Long Time-Series Urban Heat Island Monitoring and Driving Factors Analysis Using Remote Sensing and Geodetector

Urban heat island (UHI) effect decribes significant change due to rapid urbanization development. This study focused on the long time series analysis of UHI during the period 2000-2018, and analyzed the impact of land cover type and landscape metric factors on surface temperature. The results revealed that the UHI had a continuously decreasing trend in 2005–2010, and an increasing trend in 2000–2005 and 2010–2018. Cropland, built-up land, patch density (PD), Shannon Diversity Index (SHDI), and Landscape Shape Index (LSI) had a positive relationship with UHI, whereas forestland, open water, and CONTAG had a negative correlation with the UHI effect. The Geodetector analysis further revealed that PD, SHDI, and LSI had the greatest influences on LST as the three factors had the largest q values (0.287, 0.286, and 0.278). Forestland, cropland, and built-up land had greater impacts on the UHI than other land cover type factors. The explanatory power reached a maximum value of 0.408 when built-up land and cropland variables interacted. The findings of this study provide new understandings of the relationship between urban landscape and UHI, as well as important insights for urban planners to mitigate the UHI effect for the sustainable development of future urban agglomeration.

1 Introduction

Rapid urban social and economic development can lead to substantial urban ecological environment issues including environmental pollution, Urban Heat Island (UHI), traffic congestion, and so on. Among them, UHI is one of the most serious environmental problems related to urban landscape changes (Howard, 1833). In the “Guidelines for the Medium- and Long-Term National Science and Technology Development Program (2006–2020)”, the formation mechanism of the UHI effect and artificial control technology was brought forward in China as the key contents of urban studies.

Land use/cover changes deeply depend on urbanization. A study on the quantitative relationships between land use/cover type and the UHI effects is an important step for understanding the mechanism of UHI (Hou and Wen, 2020). Traditional UHI studies using the observed temperature data from fixed or mobile monitoring stations may lead to a potential bias that cannot represent the holistic urban thermal environment. Remote sensing, with the advantages of low cost and large coverage, have been widely applied to environmental monitoring that can be used to estimate the UHI effect. It also can greatly improve the identification of temporal-spatial patterns of temperature for studying climatological processes on regional and global scales (Chen et al., 2006; Flores R. et al., 2016). At the same time, remote sensing techniques have been extensively used in recent years to monitor changes in land use/cover patterns and map up-to-date landscape structures (Xian and Crane, 2006; Wu et al., 2014). Few studies have focused on the relationships between land use/cover type and the UHI effect (Du et al., 2020; Elliot et al., 2020) in depth. Analysis of the influenced mechanisms of the regional urban landscape on the urban thermal environment is still unclear (Nimish et al., 2020; Xie et al., 2020; Yao et al., 2020). Meanwhile, although the correlation analysis and regression equations used in previous studies can simply describe the degree of closeness in a relationship between factors of urban landscape and UHI, they are incapable of describing the explanatory power of interactions among multiple factors for the UHI effect (Estoque et al., 2017; Peng et al., 2018). Fortunately, a newly-developed method, the Geodetector method, can be introduced to analyze the influencing factors of the UHI effect, since the novel method contributes to developing interaction effects among multi-factors (Wang et al., 2010; Zou et al., 2017). Q-statistic in Geodetector has already been applied in many fields of natural and social sciences that can be used to measure spatial stratified heterogeneity, detect explanatory factors and analyze the interactive relationship between variables. Duan and Tan used Geodetector to identify the key factors that influence urban forest spatial differences within China (Duan and Tan, 2020). Many studies also widely applied the Geodetector method to quantify the spatial heterogeneity influences of factors and factor interactions on air pollution (Zou et al., 2017; Bai et al., 2019). To date, few studies have used Geodetector to analyze the interaction effects of factors of land cover and landscape metrics to the UHI effect.

Previous studies have revealed that urban areas can influence the local UHI circulation (Wang et al., 2020). Considering that the conclusions from studies of a single city might be limited by local conditions, few studies have attempted to investigate the UHI effect in multiple cities. For instance, Zhou et al. focused on the SUHI in 32 major Chinese cities and found the spatial pattern of the UHI effect had high spatial heterogeneities (Zhou et al., 2015). Even though spatial patterns of the UHI effect have been discussed in detail, the long-term trends of the UHI effect and associated factors are still unclear in current multi-city investigations. Therefore, a long temporal trend of the UHI effect in the urban agglomeration of the Xiangjiang river valley covering multiple cities, needs to be undertaken, because the currently reported UHI studies of Xiangjiang river valley mainly concentrate on individual cities (e.g., Changsha (Ye et al., 2017), Chang-Zhu-Tan urban agglomeration (Tang, 2018; Yuan et al., 2018; Xiong et al., 2019)).

Hence, we attempted to fill the above-mentioned gaps in this study. Overall, this study selects the urban agglomeration of the Xiangjiang river valley as the study area and collected remote sensing land surface temperature (LST) products from 2000 to 2018 to disclose the long time series characteristics of the UHI effect. The study applies the correlation analysis method to analyze the correlation coefficients between UHI and land cover types and urban landscape metric factors and further employs the Geodetector method to find the main contributors to the UHI effect. The results from this study could enhance understanding of UHI intensities with changing land cover and urban landscape patterns. In addition, important insights can be provided to urban planners and natural resource managers on how to mitigate the impact of urbanization on UHI through urban design and vegetation management for sustainable development.

2 Data and Methods

2.1 Study Area and Data

This study examines an area of urban agglomeration in the Xiangjiang river valley, including the core area as well as the regions with the most prominent ecological and environmental problems in Hunan province. The area has a dense population and rapid economic development with a complex and diverse urban landscape. According to the “overall plan for the scientific development of Xiangjiang river basin” on the website of the People’s Government of Hunan Province in 2016, the study area covers nine cities (Changsha, Zhuzhou, Xiangtan, Yueyang, Yongzhou, Shaoyang, Hengyang, Loudi, and Chenzhou), which include 68 counties or districts (Figure 1). The Xiangjiang river valley belongs to the Pacific monsoon humid climate, with rich light and hot water resources. Generally, the weather is wet and cold in winter, and humid, rainy, and hot in summer. In the context of global warming, the annual average air temperature in Xiangjiang river valley is between 16°C and 18°C. The changing urban temperature will bring effects to the spatial and temporal patterns of water resources in the Xiangjiang river valley.

FIGURE 1

FIGURE 1. Study area: Urban agglomeration of Xiangjiang river valley.

This study employs Moderate Resolution Imaging Spectroradiometer (MODIS)/Terra LST and Emissivity 8-Day L3 Global 1 km Grid SIN V006 (MOD11A2) from 2000 to 2018 for analyzing the trend of LST with a spatial resolution of 1 × 1 km and temporal resolution of 8-days, the data were collected from the website of NASA (https://ladsweb.modaps.eosdis.nasa.gov). ArcGIS 10.3 was used to convert the geographic coordinate system (Asia_Lambert_Conformal_Conic) to the appropriate projection system and tiff format for further analysis. To prepare the LST map of the study area, the mask tool in ArcGIS was used to extract the study area from the collected MOD11A2 LST data based on the vector boundary data. The mean LST of the season in the study period was calculated by the ratio of the sum of the mean daily LST to days, which indicates the number of season days. The mean LSTs of the spring season (March-May), summer season (June-August), the autumn season (September-November), and winter season (December-February) in the selected years (2000, 2005, 2010, 2015, and 2018) and for 18 years (2000–2018) were further obtained. Then, the annual average LST can be calculated based on the mean LST of the season.

2.2 Methods

To visually illustrate the process used in this study, a general technical flowchart describing the preprocessing of the spatial pattern of UHI classification, land cover/use type, landscape metrics, and factor analysis influencing UHI is shown in Figure 2.

FIGURE 2

FIGURE 2. The flowchart of the study.

2.2.1 Classification of UHI

The annual or seasonal mean LST, which was calculated using the raster calculator in ArcGIS, was inaccurate because of the existence of nodata value in the collected MOD11A2 LST data. It was therefore calculated using Matlab software by selecting the pixel with MOD11A2 LST value excluding the pixel with nodata value in the study period (2000–2018). MODIS LST data with 1 km spatial resolution was calibrated to obtain the temperature in degrees Celsius (°C) based on (Eq. (1)) (Li and Zeng, 2015).

$\text{Temperature }\left(\mathrm{°}\text{C}\right)=\left(\text{Digital Number}\ast \text{0}\text{.}02\right)-273\text{.}15(1)$

Most previous studies are focused on the spatial distribution or temporal changes by calculating the temperature difference between urban and rural areas or equally segmenting the urban surface temperatures from thermal remote sensing images. However, these methods are not suitable when weather stations in rural areas or threshold values are selected arbitrarily, and the results may not well represent the high-temperature area (Hawkins et al., 2004). In this study, a standard deviation segmenting method was thus proposed to calculate the UHI effect from the LST image for seeking a more suitable threshold value (Chen and Wang, 2009). The specific implementation was as follows. Firstly, the mean surface temperatures (μ) for the study area and their standard deviation (std) were calculated. The mean surface temperature ±0.5 times standard deviation can be determined as the background value for urban LST, and can thus be recognized as the threshold value for extracting the UHI area (strongest UHI, strong UHI, and medium UHI) and non-UHI area (strong urban cool island (UCI) and strongest UCI). The threshold of (μ+0.5*std) was used to extract the outlines of the hot island and then determine the strong UHI area by calculating the total number of pixels that the temperature is higher than (μ+0.5*std) (Wong et al., 2016). The LST classification could reflect the spatial extent and the seriousness of UHI and could be used to quantify the UHI effect. The UHI and non-UHI classifications of the study area are listed in Table 1.

TABLE 1

TABLE 1. The classification of UHI and non-UHI effects.

2.2.2 Landscape Metrics

The land cover data were used to observe the dominant causative factors influencing the UHI in this study. The land cover/use data in the years 2000, 2005, 2010. 2013 and 2017 were collected from the Geographical Information Monitoring Cloud Platform (http://www.dsac.cn/). Given the insignificant change of land cover type during one or 2 years, the land cover data in 2013 and 2017 were used to develop factor analysis instead of the land cover data in 2015 and 2018. The landscape metrics were calculated based on classification maps including six land-cover types: cropland, forestland, grassland, open water, built-up land, and unused land. The accuracy of the classification result was evaluated by the overall Kappa index as 0.85, which was acceptable for the urban scale. The landscape metrics are demonstrated in many studies to measure the composition and configuration of land cover features (Wu et al., 2010; Xu, 2015). Landscape metrics (i.e. contagion index (CONTAG), patch density (PD), Shannon Diversity Index (SHDI), and landscape shape index (LSI)) were calculated at the landscape level using Fragstats 4.0 (McGarigal et al., 2002) for describing landscape size, shape, diversity, aggregation and fragmentation.

Considering the spatial units of LST data, all the statistical variables were entered into the database of 1 km × 1 km grid cells for further processing analysis of the factor interaction detector (Figure 3A). For the spatial land cover data of 30 m × 30 m grid cells, the area percentage of each land cover type in each 1 km × 1 km grid cell was calculated. In addition, the use of land cover data for the latest year was more beneficial in providing guidance for future planning. The results of land cover data and landscape metric values in 2017 were therefore described with the classification method of natural breaks (Figures 3F–K). The landscape metric values for each grid were calculated in every 1 km × 1 km grid (Figures 3B–E). The spatial patterns of land cover data and landscape metric values in 2000, 2005, 2010, 2013, and 2017 were derived.

FIGURE 3

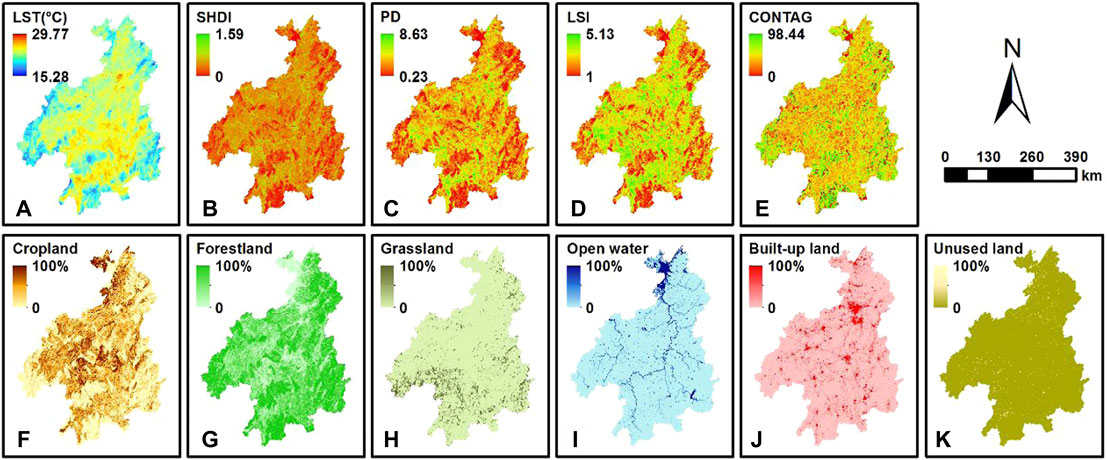
FIGURE 3. Spatial patterns of land cover types and landscape metrics in 2017. (A) LST, (B) SHDI, (C) PD, (D) LSI, (E) CONTAG, (F) Cropland, (G) Forestland, (H) Grassland, (I) Open water, (J) Built-up land, (K) Unused land.

CONTAG describes the aggregation degree and extension degree of different patch types. A smaller value indicates a higher degree of plaque dispersion. PD is the degree of fragmentation of the landscape, which reveals the complexity between landscape spatial structures. SHDI depicts the diversity of landscape types, and the higher value indicates the richer the land use type. LSI represents the size of the landscape shape. As the shape becomes more and more irregular, the LSI becomes larger, indicating that the landscape is less disturbed.

2.2.3 Geodetector

The effects of spatial configuration on LST distribution were examined by using landscape metrics. (Weng et al., 2008; Zhou et al., 2011). Geodetector represents a new spatial statistics method that is used to detect spatial heterogeneity and identify driving factors based on risk, factors, ecology, and interaction (Wang and Geodetector, 2017). The advantage of the Geodetector method is that it can examine the interactions of two driving factors affecting the dependent variable and it reveals whether the interactions of two factors are linear or nonlinear. The Geodetector method is therefore employed to find the main contributors to the UHI effect. Land cover and urban landscape factors were divided into different spatial types or subzones. A significance test for the differences of mean values of land cover and urban landscape factors was conducted to detect the relative importance of land cover and urban landscape factors. The calculation model of the explanatory power of each land cover and urban landscape factor is as Eq. 2:

$q=1-\frac{{{\displaystyle \sum }}_{i=1}^m{N}_i{\sigma }_i^2}{N{\sigma }^2}(2)$

where q is the explanatory power of land cover and urban landscape factors on LST, i = 1, … ,m are the stratification of y or factor x, that is, classification or partition. N_i and m are the number of units in i and the whole region, respectively. N and ${\sigma }^2$ are the total number of samples and the variance of y value in the whole region. ${\sigma }_i^2$ is the variance of units i. The range of q value is between 0 and 1. Note that one value means that one of the land cover and urban landscape factors completely controls the spatial distribution of LST, whereas 0 value implies a completely random spatial occurrence of LST.

Interaction detection is used to identify the interaction between land cover and urban landscape factors to evaluate the accountability of the combined effect (enhancing or weakening) and respective effect on the LST. The q values of two factors with respect to LST were calculated as follows (the symbol “∩” denotes the intersection between X₁ and X₂):

Enhance: q(X₁∩X₂)>q(X₁) or q(X₂)

Enhance, bilinear: q(X₁∩X₂)>q(X₁) and q(X₂)

Enhance, nonlinear: q(X₁∩X₂)>q(X₁)+q(X₂)

Weaken: q(X₁∩X₂)<q(X₁)+q(X₂)

Weaken, unique: q(X₁∩X₂)<q(X₁) or q(X₂)

Weaken, nonlinear: q(X₁∩X₂)<q(X₁) and q(X₂)

Independent: q(X₁∩X₂) = q(X₁)+q(X₂)

3 Results

3.1 Spatial Pattern of UHI Intensity

3.1.1 Annual UHI Intensity

The spatial pattern of the annual mean UHI effect at the city level were depicted in Figure 4. Most areas of the Xiangjiang river valley are concentrated at the medium UHI level. The strong and strongest UHI effect were located in the southern and southwestern study areas. The strong and strongest UCI area was concentrated in the western, northeastern, and southeastern study areas. The spatial pattern and area ratio of the 18-years mean UHI effect at the city level in Figure 4G shows that the medium UHI level had a larger coverage than the other levels in the six cities of Yueyang, Changsha, Xiangtan, Zhuzhou, Loudi, and Shaoyang. Thus, the total area ratios of the strong and strongest UHI effect in Yueyang, Changsha, Xiangtan, Loudi, and Shaoyang were only 1.62, 15.76, 14.60, 10.47, and 13.85% respectively, while that of the strongest UCI effect were respectively up to 23.07, 10.67, 0.47, 19.19, and 32.42%. It demonstrated that the UHI effect was insignificant in the five cities, especially in Yueyang and Shaoyang. Changsha as the provincial capital of Hunan, China has the largest administrative area. The UHI effect in Changsha was weaker than that in Hengyang, Chenzhou, Yongzhou, and Zhuzhou because Changsha had a slow urbanization increase in the earlier year. The total area ratio of the strong and strongest UHI in Zhuzhou was 40.19%, which was identified as the significant UHI effect in this city. The area ratios of the strongest UHI level in Hengyang city, Chenzhou city, and Yongzhou city were respectively 42.87, 35.20, and 34.48%, which had a higher proportion than the area of the other levels. Therefore, the three cities of Hengyang, Chenzhou, and Yongzhou experienced a significant UHI effect during the period 2000–2018. The UHI effect of Hengyang was strongest in the Xiangjiang river valley.

FIGURE 4

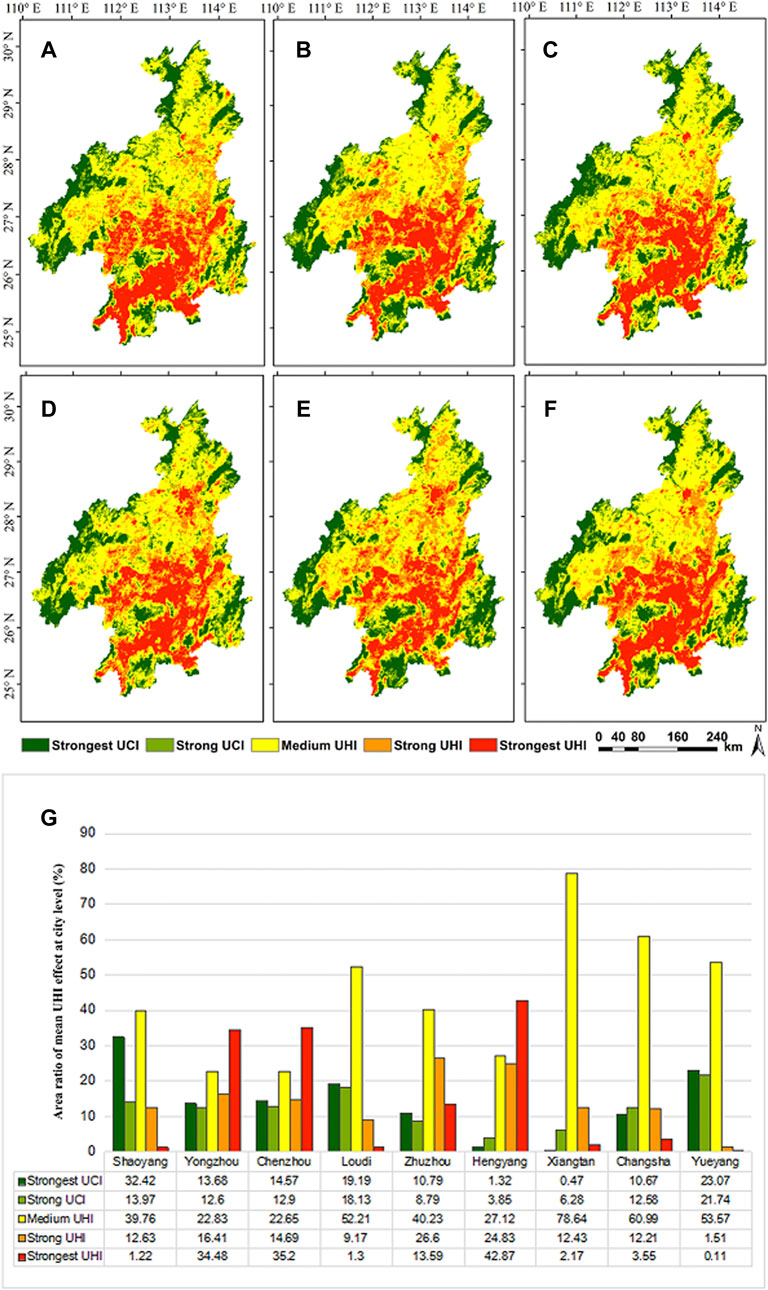
FIGURE 4. Spatial pattern of the UHI effect in (A) 2000, (B) 2005, (C) 2010, (D) 2015, (E) 2018, (F) 18-year (2000–2018), and (G) area ratio of the 18-year mean UHI effect at the city level.

3.1.2 Seasonal UHI Intensity

The seasonal mean UHI effect between 2000–2018 was calculated to describe the spatial pattern of the seasonal mean UHI (seen in Figure 5). In total, the areas of the central and southern study area had strong and strongest UHI during all the seasons. In contrast, the western areas were with UCI in different seasons. The northern areas were with medium UHI in spring (Figures 5A–F), summer (Figures 5G–L), and autumn (Figures 5M–R), and were with strong and strong UHI in winter (Figures 5S–X). The UHI the south western area was significant in winter, but in the other three seasons, it showed UCI or medium UHI in these regions. Strong UHI also happened in the north-central areas in spring, and relieved to medium UHI in summer and autumn, then changed to UCI in winter.

FIGURE 5

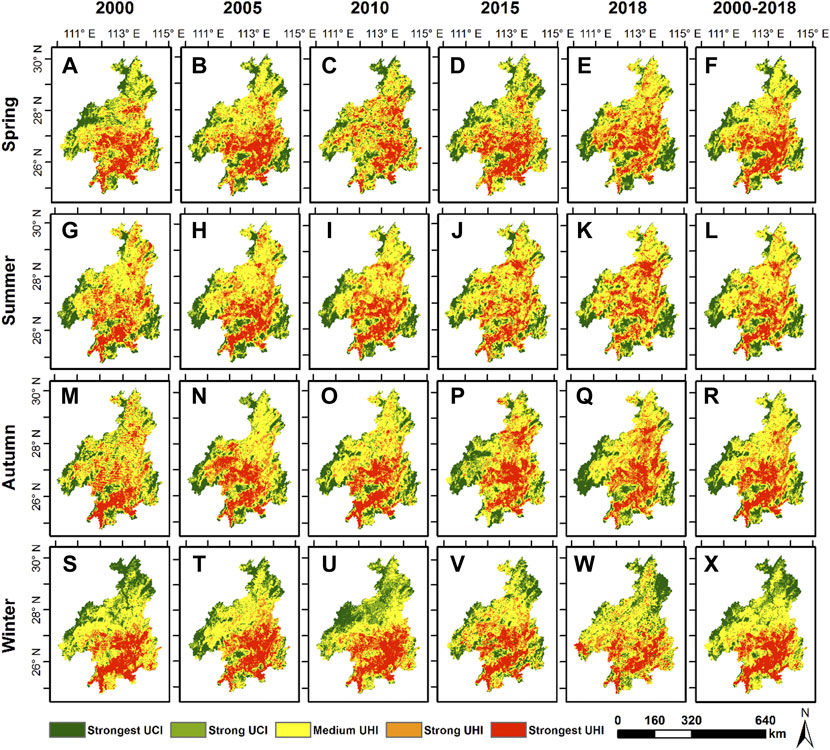
FIGURE 5. Spatial distribution map of UHI effect for the (A–F) spring, (G–L) summer, (M–R) autumn, and (S–X) winter seasons during the period 2000–2018.

3.2 Long-Time Series Analysis of UHI Intensity

3.2.1 Annual UHI Variations

The magnitude of 18-year UHI has significantly changed over time. The statistical results of five classes representing UHI and non-UHI effects in the study area based on Figure 4 are listed in Table 2. The area ratio of the different levels of the UHI effect was calculated by the ratio of the area of the different levels to the total area of the Xiangjiang river valley. The area ratio of 39.80% of medium UHI in 2000 was larger than the strong UHI (14.48%) and the strongest UHI (16.34%). The total area ratio of the strong and strongest UHI in 2005 was 33.19%, which was larger than 30.82% in 2000. There was a significant increasing trend from 2000 to 2005. The total area ratio (30.66%) of the strong and strongest UHI in 2010 compared to 2005, which had a small decrease, while the area ratio of the strongest UHI increased from 16.99 to 17.76%. The total area ratio of the strong and strongest UHI had a significant decreasing trend since 2010, then increasing until 2018, was respectively 32.44% in 2015 and 33.97% in 2018. The total area ratio of the non-UHI experienced a decreasing trend from 29.38% in 2000 to 28.89% in 2005, then increased slowly from 29.36% in 2010 to 29.57% in 2018. The area ratio of the strongest UHI was more than that of the strongest UCI, with a difference of 2.67% in 2000–2018. The total area ratio of the medium, strong, and strongest UHI was 71.65%, which demonstrated the significant UHI effect in the Xiangjiang river valley.

TABLE 2

TABLE 2. Area ratios of five levels of the UHI effect during the period 2000-2018 (unit: %).

3.2.2 Seasonal UHI Variations

The area ratio of the UHI effect for the spring, summer, autumn, and winter seasons during the period 2000–2018 are depicted in Figure 6 according to Figure 5. The area ratio of medium UHI for the spring season is noticed in the range of 36.32–40.19%. The area ratios of the strongest UHI were 17.33, 17.97, 14.97, 15.68, and 16.80% for the year 2000, 2005, 2010, 2015, and 2018, respectively. The total area ratios of the strong and strongest UHI were 31.24, 34.52, 30.74, 30.90, and 34.23% for the years 2000, 2005, 2010, 2015, and 2018, respectively. It can be concluded that the UHI effect experienced an increasing trend during the period 2000–2005 and 2010–2018, whereas had a decreasing trend during the period 2005–2010.

FIGURE 6

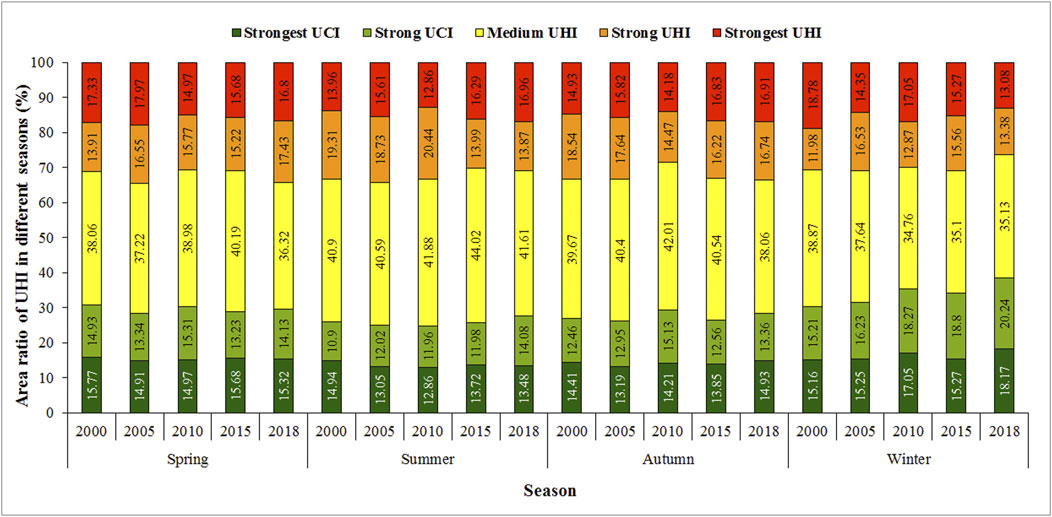
FIGURE 6. Area ratio of the UHI effect for the spring, summer, autumn, and winter seasons during the period 2000–2018.

The area ratio of medium UHI for the summer season ranged from 40.59 to 44.02%, which was the high proportion level. The area ratios of the strongest UHI were noticed as 13.96, 15.61, 12.86, 16.29, and 16.96% for the years 2000, 2005, 2010, 2015, and 2018, respectively. The total area ratios of the strong and strongest UHI were observed as 33.27, 34.34, 33.3, 30.28, and 30.83% for the years 2000, 2005, 2010, 2015, and 2018, respectively. The same changing tendency of the strongest UHI effect during the period 2000–2018 for the summer season compared to the spring season was found. However, it can be observed according to the total area ratio that there was an increasing trend during the period 2000–2005 and 2015–2018, and a decreasing trend during the 2005–2015 period.

The area ratio of medium UHI level of the high proportion for the autumn season was in the range of 38.06–42.01%. The area ratios of the strongest UHI were noticed as 14.93, 15.82, 14.18, 16.83, and 16.91% for the years 2000, 2005, 2010, 2015, and 2018, respectively. The total area ratios of the strong and strongest UHI were observed as 33.47, 33.46, 28.65, 33.05, and 33.65% for the years 2000, 2005, 2010, 2015, and 2018, respectively. It can be observed that the UHI effect experienced an increasing trend during the period 2000–2005 and 2010–2018, whereas it had a decreasing trend during the period 2005–2010. The changing tendency of the UHI effect during the period 2000–2018 for the autumn season was consistent with the summer season.

The area ratio of medium UHI level for the winter season was in the range of 34.76–38.87%, which was larger than the area ratio for the spring, summer, and autumn seasons. The area ratios of the strongest UHI were noticed as 18.78, 14.35, 17.05, 15.27, and 13.08% for the years 2000, 2005, 2010, 2015, and 2018, respectively. The total area ratios of the strong and strongest UHI were observed as 30.76, 30.88, 29.92, 30.83, and 26.46% for the years 2000, 2005, 2010, 2015, and 2018, respectively. The strongest UHI effect experienced a decreasing trend during the period 2000–2005 and 2010–2018, whereas it had an increasing trend during the period 2005–2010. The change trend of the strongest UHI effect for the winter season has the opposite result with the trend for the spring, summer, and autumn seasons. According to the total area ratio, there was an increasing trend during the period 2000–2005 and 2010–2015, and a decreasing trend during the period of 2005–2010 and 2015–2018.

The area ratio of medium UHI level of the high proportion of the 18-years UHI effect was in the range of 37.31–39.28%. The maximum total area ratio of the strong and strongest UHI was observed as 33.33% in spring, the minimum was 29.52% in winter. The total area ratio of the strong and strongest UCI level of 32.19% for the winter season compared to the spring, summer, and autumn seasons was at the highest proportion level, while the minimum of the total area ratio was 27.66% occurring in summer. Therefore, the UHI effect was the strongest for the spring season and weakest for the winter by analyzing the seasonal variation of the 18-years UHI effect.

The UHI in the Xiangjiang river valley was different and clearly show the effect of ecological context on seasonal UHI amplitudes during the period 2000–2018 (Figure 7). The high LST in a year is distributed mainly in summer, and the maximum was 40.73°C occurring in 2018 among all these years, while the low LST in a year focused on the winter season and the minimum was 1.22°C occurring similarly in 2018 among all these years. The maximum seasonal mean temperature during the period 2000–2018 was 30.36°C occurring in summer 2010. The maximum difference between the maximum and minimum temperatures was 26.52°C in summer 2015, the minimum was 13.33°C in spring 2010. The standard deviation was used to evaluate the temperature change in a season, the higher value indicated the larger temperature difference. Figure 7 shows that all standard deviations in spring, summer, autumn, and winter 2018 were greater than 2.0, which illustrated the significant temperature difference in a season. The maximum standard deviation was 2.49 in autumn 2015, while the minimum was 1.57 in winter 2010.

FIGURE 7

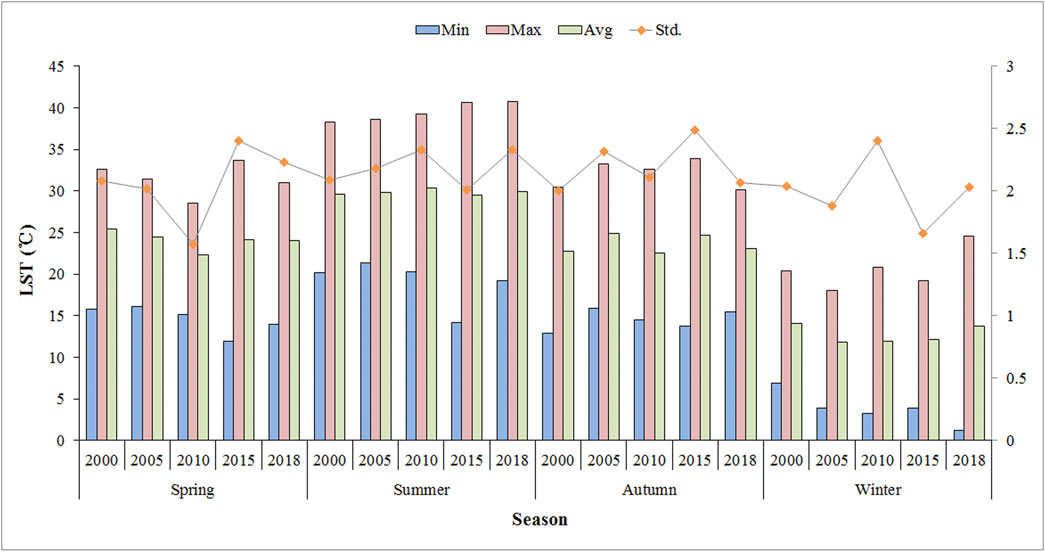
FIGURE 7. Histogram of seasonal LST during the period 2000–2018 to evaluate the temperature change in each season.

3.3 Factor Analysis Influencing UHI

3.3.1 Correlation Analysis

The correlation analysis between UHI and 10 influencing factors is obtained and summarized in Table 3. The Pearson correlation coefficients between UHI and cropland range from 0.365 to 0.498 during the 2000–2018 period, indicating increased correlated levels from 2000 to 2018. A positive Pearson correlation coefficient for an independent variable indicates that the variable has a positive effect on UHI intensity, or that UHI intensity increases with the increase of the value of that variable; whereas a negative coefficient indicates UHI intensity decreases with the increase of the value of that variable. In this study, both coefficients of percent cover of cropland and built-up land were positive, suggesting that an increase in the percent of the cover of cropland and built-up land would increase UHI intensity. In contrast, the negative coefficients of percent cover of forestland, grassland, open water, and unused land indicated that UHI intensity would decrease with the increase of relative abundances of vegetation and water. The correlation analysis also shows that several landscape metrics are significantly related to the UHI effect, as shown in Table 3. LSI, PD, and SHDI have a positive relationship with UHI, whereas CONTAG has a negative correlation with the UHI effect. These indicate that the higher the degree of plaque dispersion, the richer the land use type, and a more irregular the size of the landscape shape will lead to higher UHI intensity.

TABLE 3

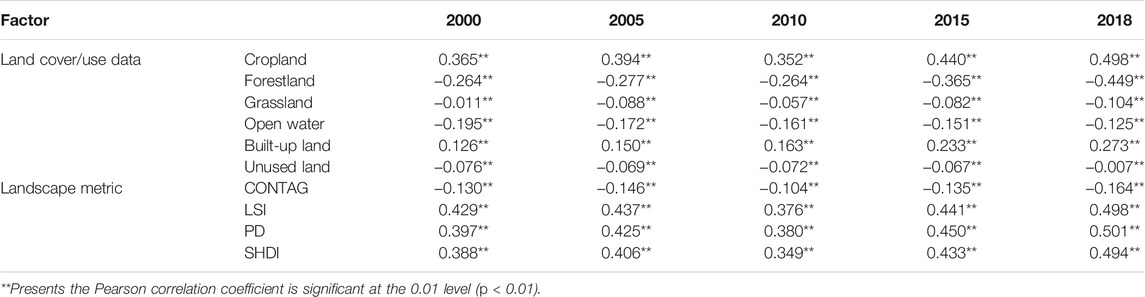
TABLE 3. Pearson correlation coefficients between UHI intensity and land cover features and landscape metrics.

3.3.2 Geodetector Analysis

Although the correlation analysis can measure how close the influencing factors are to the UHI intensity, it is unable to disclose the spatial stratification heterogeneity of the UHI effect and cannot determine the interactive influences of factors. To overcome these shortcomings, this subsection presents the analysis results of the Geodetector. In addition, the use of land cover data for the latest year was more beneficial for providing guidance for future planning.

The impact (q values) of the 10 influencing factors on the LST are obtained by means of the factor detector, the results of which are reported in Table 4. As shown in Table 4, of the 10 influencing factors, seven factors are statistically significant. The q values of these seven factors are, in descending order: Cropland (0.322) > PD (0.287) > LSI (0.286) > SHDI (0.278) > Forestland (0.273) > CONTAG (0.208) > Built-up land (0.146). Among the landscape metric factors, PD and LSI have the greatest influence on the LST as the two factors have the largest q values. Among the land cover factors, cropland, forestland, and built-up land have greater impacts on the LST than other factors. However, grassland, open water, and unused land layers among all factors have no significant influences on the LST, a possible reason being that these factors from land cover are not good proxy indicators for accurately depicting the spatial configuration of urban sprawl and growth because of the development of urbanization.

TABLE 4

TABLE 4. Results of factor and interaction detector for LST.

Among the 10 factors, a total of 45 pairs of interaction effects were obtained by means of the interaction factor, as summarized in Table 4. According to Table 4, each pair of factors is shown to be larger than the q values of each factor, and smaller than the sum of the two factors’ q values. Hence, the interactions between cropland and the other land cover types, excluding unused land or landscape metrics, exhibited binary enhancement in this analysis. If each pair of factors is shown to be equal to the sum of the two factors’ q values, two factors leading to the LST change are independent. Therefore, the relationships between unused land and cropland, built-up land, CONTAG, LSI, SHDI are independent in influencing the LST. Furthermore, the interaction effects of a few factors on the LST represent nonlinear enhancements (represented as EN), whereas most of the factors have bivariate enhanced interaction effects. The interactions between landscape metrics including CONTAG, LSI, PD, and SHDI, and land cover types excluding the unused land and grassland types revealed binary enhancement, while the interaction with grassland type exhibited nonlinear enhancement. More specifically, perspective values for forestland and grassland were 0.273 and 0.016 but their interactive q-statistic reached as high as 0.356, which is larger than the sum of the two factors’ q values. Furthermore, calculations show that when built-up land and cropland variables interacted, explanatory power reached a maximum value of 0.408. Data also show that landscape metrics can enhance the explanatory power of the land cover types. For example, perspective values for cropland and PD were 0.322 and 0.287 but their interactive q-statistic reached as high as 0.396. The q-statistic values for forestland and LSI were 0.273 and 0.286 but their interactive q-statistic reached as high as 0.359, which was higher than the q-statistic value of a single factor of the forest type. The interactive q-statistic values for forestland and land cover types including cropland, grassland, built-up land, and open water, as well as landscape metrics including LSI, PD, and SHDI, were more than 0.300, which was higher than the q-statistic value of 0.273 of the single factor. The study also tried to explore the temporal variations of single and interactive contortions of different factors. The results showed that the contribution of each factor has little temporal heterogeneity. These indicate that the interaction relationships of pair factors of cropland, forestland, grassland, built-up land, and landscape metrics were significant in influencing the LST. The conclusion may be drawn that the interaction of two factors plays a more important role in influencing the urban thermal environment than each factor separately.

4 Discussion

The ground surface in urbanized areas is a key factor influencing the spatial structure and formation of UHI. This study investigated the long term series variations of the surface temperature in nine cities in the Xiangjiang river valley in Hunan province, China. The UHI effect was the strongest for the spring season and weakest for the winter by analyzing the seasonal variation of the 18-years UHI effect. The increases in vegetation in spring exhibit a low temperature, it was therefore observed that the UHI is more intense during the spring season due to the significant thermal changes between vegetation and built-up land. As the vegetation decreased during the winter, resulting in less temperature difference, the UHI of Xiangjiang river valley is lower in the winter than in other seasons. In terms of spatial distribution, the strong and strongest heat island areas are distributed mainly in the southern and southwestern study area and expanded gradually north, for the cities of Hengyang city, Chenzhou city, Yongzhou city, and Zhuzhou. The weakest heat island areas focused on the northeastern, western, and southeastern study areas. The reason is that the study areas having a good proportion of vegetation mostly on these parts of the study area shows lower temperature as compared to the densely built-up areas in the southern and southwestern parts of the study area.

This study also presents the results of an investigation of the relationships between spatial variations of the surface temperature and the land surface attributes. Our results indicated that both the composition and configuration of land cover features significantly affect the magnitude of LST. By explicitly describing the quantitative relationships of LST with the composition and configuration of land cover features, this research expands our scientific understanding of the effects of land cover pattern on LST in urban landscapes. Our results showed that the increasing vegetation cover or surface water could significantly decrease LST, and thus help to mitigate excess heat in urban areas; whereas the increase of buildings would significantly increase LST, exacerbating the UHI phenomena. However, our results are inconsistent with those from previous research that shows an increase in the percent cover of cropland would increase UHI intensity. This is because the LST of cropland is affected by the status and type of crops, and changes with time to a certain extent. The vegetation cover on this arable land may be attributed to the intensification of agricultural activities (almost 30% of the study areas are covered by cultivated plants), such as artificial fertilizer use and irrigation (surface or groundwater). If there are no cultivated plants or agricultural activities on this arable land, the cropland is equivalent to bare land, which may lead to increased UHI intensity. In this study, the total areas of forestland and cropland are more than 90%, the insignificant cooling effect of cropland compared to forestland leads to the positive correlation between the UHI intensity and the percent cover of cropland. Cropland neighboring buildings can mitigate UHI intensity. By developing correlation analysis to cropland neighboring buildings and forestland in 2018, our study found that the correlation coefficient between the cropland neighboring building and the UHI intensity is -0.316, and the cropland neighboring forestland and the UHI intensity is 0.530. Therefore, a large area of cropland in the suburban area contributes to the mitigation of UHI intensity in this study area.

These results have important theoretical and management implications. Urban planners and natural resource managers attempting to mitigate the impact of urban development on UHI can gain insights on the importance of balancing the relative amount of various types of land cover features and optimizing their spatial distributions, especially forest conservation and crop planting for food security.

The analysis of the impact of land cover type and landscape metrics factors and their interactions on surface temperature was implemented by means of a novel spatial stratified heterogeneity analysis method, the Geodetector method. This method has a few advantages compared with classical linear regression and spatial overlay analysis. Empirical results verified that the Geodetector could not only identify the main contribution of land cover type and landscape metric factors on LST, but they could also better uncover the interaction of two factors on LST in the urban agglomeration of Xiangjiang river valley. For example, the q-statistic values were calculated using the geographic detector method and reveal that the major variables influencing LST are cropland, forestland, and built-up land. This result is similar to previously reported findings (Kumari et al., 2019; Xiong et al., 2019).

Data also show that grassland, open water, and unused land exerted no significant influence on LST. If these variables are integrated with the other variables, they act to greatly enhance the explanatory power of other variables. PD and LSI have the greatest influence on the LST among landscape metric factors. In addition, the Pearson correlation coefficient between UHI intensity and PD and LSI indicates that a high degree of fragmentation in the landscape could exert a significant influence on increased UHI intensity.

The interaction q values of cropland with landscape metrics had the greatest influence on LST in this study. The use of the Geodetector method provides a new perspective for interactive analysis of multi-factors influencing LST. The new findings obtained from the novel method indicate that only using land cover type to analyze the formation of the UHI is not comprehensive. Landscape metrics need to be further emphasized for quantitatively exploring the influence of the spatial configuration of the urban landscape on the UHI.

This study has limitations. The research was conducted for one region, using only the daytime thermal image to obtain LST. Previous studies have shown that there are diurnal and seasonal variations in the relationships between LST and land cover features (Yuan and Bauer, 2007; Buyantuyev and Wu, 2010). For example, vegetation abundance, measured by NDVI, had a strong relationship with daytime LST but was only very weakly related to nighttime LST (Wang and Geodetector, 2017). Therefore, the diurnal thermal image needs to be used to study the phenomenon of UHI and the impact factors of UHI. In addition, the difference of spatial scales based on the urban size in different climate conditions could be compared to its influence on the formation of UHI. The application of the local climate scale has to be taken into account for developing the factor analysis of the UHI effect. The reasons for this are that the percent cover of cropland near the building has a negative correlation with the UHI intensity, while the percent cover of cropland near the forestland has a positive correlation with the UHI intensity. This is also a possible reason for the local UHI intensity of built-up area at the small spatial scale surrounded by open water, cropland, or forestland would be found to be decreased from the urban landscape perspective, especially in a large study area. The magnitude of local LST differences is driven by various environmental or anthropogenic factors. It is important to investigate the effect of human activities and other impact factors on decreasing the contributions of UHI under the context of global warming.

5 Conclusion

In this study, an analysis based on multi-temporal remote sensing data was carried out to study not only the long term variations of UHI over the period 2000–2018 but the impact factors of UHI. Throughout the analyzed period, the UHI effect experienced an increasing trend during the period 2000–2005 and 2010–2018, whereas it had a decreasing trend during the period 2005–2010. The UHI effect was the strongest for the spring season and weakest for the winter by analyzing the seasonal variation of the 18-year UHI effect. The UHI effect was the strongest in spring 2005 and 2018, in autumn 2000 and 2015, and summer 2010. In terms of spatial distribution, the strong and strongest heat island areas were distributed mainly in the southern and southwestern study areas and expanded gradually north.

The correlation analysis between UHI and 10 influencing factors found that the increase in the percent cover of cropland and built-up land would aggravate UHI intensity. In contrast, the negative coefficients of percent cover of forestland, grassland, open water, and unused land indicated that UHI intensity would decrease with the increase of relative abundances of vegetation and water. However, factor interaction detector analysis revealed that grassland, open water, and unused land layers among all factors have no significant influences on the LST. PD, LSI, and SHDI are determined to have the greatest influences on the LST as the three factors have the largest q values, which are consistent with the results of correlation analysis. LSI, PD, and SHDI have a positive relationship with UHI, whereas CONTAG has a negative correlation with the UHI effect. These indicate that the higher the degree of plaque dispersion, the richer the land use type, and a more irregular the size of landscape shape will lead to a higher UHI intensity. Landscape metrics can enhance the explanatory power of land cover types. Therefore, for UHI mitigation, a prerequisite for multifactor analysis must be taken into consideration during the implementation of cropland and built-up land to alleviate urban thermal stress and thus promote urban ecological sustainability. Our findings are a good theoretical supplement for current UHI research, providing urban administrators with useful information for achieving optimized urban agglomeration development.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material,further inquiries can be directed to the corresponding author.

Author Contributions

All authors participated in the field survey and data collection. LX drafted the manuscript. LX and FP analyzed the data. SL and BZ designed the study. XF and YX revised the manuscript. All authors participated in the field survey and data collection, critically revised the manuscript, and gave final approval to the version submitted for publication.

Funding

This research was funded by the Natural Science Foundation of Hunan Province (Project NOs. 2019JJ50640, 2021JJ40022, 2021JJ50155), the Scientific Research Project of Education Department of Hunan province (Project N0. 19C0060), the Scientific Research Project of Education Department of Hunan province (Project N0. 19B107), and the Key Laboratory Open Fund Project of the Ministry of Education (Project N0. 2017ysjs07).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank the journal reviewers for providing insightful comments which improved the quality of the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2021.828230/full#supplementary-material

References

Bai, L., Jiang, L., Yang, D.-y., and Liu, Y.-b. (2019). Quantifying the Spatial Heterogeneity Influences of Natural and Socioeconomic Factors and Their Interactions on Air Pollution Using the Geographical Detector Method: A Case Study of the Yangtze River Economic Belt, China. J. Clean. Prod. 232, 692–704. doi:10.1016/j.jclepro.2019.05.342

CrossRef Full Text | Google Scholar

Buyantuyev, A., and Wu, J. (2010). Urban Heat Islands and Landscape Heterogeneity: Linking Spatiotemporal Variations in Surface Temperatures to Land-Cover and Socioeconomic Patterns. Landscape Ecol. 25 (1), 17–33. doi:10.1007/s10980-009-9402-4

CrossRef Full Text | Google Scholar

Chen, S., and Wang, T. (2009). Comparison Analyses of Equal Interval Method and Mean-Standard Deviation Method Used to Delimitate Urban Heat Island. Geo-information Sci. 11 (2), 145–150. doi:10.3724/sp.j.1047.2009.00145

CrossRef Full Text | Google Scholar

Chen, X.-L., Zhao, H.-M., Li, P.-X., and Yin, Z.-Y. (2006). Remote Sensing Image-Based Analysis of the Relationship between Urban Heat Island and Land Use/cover Changes. Remote Sensing Environ. 104, 2133–2146. doi:10.1016/j.rse.2005.11.016

CrossRef Full Text | Google Scholar

Du, H., Zhou, F., Li, C., Cai, W., Jiang, H., and Cai, Y. (2020). Analysis of the Impact of Land Use on Spatiotemporal Patterns of Surface Urban Heat Island in Rapid Urbanization, a Case Study of Shanghai, China. Sustainability 12 (3), 1171. doi:10.3390/su12031171

CrossRef Full Text | Google Scholar

Duan, Q., and Tan, M. (2020). Using a Geographical Detector to Identify the Key Factors that Influence Urban forest Spatial Differences within China. Urban For. Urban Green. 49, 126623. doi:10.1016/j.ufug.2020.126623

CrossRef Full Text | Google Scholar

Elliot, T., Babí Almenar, J., and Rugani, B. (2020). Modelling the Relationships between Urban Land Cover Change and Local Climate Regulation to Estimate Urban Heat Island Effect. Urban For. Urban Green. 50, 126650. doi:10.1016/j.ufug.2020.126650

CrossRef Full Text | Google Scholar

Estoque, R. C., Murayama, Y., and Myint, S. W. (2017). Effects of Landscape Composition and Pattern on Land Surface Temperature: An Urban Heat Island Study in the Megacities of Southeast Asia. Sci. Total Environ. 577, 349–359. doi:10.1016/j.scitotenv.2016.10.195

PubMed Abstract | CrossRef Full Text | Google Scholar

Flores R., J. L., Pereira Filho, A. J., and Karam, H. A. (2016). Estimation of Long Term Low Resolution Surface Urban Heat Island Intensities for Tropical Cities Using MODIS Remote Sensing Data. Urban Clim. 17, 32–66. doi:10.1016/j.uclim.2016.04.002

CrossRef Full Text | Google Scholar

Hawkins, T. W., Brazel, A. J., Stefanov, W. L., Bigler, W., and Saffell, E. M. (2004). The Role of Rural Variability in Urban Heat Island Determination for Phoenix, Arizona. J. Appl. Meteorol. 43 (3), 476–486. doi:10.1175/1520-0450(2004)043<0476:Trorvi>2.0.Co;2

CrossRef Full Text | Google Scholar

Hou, K., and Wen, J. (2020). Quantitative Analysis of the Relationship between Land Use and Urbanization Development in Typical Arid Areas. Environ. Sci. Pollut. Res. 27, 38758–38768. doi:10.1007/s11356-020-08577-8

CrossRef Full Text | Google Scholar

Howard, L. (1833). Climate of London Deduced from Metrological Observations. 3th ed London: Harvey and Dorton Press.

Google Scholar

Kumari, M., Sarma, K., and Sharma, R. (2019). Using Moran's I and GIS to Study the Spatial Pattern of Land Surface Temperature in Relation to Land Use/cover Around a thermal Power Plant in Singrauli District, Madhya Pradesh, India. Remote Sensing Appl. Soc. Environ. 15, 100239. doi:10.1016/j.rsase.2019.100239

CrossRef Full Text | Google Scholar

Li, X., and Zeng, S. (2015). Comparisive Research on Characteristics of Urban Heat Island Effects between Chengdu and Chongqing. Meteorol. Sci. Technol. 43 (5), 888–897.

Google Scholar

McGarigal, K., Cushman, S., Neel, M. C., and Ene, E. (2002). FRAGSTATS: Spatial Pattern Analysis Program for Categorical Maps. Availabe online: http://www.umass.edu/landeco/research/fragstats/fragstats.html.

Google Scholar

Nimish, G., Bharath, H. A., and Lalitha, A. (2020). Exploring Temperature Indices by Deriving Relationship between Land Surface Temperature and Urban Landscape. Remote Sensing Appl. Soc. Environ. 18, 100299. doi:10.1016/j.rsase.2020.100299

CrossRef Full Text | Google Scholar

Peng, J., Jia, J., Liu, Y., Li, H., and Wu, J. (2018). Seasonal Contrast of the Dominant Factors for Spatial Distribution of Land Surface Temperature in Urban Areas. Remote Sensing Environ. 215, 255–267. doi:10.1016/j.rse.2018.06.010

CrossRef Full Text | Google Scholar

Tang, Y. (2018). Effect Analysis of Land-Use Pattern with Landscape Metrics on an Urban Heat Island. J. Appl. Rem. Sens. 12 (2), 1. doi:10.1117/1.Jrs.12.026004

CrossRef Full Text | Google Scholar

Wang, J. F., and Geodetector, C. D. X. (2017). Principle and Prospective. Acta Geogr. Sin. 72 (1), 116–134.

Google Scholar

Wang, J. F., Li, X. H., Christakos, G., Liao, Y., Zhang, T., Gu, X., et al. (2010). Geographical Detectors-Based Health Risk Assessment and its Application in the Neural Tube Defects Study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 24 (1-2), 107–127. doi:10.1080/13658810802443457

CrossRef Full Text | Google Scholar

Wang, Q., Zhang, C., Ren, C., Hang, J., and Li, Y. (2020). Urban Heat Island Circulations over the Beijing-Tianjin Region under Calm and Fair Conditions. Building Environ. 180, 107063. doi:10.1016/j.buildenv.2020.107063

CrossRef Full Text | Google Scholar

Weng, Q., Liu, H., Liang, B., and Lu, D. (2008). The Spatial Variations of Urban Land Surface Temperatures: Pertinent Factors, Zoning Effect, and Seasonal Variability. IEEE J. Sel. Top. Appl. Earth Observations Remote Sensing 1 (2), 154–166. doi:10.1109/JSTARS.2008.917869

CrossRef Full Text | Google Scholar

Wong, M., Peng, F., Zou, B., Shi, W., and Wilson, G. (2016). Spatially Analyzing the Inequity of the Hong Kong Urban Heat Island by Socio-Demographic Characteristics. Ijerph 13 (3), 317. doi:10.3390/ijerph13030317

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, H., Wang, W., Wang, W., Qin, J., and Bai, X. (2010). Research on the Characteristics of Landscape Pattern and Change in Changsha-Zhuzhou-Xiangtan Metropolitan Region. Geo-information Sci. 12 (1), 133–142. doi:10.3724/sp.j.1047.2010.00133

CrossRef Full Text | Google Scholar

Wu, H., Ye, L.-P., Shi, W.-Z., and Clarke, K. C. (2014). Assessing the Effects of Land Use Spatial Structure on Urban Heat Islands Using HJ-1B Remote Sensing Imagery in Wuhan, China. Int. J. Appl. Earth Observation Geoinformation 32, 67–78. doi:10.1016/j.jag.2014.03.019

CrossRef Full Text | Google Scholar

Xian, G., and Crane, M. (2006). An Analysis of Urban thermal Characteristics and Associated Land Cover in Tampa Bay and Las Vegas Using Landsat Satellite Data. Remote Sensing Environ. 104 (2), 147–156. doi:10.1016/j.rse.2005.09.023

CrossRef Full Text | Google Scholar

Xie, M., Chen, J., Zhang, Q., Li, H., Fu, M., and Breuste, J. (2020). Dominant Landscape Indicators and Their Dominant Areas Influencing Urban thermal Environment Based on Structural Equation Model. Ecol. Indicators 111, 105992. doi:10.1016/j.ecolind.2019.105992

CrossRef Full Text | Google Scholar

Xiong, Y., Peng, F., and Zou, B. (2019). Spatiotemporal Influences of Land Use/cover Changes on the Heat Island Effect in Rapid Urbanization Area. Front. Earth Sci. 13 (3), 614–627. doi:10.1007/s11707-018-0747-3

CrossRef Full Text | Google Scholar

Xu, S. (2015). Impact Analysis of Land Use/Cover on Air Pollution. J. Geo-inf. Sci. 17 (3), 290–299.

Google Scholar

Yao, L., Li, T., Xu, M., and Xu, Y. (2020). How the Landscape Features of Urban green Space Impact Seasonal Land Surface Temperatures at a City-Block-Scale: An Urban Heat Island Study in Beijing, China. Urban For. Urban Green. 52, 126704. doi:10.1016/j.ufug.2020.126704

CrossRef Full Text | Google Scholar

Ye, Y., Qin, J., and Hu, S. (2017). Spatial-temporal Evolution of Urban Heat Island Effects in Changsha City. J. Geo-inf. Sci. 19 (4), 518–527.

Google Scholar

Yuan, F., and Bauer, M. E. (2007). Comparison of Impervious Surface Area and Normalized Difference Vegetation Index as Indicators of Surface Urban Heat Island Effects in Landsat Imagery. Remote Sensing Environ. 106 (3), 375–386. doi:10.1016/j.rse.2006.09.003

CrossRef Full Text | Google Scholar

Yuan, J., Li, J., Ye, S., Han, X., and Hu, Y. (2018). The Urban Heat Island Analysis of Changsha-Zhuzhou-Xiangtan Urban Agglomeration Aased on Modis Data. E3s Web Conf. 53, 03045. doi:10.1051/e3sconf/20185303045

CrossRef Full Text | Google Scholar

Zhou, D., Zhao, S., Zhang, L., Sun, G., and Liu, Y. (2015). The Footprint of Urban Heat Island Effect in China. Sci. Rep. 5, 11160. doi:10.1038/srep11160

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, W., Huang, G., and Cadenasso, M. L. (2011). Does Spatial Configuration Matter? Understanding the Effects of Land Cover Pattern on Land Surface Temperature in Urban Landscapes. Landscape Urban Plann. 102, 54–63. doi:10.1016/j.landurbplan.2011.03.009

CrossRef Full Text | Google Scholar

Zou, B., Xu, S., and Zhang, J. (2017). Spatial Variation Analysis of Urban Air Pollution Using GIS: A Land Use Perspective. Wuhan Univ. J. Inf. Sci. 42 (2), 216–222.

Google Scholar