- Department of Environmental Health Sciences, Mailman School of Public Health, Columbia University, New York City, NY, United States
Motivation: Gas stations chronically release gasoline vapor to the environment that contains the carcinogen benzene. However, there is no method for estimating setbacks for a gas station depending on an acceptable excess cancer risk due to the benzene emissions, sales volume, benzene content of the emissions, and inhalation dose, without performing an air dispersion simulation for each scenario.
Methods: We developed a new modeling framework, in which only one air dispersion simulation is performed for a reference gas station. Then, a new scaling law is used to estimate cancer risks and setbacks for different gas station characteristics and exposure scenarios.
Results: Our new scaling law allows estimating cancer risk vs. distance as a function of an acceptable excess cancer risk, total benzene emission rate, and frequency of exposure. Setbacks can also be determined from this scaling law or graphically from a design chart. Calculated setbacks differ only slightly from those determined from air dispersion simulations. Different emission control technologies substantially affect calculated setbacks.
Conclusions: We developed a framework that allows policy makers to examine easily how setbacks depend on regulatable measures such as emission control and acceptable cancer risk as well as on exposure characteristics. The framework also allows incorporating a safety factor to account for increased emissions. While this study was conducted in the context of US gas stations, our framework can be applied world-wide.
1. Introduction
Gas stations chronically release unburned fuel to the environment. These releases occur during fuel storage, when fuel is transferred to the tanks of customer vehicles, and when fuel storage tanks are filled by tanker trucks (1–3). Gasoline contains various toxic chemicals. Of particular concern is benzene, the inhalation of which can cause various short-term health effects (e.g., drowsiness, dizziness, rapid or irregular heartbeat, headaches, tremors, confusion, unconsciousness, and at extremely high concentrations death) but also long-term effects including cancer (4). Increased benzene concentrations have been measured in the surroundings of gas stations (5–11). Not surprisingly, gasoline emissions from gas stations have been associated with excess cancer risk of the general population in various case control studies (12–16) or based on measured or modeled outdoor benzene levels (9, 10, 17). Hence, a setback, i.e., a minimum distance between a gas station and adjacent land uses, may be required, and the magnitude of the setback is typically driven by the cancer risk posed by the fuel releases. However, setback regulations are not uniform across the world and within countries. In the US, they may exist at the state level [e.g., (18)], the county level [e.g., (19)], or not at all.
Emissions crucially depend on deployed dispensing and pollution prevention technologies including: dripless nozzles which reduce gasoline spills to the ground occurring during customer vehicle refueling, low permeation dispensing hoses; measures that reduce emissions from the vent pipes of storage tanks such as bladder tanks, membrane separators, carbon canisters or thermal oxidizers; measures that during refueling reduce vapor emission from the fuel tanks of customer vehicles including vacuum assist and pressure balance nozzles (Stage II vapor recovery) and onboard refueling vapor recovery (ORVR); and measures which minimize loading losses occurring during storage tank refueling via tanker trucks (Stage I vapor recovery). Recommendations for setback distances should ideally account for deployed pollution prevention technologies, because their efficiencies affect benzene emissions and thus cancer risk.
In the US, there is no agreement on how big an acceptable excess lifetime cancer risk due to exposure to carcinogenic chemicals such as benzene is, neither for the general population nor the work force. In a rule related to the remediation of environmental contamination, the US Environmental Protection Agency (EPA) states that for known or suspected carcinogens, acceptable exposure levels are generally concentration levels that represent an excess upper bound lifetime cancer risk to an individual of between one in 10,000 (100 per million) and one in a million (20). At the state level, e.g., the California Environmental Protection Agency & California Air Resources Board (CARB) used an acceptable cancer risk of 5 in a million to recommend setbacks for a broad range of industrial operations including gas stations (18). However, there is no consensus among the 50 US states about which threshold to use. No matter which threshold is used, policy makers should ideally use a science-based framework that allows them to determine meaningful setbacks for gas stations based on a chosen acceptable cancer risk.
The purpose of this paper is to develop a framework that allows policy makers to examine how a chosen acceptable cancer risk and applicable emission factors affect setbacks for gas stations. To that end we perform an air dispersion simulation to obtain the spatial distribution of the benzene concentration and hence cancer risk due to emissions from a reference gas station. This information is then used to develop a simple scaling law which allows estimating cancer risks and setbacks for gas stations with different benzene emission rates and for different benzene inhalation doses. The scaling law we developed allows policy makers, for the first time, to estimate cancer risk of atmospheric gasoline emissions from gas stations for a wide range of conditions without performing an AERMOD simulation for each condition, a task that can typically not be accomplished by policy makers alone, thus potentially delaying and/or negatively impacting the regulatory process.
2. Methods
2.1. Scaling law
The cancer risk associated with atmospheric emissions of unburned fuel (gasoline vapors) from gas stations is primarily due to the inhalation of benzene vapors. A simple approach for estimating the lifetime cancer risk due to carcinogen inhalation uses the concept of unit risk value : where is the average benzene concentration during the lifetime exposure and is the exposure factor which accounts for how often and how long a person is exposed (21). This approach was also used by the California Air Pollution Control Officers Association (CAPCOA) to assess the health risk due to emissions of unburned gasoline from gas stations (22).
Key to estimating the cancer risk around an emission source is knowledge of the spatial distribution of the average benzene concentration. This concentration field is controlled by the benzene emissions from the gas station and atmospheric conditions which control the dispersion of emitted benzene vapors. In the US, the AERMOD software developed by EPA to model air pollution due to emissions from a broad range of sources (23) is frequently used to assess gas station emissions with a given sales volume and assumed emission rates. To estimate the lifetime exposure, simulations are typically performed for a period of one to three years, using hourly meteorological data for that period as an input. The benzene emission rates are typically based on studies conducted by CARB.
To estimate cancer risk for gas stations with different sales volume and emission benzene content as well as different exposure frequency (without performing additional AERMOD simulations), we generalize a scaling law for cancer risk we developed in previous work, in which we examined the effects of sales volume and number of gas stations in a gas station cluster, , on cancer risk (17). In that work, we assumed an average cancer risk to be proportional to sales volume: where is the sales volume of a single gas station in the gas station cluster, r is the distance from the gas station cluster, and a and b are regression parameters. However, that approach does not allow examining how cancer risk depends on the benzene content of the emissions, and this content may vary not only because of the variable benzene content of gasoline but also because of the deployed benzene emission technologies, since they can affect the relative contributions of liquid and gaseous gasoline emissions. Moreover, cancer risk depends on and , factors for which Hsieh et al. (17) did not account. Hence, we propose here the following scaling law for cancer risk: where is the actual benzene emission rate, is the reference benzene emission rate, is the reference unit risk value, and is the reference cancer risk obtained for , , and .
2.2. Reference gas station
2.2.1. Geometry, location, and emissions
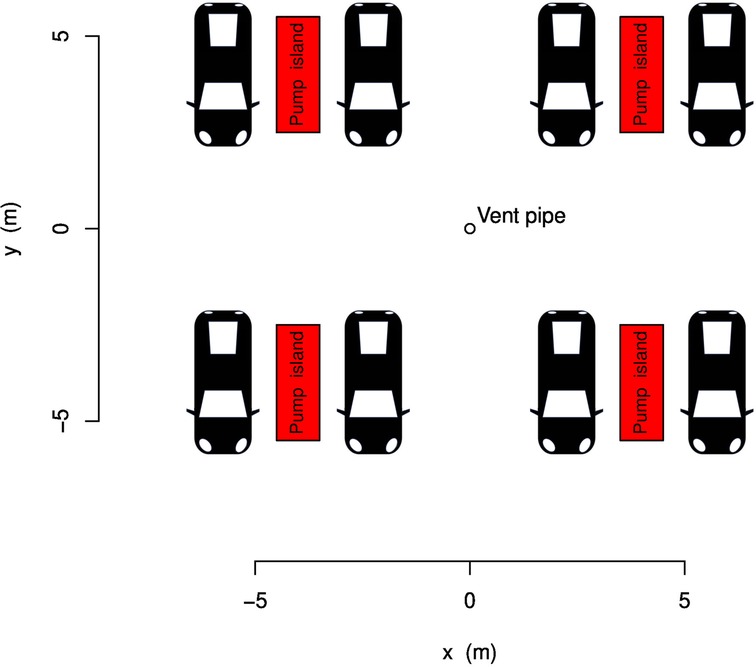
Like Hsieh et al. (17), we assumed the reference gas station to have four pump islands, from which fuel can be dispensed on both sides (Figure 1). The four centers of the pump islands are located at . The vent pipe of the underground storage tank is assumed to be located in the center of the gas station, with the vent releasing gasoline vapors at an elevation of 4 m above ground.
The gas station was assumed to be located at BWI Airport in the US state of Maryland. In the simulations, location may affect cancer risk through two factors: (1) the benzene content of the gasoline emissions due to the regionally variable benzene content of the gasoline and gasoline dispensing technology, and (2) meteorological conditions which control the atmospheric dispersion of emitted benzene vapors. We assumed a reference sales volume (14 million L/year), which according to CARB represents the lower bound of sales volumes of large gas stations (18).
Loading, breathing, refueling (of vehicles not equipped with ORVR), and spillage gasoline loss factors that should be representative for gas stations in Maryland were taken from the Gasoline Service Station Industrywide Risk Assessment Guidelines prepared by CAPCOA (22). We specifically used the values listed for a gas station with an underground storage tank, presence of Stage I vapor recovery and absence of Stage II vapor recovery. Absence of Stage II vapor recovery was assumed, because EPA (24) has allowed states not to require Stage II systems in case of widespread use of ORVR in the refueled vehicles, which has become the case in Maryland in the US. For ORVR-equipped vehicles, we assumed 95% efficiency of ORVR (24), i.e., refueling losses from ORVR-equipped vehicles are 5% of the uncontrolled losses for non-ORVR equipped vehicles. For hose permeation, the loss was taken from a report by CARB (25). We specifically used the value shown in Table VII in that report for the uncontrolled emission factor (UEF) case, for which Stage II vapor recovery is absent, exactly the assumption we made for Maryland. The first data column in Table 1 summarizes the magnitudes of the different losses in units of lbs/kgal (pounds per 1,000 gallons of gasoline dispensed). These losses are independent of the sales volume of the gas station, because they are normalized by the volume of gasoline dispensed. To convert gasoline losses into benzene losses, we assumed a gasoline density of 737 kg/m3, a benzene mass fraction of 1.2% in the liquid gasoline, and a mass fraction of 0.3% in the ullages of the storage and customer vehicle tanks. The second data column in Table 1 shows resultant benzene emissions rates for a Maryland gas station dispensing 3.6 million gallons per year in units of mass of benzene released per unit time. These are the units required by AERMOD as an input (for better readability we use mg/s in Table 1, even though AERMOD uses units of g/s).
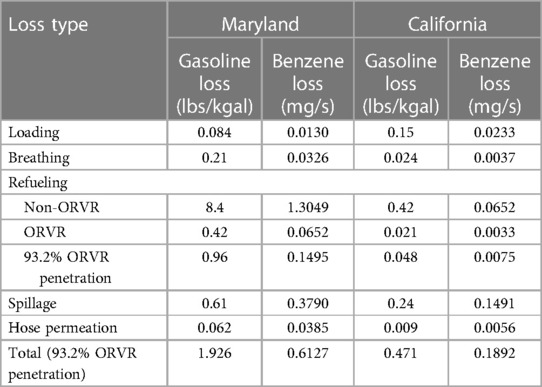
Table 1. Gasoline losses and benzene emission for a “large” gas station with a sales volume of 3.6 million gal per year in two US states.
2.2.2. Air dispersion simulations
To determine the spatial distribution of the reference cancer risk of the reference gas station at BWI Airport in Maryland, we first determined a reference benzene concentration field by performing an AERMOD simulation of the atmospheric dispersion of benzene vapors emitted from the gas station. Using the AERMOD software (23, 26), simulations were performed with the following simulation parameters:
• The numerical grid was polar with uniform angular and radial spacing. The radial coordinate r varied between 0 m and 150 m, with increments of 5 m. The angular coordinate varied between 10° and 360°, with increments of 10°.
• The benzene concentration field was simulated 1.5 m above ground (FLAGPOLE parameter in AERMOD), which is approximately within the breathing zone of adults.
• The simulated hourly benzene concentration field was averaged over the entire simulation interval, i.e., 1 year (the AVERTIME parameter in AERMOD is set to PERIOD).
• We assumed flat terrain (the FLAT option in AERMOD's MODELOPT pathway).
• Evaporative benzene emissions due to (a) gasoline spillage onto the ground during vehicle refueling, (b) hose permeation, and (c) customer vehicle tank refueling were modeled as volume sources while evaporative benzene emissions due to (a) loading, and (b) breathing of the storage tank were modeled as point sources as described and parameterized in Hsieh et al. (17) or CAPCOA (22).
• Benzene emission rates from the various sources were parameterized according to the second data column in Table 1.
• The stack exit velocity (the VS parameter in AERMOD) was set to the value obtained for the reference gas station with sales volume , i.e., VS = 0.00477 m/s, which is based on the assumption that the breathing and loading losses are released to the environment through a single vent pipe with insider diameter of 5.1 cm (2″). The stack exit velocity was also used for the other higher sales volumes we used, because we assumed that gas stations with higher sales volumes have likely more underground storage tanks and vent pipes.
• Surface meteorological data for the year 2020 was obtained for BWI Airport from the US National Climatic Data Center (NCDC). Upper air radiosonde data was obtained for the relatively nearby Sterling in Virginia from the National Oceanic and Atmospheric Administration (NOAA). Of note, a substantial portion of the meteorological data, mostly upper air data, was reported as missing giving rise to 26% of missing hourly AERMOD data.
2.2.3. Cancer risk calculations
The spatial distribution of the reference cancer risk was calculated from the simulated benzene concentration field via where is the spatial distribution of the annual average benzene concentration, and is the upper bound of the range of unit risk values reported by EPA (27). This calculation implicitly assumes an exposure factor which represents daily continuous exposure to the contaminant.
2.3. Simulations with California gasoline dispensing technology
In this paper, we also examine the hypothetical scenario of California gasoline dispensing technology being used in Maryland. Gasoline losses for loading, breathing, refueling, spillage, and hose permeation that should be representative of California dispensing technology were taken from a report by CARB (25). We specifically used the revised values for enhanced vapor recovery (EVR) emission control shown in Table I-I in that report. We determined benzene emission rates like for the Maryland gas stations. The third and fourth data column in Table 1 show the gasoline losses and benzene emission rates, respectively.
AERMOD simulations for gas stations using California dispensing technology were conducted as described in Section 2.2.2, except that the benzene emission rates from the fourth column in Table 1, scaled by the actual sales volume of the gas station, were used, and the stack exit velocity was revised according to the assumed breathing and loading emissions. For the assumed single vent pipe with insider diameter of 5.1 cm and the assumed sales volume , the stack exit velocity became VS = 0.00264 m/s, and like for the reference gas station we used this value also for higher sales volumes .
2.4. Correlation equation for reference cancer risk as a function of distance
Similar to our previous work (17), we derived a correlation equation for cancer risk as a function of distance r from the center of the gas station:
where is the maximum cancer risk observed at distance r among the 36 simulated directions (between 0° and 360°), and
is a function which describes the dependence of the reference cancer risk on distance r from the gas station with fit parameters , and . The bi-exponential terms in Equation 2 are an attempt to capture air dispersion from the various benzene emission sources, which differ in spatial extent (e.g., point and volume sources), location, and elevation. Since we are interested in estimating setbacks, this equation was like in our previous work (17) only fitted to simulated cancer risks in the far field of the gas station, where decreases monotonically ().
If in Equation 1 is interpreted as the acceptable cancer risk , the distance r becomes the setback which is given by
where
is the adjusted acceptable cancer risk, which accounts for the actual benzene emission rate, the actual unit risk value, and the exposure factor. Hence the setback can be obtained by first calculating and then applying the inverse function to this adjusted cancer risk. There is no analytical expression for . Hence, the setback distance needs to be determined numerically by inverting the function , or it can be determined graphically from a design chart which basically shows the vs. r relationship for the reference gas station according to Equation 2; however, the axes labels are renamed according to Equation 3.
To allow developing an analytical expression for the setback, we also considered a simplification of Equation 2 which assumes the simple exponential decay used in our previous work (17):
where the corresponding setback distance is then given by the following analytical expression:
We obtained the parameters and from a linear regression by log-transforming Equation 5 with resultant regression parameters and . To improve the fit closer to the emission sources we excluded distances from the regression.
Regression analyses were performed with the R statistical software, version 4.2.1. The “nls” package for nonlinear least squares regression was used to fit the simulated cancer risk vs. distance data from AERMOD to Equation 2 to obtain the fit parameters , and . Whereas the native “lm” function was used to fit the models given by Equations 5, 7 to the data via linear least square regression.
2.5. Evaluation of the scaling law
If Equation 3 is used to predict setback for a scenario that differs from the reference gas station, some error will be introduced. To quantify this error, we performed for all scenarios for which we used the scaling law also AERMOD simulations with the actual five benzene emission rates for loading, breathing, refueling, spillage, and hose permeation. Since the simulations only yield cancer risk on a uniform polar grid with 5-m spacing, we estimated the setbacks by first fitting the simulated field to Equation 1. The resultant regression parameters together with the assumed acceptable cancer risk were then used to calculate the setback using Equation 3.
3. Results
3.1. Cancer risk for the reference gas station
Figure 2 illustrates the dependence of the simulated reference cancer risk on direction and distance r for the reference gas station. The figure also illustrates the very good model fit by Equation 2. The residual standard error was only 4 × 10−8 which is 50 times smaller than the mean value of 2 × 10−6. The first data row in Table 2 lists the numerical values of the fit parameters.
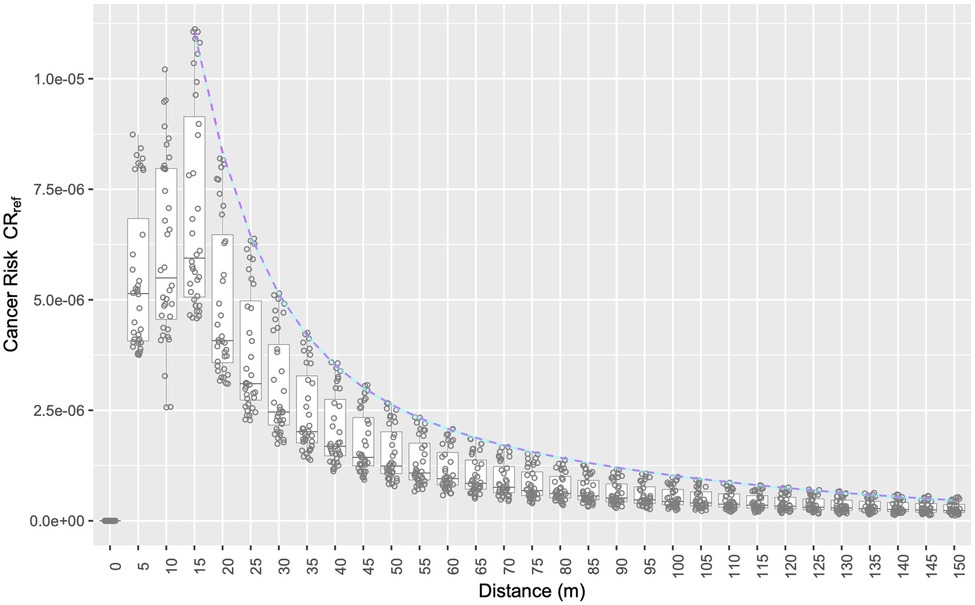
Figure 2. Reference cancer risk as a function of distance r from the reference gas station dispensing 3.6 million gallons per year. For each simulated r, a box plot illustrates the distribution of the simulated cancer risks along the 36 directions of the numerical polar grid. Magenta dashed line and cyan ribbon show the fit of maximum cancer risk to Equation 2 and the 95% confidence interval, respectively.
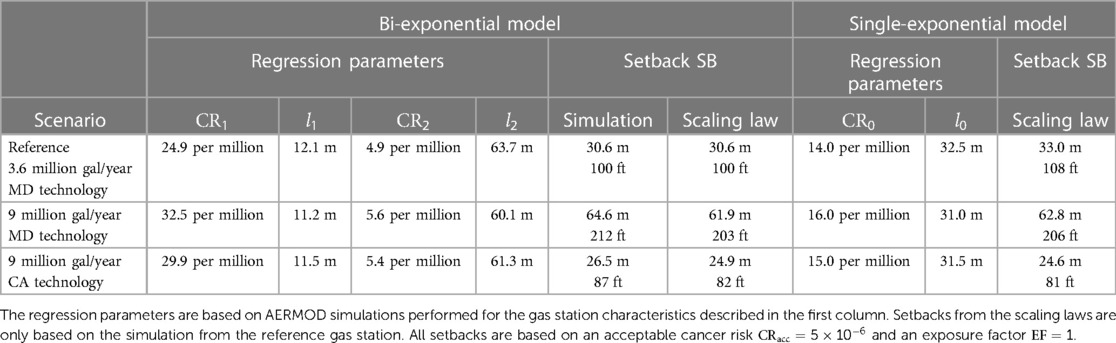
Table 2. Results of the AERMOD simulations performed for three gas stations differing in sales volume and emission controls.
Figure 3 shows the design chart we developed for estimating setbacks for gas station characteristics and exposure scenarios that differ from those assumed in the reference gas station simulation. The black solid line in Figure 3 and the magenta dashed line in Figure 2, which represents the cancer risk of the reference gas station, are numerically identical. However, the abscissa and ordinate values are reinterpreted to allow for the prediction of the other scenarios as demonstrated in Section 3.2.
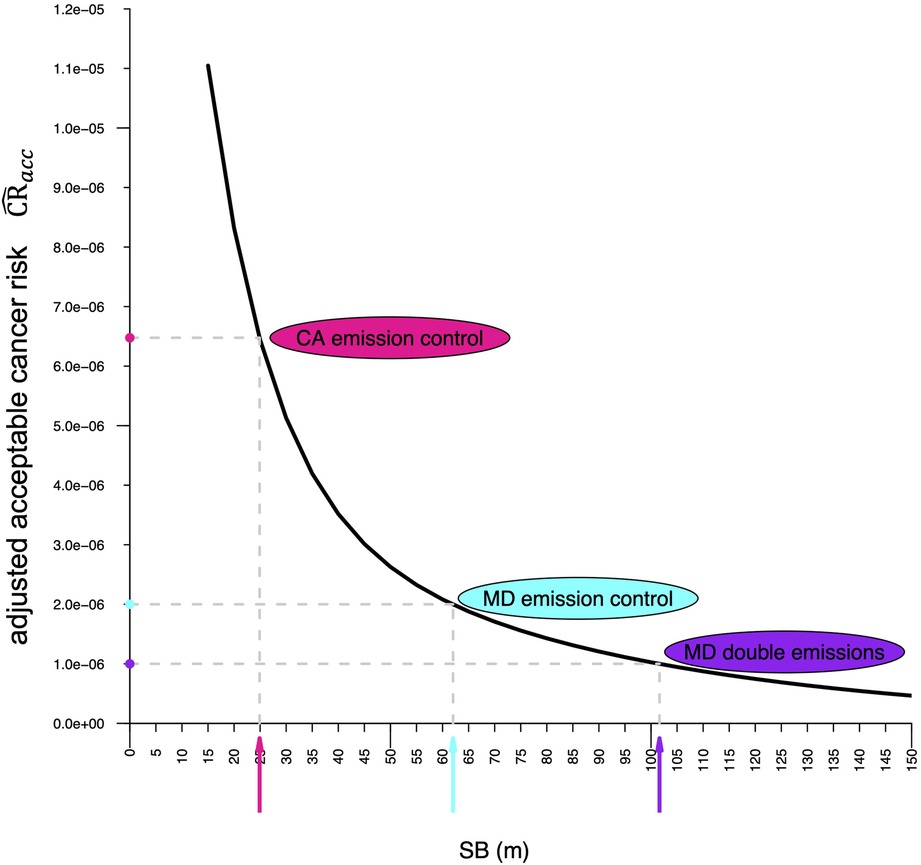
Figure 3. This design chart allows determining setback for a given acceptable cancer risk . First, the adjusted cancer risk , which accounts for the actual benzene emission rate , the actual unit risk value , and exposure factor , is calculated and graphed on the ordinate (filled circles). The setbacks are then obtained by applying the inverse function to the adjusted cancer risks, either numerically using Equation 3 or graphically as illustrated in this figure. Here the chart is used to determine setbacks for three gas stations each dispensing 9 million gallons of gasoline per year at BWI Airport in Maryland (US) but using different emission control technologies.
We note that the model residuals plotted against fitted values were not randomly distributed indicating that Equation 2 does not perfectly describe the simulated cancer risk data. This is not surprising, because the cancer risks are based on simulated benzene concentrations, which in turn are based on complex fluid mechanical flow and transport processes described by partial differential equations, which the four-parametric model given by Equation 2 cannot be expected to capture. The residuals vs. fitted values plot can be dramatically improved by fitting the following eight-parametric model to the cancer risk vs. distance data:
with equidistantly spaced, non-fitted wave numbers where is the decay length from the fit to the simple exponential decay model according to Equation 5 and the are fitted cancer risks. Equation 7 can be interpreted as a crude approximation of a Laplace transformation, which represents a given function by a superposition of exponential functions (28). However, a Laplace transformation is more general as it involves complex wave numbers (complex here means that a number may contain the imaginary unit ).
Figure 4 presents a side-by-side comparison of the three model fits examined in this paper to the cancer risk vs. distance data for the reference gas station, . The bi-exponential model given by Equation 2 provides a very good fit to the data. Including additional regression terms by use of Equation 7 results in only a slightly better match between the model prediction and the fitted data, even though the residual error distribution improves substantially. In contrast, the single-exponential model given by Equation 5 has problems with capturing the change in slope of the fitted data. While the eight-parametric regression according to Equation 7 is more satisfactory from a statistical point of view, we prefer the four-parametric model from Equation 2, because it already yields a small residual standard error, is easier to implement in a spreadsheet if predictions are of cancer risk as a function of distance are sought, and allows for better interpretability of the fit parameters.
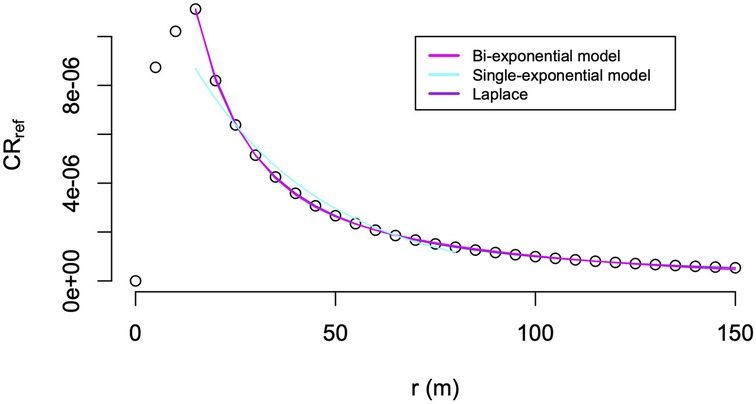
Figure 4. Comparison of the three model fits to the cancer risk vs. distance r data simulated with AERMOD (open circles).
3.2. Applications of the design chart
Using the design chart (Figure 3) as well as its mathematical basis given by Equations 3, 4, we now examine the effects that different pollution technologies have on cancer risks and setbacks for a gas station with sales volume , a value used by CARB to motivate the recommendation of a 300 ft (91.4 m) setback distance (18). We assume an acceptable cancer risk , an exposure factor , and .
We first assume the gas station to be equipped with pollution prevention technology representative for gas stations in Maryland, like our reference gas station. Hence, the benzene emission rate scales linearly with sales volume: . Since , one obtains as well. Therefore, the adjusted acceptable cancer risk becomes according to Equation 4. The setback distance according to Equation 3 is SB = 61.9 m (203 ft), a value which can also be determined graphically from the design chart.
Now we examine the effects of more efficient pollution prevention technology on cancer risk. For instance, in California gas stations have about three times lower benzene emission rates, for a gas station dispensing the reference sales volume of 3.6 million gal/year compared to for the reference gas station in Maryland (see Table 1). Using the California emission controls in Maryland would therefore result in an emission rate ratio ER/ERref= . Therefore, the adjusted acceptable cancer risk becomes according to Equation 4. The setback distance according to Equation 3 or the design chart is SB = 24.9 m (82 ft), much less than the 61.9 m obtained with Maryland emission controls.
Moreover, our modeling framework can be used in sensitivity analyses that can inform setting safety factors to account for benzene emissions that exceed the ones estimated by CARB (see Table 1), because these emission rates typically do not account for malfunctioning equipment, human error, inaccurate assumptions, or may be outdated (3, 29). For instance, if actual emissions with Maryland emission control technology were twice as high, i.e., , the adjusted acceptable cancer risk becomes according to Equation 4, and the setback would be SB = 101.6 m (333 ft) according to Equation 3 or the design chart.
To evaluate how accurately the scaling law given by Equation 3 and the design chart predict the setbacks, we compared their predictions to the ones from AERMOD simulations, which were based on the actual benzene emission rates as described in Section 2.5. The regression parameters , and obtained from the AERMOD simulations performed for the actual gas station characteristics agree quite well with those determined for the reference gas station (see columns 2–5 in Table 2). More importantly, the actual setbacks differ only slightly (≤3 m) from the ones predicted by the scaling equation (see columns 6 and 7 in Table 2). The ≤3 m difference in setback distance is less than the 5 m radial spacing of the numerical grid and seems negligible in regulatory environments where setbacks are on the order of 50 m or more, thus supporting use of Equation 3 and not necessitating AERMOD simulations for actual emission rates.
While the design chart given by Figure 3 alone allows estimating setback as a function of three parameters (), it can still be instructive to show for each of the three emission scenarios how cancer risk depends on distance. Figure 5 shows these cancer risks which we calculated with Equation 1. The setbacks for the assumed acceptable cancer risks can be determined graphically by determining the distances at which the horizontal line intersects with the vs. r curves. These setbacks are the same as the ones determined from the design chart.
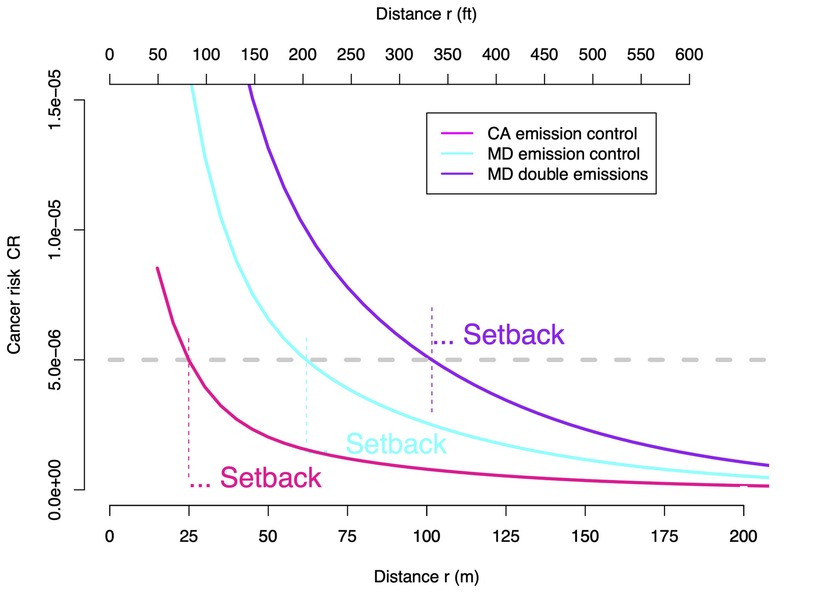
Figure 5. Cancer risk vs. distance r for three gas stations each dispensing 9 million gallons of gasoline per year at BWI Airport in Maryland (US) but using different emission control technologies. The setback distances vary substantially for an assumed acceptable cancer risk of 5 in a million.
4. Discussion
We derived a simple expression given by Equation 3 for estimating the setback from a gas station as a function of sales volume, pollution prevention technology, exposure factor, and acceptable cancer risk. Use of Equation 3 can be expected to introduce some error, because it only accounts for the total benzene emission rate but not the relative weights of the five different benzene vapor sources. However, the difference in setback predicted by the scaling law and AERMOD simulations, which accounted for the actual benzene emission rates, was within only 3 m, thus supporting use of Equation 3.
The setback can also be determined graphically. The design chart shown in Figure 3 allows examining the effects of three parameters, namely benzene emission rate, unit risk value, and exposure factor, on the setback. While one would naively expect a three-dimensional plot to be necessary to accomplish this task, this is not the case, because the plot is based on the scaling law given by Equation 1. In a way, the design chart capitalizes on dimensional analysis, which, e.g., in the field of fluid mechanics and other engineering/science disciplines is routinely used to reduce the number of independent variables. This reduction is possible because Equation 1 has been formulated in a dimensionally correct fashion (dimension refers here to the units of the variables).
For a gas station that hypothetically dispenses 9 million gal of gasoline per year using California dispensing technology, we estimated a setback distance of about 25 m (82 ft) for an acceptable cancer risk of 5 in a million (see Table 2). This setback is much less than the 300 ft that CARB recommended in 2005 in their Air Quality and Land Use Handbook (18) for gas stations in California with the same sales volume. We cannot explain the difference, because details of the cancer risk simulations that gave rise to the recommendation have not been provided in the handbook; however, we suspect that the recommendation is based on higher emission factors.
This study has limitations: (1) We assumed flat terrain when modeling the dispersion of benzene vapors. This assumption can be inadequate depending on the actual topography and built structures; however, the assumption is perhaps the least biased one when defining a generic gas station. (2) The parameterization of the cancer risk vs. distance relationship given by Equation 1 as well as the related design chart have been derived for a gas station in Maryland as meteorological conditions for that location were used as an input and cannot necessarily be applied in other locations. However, use of our parameterization may be warranted in climatically similar regions or for screening purposes. (3) 26% of the meteorological data was missing, which exceeds the 10% threshold for regulatory air dispersion modeling (30). Thus, the setbacks derived here for BWI Airport should be used with caution.
While this study has been conducted in the context of gas stations in Maryland in the US, the framework including the equations we developed for cancer risk as a function of distance from a gas station and for setback can be easily applied to other regions in the US and countries in the world. For instance, one cannot only account for different emission control technologies as demonstrated in this paper but also for a benzene content of gasoline which can differ substantially across countries (31). If our framework were to be applied in another region, one should ideally determine the reference cancer risk field (and fit parameters , and ) by performing an AERMOD simulation that uses meteorological and benzene emission data for that region. However, use of our parameterization of the scaling law and design chart could be warranted for screening purposes if the region is climatically similar to Maryland.
A study conducted in California sheds light on the effects of meteorology and hence location on cancer risk (32). The ISCST3 air dispersion modeling software (predecessor of AERMOD) was used to estimate cancer risk due to emissions from a gas station dispensing 1 million gallons annually in 35 cities geographically distributed in the South Coast Air Quality Management District. At a downwind distance of 100 m, the mean of the resultant 35 cancer risks was 0.43 per million, the standard deviation was 0.12 per million, and the range was [0.28, 0.76] per million [we inferred these values from Table 3 in AQMD (32)]. The ratio between the maximum and minimum cancer risk of about 3 shows that meteorology can have a pronounced effect on cancer risk. However, most gas stations in this district have similar cancer risks as evidenced by the relatively small relative standard deviation of 0.12/0.43 = 29%. Thus, sales volume and deployed emission control technologies can be factors much more important than meteorology since they can vary by much more than 30%, and use of our parameterization of Equation 2 might be warranted in locations other than BWI Airport when exploring the effects of sales volume and emissions controls.
Our framework easily allows accounting for uncertainties in benzene emission factors, the exposure factor , and unit risk value without the need to perform additional air dispersion simulations. For instance, to account for uncertainties in benzene emission factors developed and potentially underestimated by regulatory agencies, we multiplied the emission rate by a factor of 2, effectively accounting for a safety factor of 2. This numerical value is actually consistent with a study of vent pipe emissions from gas station storage tanks that found combined breathing and loading losses of 1.4 lbs/kgal and 1.7 lbs/kgal at the two gas stations examined (29). These values exceed the combined loss of 0.109 lbs/kgal that the CAPCOA study assumed for a gas station with Stage I and II vapor recovery technology and a pressure/vacuum valve on the vent pipe of the underground storage tank. Thus, breathing and loading losses were on average 14 times higher than reported in the CAPCOA study. If breathing and loading losses were also 14 times higher for a gas station with Maryland emission controls (no Stage II vapor recovery), the total benzene emission rate for a gas station dispensing 3.6 million gallons per year would be 1.21 mg/s, about twice the emission rate we assumed for our reference gas station . There is additional concern that the loading loss of 0.084 lbs/kgal which we assumed for Maryland emission technology is too low, because that value is based on the ad-hoc assumption of 1% uncontrolled emissions during loading (22). Indeed, CARB currently uses a loading loss of 0.15 lbs/kgal, i.e., a value two times higher, indicating that a loading loss of 0.084 lbs/kgal is too optimistic. In conclusion, a safety factor of 2 is not unreasonable, even though vent emissions should be examined at more gas stations, with broad geographical coverage.
In summary, this paper provides a science-based approach for estimating setbacks from gas stations. One should keep in mind that the acceptable cancer risk in Equation 3 only represents the excess individual cancer risk due to emission of unburned gasoline. Other emissions such as tail pipe emissions from vehicles visiting the gas station are not counted in as well as background benzene levels, all giving rise to cumulative health risks. The framework also does not account for how many people are exposed to the benzene, e.g., for population density. Moreover, there are also gas stations which dispense more than the 9 million gallons of gasoline per year, the sales volume we used to estimate setback distances in Figure 3. E.g., in 2005, CalEPA/CARB (18) noted that extremely large gas stations can have sales volumes as high as 19 million gallons per year.
Perhaps the greatest and unavoidable challenge in using our approach is choosing the acceptable cancer risk, an ethical decision which may also account for economic considerations including the cost of emission controls, which we have shown can substantially reduce setbacks, and the health, safety, and fuel savings benefits of these controls.
Data availability statement
The datasets presented in this article are not readily available from the author because: the meteorological surface and upper air data that were used as an input into the AERMOD simulations can be downloaded from ftp://ftp.ncdc.noaa.gov/pub/data/noaa and https://ruc.noaa.gov/raobs, respectively. The AERMOD and AERMET input files are available upon request to interested researchers.
Ethics statement
Ethical review and approval was not required for this study in accordance with the local legislation and institutional requirements.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
MH was partially supported by National Institute of Environmental Health Sciences grant P30 ES009089.
Acknowledgments
MH thanks Ted Tiberi for many insightful discussions of fuel vapor emissions from gas stations and emission control technologies, and for having carefully reviewed this manuscript. MH also would like to thank Jim Clary for his tutorial on how to download the AERMET input files (33).
Conflict of interest
MH has provided consultation and expert opinion on petroleum spills and emissions of petroleum vapors. MH also received funding from Booster Inc. to examine refueling losses during mobile refueling and at gas stations.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Hilpert M, Breysse PN. Infiltration and evaporation of small hydrocarbon spills at gas stations. J Contam Hydrol. (2014) 170:39–52. doi: 10.1016/j.jconhyd.2014.08.004
2. Hilpert M, Mora BA, Ni J, Rule AM, Nachman KE. Hydrocarbon release during fuel storage and transfer at gas stations: environmental and health effects. Curr Environ Health Rep. (2015) 2(4):412–22. doi: 10.1007/s40572-015-0074-8
3. Health Canada. “Benzene releases from gasoline stations: Implications for human health.” Government of Canada. Pub.: 220706 (2023).
4. ATSDR. “Toxicological Profile for Benzene.” Agency for Toxic Substances and Disease Registry. CAS#: 71-43-2 (2007).
5. Akland GG. Exposure of the general population to gasoline. Environ Health Perspect. (1993) 101(Suppl 6):27–32. doi: 10.1289/ehp.93101s627
6. Jo WK, Moon KC. Housewives’ exposure to volatile organic compounds relative to proximity to roadside service stations. Atmos Environ. (1999) 33(18):2921–8. doi: 10.1016/S1352-2310(99)00097-7
7. Jo WK, Oh JW. Exposure to methyl tertiary butyl ether and benzene in close proximity to service stations. J Air Waste Manage Assoc. (2001) 51(8):1122–8. doi: 10.1080/10473289.2001.10464339
8. Terres IMM, Minarro MD, Ferradas EG, Caracena AB, Rico JB. Assessing the impact of petrol stations on their immediate surroundings. J Environ Manag. (2010) 91(12):2754–62. doi: 10.1016/j.jenvman.2010.08.009
9. Dehghani M, Fazlzadeh M, Sorooshian A, Tabatabaee HR, Miri M, Baghani AN, et al. Characteristics and health effects of BTEX in a hot spot for urban pollution. Ecotoxicol Environ Saf. (2018) 155:133–43. doi: 10.1016/j.ecoenv.2018.02.065
10. Baghani AN, Sorooshian A, Heydari M, Sheikhi R, Golbaz S, Ashournejad Q, et al. A case study of BTEX characteristics and health effects by major point sources of pollution during winter in Iran. Environ Pollut. (2019) 247:607–17. doi: 10.1016/j.envpol.2019.01.070
11. Barros N, Carvalho M, Silva C, Fontes T, Prata JC, Sousa A, et al. Environmental and biological monitoring of benzene, toluene, ethylbenzene and xylene (BTEX) exposure in residents living near gas stations. J Toxicol Environ Health A. (2019) 82(9):550–63. doi: 10.1080/15287394.2019.1634380
12. Harrison RM, Leung PL, Somervaille L, Smith R, Gilman E. Analysis of incidence of childhood cancer in the west midlands of the United Kingdom in relation to proximity to main roads and petrol stations. Occup Environ Med. (1999) 56(11):774–80. doi: 10.1136/oem.56.11.774
13. Steffen C, Auclerc MF, Auvrignon A, Baruchel A, Kebaili K, Lambilliotte A, et al. Acute childhood leukaemia and environmental exposure to potential sources of benzene and other hydrocarbons; a case-control study. Occup Environ Med. (2004) 61(9):773–8. doi: 10.1136/oem.2003.010868
14. Brosselin P, Rudant J, Orsi L, Leverger G, Baruchel A, Bertrand Y, et al. Acute childhood leukaemia and residence next to petrol stations and automotive repair garages: the ESCALE study (SFCE). Occup Environ Med. (2009) 66(9):598–606. doi: 10.1136/oem.2008.042432
15. Infante PF. Residential proximity to gasoline stations and risk of childhood leukemia. Am J Epidemiol. (2017) 185(1):1–4. doi: 10.1093/aje/kww130
16. Mazzei A, Konstantinoudis G, Kreis C, Diezi M, Ammann RA, Zwahlen M, et al. Childhood cancer and residential proximity to petrol stations: a nationwide registry-based case-control study in Switzerland and an updated meta-analysis. Int Arch Occup Environ Health. (2022) 95(5):927–38. doi: 10.1007/s00420-021-01767-y
17. Hsieh PY, Shearston JA, Hilpert M. Benzene emissions from gas station clusters: a new framework for estimating lifetime cancer risk. J Environ Health Sci Eng. (2021) 19(1):273–83. doi: 10.1007/s40201-020-00601-w
18. CalEPA/CARB. Air Quality and Land Use Handbook: A Community Health Perspective, California Environmental Protection Agency & California Air Resources Board (2005).
19. Montgomery County Council. “Zoning Text amendments: filling station—use standards ZTA-15-07.” (2015). Available at: https://www.montgomerycountymd.gov/COUNCIL/Resources/Files/zta/2015/20151201_18-07.pdf
20. EPA. Remedial investigation/feasibility study and selection of remedy. 40 CFR § 300.430. Environmental Protection Agency (2011).
21. ATSDR. “Guidance for Inhalation Exposures.” Agency for Toxic Substances and Disease Registry, U.S. Department of Health and Human Services, Public Health Service (2020).
22. CAPCOA. “Gasoline service station industrywide risk assessment guidelines.” Toxics Committee of the California Air Pollution Control Officers Association (1997).
23. Cimorelli AJ, Perry SG, Venkatram A, Weil JC, Paine RJ, Wilson RB, et al. AERMOD: a dispersion model for industrial source applications. Part I: general model formulation and boundary layer characterization. Journal of Applied Meteorology. (2005) 44(5):682–93. doi: 10.1175/JAM2227.1
24. EPA. “Air Quality: Widespread Use for Onboard Refueling Vapor Recovery and Stage II Waiver.” Federal Register 40 CFR 51: 28772-28782 (2012).
25. CARB. “Revised Emission Factors for Gasoline Marketing Operations at California Gasoline Dispensing Facilities.” California Air Resources Board. Monitoring and Laboratory Division. (2013).
26. EPA. “User’s Guide for the AERMOD Meteorological Preprocessor (AERMET).” U.S. Environmental Protection Agency (2016).
27. EPA. Benzene; CASRN 71-43-2. Integrated Risk Information System (IRIS) U.S. Environmental Protection Agency (2000).
29. Hilpert M, Rule AM, Adria-Mora B, Tiberi T. Vent pipe emissions from storage tanks at gas stations: implications for setback distances. Sci Total Environ. (2019) 650(Pt 2):2239–50. doi: 10.1016/j.scitotenv.2018.09.303
30. EPA. “Meteorological Monitoring Guidance for Regulatory Modeling Applications.” US Environmental Protection Agency. EP A-454/R-99-005 (2000).
31. IARC. IARC monographs on the evaluation of carcinogenic risks to humans. Benzene. (2018) 120. ISBN 978-92-832-0187-8.
32. AQMD. "Emission Inventory and Risk Assessment Guidelines for Gasoline Dispensing Stations.” South Coast Air Quality Management District (2007).
33. AERMODtraining.com. “How to Download Meteorology Data for AERMET & AERMINUTE|AERMOD Training.” (2016). Available at: https://www.youtube.com/watch?v=xk8TJ4y1pu0
Keywords: gas station, setback, cancer risk, benzene, air dispersion modeling
Citation: Hilpert M (2023) Setbacks for gas stations in a world with regionally varying emissions factors and acceptable health risks. Front. Environ. Health 2:1214376. doi: 10.3389/fenvh.2023.1214376
Received: 29 April 2023; Accepted: 5 June 2023;
Published: 23 June 2023.
Edited by:
Sourangsu Chowdhury, Centre for International Climate and Environmental Research (CICERO), NorwayReviewed by:
Poonam Mangaraj, National Institute of Advanced Studies, IndiaEmina Kristina Petrovic, Victoria University of Wellington, New Zealand
© 2023 Hilpert. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Markus Hilpert bWgzNjMyQGNvbHVtYmlhLmVkdQ==
 Markus Hilpert
Markus Hilpert