Method for calculating a water surface profile at the watershed scale with little observed data based on ASTER GDEM: a case study in the Naoli River, northeast China

The calculation of a river water surface profile is a very important problem in the field of hydraulic engineering. With the development of research on surface and groundwater coupled simulation, the river water surface profile has become an indispensable boundary condition for simulating the inter-relationship between surface water and groundwater. River channel large-section data are the basic prerequisites for building most hydrodynamic models, and obtaining field data can consume considerable effort and material resources. We extracted river sections using ArcGIS based on the ASTER GDEM data and interpolated the corresponding water levels of different guarantee flow rates in Baoqing and Caizuizi stations. We analyzed the variation of upstream water levels under different Manning coefficients n, and the bed resistance of the Naoli River was determined to be 0.025. In order to ensure the rationality of the model and the reliability of the operation results, three indexes (non-scouring velocity, the shear stress of the riverbed, and the water surface slope) were used to analyze and test the rationality of the simulation results. Ultimately, the calculation of the water surface profile from the Baoqing hydrologic station to the Caizuizi hydrologic station in the Naoli River was achieved using the MIKE 11 hydrodynamics model under the guarantee flow rates of 20%, 50%, 75%, and 95%. Calculating the water surface profile can provide hydrological boundary conditions for surface and groundwater conversion and the combined simulation. Furthermore, the present study can provide a feasible method for calculating a river water surface profile in areas that lack measured section data.

1 Introduction

A river water surface profile is based on the data of river topography, transverse and longitudinal sections, and roughness to calculate the water level of each section under a certain fixed flow value and connect the water level value into a curve. As an important part of hydraulics research, the water surface profile plays an important role in surface and underground coupled river basin simulation. The results of water surface line calculations can provide hydrological boundary conditions for a numerical groundwater calculation model, which is the basis for the successful operation of the model. Based on the Advanced Spaceborne Thermal Emission and Reflection Radiometer Global Digital Elevation Model (ASTER GDEM) data, the hydrodynamic simulation software MIKE 11, which is widely used and has a high accuracy of calculation results, is adopted in this paper for hydrodynamic calculation, aiming to deduce the river water surface profile under different working conditions in the region without a cross section of the measured river.

In the past 20 years, the principles of river hydraulic calculation have been widely used in many river basins worldwide. In 1871, Saint-Venant (1871) proposed an explicit unsteady flow differential equation, namely Saint-Venant’s equation. The spatio-temporal changes in river water level and flow rate are usually calculated using Saint-Venant’s formula (Strelkoff, 1970; Tayfur et al., 1993; Popescu, 2014), which is based on the conservation of mass and momentum. The calculation of the Saint-Venant formula was very complicated and difficult. In the 1950s, with the development of computer technology and the finite difference method, the numerical simulation of one-dimensional, shallow open channel flow gradually developed and matured. By the 1960s, finite element, finite volume, and other numerical methods were continuously applied to computational fluid dynamics, and two-dimensional and three-dimensional shallow hydrodynamic models emerged. Since the 1990s, several mature commercial software packages for river hydrodynamic models, such as SMS and HEC-RAS, have appeared. At present, the numerical methods to calculate Saint-Venant mainly include the finite difference method (FDM), the finite element method (FEM), and the finite volume method (FVM). After 2000, based on the above numerical methods, researchers began to calculate river dynamics with different hydrodynamic models (Bates and De Roo, 2000; Hunter et al., 2007).

The MIKE series is a piece of commercial software developed by the Danish Institute of Hydraulic Research (DHI) and is composed of MIKE 11, MIKE 21, MIKE NAM, and other parts. MIKE 11 applications, more than any other simulation software, can deal with flood, navigation, water quality, prediction, sediment transport, and other practical problems (Danish Hydraulic Insititute, 2012). MIKE 11 makes use of the finite difference method (FDM), the finite element method (FEM), the finite volume method (FVM), and other numerical methods to calculate different grid points along the flow direction of water level and flow of the hydrodynamic simulation software. This software has the advantages of reliable algorithms, stable calculation, simple processing, and strong regulation functions for hydraulic structures. The MIKE 11 model used in this study can satisfy the hydraulic calculation under complex river channels and different flood flow patterns, with strong adaptability and a wide application range.

At present, MIKE 11 software is widely used in flood control, flood prediction, water quality evaluation and prediction, as well as research, planning, design, management, and evaluation of water conservancy projects. MIKE 11 has been well applied in many countries. As a world-class standard for dynamic simulation of rivers and waterways, MIKE 11 has unlimited river simulation capacity and has become the most powerful and comprehensive method for river hydrodynamic and environmental simulation. This paper used the numerical method of MIKE 11 (HD) to calculate the relationship between the flow rate and water level at different points in the river and to explore the calculation of the water surface line under different working conditions.

River profile data are the basic input into the MIKE 11 hydrodynamic model for simulating water levels. Because obtaining river profile data and hydrological data measured in the field can consume considerable effort and material resources, this paper used the elevation data provided by satellite to complete the section extraction. ASTER GDEM is a global digital elevation model of the land surface of the earth jointly launched by Japan’s METI and the United States NASA on 29 July 2009. ASTER GDEM is a model that can provide global digital elevation data to the public free of charge. It provides elevation data with a plane accuracy of 30 m and a vertical accuracy of 20 m (Chrysoulakis et al., 2011). This is higher than the elevation data accuracy provided by SRTM, which is also widely used at present.

In this paper, ASTER GDEM precision is used to extract the river section as the input for the MIKE 11 hydrodynamic model. ASTER GDEM can provide global digital elevation data to the public free of charge. It has made good progress in hydrological process simulation, engineering planning and design, landform analysis, and geological hazard assessment. In this paper, ASTER GDEM data is used to extract river sections in areas with scarce river section data, and a feasible method is explored to determine the river surface line under different guarantee rates (20%, 50%, 75%, and 95%) in areas without measured river sections. This work can provide information for flood control and reduction of the damage caused by flooding and drought. Moreover, the river water level at different design flood guarantee rates can be used as the boundary conditions in the groundwater numerical model.

2 Methods

Limited by time, cost, site, or test instruments, it is difficult to carry out experimental research on the actual river model for all projects. Therefore, hydrodynamic simulation software is usually used by researchers to deduce the water surface line of the natural river so as to achieve the expected purpose. At present, there are many calculation methods for river surface lines. The common methods can be generally summarized as artificial trial algorithms and hydrodynamic simulation software calculation methods, and the most widely used method is the hydrodynamic simulation software calculation method.

The MIKE 11 model is a widely used hydrologic simulation system developed by the Danish Institute of Hydraulic Research (MIKE11, 2013). The MIKE 11 model is mainly used to simulate surface runoff, water flow, sediment transport, and river and estuary water quality (Rahman et al., 2011; Thompson et al., 2004; Liu et al., 2007; Keskin et al., 2008). The models include hydrodynamic (HD), convection-dispersion (AD), flood prediction (FF), sediment transport (ST), and rainfall-runoff (RR). MIKE 11 has the advantages of wide applicability, friendly interface, strong scalability, stability, and efficient calculation. Based on the above advantages and the universality of their applications, this study will use the hydrodynamic model of MIKE 11 to complete the water surface profile estimation of the basin.

The hydrodynamic module of MIKE 11, which is the most widely used, is the application basis of other modules such as convection-dispersion, flood prediction, sediment migration, and rainfall-runoff. Establishing the HD model includes simplifying the formula of the control equations, discretizing the equation, solving the numerical value of the control equations, determining the initial and boundary conditions of the model, parameter calibration, model verification, sensitivity analysis, and other steps.

The operation of the MIKE 11 model is based on the dynamic, diffusion, or fully dynamic, vertically integrated mass and momentum equations, namely, Saint-Venant equations, including the continuous equation (Formula 1) and the momentum equation (Formula 2). The solution of these equations is based on the implicit finite difference scheme because this scheme is not subject to the dynamic, diffusion, and other wave conditions (Kamel et al., 2008).

$\frac{\mathit{\partial }\mathrm{A}}{\mathit{\partial }\mathit{t}}+\frac{\mathit{\partial }\mathrm{Q}}{\mathit{\partial }\mathrm{x}}=\mathrm{q}.(1)$

$\frac{\mathit{\partial }\mathrm{Q}}{\mathit{\partial }\mathrm{t}}+\frac{\mathit{\partial }\left(\mathrm{\alpha }\frac{{\mathrm{Q}}^2}{\mathrm{A}}\right)}{\mathit{\partial }\mathrm{x}}+\mathrm{g}\frac{\mathrm{Q}\left|\mathrm{Q}\right|}{{\mathrm{C}}^{2}AR}=0.(2)$

In this formula, A is the discharge section area (m²);t is (s);Q is the section runoff (m³/s);x is the distance along the direction of the current (m);q is the lateral inflow per unit length of reach (m²/s);α is the momentum distribution coefficient;g is the gravitational acceleration (m²/s);C is the Chezy coefficient (m^1/2/s);R is the hydraulic radius (m).

MIKE 11 (HD) solves Saint-Venant equations based on the following assumptions:

(1) the water flow is incompressible, and flow is uniform (such as small changes in density);

(2) the wavelength is larger than the water depth, assuming that the water flow and the bottom of the riverbed are parallel (for example, vertical acceleration can be ignored, assuming that the vertical hydrostatic pressure changes);

(3) the natural gradient of the riverbed is small, and the approximate riverbed angle cosine is 1;

(4) the flow is subcritical flow (MIKE 11 can simulate supercritical flow, but the application conditions are more stringent).

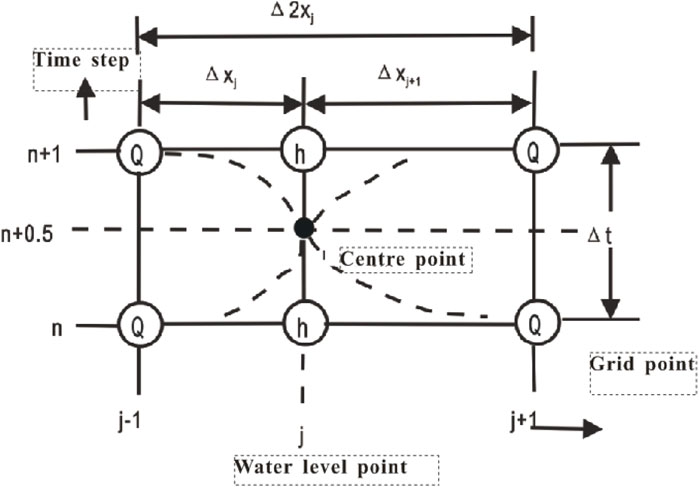
In the MIKE 11 workflow, the river and floodplain are described as a river network system with interconnected tributaries. Abbott’s six-point central implicit difference (discrete) scheme is adopted to solve Saint-Venant equations using the “double-sweep” algorithm. This discrete format is very stable under any conditions. Even though the data volume is very large, it can still maintain the computational stability of the model and efficiently complete the hydrodynamic calculation of rivers and river networks. The change of water level (h) and flow rate (Q) with time is calculated alternately in the order of h-q-h at each node along the flow direction. The model operation is based on the topographic information of rivers and floodplains, and the specific calculation sequence is shown in Figure 1.

Figure 1

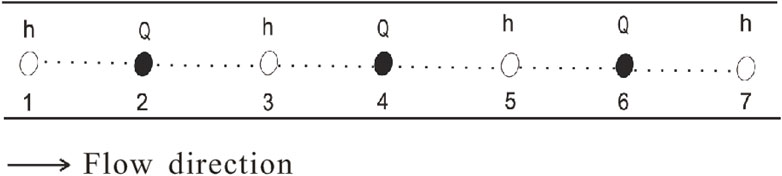
Figure 1. Schematic diagram of the alternating calculation of water level and flow at section nodes.

The specific discrete format of the Saint-Venant flow continuity equation is expressed in Figure 2. In the flow continuity equation, after introducing channel width Bs, the equation can be expressed as Formulas 3–5.

$\frac{\mathit{\partial }\mathrm{Q}}{\mathit{\partial }\mathrm{x}}=\frac{\frac{{\mathrm{Q}}_{\mathrm{j}+1}^{\mathrm{n}+1}+{\mathrm{Q}}_{\mathrm{j}+2}^{\mathrm{n}}}{2}+\frac{{\mathrm{Q}}_{\mathrm{j}+1}^{\mathrm{n}+1}+{\mathrm{Q}}_{\mathrm{j}+2}^{\mathrm{n}}}{2}}{∆2{\mathrm{x}}_{\mathrm{j}}}.(3)$

$\frac{\mathit{\partial }\mathrm{h}}{\mathit{\partial }\mathrm{t}}\approx \frac{{\mathrm{h}}_{\mathrm{j}}^{\mathrm{n}+1}-{\mathrm{h}}_{\mathrm{j}}^{\mathrm{n}}.}{∆\mathrm{t}}(4)$

${\mathrm{B}}_{\mathrm{s}}=\frac{{\mathrm{A}}_{0,\mathrm{j}}+{\mathrm{A}}_{0,\mathrm{j}+1}}{∆2{\mathrm{x}}_{\mathrm{j}}}.(5)$

In this formula: ${\mathrm{A}}_{0,\mathrm{j}}$ is the surface area between lattice point j − 1 and lattice point j (m²);${\mathrm{A}}_{0,\mathrm{j}+1}$ is the surface area between lattice point j and lattice point j + 1 (m²);$∆2{\mathrm{x}}_{\mathrm{j}}$ is the spacing between lattice point j − 1 and lattice point j + 1 (m).

Figure 2

Figure 2. Abbott six-point hermit difference scheme for Saint-Venant continuous equations.

Based on the above equations, the discrete format of the continuous equation can be summarized as shown in Formula 6, which can be further simplified to Formula 7.

${\mathrm{B}}_{\mathrm{s}}\frac{{\mathrm{h}}_{\mathrm{j}}^{\mathrm{n}+1}-{\mathrm{h}}_{\mathrm{j}}^{\mathrm{n}}}{∆\mathrm{t}}+\frac{\frac{{\mathrm{Q}}_{\mathrm{j}+1}^{\mathrm{n}+1}+{\mathrm{Q}}_{\mathrm{j}+1}^{\mathrm{n}}}{2}-\frac{{\mathrm{Q}}_{\mathrm{j}-1}^{\mathrm{n}+1}+{\mathrm{Q}}_{\mathrm{j}-1}^{\mathrm{n}}}{2}}{∆2{\mathrm{x}}_{\mathrm{j}}}={\mathrm{q}}_{\mathrm{j}.}(6)$

${\mathrm{\alpha }}_{\mathrm{j}}{\mathrm{Q}}_{\mathrm{j}-1}^{\mathrm{n}+1}+{\mathrm{\beta }}_{\mathrm{j}}{\mathrm{h}}_{\mathrm{j}}^{\mathrm{n}+1}+{\mathrm{\gamma }}_{\mathrm{j}}{\mathrm{Q}}_{\mathrm{j}+1}^{\mathrm{n}+1}={\mathrm{q}}_{\mathrm{j}.}(7)$

Saint-Venant equations are solved by the “double scan” algorithm.

After the Saint-Venant equations are discretized, the hydraulic parameters (W) at any point in the river channel, including water level and flow, are related to the adjacent grid point W, which can be expressed as the following linear equation (Formula 8).

${\mathrm{\alpha }}_{\mathrm{j}}{\mathrm{W}}_{\mathrm{j}}^{\mathrm{n}+1}+\mathrm{\beta }{\mathrm{W}}_{\mathrm{j}}^{\mathrm{n}+1}+{\mathrm{\gamma }}_{\mathrm{j}}{\mathrm{W}}_{\mathrm{j}+1}^{\mathrm{n}+1}={\mathrm{\delta }}_{\mathrm{j}.}(8)$

In this formula, n+1 is the Time step;bj − 1, j, j+1 is the Node location;$\mathrm{\alpha },\mathrm{\beta }\mathrm{\gamma }\mathrm{\delta }$ is the water level node calculated by the discretized flow continuity equation. A flow node is calculated by the discrete momentum equation. If a river has n (odd) nodes, the equations are composed of n linear equations, as follows (Formula 9):

${\mathrm{\alpha }}_1{\mathrm{H}}_{\text{us}}^{\mathrm{n}+1}+{\mathrm{\beta }}_1{\mathrm{h}}_1^{\mathrm{n}+1}+{\mathrm{\gamma }}_1{\mathrm{Q}}_2^{\mathrm{n}+1}={\mathrm{\delta }}_{1.}$

${\mathrm{\alpha }}_2{\mathrm{H}}_1^{\mathrm{n}+1}+{\mathrm{\beta }}_1{\mathrm{h}}_2^{\mathrm{n}+1}+{\mathrm{\gamma }}_1{\mathrm{h}}_3^{\mathrm{n}+1}={\mathrm{\delta }}_{2.}$

$\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots .$

${\mathrm{\alpha }}_{\mathrm{n}-1}{\mathrm{H}}_1^{\mathrm{n}+1}+{\mathrm{\beta }}_1{\mathrm{Q}}_{\mathrm{n}-1}^{\mathrm{n}+1}+{\mathrm{\gamma }}_{\mathrm{n}-1}{\mathrm{h}}_{\mathrm{n}}^{\mathrm{n}+1}={\mathrm{\delta }}_{\mathrm{n}-1.}$

${\mathrm{\alpha }}_{\mathrm{n}}{\mathrm{Q}}_{\mathrm{n}-1}^{\mathrm{n}+1}+{\mathrm{\beta }}_{\mathrm{n}}{\mathrm{h}}_{\mathrm{n}}^{\mathrm{n}+1}+{\mathrm{\gamma }}_{\mathrm{n}}{\mathrm{H}}_{\text{ds}}^{\mathrm{n}+1}={\mathrm{\delta }}_{\mathrm{n}}.(9)$

In this formula, H_us is the water level of the upstream node (h);H_ds is the water level of the downstream node (h).At the first section in MIKE 11, h₁= H_us; at the last section, h_m= H_ds.

The above equations are easy to solve if there is no major tributary inflow on the reach and the upper and lower water level boundaries of the reach are known (they are usually obtained from the measured value of the hydrological station).

3 Examples

3.1 Study area

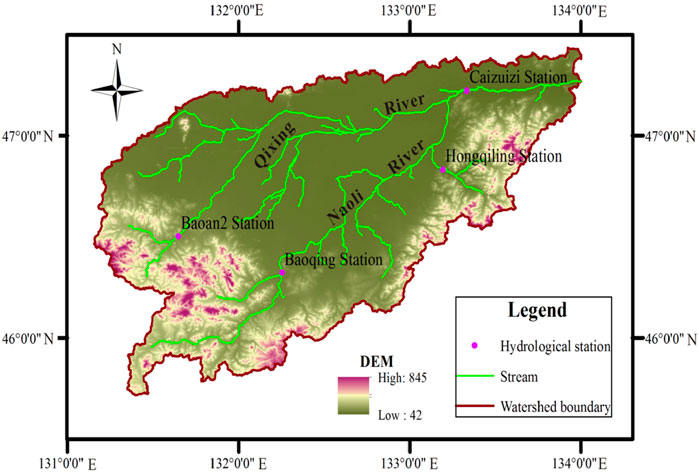
The Naoli River basin is located in northeast Heilongjiang province, the heart of the Sanjiang plain, at east longitude 131°31′∼134°10′, north latitude 45°43′∼ 47°45′. It is a tributary of the Ussuri River, originating from the north slope of the Wanda mountain, with a total length of approximately 596 km. It is the largest inland river in the Sanjiang plain, with a total basin area of 24,800 km², and finally converges with the Qixing River into the Wusuli River. In this basin, the mountainous area accounts for 38.3% of the total area, mainly distributed in the southwest and south of the basin, with the plain accounting for 61.7% of the total area, distributed in the north and middle of the basin (Figure 3).

Figure 3

Figure 3. The location of the research area.

The average annual precipitation in the Naoli River basin is approximately 518 mm (Liu et al., 2013). In 1960, the maximum precipitation was 813 mm, while in 1967, the minimum precipitation was only 351 mm. Over the past 60 years in this basin, the average temperature was 3.14°C, the highest average temperature of 4.49°C occurred in 1990 and 2008, and the lowest average temperature of 1.06°C occurred in 1969. The average relative humidity is 66% in many years and ranges from 70% to 80% in summer and 60%∼70% in winter. The annual average wind speed is between 3.7 m/s and 4.2 m/s. The perennial average sunshine hours were 2509 h. The average solar radiation over the years is between 99 kcal/cm² and 110 kcal/cm² (Song, 2012).

The Naoli River is the main branch of the Wusuli River in China, flowing from southwest to northeast. The main tributaries are on the right bank of the river: Big Suolun River, Small Suolun River, Hamatong River, Qing River, Qiliqin River, Big Jia River, and Small Jia River. On the left bank of the river are tributaries of the Qixing River. After the river enters the plain, the bending coefficient is generally above 1.8, and the local reach reaches approximately 3. The river slope changes greatly, including 1/200∼1/800 in the upper reaches of the Naoli River, 1/4,000∼1/15,000 in the middle reaches, and 1/8,000 in the lower reaches. The main stream of the Naoli River originates from the north slope of Wanda mountain in Qitaihe city and flows into the Wusuli River. The Qixing River originates from the Qixing pleated mountain in Shuangyashan city and flows into the Naoli River after passing through the Qixing River wetland reserve.

There are two main hydrological stations in the study river: Baoqing hydrological station and Caizuizi hydrological station. Baoqing station was established in August 1949 and is located in Heilongjiang province, Shuangyashan city, Baoqing town, with geographical coordinates of longitude 132°18′ and north latitude 46°18′. In the catchment area of 3,689 km², 439 km from the estuary, is a national second-class precision hydrological station. Caizuizi Hydrological Station was established in 1956. It is located in the mountains of Heilongjiang province, Jixi city, Caizuizi village, and its geographical coordinates are longitude 133°20′ north, latitude 47°12′. The catchment area is 20,556 km². It is the Naoli River downstream control station, and it is a news station at the national level.

3.2 Build model

The river network file, section file, boundary file, and roughness file are needed for model construction.

3.2.1 River network

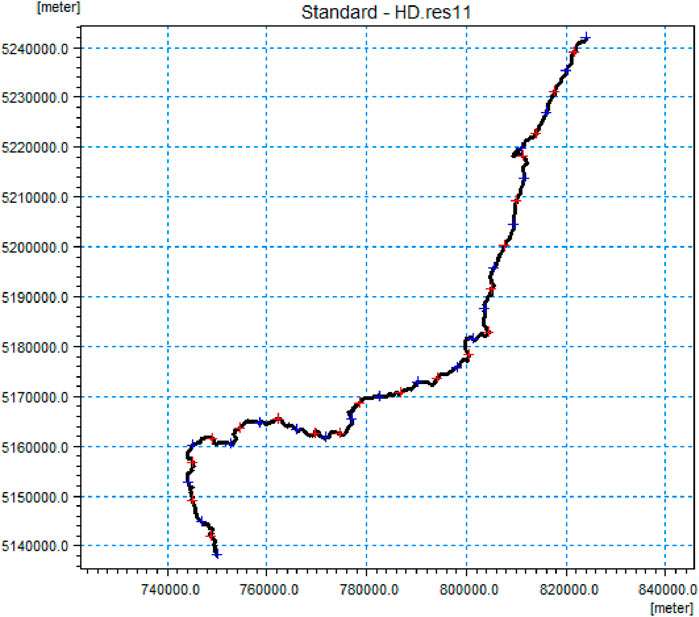
River network documents mainly include the geometric shapes, lengths, and trends of rivers, estuaries, and river networks, or numerical maps of GIS. The river network file in this study is based on elevation data extraction, and GIS software is used to generate the Shp file, which is input needed by the MIKE 11 model. The river network file extracted from Baoqing station to Caizuizi station along the Naoli River is shown in Figure 4. The total length of the reach is 198.725 km.

Figure 4

Figure 4. Schematic diagram of the research river network (note: marked with geodetic coordinates in the figure).

3.2.2 River section

The section file contains river section information, and the section is arranged according to the research purpose. The section is used to reflect the section shape of the studied section for hydraulic calculation. In this study, the sections of the initial upper boundary Baoqing station and the lower boundary Caizuizi station were physically measured. Other sections between these two were extracted by using ArcGIS and ASTER GDEM elevation data. Every section was arranged every 10 km along the main stream of the Naoli River from Baoqing station to Caizuizi station, and every elevation sampling point was arranged every 30 m vertically along each extracted section from left to right. Nineteen sections were extracted by ASTER GDEM. The layout of all sections is shown in Figure 5.

Figure 5

Figure 5. All sections of the river network (note: marked with geodetic coordinates in the figure).

The position x and riverbed elevation z data of each sampling point in the section were imported into MS EXCEL. The section data were edited into TEXT according to the format required by the MIKE 11 model (format conversion can be realized by using self-programming programs such as FORTRAN, BASIC, and EXCEL VBA). Then, the actual measured sections and extracted section data were input into the MIKE 11 model in the specified format. The actual measured sections of the Baoqing station and the Caizuizi station are shown in Figure 6, and part of the sections extracted from ASTER GDEM elevation data are shown in Figure 7.

Figure 6

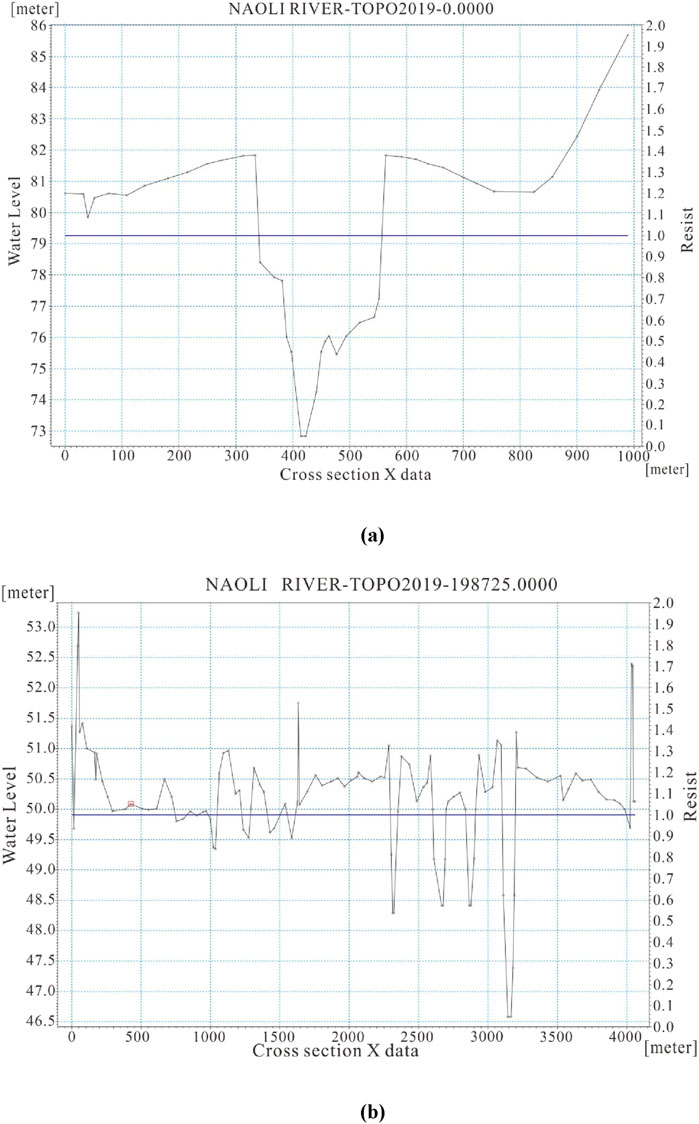
Figure 6. The actual measured sections of Baoqing station (A) and Caizuizi station (B) in the main stream of the Naoli River.

Figure 7

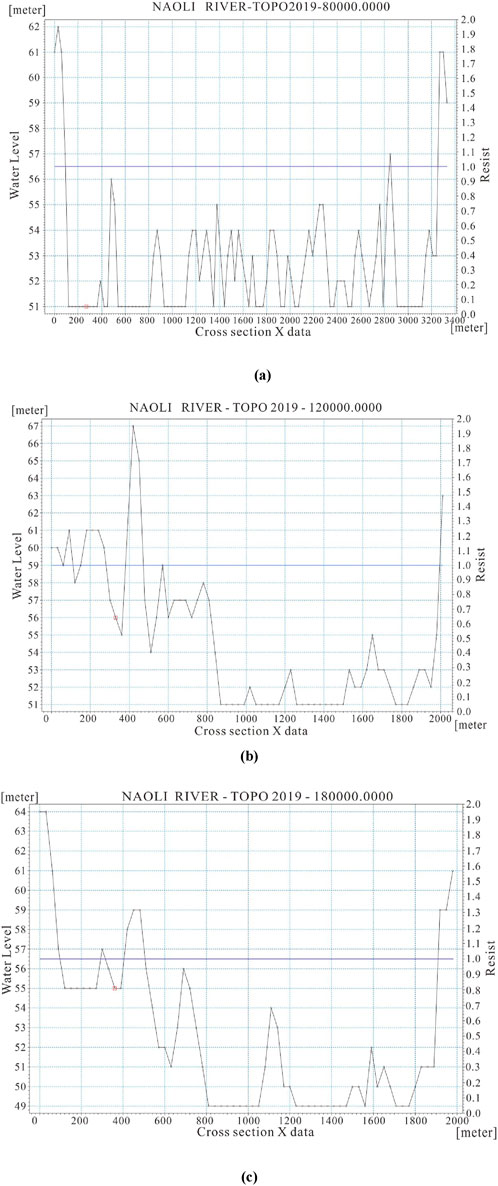
Figure 7. The part sections (A) 80 km, (B) 120 km, and (C) 180 km were extracted by ASTER GDEM elevation data in the main stream of the Naoli River.

3.2.3 Model boundary

When using MIKE (HD) to deduce the water profile line, the upstream flow and downstream water level values must be input into the model. Groundwater numerical modeling requires boundary conditions. Mike 11 (Patro et al., 2009; Panda et al., 2010; DHI, 2007) can be used to calculate the water level at different guarantee rates (20%, 50%, 75%, and 95%). As the boundary conditions of the model simulation, the water level and flow of the river sections are calculated to provide data for the numerical simulation of groundwater.

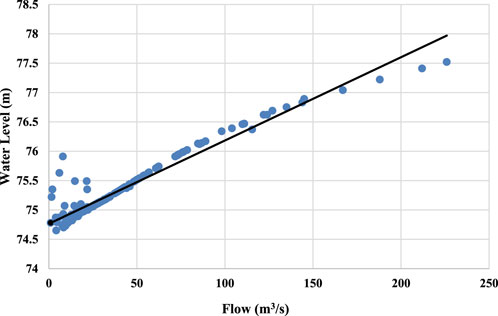
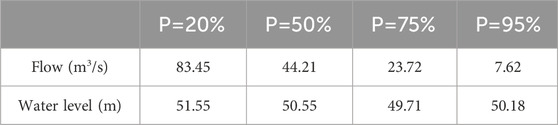
The flow boundary of the Naoli River trunk stream is determined by the measured data from the Baoqing station upstream and the Caizui station downstream. The relationship between water level and flow in the Baoqing station is shown in Figure 8. It was found that the water level relation law corresponding to small flow and large flow was different in the Caizuizi station. Therefore, the water level flow relationship curve of small flow and large flow was made, respectively, and the water level was interpolated according to the flow value under different guarantee rates in Caizuizi station, as shown in Figure 9. The corresponding water levels of different guaranteed flow rates in Baoqing station and Caizui station were interpolated according to the data of daily water level flow in 2013, as shown in Tables 1, 2.

Figure 8

Figure 8. The relationship between water level and flow in Baoqing station.

Figure 9

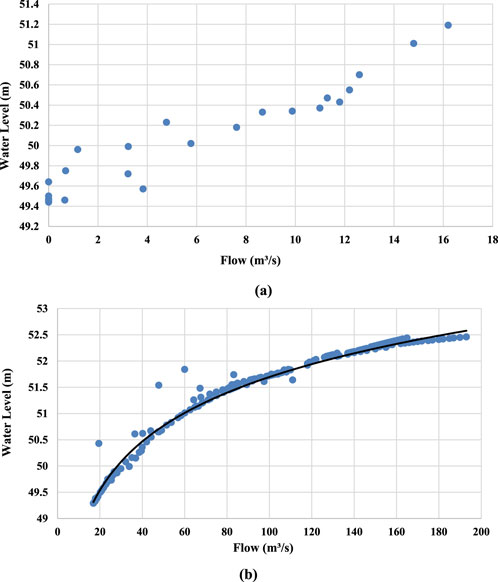
Figure 9. The relationship between water level and flow in Caizuizi station under flow<17 m³/s and flow≥17 m³/s conditions.

Table 1

Table 1. The corresponding water level of different guarantee flow rates in Baoqing station.

Table 2

Table 2. The corresponding water level of different guarantee flow rates in Caizuizi station.

3.2.4 Model roughness

The bed roughness reflects the riverbed resistance and directly affects the flow speed and flow rate. In the course of flood propagation, roughness affects not only the propagation speed but also the water level. However, bed roughness is determined by many factors, such as the shape of the section, roughness of the bed surface, vegetation coverage, degree of river bend, and water level. Bed roughness is an important sensitive parameter of hydraulic calculation (Xu, 2010; Jia and Zu, 2014). In the hydraulic calculation of a natural river channel, the selection of bed roughness affects the calculation accuracy of the hydrodynamic model. The Manning roughness coefficient n is considered in the parameter calibration of the hydrodynamic model. n is an important coefficient to measure the influence of riverbed wall roughness on water flow and carry out corresponding hydrological analysis. Its value is the key to a one-dimensional numerical simulation of the river channel. The accuracy of n directly affects the calculation accuracy of the hydrodynamic model. In this article, the value of Manning’s coefficient n is determined by a trial algorithm.

4 Results and discussion

4.1 Determination of Manning’s coefficient

The parameter calibration of MIKE 11 is the calibration of Manning roughness (n), which is used to improve the rationality of the model. The essence of parameter calibration is that a roughness value is assumed and substituted into the MIKE 11 model for calculation, and then the water level calculation result of the upper station is obtained. The calculated water level of the model is compared with the measured water level of the upper station. If the difference between the calculated value and the measured value meets the allowable range of error, the roughness value can be used as the channel parameter under this flow. If the difference value is greater than the error range, the roughness value is adjusted and substituted into the model again for calculation. The above process is repeated and repeatedly debugged until the difference between the calculated water level and the measured water level is less than 2 cm; then, the roughness calibration is completed.

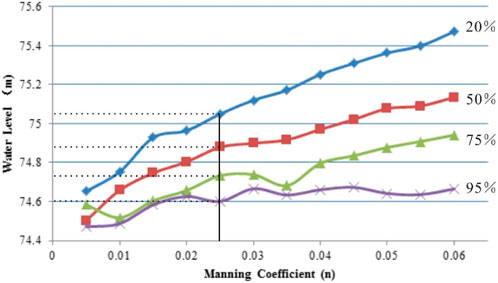
In this paper, we used the existing measured water level and flow data, the flow of Baoqing station as the upper boundary, and the water level of Caizuizi station as the downstream boundary. The boundary conditions are input into the Mike 11 model, which can calculate the water level of the upstream Baoqing station according to the water level boundary of the downstream Caizui station under different guarantee rates (20%, 50%, 75%, and 95%). The water level of Baoqing station corresponding to different Manning coefficients is shown in Figure 10. By comparing the calculated error with the measured water level of the Baoqing station under different guarantee rates, the Manning coefficient n was determined to be 0.025. Combined with the current situation of the river, the Manning coefficient is reasonable. Using this Manning coefficient, the errors between the calculated water level and the measured water level in Baoqing station under different guarantee rates are shown in Table 3.

Figure 10

Figure 10. The water level of Baoqing station at different Manning coefficients n.

Table 3

Table 3. The calculated water level and the measured water level of Baoqing station under different guarantee rates when the Manning coefficient is 0.025.

4.2 Rationality analysis

Because ASTER GDEM elevation data have a vertical accuracy of 20 m and a horizontal accuracy of 30 m, the river section generated based on this elevation data is uncertain, which will affect the accuracy of the calculation results of the water surface profile. In order to ensure the rationality of the model and the reliability of the operation results, three indexes are used to analyze and test the rationality of the simulation results. The indexes of the test are the non-scouring velocity, the shear stress of the riverbed, and the water surface slope.

4.2.1 Non-scouring velocity

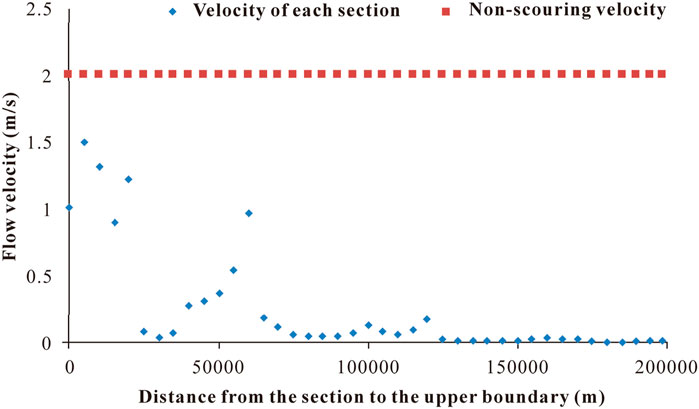
According to the current situation of the riverbed, which is lined with pebbles, the non-scouring velocity should be less than 2.0 m/s. Therefore, it is necessary to check whether the velocity of each section of the water surface line exceeds the non-scouring velocity. If there is a section that exceeds the non-scouring velocity, it is necessary to correct the section. Under the condition that the guarantee rate is 20%, the velocity of each section is shown in Figure 11. Compared with the non-scouring velocity, it can be seen that the calculated flow velocity does not exceed the non-scouring velocity, indicating that the calculation results are reasonable.

Figure 11

Figure 11. The velocity of each section under the condition that the guarantee rate is 20%.

4.2.2 Bed shear stress

The shear stress formula of the riverbed is

$\mathrm{\tau }=\mathrm{\rho }\text{gH\hspace{0.17em}}\left({\mathrm{n}}^2{\mathrm{V}}^2\right)/{\mathrm{R}}^{\left(\frac{4}{3}\right)}.$

In this formula, H is the depth of the water (m);n is the Manning roughness;V is the velocity;R is the hydraulic radius;ρg is the specific gravity of water.

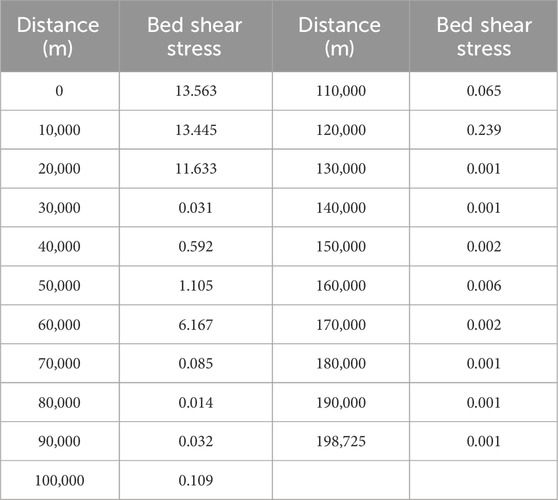
The shear stress value of the riverbed can be obtained according to the formula calculation. Under the condition of a 20% guarantee rate, the shear stress of each section is shown in Table 4. It can be seen there is no extra-large value of bed shear stress in the calculated results, indicating that the calculation results are reasonable.

Table 4

Table 4. Bed shear stress of each section under a 20% guarantee rate.

4.2.3 Water surface slope

The average water surface slope refers to the difference in the water level between the upper and lower reaches of the unit river section horizontal distance along the water flow direction according to Formula 10. The accuracy of the water surface line calculation results is verified by the consistency between the calculated water surface slope and the actual river channel slope.

$\mathrm{J}=\frac{∆\mathrm{H}}{\mathrm{L}}.(10)$

In this formula, ∆H is the difference in water levels between two ends of reach, and L is the length of the reach.

Based on the measured upstream and downstream boundary sections, it can be calculated that the average ratio of Baoqing station to Caizui station is 0.133‰. The average water surface slope calculated by the hydrodynamic model of MIKE 11 under different conditions is between 0.118‰ and 0.126‰. Therefore, the hydrodynamic model of MIKE 11 established in this study is reasonable. The water surface line results calculated by this model are scientific and reasonable and can be used as the hydrological boundary conditions for the numerical simulation of groundwater flow.

4.3 River water surface profile

Numerical groundwater modeling requires boundary conditions, and Mike 11 can be used to calculate the water level at different guarantee rates (20%, 50%, 75%, and 95%). As the boundary conditions of the model simulation, the water level flow of the section laid in the river section is calculated to provide data for a numerical simulation of groundwater. In the following studies, water level and flow data were used to calculate guarantee rates of 20%, 50%, 75%, and 95%, which can provide the boundary conditions of the groundwater numerical model, as shown in Figure 12.

Figure 12

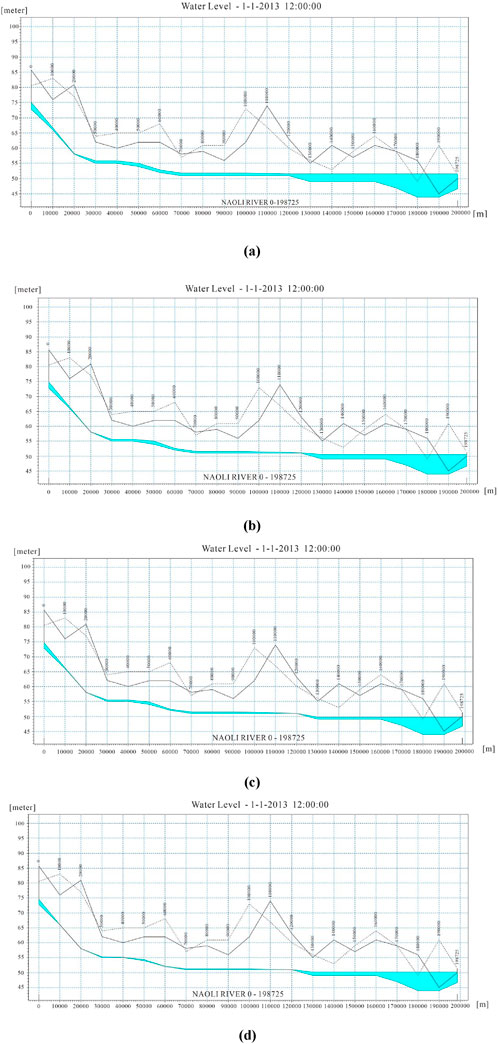
Figure 12. Water surface profile under different guarantee rates of 20% (A), 50% (B), 75% (C), and 95% (D).

5 Conclusion

River channel section data are the basic prerequisite for building most hydrodynamic models, and obtaining such data can consume considerable effort and material resources. In this paper, the feasibility of using ASTER GDEM to extract river section data for the MIKE 11 operation to calculate water surface line at different guarantee rates (20%, 50%, 75%, and 95%) to provide hydrological boundary conditions for surface and groundwater conversion and simulation is examined.

(1) The flow boundary of the Naoli River trunk stream is determined by the measured data from the Baoqing station upstream and the Caizui station downstream. It was found that the water level relation law corresponding to small flow and large flow was different in Caizuizi station. Therefore, water level flow relationship curves of small flow (<17 m³/s) and large flow (≧17 m³/s) were made. The corresponding water levels of different guaranteed flow rates in Baoqing station and Caizui station were interpolated according to the daily water level flow data.

(2) When applying the cross-section data extracted by ASTER GDEM to MIKE 11, the Manning roughness (n) parameter value must be estimated to ensure that the error of the calculated upstream water level and the measured water level meet the allowable error (≤2 cm). Finally, the Manning coefficient was determined to be 0.025.

(3) In view of the uncertainty of the section caused by the accuracy of the ASTER GDEM, in this study, three indexes (non-scouring velocity, the shear stress of the riverbed, and water surface slope) are used to analyze and test the rationality of the simulation results. All three indexes verify the reliability of the model results. Finally, we used the Mike 11 model to calculate the river water level at different guarantee rates (20%, 50%, 75%, and 95%). This can be used as the boundary conditions in the groundwater numerical model. This study can also provide a feasible method for the estimation of water surface lines in some regions with little measured section data of the river.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LT: conceptualization and writing–original draft. YW: software and writing–review and editing. SW: writing–review and editing. GZ: writing–review and editing. CZ: writing–review and editing. XH: writing–review and editing. WH: writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors hereby would like to express deep gratitude to the key special project of Natural Science Foundation of Jilin Province (YDZJ202201ZYTS492).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bates, P. D., and De Roo, A. (2000). A simple raster-based model for flood inundation simulation. J. Hydrology 236 (1), 54–77. doi:10.1016/s0022-1694(00)00278-x

CrossRef Full Text | Google Scholar

Chrysoulakis, N., Abrams, M., Kamarianakis, Y., and Stanislawski, M. (2011). Validation of ASTER GDEM for the area of Greece. Photogrammetric Eng. and Remote Sens. 77 (2), 157–165. doi:10.14358/pers.77.2.157

CrossRef Full Text | Google Scholar

Danish Hydraulic Insititute (2012). MIKE11 user manual. Copenhagen: DHI.

Google Scholar

DHI (2007). A modeling system for rivers and channels reference manual. DHI Water and Environment.

Google Scholar

Hunter, N. M., Bates, P. D., Horritt, M. S., and Wilson, M. D. (2007). Simple spatially-distributed models for predicting flood inundation: a review. Geomorphology 90 (3–4), 208–225. doi:10.1016/j.geomorph.2006.10.021

CrossRef Full Text | Google Scholar

Jia, E. H., and Zu, G. K. (2014). Discussion on determination method of roughness of natural channel. Water Technol. Econ. 20 (7), 72–73. doi:10.3969/j.issn.1006-7175.2014.07.028

CrossRef Full Text | Google Scholar

Kamel, A. H., Ammar, I., and Kamel, H. (2008). Application of A hydrodynamic Mike 11 model for the euphrates river in Iraq. Slovak J. Civ. Eng. 2, 1–7.

Google Scholar

Keskin, F., Aynur Sensoy, A., Arda Sorman, A., and Sorman, U. (2008). Application of Mike11 model for the simulation of snowmelt runoff in Yuvacik dam basin, Turkey.

Google Scholar

Liu, G. H., Luan, Z. Q., and Yan, B. X. (2013). Spatial and temporal distribution characteristics of precipitation in the Naoli river basin of Sanjiang plain in recent 50 years. Resour. Environ. Arid Areas 27 (2). doi:10.13448/j.cnki.jalre.2013.02.028

CrossRef Full Text | Google Scholar

Liu, H. L., Chen, X., Bao, A. M., and Wang, L. (2007). Investigation of groundwater response to overland flow and topography using a coupled MIKE SHE/MIKE 11 modeling system for an arid watershed. J. Hydrology 347 (3–4), 448–459. doi:10.1016/j.jhydrol.2007.09.053

CrossRef Full Text | Google Scholar

MIKE11 (2013). MIKE11.User manual.

Google Scholar

Panda, R. K., Pramanik, N., and Bala, B. (2010). Simulation of river stage using artificial neural network and MIKE 11 hydrodynamic model. Comput. and Geosciences 36 (6), 735–745. doi:10.1016/j.cageo.2009.07.012

CrossRef Full Text | Google Scholar

Patro, S., Chatterjee, C., Mohanty, S., Singh, R., and Raghuwanshi, N. S. (2009). Flood inundation modeling using MIKE FLOOD and remote sensing data. J. Indian Soc. Remote Sens. 37 (1), 107–118. doi:10.1007/s12524-009-0002-1

CrossRef Full Text | Google Scholar

Popescu, I. (2014). Computational hydraulics. IWA: Environmental Management. doi:10.2166/9781780400457

CrossRef Full Text | Google Scholar

Rahman, M. M., Arya, D. S., Goel, N. K., and Dhamy, A. P. (2011). Design flow and stage computations in the teesta river, Bangladesh using frequency analysis and MIKE 11 modeling. J. Hydrologic Eng. 16 (2), 176–186. doi:10.1061/(asce)he.1943-5584.0000299

CrossRef Full Text | Google Scholar

Saint-Venant, A. J. C. (1871). Theorie du movement non permanent des eaux, avec application aux crues des rivieres et al’introduction des marées dans leur lit. Comptes Rendus de l'Académie des Sciences de Paris, vol. 73, 147–154. Available at: https://www.scienceopen.com/document?vid=f5cb5154-4993-41d2-b580-97325873acb0

Google Scholar

Song, X. L., Lu, X. G., Liu, Z. M., and Sun, Y. (2012). Runoff change of Naoli river in Northeast China in 1955–2009 and its influencing factors. Chine. Geographi. Sci. 22 (2), 144–153.

CrossRef Full Text | Google Scholar

Strelkoff, T. (1970). Numerical solution of saint-venant equations. J. Hydraulics Div. 96 (1), 223–252. doi:10.1061/jyceaj.0002262

CrossRef Full Text | Google Scholar

Tayfur, G., Levent Kavvas, M., Govindaraju, S. G., and Storm, D. E. (1993). Venant equations for two-dimensional overland flows over rough infiltrating surfaces. J. Hydraulic Eng. 119 (1), 51–63. doi:10.1061/(ASCE)0733-942911993)119:1(51)

CrossRef Full Text | Google Scholar

Thompson, J. R., Sørenson, H. R., Gavin, H., and Refsgaard, A. (2004). Application of the coupled MIKE SHE/MIKE 11 modelling system to a lowland wet grassland in southeast England. J. Hydrology 293 (1), 151–179. doi:10.1016/s0022-1694(04)00062-9

CrossRef Full Text | Google Scholar

Xu, H. M. (2010). Study on channel roughness in hydraulic engineering. Water Technol. Econ. 16 (11), 1253–1256. doi:10.3969/j.issn.1006-7175.2010.11.023

CrossRef Full Text | Google Scholar