- 1Faculty of Business Administration, Technische Universität Bergakademie Freiberg, Freiberg, Germany
- 2Center for Environmental Management, Resources and Energy, Ruhr Universität Bochum, Bochum, Germany
Effective combat of international environmental problems regularly necessitates a minimum number of participating countries. Some international environmental treaties like the Paris Agreement combating global warming and the Montreal Protocol protecting the ozone layer required that a minimum participation threshold be met before they entered into force. Albeit the immense challenge to protect the global climate, the Paris Agreement additionally demands to address sustainable development and therefore seeks to take advantage of potential co-benefits of climate protection measures. This article is, to the authors' knowledge, the first to investigate in 3 × 3 normal form games the prospects for effective international cooperation on climate protection if effectiveness requires a minimum number of participating countries. The main findings are, first, that sustainable development co-benefits from mitigation might increase the chance that the minimum participation threshold is met and climate policy will be effective in the end; and second, if domestic ancillary benefits from mitigation are rather small, new organizational designs could create additional sustainability benefits that are limited to mitigating countries. For example, a win-win situation – regarding climate and sustainability – could be achieved by international policy designs that create additional co-benefit spillovers via the establishment of a club pursuing sustainable innovations (in line with UN Sustainable Development Goal 9).
1. Introduction
Global environmental problems, above all, climate change, can usually be addressed effectively only if a sufficient number of countries cooperate. Unilateral action will not be enough. However, there is no institution that can force sovereign countries to reduce their greenhouse gas (GHG) emissions. Therefore, international environmental agreements are essential to coordinate countries' efforts. In order to have the desired impact, they often demand a certain minimum participation level before entering into force. The minimum participation requirement is designed as an incentive to deter free-riding (Black et al., 1993; Weikard et al., 2015), thereby increasing the environmental effectiveness of the treaty (Carraro et al., 2009) and potentially curbing carbon leakage (Barrett and Stavins, 2003). In a dynamic setting, minimum participation might also ensure the stability of an environmental treaty (Breton et al., 2010). Both the Paris Agreement (PA), adopted in 2015, and its predecessor, the Kyoto Protocol (KP), were subject to such a minimum participation rule. The PA entered into force 30 days after its ratification by 55 countries that were jointly responsible for at least 55% of global GHG emissions, on 4 November 2016 (UNFCCC, 2022a). In the case of the KP that was already signed in 1997, it took 7 years to achieve ratification by 55 countries that made up 55% of CO2 emissions of Annex I countries, so it could not enter into force until 16 February 2005. After the first commitment period, which lasted from 2008 to 2012, “Kyoto II” was supposed to cover the period from 2013 to 2020. However, its participation threshold – ratification by 144 countries except the European Union – was not met before 2 October 2020, so it effectively entered into force on 31 December 2020, only a few hours before its predetermined end (UNFCCC, 2022c).1 Particularly the failure of “Kyoto II” demonstrates the challenges associated with global coordination in the context of climate change.
The difficulties observed in the ratification processes of international climate agreements and in the implementation of effective climate policy measures, in general, are due to the global public good nature of climate policy, i.e., the worldwide non-excludability from its benefits and non-rivalry in consumption (Buchholz and Sandler, 2021). Mayrhofer and Gupta (2016), p. 27, describe climate policy as “a ‘wicked' problem”: its benefits occur with temporal delay and are dispersed globally, whereas its costs occur immediately to the agent (e.g., country) pursuing this policy (see also Nordhaus, 2015). Co-benefits of climate policy can then foster its acceptance as they are often perceptible relatively quickly, on a local scale, and may have a positive impact on policy areas that are considered more urgent (Mayrhofer and Gupta, 2016). For example, it is frequently argued that climate change mitigation goes hand in hand with sustainable development (SD) (IPCC, 2018; McCollum et al., 2018; Tolliver et al., 2019). The PA stresses the need not only to protect the climate but also to do this in a sustainable way. The SD context is highlighted in Articles 2 and 4.1 and the guidelines for voluntary cooperation in Article 6.
Against this background, this article links the aspects of minimum participation requirements and of SD co-benefits to observe their influence on climate policy. The research also examines international policy design options that create additional co-benefit spillovers via the establishment of a club pursuing sustainable innovations (in line with UN Sustainable Development Goal 9). In doing so, it contributes to the game-theoretic strand of literature. In general, the game structure depends on the underlying assumptions regarding countries' relative power and the ratio of possible outcomes (payoffs). If countries are small and have a negligible impact on the overall public good provision, so their individual benefit from contributing is always smaller than their abatement costs, the situation is best represented by a prisoners' dilemma game (Lange and Vogt, 2003). If, instead, countries are large (or a coalition of countries jointly has a big impact) and cooperation by a single country (or coalition) is already beneficial, the chicken game is more appropriate (Pittel and Rübbelke, 2012). In the chicken game, mutual defection would result in a catastrophic outcome, so there is an incentive for one player to cooperate in order to avoid that. In contrast, if there is a threshold for minimum participation for an environmental problem to be solved, a coordination game, such as a stag-hunt game, is suitable (Sandler and Sargent, 1995). Finally, if environmental benefits are so high that it always pays for an agent to cooperate, the harmony game, or no-conflict game, should be employed (Finus, 2001; p. 31).
The voluntary provision of public goods, such as climate protection, and strategic behavior are often illustrated as a prisoners' dilemma game where defection is the dominant strategy (Helm, 2008; Hattori, 2015; Carrozzo Magli and Manfredi, 2022). Mutual defection can, in the context of the prisoners' dilemma, be overcome if side payments are introduced so that some countries are convinced of cooperating with some financial reward (Barrett, 2001).2 Alternatively, reciprocity preferences can serve as a stimulus to cooperation (Buchholz et al., 2018).
However, Carraro and Siniscalco (1993) suggest that the decision to cooperate or defect in international climate policy resembles a chicken game rather than a prisoners' dilemma game, opening up the possibility of stable partial climate coalitions even without side payments, as observed in the real world. Similarly, Rotillon and Tazdaït (1996) argue that a group of countries will act as leaders and cooperate on international environmental issues. They will then try to enlarge the coalition by offering transfers to non-participating countries. This bargaining process will induce a coordinative game structure and can turn the previous prisoners' dilemma game into a chicken game where, as in Carraro and Siniscalco (1993), partial cooperation results. DeCanio and Fremstad (2013) also argue that bilateral climate policy negotiations are better represented by a coordinative game structure, such as a stag-hunt. In the stag-hunt game, the player who cooperates unilaterally receives the lowest payoff, as in the prisoners' dilemma game, because unilateral action is not sufficient. There are two Nash equilibria in pure strategies, where either both countries cooperate or both countries defect. Mutual defection, however, is the less favorable outcome since the risk of climate change is so severe.3
If three different strategies are to be considered in a normal form game, it can be displayed in a 3 × 3 matrix (see, e.g., Olszowiec, 2018; Fourny and Sulser, 2021). For instance, two prisoners' dilemma games can be combined into a 3 × 3 game where agents decide, e.g., between public good provision, inaction, and depletion of the commons (Arce and Sandler, 2005b). Similar 3 × 3 games have also been applied to counterterrorism (Arce and Sandler, 2005a; Sandler and Arce, 2007; Sandler and Siqueira, 2009). It is also possible to combine two different kinds of games in a 3 × 3 matrix. Endres and Ohl (2002) discuss international environmental policy and introduce three different strategies: defection and two policy instruments that differ with respect to efficiency and propensity to cooperation. They combine a chicken game and a stag-hunt game. Pittel and Rübbelke (2012) analyze climate policy by combining a prisoners' dilemma game and a chicken game into a 3 × 3 normal form game comprising the three strategies “mitigate”, “neutral” and “increase”.
A few studies also account for the co-benefits of climate policy in a game-theoretic framework.4 Pittel and Rübbelke (2008) and Pittel et al. (2022) include private co-benefits of climate change mitigation into a 2 × 2 chicken game and find that the presence of co-benefits increases the likelihood of cooperation. As some co-benefits are inherent to climate policy, they can potentially substitute for side payments and serve the same purpose, i.e., provide an additional private benefit from cooperation. Pittel and Rübbelke (2012) conclude that in their 3 × 3 normal form game, the inclusion of co-benefits can also be beneficial: it raises the scope for mitigation and reduces the chance that countries will increase their emissions.
What is currently missing in the literature is an analysis of a normal form game of international climate policy that (i) considers the three strategies mitigate, neutral and increase; (ii) takes into account the threshold public good nature of climate policy, i.e., recognizes the decision between mitigate and neutral as a stag-hunt game, while at the same time the decision between neutral and increase corresponds to a harmony game, assuming that the impact of even one country increasing its emissions will adversely affect both; (iii) addresses the impact of private co-benefits of mitigation; and (iv) suggests issue linkage within that framework as a further incentive for countries to engage in mitigation. This study attempts to close that gap.
The study will proceed as follows: In Section 2, the concept of SD co-benefits of climate policy is briefly discussed. Section 3 then demonstrates the impact of minimum participation requirements in international climate policy by introducing a 3 × 3 normal form game where two large countries can either mitigate, keep their emissions unchanged, or increase them. Section 4 introduces private co-benefits of mitigation and observes how the outcome changes. Section 5 focuses on the stag-hunt game with the strategies mitigate and neutral and extends the setting to more than two players. In particular, the implications of a technological partnership are discussed where mitigating countries can form a club in order to gain additional spillover co-benefits that are exclusive to the club members. Section 6 provides the conclusion.
2. Sustainable development co-effects of climate policy
The term “co-benefits” in general describes the effects of a single policy measure when there is a win-win situation with respect to several objectives (Mayrhofer and Gupta, 2016). A prioritization of policy areas is not necessarily included, unlike in the concept of “secondary benefits” that was mainly used in the 1990s. The climate protection benefits were then called the “primary benefits”. Meanwhile, the wording changed to co-benefits or, interchangeably, ancillary benefits (IPCC, 2007), giving more weight to these additional benefits of climate policy. The expression “multiple benefits” completely abandons the emphasis on climate protection (Ürge-Vorsatz et al., 2014). The latter expression would be most suitable when one seeks policies that serve simultaneously both the objectives of climate change mitigation and SD.
More neutral are the terms “co-effects” or “co-impacts”, covering both positive and negative interactions, i.e., synergies and trade-offs between different policy areas (Cohen et al., 2021). As co-effects are quite heterogeneous, it is difficult to characterize them consistently. Yet, it is frequently assessed that co-effects differ from the climate-protecting effect with regard to the following characteristics:
• Geographical scope (see, e.g., Rübbelke, 2002; Klemun et al., 2020); with important strategic implications for international climate policy.
• Timing of occurrence; this will affect the choice of discount factors (see the discussion of discount factors, e.g., by Nordhaus, 2007; Stern, 2007).5
• The capture of effects and their modes of actions; in order to conduct a valuation of the effects, which is a prerequisite for cost-benefit assessments, the impacts should be recorded as precisely as possible (Boyd et al., 1995; Ürge-Vorsatz et al., 2014).
Co-effects can have a positive impact on social acceptance of climate policy measures. Emphasizing personal co-benefits of climate change mitigation can be a promising way to increase public support for those policies. Although climate protection measures are sometimes perceived as uncomfortable, like policies aimed at reducing car traffic, people are more likely to be supportive if co-benefits with respect to improved air quality, health, or road safety are stressed (Walker et al., 2018). It has been demonstrated that even climate change deniers can be convinced of climate policies if communication is focused on the non-climate benefits of the same policies (Bain et al., 2012). Particularly, co-benefits in the fields of development and benevolence can motivate action in many countries (Parnphumeesup and Kerr, 2015; Bain et al., 2016), which can open up a chance to address climate and SD issues simultaneously (Cohen et al., 2021).
There are now numerous research studies highlighting the synergies between pursuing the goals of the PA and SD (McCollum et al., 2018; Tolliver et al., 2019). An extensive analysis of synergies and trade-offs between climate change mitigation and the Sustainable Development Goals (SDGs) is provided by the IPCC (2018). In particular, this Special Report highlights that achieving the SDGs is less likely in the case of advancing climate change (Allen et al., 2018). An ambitious 1.5°C target would, in contrast, facilitate the achievement of some SDGs, such as zero hunger, good health and wellbeing, clean water and sanitation, sustainable cities and communities, and life on land (Roy et al., 2018). Olsen et al. (2019) suggest that climate policies should take into account both climate and sustainability targets and use the SDG global indicator framework to evaluate SD aspects of mitigation activities. This is particularly important when it comes to Articles 6.4 through 6.7 of the PA that establish mechanisms for market-based cooperation, contributing to the mitigation of greenhouse gas emissions and supporting SD at the same time. The final rules for Article 6 mechanisms have only been agreed upon at COP 26 in 2021.6 The Article 6.4 mechanism shares similarities with the Clean Development Mechanism (CDM) that was established under the KP and also jointly pursued the twin goals of stimulating emission reductions and SD. The Article 6.4 mechanism has been designed as a baseline-and-credit system and allows offsets from the CDM since 2013 to be transferred to the new mechanism. The important issue of avoiding double counting is delegated to the host countries of projects that are responsible for deciding where emission reductions are to be credited. As the CDM, the Article 6.4 mechanism also requires a share of proceeds to be spent on the Adaptation Fund and for administration (Ahonen et al., 2022; UNFCCC, 2022b).
3. A game-theoretic approach to international climate policy
The approach in this study is similar to the suggestions of Arce and Sandler (2005b) and Pittel and Rübbelke (2012) to combine a public good provision game with a commons game. Whereas the decision to mitigate or remain neutral is concerned with the provision of the global public good “climate policy”, the decision to remain neutral or increase emissions refers to the depletion of the atmosphere as a global common-pool resource. Two countries are considered7 that have three possible strategies with respect to their GHG emissions: mitigate, neutral, and increase. Mitigate means that countries contribute actively to the global public good “climate policy” and reduce emissions; neutral implies that they emit an unchanged amount of GHGs; and increase means raising emissions beyond the present level. Therefore, the game will be displayed as a 3 × 3 normal form game. It is assumed that climate policy will only be successful if both countries choose to mitigate their emissions. A unilateral mitigation action is not sufficient to bring about benefits. Hence, the choice among the strategies mitigate and neutral is represented as a stag-hunt game. The choice between neutral and increase is characterized as a harmony game because it is assumed that players' increases in emissions will result in large damages. Therefore, the 3 × 3 matrix displayed in Figure 1 results where 2B > C > 0, X > c > b > 0, and γ > c are assumed.
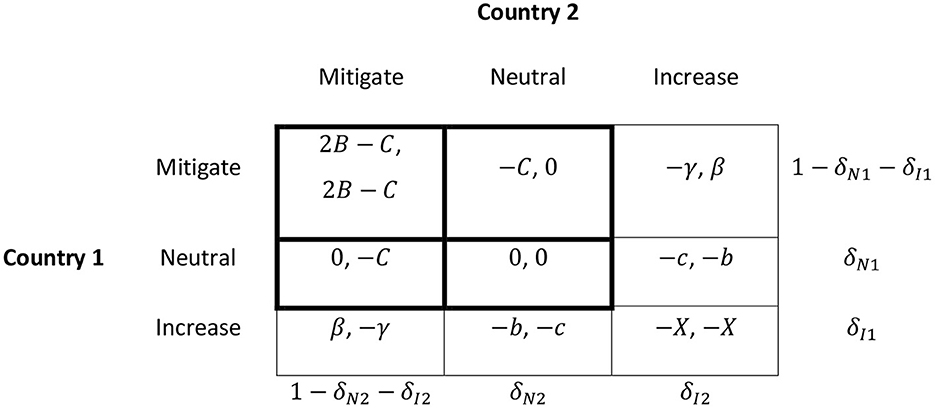
Figure 1. International climate policy in a 3 × 3 normal form game, combining a stag-hunt and a harmony game.
The bold-framed 2 × 2 matrix in the upper left corner depicts a stag-hunt game that has two symmetric Nash equilibria in pure strategies – (mitigate, mitigate) and (neutral, neutral) – and a Nash equilibrium in mixed strategies. The 2 × 2 matrix in the bottom right corner illustrates a harmony game that has (neutral, neutral) as the only Nash equilibrium.
3.1. Case 1: Detrimental impact of increased emissions (β ≤ 0)
Two cases concerning β must be distinguished: At first, β ≤ 0 can be assumed, i.e., the consequences to a country that increases its emissions are never beneficial, so the strategy increase will not be chosen. The increase strategy can then be eliminated since, due to the parameter constellation, the mitigate and neutral strategies dominate the increase strategy. Therefore, the original 3 × 3 matrix can be reduced to the bold-framed 2 × 2 stag-hunt game.
Nash equilibria in pure strategies for the stag-hunt game are (mitigate, mitigate) and (neutral, neutral), as aforementioned. However, the second Nash equilibrium is Pareto-dominated by the first one where both agents have strictly positive payoffs.8
Additional to the two Nash equilibria in pure strategies, there is a mixed-strategy equilibrium. Mixed strategies can be applied when there is uncertainty about the opponent's behavior. A player determines their strategic choice by comparing the expected payoffs (which can also be interpreted as expected utilities) of either strategy. Country 1 will be indifferent between mitigate and neutral if the expected payoffs of both strategies are equal. As the strategy increase has already been eliminated, set δI2 = 0 to obtain:
The left-hand side of this equation is country 1's expected payoff of playing mitigate, given that country 2 will play mitigate with probability 1−δN2 and neutral with probability δN2 if δI2 = 0. The right-hand side illustrates that country 1 will obtain a payoff of zero if it chooses to play neutral, no matter if country 2 plays mitigate or neutral (see also Figure 1).
Consequently,
i.e., country 1 will be indifferent between playing neutral or mitigate if it expects country 2 to play neutral with a probability of and mitigate with a probability of . If it expects , country 1 will play neutral, and in the case (or, equivalently, ), it will choose mitigate. As both countries are symmetric, the same reasoning applies to country 2. Therefore, climate policy is more likely to be successful if and are small and and are rather large. This in turn holds if costs of climate policy C are low and associated benefits B are large, which is a quite intuitive result. Regardless, the good news is that no country will increase its emissions in this case, which can occur if β > 0, as will be argued in the following.
3.2. Case 2: Possible benefit from unilaterally increased emissions (β > 0)
In this case, increase can no longer be excluded, but all three possible strategies have to be considered. Now two sub-cases have to be distinguished:
• Case 2A: β > 2B −C.
• If the payoff from unilaterally increasing emissions while the other country mitigates emissions exceeds the payoff a country can obtain from mutual mitigation, (mitigate, mitigate) can no longer be an equilibrium and (neutral, neutral) will be the only Nash equilibrium in pure strategies.
• Case 2B: β < 2B −C.
• If the opposite applies, two Nash equilibria in pure strategies will result as in case 1 earlier: (mitigate, mitigate) and (neutral, neutral).
Mixed strategies again result from equating the expected payoffs of the available strategies. For country 1 those expected payoffs are as follows:
(1 − δN2 − δI2)(2B − C) − δN2C − δI2γ for choosing mitigate,
− δI2c for choosing neutral,
(1 − δN2 − δI2)β − δN2b − δI2X for choosing increase.
Solving for the probabilities yields
As earlier, those values indicate the probabilities of country 2 playing either strategy that make country 1 indifferent between its three strategy choices. If the expected probabilities deviate from , and/or , however, the outcome is not always as clear as in case 1.
Consider first the case that , i.e., country 1 expects country 2 to play increase with a probability greater than . The expected payoff of the neutral strategy will then decrease by less than the expected payoffs of the other two strategies because both γ > c and X > c by assumption. However, if , either or must hold at the same time as the three probabilities still have to sum up to 1.9 If , the expected payoffs of the mitigate and increase strategies will rise, but the payoff of the neutral strategy is left unchanged, so the overall impact is ambiguous. If, on the contrary, 1 − δN2 − δI2 falls short of , the expected payoffs of the mitigate and increase strategies both decrease even more whereas the expected payoff of remaining neutral is unaffected. In this latter case, country 1 will always choose the neutral strategy.
Next, the case is investigated, i.e., country 1 expects country 2 to play neutral with a probability exceeding . This will reduce the expected payoffs of the mitigate and increase strategies but leave the expected payoff of the neutral strategy unchanged. If at the same time, the expected payoffs of all three strategies increase, but the rise of the expected payoff for the mitigate and increase strategies is numerically greater than that of the neutral strategy. Yet, the relationship between those changes is ambiguous and a general conclusion with respect to the overall impact is not possible. If instead is accompanied by , the neutral strategy will be chosen as the expected payoffs of the other two strategies are affected negatively.
Finally, the case remains to be discussed, which implies that country 1 expects country 2 to play mitigate with a probability greater than . Then, the expected payoffs of the mitigate and increase strategies both rise, but the relationship between them is unclear. The expected payoff of the neutral strategy does not change. If comes with , the payoffs of the mitigate and increase strategies will rise even more whereas the payoff of the neutral strategy remains unchanged. Consequently, either the mitigate or increase strategy will be chosen. The same result holds if instead because the expected payoffs of the mitigate and increase strategies rise by more than that of the neutral strategy. In general, it is more likely that country 1 will play mitigate instead of increase if 2B − C > β, i.e., in case 2B, where the net benefit from mutual mitigation exceeds the benefit from unilaterally increasing emissions when the other country mitigates.
3.3. Comparison of cases 1 and 2
First, it is notable that in case 1 (detrimental impact of increased emissions), the increase strategy was eliminated, so the worst outcomes of the game where both countries lose could not occur. If in case 2 (possible benefit from unilaterally increased emissions), the benefit from unilaterally increasing emissions when the other country mitigates exceeds the net benefit from mutual mitigation (sub-case 2A), the pure-strategy equilibrium implies both countries playing neutral. If the opposite holds (sub-case 2B), the same two pure-strategy Nash equilibria as in case 1 can arise, i.e., either both countries mitigate or both remain neutral.
Regarding mixed strategies, if the expected probability of country 2 playing increase exceeds , country 1 will play neutral if it expects the probability at the same time. That way, country 1 can avoid mitigation costs that would exceed its benefits if it pursued a unilateral climate policy, and it can still prevent the catastrophic outcome that would result if both countries increased their emissions. If, however, it expects along with , no general statement is possible.
In case 1, it turned out that country 1 will always play neutral if . In case 2, this will only apply to a certain parameter constellation. In general, the outcome can be better, worse, or unchanged compared to case 1, depending on the accompanying adjustments of δI2 or 1 − δN2 − δI2.
If the expected probability of the mitigate strategy is , country 1 will definitely play mitigate in case 1, but in case 2, it is only certain that it will not choose neutral. In general, allowing for benefits from unilaterally increased emissions (case 2) makes the outcome more uncertain. Successful climate policy will be more likely if the payoff of mutual mitigation exceeds the payoff of increasing emissions while the opponent mitigates, i.e., if 2B − C > β as in case 2B.
4. Inclusion of ancillary benefits
In the previous section, climate policy has been treated as a pure public good. However, several studies have shown that it also yields considerable co-benefits or ancillary benefits that accrue locally in the regions reducing their emissions (for an overview see, e.g., Rübbelke, 2003; Karlsson et al., 2020). These ancillary benefits include, but are not limited to, a reduction of local air pollutants and associated health issues, improved soil and water quality, higher energy security, or conflict and disaster resilience (see also Deng et al., 2017). Climate policy is therefore referred to as an impure public good that simultaneously generates both global public benefits and local private benefits.10
For the normal form game it follows that, if co-benefits are accounted for, the payoff to a country increases by the amount of the ancillary benefit A > 0 if and only if it undertakes mitigation measures itself.11 The modified payoffs are displayed in Figure 2. As in Section 3 without co-benefits, it is still assumed that 2B > C > 0, X > c > b > 0, and γ > c.
The expected payoff of the mitigate strategy then is
Since the probabilities must still add up to one, the expected payoff of the mitigate strategy can alternatively be written as
The expected payoffs of the neutral and increase strategies remain unchanged.
4.1. Case 3: Detrimental impact of increased emissions (β ≤ 0) and co-benefits from mitigation
As aforementioned in case 1, if β ≤ 0 holds, i.e., increasing emissions is a harmful strategy for the polluting country itself, increase will be dominated by the neutral and mitigate strategies and can again be eliminated. In general, the impact of ancillary benefits depends on their magnitude. As the interest of this article lies in the implications of a minimum participation threshold, the focus is on the case that ancillary benefits are smaller than abatement costs, i.e., A < C, in order to retain the stag-hunt game structure in the bold-framed part of Figure 2.12 The pure-strategy Nash equilibria will then be mutual mitigation and mutual neutrality.
Due to the inclusion of ancillary benefits, mixed strategies now result from
and the probabilities that make country 1 indifferent between playing neutral or mitigate are
Comparing the results to those without co-benefits in case 1, observe that is now larger and smaller than without co-benefits. Since the neutral strategy is chosen by country 1 if it expects , this is now less likely. Instead, as the mitigate strategy is chosen whenever , it is more likely that country 1 will play mitigate.
4.2. Case 4: Possible benefit from unilaterally increased emissions (β > 0) and co-benefits from mitigation
If β > 0, the increase strategy can no longer be eliminated. Again, a distinction of sub-cases is necessary. As in case 3, A<C is still assumed.
• Case 4A: β > A+2B − C and A > γ − c.
In this case, there are three Nash equilibria in pure strategies: (neutral, neutral), (mitigate, increase), and (increase, mitigate). The latter two equilibria have not been possible without ancillary benefits, i.e., for A = 0, because γ > c is assumed throughout.
• Case 4B: β > A+2B − C and A < γ − c.
Here the only pure-strategy Nash equilibrium will be (neutral, neutral).
• Case 4C: β < A+2B − C.
In this parameter constellation, the resulting Nash equilibria in pure strategies are (mitigate, mitigate) and (neutral, neutral).
Following the same procedure as earlier, i.e., equating the expected payoffs of the three strategies, the mixed-strategy equilibria are as follows:
Comparing these mixed strategies to those in case 2 earlier, where the framework with possible benefits from unilaterally increased emissions (β > 0) was identical, the inclusion of ancillary benefits will raise the equilibrium probability of the increase strategy whereas the equilibrium probability of the neutral strategy decreases. The increase of will reduce the expected payoffs of all three strategies, but the expected payoff of the neutral strategy decreases the least, making neutral a more attractive strategy than in the previous case without co-benefits. However, the decrease of implies that the expected payoffs of the mitigate and increase strategies both rise whereas that of the neutral strategy is unaffected, which in turn means that mitigate and increase become more worthwhile than in the absence of co-benefits. A general statement is therefore not possible with respect to the impact of and .
The impact on the equilibrium probability of mitigation, , depends on the specific parameter values: if X > b+c, it will increase, but if X < b+c, it will decrease. Therefore, if the damage from mutually increased GHG emissions is relatively large, represented by a large value of X, it is more likely that rises. Then the expected payoffs of the mitigate and increase strategies rise and that of the neutral strategy is unaffected again. If ancillary benefits A are sufficiently small, as in cases 4A and 4B (i.e., β > A+2B − C), it can happen that the rise of the expected payoff of the increase strategy dominates the rise of the expected payoff of the mitigate strategy. This is, of course, less likely in the presence of strictly positive co-benefits A > 0 than without co-benefits. If, on the contrary, the damage of mutually increased emissions is less severe and decreases, the reverse will apply. In general, due to the introduction of co-benefits A > 0, the payoff of the mitigate strategy unambiguously increases whereas the payoffs of the neutral and increase strategies are unaffected. This creates an additional incentive for a country to participate in climate policy.
The empirical literature largely confirms this finding. In their review article, Karlsson et al. (2020) state that policymakers often overlook the ancillary benefits of climate change mitigation, which leads to insufficiently low mitigation efforts. Therefore, if ancillary benefits are included in the analysis, mitigation becomes more likely. On the level of individual citizens, Longo et al. (2012) conclude, for instance, that accounting for co-benefits increases the willingness to pay for climate policy by more than 50%. In this context, see also Bain et al. (2012) and Walker et al. (2018) on the positive impact of ancillary benefits on the social acceptance of climate policy measures.
5. An extension to more than two players
The stag-hunt game for the choice among the mitigate and neutral strategies is now extended to more than two players in order to analyze partial cooperation options. Sandler and Sargent (1995) state that, as the number of agents required for a minimal-sized coalition increases, it becomes more unlikely that an agreement can be reached if individual countries' probabilities are independent.13
The analysis starts with three players in Section 5.1 and then demonstrates how the setting can be generalized to an arbitrary number of players in Section 5.2. In Section 5.3, the three-player case is discussed when technology spillover co-benefits can arise from the cooperation of at least two countries.
5.1. The stag-hunt game with three players
Suppose that three large countries, or groups of countries, interact with respect to climate policy and their available strategies are mitigate and neutral. The minimum participation requirement still holds, but in contrast to the two-player case where only mutual mitigation could bring about the desired effect, in the three-player case, a partial coalition of two countries may be sufficient. As before, mitigation causes a private cost of C for the contributing country. Benefits are zero if fewer than two countries engage in mitigation. As soon as two or more countries mitigate, the benefits are nB, where n denotes the number of mitigating countries, and those benefits are globally public. Moreover, 2B > C > B > 0 holds. The game can then be depicted by two 2 × 2 matrices, as shown in Figure 3.14 The players are countries 1, 2, and 3, and their strategies are abbreviated by M for mitigate and N for neutral.
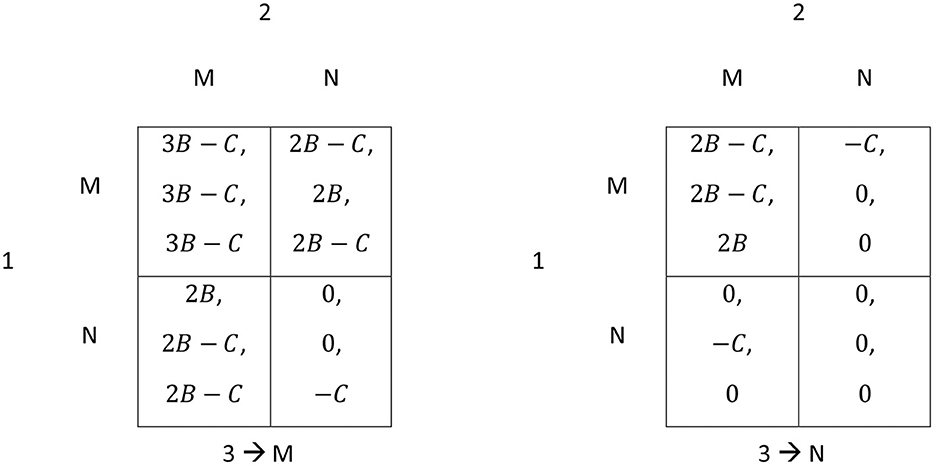
Figure 3. International climate policy as a three-country game. The matrix on the left-hand side shows the payoffs if country 3 always mitigates. The matrix on the right-hand side shows the payoffs if country 3 always remains neutral. Payoffs in each cell are arranged in the sequence for countries 1, 2, and 3.
There are now four Nash equilibria in pure strategies where either exactly two countries mitigate (1 and 2, or 2 and 3, or 1 and 3) or no one mitigates. As can be seen on the left-hand side of Figure 3, it is not worthwhile for a third country to reduce its emissions, provided that the other two countries already mitigate, because the private cost C would exceed its additional benefit B. From the perspective of the two countries that already engage in climate policy, however, the participation of the third agent would be beneficial, but they will nevertheless remain in the two-country coalition since they are still better off with partial cooperation than in the absence of climate policy (i.e., mitigation by fewer than two countries).
5.2. The stag-hunt game with more than three players
In the case of many influential blocks of countries, international climate policy can be visualized as a stag-hunt game with more than three players. Peinhardt and Sandler (2015); p. 93, suggest an illustration of a stag-hunt game with six players, a generalized version of which is displayed in Figure 4. It accounts for an arbitrary number j of players, and payoffs are adjusted to the previous assumptions in this article: mitigation causes a private cost of C; globally public benefits are nB, where n denotes the number of mitigating countries, if the minimum threshold of three contributors is met15 and zero otherwise, and 2B > C > B > 0. The payoffs indicated in each cell are for country i. Since all countries are homogeneous in this depiction, they are interchangeable, and the analysis applies to all of them equally.
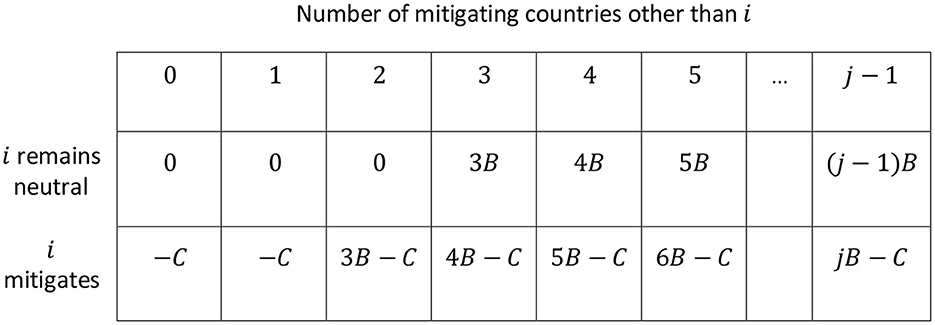
Figure 4. International climate policy as a stag-hunt game with an arbitrary number of j homogeneous countries.
As in the three-country case in Section 5.1, the Nash equilibria in Figure 4 are located where either no one mitigates or where exactly three countries mitigate, i.e., the minimum participation requirement is just met. In total there are j!/(j − t)!t!+1 Nash equilibria, where t denotes the threshold number of countries. For the example with six countries and a threshold of three, this yields 21 Nash equilibria. The large number is due to the different possibilities to choose three out of six countries, as the equation shows. In the case of homogeneous countries, therefore, an equilibrium selection problem arises for the decision of which countries will mitigate (if any). This coordination issue can, at least to some extent, be relieved if countries are heterogeneous. Then those with higher net benefits will possibly go forward and mitigate, making the achievement of the minimum participation requirement more likely (Peinhardt and Sandler, 2015, p. 94–95).
5.3. The stag-hunt game with three players and technology spillover co-benefits
Let us return to the case with three (groups of) countries, but now assume that there are two types of co-benefits from mitigation. First, there is again a domestic ancillary benefit A to any mitigating country, as introduced in Section 4. Second, mitigating countries decide to link the issue of climate protection with the formation of a technological partnership among mitigating countries, i.e., they establish a club seeking to enhance technological progress. Innovation benefits S are then only jointly enjoyed by the members of the club, but free-riders in climate protection are excluded. This creation of innovation co-benefits is also pursued by SDG 9, e.g., Target 9.5 includes the requirement to “[e]nhance scientific research, upgrade the technological capabilities of industrial sectors in all countries”.
The adjusted payoff matrix is shown in Figure 5. The interpretation is analogous to Figure 3.
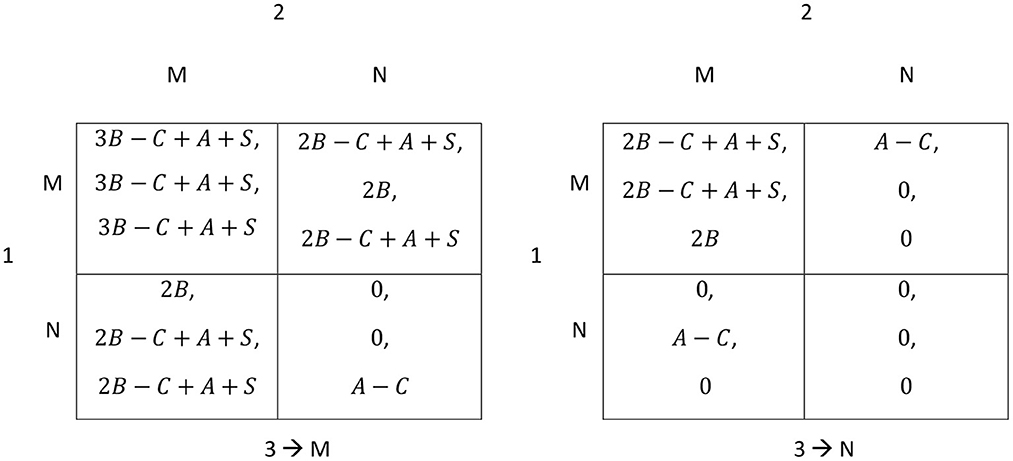
Figure 5. International climate policy as a three-country game, including ancillary benefits A from mitigation and technology spillover co-benefits S if at least two countries join a technological partnership.
It is assumed, first, that ancillary benefits A are rather small, so A < C. Second, the innovation co-benefit S is supposed to be sufficiently large to generate a strictly positive payoff from mitigation if at least two countries form a club: 2B+A+S > C. From Figure 5 it can be observed that linking the issues of innovation and climate protection by forming a club seeking to enhance innovations can make a difference in global climate protection. Let us consider two cases with ancillary benefits.
• Case A: No club creating innovation benefits that spillover only between club members is established and only domestic co-benefits A arise. Then, no country will have the incentive to reduce GHG emissions. The only Nash equilibrium is mutually playing neutral. Mitigation of one or two countries is not worthwhile because it yields a negative payoff and countries can instead get a payoff of zero if they remain neutral. Even if two countries already mitigate, the third one will not join because its additional benefit B+A is smaller than the associated cost C (see the left-hand panel of Figure 5 and the first assumption earlier).
• Case B: A club creating innovation benefits that spillover only between club members is established. If a technological partnership between at least two countries is established, each of them will receive an additional spillover co-benefit S > 0. Due to the second assumption, this technology spillover effect is sufficient to restore the coordination game structure. Even though mutual neutrality remains as a Nash equilibrium, there are now additional Nash equilibria where at least two countries mitigate and form a technological partnership. If S is not too large, so that C − B − A > S > C − 2B − A, any two-country coalition will be a Nash equilibrium. The first part of the inequality states that joining an existing two-country coalition does not pay for the third country, and the second part is a direct implication of the second assumption. If, however, the spillover co-benefit is large and S > C − B − A, the Nash equilibrium is established when all three players mitigate.
This example shows that, even if domestic ancillary benefits from an active climate policy (denoted by A) are too small to induce mitigation by countries, new organizational designs might help to overcome lacking mitigation incentives by creating international spillovers that are limited to mitigating countries.
6. Conclusion
Climate change mitigation will only be successful if a sufficient number of countries cooperate. SD co-benefits from mitigation might increase the chance that the minimum participation threshold is surpassed and climate policy will be effective in the end.
If domestic ancillary benefits from mitigation are rather small, new organizational designs could create additional sustainability benefits that are limited to mitigating countries. The idea of issue linkage has been applied in this study (see also Carraro and Siniscalco, 1997; Paroussos et al., 2019; Currarini and Marchiori, 2022), e.g., the issues of climate protection and technological development could be linked in the framework of the analysis in normal form games. As a policy implication, it follows that domestic co-benefits from mitigation should, in general, be taken into account when deciding about climate policies. Moreover, ancillary benefits can be intentionally created by forming a club of mitigating countries that jointly engage in technological innovation, which in turn can raise the attractiveness of mitigation efforts and thereby generate global benefits as well.
In spite of the significant and diverse co-effects that climate policy might bring about (see, e.g., Nemet et al., 2010; Rive and Rübbelke, 2010), the strategy of killing two birds with one stone is also criticized as creating coordination issues and possibly being inefficient (Mann, 2005). Policymakers should therefore be cautious not to overload a policy instrument with too many different objectives. Rather, it would be advisable to address independent objectives by specific individual instruments, as suggested already by the Tinbergen Rule (Tinbergen, 1952). Otherwise, particularly in the context of climate finance, a trade-off between distributive and allocative goals can occur if recipient countries prefer policies that contribute mainly to their private SD co-benefits, but little to climate protection (Buchholz and Rübbelke, 2021).16 In this article, the risk that the creation of ancillary benefits could be at the expense of global benefits has been disregarded. In other words, additional co-benefits do not raise marginal costs of global climate protection in the approach of this article, but they simply arise additionally. To put the results into perspective, due to the heterogeneity of climate policies and the induced multiple effects, the disregard of possible trade-offs between attaining climate and (non-climate) sustainability goals might distort the results obtained from the analysis. As a future research direction, more empirical analyses on policies' synergies and trade-offs concerning different goals could help to better adapt the respective game theoretic modeling to reality.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
Both authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
Open Access Funding by the Publication Fund of the TU Bergakademie Freiberg.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^Already the Montreal Protocol on Substances that Deplete the Ozone Layer from 1987 that is considered as one of the most successful environmental treaties (UNEP, 2022) came into force only after ratification by eleven states representing at least two thirds of estimated emitted substances in 1986. In contrast to the later climate agreements, its threshold was quickly passed, and it entered into force on 1 January 1989. The main reason for its success was the very favorable benefit-cost ratio that was much higher for the protection of the ozone layer than for climate change mitigation (Barrett, 2007). For a detailed discussion, see also Barrett (2012) and Sandler (2017).
2. ^For a discussion of side payments and preplay negotiations in general, see, e.g., Kalai (1981) and Goranko and Turrini (2016). A rather pessimistic view on their prospects of success in voluntary public good provision games is expressed by Jackson and Wilkie (2005).
3. ^Recently, Kendall (2022) pointed out the relevance of the behavioral component in 2 × 2 stag-hunt games and thereby explains why experiments find systematic variations in the outcomes of stag-hunt games that established theory would not predict.
4. ^Among the exceptions is Kemfert (2004) using climate control coalition games to investigate technological co-benefits. Rübbelke (2006) models ancillary benefits of climate policy in a matching game. Finus and Rübbelke (2013) examine the implications of ancillary benefits in a setting of non-cooperative coalition formation. Hannam et al. (2017) employ an evolutionary-game-theoretic model to analyze regimes that yield domestic incentives to contribute to public goods provision. Takashima (2017, 2020) investigates the effects of ancillary benefits on IEAs in a repeated game framework.
5. ^In a dynamic impure public good framework, Pittel and Rübbelke (2017) model the local co-effects of a GHG emitting activity via flow pollutants and the global effects via stock pollutants in order to capture diverging time scales.
6. ^See also Ahonen et al. (2022) for a discussion of these rules.
7. ^In a first step, in Sections 3 and 4, the game will be kept simple by assuming only two players. In doing so, it is argued that players do not have to be interpreted as individual countries. Instead, it has been observed in recent climate negotiations that countries join alliances with similar interests. For an overview, see https://unfccc.int/process-and-meetings/parties-non-party-stakeholders/parties/party-groupings. Section 5 presents an extension of the stag-hunt game to more than two players.
8. ^The equilibrium selection problem can be solved in a sequential game if one player acts as a leader and chooses the mitigation strategy (Peinhardt and Sandler, 2015, p. 29). The other player will then follow the example and mitigate as well. It can easily be demonstrated that in a sequential game mutual mitigation is the subgame perfect equilibrium. The leader country anticipates that the follower will choose the same strategy and is aware that its payoff of mutual mitigation exceeds its payoff of mutual neutrality.
9. ^It is also possible that all three probabilities change at the same time, but in this study attention is restricted to the case where only two of them vary to ensure traceability.
10. ^The standard impure public good model has been developed by Cornes and Sandler (1984) (see also Cornes and Sandler, 1996).
11. ^In this article ancillary benefits are assumed to be equal for both players. See Pittel et al. (2022) for an analysis of a 2 × 2 chicken game where ancillary benefits are larger in developing countries than in industrialized countries. They conclude that the inclusion of ancillary benefits will increase the likelihood of cooperation for both countries, particularly for the developing country.
12. ^If ancillary benefits exceeded abatement costs, the bold-framed 2 × 2 matrix would turn into a harmony game where mitigate would result as the dominant strategy for both countries. Mitigation would then be a no-regret policy for the countries, as discussed, e.g., by Hourcade and Chapuis (1995).
13. ^In case probabilities are not independent, cooperation prospects may improve, e.g., when there is leadership of an influential country inducing other countries to also mitigate (Buchholz and Sandler, 2017).
14. ^For simplicity three homogeneous countries are assumed. The exposition would also allow for heterogeneous agents. Then the payoffs would have to be adjusted to illustrate differences in mitigation costs and/or benefits.
15. ^Figure 4 can easily be modified if the threshold is supposed to be greater or smaller than three.
16. ^This concern is supported empirically by the finding that climate action (SDG 13) faces a potential trade-off with the no-poverty goal (SDG 1) (Barbier and Burgess, 2021, p. 93). On the other hand, SDG 13 is expected to have synergies mainly with other environmental goals, above all, sustainable cities and communities (SDG 11) (Pradhan et al., 2017), as well as water (SDG 6), energy (SDG 7), food (SDG 2) and life on land (SDG 15) (IPCC, 2018).
References
Ahonen, H.-M., Kessler, J., Michaelowa, A., Espelage, A., Hoch, S. (2022). Governance of fragmented compliance and voluntary carbon markets under the paris agreement. Polit. Gover. 10, 235–245. doi: 10.17645/pag.v10i1.4759
Allen, M. R., Dube, O. P., Solecki, W., Aragón-Durand, F., Cramer, W., Humphreys, S., et al. (2018). “Framing and Context,” in Global Warming of 1.5°C. An IPCC Special Report on the impacts of global warming of 1.5°C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty, eds. IPCC. Geneva: IPCC. 49–91.
Arce, M. D. G., Sandler, T. (2005a). Counterterrorism: A game-theoretic analysis. J. Conf. Resol. 49, 183–200. doi: 10.1177/0022002704272863
Arce, M. D. G., Sandler, T. (2005b). The dilemma of the prisoners' dilemmas. Kyklos, 58, 3–24. doi: 10.1111/j.0023-5962.2005.00275.x
Bain, P. G., Hornsey, M. J., Bongiorno, R., Jeffries, C. (2012). Promoting pro-environmental action in climate change deniers. Nat. Clim. Change. 2, 600–603. doi: 10.1038/nclimate1532
Bain, P. G., Milfont, T. L., Kashima, Y., Bilewicz, M., Doron, G., Garð*arsdóttir, R. B., et al. (2016). Co-benefits of addressing climate change can motivate action around the world. Nat. Clim. Change. 6, 154–157. doi: 10.1038/nclimate2814
Barbier, E. B., Burgess, J. C. (2021). Economics of the SDGs. Cham: Springer International Publishing. doi: 10.1007/978-3-030-78698-4
Barrett, S. (2001). International cooperation for sale. Eur. Econ. Rev. 45, 1835–1850. doi: 10.1016/S0014-2921(01)00082-4
Barrett, S. (2007). Why Cooperate? The Incentive to Supply Global Public Goods. Oxford: Oxford University Press. doi: 10.1093/acprof:oso/9780199211890.001.0001
Barrett, S. (2012). Environment and Statecraft: The Strategy of Environmental Treaty-Making. Oxford: Oxford University Press.
Barrett, S., Stavins, R. (2003). Increasing participation and compliance in international climate change agreements. Int. Environ. Agree. 3, 349–376. doi: 10.1023/B:INEA.0000005767.67689.28
Black, J., Levi, M. D., Meza, D. de (1993). Creating a good atmosphere: minimum participation for tackling the ‘greenhouse effect'. Economica. 60, 281. doi: 10.2307/2554852
Boyd, R., Krutilla, K., Viscusi, W. K. (1995). Energy taxation as a policy instrument to reduce CO2 emissions: a net benefit analysis. J. Environ. Econ. Manag. 29, 1–24. doi: 10.1006/jeem.1995.1028
Breton, M., Sbragia, L., Zaccour, G. (2010). A dynamic model for international environmental agreements. Environ. Resour. Econ. 45, 25–48. doi: 10.1007/s10640-009-9304-6
Buchholz, W., Peters, W., Ufert, A. (2018). International environmental agreements on climate protection: a binary choice model with heterogeneous agents. J. Econ. Behav. Organiz. 154, 191–205. doi: 10.1016/j.jebo.2018.08.015
Buchholz, W., Rübbelke, D. (2021). Overstraining international climate finance: when conflicts of objectives threaten its success. Int. J. Clim. Change Strat. Manage. 13, 547–563. doi: 10.1108/IJCCSM-06-2021-0071
Buchholz, W., Sandler, T. (2017). Successful leadership in global public good provision: incorporating behavioural approaches. Environ. Resour. Econ. 67, 591–607. doi: 10.1007/s10640-016-9997-2
Buchholz, W., Sandler, T. (2021). Global public goods: a survey. J. Econ. Liter. 59, 488–545. doi: 10.1257/jel.20191546
Carraro, C., Marchiori, C., Oreffice, S. (2009). Endogenous minimum participation in international environmental treaties. Environ. Resour. Econ. 42, 411–425. doi: 10.1007/s10640-009-9264-x
Carraro, C., Siniscalco, D. (1993). Strategies for the International Protection of the Environment. J. Public Econ. 52, 309–328. doi: 10.1016/0047-2727(93)90037-T
Carraro, C., Siniscalco, D. (1997). “RandD cooperation and the stability of international environmental agreements,” in International Environmental Negotiations: Strategic Policy Issues, eds. C. Carraro (Cheltenham, UK, Brookfield, US: Edward Elgar Publishing) 71–96.
Carrozzo Magli, A., Manfredi, P. (2022). Coordination games vs prisoner's dilemma in sustainability games: a critique of recent contributions and a discussion of policy implications. Ecol. Econ. 192, 107268. doi: 10.1016/j.ecolecon.2021.107268
Cohen, B., Cowie, A., Babiker, M., Leip, A., Smith, P. (2021). Co-benefits and trade-offs of climate change mitigation actions and the sustainable development goals. Sustain. Prod. Consumpt. 26, 805–813. doi: 10.1016/j.spc.2020.12.034
Cornes, R., Sandler, T. (1984). Easy riders, joint production, and public goods. Econ. J. 94, 580–598. doi: 10.2307/2232704
Cornes, R., Sandler, T. (1996). The Theory of Externalities, Public Goods and Club Goods (2nd ed.). New York: Cambridge University Press. doi: 10.1017/CBO9781139174312
Currarini, S., Marchiori, C. (2022). Issue linkage. Games Econ. Behav. 135, 16–40. doi: 10.1016/j.geb.2022.05.009
DeCanio, S. J., Fremstad, A. (2013). Game theory and climate diplomacy. Ecol. Econ. 85, 177–187. doi: 10.1016/j.ecolecon.2011.04.016
Deng, H.-M., Liang, Q.-M., Liu, L.-J., Anadon, L. D. (2017). Co-benefits of greenhouse gas mitigation: a review and classification by type, mitigation sector, and geography. Environ. Res. Lett. 12, 123001. doi: 10.1088/1748-9326/aa98d2
Endres, A., Ohl, C. (2002). Introducing “cooperative push”: how inefficient environmental policy (sometimes!) protects the global commons better. Public Choice. 111, 285–302. doi: 10.1023/A:1014916012640
Finus, M. (2001). Game Theory and International Environmental Cooperation. Cheltenham, UK, Northampton, USA: Edward Elgar Publishing. doi: 10.4337/9781843762898
Finus, M., Rübbelke, D. (2013). Public good provision and ancillary benefits: the case of climate agreements. Environ. Resour. Econ. 56, 211–226. doi: 10.1007/s10640-012-9570-6
Fourny, G., Sulser, F. (2021). Data on the existence ratio and social utility of nash equilibria and of the perfectly transparent equilibrium. Data Brief. 34, 106623. doi: 10.1016/j.dib.2020.106623
Goranko, V., Turrini, P. (2016). Two-player preplay negotiation games with conditional offers. Int. Game Theory Rev. 18, 1550017. doi: 10.1142/S0219198915500176
Hannam, P. M., Vasconcelos, V. V., Levin, S. A., Pacheco, J. M. (2017). Incomplete cooperation and co-benefits: deepening climate cooperation with a proliferation of small agreements. Clim. Change. 144, 65–79. doi: 10.1007/s10584-015-1511-2
Hattori, K. (2015). Within-group cooperation and between-group externalities in the provision of public goods. Int. Tax Public Finan. 22, 252–273. doi: 10.1007/s10797-014-9308-1
Helm, D. (2008). Climate-change policy: why has so little been achieved? Oxford Rev. Econ. Policy. 24, 211–238. doi: 10.1093/oxrep/grn014
Hourcade, J.-C., Chapuis, T. (1995). No-regret potentials and technical innovation. Energy Policy. 23, 433–445. doi: 10.1016/0301-4215(95)90168-7
IPCC (2007). Climate Change 2007: Mitigation of Climate Change. Contribution of Working Group III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, UK, New York: Cambridge University Press.
IPCC (2018). Global Warming of 1.5°C. An IPCC Special Report on the impacts of global warming of 1.5°C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty. Geneva.
Jackson, M. O., Wilkie, S. (2005). Endogenous games and mechanisms: side payments among players. Rev. Econ. Stud. 72, 543–566. doi: 10.1111/j.1467-937X.2005.00342.x
Kalai, E. (1981). Preplay negotiations and the prisoner's dilemma. Mathem. Soc. Sci. 1, 375–379. doi: 10.1016/0165-4896(81)90015-9
Karlsson, M., Alfredsson, E., Westling, N. (2020). Climate policy co-benefits: a review. Clim. Policy. 20, 292–316. doi: 10.1080/14693062.2020.1724070
Kemfert, C. (2004). Climate coalitions and international trade: assessment of cooperation incentives by issue linkage. Energy Policy. 32, 455–465. doi: 10.1016/S0301-4215(03)00148-4
Kendall, R. (2022). Decomposing coordination failure in stag hunt games. Exper. Econ. 25, 1109–1145. doi: 10.1007/s10683-022-09745-y
Klemun, M. M., Edwards, M. R., Trancik, J. E. (2020). Research priorities for supporting subnational climate policies. Wiley Interdisc. Rev. 11, e646. doi: 10.1002/wcc.646
Lange, A., Vogt, C. (2003). Cooperation in international environmental negotiations due to a preference for equity. J. Public Econ. 87, 2049–2067. doi: 10.1016/S0047-2727(02)00044-0
Longo, A., Hoyos, D., Markandya, A. (2012). Willingness to pay for ancillary benefits of climate change mitigation. Environ. Resour. Econ. 51, 119–140. doi: 10.1007/s10640-011-9491-9
Mann, S. (2005). Different perspectives on cross-compliance. Environ. Value. 14, 471–482. doi: 10.3197/096327105774462719
Mayrhofer, J., Gupta, J. (2016). The science and politics of co-benefits in climate policy. Environ. Sci. Policy. 57, 22–30. doi: 10.1016/j.envsci.2015.11.005
McCollum, D. L., Zhou, W., Bertram, C., Boer, H.-S., de, Bosetti, V., Busch, S., et al. (2018). Energy investment needs for fulfilling the paris agreement and achieving the sustainable development goals. Nat. Energy, 3, 589–599. doi: 10.1038/s41560-018-0179-z
Nemet, G. F., Holloway, T., Meier, P. (2010). Implications of incorporating air-quality co-benefits into climate change policymaking. Environ. Res. Lett. 5, 14007. doi: 10.1088/1748-9326/5/1/014007
Nordhaus, W. (2007). Critical assumptions in the stern review on climate change. Science. 317, 201–202. doi: 10.1126/science.1137316
Nordhaus, W. (2015). Climate clubs: overcoming free-riding in international climate policy. Am. Econ. Rev. 105, 1339–1370. doi: 10.1257/aer.15000001
Olsen, K. H., Bakhtiari, F., Duggal, V. K., Fenhann, J. V. (2019). Sustainability labelling as a tool for reporting the sustainable development impacts of climate actions relevant to article 6 of the paris agreement. Int. Environ. Agree. 19, 225–251. doi: 10.1007/s10784-018-09428-1
Parnphumeesup, P., Kerr, S. A. (2015). Willingness to pay for gold standard carbon credits. Energy Sourc. Part B 10, 412–417. doi: 10.1080/15567249.2010.551251
Paroussos, L., Mandel, A., Fragkiadakis, K., Fragkos, P., Hinkel, J., Vrontisi, Z. (2019). Climate clubs and the macro-economic benefits of international cooperation on climate policy. Nat. Clim. Change. 9, 542–546. doi: 10.1038/s41558-019-0501-1
Peinhardt, C., Sandler, T. (2015). Transnational Cooperation: An Issue-based Approach. New York: Oxford Univ. Press. doi: 10.1093/acprof:oso/9780199398607.001.0001
Pittel, K., Ringel, M., Rübbelke, D., Vögele, S., Ball, C., Stahlke, T. (2022). “International climate policy and economic perspectives,” in Handbook of Climate Change Mitigation and Adaptation, eds. M. Lackner, B. Sajjadi and W.-Y. Chen (Cham: Springer) 3559–3609. doi: 10.1007/978-3-030-72579-2_4
Pittel, K., Rübbelke, D. (2008). Climate policy and ancillary benefits: a survey and integration into the modelling of international negotiations on climate change. Ecol. Econ. 68, 210–220. doi: 10.1016/j.ecolecon.2008.02.020
Pittel, K., Rübbelke, D. (2012). Transitions in the negotiations on climate change: from prisoner's dilemma to chicken and beyond. Int. Environ. Agree. 12, 23–39. doi: 10.1007/s10784-010-9126-6
Pittel, K., Rübbelke, D. (2017). “Thinking local but acting global? the interplay between local and global internalization of externalities,” in The Theory of Externalities and Public Goods: Essays in Memory of Richard C. Cornes, eds. W. Buchholz and D. Rübbelke (Cham: Springer), 271–297. doi: 10.1007/978-3-319-49442-5_14
Pradhan, P., Costa, L., Rybski, D., Lucht, W., Kropp, J. P. (2017). A systematic study of sustainable development goal (SDG) interactions. Earth's Future. 5, 1169–1179. doi: 10.1002/2017EF000632
Rive, N., Rübbelke, D. (2010). International environmental policy and poverty alleviation. Rev. World Econ. 146, 515–543. doi: 10.1007/s10290-010-0063-9
Rotillon, G., Tazdaït, T. (1996). International bargaining in the presence of global environmental change. Environ. Resour. Econ. 8, 293–314.
Roy, J., Tschakert, P., Waisman, H., Abdul Halim, S., Antwi-Agyei, P., Dasgupta, P., et al. (2018). “Sustainable development, poverty eradication and reducing inequalities,” in Global Warming of 1.5°C. An IPCC Special Report on the impacts of global warming of 1.5°C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty, eds. IPCC (Geneva: IPCC) 445–538.
Rübbelke, D. (2002). International Climate Policy to Combat Global Warming: An Analysis of the Ancillary Benefits of Reducing Carbon Emissions. Cheltenham, UK, Northampton, USA: Edward Elgar Publishing. doi: 10.4337/9781782542742
Rübbelke, D. (2003). An analysis of differing abatement incentives. Resour. Energy Econ. 25, 269–294. doi: 10.1016/S0928-7655(03)00032-0
Rübbelke, D. (2006). Analysis of an international environmental matching agreement. Environ. Econ. Policy Stud. 8, 1–31. doi: 10.1007/BF03353991
Sandler, T. (2017). Environmental cooperation: contrasting international environmental agreements. Oxford Econ. 69, 345–364. doi: 10.1093/oep/gpw062
Sandler, T., Arce, M. D. G. (2007). “Chapter 25 terrorism: a game-theoretic approach,” in Handbooks in economics: Vol. 12. Handbook of Defense Economics: Volume 2, Defense in a Globalized World, eds. T. Sandler and K. Hartley (Amsterdam, New York: Elsevier) 775–813. doi: 10.1016/S1574-0013(06)02025-4
Sandler, T., Sargent, K. (1995). Management of transnational commons: coordination, publicness, and treaty formation. Land Econ. 71, 145. doi: 10.2307/3146497
Sandler, T., Siqueira, K. (2009). Games and terrorism. Simul. Gam. 40, 164–192. doi: 10.1177/1046878108314772
Stern, N. (2007). The Economics of Climate Change: The Stern Review. Oxford: Cambridge University Press. doi: 10.1017/CBO9780511817434
Takashima, N. (2017). International environmental agreements with ancillary benefits: repeated games analysis. Econ. Model. 61, 312–320. doi: 10.1016/j.econmod.2016.10.011
Takashima, N. (2020). “Sustainable International Cooperation with Ancillary Benefits of Climate Policy,” in Ancillary Benefits of Climate Policy: New Theoretical Developments and Empirical Findings, eds. W. Buchholz, A. Markandya, D. Rübbelke and S. Vögele (Cham: Springer International Publishing) 91–108. doi: 10.1007/978-3-030-30978-7_5
Tolliver, C., Keeley, A. R., Managi, S. (2019). Green bonds for the paris agreement and sustainable development goals. Environ. Res. Lett. 14, 64009. doi: 10.1088/1748-9326/ab1118
UNEP (2022). About Montreal Protocol. Available online at: https://www.unep.org/ozonaction/who-we-are/about-montreal-protocol (accessed November 23, 2022).
UNFCCC (2022a). Paris Agreement – Status of Ratification. Available online at: https://unfccc.int/process/the-paris-agreement/status-of-ratification (accessed November 23, 2022).
UNFCCC (2022b). Report of the Conference of the Parties serving as the meeting of the Parties to the Paris Agreement on its third session, held in Glasgow from 31 October to 13 November 2021.
UNFCCC (2022c). What is the Kyoto Protocol? Available online at: https://unfccc.int/kyoto_protocol (accessed November 23, 2022).
Ürge-Vorsatz, D., Herrero, S. T., Dubash, N. K., Lecocq, F. (2014). Measuring the co-benefits of climate change mitigation. Ann. Rev. Environ. Resour. 39, 549–582. doi: 10.1146/annurev-environ-031312-125456
Walker, B. J. A., Kurz, T., Russel, D. (2018). Towards an understanding of when non-climate frames can generate public support for climate change policy. Environ. Behav. 50, 781–806. doi: 10.1177/0013916517713299
Keywords: ancillary benefits, climate policy, minimum participation threshold, mitigation, sustainable development
Citation: Brumme A and Rübbelke D (2023) Minimum participation requirements and the role of co-benefits in international climate policy. Front. Environ. Econ. 1:1106186. doi: 10.3389/frevc.2022.1106186
Received: 23 November 2022; Accepted: 22 December 2022;
Published: 13 January 2023.
Edited by:
Rabindra Nepal, University of Wollongong, AustraliaReviewed by:
Abdulrasheed Zakari, Alma Mater Europaea, SloveniaLiton Chandra Voumik, Noakhali Science and Technology University, Bangladesh
Muhammad Tayyab Ayaz, University of Kotli Azad Jammu and Kashmir, Pakistan
Copyright © 2023 Brumme and Rübbelke. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anja Brumme,  YW5qYS5icnVtbWVAdndsLnR1LWZyZWliZXJnLmRl
YW5qYS5icnVtbWVAdndsLnR1LWZyZWliZXJnLmRl
 Anja Brumme
Anja Brumme Dirk Rübbelke1,2
Dirk Rübbelke1,2