Hydrodynamic-aerodynamic performance of a barge-type floating offshore wind turbine with four moonpools and moorings

Introduction: This study investigates the hydrodynamic and aerodynamic performance of a barge-type floating offshore wind turbine (FOWT) equipped with four moonpools and horizontal springs as mooring lines. The integration of moonpools enhances the platform’s hydrodynamic performance by increasing the moment of inertia, recovery torque, and damping effects, while the horizontal springs mitigate the tilt angle caused by wind-induced thrust moments.

Methods: Numerical simulations are conducted using viscous flow theory, the Finite Volume Method (FVM), and the Volume of Fluid (VOF) method to model the fluid domain under varying wind and wave conditions.

Results: The motion responses and the wind thrust at different wave periods and wind speeds are provided.

Discussion: The results demonstrate that the springs effectively reduce the tilt angle and restrain heave motion across different wind speeds and waves.

1 Introduction

Energy has become a critical factor constraining social and economic development. With an increasing focus on sustainable development, the robust advancement of green energy, particularly wind energy, has become a key component of national development strategies (Shi et al., 2023). Offshore wind farms, compared to their onshore counterparts, benefit from vast areas and higher wind speeds, making them ideal for wind power generation. Additionally, the absence of terrain restrictions allows for extensive installation of wind power infrastructure (Breton and Moe, 2009).

Several types of Floating Offshore Wind Turbines (FOWT) exist, including Spar-type, tension leg platform type, semi-submersible type, and barge-type platforms. Among these, the barge-type platform, exemplified by Ideol, exhibits significant application potential because of its shallow draft, straightforward design, and ease of installation and maintenance (Ikoma et al., 2021).

Various studies have been conducted on barge-type platforms. For instance, Beyer et al. (2015) and Borisade et al. (2016) explored the motion response characteristics of the Ideol-Floatgen FOWT utilizing computational fluid dynamics (CFD) and model testing. Mayilvahanan and Selvam (2011) investigated barge-type foundations with differing aspect ratios and found that the longitudinal pitch response amplitude operator (RAO) is minimized when the aspect ratio is 1. Yang et al. (2022) and Chuang et al. (2021) optimized the principal dimensions of barge-type FOWT, assessing motion response and mooring loads through pool experiments and numerical simulations. Ikoma et al. (2019) demonstrated through numerical simulations that increasing the number of moonpools significantly enhances the hydrodynamic performance of the platform compared to using a single moonpool. Although Ikoma investigated the motion characteristics of the four moonpools floating offshore wind turbine (FOWT) equipped with a vertical axis wind turbine (VAWT), the performance of the four moonpools FOWT with a horizontal axis wind turbine (HAWT) remains uncertain. Additionally, Ikoma’s study did not account for the effects of wind.

When applying multiple moonpools, the interactions between the vibrations of water in different moonpools may affect the resonance characteristics (Lu et al., 2010; Ning et al., 2015). Tan et al. (2021) examined a barge-type platform with four moonpools to analyze the effect of the number of openings in the moonpools on the average second-order drift force that the platform experiences. Additionally, Zhai et al. (2024) and Vijay et al. (2016) combined the barge-type FOWT with aquaculture cages and wave energy devices, thereby enhancing the applicability of floating platforms.

In the study of floating wind turbines, the theoretical framework is primarily based on linear potential flow theory. While this approach simplifies the problem by disregarding the effects of fluid viscosity and nonlinear terms, such factors become critical when analyzing floating structures with a moon pool. Consequently, we utilize viscous flow theory along with the finite volume method (FVM) and volume of fluid (VOF) method to simulate the behavior of a barge-type floating wind turbine (FOWT) equipped with a moonpool under varying wind and wave conditions. Under the effect of the wind, the rotation of the turbine blades generates a thrust moment, which can lead to significant tilt of the FOWT. One important method to reduce the tilt is adding moorings to the platform, in present work we used horizontal springs to replace the moorings, and hydrodynamic and aerodynamics performance of a barge-type wind turbine are investigated systematically.

In Section 2, we introduce the physical models of the wind turbine and the barge-type floating structure. In Section 3, we outline the governing equations employed, including the RANS equations, continuity equation, VOF method, and motion equations. In Section 4, we first present the configuration for simulating the wave environment, followed by a convergence analysis, and subsequently analyze the numerical results of the motion response with respect to the effects of wind and waves.

2 Description of the system

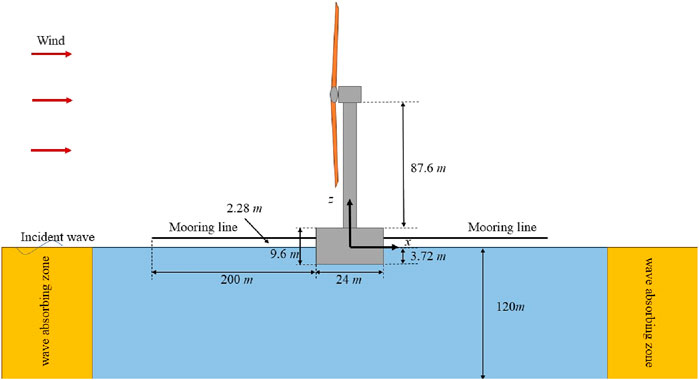
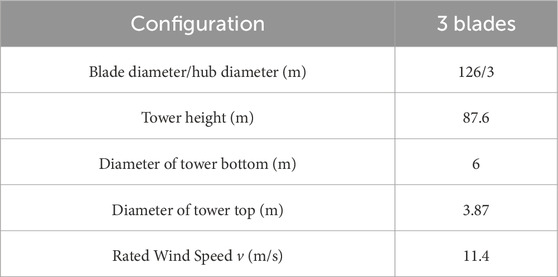
Figure 1 illustrates a barge-type floating wind turbine featuring four moonpools within a marine environment and some of geometric dimensions of the floating structure. Figure 2 provides a side view of the platform. The structure measures 54 m in length, 24 m in width, 9.6 m in overall height, and has a draft of 3.72 m. Within this structure, there are four moonpools, each with dimensions of 18 m in length and 6 m in width. A 5 MW wind turbine, sourced from the National Renewable Energy Laboratory (NREL), is centrally installed within the structure, as depicted in Figure 1, with the turbine’s specifications detailed in Table 1. In Figure 2, the origin of the Cartesian coordinate system is positioned at the still water surface: the x-axis is aligned with the direction of wave and wind propagation, the z-axis is perpendicular to the x-axis and oriented upward, while the y-axis is perpendicular to both the x-axis and z-axis. The total mass of the floating offshore wind turbine (FOWT) including the rotor, tower, and floating structure—is 3,198,960 kg, with the center of mass situated at the coordinates (0, 0, 2.28). Two springs have been implemented to provide mooring force, each measuring 200 m in length and exhibiting a stiffness of $3.71\times {10}^7$ N/m, and are positioned parallel to the x-axis at a height of 2.28 m above the water surface,the initial tension is zero. Three degrees of freedom are accounted for in the motion: surge along the x-axis, heave along the z-axis, and pitch about the y-axis, with the center of rotation aligned with the center of mass. Under the effects of wind, the tower will deviate from the vertical position, forming a tilt angle between the tower and the vertical line.

Figure 1

Figure 1. Visualization of a barge-type floating offshore wind turbine in the ocean.

Figure 2

Figure 2. Side view of wind turbine supported by a four-moonpool barge-type floating foundation.

Table 1

Table 1. Main parameters of the NREL 5 MW wind turbine.

3 Mathematical equations

A numerical model for incompressible fluids is established based on viscous flow theory. The computational domain is discretized using the Finite Volume Method (FVM), while the capturing of the free surface is achieved through the Volume of Fluid (VOF) method. Fluid flow is governed by the Reynolds-Averaged Navier-Stokes (RANS) equations and the continuity equation. RANS are derived from the Navier-Stokes equations by separating the flow variables into mean and fluctuating components and then averaging the resulting equations over time. For an incompressible fluid, the time averaged continuity equation and RANS can be expressed in a tensor form:

$\frac{\mathrm{\partial }\rho {\overline{u}}_i}{\mathrm{\partial }{x}_i}=0(1)$

$\frac{\mathrm{\partial }\rho {\overline{u}}_i}{\mathrm{\partial }t}+u_j\frac{\mathrm{\partial }\rho {\overline{u}}_i}{\mathrm{\partial }{x}_j}=-\frac{\mathrm{\partial }\overline{p}}{\mathrm{\partial }{x}_i}+\rho {\overline{f}}_i+\frac{\mathrm{\partial }}{\mathrm{\partial }{x}_j}\left[\mu \left(\frac{\mathrm{\partial }{\overline{u}}_i}{\mathrm{\partial }{x}_j}+\frac{\mathrm{\partial }{\overline{u}}_j}{\mathrm{\partial }{x}_i}\right)\right]-\frac{\rho \mathrm{\partial }\overline{u_i^{\prime }{u}_j^{\prime }}}{\mathrm{\partial }{x}_j}(2)$

where $\rho$ is the fluid density, $\mu$ is the fluid viscosity, $\overline{p}$ is mean pressure, ${\overline{u}}_i$, ${\overline{u}}_j$ indicates the component of the average velocity, and the subscript specifies the direction (x, y, z), ${\overline{f}}_i$ is defined as the average mass force, which typically refers to gravitational acceleration within a gravitational field. The direct solution of Equations 1, 2 is particularly challenging due to the presence of Reynolds stress terms. To address this issue, the SST $k-\omega$ turbulence model (Menter, 1994) is employed to close the system of equations. The Volume of Fluid (VOF) method is used to approximate the free liquid surface.

The equations of motion including surge, heave and pitch can be written as the following Equation 3

$\left(\begin{array}{ccc}m& m& -m\left(z_m-z_c\right)\\ m& m& -m\left(x_m-x_c\right)\\ -m\left(z_m-z_c\right)& -m\left(x_m-x_c\right)& I\end{array}\right)\left(\begin{array}{c}\frac{d{v}_x}{dt}\\ \frac{d{v}_z}{dt}\\ \frac{d\omega }{dt}\end{array}\right)=\left(\begin{array}{c}{f}_x\\ f_z\\ n\end{array}\right)(3)$

where $v_x$ and $v_z$ are the translational velocities in x and z direction and ω is the pitch velocity with respect to y-axis of the floating body. m and I represent the total mass and rotational inertia, respectively, accounting for the contribution from the floating foundation, tower and rotor. $x_m-x_c$ and $z_m-z_c$ are the horizontal distance and vertical distance respectively between the mass center and rotational center. $f_x$ and $f_z$ and $n$ are the resultant force in the x and z direction and the resultant moment about the y-axis, respectively, including the effects of buoyancy, gravity, wave forces, and the thrust of the wind turbine.

Using a linear spring as the mooring force, the expression for the spring restoring force takes the form of Equation 4

$f_1\left(x\right)=k\left(x-x_0\right),\hspace{1em}{f}_2\left(x\right)=-f_1\left(x\right)(4)$

where $f_1\left(x\right)$ is the resilience at the first endpoint, $f_2\left(x\right)$ is the resilience at the second endpoint, $k$ is the stiffness of spring, $x$ is the distance between the two endpoints of the spring, and $x_0$ is the length of the spring in its relaxed state.

4 Numerical results and discussions

The Star CCM + solver is used to resolve the fluid control and motion equations. The specifications of the computational domain include a length of 900 m (along the x-axis, representing the wave propagation direction), a width of 180 m (along the y-axis), and a total height of 370 m, with 120 m beneath the mean water surface, while the remainder is air. To mitigate the effects of reflective waves from the body, damping zones are implemented on both the left and right sides of the basin, utilizing wave force techniques. Furthermore, a wind field is established at a speed of 11.4 m/s, with its propagation direction aligning with that of the waves, allowing the wind turbine to achieve its rated speed of 12 rpm.

4.1 The set of mesh and time step and comparison

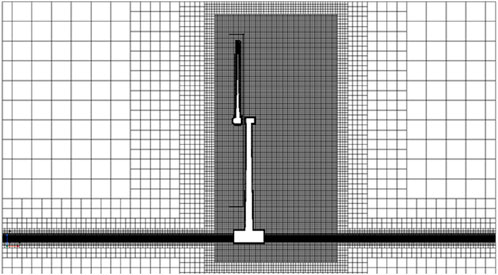
This section addresses the convergence of the grid and time step. The mesh grid for the simulation is shown in Figure 3, the entire simulation area employs a cut-cell grid generator. The cut-cell grid is produced under size constraints using a hexagonal cuboid grid template, which is subsequently refined by removing the excess grid based on the surface of the input object, thereby creating the object grid. The rotational motion of the wind turbine blades is facilitated through sliding grids, while the movement of the FOWT is executed using overlapping grids. The range of the overlapping domain is at $xϵ\left(-30,70\right)$, $yϵ\left(-70,70\right)$, $zϵ\left(-20,181\right)$, two grid sizes (l = 1 m and l = 0.5 m) were employed in the overlapping region. Beyond the overlapping domain, the mesh size decreases gradually, and the largest mesh size is $l=16$. The free surface ranging from z = −2.1 to z = 2.1 m is gradually encrypted 16 times in x direction and 64 times in z direction relative to the smallest mesh size.

Figure 3

Figure 3. Sketch of grids for the calculation.

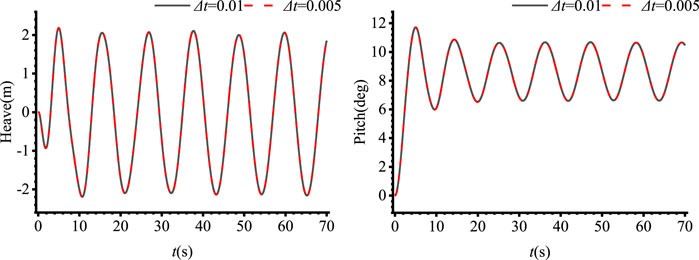
To verify time step convergence, two time steps, Δt = 0.01 s and Δt = 0.005 s, are considered. The wave period is 8.13 s, and the wave height is 4.2 m. The spring parameters can be found in Section 2. The motion curves of heave and pitch for the different grid sizes and time steps are presented in Figures 4, 5. Analysis of these figures shows that the motion curves are in a good agreement, confirming that both the grid sizes and time steps are convergent. Consequently, to minimize computational time costs, a grid size of l = 1 m and a time step of Δt = 0.01 s were selected for subsequent analysis.

Figure 4

Figure 4. Mesh convergence study.

Figure 5

Figure 5. Time step convergence study.

4.2 Barge-type floating foundation with moonpools and springs for mooring lines

Under the effects of wind, a significant tilt angle poses considerable risks for FOWT, adding mooring lines is an effective method to decrease the tilt angle, in present work we use the horizontal springs to realize the effect of mooring lines. Under the effects of wave, the body will undertake periodic motion in three degrees of freedom, namely, surge, heave, pitch, and moonpools will exert important effects in reducing them. The wind speed is maintained at 11.4 m/s, the rotor speed at 12 rpm, and the regular wave period T and wave height H are set as 10 s and 4.2 m, respectively.

Figure 6 illustrates the time histories of motion responses and aerodynamic thrust with and without springs. For the case with springs, surge along x direction is released, while without springs, surge is fixed. It can be found that heave motion in Figure 6A is less affected by the springs, and this is also true for the amplitude of wind thrust in Figure 6C. The tilt angle with spring in Figure 6B is noticeably smaller than that without spring, this is because the spring provide additional restoring force.

Figure 6

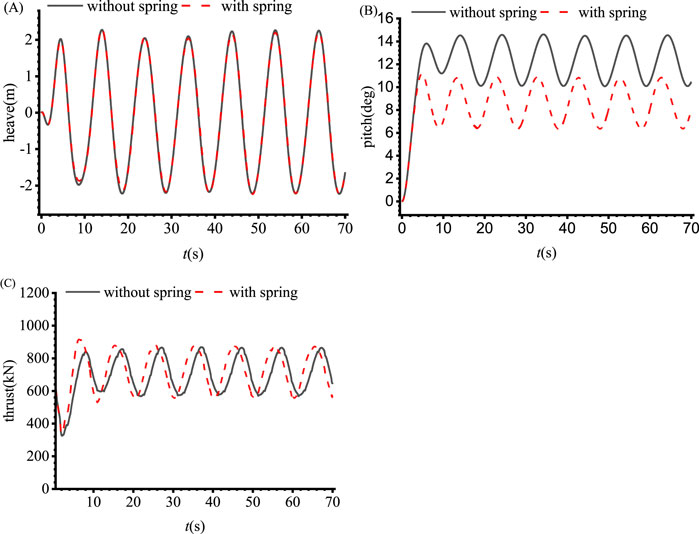
Figure 6. Time histories of motion responses of the platform and thrust of wind turbine: (A) heave, (B) pitch and (C) thrust.

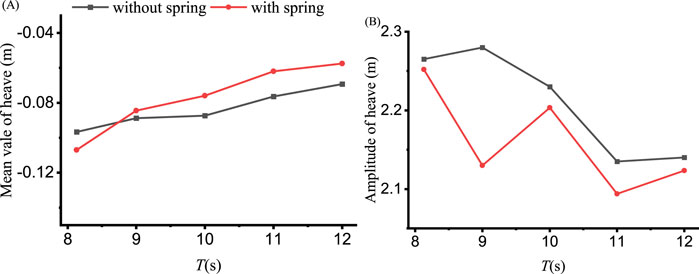
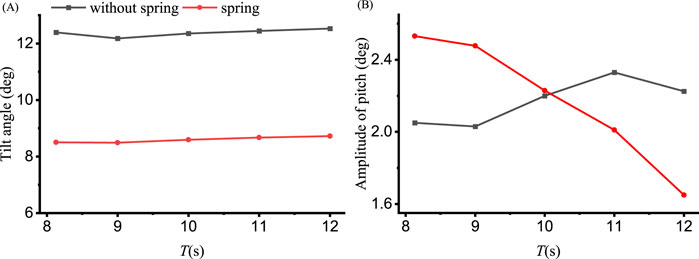
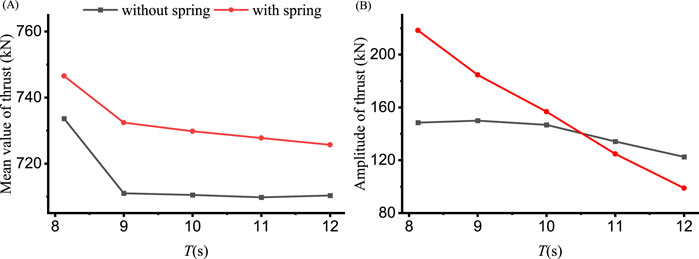
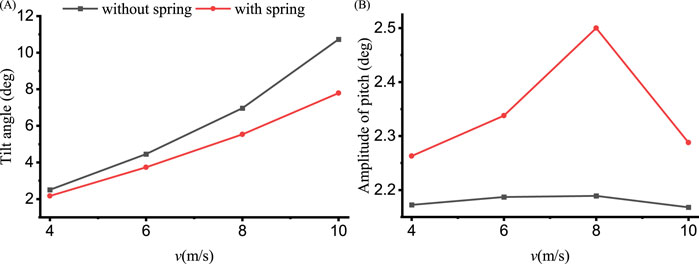
Figure 7 illustrates the mean values and amplitudes of heave under different wave periods (T), while Figures 8, 9 depict the pitch and thrust values, respectively. The wave height for these conditions is consistently maintained at 4.2 m. In Figure 7A, the order of mean value of heave is 10⁻², and the effect of the spring is not prominent. In Figure 7B, the amplitude of heave with spring becomes smaller, the reason for this is the spring provides additional restoring force in heave direction. The spring will provide larger restoring force in rotational direction, directly reducing the tilt angle prominently, and this can be found in Figure 8A. But this is not true for the pitch amplitude in 8(B), which is also affected by the wave force, and both effects lead to larger pitch amplitude under smaller wave periods and smaller pitch amplitude at larger wave periods. The tilt angle in 8(A) becomes noticeably smaller with the spring, but the thrust with spring whereas becomes slightly larger, and this is because the effective inlet area of the fan becomes larger when tilt angle becomes smaller. The thrust amplitude in 9(B) is larger under smaller wave periods and smaller under larger wave periods with spring.

Figure 7

Figure 7. (A) Mean values and (B) amplitudes of heave at different wave periods.

Figure 8

Figure 8. (A) Tilt angles and (B) amplitudes of pitch at different wave periods.

Figure 9

Figure 9. (A) Mean values and (B) amplitudes of thrust at different wave periods.

4.3 Barge-type floating foundation with moonpools with different wind speed

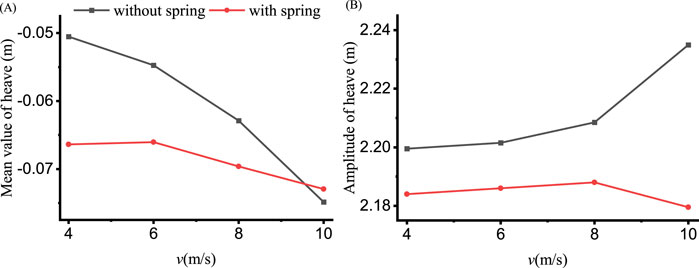
Figure 10 provides the time histories of motion responses of the platform and the thrust of the wind turbine at different wind speeds, respectively at v = 11.4 m/s, 10 m/s, 8 m/s, 6 m/s and 4 m/s, the surge degree is released through connecting two springs, and the spring parameters are the same as the above case. As the wind speed decreases, the heave in 10(A) is less affected, but both the pitch angle and aerodynamic thrust exhibit a markable decline, as illustrated in Figures 10B, D, and this is because the thrust is approximately proportional to the square of the wind speed, and directly affect the pitch angle. It is of great interest to see that the surge motion in Figure 10D actually increases at lower wind speeds, this is because at the higher wind, the tension of the spring at the windward side becomes larger, and it will restrain the surge motion of the platform.

Figure 10

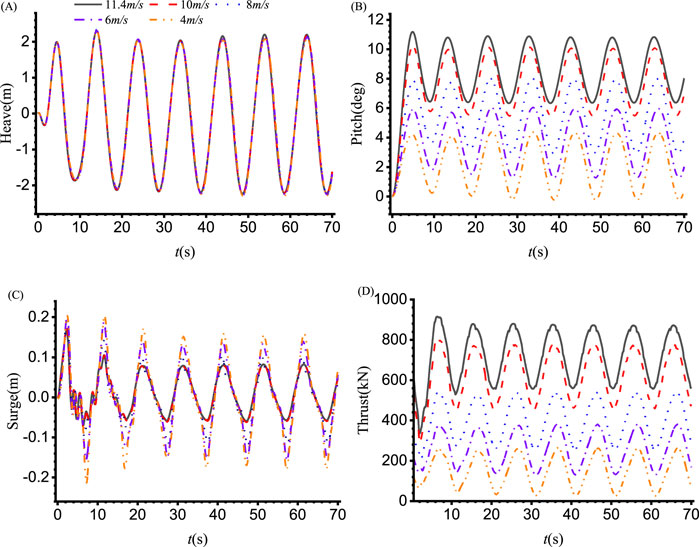
Figure 10. The time histories of motion responses and thrust of wind turbine at different wind speeds: (A) heave, (B) pitch, (C) surge and (D) thrust.

Figures 11–13 depict the heave, pitch, and aerodynamic thrust values across varying wind speeds, with a wave period (T) of 10 s and a wave height (H) of 4.2 m. In Figure 11A, it is evident that as the wind speed increases, the mean heave values are on the order of ${10}^{-2}$, significantly smaller than the heave amplitudes shown in Figure 11B. The heave amplitude in Figure 11B is notably smaller for the case with springs compared to that without springs. This difference arises because the springs provide an additional restoring force. As the wind speed increases, the heave amplitude without springs grows with wind speed, while only minor changes are observed for the case with springs. This demonstrates that the springs effectively restrain heave motion across varying wind speeds. In Figure 12A, the tilt angle increases with wind speed for both cases, with and without springs. This is directly attributed to the thrust being proportional to the square of the wind speed, as illustrated in Figure 13A. However, under the influence of the spring force, the tilt angle with springs is smaller than that without springs, and this difference becomes more pronounced at higher wind speeds. This indicates that the spring’s inhibitory effect on tilt becomes increasingly significant under stronger wind conditions. Although the springs reduce the platform’s tilt, they amplify the pitch amplitude and thrust amplitude. This occurs because the periodic wave force plays a more dominant role when the tilt angle is smaller.

Figure 11

Figure 11. (A) Mean values and (B) amplitudes of heave at different wind speeds.

Figure 12

Figure 12. (A) Tilt angles and (B) pitch amplitudes at different wind speeds.

Figure 13

Figure 13. (A) Mean values and (B) amplitudes of thrust at different wind speeds.

5 Conclusion

This study comprehensively analyzed the hydrodynamic and aerodynamic performance of a barge-type floating wind turbine equipped with four moonpools and horizontal springs as mooring lines. The work is beneficial for the choice of mooring system and vibration damping design in the real-word offshore wind farm installations.

The key findings are summarized as follows:

(1) Because the spring provides additional restoring force, the heave amplitude becomes slightly smaller under various wave periods and wind speeds, and the mean position of heave is less affected.

(2) Under the influence of the spring force, the tilt angles with springs are noticeably smaller than those without springs at various wave periods, and due to the thrust being proportional to the square of the wind speed, the difference of the tilt angle with and without spring becomes more pronounced at higher wind speeds. But for the amplitude of pitch, the effect of spring, wave period and wind speed all take noticeable effects.

(3) When considering the spring, the mean value of thrust becomes slightly larger, and this is because the effective inlet area of the fan becomes larger at smaller tilt angle.

(4) The surge motion may be larger at lower wind speeds, this is because at the higher wind, the tension force of the spring at the windward side becomes larger to withstand the tilt of the platform, and it will restrain the surge motion of the platform more tightly.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

YL: Writing – original draft. SS: Funding acquisition, Writing – original draft, Writing – review and editing. JC: Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work is supported by the Royal Society (Grant No. IEC\NSFC\223358), with Shi Yan Sun serving as a Co-Investigator. We thank Kang Ren from UCL (now from University of Southampton) for the insightful discussions and helpful comments on this work. This work is also supported by the National Natural Science Foundation of China (Grant No. 52271276, 52271319), and the Natural Science Foundation of Jiangsu Province of China (BK20231525).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Beyer, F., Choisnet, T., Kretschmer, M., and Cheng, P. W. (2015). “Coupled MBS-CFD simulation of the IDEOL floating offshore wind turbine foundation compared to wave tank model test data,” in ISOPE International Ocean and Polar Engineering Conference: ISOPE.

Google Scholar

Borisade, F., Choisnet, T., and Cheng, P. W. (2016). Design study and full scale MBS-CFD simulation of the IDEOL floating offshore wind turbine foundation. J. Phys. Conf. Ser. 753, 092002. doi:10.1088/1742-6596/753/9/092002

CrossRef Full Text | Google Scholar

Breton, S. P., and Moe, G. (2009). Status, plans and technologies for offshore wind turbines in Europe and North America. Renew. Energy 34 (3), 646–654. doi:10.1016/j.renene.2008.05.040

CrossRef Full Text | Google Scholar

Chuang, T. C., Yang, W. H., and Yang, R. Y. (2021). Experimental and numerical study of a barge-type FOWT platform under wind and wave load. Ocean. Eng. 230, 109015. doi:10.1016/j.oceaneng.2021.109015

CrossRef Full Text | Google Scholar

Ikoma, T., Nakamura, M., Moritsu, S., Aida, Y., Masuda, K., and Eto, H. (2019). “Effects of four moon pools on a floating system installed with twin-VAWTs,” in International Conference on Offshore Mechanics and Arctic Engineering (American Society of Mechanical Engineers).

CrossRef Full Text | Google Scholar

Ikoma, T., Tan, L., Moritsu, S., Aida, Y., and Masuda, K. (2021). Motion characteristics of a barge-type floating vertical-axis wind turbine with moonpools. Ocean. Eng. 230, 109006. doi:10.1016/j.oceaneng.2021.109006

CrossRef Full Text | Google Scholar

Lu, L., Teng, B., Cheng, L., Sun, L., and Chen, X. (2010). Modelling of multi-bodies in close proximity under water waves—fluid resonance in narrow gaps. Sci. China Phys. Mech. Astronomy 54 (1), 16–25. doi:10.1007/s11433-010-4194-8

CrossRef Full Text | Google Scholar

Mayilvahanan, A., and Selvam, P. R. (2011). Time domain response analysis of barge floater supporting an offshore wind turbine. Int. J. Ocean Clim. Syst. 2 (4), 303–314. doi:10.1260/1759-3131.2.4.303

CrossRef Full Text | Google Scholar

Menter, F. R. (1994). Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 32 (8), 1598–1605. doi:10.2514/3.12149

CrossRef Full Text | Google Scholar

Ning, D., Su, X., Zhao, M., and Teng, B. J. (2015). Numerical study of resonance induced by wave action on multiple rectangular boxes with narrow gaps. Acta Oceanol. Sin. 34, 92–102. doi:10.1007/s13131-015-0672-1

CrossRef Full Text | Google Scholar

Shi, W., Zhang, L., Karimirad, M., Michailides, C., Jiang, Z., and Li, X. (2023). Combined effects of aerodynamic and second-order hydrodynamic loads for floating wind turbines at different water depths. Appl. Ocean Res. 130, 103416. doi:10.1016/j.apor.2022.103416

CrossRef Full Text | Google Scholar

Tan, L., Ikoma, T., Aida, Y., and Masuda, K. (2021). Mean wave drift forces on a barge-type floating wind turbine platform with moonpools. J. Mar. Sci. Eng. 9 (7), 709. doi:10.3390/jmse9070709

CrossRef Full Text | Google Scholar

Vijay, K., Karmakar, D., Uzunoglu, E., and Soares, C. G. (2016). “Performance of barge-type floaters for floating wind turbine,” in Proceedings of the 2nd International Conference of Renewable Energies Offshore (Renew 2016), Lisbon, Portugal, 24–26.

Google Scholar

Yang, R. Y., Wang, C. W., Huang, C. C., Chung, C. H., Chen, C. P., and Huang, C. J. (2022). The 1:20 scaled hydraulic model test and field experiment of barge-type floating offshore wind turbine system. Ocean. Eng. 247, 110486. doi:10.1016/j.oceaneng.2021.110486

CrossRef Full Text | Google Scholar

Zhai, Y., Zhao, H., Li, X., Feng, M., and Zhou, Y. (2024). Effects of aquaculture cage and netting on dynamic responses of novel 10 MW barge-type floating offshore wind turbine. Ocean. Eng. 295, 116896. doi:10.1016/j.oceaneng.2024.116896

CrossRef Full Text | Google Scholar