Unbalance mitigation strategy and power quality improvement in microgrids using a state feedback controller and voltage profile improvement with an electric spring

One of the most important issues with microgrids is the optimal allocation of power between distributed generation sources and the mains, so that DG sources connected to the microgrid by electronic-power interfaces must be able to share the needs for their local loads and common loads properly. This paper will present a control method using a mode feedback controller to control the switching of interface converters and compensate unbalanced and nonlinear loads. This controller will use a linear grade 2 regulator to generate a suitable interest margin and will optimally distribute the load between distributed generation sources. The proposed compensator can balance the load, compensate the harmony, and control the reactive power and provides the actual power required by the network. Additionally, unfavorable voltage profiles and voltage fluctuations due to load change and variable generation of renewable sources are the problems of microgrids. Recently, a device called an electric spring has been introduced to respond to the load dynamics and improve the voltage profile in the microgrid. This paper also proposes a comprehensive strategy to use electric springs in order to improve the voltage profile.

1 Introduction

The evolution of power systems towards greater sustainability and resilience has necessitated the increasing integration of Distributed Generation (DG) sources within microgrids. This shift is driven by the need to reduce carbon dioxide emissions, enhance energy storage capabilities, and improve grid reliability (Konneh et al., 2022a; Mancera et al., 2022; Sheykhi et al., 2022; Hamza et al., 2022; Roslan et al., 2022; Chandak et al., 2022). Microgrids, characterized by their decentralized structure and ability to operate independently or in conjunction with the main grid, present unique challenges and opportunities in power allocation and voltage regulation (Konneh et al., 2022a). One of the critical challenges in microgrid operation is the optimal allocation of power among various DG sources and the mains to ensure efficient and stable power delivery to both local and common loads. Existing control strategies, such as Droop Control, Power Factor Correction (PFC), and Passive Filtering, have been widely employed to manage load sharing and voltage regulation (Konneh et al., 2022b; Bizon and Thounthong, 2020; Babazadeh and Nobakhti, 2018; Aderibole et al., 2019). However, these methods exhibit significant limitations that hinder their effectiveness in dynamic and complex microgrid environments.

Droop Control is a prevalent method used for load sharing among parallel DGs by mimicking the behavior of synchronous generators. While Droop Control effectively balances real and reactive power outputs based on frequency and voltage droop characteristics, it lacks the capability to compensate for harmonic distortions and unbalanced loads, leading to degraded power quality and voltage instability under fluctuating load conditions (Sheykhi et al., 2022; Konneh et al., 2022b). Additionally, Droop Control’s performance is sensitive to system parameter variations, which can result in suboptimal power distribution and increased power losses (Babazadeh and Nobakhti, 2018).

Power Factor Correction (PFC) techniques aim to improve the power factor by compensating for reactive power demand, thereby enhancing energy efficiency. However, PFC methods primarily focus on maintaining a desirable power factor and do not address the issues of load imbalance or voltage regulation comprehensively. This limitation can result in inadequate voltage support during peak load times or when integrating renewable energy sources with variable outputs (Roslan et al., 2022; Aderibole et al., 2019).

Linear optimal control techniques provide an intuitive approach to the design of linear state feedback control. If the states and inputs of a given plant relate to physical quantities,it is often possible to establish a good understanding on how to design a quadratic objective function such that the resulting linear quadratic regulator (LQR) shapes the closedloop dynamics in a desired manner (Schaub and Ulrich, 2023). A decentralized stabilizing control scheme based on optimal state feedback for weak grid-connected inverter interfaces is proposed in the study (Sharma et al., 2023). Feedback control options based on linear quadratic regulator (LQR) are investigated for small signal disturbances in the reference signals, and in the control gains for the same case. It is shown that with full state feedback of local control variables, the stability enhancement with gain disturbances is not very effective. Instead, changing the reference setpoint is shown to stabilize the inverter. Power system instability is identifed as a key problem which modern grids with power inverters are about to face in the future. Taming the intermittent power and Electric Spring Review: Analysis, Control and Applications Electric spring technology has been identi¯ed as one of the demand-side management techniques which is capable of sorting out this problem (Subramani and Ramanand, 2018). This paper points out the various analyses, control schemes and applications that are applicable for electric spring, in hope of its technical advancement in smart grid. In reference (Mohanty et al., 2024), an innovative solution is proposed to address the intermittent challenges in islanded microgrids based on self-excited induction generators. This approach uses an electric spring to maintain a constant voltage at critical loads. In addition, a first-order sliding mode controller is proposed to enhance the voltage and frequency regulation, stability, and overall efficiency of the system. This control strategy is designed to linearize voltage errors and provide fast responses under different steady and transient conditions. To verify the effectiveness of the proposed scheme, the model is compared with the widely used square voltage injection scheme under different load and torque conditions. Furthermore, the system exhibits a fast settling time, typically requiring only one to two cycles to stabilize, which confirms the robustness and stability of the controller.

Passive Filtering is employed to mitigate harmonic distortions by filtering out unwanted frequency components from the power system. While effective in improving power quality, Passive Filtering does not contribute to load balancing or voltage regulation. Its performance is also limited in dynamic environments where harmonic content varies with changing load and generation conditions (Bizon and Thounthong, 2020; Yin et al., 2022). Moreover, Passive Filters require careful tuning and are less effective in handling non-linear and unbalanced loads, making them unsuitable for adaptive control scenarios (Shahzad et al., 2022). To address these limitations, This study proposes a novel control method that integrates a Linear Quadratic Regulator (LQR) with Electric Springs (ES) to achieve optimal power allocation, load balancing, and voltage regulation in microgrids. The LQR is employed to design a state feedback controller that optimizes the system performance by minimizing a predefined cost function, ensuring precise control over power distribution and voltage levels (Cheng et al., 2018). Electric Springs (ES), modeled as current-controlled voltage sources, provide dynamic voltage support by adjusting their voltage offset and phase angle in response to load changes and renewable energy fluctuations (Yin et al., 2022; Alwal et al., 2022). The integration of LQR with ES offers several advantages over standalone approaches:Optimal Power Allocation: The LQR-based state feedback controller ensures that power is distributed efficiently among DG sources and the mains, minimizing power losses and enhancing system reliability (Cheng et al., 2018). Enhanced Voltage Regulation: ES provides real-time voltage support, mitigating voltage drops and fluctuations caused by unbalanced and nonlinear loads, thereby maintaining a stable voltage profile (Yin et al., 2022; Alwal et al., 2022). Harmonic Compensation: The combined approach effectively compensates for harmonic distortions and unbalanced currents, improving overall power quality and reducing the need for additional filtering components (Shahzad et al., 2022).

An ES can transform a connected non-critical load into a smart load that provides voltage support and voltage suppression functions. This study (Zheng et al., 2020) addresses the optimal allocation of smart electric spring load (ES) devices in radial distribution systems for voltage regulation.

In this paper, a risk-limiting ES scheduling method is proposed to obtain the optimal ES configuration (number, locations, capacities, and types) to mitigate voltage violations caused by uncertainty in distributed renewable generation. Droop control algorithm is widely used in microgrids, some shortcoming of the droop control, such as poor disturbance rejection and slowtransient response, seriously affect the power quality and stabilityin islanded microgrid. Moreover, when the power consumptionof the demand exceeds the generated power of the distributedgenerators in microgrid, the decreased frequency will lead to the microgrid blackout owing to the slow load shedding characteristics of the droop control (Lin et al., 2022). In this study, an online trained Petriprobabilistic wavelet fuzzy neural network (PPWFNN) controller is developed as the voltage controller to replace the traditional proportional–integral controller in a battery energy storage system for an islanded microgrid with droop control to achieve fast load shedding.

Scalability and Flexibility: The proposed method is highly scalable, making it suitable for large-scale microgrids with multiple DG sources and diverse load profiles (Badoni et al., 2021). Resilience to Dynamic Conditions: By leveraging ES’s ability to dynamically adjust voltage support and LQR’s optimal control capabilities, the system exhibits enhanced resilience to rapid load changes and renewable energy intermittency (Chauhan and Singh, 2022). The necessity of this research is underscored by the growing complexity of modern microgrids, which require advanced control mechanisms to manage the interplay between distributed generation sources, variable renewable energy inputs, and fluctuating loads. Traditional methods fall short in providing the required flexibility and precision needed for optimal operation in such dynamic environments. By integrating LQR with ES, this study presents a comprehensive solution that not only addresses the limitations of existing control strategies but also enhances the overall performance and reliability of microgrids (Yang et al., 2018; Córdova et al., 2022; da Costa et al., 2024).

Cyber-physical systems (CPS) are quite popular in modern industrial communities, especially the energy and electric power sectors (Adiche et al., 2024). This study have implemented distributed energy management (DEM) of a small-scale microgrid to preliminarily verify the feasibility of the RoboEC. The case study of this microgrid with demand response demonstrates that the idea of RoboEC based on CPSS can effectively achieve the human-computer collaboration and rapidly obtain a higher quality optimum of DEM compared with other centralized heuristic algorithms. The simulation results obviously demonstrate that the increasing virtual artificial systems (VAS) can generate a potential higher quality optimal solution via a deeper exploitation and exploration with various decision behaviors. However, the parallel learning algorithms require more computation capability and consume more execution time. Furthermore, the execution time of parallel learning is slightly larger than that of GA, PSO, and GSO since each game agent requires a linear programming computation to search an optimal correlated equilibrium policy in each time of iteration.

2 Methodology

2.1 Connection of distributed generation sources by the inverter to the power grid

The presence of unbalanced and nonlinear loads in the microgrid can disrupt the performance of the system and cause unbalanced voltage and power. Another important issue with microgrids is the issue of load allocation between distributed generation sources, meaning that DG sources connected to the microgrid by electronic-power interfaces must have the power required for their local loads and share common loads appropriately between themselves and the main network. Therefore, in a microgrid, there is a need for a controller compensating for the effects of imbalance and nonlinearity of the load and helps the distributed generation sources to distribute the loads properly. In this chapter, we will introduce a sample structure for microgrids such as loads and distributed generation sources, and then will present effective control methods for load compensation as well as optimal load alocation.

Unlike large generators, which are often 50 or 60 Hz synchronous machines, DGs include variable frequency sources (variable speed) such as wind power and high frequency sources like microturbine converters and direct energy conversion sources that produce DC voltage and current such as fuel cells and photovoltaics. This type of DG unit requires a voltage source converter to assist the DG connection to the grid. In DG sources with inverters, inverters are the most important component of the circuit. Figure 1 shows the power circuit of a DG unit connected to the inverter and the corresponding control function. The figure depicts a three-part VSI with a common load on the AC side of the power circuit and various control circuits of the converter control structure.

Figure 1

Figure 1. Power circuit and control function of a DG connected to the inverter.

Figure 2 shows the structure of a microgrid, consisting of two DG sources and unbalanced and nonlinear loads, in which P and Q denote the real and reactive power, respectively. The microgrid is connected to the mains at the PCC point. Both DG1 and DG2 sources are connected directly to the microgrid by CB-3 and CB-4 breaker circuits, respectively.

Figure 2

Figure 2. The structure of a microgrid consisting of local and common loads.

One of the tasks of DGs is to compensate for the imbalance and nonlinearity of the local load. When connected to the mains, DG sources share a percentage of their local load with the mains, while the shared load is supplied entirely by the mains.

During the islanding process, each DG resource provides its own local load, and the common load is shared between the DG resources. The mixed power drawn by the loads in the region is P_L1 + jQ_L1 and P_L2 + jQ_L2.

The common load draws current from the network and consumes P_LC + jQ_LC complex power.

Local loads at points PCC1 and PCC2 are connected to DG sources with voltages, respectively. P1, Q1, P2, and Q2 denote the actual and reactive power supplied by distributed generation sources, respectively. It is assumed that the microgrids are mainly resistive and at the distribution level and have line impedances. The main power supply is indicated by resistance Rs and inductor Ls of the feeder and, respectively The mains injects P_G and Q_G capacities into the microgrid. The CB1 can disconnect the microgrid from the mains.

The main purpose of the compensator is to eliminate the effects of imbalance and the harmonic components of the region load in a state where a predetermined amount of real and reactive power is provided for the load. If this compensator does its job well, the ig1 current will be balanced, and the voltage vp1 supplied by the vs. source will be balanced. Here the phases are marked with subtitles a, b and c, respectively. Therefore, since ig1 is balanced, we have:

$i_{g1a}+i_{g1b}+i_{g1c}=0(1)$

Using Figure 2 and the KVL rule at point vp we have:

$i_{1k}+i_{g1k}=i_{L1k},k=a,b,c(2)$

By combining Equations 1 and summing the currents, we will have three phases:

$i_{1a}+i_{1b}+i_{1c}=i_{l1a}+i_{l1b}+i_{l1c}(3)$

Owing to the compensator function, the current i_g1 is balanced and consequently, the voltage v_p1 will be balanced. Accordingly, the true power of the moment will be equal to its mean value (PG1). Here one can write

$v_{p1a}{i}_{g1a}+v_{p1b}{i}_{g1b}+v_{p1c}{i}_{g1c}=p_{G1}+P_{G1}(4)$

Using KCL and Equations 2, 4 we can write:

$v_{p1a}\left(i_{L1a}-i_{1a}\right)+v_{p1b}\left(i_{L1b}-i_{1b}\right)+v_{p1c}\left(i_{L1c}-i_{1c}\right)=P_{G1}(5)$

Similarly, the reactive power will be equal to its instantaneous components, and we will have:

$\left(v_{p1b}-v_{p1c}\right)i_{g1a}+\left(v_{p1c}-v_{p1a}\right)i_{g1b}+\left(v_{p1a}-v_{p1b}\right)i_{g1c}=\sqrt{3}\times Q_{G1}(6)$

Using KCL law, relationships Equations 3, 6 can be rewritten as follows:

$\left(v_{p1b}-v_{p1c}\right)\left(i_{L1a}-i_{1a}\right)+\left(v_{p1c}-v_{p1a}\right)\left(i_{L1b}-i_{1b}\right)+\left(v_{p1a}-v_{p1b}\right)\left(i_{L1c}-i_{1c}\right)=\sqrt{3}\times Q_{G1}(7)$

Equations 3, 5, 7 form the basis of the algorithm for calculating the amount of the compensatory reference current.

Using these equations, we can write:

$A\left[\begin{array}{c}{i}_{1a}\\ i_{1b}\\ i_{1c}\end{array}\right]=A\left[\begin{array}{c}{i}_{L1a}\\ i_{L1b}\\ i_{L1c}\end{array}\right]+\left[\begin{array}{c}0\\ {-P}_{G1}\\ -\sqrt{3}{Q}_{G1}\end{array}\right](8)$

Where A is:

$A=\left[\begin{array}{ccc}1& 1& 1\\ v_{pla}& v_{p1b}& v_{p1c}\\ v_{p1b}-v_{p1c}& v_{p1c}-v_{p1a}& v_{p1a}-v_{p1b}\end{array}\right](9)$

The determinant of matrix 9 can be calculated as follows:

$\left|A\right|=v_{p1a}\left(v_{p1c}+v_{p1b}-2v_{p1a}\right)+v_{p1b}\left(v_{p1a}+v_{p1c}-2v_{p1b}\right)+v_{p1c}\left(v_{p1b}+v_{p1a}-2v_{p1c}\right)(10)$

If vp1 is balanced we will have:

$v_{p1a}+v_{p1b}+v_{p1c}=0(11)$

By placing Equation 11 in the Equation 10 we get

$\left|A\right|=-K$

where the value of K is calculated from the Equation 12:

$K=3\left({v_{p1a}}^2+{V_{p1b}}^2+{v_{p1c}}^2\right)(12)$

By solving Equation 8 we will have:

$\left[\begin{array}{c}{i}_{1a}\\ i_{1b}\\ i_{1c}\end{array}\right]=\left[\begin{array}{c}{i}_{L1a}\\ i_{L1b}\\ i_{L1c}\end{array}\right]-\frac{1}{K}\left[\begin{array}{c}3P_{G1}{v}_{p1a}+\sqrt{3}{Q}_{G1}\left(v_{p1b}-v_{p1c}\right)\\ 3P_{G1}{v}_{p1b}+\sqrt{3}{Q}_{G1}\left(v_{p1c}-v_{p1a}\right)\\ 3P_{G1}{v}_{p1c}+\sqrt{3}{Q}_{G1}\left(v_{p1a}-v_{p1b}\right)\end{array}\right](13)$

As mentioned earlier, the DG-1 provides a fraction of the actual reactive power required by the local load, so it can be written:

$P_1={\lambda }_{1p}\times P_{L1av}$

$Q_1={\lambda }_{1Q}\times Q_{L1av}(14)$

where in Equation 14, PLav and QLav are the actual and reactive power requested by the local load, respectively, and p1p and λ1Q are the fraction of the actual and inactive power supplied by the DG-1, respectively. It should be noted that real and reactive powers have double frequency and distortion around their mean components. DG-1 provides this double frequency and distorted components to compensate for imbalances and harmonics. As a result, the active power (PG1) and reactive power (QG1) supplied by the network will not include any double frequencies and distorted components. As mentioned, the DG-1 provides some of the power required by the load. Therefore, the real and reactive power supplied by the network using KCL law will be equal to Equation 15:

${P_{G1}=P}_{L1av}-{\lambda }_{1P}\times P_{L1av}=P_{L1av}\left(1-{\lambda }_{1P}\right)$

${Q_{G1}=Q}_{L1av}-{\lambda }_{1Q}\times Q_{L1av}=Q_{L1av}\left(1-{\lambda }_{1Q}\right)(15)$

By modifying relation Equation 13, the Equation 16 can be achieved for the reference flow:

$\left[\begin{array}{c}{i}_{1a}\\ i_{1b}\\ i_{1c}\end{array}\right]=\left[\begin{array}{c}{i}_{L1a}\\ i_{L1b}\\ i_{L1c}\end{array}\right]-\frac{1}{K}\left[\begin{array}{c}3P_{L1av}\left(1-{\lambda }_{1P}\right)v_{p1a}+\sqrt{3}{Q}_{L1av}\left(1-{\lambda }_{1Q}\right)\left(v_{p1b}-v_{p1c}\right)\\ 3P_{L1av}\left(1-{\lambda }_{1P}\right)v_{p1b}+\sqrt{3}{Q}_{L1av}\left(1-{\lambda }_{1Q}\right)\left(v_{p1c}-v_{p1a}\right)\\ 3P_{L1av}\left(1-{\lambda }_{1P}\right)v_{p1c}+\sqrt{3}{Q}_{L1av}\left(1-{\lambda }_{1Q}\right)\left(v_{p1a}-v_{p1b}\right)\end{array}\right](16)$

Similarly, the reference current for DG-2 can be calculated as Equation 17:

$\left[\begin{array}{c}{i}_{2a}\\ i_{2b}\\ i_{2c}\end{array}\right]=\left[\begin{array}{c}{i}_{L2a}\\ i_{L2b}\\ i_{L2c}\end{array}\right]-\frac{1}{K}\left[\begin{array}{c}3P_{L2av}\left(1-{\lambda }_{2P}\right)v_{p2a}+\sqrt{3}{Q}_{L2av}\left(1-{\lambda }_{2Q}\right)\left(v_{p2b}-v_{p2c}\right)\\ 3P_{L2av}\left(1-{\lambda }_{2P}\right)v_{p2b}+\sqrt{3}{Q}_{L2av}\left(1-{\lambda }_{2Q}\right)\left(v_{p2c}-v_{p2a}\right)\\ 3P_{L2av}\left(1-{\lambda }_{2P}\right)v_{p2c}+\sqrt{3}{Q}_{L2av}\left(1-{\lambda }_{2Q}\right)\left(v_{p2a}-v_{p2b}\right)\end{array}\right](17)$

Using the concept of mechanical spring, electric spring has the functions of supporting the electrical voltage, storing the electrical energy, and reducing electrical fluctuations. The electric spring can be represented by a current-controlled voltage source. Figure 3 depicts the location of the spring in the system. The spring-loaded output is connected in series to a non-sensitive charge to create an intelligent load. An insensitive charge is a single charge or a group of electrical charges that can withstand voltage changes to the permissible level without causing significant inconvenience to the user. The series of the electric current and the load and their sum in parallel with the sensitive load causes the voltage of the sensitive load, which is the same as the voltage of the ac power network, to be kept constant at its nominal reference value.

Figure 3

Figure 3. Installation of an electric spring in the system.

In electronegativity, the VES and Io vectors can be perpendicular to each other, so that no active power is injected into the grid by ES. The sum of the insensitive load voltage Vo and the offset voltage VES is equal to the supply voltage Vs. Vo can be increased or decreased by Ves generated by the spring electricity. As a result, insensitive load power consumption can be controlled. Figure 2 presents the phasor diagram of a spring-loaded operation. The electric spring acts as a series compensator that can supply the variable voltage ac of the insensitive load Zo, thereby changing the current to the load, without changing the line voltage Vs. and the load Zo. According to Figure 4, the electric spring can be implemented using a controlled voltage source. A PLL is used to access the phase angle information.

Figure 4

Figure 4. Control strategy.

One of the aims of the present paper is to investigate the performance of ES in improving the voltage profile and maintaining the line voltage level in desired conditions in the microgrid system, in normal conditions, and in variable renewable energy sources and load variability conditions. The system under consideration is the system depicted in Figure 5.

Figure 5

Figure 5. The system including ES.

2.2 State feedback controller

A two-line regulator is used to produce an unlimited gain margin and a phase margin of at least 60°. As Figure 6 demonstrates, another important feature of LQR is that it is highly flexible against the nonlinear input. When the error is large and the control is limited between 1 and -1, then the K-matrix ip’s components should be small. For the decreasing sets of R values, we obtain the corresponding increasing set of K values.

Figure 6

Figure 6. Regulators in the linear quadratic state feedback.

Figure 6 shows a block diagram of a state feedback controller with a linear quadratic regulator. In this block diagram, the x parameter represents the system states, and the z parameter is called the system control output. The value of z is equal to: Equation 18

$\dot{Z}=Gx+Hu(18)$

2.3 State Feedback Controller with Linear Quadratic Regulator (LQR)

The proposed control method employs a State Feedback Controller integrated with a Linear Quadratic Regulator (LQR) to achieve optimal load distribution and voltage stabilization in the microgrid. The LQR is designed to minimize the cost function 19:

$J={\int }_0^{\infty }\left({\mathrm{x}}^T{\mathrm{Q}}_x+{\mathrm{u}}^{T}Ru\right)dt(19)$

where:

*$\mathrm{x}\in {\mathbb{R}}^{\mathbb{n}}$: State vector representing the system states.

*$u\in {\mathbb{R}}^m$: Control input vector.

*$\mathrm{Q}\in {\mathbb{R}}^{\mathbb{n}\mathbb{ˣ}\mathbb{n}}$: State weighting matrix. This matrix determines the relative importance of each state variable in the cost function. Higher values in Q will result in a stronger emphasis on minimizing deviations in the corresponding state variables.

*$R\in {\mathbb{R}}^{m*m}$: Control weighting matrix. This matrix penalizes excessive control effort. Higher values in R will discourage large control signals, which can lead to instability or rapid wear and tear on control components.

2.3.1 State vector (x):

$\mathrm{x}=\left[\text{PQV}\right]$

where:

P: Represents the active power.

Q: Represents the reactive power.

V: Represents the voltage.

2.3.2 In essence

The LQR method seeks to find the optimal control inputs (u) that minimize the cost function J. This minimization is achieved by carefully balancing the desired system performance (as defined by the state weighting matrix Q) with the need to limit excessive control effort (as defined by the control weighting matrix R).

2.3.3 Key considerations

State Space Model: To implement this control scheme, a linear state-space model of the microgrid system is necessary. This model will describe the dynamics of the system in terms of its states (x) and inputs (u).

Tuning: The effectiveness of the LQR controller heavily relies on the appropriate selection of the weighting matrices Q and R. This often involves a trial-and-error process or more sophisticated tuning methods to achieve the desired control performance.

2.4 Detailed influence of parameters on system performance

Understanding the role of each parameter is crucial for optimizing the microgrid’s performance: Below is a brief explanation for better understanding.

2.5 State weighting matrix (SWM)

• Impact: Determines the relative importance of state variables in the control objective. By increasing q2q_2q2 and q3q_3q3, the controller prioritizes reactive power and voltage stability over real power adjustments.

• Performance: Higher weights on reactive power and voltage lead to better voltage regulation and reduced reactive power fluctuations, enhancing overall power quality.

2.6 Control weighting matrix (CWM)

• Impact: Balances the trade-off between minimizing the cost function and the magnitude of control inputs. A smaller CWM allows for more aggressive control actions, while a larger CWM enforces smoother control responses.

• Performance: Proper tuning of CWM ensures that the system responds swiftly to disturbances without inducing excessive control efforts, maintaining stability and preventing oscillations.

2.7 Electric spring voltage offset (VESV_{ES}VES)

• Impact: Directly influences the voltage support provided to the microgrid. Adjusting VESV_{ES}VES allows the ES to compensate for voltage drops caused by load variations or renewable energy intermittency.

• Performance: Effective management of VESV_{ES}VES results in stable voltage levels, reducing the likelihood of voltage sags or swells, and enhancing the reliability of power supply to sensitive loads.

2.8 Electric spring phase angle (θ\thetaθ)

• Impact: Controls the reactive power injection or absorption by the ES. Adjusting θ\thetaθ ensures that the ES contributes appropriately to reactive power management, aiding in voltage regulation.

• Performance: Accurate phase angle adjustments prevent harmonic distortions and ensure that reactive power flows harmoniously within the microgrid, maintaining power quality and system stability.

2.9 Electric spring control gain (KESK_{ES}KES)

• Impact: Dictates the responsiveness of the ES to voltage deviations. A higher KESK_{ES}KES allows the ES to react more swiftly to voltage changes.

• Performance: While increased responsiveness can enhance voltage stability, it is essential to balance KESK_{ES}KES to avoid potential overcompensation and system instability.

Table 1 provides definitions and justifications for the parameters.

Table 1

Table 1. Parameter definitions and justifications.

2.10 Detailed algorithmic breakdown

To facilitate reproducibility, the following algorithm and pseudocode 1 outlines the step-by-step implementation of the proposed LQR + ES control strategy.

1. Initialization: Define the initial states, control inputs, and weighting matrices for the LQR. Calculate the optimal gain matrix using the LQR design.

2. State Measurement: Continuously monitor the current real power (P), reactive power (Q), and voltage (V) levels within the microgrid.

3. Control Input Computation: Utilize the LQR to compute the optimal control inputs (ΔP\Delta PΔP, ΔQ\Delta QΔQ, ΔVES\Delta V_{ES}ΔVES) that minimize the cost function, ensuring efficient power allocation and voltage regulation.

4. Electric Spring Adjustment: Update the ES voltage offset (VESV_{ES}VES) and phase angle (θ\thetaθ) based on the computed control inputs to provide dynamic voltage support.

5. Application of Control Inputs: Adjust the DG outputs and set the ES parameters accordingly to influence the microgrid’s power flow and voltage levels.

6. System State Update: Update the system’s real power, reactive power, and voltage states based on the applied control actions and the resulting power flows.

7. Performance Monitoring: Log key performance metrics such as efficiency, load balancing capability, and voltage profile improvements for analysis.

8. Stability Check: Ensure that the system remains stable within predefined thresholds. If instability is detected, adjust control parameters or activate safety mechanisms to maintain system integrity.

Scalability considerations: The proposed LQR + ES control strategy is designed with scalability in mind, making it adaptable to microgrids of varying sizes and complexities. Key scalability features include:

• Modular Controller Design: The LQR controller can be extended to accommodate additional DG sources without significant redesign, facilitating easy integration into larger systems.

• Dynamic ES Allocation: Multiple ES devices can be deployed across different points in the microgrid to provide localized voltage support, enhancing the system’s ability to handle diverse load profiles.

• Computational Efficiency: The LQR algorithm is computationally efficient, enabling real-time control even in large-scale microgrid environments with numerous control inputs and state variables.

pseudocode 1. Combined LQR and electric spring control strategy.

Define state vector x = [P, Q, V]^T

Define control input vector u = [ΔP, ΔQ, ΔV_ES]^T

Define state weighting matrix Q = diag(q1, q2, q3)

Define control weighting matrix R = r *I

Initialize Parameters

Calculate LQR gain matrix K using Q and R

Initialize Electric Spring parameters:

V_ES = V_initial

θ = θ_initial

Set simulation time step h = 0.001 s

Begin Simulation Loop for each time step:

1. Measure Current State:

x = [P_current, Q_current, V_current]^T

2. Compute Control Inputs using LQR:

u = -K *x

ΔP = u[0]

ΔQ = u[1]

ΔV_ES = u[2]

3. Update Electric Spring Parameters:

V_ES = V_ES + ΔV_ES

θ = θ + Δθ//Δθ can be a function of ΔQ or predefined

4. Apply Control Inputs:

Adjust DG outputs based on ΔP and ΔQ

Set ES voltage to V_ES with phase angle θ

5. Update System States:

Update P, Q, V based on power flow equations and control actions

6. Log and Monitor Performance Metrics: Record efficiency, load balancing, and voltage profiles

7. Check for Convergence or Stability:

If system is stable within desired thresholds, continue

Else, adjust control parameters or trigger safety mechanisms

End Simulation Loop

2.11 Simulation environment and computational setup

To ensure the reproducibility of the proposed control strategy, the simulations were conducted using MATLAB/Simulink (Version R2024a), a widely recognized platform for modeling, simulating, and analyzing dynamic systems. The computational setup utilized for the simulations was as follows:

• Hardware Specifications:

• Processor: Intel Core i7-12700K CPU @ 3.60 GHz

• Memory: 32 GB DDR4 RAM

• Operating System: Windows 10 Pro, 64-bit

• Software Specifications:

• MATLAB/Simulink: Version R2024a

• Toolboxes:

• Simulink Control Design Toolbox

• SimPowerSystems Toolbox

• Stateflow Toolbox

2.12 Simulation parameters

• Time Step: Fixed-step solver with a step size of 0.001 s

• Simulation Duration: 10 s per scenario to capture transient and steady-state behaviors

• Model Configuration: The microgrid model comprised two Distributed Generators (DG1 and DG2), an Electric Spring (ES), local and common loads, and a Point of Common Coupling (PCC). Protective devices and measurement units were incorporated to accurately monitor system states and control actions.

2.13 Simulation scenarios

The proposed LQR + ES control strategy was evaluated under various scenarios to assess its performance in mitigating unbalanced loads and enhancing voltage profiles. The primary scenarios included:

1. Load Variability: Simulating dynamic changes in load demands to test the controller’s responsiveness and stability.

2. Renewable Generation Integration: Incorporating intermittent renewable energy sources (e.g., photovoltaic panels) to evaluate the controller’s ability to handle fluctuations in generation.

Each scenario was simulated in both connected mode (microgrid operating in parallel with the main grid) and islanded mode (microgrid operating independently). The detailed simulation results are presented below.

3 Test results

The microgrid study includes one DG. As Figure 7 shows, the system considered in this section includes a DG source. The microgrid is connected to the mains at the PCC point. The DG source has a local load that includes unbalanced and nonlinear loads. When connected to the mains, the common load is fully powered by the mains, and the DG-1 source and the mains jointly supply the required local load power. In island mode, when CB-1 is opened and the microgrid is disconnected from the mains, DG-1 must provide all the power required for both local and common loads. In the following sections, we will consider both modes.

Figure 7

Figure 7. One-line diagram of the system, including the microgrid, mains, and local and common loads.

Suppose that at t = 0.5 (s) the impedance of the common load is reduced by half of the initial value. Figure 8 shows the actual and passive capacities for the DG-1 source this figure shows the point voltage (PCC1) and the ig1 current. Allocation of load in the same desired ratios as well as the voltage balance even after changing the amount of the common load indicates stable performance for the network. Notably, the state feedback control law expressed in the previous sections was used to establish balance in the network and allocate the optimal load.

Figure 8

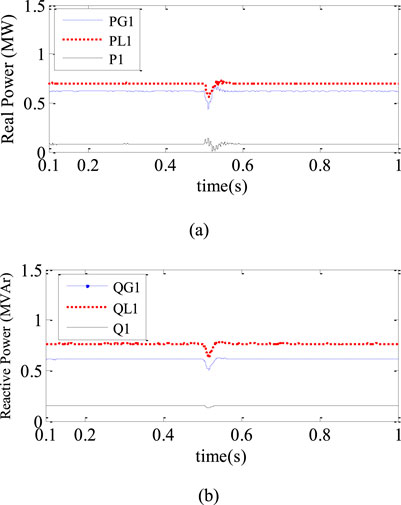
Figure 8. Assignment of real and passive capabilities while connected to the network (for a system including a DG): (a) active power (MW) (b) reactive (MVAR).

Here, for proper network performance, the LQR index parameters are selected as follows: $Q=diag\left[011\right]R=0.05\rho =1$, K = [8.1109 3.2170 0.1170].

Where diag is a diagonal matrix. The two variables that are crucial for control are the i2 current and the vcf voltage. The choice of the Q matrix demonstrates the importance of the states. Figures 8, 9 clearly show the voltage drop resulting loss of real and reactive power at the moment of load change, i.e., (time 0.5 s). After a short time (approximately 0.025 s), the voltage, current and power return to equilibrium twice.

Figure 9

Figure 9. (a) Three-phase voltage at point PCC1. (b) Network injection current to the PCC1 point.

In Figures 8, 9, the voltage drop and as a result the real and reactive power drop at the moment of load change, i.e., (time 0.5 s), can be clearly seen. After a short period of time (about 0.025 s), the voltage, current and powers return to the equilibrium state twice. Table 2 shows some numerical results obtained from these graphs.

Table 2

Table 2. Numerical results of connected state.

3.1 The microgrid study consisted of two DGs

Figure 10 shows a single-line diagram of a power system containing two DG sources. The microgrid is connected to the mains at the PCC point. Both DG1 and DG2 sources are directly connected to the microgrid by the CB-3 and CB-4 circuits breaker, respectively. As mentioned in the previous sections, both DGs have regional loads that may be nonlinear and unbalanced. In addition, the microgrid may have a common load that is assumed to be balanced and located at a great distance from the DGs. One of the tasks of DGs is to correct the imbalance and nonlinearity of the local load. When connected to the mains, DG sources share a percentage of their local load with the mains, while the shared load is fully supplied by the mains. In all the states stated for the network in this section, a state feedback controller with the presence of a quadratic linear regulator will be used to control the network and correct unbalanced loads. The block diagram of this controller is shown in Figure 11. Here, in order to achieve the desired answers, the value of h is considered equal to 0.001.

Figure 10

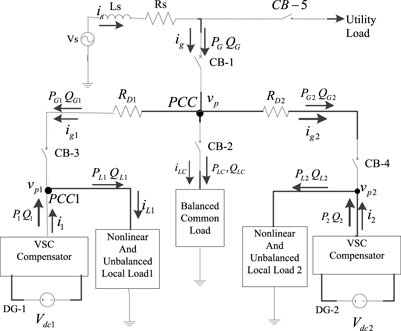
Figure 10. The single-line diagram of the microgrid and the power grid under study witch includes two distributed generation sources.

Figure 11

Figure 11. State feedback control diagram block.

Figure 12 shows the allocation of real and reactive capabilities of DG-1 and DG-2 resources. The point voltages (PCC1) and (PCC2) as well as the ig1 current are shown in Figure 13.

Figure 12

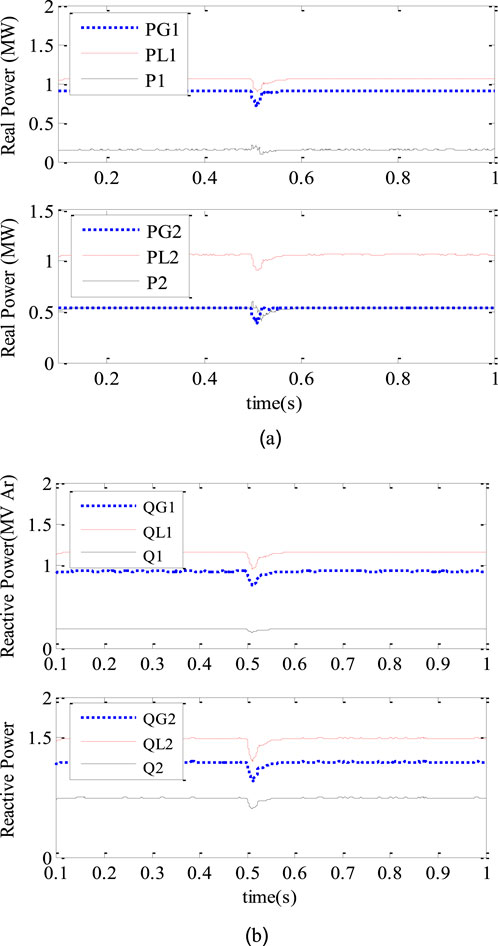
Figure 12. Allocation of the real and reactive power in DG-1 and DG-2. (a) Real power distribution (MW) (b) Reactive power distribution (MVAR).

Figure 13

Figure 13. (a) Three-phase voltage at points PCC1 and PCC2. (b) Injection current to point PCC1.

As the figure shows, by decreasing the amount of the common load at the moment t = 0.5 s, the points PCC1 and PCC2 have a voltage drop and consequently at this moment, the values of real and reactive power are slightly reduced, After a short time, the system returns to its equilibrium state.

Table 3 shows the numerical results of the simulations for the first and second modes of choosing R and Q. According to this table and using the voltage and power waveforms, it can be seen that in the second case, the voltages and powers will have a smaller drop at the moment of common load reduction than in the first case.

Table 3

Table 3. Numerical results for 2 DG.

To show the effect of adding an electric spring, we present the results of the voltage profile for the microgrid for both cases of with and without electric springs.

According to Figure 14, the system without ES is in good condition in terms of voltage regulation and has a voltage level of 0.986 prionite. In 4 s, when the switch is connected, load 4 enters the system with a power of 1 j + 1 MVA, and then the voltage drops to 0.979 pronate in Figure 15a, electric current is introduced into the circuit, which in this part, by producing a voltage level of 600 V, causes the system voltage level to increase from 0.986 prionite to 0.988 prionite according to Figure 15b. Since, according to Figure 14, by switching the load (load4) in 4 s, the voltage across the two sensitive loads has dropped more ¬, as compared to Figure 15b and Figure 14, ES increases the voltage level V¬2000 by producing a voltage level. The sensitive charge voltage is prionized from 0.98 prionite to 0.988 prionite, so the voltage drop is reduced by 0.8%. Finally, when the load is cut off, the output voltage of the ES reaches the normal value of V600. As shown in Figures 15b, c, the constant presence of ES in the microgrid causes the system voltage to always be at its desired level and in the event of an error can reduce voltage fluctuations. It should be noted that according to Figure 15c, in the use of ES, the insensitive load voltage has also increased from 0.985 prionite to 0.989 prionite.

Figure 14

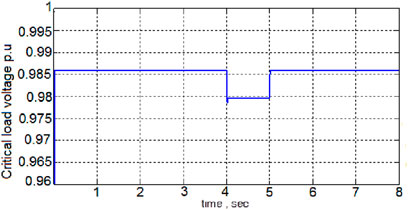
Figure 14. Sensitive load voltage, in a system with theFi optimal voltage setting with load switching, without ES.

Figure 15

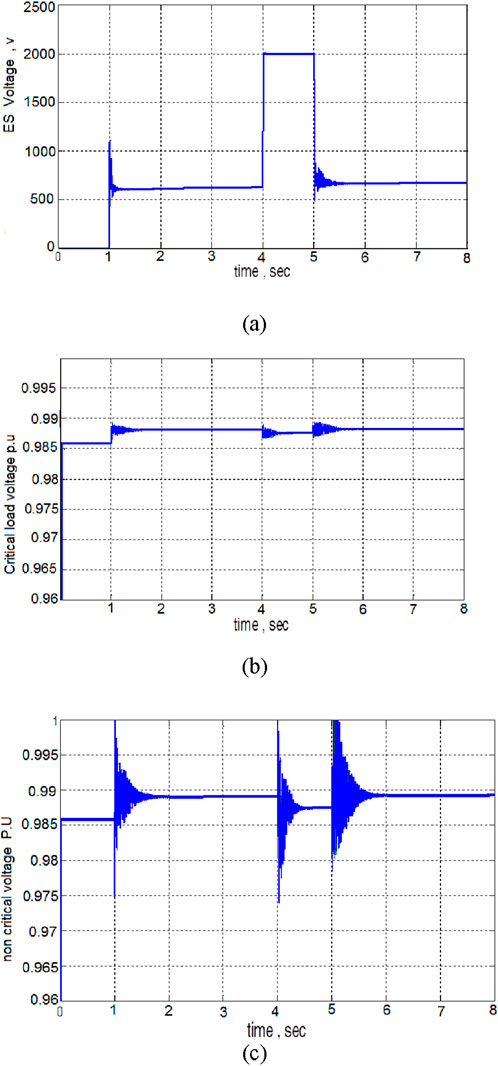
Figure 15. (a) ES output voltage, in the system with the optimal voltage regulation with load switching. (b) Sensitive load voltage, in a system with the optimal voltage. regulation with load switching, with ES. (c) Insensitive load voltage, in a system with optimal voltage.

Proposed Method: The proposed method demonstrates high efficiency in power allocation and ensures optimal power distribution. It is designed to improve the allocation of power between distributed generation sources and the mains, resulting in an optimized distribution of power among different sources.

Traditional Rule-Based Approach: This method shows a moderate level of efficiency in power allocation. However, it does not achieve optimal power distribution. It relies on rule-based strategies or simplistic algorithms, which may lead to suboptimal power distribution among the sources.

Simple Load-Sharing Scheme: This method exhibits low efficiency in power allocation. It does not achieve optimal power distribution among the sources. The load-sharing scheme employed in this method is inefficient and does not effectively allocate power based on the needs and capabilities of the sources.

The remarks/advantages column provides additional information about each method:

Proposed method: The proposed method offers improved power allocation, ensuring that power is distributed optimally among the distributed generation sources and the mains. It takes into account the specific requirements of local loads and common loads, resulting in efficient power sharing.

Traditional rule-based approach: The traditional rule-based approach is simple to implement but falls short in achieving optimal power distribution. It may overlook the specific characteristics and capabilities of the different generation sources, leading to suboptimal allocation of power.

Simple load-sharing scheme: The simple load-sharing scheme lacks efficiency in power allocation. It does not consider the specific requirements and capabilities of individual sources, resulting in inefficient allocation of power among the sources.

Overall, the table highlights the advantages of the proposed method in terms of high efficiency and optimal power distribution compared to the traditional rule-based approach and simple load-sharing scheme.

Table 4 compares different methods for power allocation in a microgrid. It provides information on the efficiency, optimal power distribution, and remarks/advantages of each method.

Table 4

Table 4. Power allocation comparison.

Table 5 compares different methods for load balancing and harmonics compensation in a microgrid. It provides information on the load balancing capability, harmonics compensation, and remarks/advantages of each method.

• Proposed Method: The proposed method demonstrates effective load balancing and harmonics control. It is designed to balance the load among different distributed generation sources and compensates for harmonics, resulting in efficient load management and improved power quality.

• Droop Control: Droop control exhibits partial load balancing capability but does not provide harmonics compensation. It regulates the power output of the sources based on the frequency and voltage droop characteristics, but it may not achieve precise load balancing and lacks harmonics compensation features.

• Passive Filtering: Passive filtering does not offer load balancing capability but provides harmonics compensation. It utilizes passive components to filter out harmonic components from the power system, improving the power quality by reducing harmonics. However, it does not actively balance the load among the sources.

Table 5

Table 5. Load balancing and harmonics compensation comparison.

The remarks/advantages column provides additional information about each method:

• Proposed Method: The proposed method excels in load balancing, effectively distributing the load among the distributed generation sources. It also provides harmonics compensation, ensuring a clean and high-quality power supply. This approach offers comprehensive control and management of load and harmonics.

• Droop Control: Droop control has limited load balancing capability as it adjusts the power output of the sources based on droop characteristics. However, it does not address harmonics compensation, which may result in a suboptimal power quality in the microgrid.

• Passive Filtering: Passive filtering specializes in harmonics compensation by reducing harmonic components in the power system. However, it does not actively balance the load among the sources. It can be advantageous in mitigating harmonics-related issues but may not address load balancing requirements.

Overall, the table highlights the advantages of the proposed method in terms of effective load balancing and harmonics control compared to droop control and passive filtering. It offers a comprehensive solution for managing load distribution and improving power quality in the microgrid.

Table 6 compares different methods for reactive power control in a power system. It provides information on the accuracy, responsiveness, stability, and remarks/advantages of each method.

• Proposed Method: The proposed method demonstrates high accuracy in reactive power control. It is designed to provide precise and reliable control of reactive power in the system. It also exhibits high responsiveness, meaning it can quickly adjust the reactive power output in response to system dynamics. The proposed method is stable, ensuring consistent and reliable reactive power control.

• Power Factor Correction: Power factor correction methods show moderate accuracy and responsiveness in reactive power control. They are designed to adjust the power factor of the system by compensating for reactive power. These methods provide basic reactive power control, but they may not offer the same level of accuracy and responsiveness as the proposed method. They are stable, ensuring a steady power factor correction.

• Static VAR Compensator (SVC): SVCs offer high accuracy in reactive power control. They are capable of precise control of reactive power output in the system. However, their responsiveness is moderate, meaning they may have a slower response time compared to the proposed method. SVCs provide additional features, such as voltage control and power factor correction. They are stable, ensuring reliable reactive power control with enhanced capabilities.

Table 6

Table 6. Reactive power control comparison.

The remarks/advantages column provides additional information about each method:

• Proposed Method: The proposed method excels in accuracy, responsiveness, and stability in reactive power control. It ensures accurate control of reactive power and can quickly respond to system dynamics. This method provides reliable and consistent reactive power control, meeting the specific requirements of the power system.

• Power Factor Correction: Power factor correction methods offer basic reactive power control, adjusting the power factor of the system. They provide moderate accuracy and responsiveness, ensuring stable power factor correction. These methods are suitable for improving the power factor but may not provide the same level of accuracy as the proposed method.

• Static VAR Compensator (SVC): SVCs deliver high accuracy in reactive power control. They offer precise control of reactive power and provide additional features such as voltage control and power factor correction. However, their responsiveness may be slower compared to the proposed method. SVCs provide stable reactive power control with added functionalities.

Overall, the table highlights the advantages of the proposed method in terms of accurate and responsive reactive power control. While power factor correction methods and SVCs have their advantages, the proposed method stands out in terms of accuracy and responsiveness, ensuring stable and reliable reactive power control in the power system.

Table 7 compares different methods for improving the voltage profile in a power system. It provides information on voltage fluctuations, voltage profile improvement, and remarks/advantages of each method.

• Proposed Method: The proposed method demonstrates reduced voltage fluctuations and improved voltage profile in the power system. It effectively reduces the variations in voltage levels and enhances the overall voltage profile. This method offers an effective solution for improving the voltage profile in the system.

• Voltage Regulation Schemes: Voltage regulation schemes partially reduce voltage fluctuations and partially improve the voltage profile. These schemes aim to regulate the voltage levels within certain limits. While they contribute to some improvement in the voltage profile, their impact may be limited compared to the proposed method.

• Voltage Control Devices: Voltage control devices have limited effects on voltage fluctuations and voltage profile improvement. These devices are designed to control voltage levels in specific locations or sections of the power system. However, their impact on the overall voltage profile improvement may be minimal.

Table 7

Table 7. Voltage profile improvement comparison.

The remarks/advantages column provides additional information about each method:

• Proposed Method: The proposed method effectively reduces voltage fluctuations and significantly improves the voltage profile in the power system. It provides a reliable and efficient solution for achieving an improved voltage profile.

• Voltage Regulation Schemes: Voltage regulation schemes offer partial reduction in voltage fluctuations and partial improvement in the voltage profile. While they contribute to maintaining voltage levels within acceptable limits, their impact on overall voltage profile improvement may be limited.

• Voltage Control Devices: Voltage control devices have limited effects on voltage fluctuations and voltage profile improvement. They provide localized voltage control but may not have a significant impact on improving the overall voltage profile.

• Overall, the table highlights the advantages of the proposed method in terms of reduced voltage fluctuations and improved voltage profile. While voltage regulation schemes and voltage control devices have their merits, the proposed method stands out in terms of effective voltage profile improvement. It offers a comprehensive solution for enhancing the voltage profile in the power system.

3.2 Quantitative comparison table

Table 8 presents a quantitative comparison of three prominent control strategies—LQR + ES, Droop Control, and Passive Filtering—across four critical performance metrics: Efficiency (%), Load Balancing Capability (%), Voltage Profile Improvement (%), and Scalability. Efficiency measures the system’s ability to minimize power losses during operation, reflecting how effectively each strategy conserves energy within the microgrid. Load Balancing Capability assesses the effectiveness of the control strategy in distributing power among Distributed Generators (DGs) and the mains, which is crucial for maintaining system stability and preventing overloading of individual components. Voltage Profile Improvement evaluates the strategy’s success in stabilizing voltage levels and mitigating fluctuations, thereby ensuring reliable power quality for sensitive loads. Lastly, Scalability indicates the ease with which each control strategy can be adapted to larger and more complex microgrid configurations, highlighting the strategy’s flexibility and applicability in diverse operational scenarios.

Table 8

Table 8. Quantitative comparison of control strategies.

The integration of a Linear Quadratic Regulator (LQR) with Electric Springs (ES), referred to as LQR + ES, significantly outperforms traditional control methods such as Droop Control and Passive Filtering across all evaluated performance metrics. Specifically, LQR + ES achieves an impressive 95% efficiency, demonstrating its superior capability in minimizing power losses and optimizing energy utilization within the microgrid. Additionally, it exhibits a 95% Load Balancing Capability, indicating highly effective distribution of power among DG sources and the mains, which is essential for maintaining system equilibrium and preventing the overburdening of individual generators. In terms of voltage regulation, LQR + ES offers a 90% Voltage Profile Improvement, showcasing its robust ability to stabilize voltage levels and mitigate fluctuations, thereby enhancing overall power quality and reliability.

In contrast, Droop Control demonstrates moderate performance with a 75% efficiency and 60% Load Balancing Capability, indicating that while it can effectively distribute power to some extent, it falls short in optimizing energy use and maintaining balanced loads under varying conditions. Moreover, its ability to improve voltage profiles is limited, achieving only a 50% Voltage Profile Improvement. This suggests that Droop Control may struggle to maintain voltage stability in the face of significant load changes or renewable energy integration, potentially leading to power quality issues.

Passive Filtering, on the other hand, excels in enhancing voltage profiles, achieving an 85% Voltage Profile Improvement, which underscores its effectiveness in mitigating harmonic distortions and stabilizing voltage levels. However, it lacks in other critical areas, with a 60% efficiency and 0% Load Balancing Capability, indicating that while it can improve power quality, it does not contribute to the distribution of power among DGs and the mains. Consequently, Passive Filtering may not address fundamental issues related to load imbalance and energy optimization, limiting its overall effectiveness as a standalone control strategy.

Furthermore, the Scalability of each control strategy varies significantly. LQR + ES is rated as High, highlighting its adaptability and suitability for large-scale microgrid implementations with multiple DG sources and complex load profiles. Droop Control is rated as Moderate, suggesting that while it can be applied to larger systems, its performance may degrade as system complexity increases. Passive Filtering is rated as Low in scalability, indicating limited applicability in expansive or highly dynamic microgrid environments where flexible and adaptive control mechanisms are required.

In summary, the LQR + ES combination offers a comprehensive and highly effective control solution that not only optimizes energy efficiency and load distribution but also ensures robust voltage regulation and scalability. This integrated approach addresses the shortcomings of traditional methods, making it a superior choice for modern microgrids aiming for enhanced performance, reliability, and adaptability.

4 Conclusion

Connection of distributed generation to the network through electronic power converters increase concerns about the quality and proper allocation of power between different DG sources and the network. Microgrids could generally be considered a bunch of distributed generation sources, usually connected to the mains by some voltage source converters. Unbalanced and nonlinear loads can interfere with the microgrid performance. Additionally, voltage source converters, including DG sources, are themselves the source of the harmonic output. Accordingly, the structure of a compensator was introduced to solve problems caused by unbalanced loads and harmonics due to switching. The proposed compensator was designed to be suitable for supplying the microgrid electrical power while compensating for the effects of load imbalance and nonlinearity. Next, to control the compensators and perform the optimal and stable switching, we designed a state feedback controller with the presence of a linear quadratic regulator. In this mode feedback controller, local signals were used as feedback to control the converter. In designing the state feedback controller to control the compensators, to balance the network and compensate for the imbalances, the voltage and current of the converter must follow a series of reference values. In the case of islands, the power allocation between distributed generation sources is based on the drop characteristic, and the drop coefficients are selected using the nominal values of DGs. After reviewing the performance of the proposed LQR controller in both island and grid-connected modes, it Is observed that this controller performed relatively well in establishing network balance and improving the power quality in both modes.

This paper also proposed a control strategy to improve voltage regulation using electronic switch (ES), in microgrids in normal condition and in load change and variability of renewable energy sources conditions. In this control method, by adjusting the phase angle and ES amplitude, voltage support is provided to prevent the voltage drop and improve the voltage regulation. The results of the studies indicate that the use of ES not only enhances the voltage regulation by improving the system voltage level in the network, but also does not disrupt the insensitive load voltage. Thus, the permanent presence of ES in the network improves voltage profile. As explained in the introduction, in the future, intelligent methods will replace algorithms such as GA, PSO and GSO, but they have weaknesses such as computational delay. With the advancement of technology, these algorithms can be used to increase the accuracy and reduce the error of intelligent methods before applying them to the system.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Ethics statement

The studies involving humans were approved by ISLAMIC AZAD UNIVERSITY BYAZD BRANCH. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

HA: Writing–original draft, Writing–review and editing, Project administration, Methodology. MS: Software, Writing–original draft, Writing–review and editing. ZB: Methodology, Software, Writing–original draft, Writing–review and editing. SM: Methodology, Software, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aderibole, A., Zeineldin, H. H., Al Hosani, M., and El-Saadany, E. F. (2019). Demand side management strategy for droop-based autonomous microgrids through voltage reduction. IEEE Trans. Energy Convers. 34, 878–888. doi:10.1109/tec.2018.2877750

CrossRef Full Text | Google Scholar

Adiche, S., Larbi, M., Toumi, D., Bouddou, R., Bajaj, M., Bouchikhi, N., et al. (2024). Advanced control strategy for AC microgrids: a hybrid ANN-based adaptive PI controller with droop control and virtual impedance technique. Sci. Rep. 14, 31057. doi:10.1038/s41598-024-82193-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Alwal, L. A., Kihato, P. K., and Kamau, S. I. (2022). “A review of control strategies for microgrid with PV-wind hybrid generation systems,” in Proceedings of the sustainable research and innovation conference, 243–250.

Google Scholar

Babazadeh, M., and Nobakhti, A. (2018). Robust decomposition and structured control of an islanded multi-DG microgrid. IEEE Trans. Smart Grid 10, 2463–2474. doi:10.1109/tsg.2018.2798617

CrossRef Full Text | Google Scholar

Badoni, M., Singh, A., Singh, A. K., Saxena, H., and Kumar, R. (2021). Grid tied solar PV system with power quality enhancement using adaptive generalized maximum Versoria criterion. CSEE J. Power Energy Syst. doi:10.17775/CSEEJPES.2020.04820

CrossRef Full Text | Google Scholar

Bizon, N., and Thounthong, P. (2020). Energy efficiency and fuel economy of a fuel cell/renewable energy sources hybrid power system with the load-following control of the fueling regulators. Mathematics 8, 151. doi:10.3390/math8020151

CrossRef Full Text | Google Scholar

Chandak, S., Sahoo, B., Kumar Rout, P., Mishra, S., and Mishra, M. (2022). “A brief analysis on microgrid control,” in Innovation in electrical power engineering, communication, and computing technology (Singapore: Springer), 541–553.

CrossRef Full Text | Google Scholar

Chauhan, S., and Singh, B. (2022). Utility intertie multi-photovoltaic-inverters-based microgrid control for solar rooftop. IET Energy Syst. Integr. 4, 247–266. doi:10.1049/esi2.12058

CrossRef Full Text | Google Scholar

Chen, J., Yan, S., Yang, T., Tan, S. C., Hui, S. Y. R., and Hui, R. (2018a). Practical evaluation of droop and consensus control of distributed electric springs for both voltage and frequency regulation in microgrid. IEEE Trans. Power Electron. 34, 6947–6959. doi:10.1109/tpel.2018.2874495

CrossRef Full Text | Google Scholar

Cheng, L., Yu, T., Zhang, X., and Yang, B. (2018). Parallel cyber-physical-social systems based smart energy robotic dispatcher and knowledge automation: concepts, architectures, and challenges. IEEE Intell. Syst. 34 (2), 54–64. doi:10.1109/mis.2018.2882360

CrossRef Full Text | Google Scholar

Córdova, S., Cañizares, C. A., Lorca, Á., and Olivares, D. E. (2022). Frequency-constrained energy management system for isolated microgrids. IEEE Trans. Smart Grid 13, 3394–3407. doi:10.1109/tsg.2022.3170871

CrossRef Full Text | Google Scholar

da Costa, J. N. N., Passos Filho, J. A., and Peres, W. (2024). Development of steady-state voltage control techniques applied to microgrids. IEEE Access 12, 83887–83899. doi:10.1109/access.2024.3410955

CrossRef Full Text | Google Scholar

Hamza, A., Hussain Rizvi, S. T., Safder, M. U., and Asif, H. (2022). A novel mathematical approach to model multi-agent-based main grid and microgrid networks for complete system analysis. Machines 10 (2), 110. doi:10.3390/machines10020110

CrossRef Full Text | Google Scholar

Konneh, K. V., Bode Adewuyi, O., Elsayed Lotfy, M., Sun, Y., and Senjyu, T. (2022a). Application strategies of model predictive control for the design and operations of renewable energy-based microgrid: a survey. Electronics 11 (4), 554. doi:10.3390/electronics11040554

CrossRef Full Text | Google Scholar

Konneh, K. V., Bode Adewuyi, O., Elsayed Lotfy, M., Sun, Y., and Senjyu, T. (2022b). Application strategies of model predictive control for the design and operations of renewable energy-based microgrid: a survey. Electronics 11 (4), 554. doi:10.3390/electronics11040554

CrossRef Full Text | Google Scholar

Lin, F.-J., Tan, K.-H., Chang, C.-Fu, Li, M.-Y., and Tseng, T.-Yu (2022). Development of intelligent controlled microgrid for power sharing and load shedding. IEEE Trans. Power Electron. 37, 7928–7940. doi:10.1109/tpel.2022.3152167

CrossRef Full Text | Google Scholar

Mancera, J. J. C., Saenz, J. L., López, E., Andújar, J. M., Manzano, F. S., Vivas, F. J., et al. (2022). Experimental analysis of the effects of supercapacitor banks in a renewable DC microgrid. Appl. Energy 308, 118355. doi:10.1016/j.apenergy.2021.118355

CrossRef Full Text | Google Scholar

Mohanty, S., Pati, S., and Kar, S. K. (2024). Improved islanded microgrid performance with sliding mode controller based electric spring. Renew. Energy Focus 48, 100535. doi:10.1016/j.ref.2023.100535

CrossRef Full Text | Google Scholar

Roslan, M. F., Hannan, M. A., Jern Ker, P., Mannan, M., Muttaqi, K. M., and Mahlia, T. M. I. (2022). Microgrid control methods toward achieving sustainable energy management: a bibliometric analysis for future directions. J. Clean. Prod. 348, 131340. doi:10.1016/j.jclepro.2022.131340

CrossRef Full Text | Google Scholar

Schaub, P., and Ulrich, K. (2023). 2023 27th international conference on system theory, control and computing (ICSTCC). Structured linear quadratic regulator design.

Google Scholar

Shahzad, E., Khan, A. U., Iqbal, M., Saeed, A., Hafeez, G., Waseem, A., et al. (2022). Sensor Fault-tolerant control of microgrid using robust sliding-mode observer. Sensors 22 (7), 2524. doi:10.3390/s22072524

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharma, A., Achlerkar, P. D., and Bijaya, K. P. (2023). Assessment of linear quadratic regulator based optimal stabilization of weak-grid-following inverter interface. IEEE Trans. Power Deliv. 38 (5), 3647–3659. doi:10.1109/tpwrd.2023.3283280

CrossRef Full Text | Google Scholar

Sheykhi, N., Salami, A., Guerrero, J. M., Agundis-Tinajero, G. D., and Faghihi, T. (2022). A comprehensive review on telecommunication challenges of microgrids secondary control. Int. J. Electr. Power and Energy Syst. 140, 108081. doi:10.1016/j.ijepes.2022.108081

CrossRef Full Text | Google Scholar

Subramani, C., and Ramanand, K. R. (2018). A brief review on electric spring: analysis, control and applications. J. Circuits, Syst. Comput. 27 (05), 1830002. doi:10.1142/s0218126618300027

CrossRef Full Text | Google Scholar

Yang, T., Liu, T., Chen, J., Yan, S., Hui, S. Y. R., and Hui, R. (2018). Dynamic modular modeling of smart loads associated with electric springs and control. IEEE Trans. Power Electron. 33, 10071–10085. doi:10.1109/tpel.2018.2794516

CrossRef Full Text | Google Scholar

Yin, F., Wang, C., and Wang, W. (2022). Adaptive sliding-mode control for electric spring in microgrids with distributed renewable energy. Energies 15, 4842. doi:10.3390/en15134842

CrossRef Full Text | Google Scholar

Zheng, Y., Hill, D. J., Song, Y., Zhao, J., and Hui, S. Y. R. (2020). Optimal electric spring allocation for risk-limiting voltage regulation in distribution systems. IEEE Trans. Power Syst. 35, 273–283. doi:10.1109/tpwrs.2019.2933240

CrossRef Full Text | Google Scholar