Optimal dispatch of integrated energy system considering time-space dimensional demand response based on time-of-use electricity price

Demand response has significant potential for enhancing energy utilization, thereby contributing to the advancement of integrated energy systems (IES). In this paper, an optimal IES dispatch model fully incorporating flexible loads on the demand sides is established. Firstly, based on time-of-use (ToU) electricity pricing, a flexible two-dimensional integrated demand response (IDR) model is presented, which is characterized by considering tightly spatial-temporal coupling characteristics of different loads. Subsequently, a day-ahead dispatch model for IES, incorporating ToU-based IDR, is developed to minimize the total operational cost. In this model, the optimal ToU pricing scheme is determined by comparing their economic efficiencies. The Particle Swarm Optimization (PSO) algorithm is then applied to solve the complex dispatch problem. Finally, the case study is conducted and the comparative results confirm that: 1) implementation of the IDR in time-space dimension can flatten the loads curves; 2) the time-space IDR significantly promotes the economic benefits of IES dispatch; 3) the proposed dispatch model is able to coordinate and optimize various types of energy and flexible loads.

1 Introduction

Energy shortages and environmental pollution have been critical challenges in the development of countries worldwide. In terms of the utilization of renewable energy, the ongoing development and deployment of renewable energy sources such as wind power, photovoltaics, and hydroelectric power generation have become hot topics. Traditionally, the power system scheduling has focused primarily on the supply side, coordinating the output of various types of generators to minimize scheduling cost. The research on power system optimal scheduling mainly includes unit combination methods, multi-time scale optimization scheduling strategies, and uncertain scheduling of the power grid. From the perspective of improving energy efficiency, the integrated energy system (IES) technology has emerged (Zhang et al., 2022; Dou et al., 2024). IES is an important form of coupling multiple energy sources such as electricity, gas and heat, enabling the comprehensive planning and unified dispatch of different energy systems. IES facilitates cascaded energy utilization, which not only improves energy efficiency but also promotes the integration of renewable energy sources. Scholars began to explore the flexibility of user-side scheduling, aiming to enhance the grid’s regulation capacity. This is referred to demand-side response. The demand response technologies in IES are evolving toward large-scale integrated demand response (IDR) (Zhang et al., 2022; Dou et al., 2024; Hossein Yaghmaee, 2024; Li et al., 2023; Gu et al., 2023; Wang et al., 2023; Feng et al., 2020; Yang Cui et al., 2022; Yang et al., 2020; Duan et al., 2022; Yang Li et al., 2022; Liang et al., 2022; Shao et al., 2021). IDR is a promising approach, which adjusts energy consumption patterns based on temporal characteristics and price signals within the IES. By improving the flexibility of energy consumption, IDR has emerged as a crucial technology for balancing supply and demand, gaining significant attention in recent years.

IDR plays a pivotal role in advancing energy conservation, reducing emissions, and supporting the achievement of carbon emission reduction goals. IDR achieves cascaded energy utilization and enhance energy efficiency through the conversion between different forms of energy and the complementary characteristics of load energy consumption patterns. Significant research has been conducted on IDR strategies and the optimal operation considering IDR in IES. Reference (Zhang et al., 2022; Dou et al., 2024) proposes an IES optimization scheduling model that incorporates IDR and dynamic energy prices, aiming to maximize the economic benefits for both users and suppliers while considering the interests of multiple stakeholders. Reference (Zhang et al., 2022; Dou et al., 2024) introduces a low-carbon economic dispatch model for source-load coordination in IES, which accounts for generalized electric-thermal demand response. This model improves carbon capture at power plants during peak load periods, thus balancing economic and environmental objectives. Reference (Zhang et al., 2022; Dou et al., 2024) suggests an optimization approach for the source-network-load scheduling in IES through IDR participation. This method decouples the operation mode of combined cooling heating, and power (CCHP) systems and wind curtailment, thereby enhancing the integration of wind power within the system. Reference (Zhang et al., 2022; Dou et al., 2024) presents an optimization method for electricity and natural gas coupled systems that accounts for IDR uncertainty based on opportunity constraints. Reference (Zhang et al., 2022; Dou et al., 2024) explores the uncertain optimization scheduling problem of community IES considering comprehensive demand response and electric vehicles, with the goals of minimizing system operating costs. Reference (Zhang et al., 2022; Dou et al., 2024) conducts a detailed classification study on load types in IDR, establishing models for uncontrollable loads, transferable loads, reducible loads, and substitutable loads, and conducting systematic two-level optimizations. Reference (Zhang et al., 2022; Dou et al., 2024) introduces an IDR model for electric-power systems based on energy hubs, which optimizes both upper-level unit combination and lower-level economic scheduling.

Although IDR technology has become a significant research focus and has yielded valuable results, there are issues that need further exploration. The major motivations of this paper are shown as follows. 1) Current research primarily concentrates on adjusting load profiles on the time dimensional IDR, with insufficient attention given to load adjustment strategies on the spatial dimension. Therefore, IDR considering the substitution characteristics of different energy across different domains remains underdeveloped. 2) The electricity, heating, and cooling loads within IES exhibit flexible characteristics, which not only help reduce peak-to-valley differences but also contribute to deducing operational costs alongside generation. Integrating comprehensive IDR across various dimensions with IES dispatch represents a promising pathway for enhancing the efficiency of IES operations. 3) Demand-side participation in the optimized operation of IES presents a complex, nonlinear, multidimensional, uncertain, and multi-party optimization challenge. How to solve the IES dispatch model with IDR is an important issue.

In conclusion, the main contributions of this paper are shown as follows. 1) This paper proposed a two-dimensional IDR model based on ToU price scheme to further explore the elasticity of demand sides. It conducts in-depth research on the time-shiftable characteristics of flexible loads and the spatial energy complementary substitution dynamics. 2) The paper explores the potential contributions of the demand side to IES dispatch optimization. An optimal IES dispatch model incorporating comprehensive IDR is developed with the goal of enhancing the economic benefits. 3) Finally, the effectiveness of the two-dimensional IDR mechanism proposed in this paper and the practicality of the IES scheduling method considering IDR are verified through simulation cases.

The rest of the paper is organized as follows. The two dimensional IDR in IES is established in Section 2. Section 3 proposes the IES dispatch model integrated with IDR strategy, which is followed by model solution algorithm description in Section 4. Case study is given in Section 5. Finally, conclusion is shown in Section 6.

2 Integrated demand response modeling in IES

Flexible load plays an important role in peak-load shifting, promoting renewable energy consumption and increasing IES economic benefits. In proposed IES dispatch with IDR problem, three forms of loads are covered, which are electricity loads, heating loads and cooling loads. The consumers can change their energy usage behaviors by price-based IDR. Not only can they directly decrease or shift a portion of the loads, but also change the form of the energy through the coupling devices (Liu et al., 2020; Siqing et al., 2024; Chen et al., 2022; Safta et al., 2017; Zeng et al., 2018; Wu et al., 2017; Cheng et al., 2022).

In ToU based IDR, the goal is to determine the optimal electricity price for the valley period (${\rho }_{valley}$), the off-peak period (${\rho }_{\text{off}-\text{peak}}$) and the peak period (${\rho }_{\text{peak}}$) in Equation 1.

$\rho =\left[\begin{array}{l}{\rho }_{Peak}\\ {\rho }_{Off-peak}\\ {\rho }_{Valley}\end{array}\right]=\left[\begin{array}{l}{\rho }_{ave}\left(1+\sigma \right)\\ {\rho }_{ave}\\ {\rho }_{ave}\left(1-\sigma \right)\end{array}\right](1)$

where $\rho$ is the electricity matrix in a typical day, ${\rho }_{\mathrm{a}ve}$ is the average price. $\sigma$ represents the ration of up and down in peak period and the valley period, respectively.

2.1 Time-space dimension based IDR

In IES, controllable loads on the demand side represent a valuable flexible resource. Demand response can not only adjust energy consumption in the time dimension through load shedding and load shifting, but also in the spatial dimension by enabling the flexible switching between different forms of energy consumption, including electricity, gas, heating, and cooling, thereby facilitating complementary substitution of energy sources (Liu et al., 2020; Siqing et al., 2024; Chen et al., 2022; Safta et al., 2017; Zeng et al., 2018; Wu et al., 2017; Cheng et al., 2022). In the time dimension, users adjust their energy consumption patterns and shift energy use to periods of lower prices based on electricity price signals. In the spatial dimension, the price curves for electricity and natural gas typically exhibit temporal variations. During peak pricing periods for a specific energy form, users can shift alternative energy sources, optimizing their energy consumption decisions and enabling flexible adjustments in response to spatial price variations. The specific model for two-dimensional demand response within IES is formulated as Equation 2:

$\begin{array}{l}{d}_{DR,af}^{*}\left(t\right)=d_{DR,ini}^{*}\left(t\right)+\Delta d_{DR,Te}^{*}\left(t\right)+\Delta d_{DR,Sp}^{*}\left(t\right)\\ *\in \left\{electricity,heat,cool\right\}\end{array}(2)$

where $d_{DR,af}^{*}\left(t\right)$ is the load demand after IDR; $d_{DR,ini}^{*}\left(t\right)$ is the initial load demand before IDR; $\Delta d_{DR,Te}^{*}\left(t\right)$ is the load increment in time dimensional IDR; $\Delta d_{DR,Sp}^{*}\left(t\right)$ is the demand response load increment in spatial dimensional IDR.

2.1.1 IDR in time dimension

In time-dimensional IDR (TE-IDR) model, the relationship between user response and electricity/gas prices is represented by the demand price elasticity. Demand price elasticity is defined as the sensitivity of users’ electricity consumption to changes in electricity prices, specifically representing the relationship between the rate of change in consumption and the rate of change in electricity or gas prices. At any certain moment, the energy consumption of users is not only influenced by the current price of the energy, but also by the price of the energy at previous or future time points (Zhang et al., 2022; Cheng et al., 2022). The price elasticity is defined as Equation 3:

$E\left(t,t^{\prime }\right)=\frac{\mathrm{\partial }d\left(t\right)/d_0\left(t\right)}{\mathrm{\partial }{\rho }_E\left(t^{\prime }\right)/{{\rho }_{E,}}_0\left(t^{\prime }\right)}(3)$

where E is the elasticity, d(t) and d₀(t) are the electricity load demand after and before the IDR, respectively, and ${\rho }_E$ and ${{\rho }_{E,}}_0$ are the electricity price after and before the IDR, respectively.

For 24 h in a day, self and cross elasticity values can be formulated as the matrix in Equation 4:

$\left[\begin{array}{l}\frac{\Delta d\left(1\right)}{d_o\left(1\right)}\\ \frac{\Delta d\left(2\right)}{d_o\left(2\right)}\\ ...\\ \frac{\Delta d\left(24\right)}{d_o\left(24\right)}\end{array}\right]=\left[\begin{array}{ccc}E\left(1,1\right)& ...& E\left(1,24\right)\\ ...& ...& ...\\ E\left(24,1\right)& ...& E\left(24,24\right)\end{array}\right]\times \left[\begin{array}{l}\frac{\Delta {\rho }_E\left(1\right)}{{\rho }_{E,o}\left(1\right)}\\ \frac{\Delta {\rho }_E\left(2\right)}{{\rho }_{E,o}\left(2\right)}\\ ...\\ \frac{\Delta {\rho }_E\left(24\right)}{{\rho }_{E,o}\left(24\right)}\end{array}\right](4)$

In multi-energy system, the price-based load responsive model in Equation 5 base on cross elasticity of different loads in multiple periods (24 h) is:

$\begin{array}{l}{\mathit{d}}^{*}\left(\mathit{t}\right)={\mathit{d}}_{\mathit{0}}^{*}\left(\mathit{t}\right)\times \left(1+{\displaystyle \sum _{{\mathit{t}}^{\prime }=1}^{24}}\frac{{\mathit{\rho }}_{\mathit{E}}\left({\mathit{t}}^{\prime }\right)-{{\mathit{\rho }}_{\mathit{E},}}_0\left({\mathit{t}}^{\prime }\right)}{{\mathit{\rho }}_{\mathit{E},0}\left(\mathit{t}\right)}{\mathrm{E}}_{\mathit{\text{Te}}}^{*}\left(\mathit{t},{\mathit{t}}^{\prime }\right)\right)\\ *\in \left\{\mathit{\text{electricity}},\mathit{\text{heat}},\mathit{\text{cool}}\right\}\end{array}(5)$

Therefore, in the time dimension, the energy demand for electricity, heating and cooling loads participating in the demand response is in Equation 6:

$\left.\Delta d_{DR,Te}^{*}\left(t\right)=d_{\mathit{0}}^{*}\left(t\right)\times {\lambda }_{user}{\displaystyle \sum _{t^{\prime }=1}^{24}}\frac{{\rho }_E\left(t^{\prime }\right)-{{\rho }_{E,}}_0\left(t^{\prime }\right)}{{\rho }_{E,0}\left(t\right)}{\mathrm{E}}_{Te}^{*}\left(t,t^{\prime }\right)\right))(6)$

where ${\mathrm{E}}_{Te}^{*}$ is the elasticity coefficient of different load in time-dimensional IDR; ${\lambda }_{user}$ is the participation percentage of customers in a IDR program.

2.1.2 IDR in spatial dimension

Energy prices and load curves vary across different forms of energy. Users can choose the energy source that best aligns with their quality requirements, taking into account the relative price differences between various energy types. This enables the complementary substitution of energy in the spatial dimension, thereby promoting the rational utilization of resources and achieving flexibility in IES regulation. Equations 7, 8 show the coupling characteristics between loads:

$\left\{\begin{array}{l}{d}_E\left(t\right)=d_{EE}\left(t\right)+d_{EH}\left(t\right)+d_{EC}\left(t\right)\\ d_H\left(t\right)=d_{HH}\left(t\right)+d_{HE}\left(t\right)+d_{HC}\left(t\right)\\ d_C\left(t\right)=d_{CC}\left(t\right)+d_{CE}\left(t\right)+d_{CH}\left(t\right)\end{array}\right.(7)$

$d_{\xi ,{\xi }^{\prime }}\left(t\right)=-d_{{\xi }^{\prime },\xi }\left(t\right)(8)$

where E, H and C stand for electricity, heating and cooling symbol, respectively; $d_E\left(t\right),d_H\left(t\right),d_C\left(t\right)$ represents load demand of electricity, heating and cooling, respectively; $d_{\xi ,{\xi }^{\prime }}\left(t\right)\left(\xi ,{\xi }^{\prime }\in \left\{E,H,C\right\}\right)$ are coupling between two forms of loads.

In the space-dimensional IDR (SP-IDR), the energy load increment for electricity, heating, and cooling loads involved in IDR is expressed as Equation 9:

$\begin{array}{l}\Delta d_{DR,Sp}^E\left(t\right)={\lambda }_{user}{\eta }_{EH}{d}_{EH}\left(t\right)+{\lambda }_{user}{\eta }_{EC}{d}_{EC}\left(t\right)\\ \Delta d_{DR,Sp}^H\left(t\right)={\lambda }_{user}{\eta }_{HE}{d}_{HE}\left(t\right)+{\lambda }_{user}{\eta }_{HC}{d}_{HC}\left(t\right)\\ \Delta d_{DR,Sp}^C\left(t\right)={\lambda }_{user}{\eta }_{CE}{d}_{CE}\left(t\right)+{\lambda }_{user}{\eta }_{CH}{d}_{CH}\left(t\right)\end{array}(9)$

where ${\lambda }_{user}$ denotes the probability of selecting an energy complementary alternative for various types of loads at time t; ${\eta }_{\xi ,{\xi }^{\prime }}\left(t\right)\left(\xi ,{\xi }^{\prime }\in \left\{E,H,C\right\}\right)$ represents the energy conversion coefficients between different energy types.

In price-based IDR, transformable loads adjust the form of consumed energy based on the price difference signal between electricity and gas prices. For simplicity, electricity, heating, and cooling loads are converted to gas demand either directly or indirectly. In this context, the space-dimensional IDR is regarded as a virtual energy converter. Considering the coupling characteristics of the loads, the price-based IDR in the space dimension can be expressed as Equation 10.

$\begin{array}{c}\Delta d_{DR,Sp}^{*}\left(t\right)=d_{\mathit{0}}^{*}\left(t\right)\times {\lambda }_{user}\frac{{\rho }_E\left(t\right)-{\rho }_G\left(t\right)}{{\rho }_G\left(t\right)}{\mathrm{E}}_{Sp}^{*}\left(t\right)\\ *\in \left\{electricity,heat,cool\right\}\end{array}(10)$

$\Delta d_{DR,Sp}^{*}\left(t\right)={\eta }_{*,g}\cdot \Delta d_{DR,Sp}^{Gas}\left(t\right)(11)$

where $d_0^{*}\left(t\right)$ is the load demand under basic electricity price and gas price; ${\mathrm{E}}_{Sp}^{*}$ denotes the elasticity coefficient of different load in spatial-dimensional IDR; ${\rho }_G$ is the natural gas price; ${\eta }_{*,g}$ represents the conversion efficiency of electricity/heating/cooling loads to gas demand; $\Delta d_{DR,Sp}^{Gas}$ is the amount of load increment converted to the natural gas loads.

3 IES dispatch formulation with two-dimensional IDR

The IES dispatch problem is crucial for the development of energy systems. In an IES, parts of generations and controllable loads are both adjustable units. The specific IES architecture in this paper is illustrated in Figure 1. It mainly includes power to gas (P2G), combined cooling heating power (CCHP) system, electric boiler (EB), electric chiller (EC), absorption chiller (AC) and gas boiler (GB). For electricity load, it is serviced by main power grid, P2G and CHP. If there is any remaining electricity, it will be sold excess power to the gird. The heating and cooling load must be supplied by coupled devices. For heating load, it is jointly provided by the EB, GB and CCHP. For cooling load, it is supplied by EC, CCHP and AC. Meanwhile, consumers can change the energy demand by ToU-based IDR.

Figure 1

Figure 1. IES structure.

3.1 Problem description

Various load curves generated by price-based IDR under different energy prices lead to distinct optimal dispatch results. Therefore, if the electricity price is taken as the variables of IES dispatch problems, the adjustment of IES will be improved. However, treating electricity prices as decision variables in the dispatch model result in excessively large computational scales and low calculation efficiency. The structure of the IES dispatch problem incorporating IDR is illustrated in Figure 2. Different electricity price schemes are used as input variables, and a set of load curves is generated under two-dimensional IDR. Then, based on these different load curve schemes, the IES dispatch model considering IDR is developed. Next, the best IES dispatch solution under a load curve is obtained based on PSO algorithm. Finally, the most economic dispatch scheme with different load curves is selected and optimal ToU electricity price is determined.

Figure 2

Figure 2. Block diagram of IES dispatch considering IDR.

3.2 IES dispatch considering IDR

3.2.1 Objective functions

Based on the established time-space dimensional IDR, the load curves are optimized. The goal of the IES dispatch is to achieve economically optimal operation for supplying various type of loads [Liu et al., 2020]. It considers the operation costs of different components in the IES, which can be expressed as Equations 12–15:

$\mathit{min}f={\displaystyle \sum _{t=1}^T}{C}_{Ope}\left(t\right)(12)$

The operation cost C_ope represents the operation cost in a typical day. It consists of purchased cost of electricity and gas C_pur, as well as the income generated from the sale of electricity C_sel.

$C_{ope}\left(t\right)=C_{pur}\left(t\right)-C_{Sel}\left(t\right)(13)$

$C_{pur}\left(t\right)={\rho }_{pur,Gas}\left(t\right)\left(V_{gas}\left(t\right)+\Delta d_{DR,Sp}^{Gas}\left(t\right)\right)+{\rho }_{pur,Ele}\left(t\right)P_{pur}\left(t\right)(14)$

$C_{Sel}\left(t\right)={\rho }_{Sel,Ele}\left(t\right)P_{sel}\left(t\right)(15)$

where ${\rho }_{pur,Gas}$ and ${\rho }_{pur,Ele}$ are purchased price of gas and electricity from natural gas system or main grid; ${\rho }_{Sel,Ele}$ is the price of electricity sold to main grid; $P_{pur}$ and $P_{sel}$ are purchased power from main grid and sold power to main grid respectively; $V_{gas}$ is the volume of gas purchased from natural gas system; $\Delta d_{DR,Sp}^{Gas}\left(t\right)$ represents the amount of the electricity/heating/cooling load converted to gas demand in space-dimensional IDR.

3.2.2 Decision variables

In IES dispatch process, the primary goal is to optimize the quantities of electricity and natural gas to be purchased or sold, as well as the operation of the coupling devices. Therefore, in IES dispatch model considering IDR, the decisions variables are represented by matrix in Equations 16–18:

$X=\left[\sigma ,X_{ope}\right](16)$

$X_{ope}=\left[X_{ope}\left(1\right),X_{ope}\left(2\right),......,X_{ope}\left(t\right),....X_{ope}\left(T\right)\right](17)$

$\begin{array}{l}{X}_{ope}\left(t\right)=\left[P_{pur}\left(t\right),P_{sel}\left(t\right),P_{P2G}\left(t\right),P_{EB}\left(t\right),P_{EC}\left(t\right),V_{gas}\left(t\right),V_{CCHP}\left(t\right),V_{GB}\left(t\right),H_{AC}\left(t\right)\right]\\ t=1,...,T\end{array}(18)$

where T (T = 24) is the time slots number in a typical day.

3.2.3 Constraints

The IES purchases electricity and natural gas from the external network to meet the load demand, while the heating and cooling loads are supplied by the coupling equipment (Safta et al., 2017; Zeng et al., 2018; Wu et al., 2017; Cheng et al., 2022; Lu et al., 2021). To ensure the system operates efficiently, the following energy balance constraints must be satisfied, including power balance (Equation 19), gas balance (Equation 20), heating balance (Equation 21), and cooling balance (Equation 22).

$P_{pur}\left(t\right)-P_{sel}\left(t\right)=P_{P2G}\left(t\right)-P_{CCHP}\left(t\right)+P_{EB}\left(t\right)+P_{EC}\left(t\right)+d_E\left(t\right)(19)$

$V_{gas}\left(t\right)+V_{P2G}\left(t\right)=V_{CCHP}\left(t\right)+V_{GB}\left(t\right)(20)$

$H_{CCHP}\left(t\right)+H_{EB}\left(t\right)+H_{GB}\left(t\right)=H_{AC}\left(t\right)+d_H\left(t\right)(21)$

$C_{CCHP}\left(t\right)+C_{AC}\left(t\right)+C_{EC}\left(t\right)=d_C\left(t\right)(22)$

where $P_{P2G}$ and $V_{P2G}$ are input and output of P2G device; $V_{CCHP}$ is the input of device CCHP, $P_{CCHP}$, $H_{CCHP}$ and $C_{CCHP}$ are electricity output, heating output and cooling output of device CCHP; $P_{EB},H_{EB}$ are input and output of EB device; $P_{GB},H_{GB}$ are input and output of GB device; $P_{EC},C_{EC}$ are input and output of EC device; $H_{AC},C_{AC}$ are input and output of AC device.

The energy conversion of different coupling devices is shown in Equations 23–30:

$V_{P2G}={\eta }_{P2G}{P}_{P2G}(23)$

$P_{CCHP}={\eta }_P{V}_{CCHP}(24)$

$H_{CCHP}={\eta }_H{V}_{CCHP}(25)$

$C_{CCHP}={\eta }_C{V}_{CCHP}(26)$

$H_{EB}={\eta }_{EB}{P}_{EB}(27)$

$H_{GB}={\eta }_{GB}{P}_{GB}(28)$

$C_{EC}={\eta }_{EC}{P}_{EC}(29)$

$C_{AC}={\eta }_{AC}{H}_{AC}(30)$

where ${\eta }_{P2G}$ is energy conversion efficiency of P2G; ${\eta }_P$, ${\eta }_H$ and ${\eta }_C$ are energy conversion efficiency of CCHP; ${\eta }_{EB}$ is energy conversion efficiency of EB; ${\eta }_{GB}$ is energy conversion efficiency of GB; ${\eta }_{EC}$ is energy conversion coefficient of EC; ${\eta }_{AC}$ is energy conversion coefficient of AC.

The IES can directly purchase or sell electricity to/from the external power grid. However, simultaneous purchasing and selling of electricity is not permitted. The constraint is shown in Equation 31.

$P_{pur}\left(t\right)·P_{sel}\left(t\right)=0(31)$

Equipment operation limits constraints are shown in Equation 32.

$P_{i,\min }\le P_i\left(t\right)\le P_{i,\max }(32)$

where P_i,max and P_i,min denote the maximum and minimum output value of the ith device, respectively.

4 Model solution

In this paper, an optimal IES dispatch model considering time-space dimensional IDR is proposed. Firstly, IDR model of time-space dimensions based on price elasticity is developed. The ToU electricity prices are adjusted by modifying the peak-valley price differential. A series of load curves are fitted based on ToU electricity price. Next, the IES dispatch model with IDR is established. Finally, particle swarm optimization (PSO), a popular and widely used optimization algorithm based on swarm intelligence is applied to solve the problem. The outlines of model solution based on PSO are shown as follows.

Step 1: Construct the IES. Input the devices parameters, different type of load data and energy prices.

Step 2: Choose the parameters of PSO algorithm. Initiate population P randomly: position, velocity, personal best (pbest) of PSO. Select global best (gbest) of the population.

Step 3: Calculate the fitness of each particle according to Equations 12–15 and judge the constraints in Section 3.2. If constraints are violated, handle the constraints using penalty function method.

Step 4: Determine whether the maximum number of iterations has been reached. If it has not, the iterative process continues and returns to Step 3. Otherwise, output the optimal solution.

5 Case study

5.1 Case introduction

In this paper, a district IES with a specific structure, as shown in Figure 1, is selected to optimize the IES dispatch problem. The price of natural gas is 2.63 yuan/m³, while the basic electricity price for purchasing from and selling to the main power grid are 0.5 yuan/kWh and 0.4 yuan/kWh, respectively. The electricity/heating/cooling loads on a typical day in summer are shown in Figure 3. Periods of time-of-use in IES are described in Table 1. The parameters of the energy conversion devices are shown it Table 2.

Figure 3

Figure 3. The electricity, cooling and heating load on a typical day.

Table 1

Table 1. Period of time-of-use.

Table 2

Table 2. Parameters of the conversion devices.

The following four different cases are conducted and compared to verify the proposed strategy in this paper.

Case 1. Optimal dispatch of IES without any IDR.

Case 2. Optimal dispatch of IES only with time-dimensional IDR.

Case 3. Optimal dispatch of IES only with space-dimensional IDR.

Case 4. Optimal dispatch of IES with time-space dimensional IDR.

5.2 Result analysis

The comparison results of IES operation cost in different Cases, with IDR participation percentage of 30%, are shown in Table 3. The analysis reveals that Case 4 has the lowest operation cost. A comparative analysis of the four cases yields the following observations.

1) Compared with Case 1, Case 2 introduces time-dimensional IDR, which reduces the peak-valley price difference by shifting load from peak to valley periods based on the ToU electricity pricing. As a result, the optimal operation cost in Case 2 is reduced by 111.84 yuan compared to Case 1.

2) Compared with Case 1, Case 3 incorporates space-dimensional IDR, which leads to a reduction in the IES operation cost to 242.77 yuan, representing a 126.86 yuan decreasing compared to Case 1. This demonstrates that the space-dimensional IDR is effective in improving the economic efficiency of the IES dispatch.

3) The operation costs of Case 2, Case 3and Case 4 are lower than that in Case 1. It is illustrated that single IDR in time dimension, single IDR in space dimension and two-dimensional IDR all contributed to the IES operation optimization.

Table 3

Table 3. Comparison result of different cases.

5.3 Comparison analysis

5.3.1 Analysis of ToU schemes in different Cases

The electricity price schemes of optimal IES dispatch under different cases are presented in Table 4. As shown in both Tables 3 and 4, compared to the basic single electricity price in Case 1, it is evident that the load curves are adjusted according to the varying ToU pricing schemes. Analyzing the ToU schemes in Table 4 reveals that the pull-open ratio in Case 2 and Case 3 is significantly higher than that in Case 4. In Case 2, which involves only time-dimensional IDR, the large price differential encourages customers to shift a substantial amount of load from peak to valley periods. A similar pattern is observed in Case 3. However, in Case 4, the smaller price differential, resulting from the combined time-space dimensional IDR, leads to load curve optimization through a dual effect. This indicates that the smaller pull-open distance in Case 4 enables more refined load shifting, benefiting from the integration of two dimensional IDR. In summary, the optimization of load curves in Case 4 is influenced by the combined effects of time-dimensional IDR and space-dimensional IDR.

Table 4

Table 4. Optimal purchased ToU schemes in 4 Cases.

5.3.2 The optimized loads curves in different Cases

The overall loads of electricity, heating and cooling in a typical day are represented in Table 5. It is evident that overall load of different energy demand varies with the guide of electricity price. Compared with the traditional unified fix electricity price in Case 1, the load demands with IDR based on ToU schemes in Case 2, Case 3 and Case 4 are all reduced. In Case 4 which employs two-dimensional IDR, the overall electricity load, heating load and cooling load are reduced by 56.2 kW, 31.3 kW,186 kW respectively. Notably, the reduction in cooling load is the most significant.

Table 5

Table 5. Total loads in a typical day.

Moreover, in order to further highlight the necessity of implementation of IDR in both time dimension and space dimension, electricity/heating/cooling loads curves with and without IDR are shown in Figure 4. It is clear that the implementation of the IDR in time dimension and space dimension can both effectively achieve the peaking-shaving and valley filling, thereby flattening the electricity/heating/cooling loads curves. While the overall trends of the different load curves are similar, the optimization of the load curves is most pronounced when both time and space dimensional IDR are applied. Meanwhile, it is shown in Figure 4 that the load curves after implementing single-time-dimension IDR in Case 2 and single-space-dimension IDR in Case 3, demonstrate improvements over the original load curves. This indicates that each dimension IDR contributes individually to optimize the IES dispatch. However, the most significant improvement is observed when two-dimensional IDR is applied, underscoring the effectiveness of the two-dimensional IDR approach proposed in this study.

Figure 4

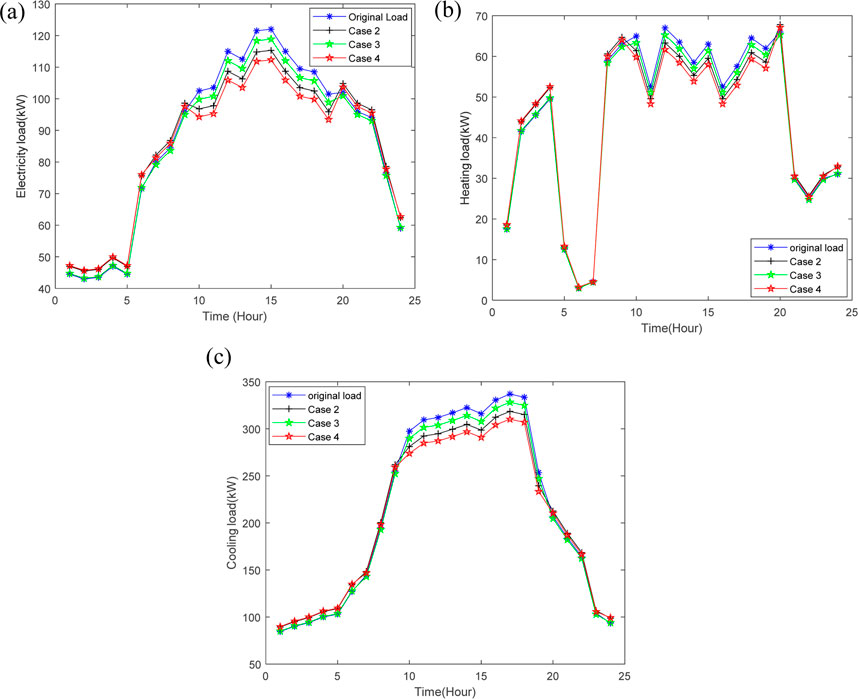
Figure 4. Different type loads before and after IDR. (A) Electricity load, (B) Heating load (C) Cooling load.

In Case 2, when IDR is applied in the time dimension, customers adjust their load demands by either reducing unnecessary loads or shifting loads from peak periods to off-peak and valley periods in response to price signals. As seen from Figure 4, the demand for electricity, heating, and cooling during 9:00–20:00 are decreased significantly, whereas those in the valley periods (0:00–6:00, 23:00–24:00) increase substantially. This demonstrates the typical peak-shifting and valley-filling effects of time-based IDR. Customers respond effectively to the ToU price, adjusting their demand according to the price fluctuations.

In Case 3, where IDR is applied in the spatial dimension, the demand for electricity, heating, and cooling is moderately reduced during the hours of 7:00–23:00, while only slight reductions are observed during other periods. The variation in the load curves in Case 3 is smaller compared to Case 2. This difference can be attributed to the fact that, in Case 3, the demand response is primarily influenced by the relative price between electricity and gas during specific periods. In contrast, in Case 2, the demand response is driven by electricity prices across all periods, resulting in a more pronounced effect on load variation.

In Case 4, where the two-dimensional IDR is implemented, Figure 4 illustrates that the electricity, heating, and cooling loads are significantly reduced during peak periods and correspondingly increased during off-peak periods. This demonstrates that the two-dimensional IDR approach proposed in this study not only optimizes the load curves but also effectively reduces the operational costs of the IES to the greatest extent possible.

5.3.3 Operation results of different units in IES

The optimal power dispatch for different units in Case 4 is shown in Figure 5. It is evident that P2G operates primarily during valley periods when electricity prices are low. The utilization rate of the EB is noticeably higher during periods of low electricity prices compared to periods of high prices. As illustrated in Figure 5B, purchased electricity remains the dominant source of energy throughout the 24-h period. The EC is more frequently used during high electricity price periods, primarily due to the heavy cooling demand in the typical summer day. Conversely, the use of AC is reduced during peak electricity price periods. Additionally, the purchase of gas increases significantly during periods of high electricity prices. This is largely due to the spatial dimension of the IDR, which influences demand response behavior.

Figure 5

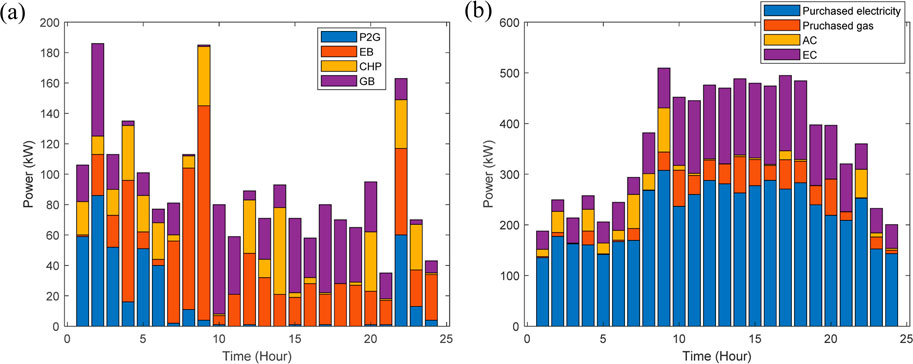
Figure 5. Optimal dispatched power of different units in Case 4. (A) P2G, EB, CHP,GB power, (B) Purchased electicty, gas, AC, EC power.

6 Conclusion

In this paper, a two-dimensional IDR based on ToU electricity price is proposed and integrated into IES dispatched problem. Firstly, a two-dimensional IDR model is constructed considering temporal-spatial coupling characteristics based on ToU. Compared to original electricity/heating/cooling loads profiles, the loads curves under time-space dimensional IDR are optimized through peak shaving and valley filling. Subsequently, an optimal dispatch model for the IES is formulated, incorporating the IDR to enhance economic performance. On this basis, the proposed IDR can further reduce IES operation cost. Finally, in the case study, the proposed methodology is demonstrated and compared with different strategies. The analysis of the case study confirms that proposed IES optimal dispatch model integrated with IDR is effective. Also, the comparative results verify the benefits of proposed two-dimensional IDR, both in terms of demand-side management and overall system operation. This can provide valuable insights for the coordinated operation of a deep multi-energy coupling IES. In the future, the uncertainty of load prediction and IDR participation degree will be further explored. The study will balance the economy and reliability of the IES system, offering practical significance for the development of efficient and resilient energy systems.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

TC: Writing–original draft. LZ: Conceptualization, Writing–review and editing. HT: Supervision, Writing–review and editing. YZ: Resources, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was financially supported by the Visiting Scholarship of State Key Laboratory of Power Transmission Equipment & System Security and New Technology (Chongqing University) (No. 2007DA10512718405) and National Natural Science Foundation of China (No. 62273130).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, L., Tang, H., Wu, J., Li, C., and Wang, Y. (2022). A robust optimization framework for energy management of CCHP users with integrated demand response in electricity market. Int. J. Electr. power energy Syst. 141, 108181. doi:10.1016/j.ijepes.2022.108181

CrossRef Full Text | Google Scholar

Cheng, T., Yang, Z., Dong, B., Li, Bo, Zhang, Y., Zeng, L., et al. (2022). Dynamic multiobjective optimal dispatch of distribution network considering time of use–based demand response. J. Energy Eng. 1 (2). doi:10.1061/(asce)ey.1943-7897.0000808

CrossRef Full Text | Google Scholar

Dou, X., Wang, J., Zhang, Z., and Gao, M. (2024). Optimal configuration of multitype energy storagefor integrated energy systems considering system reserve value. CSEE J. Power Energy Syst. 10 (5), 2114–2126.

Google Scholar

Duan, J., Liu, F., and Yang, Y. (2022). Optimal operation for integrated electricity and natural gas systems considering demand response uncertainties. Appl. Energy 323, 119455. doi:10.1016/j.apenergy.2022.119455

CrossRef Full Text | Google Scholar

Feng, T., Jia, Y., Ren, H., and Yun, B. A. I. (2020). Source-load low-carbon economic dispatch of integrated enrgy system considering carbon capture system. Power Syst. Technol. 44 (09), 3346–3355.

Google Scholar

Gu, Z., Pan, G., Gu, W., and Gu, W. (2023). Shuai Lu Robust optimization of scale and revenue for integrated power-to-hydrogen systems within energy, ancillary services, and hydrogen markets. IEEE Trans. Power Syst. 39 (3), 50058–55023.

Google Scholar

Hossein Yaghmaee, M. (2024). Incentive-based demand response program for Block chain network. IEEE Syst. Hournal 18 (1), 134–145. doi:10.1109/jsyst.2023.3342846

CrossRef Full Text | Google Scholar

Li, Bo, Qin, C., YuWei Dai, R., Shen, M., Ma, Z., Wang, J., et al. (2023). Fast solution method for the large-scale unit commitment problem with long-term storage. Chin. J. Electr. Eng. 9 (3), 39–49. doi:10.23919/cjee.2023.000033

CrossRef Full Text | Google Scholar

Liang, Z., Chen, L., Zhu, W., Lyu, L., Cai, G., and Hai, K. L. (2022). Research on the optimal allocation method of source and storage capacity of integrated energy system considering integrated demand response. Energy Rep. 8, 10434–10448. doi:10.1016/j.egyr.2022.08.184

CrossRef Full Text | Google Scholar

Liu, W., Huang, Y., Li, Z., Yang, Y., and Yi, F. (2020). Optimal allocation for coupling device in an integrated energy system considering complex uncertainties of demand response. Energy 198, 117279–117313. doi:10.1016/j.energy.2020.117279

CrossRef Full Text | Google Scholar

Lu, J., Liu, T., He, C., Nan, Lu, and Hu, X. (2021). Robust day-ahead coordinated scheduling of multi-energy systems with integrated heat-electricity demand response and high penetration of renewable energy. Renew. Energy 178 (178), 466–482. doi:10.1016/j.renene.2021.05.164

CrossRef Full Text | Google Scholar

Safta, C., Chen, R. L.-Y., Najm, H. N., Pinar, A., and Jean-Paul, W. (2017). Efficient uncertainty quantification in stochastic economic dispatch. IEEE Transaction Power Syst. 32 (4), 2535–2546. doi:10.1109/tpwrs.2016.2615334

CrossRef Full Text | Google Scholar

Shao, C., Ding, Yi, Siano, P., and Song, Y. (2021). Optimal scheduling of the integrated electricity and natural gas systems considering the integrated demand response of energy hubs. IEEE Syst. J. 15 (3), 4545–4553. doi:10.1109/jsyst.2020.3020063

CrossRef Full Text | Google Scholar

Siqing, S., Zhang, J., and Ran, Li (2024). Demand response benefit evaluation of integrated energy system based on combination weighting and gray cloud model. J. Of North China Electr. Power Univ. 51 (2), 41–52.

Google Scholar

Wang, J., Qi, An, Yue, Z., Pan, G., Song, J., Hu, Q., et al. (2023). Role of electrolytic hydrogen in smart city decarbonization in China. Appl. Energy 336, 120699. doi:10.1016/j.apenergy.2023.120699

CrossRef Full Text | Google Scholar

Wu, H., Xu, J., Ji, Yu, and Wu, M. (2017). Uncertain flow calculations of a distribution network containing DG based on blind number theory. IET Generation Transm. & Distribution 11 (6), 1591–1597. doi:10.1049/iet-gtd.2016.1530

CrossRef Full Text | Google Scholar

Yang, C., Gu, C., Fu, X., Deng, G., Yuting, Z., and Tang, Y. (2022a). Low-carbon economic dispatch of integrated energy system with carbon capture power plants considering generalized electric heating demand response. Proc. CSEE 42 (23), 8431–8445.

Google Scholar

Yang, C., Tao, J., Zhang, W., Cui, C., and Yuting, Z. (2020). Source-load coordination economic dispatch method for regional integrated energy system considering wind power accommodation. Power Syst. Technol. 44 (07), 2474–2483.

Google Scholar

Yang, Li, Wang, B., Yang, Z., and Li, J. (2022b). Optimal scheduling of integrated demand response-enabled community-integrated energy systems in uncertain environments. IEEE Trans. Industry Appl. 58 (2), 2640–2651. doi:10.1109/tia.2021.3106573

CrossRef Full Text | Google Scholar

Zeng, Bo, Wei, X., Zhao, D., Singh, C., and Zhang, J. (2018). Hybrid probabilistic-possibilistic approach for capacity credit evaluation of demand response considering both exogenous and endogenous uncertainties. Appl. Energy 229, 186–200. doi:10.1016/j.apenergy.2018.07.111

CrossRef Full Text | Google Scholar

Zhang, D., Zhu, H., Zhang, H., Goh, H. H., Liu, H., and Wu, T. (2022). Multi-Objective optimization for smart integrated energy system considering demand responses and dynamic prices. IEEE Trans. smart grid 13 (2), 1100–1112. doi:10.1109/tsg.2021.3128547

CrossRef Full Text | Google Scholar