Energy interaction strategy for multi-prosumer distribution systems based on game theory

In flexible distribution systems, the strong uncertainty of generation and load demand poses challenges for energy interaction and resource coordination. However, existing energy interaction strategies generally focus only on economic benefits, neglecting safety performance, and are insufficient to ensure the reliable operation of the system. To address these issues, this paper proposes an energy interaction strategy for multi-prosumer flexible distribution systems, considering the economic benefits of all parties and the voltage safety of the system. First, a multi-agent energy interaction framework based on the Stackelberg game is established, and a bi-level optimization model for the distribution network operator and prosumers is constructed. Second, the paper innovatively introduces soft open point-based power flow control technology into the energy trading market. Then, the KKT conditions, dual theory, linearization, and relaxation techniques are applied to transform the original bi-level game problem into a single-level mixed-integer second-order cone programming problem, improving computational efficiency. Finally, the improved IEEE 33-bus distribution system is simulated and compared with two other scenarios. The results show that the proposed strategy can significantly improve the economic and safety performance of the energy interaction system, optimize the power flow distribution, and effectively enhance power quality. The approach offers a promising solution to the growing challenges of managing distributed energy resources in the context of flexible and reliable grid operation.

1 Introduction

With the proposal of the “dual carbon” goal, the widespread access of distributed energy and flexible resources has significantly increased the participation of prosumers in the power market (Yang et al., 2024). Under this background, the operation mode of power distribution system is changing to multi-direction and multi-agent. Flexible distribution systems refer to advanced distribution networks that integrate multiple energy resources and flexible control technologies and are capable of dynamic reconfiguration and real-time power flow adjustment to adapt to changing demand and supply conditions (Li et al., 2023). By incorporating advanced control strategies, flexible distribution systems have the potential to significantly enhance energy interaction capabilities, increase renewable energy utilization, and provide strong support for system stability.

Prosumers play a crucial role in reducing energy costs and promoting renewable energy. Under coordinated feed-in tariffs, prosumers can engage in energy trading with the distribution network (DN) to maintain energy supply-demand balance, thereby providing new support for enhancing the flexibility and reliability of power systems (Seppälä and Järventausta, 2024). However, as the share of prosumers in distribution systems continues to grow, energy interactions among multiple entities are becoming increasingly complex. The presence of intermittent demand response (DR) introduces additional challenges to maintaining power system balance. Consequently, there is an urgent need for more advanced strategies to effectively regulate and manage multi-agent energy interactions, ensuring the stability, economic efficiency, and flexibility of distribution networks.

Existing energy interaction methods for multiple prosumers can be broadly categorized into two types: direct control and regional market-based control (Manchalwar et al., 2024). Direct control, also referred to as prosumer-to-grid control, involves the upper-level grid directly accessing information from individual prosumers and directly managing all controllable resources for energy interaction as needed. While this method is straightforward in operation, it suffers from drawbacks such as transaction congestion, poor privacy protection, and limitations on prosumers’ autonomy. In contrast, regional market-based control is a distributed control approach based on local energy trading markets and can be viewed as prosumer-to-distribution network operator (DNO) control. Under this framework, the DNO has pricing authority, and prosumers can adjust their flexible resources proactively based on the DNO’s pricing signals, thereby autonomously determining energy exchange while indirectly influencing the DNO’s pricing. This method balances the interests of all participants by coordinating dispersed prosumers to form a regional platform for energy generation and consumption, achieving resource sharing and preserving prosumer autonomy. Moreover, it offers excellent scalability. For instance, various approaches such as distributed trading mechanisms for demand-side energy interaction (Lou et al., 2023), optimization methods targeting models, solution techniques, and information transmission (Hou et al., 2022), dual-chain implementation methods for electricity rights trading (Gao et al., 2024), and multi-agent deep learning-based energy management techniques (Miyamoto et al., 2020) have been explored. Although these studies have achieved significant progress in energy interaction among multiple prosumers, they also exhibit notable limitations. Lou et al. (2023); Hu et al. (2022); Gao et al. (2024) neglect power quality issues and fail to account for voltage regulation, which may impact system stability. Similarly Miyamoto et al. (2020), focuses solely on power optimization without integrating economic considerations in market energy trading and distribution network regulation, potentially limiting the economic benefits for participants.

Economic efficiency and system security are two critical concerns for users, operators, and power grids. In practical applications, economic and security objectives often conflict with each other. For instance, prioritizing the economic benefits of transactions between prosumers and the distribution network operator (DNO) may compromise the reliability and safety of system operations, potentially leading to severe voltage violations or excessive utilization of grid assets (Tao et al., 2024). Moreover, the autonomous nature of prosumers, coupled with intermittent and concentrated power usage patterns, can result in imbalances between generation and consumption. This imbalance often causes power flow discrepancies across feeders, leading to frequent feeder power fluctuations and increased system losses (Liu et al., 2024). As a result, transaction control strategies that balance economic efficiency and system security have become a prominent research focus. Examples include transaction control algorithms based on attention mechanisms (Zheng et al., 2021), scheduling methods leveraging double-agent Q-learning (Liu et al., 2023), and game-theoretic scheduling strategies (Xiao et al., 2024; Guan and Hou, 2024; Zheng et al., 2024). These studies, through either deep learning algorithms or game-theory-based approaches, have demonstrated the ability to enhance DNO revenues, reduce prosumers’ electricity costs, stabilize system operations, and maximize social welfare. However, they have not adequately addressed the challenge of handling surplus energy, leaving room for further improvement in energy management strategies.

The concept of “clearing price” has been widely discussed in recent studies (Izadi and Rastegar, 2024; Meng et al., 2024; Mohammadreza et al., 2024; Wu et al., 2024), where game-theoretic methods have been applied to achieve economic dispatch and system regulation within energy communities (Izadi and Rastegar, 2024). For instance, one study explored economic coordination and regulation using game theory (Meng et al., 2024), while another incorporated energy clearing and voltage regulation through a leader-follower (Stackelberg) game-based pricing mechanism to realize mutual benefits for the DNO and prosumers. By leveraging “clearing price” as an interaction signal within the Stackelberg game framework, these approaches facilitate communication between the upper-level leader (DNO) and lower-level followers (prosumers). This methodology prioritizes internal transactions in local energy markets, effectively managing surplus energy, promoting local energy utilization, and ensuring the system’s economic efficiency. Additionally, the focus on price and power exchange as communication variables ensures robust user privacy protection (Mohammadreza et al., 2024). Despite their ability to enhance system revenues and operational security, these strategies lack consideration of active regulation in the distribution network (DN). Addressing this gap is essential to further improve system reliability and operational flexibility.

Network reconfiguration has been proposed as a method to adjust the topology of distribution networks (DN) for power flow optimization (Liang et al., 2024; Ashrafi et al., 2024), aiming to reduce power losses, lower operational costs, and prevent voltage violations. However, this approach is constrained by the operating frequency of tie switches, the need for more advanced control devices. Multi-Terminal Soft Open Points (MOP), are power electronic devices designed for efficient power transmission in electric power systems (Deakin et al., 2022; Taher et al., 2024; Li et al., 2024). MOP actively regulates active and reactive power on connected feeders, optimizes power flow distribution, and improves resource allocation, thereby increasing the flexibility and reliability of the network. Studies have demonstrated that MOP outperforms traditional network reconfiguration in power flow regulation and offers greater adaptability compared to conventional Soft Open Points (SOP) (Deakin et al., 2022), as it enables simultaneous control and optimization of multiple branch lines, providing more versatile power distribution capabilities. Nevertheless, research and applications of MOP in the context of energy interaction remain limited, suggesting significant potential for further exploration in this area.

Therefore, based on the analysis of the aforementioned background, this paper comprehensively considers the energy interaction strategy between the DNO and multiple prosumers in a flexible distribution system. This strategy involves factors such as energy storage system (ESS) charging and discharging, MOP active regulation, DR, internal pricing, and voltage stability. A game-theoretic energy interaction model and strategy for multi-prosumer distribution systems are proposed, and mathematical methods such as Karush-Kuhn-Tucker (KKT) conditions are utilized to simplify the model solution process. The KKT conditions are a set of mathematical optimization conditions widely used in optimization problems to characterize the solutions of constrained nonlinear programming (Dempe and Franke, 2019). Unlike traditional iterative methods, which typically require extensive computation and data exchange between decision-making layers, the KKT-based transformation simplifies the optimization process by reducing the bi-level optimization problem to a single-layer form. This approach not only enhances computational efficiency but also ensures privacy by limiting the exchange of sensitive data.

This paper proposes a multi-agent energy interaction strategy based on MOP to solve the balance between economic benefits and operational security, so as to promote the construction of new power systems. Through the comparison with the existing research, the innovation of this paper is as follows:

1) A multi-agent energy interaction framework based on the Stackelberg game is developed in this study. Unlike most research that focuses solely on economic aspects without considering system security, or existing studies that prioritize voltage regulation without addressing flexible resource allocation, this work establishes an interaction framework that considers economic benefits, power quality, and demand response. This framework simultaneously addresses the economic and security issues of the DNO-multi-prosumer distribution network. Furthermore, in terms of power flow optimization for the distribution network (DN), this study introduces MOP for the active regulation of active and reactive power on the connected feeders, which not only reduces network losses but also prevent voltage over-limit rate, further enhancing the system’s economic efficiency and security.

2) Different from most traditional approaches that use iterative methods to solve the Stackelberg bi-level optimization model for price determination, this study employs KKT conditions, dual theory, linearization techniques, relaxation methods, and the Big-M method to transform the bi-level model into a single-level mixed-integer second-order cone programming (MISOCP) problem. This transformation allows for solving the model using commercial solvers, thereby improving solution efficiency.

The remainder of this paper is organized as follows: Section 2 introduces the energy interaction framework for the DNO-multi-prosumer distribution system; Section 3 develops the DNO-prosumer optimization model based on the Stackelberg leader-follower game; Section 4 applies KKT conditions, linearization, and relaxation techniques to transform the bi-level model into a single-level model; Section 5 provides case studies and analysis; Section 6 presents the conclusion.

2 Energy interaction framework for multiple consumer distribution systems

2.1 Energy market interaction framework

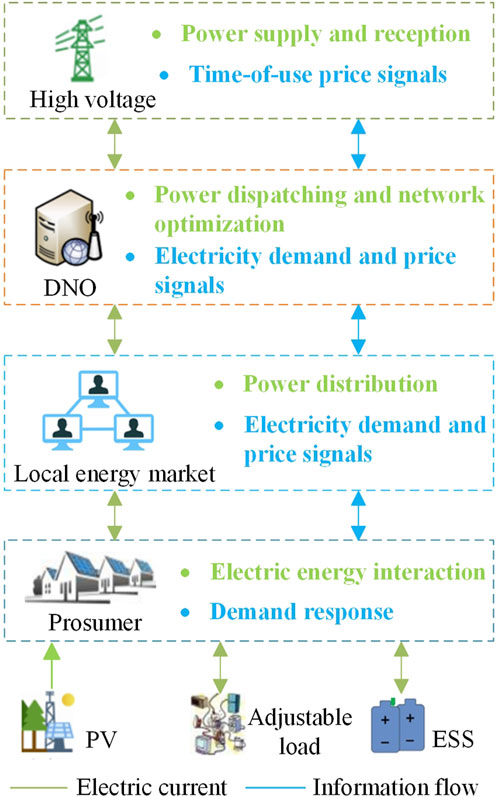
An energy market interaction framework that considers energy management issues between DNO and multiple prosumer is shown in Figure 1. The figure includes the high-voltage (HV) grid, which provides the required electrical energy and receives excess energy, the local energy interaction market that distributes electrical energy and transmits energy demand and price signals, and two key participants: the DNO, which serves as an intermediary for transactions between the HV grid and prosumers, and the photovoltaic prosumers who generate and consume their own electricity.

Figure 1

Figure 1. Energy market interaction framework.

As the energy interaction intermediary, the DNO acts as the operator of the distribution network (DN) and the internal price setter. Its responsibilities include: 1) overseeing the operation of the distribution network to ensure system safety and stability while meeting high-quality power requirements from users; 2) participating in the energy market and engaging in energy transactions with the HV grid to balance supply and demand when internal imbalances occur; 3) coordinating internal energy transactions by dynamically setting internal transaction prices based on economic and safety considerations, referencing users’ electricity demand and feed-in tariffs, and allocating internal energy to improve consumption capacity.

As the main participants in the energy market, prosumers consist of photovoltaic (PV) systems, loads (both fixed and flexible), and energy storage systems (ESS). Among these, flexible loads, also referred to as transferable loads, are controllable loads that do not affect basic living needs, enabling demand response. This allows prosumers to adjust their loads based on the transaction prices set by the DNO and develop their own electricity consumption strategies. Additionally, to enhance the network optimization level of the DNO, Multi-Terminal Soft Open Points (MOP) are installed within the distribution network (DN).

2.2 Energy interactive game framework

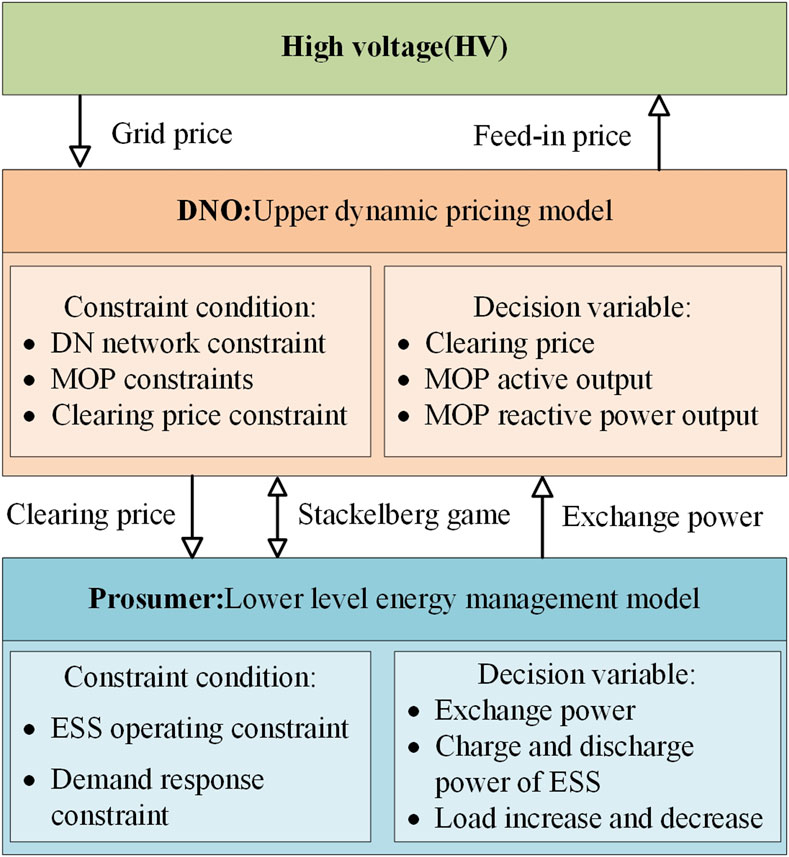
As shown in Figure 2, this paper explores a bi-level energy trading framework based on the Stackelberg game, which shows the leader-follower relationship between DNO and prosumers, and both play interest games with exchanged power through clearing prices.

Figure 2

Figure 2. Energy interactive game framework.

The upper-level leader, the DNO, can determine the operational strategy of the MOP and the internal clearing prices based on time-varying grid prices, feed-in tariffs, the exchange power between prosumers and the DNO, and the operational status of the distribution network (DN), aiming to maximize social welfare. Meanwhile, the lower-level follower, the prosumer, can adjust its electricity consumption and ESS charging/discharging strategy according to the clearing prices set by the DNO, and determine the exchange power with the DNO, in order to minimize its own costs.

It can be observed that this is a bi-directional decision-making problem, where the clearing price and exchange power serve as the communication bridge between the upper and lower levels. The DNO sets the clearing price based on the exchange power with the prosumers, while prosumers respond to the DNO’s clearing price by determining their own energy scheduling plans. Therefore, although the DNO holds priority in the decision-making process, it must take into account the demand response (DR) of each prosumer, thus forming a leader-follower game of interests.

In summary, the proposed energy market interaction and game framework effectively solves the complexity of energy trading in flexible distribution networks involving multiple production-consumers. By integrating dynamic clearing prices, DR, and MOP-based network optimization, bidirectional coordination between DNO and prosumers is achieved, ensuring joint achievement of economic and operational objectives.

3 Energy interaction model of distribution system for prolific consumer

This chapter develops an energy interaction model based on the aforementioned framework. First, the objective of minimizing the DNO’s operational costs is defined, along with the constraints for the distribution network (DN) operation. Next, the cost minimization objective for prosumers is outlined based on their characteristics, and the corresponding operational constraints are established. Finally, for the bi-level game problem, instead of using the traditional iterative methods, which are cumbersome, the study employs KKT conditions, the Big-M method, second-order cone relaxation techniques, and dual theory to transform the bi-level optimization model into a single-level model.

3.1 Optimization model of distribution network operator

3.1.1 Optimization objective

The DNO, as the coordinator between the grid and users, has the core objective of maximizing social welfare. This is specifically manifested in minimizing the transaction costs between the DNO, the HV, and prosumers, reducing network losses and voltage fluctuations in the DN, and enhancing the economic efficiency and stability of the system. Therefore, the objective function of the DNO can be expressed as:

$\min F_{DNO}=a_o\left(f_{Grid}+f_{loss}-f_{inc}\right)+b_v{f}_{vd}(1)$

$\left\{\begin{array}{l}{f}_{Grid}={\displaystyle \sum _{t=1}^{N_T}}\left(\frac{X_t-W_t}{2}\left|g_t\right|+\frac{X_t+W_t}{2}{g}_t\right)\Delta t\\ f_{loss}=C_{loss}\left({\displaystyle \sum _{t=1}^{N_T}}{\displaystyle \sum _{ij\in {\mathrm{\Omega }}_l}}{r}_{ij}{I}_{t.ij}^2+{\displaystyle \sum _{t=1}^{N_T}}{\displaystyle \sum _{i=1}^{N_N}}{P}_{t,i}^{mop,loss}\right)\Delta t\\ f_{inc}={\displaystyle \sum _{t=1}^{N_T}}{\displaystyle \sum _{n=1}^{N_p}}{\lambda }_t{P}_{t,n}^p\Delta t\\ f_{vd}={\displaystyle \sum _{t=1}^{N_T}}{\displaystyle \sum _{i=1}^{N_N}}\left|U_{t,i}^2-{\stackrel{\sim }{U}}_{ref}^2\right|\end{array}\right.(2)$

Equation 1 represents the general form of the DNO optimization objective function, which is a linear weighted combination of operational costs and voltage deviation minimization. Where, $a_o$ and $b_v$ are the weight coefficients (Yang et al., 2023), which represent the relative importance of each element in the objective, with their sum being equal to 1; $f_{Grid}$ and $f_{inc}$ represent the transaction costs incurred between the DNO and HV, as well as the total revenue from transactions between the DNO and the prosumers, respectively. $f_{loss}$ refers to the network loss cost of the DN, while $f_{vd}$ represents the total voltage deviation. Equation 2 provides detailed expressions for each component, where $X_t$ and $W_t$ denote the purchase and sale prices of electrical energy between the DN and the HV grid, respectively; $g_t$ represents the net load of the DN, with $g_t$ indicating a positive value when the DN purchases energy from the HV grid and $g_t$ indicating a negative value when the DN sells energy to the HV grid; $C_{loss}$ refers to the cost coefficient associated with network losses; $r_{ij}$ and $x_{ij}$ represent the resistance and reactance of branch; $I_{t.ij}$ denotes the current flowing through branch $ij$ at period t; $P_{t,i}^{mop,loss}$ accounts for the active power loss generated by the MOP during period t; $N_T$, $N_N$, and $N_P$ represent the total time periods, total nodes, and total number of prosumers in the DN, respectively; $\Delta t$ denotes the time interval; ${\mathrm{\Omega }}_l$ refers to the set of all branches; ${\lambda }_t$ represents the clearing price in the internal energy trading market at period t; $P_{t,n}^p$ denotes the net load of the nth prosumer at period t, which corresponds to its exchange power with the DN; $U_{t.i}$ is the voltage of bus i at period t; ${\stackrel{\sim }{U}}_{ref}$ is the reference voltage of the buses.

3.1.2 Constraint condition

3.1.2.1 Network constraints of the DN

The DN is modeled using the widely adopted Distflow branch model.

${\displaystyle \sum _{ji\in {\mathrm{\Omega }}_b}}\left(P_{t,ji}-r_{ji}{I}_{t,ji}^2\right)+P_{t,i}={\displaystyle \sum _{ik\in {\mathrm{\Omega }}_b}}{P}_{t,ik}(3)$

${\displaystyle \sum _{ji\in {\mathrm{\Omega }}_b}}\left(Q_{t,ji}-x_{ji}{I}_{t,ji}^2\right)+Q_{t,i}={\displaystyle \sum _{ik\in {\mathrm{\Omega }}_b}}{Q}_{t,ik}(4)$

$U_{t,i}^2-U_{t,j}^2-2\left(r_{ij}{P}_{t,ij}+x_{ij}{Q}_{t,ij}\right)+\left(r_{ij}^2+x_{ij}^2\right)I_{ij}^2=0(5)$

$I_{t,ij}^2{U}_{t,i}^2=P_{t,ij}^2+Q_{t,ij}^2(6)$

$\begin{array}{l}{P}_{t,i}=P_{t,i}^{PV}+P_{t,i}^{MOP}-P_{t,i}^L+P_{t,i}^{L,move}\\ +\left(P_{t,i}^{ess,c}-P_{t,i}^{ess,d}\right)\end{array}(7)$

$Q_{t,i}=Q_{t,i}^{MOP}-Q_{t,i}^L(8)$

Equations 3, 4 represent the active and reactive power balance for the branch, where $P_{t,ji}$ and $Q_{t,ji}$ are the active and reactive power flowing through branch ij at time t, $P_{t,i}$ and $Q_{t,i}$ are the active and reactive power injected at bus i at time t. Equations 5, 6 represent the voltage and branch current level constraints at bus i at period t. Equations 7, 8 represent the active and reactive power balance at the bus, where $P_{t,i}^{PV}$, $P_{t,i}^{VSC}$, $Q_{t,i}^{VSC}$ are the active and reactive power injected into bus i at period t by the PV and MOP, respectively. $P_{t,i}^L$ and $P_{t,i}^{L,move}$ are the fixed and transferable loads of the prosumer at period t, with a positive value indicating an increase in load demand and a negative value indicating a decrease. $P_{t,i}^{ess,c}$ and $P_{t,i}^{ess,d}$ represent the charging and discharging power of the ESS at period t at bus i.

3.1.2.2 Security constraints of the DN

DN During normal operation, the bus voltage and branch current cannot exceed the safety limit.

${\underset{\_}{U}}^2\le U_{t,i}^2\le {\overline{U}}^2(9)$

$I_{t,ij}^2\le {\overline{I}}^2(10)$

where, $\underset{\_}{U}$ and $\overline{U}$ are the upper and lower limits of voltage of buses respectively; $\overline{I}$ is the maximum current limit of the branch.

3.1.2.3 Operation constraints of MOP

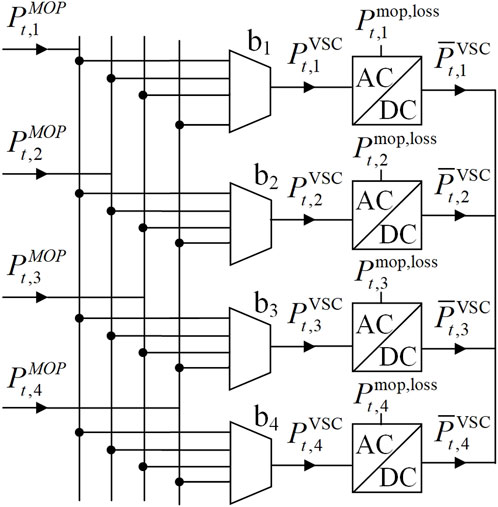
The ideal MOP of 4 feeder lines is shown in Figure 3, and $P_{t,i}^{\text{VSC}}$ in the figure is the power of the feeder connected to MOP flowing to MOP. It can be seen that it is determined by the feeder selection switch state $b_i$ and the active power $P_{t,i}^{\text{VSC}}$ transmitted by $VS{C}_i$, that is, MOP controls $P_{t,i}^{\text{VSC}}$ and $Q_{t,i}^{\text{VSC}}$ by controlling these two variables, and then controls the active and reactive power of the connected feeder.

${\overline{P}}_{t,i}^{\text{VSC}}+P_{t,i}^{\text{mop},\text{loss}}=P_{t,i}^{\text{VSC}},\forall t,i\in {\mathrm{\Omega }}_{\text{VSC}}(11)$

${\displaystyle \sum _{i=1}^{N_m}}{\overline{P}}_{t,i}^{\text{VSC}}=0,\forall t,i\in {\mathrm{\Omega }}_{\text{VSC}}(12)$

$P_{t,i}^{\text{mop},\text{loss}}=A_i^{\text{VSC}}{S}_i^{\mathrm{L}},\forall t,i\in {\mathrm{\Omega }}_{\text{VSC}}(13)$

$\begin{array}{l}\sqrt{{\left(P_{t,i}^{\text{VSC}}\right)}^2+{\left(Q_{t,i}^{\text{VSC}}\right)}^2}\le S_i^{\text{VSC}},\\ \forall t,i\in {\mathrm{\Omega }}_{\text{VSC}}\end{array}(14)$

$\begin{array}{l}{S}_n^{\mathrm{L}}\le B_{i,n}{S}_i^{\text{VSC}},\forall t,i\in {\mathrm{\Omega }}_{\text{VSC}},\\ n\in \left\{1,2,3,...N_m\right\}\end{array}(15)$

${\displaystyle \sum _{n=1}^N}{B}_{i,n}=1,\forall i\in {\mathrm{\Omega }}_{\text{VSC}}(16)$

$-{\overline{Q}}_i^{\text{VSC}}\le Q_{t,i}^{\text{VSC}}\le {\overline{Q}}_i^{\text{VSC}},\forall t,i\in {\mathrm{\Omega }}_{\text{VSC}}(17)$

Figure 3

Figure 3. MOP Topology view.

Equations 11–13 represent the power balance constraints, where ${\overline{P}}_{t,i}^{\text{VSC}}$ denotes the active power on the DC side of the VSC at bus i at period t, $P_{t,i}^{\text{VSC}}$ represents the actual transmitted active power of $VS{C}_i$ at period t, $P_{t,i}^{\text{mop},\text{loss}}$ is the active power loss of $MO{P}_i$ at period t, $A_i^{\text{VSC}}$ represents the loss coefficient of $VS{C}_i$, and ${\mathrm{\Omega }}_{\text{VSC}}$ denotes the set of VSCs. Equations 14–17 describe the MOP capacity constraints, where $S_n^{\mathrm{L}}$ represents the power transmission capacity of the branch n connected to the MOP, $S_i^{\text{VSC}}$ denotes the capacity of $VS{C}_i$, $Q_{t,i}^{\text{VSC}}$ is the actual reactive power transmitted by $VS{C}_i$ at period t, ${\overline{Q}}_i^{\text{VSC}}$ denotes the reactive power output limit of $VS{C}_i$, and $N_m$ represents the total number of branches connected to the MOP.

3.1.2.4 Price constraint

When determining the clearing price, the DNO must consider the responses of the prosumers. To encourage prosumers to actively participate in the internal energy market and ensure that they do not bypass the DNO to trade directly with the HV grid, the clearing price must satisfy certain constraints.

${\lambda }_t^{\min }\le {\lambda }_t\le {\lambda }_t^{\max }(18)$

$\frac{1}{T}{\displaystyle \sum _{t=1}^T}{\lambda }_t\le \frac{1}{T}{\displaystyle \sum _{t=1}^T}{X}_t(19)$

Equation 18 specifies that ${\lambda }_t$ must remain within the upper and lower bounds ${\lambda }_t^{\max }$ and ${\lambda }_t^{\min }$ to prevent excessive pricing, which could discourage prosumers from purchasing electricity and thereby affect their normal daily activities. Equation 19 ensures that the average clearing price does not exceed the average price of purchasing electricity from the HV grid, thereby protecting the interests of users.

3.2 Optimization model of prosumer

3.2.1 Optimization objective

Prosumers can respond to the clearing price set by the DNO by adjusting their electricity usage plans and energy storage utilization in the internal energy trading market, with the objective of minimizing their operational costs. Accordingly, the objective function for an individual prosumer is formulated as follows:

$\min J_n={\displaystyle \sum _{t=1}^T}{\lambda }_t{P}_{t,n}^p\Delta t+{\displaystyle \sum _{t=1}^T}{v}_n^{Disc}\left(P_{t,i}^{L,move}\right)\Delta t+{\displaystyle \sum _{t=1}^T}{l}_{\mathrm{deg}}\left(P_{t,i}^{ess,c}{\eta }^{ess,c}+\frac{P_{t,i}^{ess,d}}{{\eta }^{ess,d}}\right)\Delta t(20)$

$P_{t,n}^p=P_{t,i}^L+P_{t,i}^{L,move}-P_{t,i}^{PV}+{\displaystyle \sum _{e=1}^{N_e}}\left(P_{t,i}^{ess,c}-P_{t,i}^{ess,d}\right)(21)$

Equation 20 represents the general formulation of the prosumer’s optimization objective. The first term corresponds to the cost of participating in energy transactions, the second term represents the utility cost associated with load adjustments, and the third term accounts for the degradation cost of ESS operation. where $v_n^{Disc}$ denotes the sensitivity coefficient of the prosumer n to load variation discomfort, ${\eta }^{ess,c}$ and ${\eta }^{ess,d}$ represent the charging and discharging efficiencies of the ESS, respectively, and $l_{\mathrm{deg}}$ indicates the degradation coefficient of the ESS. Equation 21 is the exchanged power between the prosumer and DNO, where a positive value represents the transmission power from DNO to the prosumer.

3.2.2 Constraint condition

3.2.2.1 Constraints of ESS

ESS must meet the relevant constraints of energy storage, charge and discharge power

$\left\{\begin{array}{l}0\le P_{t,i}^{ess,c}\le u_{t,e}^{ess}{P}_e^{c,rat}\\ 0\le P_{t,i}^{ess,d}\le \left(1-u_{t,e}^{ess}\right)P_e^{d,rat}\end{array}\right.(22)$

$S_{t,e}=S_{t-1,e}+\left(\frac{P_{t,i}^{ess,c}{\eta }^{ess,c}}{Ca{p}_e^{ess}}-\frac{P_{t,i}^{ess,d}}{Ca{p}_e^{ess}{\eta }^{ess,d}}\right)\Delta t(23)$

$S_e^{\min }\le S_{t,e}\le S_e^{\max }(24)$

$S_{1,e}=S_{N_T,e}(25)$

Equation 22 defines the charging and discharging power constraints of the ESS, where $u_{t,e}^{ess}$ represents the operational state of the ESS e at period t (1 for charging, 0 for discharging), $P_e^{c,rat}$ and $P_e^{d,rat}$ are the maximum charging and discharging powers of the ESS e, respectively. The constraints Equations 23, 24 are expressed as the energy storage constraints of the ESS. where $S_{t,e}$ represents the current energy stored in the ESS e at period t, while $S_{t-1,e}$ represents its energy level at the previous period step, with the two having a recursive relationship. $S_e^{\min }$ and $S_e^{\max }$ denote the lower and upper bounds of the ESS’s energy storage, and $Ca{p}_e^{ess}$ represents its maximum capacity. Constraint Equation 25 is expressed as the equality between the initial energy storage $S_{1,e}$ and the final energy storage $S_{N_T,e}$ of the ESS.

3.2.2.2 Constraints on demand response

Prosumers can adjust their electricity demand based on the clearing price set by the DNO; however, to ensure their basic living needs, the following constraints must be satisfied:

$L^{\min }\le P_{t,i}^{L,move}\le L^{\max }(26)$

${\displaystyle \sum _{t=1}^{N_T}}{P}_{t,i}^{L,move}=0(27)$

Equation 26 indicates that the adjustment of the prosumer’s transferable load cannot exceed the specified range $\left[L^{\min },L^{\max }\right]$. Constraint Equation 27 shows that the total load demand of the prosumer remains constant throughout the day.

4 Processing and transformation of the model

The optimization objective and constraints in the above model contain numerous nonlinear functions, which cannot be solved by existing commercial solvers. Therefore, in this section, linearization methods and second-order cone relaxation techniques are applied to process the model, converting it into a mixed-integer second-order cone programming (MISOCP) model. At the same period, to simplify the model’s solution process, the bi-level optimization model is converted into a single-level optimization model.

4.1 Linearization

4.1.1 Processing of quadratic terms

Due to the nonlinear forms, such as current and voltage squared, in Equations 2–6, 9, 10, $v_{t,i}$ and $l_{t,ij}$ are used to replace $U_{t,i}^2$ and $I_{t,ij}^2$. The transformed function looks like Equations 28–34:

$f_{loss}=C_{loss}\left({\displaystyle \sum _{t=1}^{N_T}}{\displaystyle \sum _{ij\in {\mathrm{\Omega }}_l}}{r}_{ij}{l}_{t.ij}\Delta t+{\displaystyle \sum _{t=1}^{N_T}}{\displaystyle \sum _{t=1}^{N_N}}{P}_{t,i}^{VSC,loss}\Delta t\right)(28)$

${\displaystyle \sum _{ji\in {\mathrm{\Omega }}_b}}\left(P_{t,ji}-r_{ji}{l}_{t,ij}\right)+P_{t,i}={\displaystyle \sum _{ik\in {\mathrm{\Omega }}_b}}{P}_{t,ik}(29)$

${\displaystyle \sum _{ji\in {\mathrm{\Omega }}_b}}\left(Q_{t,ji}-x_{ji}{l}_{t,ij}\right)+Q_{t,i}={\displaystyle \sum _{ik\in {\mathrm{\Omega }}_b}}{Q}_{t,ik}(30)$

$\begin{array}{l}{v}_{t,i}-v_{t,j}-2\left(r_{ij}{P}_{t,ij}+x_{ij}{Q}_{t,ij}\right)\\ +\left(r_{ij}^2+x_{ij}^2\right)l_{t,ij}=0\end{array}(31)$

$l_{t,ij}{v}_{t,i}=P_{t,ij}^2+Q_{t,ij}^2(32)$

${\underset{\_}{U}}^2\le v_{t,i}\le {\overline{U}}^2(33)$

$l_{t,ij}\le {\overline{I}}^2(34)$

4.1.2 Handling of absolute value terms

Due to the absolute value term of the voltage deviation in Equation 2, an auxiliary variable $Au{x}_{t,i}$ is introduced to linearize it. The converted function is shown in Equations 35–38:

$f_{vd}={\displaystyle \sum _{t=1}^{N_T}}{\displaystyle \sum _{i=1}^{N_N}}Au{x}_{t,i}(35)$

$Au{x}_{t,i}\ge 0(36)$

$Au{x}_{t,i}\ge {\stackrel{\sim }{U}}_{ref}^2-v_{t,i}(37)$

$Au{x}_{t,i}\ge v_{t,i}-{\stackrel{\sim }{U}}_{ref}^2(38)$

4.2 Second-order cone transformation

Even after linearization in Equation 32, quadratic nonlinear terms in the form of $l_{t,ij}{v}_{t,i}$ still exist. Therefore, further processing is required, and the convex relaxation of the function is expressed as follows:

${‖\begin{array}{l}2P_{t,ij}\\ 2Q_{t,ij}\\ l_{t,ij}-v_{t,i}\end{array}‖}_2\le l_{t,ij}+v_{t,ij},\forall t(39)$

Similarly, Equation 14 also contains quadratic nonlinear terms, and the transformed second-order cone constraint is as follows:

${\left(P_{t,i}^{VSC}\right)}^2+{\left(Q_{t,i}^{VSC}\right)}^2\le 2\frac{S_{t,i}^{VSC}}{\sqrt{2}}\frac{S_{t,i}^{VSC}}{\sqrt{2}}(40)$

Equation 41 is defined to verify the constraint effect. If the gap value is sufficiently small, it is considered that the accuracy after relaxation is reasonable, which also means that the initial model can be transformed into a model that can be solved by commercial solvers using the two processing methods described above.

$\text{gap}={‖l_{t,ij}-\frac{P_{t,ij}^2+Q_{t,ij}^2}{v_{t,i}}‖}_{\infty }(41)$

4.3 Transformation of two-layer model

Based on the Stackelberg leader-follower game, and combining the above framework and model, the following bi-level optimization problem is formulated:

Upper level: $\min F_{DNO}$;

Subject to: Equations 7, 8, 11–13, 15–19, 29–31, 33, 34, 36–40;

Variables: ${\lambda }_t,P_{t,i}^{VSC},Q_{t,i}^{VSC},l_{t,ij},v_{t,i},Au{x}_{t,i}$

${\lambda }_t\downarrow \downarrow$ $P_{t,n}^P\uparrow \uparrow$

Lower level: $\min J_n$;

Subject to: Equations 22–27;

Variables: $P_{t,n}^P,P_{t,i}^{L,move},P_{t,i}^{ess,c},P_{t,i}^{ess,d},S_{t,e}$;

For the two-layer optimization model, the traditional iterative method is adopted, and the solving process is relatively complicated.

Furthermore, considering user privacy and security, and to avoid unnecessary information exchange between prosumers and the DNO, this paper applies the KKT conditions to transform the above bi-level model, thereby improving computational efficiency and protecting user privacy.

Let $\mu$ be the dual variable for the inequality constraints of the lower-level optimization problem, and $\lambda$ be the dual variable for the equality constraints of the lower-level optimization problem. As shown in Equations 42, 43, the general form of the KKT condition obtained by the transformation is:

$\nabla L=\left(P_{t,i}^{L,move},P_{t,i}^{ess,c},P_{t,i}^{ess,d},S_{t,e},{\mu }_i,{\lambda }_i\right)=0(42)$

$0\le \mu \perp g\left(x\right)\ge 0(43)$

where, $\nabla L$ is the Lagrange function written using the KKT conditions (Zhu et al., 2022), $g\left(x\right)\ge 0$ representing the inequality constraints in the optimization problem. The specific expression is as follows:

1) Introduce the optimization objectives and constraints of the lower prosumers to write the Lagrange function:

$\begin{array}{l}\nabla L={\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\lambda }_t\left[P_{t,i}^L+P_{t,i}^{L,move}-P_{t,i}^{PV}+{\displaystyle \sum _{e=1}^{N_e}}\left(P_{t,i}^{ess,c}-P_{t,i}^{ess,d}\right)\right]\Delta t+{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{v}_n^{Disc}{P}_{t,i}^{L,move}\Delta t\\ +{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{e=1}^{Ne}}{l}_{\mathrm{deg}}\left(P_{t,i}^{ess,c}{\eta }^{ess,c}+\frac{P_{t,i}^{ess,d}}{{\eta }^{ess,d}}\right)\Delta t\\ -{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{e=1}^{Ne}}\left[{\mu }_{1,t,n}^{ess,c}{P}_{t,i}^{ess,c}-{\mu }_{2,t,n}^{ess,c}\left(P_{t,i}^{ess,c}-u_{t,e}^{ess}{P}_e^{c,rat}\right)\right]\\ -{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{e=1}^{Ne}}\left\{{\mu }_{1,t,n}^{ess,d}{P}_{t,i}^{ess,d}-{\mu }_{2,t,n}^{ess,d}\left[P_{t,i}^{ess,d}-\left(1-u_{t,e}^{ess}\right)P_e^{d,rat}\right]\right\}\\ +{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{e=1}^{Ne}}\left[{\mu }_{1,t,n}^S\left(S_e^{\min }-S_{t,e}\right)+{\mu }_{2,t,n}^S\left(S_{t,e}-S_e^{\max }\right)\right]\\ +{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}\left[{\mu }_{1,t,n}^{L,move}\left(L^{\min }-P_{t,i}^{L,move}\right)+{\mu }_{2,t,n}^{L,move}\left(P_{t,i}^{L,move}-L^{\max }\right)\right]\\ +{\displaystyle \sum _{n=1}^N}{\lambda }_{1,n}\left({\displaystyle \sum _{t=1}^T}{P}_{t,i}^{L,move}\right)+{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{e=1}^{Ne}}{\lambda }_{2,n}\left(S_{1,e}-S_{T,e}\right)\\ +{\displaystyle \sum _{t=1}^{T-1}}{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{e=1}^{Ne}}\left[{\lambda }_{3,t,n}\left(S_{t,e}-S_{t-1,e}-\frac{P_{t,i}^{ess,c}{\eta }^{ess,c}\Delta t}{Ca{p}_e^{ess}}-\frac{P_{t,i}^{ess,d}}{{\eta }^{ess,d}Ca{p}_e^{ess}}\Delta t\right)\right]\end{array}(44)$

2) Taking the partial derivative with respect to $\nabla L$ yields the equality constraint:

$\frac{\mathrm{\partial }L}{\mathrm{\partial }{P}_{t,i}^{L,move}}={\lambda }_t\Delta t+v_n^{Disc}\Delta t-{\mu }_{1,t,n}^{L,move}+{\mu }_{2,t,n}^{L,move}+{\lambda }_{1,n}=0\mathrm{T}\in \left[1,t\right](45)$

$\frac{\mathrm{\partial }L}{\mathrm{\partial }{P}_{t,i}^{ess,c}}=\left\{\begin{array}{l}{\lambda }_t\Delta t+l_{\mathrm{deg}}{\eta }^{ess,c}\Delta t-{\mu }_{1,t,n}^{ess,c}+{\mu }_{2,t,n}^{ess,c}-{\lambda }_{3,t,n}{\eta }^{ess,c}\Delta t/Ca{p}_e^{ess}=0\mathrm{t}\in \left[1,T-1\right]\\ {\lambda }_t\Delta t+l_{\mathrm{deg}}{\eta }^{ess,c}\Delta t-{\mu }_{1,t,n}^{ess,c}+{\mu }_{2,t,n}^{ess,c}=0\mathrm{t}=T\end{array}\right.(46)$

$\frac{\mathrm{\partial }L}{\mathrm{\partial }{P}_{t,i}^{ess,d}}=\left\{\begin{array}{l}-{\lambda }_t\Delta t+\frac{l_{\mathrm{deg}}\Delta t}{{\eta }^{ess,d}}-{\mu }_{1,t,n}^{ess,d}+{\mu }_{2,t,n}^{ess,d}-\frac{{\lambda }_{3,t,n}\Delta t}{{\eta }^{ess,d}Ca{p}_e^{ess}}=0\mathrm{t}\in \left[1,T-1\right]\\ -{\lambda }_t\Delta t-\frac{l_{\mathrm{deg}}\Delta t}{{\eta }^{ess,d}}-{\mu }_{1,t,n}^{ess,d}+{\mu }_{2,t,n}^{ess,d}=0\mathrm{t}=T\end{array}\right.(47)$

$\frac{\mathrm{\partial }L}{\mathrm{\partial }{S}_{t,e}}=\left\{\begin{array}{l}-{\mu }_{1,t,n}^S+{\mu }_{2,t,n}^S+{\lambda }_{2,n}-{\lambda }_{3,t,n}=0\mathrm{t}=1\\ -{\mu }_{1,t,n}^S+{\mu }_{2,t,n}^S+{\lambda }_{3,t-1,n}-{\lambda }_{3,t,n}=0\mathrm{t}\in \left[2,T-1\right]\\ -{\mu }_{1,t,n}^S+{\mu }_{2,t,n}^S-{\lambda }_{2,n}+{\lambda }_{3,t-1,n}=0\mathrm{t}=T\end{array}\right.(48)$

$\frac{\mathrm{\partial }L}{\mathrm{\partial }{\lambda }_{1,n}}={\displaystyle \sum _{t=1}^T}{P}_{t,i}^{L,move}=0(49)$

$\frac{\mathrm{\partial }L}{\mathrm{\partial }{\lambda }_{2,n}}=S_{1,e}-S_{T,e}=0(50)$

$\frac{\mathrm{\partial }L}{\mathrm{\partial }{\lambda }_{3,t,n}}=S_{t,e}-S_{t-1,e}-\frac{P_{t,i}^{ess,c}{\eta }^{ess,c}}{Ca{p}_e^{ess}}+\frac{P_{t,i}^{ess,d}/{\eta }^{ess,d}}{Ca{p}_e^{ess}}\Delta t=0\mathrm{t}\in \left[1,T-1\right](51)$

3) The inequality constraint is constructed by large M method

Since the complementary slack variables in the KKT condition have nonlinear terms of the form ${\mu }_i{g}_i\left(x\right)=0$, a Boolean variable $\epsilon$ and a maximum positive number M are introduced to construct the following linear inequalities:

$\left\{\begin{array}{l}0\le P_{t,i}^{ess,c}\le {\epsilon }_1^{ess,c}M\\ 0\le {\mu }_{1,t,n}^{ess,c}\le \left(1-{\epsilon }_1^{ess,c}\right)M\end{array}\right.\mathrm{t}\in \left[1,T\right](52)$

$\left\{\begin{array}{l}0\le u_{t,e}^{ess}{P}_e^{c,rat}-P_{t,i}^{ess,c}\le {\epsilon }_2^{ess,c}M\\ 0\le {\mu }_{2,t,n}^{ess,c}\le \left(1-{\epsilon }_2^{ess,c}\right)M\end{array}\right.\mathrm{t}\in \left[1,T\right](53)$

$\left\{\begin{array}{l}0\le P_{t,i}^{ess,d}\le {\epsilon }_1^{ess,d}M\\ 0\le {\mu }_{1,t,n}^{ess,d}\le \left(1-{\epsilon }_1^{ess,d}\right)M\end{array}\right.\mathrm{t}\in \left[1,T\right](54)$

$\left\{\begin{array}{l}0\le \left(1-u_{t,e}^{ess}\right)P_e^{d,rat}-P_{t,i}^{ess,d}\le {\epsilon }_2^{ess,d}M\\ 0\le {\mu }_{2,t,n}^{ess,d}\le \left(1-{\epsilon }_2^{ess,d}\right)M\end{array}\right.\mathrm{t}\in \left[1,T\right](55)$

$\left\{\begin{array}{l}0\le S_{t,e}-S_e^{\min }\le {\epsilon }_1^{S}M\\ 0\le {\mu }_{1,t,n}^S\le \left(1-{\epsilon }_1^S\right)M\end{array}\right.\mathrm{t}\in \left[1,T\right](56)$

$\left\{\begin{array}{l}0\le S_e^{\max }-S_{t,e}\le {\epsilon }_2^{S}M\\ 0\le {\mu }_{2,t,n}^S\le \left(1-{\epsilon }_2^S\right)M\end{array}\right.\mathrm{t}\in \left[1,T\right](57)$

$\left\{\begin{array}{l}0\le P_{t,i}^{L,move}-L^{\min }\le {\epsilon }_1^{L,move}M\\ 0\le {\mu }_{1,t,n}^{L,move}\le \left(1-{\epsilon }_1^{L,move}\right)M\end{array}\right.\mathrm{t}\in \left[1,T\right](58)$

$\left\{\begin{array}{l}0\le L^{\max }-P_{t,i}^{L,move}\le {\epsilon }_2^{L,move}M\\ 0\le {\mu }_{2,t,n}^{L,move}\le \left(1-{\epsilon }_2^{L,move}\right)M\end{array}\right.\mathrm{t}\in \left[1,T\right](59)$

4) Single layer optimization model

Substituting Equations 45–51 into Equation 44 can be obtained as follows:

$\begin{array}{l}\nabla L={\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\lambda }_t\left(P_{t,i}^L-P_{t,i}^{PV}\right)\Delta t-{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\mu }_{2,t,n}^{ess,c}{u}_{t,e}^{ess}{P}_e^{c,rat}-{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\mu }_{2,t,n}^{ess,d}\left(1-u_{t,e}^{ess}\right)P_e^{d,rat}\\ +{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\mu }_{1,t,n}^S{S}_e^{\min }-{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\mu }_{2,t,n}^S{S}_e^{\max }+{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\mu }_{1,t,n}^{L,move}{L}^{\min }-{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\mu }_{2,t,n}^{L,move}{L}^{\max }\end{array}(60)$

Equation 60 is combined with the upper DNO optimization objective Equation 1 to obtain the optimization objective of the single-layer optimization model as shown in Equation 61:

$\begin{array}{l}\min F=a_o\left[f_{Grid}+f_{loss}+f_{switch}-{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}{\lambda }_t\left(P_{t,i}^L-P_{t,i}^{PV}\right)\Delta t\right]+b_v{f}_{vd}+\\ {\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}\left({\mu }_{1,t,n}^{L,move}{L}^{\min }-{\mu }_{2,t,n}^{L,move}{L}^{\max }\right)\\ +{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}\left[-{\mu }_{2,t,n}^{ess,c}{u}_{t,e}^{ess}{P}_e^{c,rat}-{\mu }_{2,t,n}^{ess,d}\left(1-u_{t,e}^{ess}\right)P_e^{d,rat}\right]\\ +{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}\left[{\mu }_{1,t,n}^S{S}_e^{\min }-{\mu }_{2,t,n}^S{S}_e^{\max }\right]\end{array}(61)$

Subject to: Equations 7, 8, 11–13, 15–19, 29–31, 33–34, 36–40, 45–59;

Variables: ${\lambda }_t,P_{t,i}^{VSC},Q_{t,i}^{VSC},P_{t,n}^P,P_{t,i}^{L,move},P_{t,i}^{ess,c},P_{t,i}^{ess,d},S_{t,e}$;

By the above methods, the two-layer game optimization problem has been transformed into a single-layer optimization problem.

5 Simulation and analysis

To verify the accuracy and feasibility of the proposed model, programming was implemented using MATLAB R2021b software. The optimization was solved in a 64-bit Windows environment, utilizing the YALMIP toolbox and the Gurobi solver. The hardware environment for optimization calculations was an Intel(R) Core(TM) i9-13900 K @ 3.00 GHz processor with 128 GB of memory.

5.1 Parameter setting

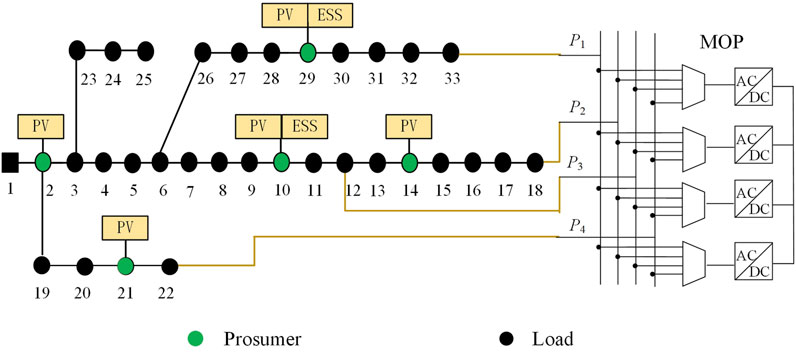
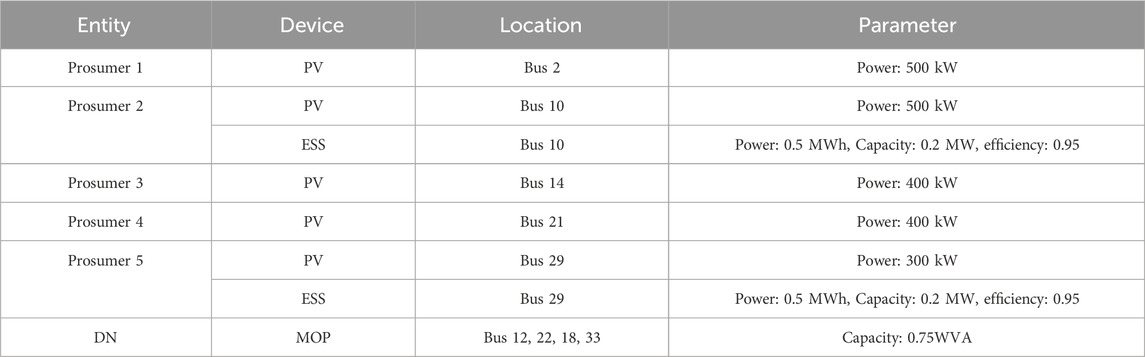
In the simulation tests, the modified IEEE-33 bus distribution system is used for analysis, which includes five prosumers with PV systems. Among them, the prosumers at buses 10 and 29 are equipped with ESS, as shown in Figure 4. The whole DN contains five PVS, two ESS and one four-feeder MOP. The relevant parameters are shown in Table 1, and the other bus branch parameters are the standard IEEE-33 bus system.

Figure 4

Figure 4. Diagram of the improved IEEE 33-bus system.

Table 1

Table 1. IEEE 33-bus test system related parameters.

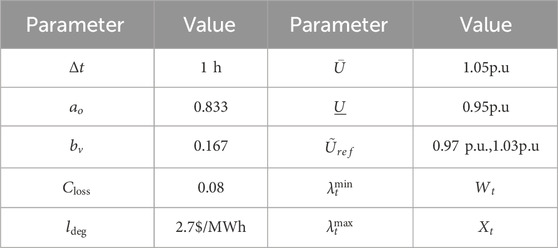
The DNO is set from the HV power purchase price reference (Qiao et al., 2025), and the DNO selling price is set to 400 ¥/MWh, without considering the reactive power influence of renewable energy. Other parameter Settings are shown in Table 2 (Yang et al., 2023).

Table 2

Table 2. Parameter settings.

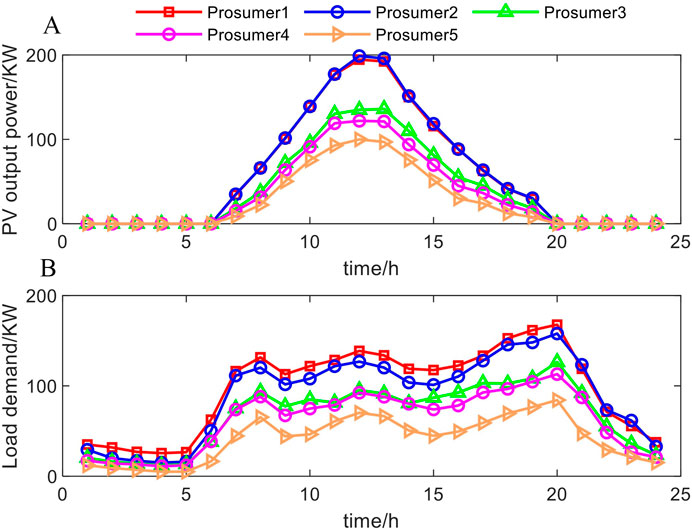
The PV output and load demand forecast of each prosumer are shown in Figures 5A, B.

Figure 5

Figure 5. Initial data of each prosumer: (A) PV output; (B) Load demand.

5.2 Results and analysis

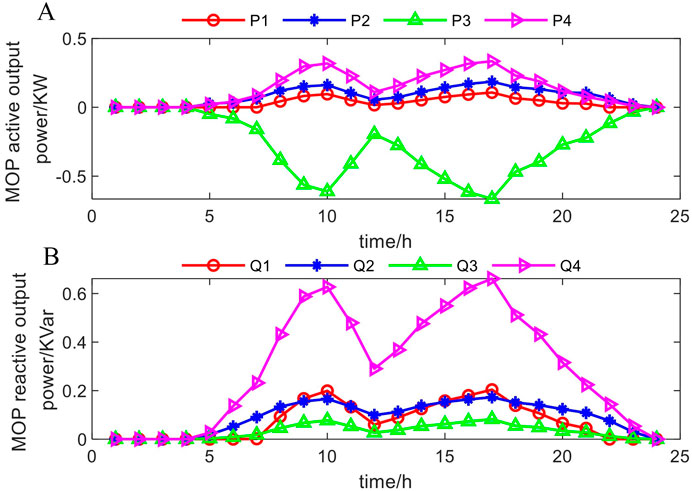
In the energy trading market, DNO, as the leader, has the pricing power, and the settlement price determined is shown in Figure 6.

Figure 6

Figure 6. Clearing price.

As followers, prosumer adjust their electricity consumption strategies according to the internal settlement price. The transferable load of each prosumer is shown in Figure 7A, and the total exchange power with DNO is shown in Figure 7B. The charging and discharging power of ESS1 connected to prosumer 2 is shown in Figure 8A, and the energy storage of each ESS is shown in Figure 8B.

Figure 7

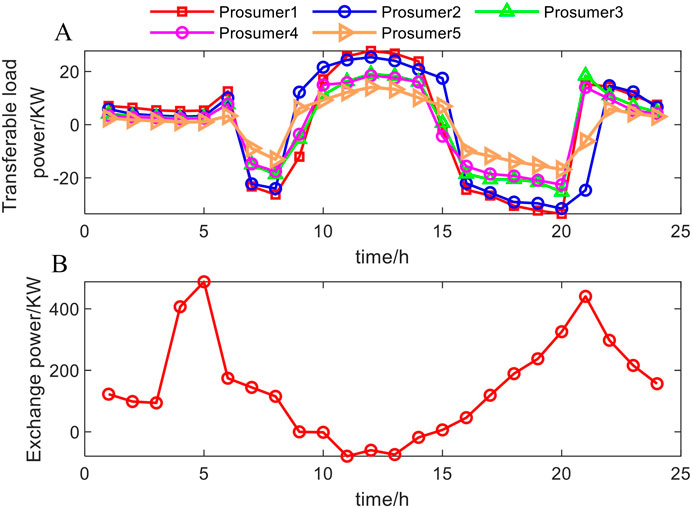
Figure 7. Load regulation strategies of prosumer: (A) Changes in transferable loads; (B) Exchange power.

Figure 8

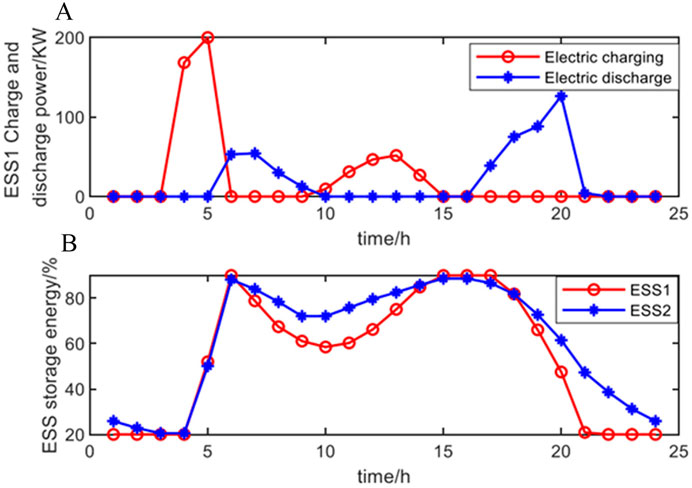
Figure 8. ESS control strategy: (A) Charge and discharge power of ESS1; (B) Energy storage of each ESS.

As observed from Figures 5–8, the formulation of the electricity consumption strategy of the prosumer is affected by the clearing price set by the DNO, which is specifically shown as follows:

Between 0:00 and 5:00, with zero PV output and low prosumer loads, prosumers purchase electricity to maintain normal operations. Clearing prices remain high due to economic principles but are capped by time-of-use pricing. During this period, the ESS charges and the prosumer increases the transferable load. From 3:00 to 5:00, as the electricity price decreases, the ESS charging increases, resulting in a sharp rise in the exchanged power. Between 6:00 and 8:00, the PV generation and consumer load gradually rise, but the supply is still insufficient, leading to an increase in the clearing price. At the same time as the ESS discharges, the prosumer reduces the transferable load, which reduces the exchanged power. Between 9:00 and 10:00, higher PV generation and less load can achieve energy balance through energy interaction and resource adjustment without purchasing DNO, thus achieving price reduction and zero exchanged power. From 11:00 to 13:00, peak PV output exceeds demand, enabling prosumers to charge ESS, consume transferable loads, and sell surplus energy to the DNO. Exchange power becomes negative, and clearing prices drop to the minimum limit. Between 14:00 and 17:00, as PV generation and load are reduced, the supply temporarily meets the demand and maintains the minimum price. After that, the energy internal supply exceeds the demand leading to the clearing price increase, prompting the prosumer to reduce the load and the ESS discharge, so that the exchange power is positive. From 18:00 to 20:00, insufficient PV generation and gradually rising electricity demand lead to the maximum clearing price. The prosumer reduces the transferable load and the ESS discharges, at which point, the exchanged power reaches its peak. Between 21:00 and 24:00, demand remains high, but prices stabilize due to time-of-use pricing. Prosumers remaining transferable loads and discharge surplus ESS energy, reducing costs and exchange power as load demand declines.

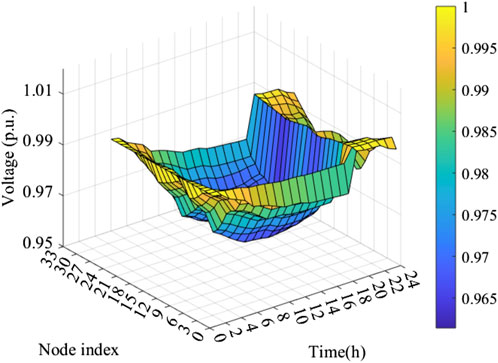
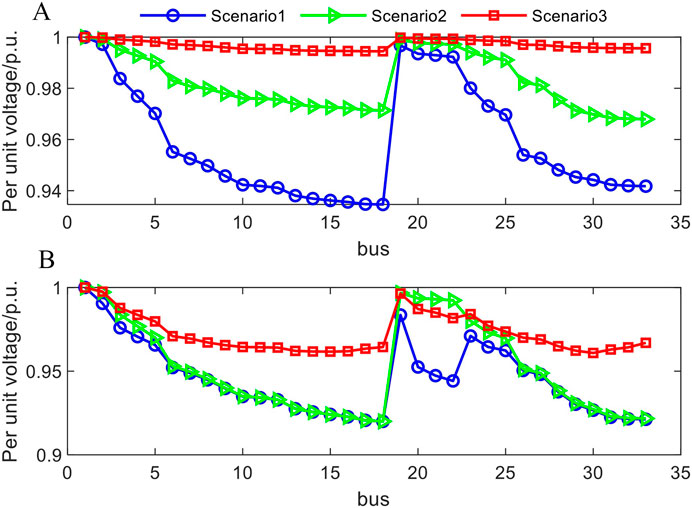
The voltage situation of each bus within 24 h of the test system is shown in Figure 9. It can be seen that the per unit voltage value of each bus is within the expected range (0.96 p.u.–1.04p.u.), which meets the safety of the system operation.

Figure 9

Figure 9. Voltage profiles of all 33 nodes.

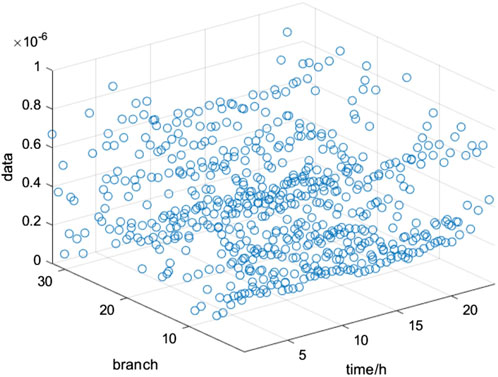
The gap value of 24 h is shown in Figure 10. Combined with the definition of Equation 41, it can be found that the gap value of each time period is at the level of 10-6, so it can be proved that convex relaxation is accurate.

Figure 10

Figure 10. Gap value.

5.3 Scenario comparison and analysis

In order to verify the effectiveness and superiority of the proposed strategy, the following three scenarios are set in this section:

Scenario 1: Only the economy of the system is considered, and safety issues such as MOP power flow optimization, power loss, and voltage deviation are not considered.

Scenario 2: The adjustment of MOP is not considered in the proposed strategy.

Scenario 3: The strategy presented in this article.

As can be seen in Figures 11A, B and Figures 12 A, B, the voltage quality of scenario 3 is better than that of the comparison scenario, indicating that the proposed strategy can improve the stability of the system. Moreover, the action of MOP is consistent with that of energy storage, which indicates that MOP can optimize the power flow distribution and improve power quality by adjusting the active and reactive power of the connected feeders.

Figure 11

Figure 11. Comparison of voltage per unit value: (A) Maximum voltage; (B) Minimum voltage.

Figure 12

Figure 12. Power output of MOP: (A) The output of active power; (B) The output of reactive power.

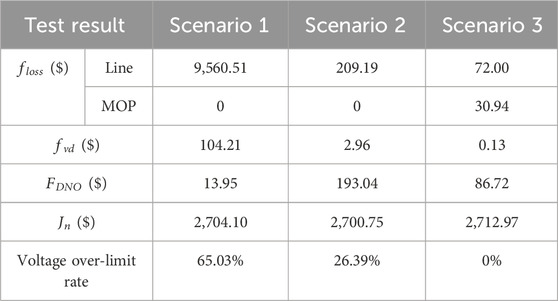
The test results are compared as shown in Table 3, including the system power loss cost ($f_{loss}$, including line power loss and MOP power loss), the converted voltage deviation cost ($f_{vd}$), the total operating cost of DNO ($F_{DNO}$), the total operating cost of the prosumer ($J_n$) and voltage over-limit rate. The voltage compliance range specified in this paper is 0.95p.u.–1.05p.u.

Table 3

Table 3. Test data comparison.

As shown in Table 3, the daily total operating cost of the DNO in Scenario 1, which considers only economic benefits, is $13.95, representing a reduction of approximately 83.9% compared to $86.72 in Scenario 3. However, the voltage deviation cost increases from $0.13 to $104.21, an increase of nearly 800 times, and the voltage over-limit rate increases from 0% to 26.39%. This indicates that in scenarios where safety performance is not considered, all controllable resources are allocated to maximize profits. While this approach effectively reduces system operating costs, it leads to significant grid fluctuations, poor power quality, and substantial safety risks, which are detrimental to the reliable operation of the system.

Compared to Scenario 2, Scenario 3 introduces the MOP, which increases the power loss cost of the MOP by $30.94. However, both network loss and voltage deviation costs are reduced, resulting in a decrease in the total operating cost of the DNO from $193.04 to $86.72, a reduction of approximately 55.1%. Moreover, the voltage over-limit rate is reduced from 65.03% to 0. This demonstrates a significant improvement in both economic efficiency and operational safety.

In summary, the proposed strategy not only addresses the energy transaction challenges in multi-prosumer distribution systems and ensures the economic benefits of all participants but also enhances the safety performance of the system. Additionally, it provides a novel solution for promoting local renewable energy utilization and optimizing energy interactions.

6 Conclusion

This study investigates the energy interaction challenges in flexible distribution systems with multiple prosumers. By analyzing the factors influencing the economic benefits of the DNO and prosumers, as well as the network security of the DN, a Stackelberg game-based energy interaction strategy for multi-prosumer distribution systems is proposed, considering both economic and safety aspects. Unlike previous studies, this strategy not only addresses the economic issues between the DNO and prosumers but also optimizes DN operation by regulating the MOP, ensuring system operational safety and improving power quality. Additionally, the original bi-level energy interaction model is transformed using KKT conditions, enhancing computational efficiency. The main conclusions are as follows:

1) Different from traditional energy interaction models for multi-prosumer distribution systems, this paper proposes a novel energy interaction strategy based on game theory, considering the interests of all participants and the operational safety of the system. This strategy not only maximizes the benefits for all parties but also promotes the local utilization of PV energy while protecting user privacy.

2) The influencing factors in the energy interaction process were analyzed, and the MOP was introduced into the energy trading market. Different from traditional interaction models that focus solely on the coordination between the DNO and prosumers, this strategy also considers power flow regulation in the DN. Although the introduction of MOP increases device costs, it significantly reduces power losses across the system, improves power quality, and ensures the long-term operation of the system.

3) Different from traditional iterative methods for solving bi-level energy interaction game models to determine transaction prices, this paper employs KKT conditions, dual theory, linearization methods, and relaxation techniques to transform the bi-level optimization model, simplifying the solution process.

This study focuses on exploiting the potential of game theory in enhancing energy interaction in flexible distribution systems and innovating the introduction of interconnected devices to improve the regulation performance of distribution networks, but voltage overruns still exist. Therefore, future research should be oriented to dynamic uncertainty and real-time operation, and explore data-driven based intelligent control to further optimize energy trading, improve scalability, and ensure reliable grid operation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

WL: Funding acquisition, Project administration, Writing–review and editing, Methodology. SZ: Investigation, Supervision, Writing–original draft. XZ: Methodology, Software, Writing–original draft. SQ: Data curation, Supervision, Writing–review and editing. BL: Formal Analysis, Writing–review and editing. YZ: Formal Analysis, Supervision, Writing–review and editing. JC: Writing–review and editing. QG: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was financially supported by Technology Project of State Grid Anhui Electric Power Co., Ltd. China “Research on multi-agent interactive energy control technology of high proportion distributed photovoltaic flexible distribution system” (B31205230006).

Conflict of interest

Authors WL, SZ, and SQ were employed by Electric Power Research Institute of State Grid Anhui Electric Power Co., Ltd. Authors BL, YZ, JC, and QG were employed by State Grid Anhui Electric Power Co., Ltd., Chuzhou Power Supply Company.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from Technology Project of State Grid Anhui Electric Power Co., Ltd. The funder had the following involvement in the study: study design, decision to publish, and preparation of the manuscript.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ashrafi, M., Abbaspour, A., Firuzabad, M., Dehkordi, S., Bacha, S., and Caire, R. (2024). Fault-resilient energy management of grid-connected energy communities in presence of distance-driven P2P and P2G energy transactions. Electr. Power Syst. Res. 233, 110468. doi:10.1016/J.EPSR.2024.110468

CrossRef Full Text | Google Scholar

Deakin, M., Taylor, P., Bialek, J., and Ming, W. (2022). Design and operation of hybrid multi-terminal soft open points using feeder selector switches for flexible distribution system interconnection. Electr. Power Syst. Res. 212, 108516. doi:10.1016/J.EPSR.2022.108516

CrossRef Full Text | Google Scholar

Dempe, S., and Franke, S. (2019). Solution of bilevel optimization problems using the KKT approach. Optimization 68 (8), 1471–1489. doi:10.1080/02331934.2019.1581192

CrossRef Full Text | Google Scholar

Gao, J., Shao, Z., Chen, F., and Lak, M. (2024). Robust optimization for integrated energy systems based on multi-energy trading. Energy 308, 132302. doi:10.1016/J.ENERGY.2024.132302

CrossRef Full Text | Google Scholar

Guan, Y., and Hou, Q. (2024). Design of distributed trading mechanism for prosumers considering the psychological gap effect in community electricity markets. Electr. Power Syst. Res. 232, 110410. doi:10.1016/J.EPSR.2024.110410

CrossRef Full Text | Google Scholar

Hou, P., Yang, G., Hu, J., Douglass, P., and Xue, Y. (2022). A distributed transactive energy mechanism for integrating PV and storage prosumers in market operation. Engineering 12, 171–182. doi:10.1016/J.ENG.2022.03.001

CrossRef Full Text | Google Scholar

Izadi, A., and Rastegar, M. (2024). A stochastic iterative peer-to-peer energy market clearing in smart energy communities considering participation priorities of prosumers. Sustain. Cities Soc. 114, 105728. doi:10.1016/J.SCS.2024.105728

CrossRef Full Text | Google Scholar

Li, J., Zhang, L., Zhang, B., and Tang, W. (2023). Coordinated planning for flexible interconnection and energy storage system in low-voltage distribution networks to improve the accommodation capacity of photovoltaic. Glob. Energy Interconnect. 6 (6), 700–713. doi:10.1016/J.GLOEI.2023.11.004

CrossRef Full Text | Google Scholar

Li, J., Zhang, Y., Lv, C., Liu, G., Ruan, Z., and Zhang, F. (2024). Coordinated planning of soft open points and energy storage systems to enhance flexibility of distribution networks. Appl. Sci. 14 (18), 8309. doi:10.3390/APP14188309

CrossRef Full Text | Google Scholar

Liang, J., Zhou, J., Yuan, X., Huang, W., Gong, X., and Zhang, G. (2024). An active distribution network voltage optimization method based on source-network-load-storage coordination and interaction. Energies 17 (18), 4645. doi:10.3390/EN17184645

CrossRef Full Text | Google Scholar

Liu, D., Cheng, P., Cheng, J., Liu, J., Lu, M., and Jiang, F. (2023). Improved reinforcement learning-based real-time energy scheduling for prosumer with elastic loads in smart grid. Knowledge-Based Syst. 280, 111004. doi:10.1016/J.KNOSYS.2023.111004

CrossRef Full Text | Google Scholar

Liu, J., Meng, X., and Wu, J. (2024). Multi-stage cooperative planning among shared energy storage operator and multiple prosumers in regional integrated energy system considering long-term uncertainty. J. Energy Storage 103 (PA), 114244. doi:10.1016/J.EST.2024.114244

CrossRef Full Text | Google Scholar

Lou, W., Zhu, S., Ding, J., Zhu, T., Wang, M., Sun, L., et al. (2023). Transactive demand–response framework for high renewable penetrated multi-energy prosumer aggregators in the context of a smart grid. Appl. Sci. 13 (18), 10083. doi:10.3390/APP131810083

CrossRef Full Text | Google Scholar

Manchalwar, A. D., Patne, N. R., Morey, C. D., and Pemmada, S. (2024). Prosumers and retailers based decentralized energy trading model in the smart grid considering network constraints. Int. J. Electr. Power Energy Syst. 160, 110108. doi:10.1016/J.IJEPES.2024.110108

CrossRef Full Text | Google Scholar

Meng, H., Jia, H., Xu, T., Sun, J., Wang, R., and Wang, J. (2024). Trading mechanism of distributed shared energy storage system considering voltage regulation. Appl. Energy 374, 123904. doi:10.1016/J.APENERGY.2024.123904

CrossRef Full Text | Google Scholar

Miyamoto, T., Kitamura, S., Naito, K., Mori, K., and Izui, Y. (2020). Distributed day-ahead scheduling of community energy management system group considering uncertain market prices using stochastic optimization. IEEJ Trans. Electr. Electron. Eng. 15 (3), 401–408. doi:10.1002/tee.23068

CrossRef Full Text | Google Scholar

Mohammadreza, A., Taher, N., and Hossein, J. (2024). Economic operation of networked flexi-renewable energy hubs with thermal and hydrogen storage systems based on the market clearing price model. Int. J. Hydrogen Energy 50 (PD), 1–18. doi:10.1016/J.IJHYDENE.2023.06.144

CrossRef Full Text | Google Scholar

Qiao, J., Mi, Y., Shen, J., Lu, C., Cai, P., Ma, S., et al. (2025). Optimization schedule strategy of active distribution network based on microgrid group and shared energy storage. Appl. Energy 377 (PD), 124681. doi:10.1016/J.APENERGY.2024.124681

CrossRef Full Text | Google Scholar

Seppälä, J., and Järventausta, P. (2024). Analyzing supply reliability incentive in pricing regulation of electricity distribution operators. Energies 17 (6), 1451. doi:10.3390/EN17061451

CrossRef Full Text | Google Scholar

Taher, A., Hasanien, H., Alsaleh, I., Aleem, A., Alassaf, A., and Almalaq, A. (2024). Optimizing active distribution microgrids with multi-terminal soft open point and hybrid hydrogen storage systems for enhanced frequency stability. J. Energy Storage 99 (PA), 113369. doi:10.1016/J.EST.2024.113369

CrossRef Full Text | Google Scholar

Tao, C., Duan, Y., Gao, F., and Zhang, J. (2024). A game model based optimisation approach for generalised shared energy storage and integrated energy system trading. J. Eng. Appl. Sci. 71 (1), 172. doi:10.1186/S44147-024-00506-7

CrossRef Full Text | Google Scholar

Wu, Y., Tian, X., Gai, L., Lim, B., Wu, T., Xu, D., et al. (2024). Energy management for PV prosumers inside microgrids based on Stackelberg–Nash game considering demand response. Sustain. Energy Technol. Assessments 68, 103856. doi:10.1016/J.SETA.2024.103856

CrossRef Full Text | Google Scholar

Xiao, Y., Lin, X., Lei, Y., Gu, Y., Tang, J., Zhang, F., et al. (2024). Blockchain-assisted secure energy trading in electricity markets: a tiny deep reinforcement learning-based Stackelberg game approach. Electronics 13 (18), 3647. doi:10.3390/ELECTRONICS13183647

CrossRef Full Text | Google Scholar

Yang, X., Song, Z., Wen, J., Ding, L., Zhang, M., Wu, Q., et al. (2023). Network-constrained transactive control for multi-microgrids-based distribution networks with soft open points. IEEE Trans. Sustain. Energy 14, 1769–1783. doi:10.1109/TSTE.2023.3246360

CrossRef Full Text | Google Scholar

Yang, Y., Xu, X., Pan, L., Liu, J., Liu, J., and Hu, W. (2024). Distributed prosumer trading in the electricity and carbon markets considering user utility. Renew. Energy 228, 120669. doi:10.1016/J.RENENE.2024.120669

CrossRef Full Text | Google Scholar

Zheng, S., Huang, G., and Lai, A. C. K. (2021). Techno-economic performance analysis of synergistic energy sharing strategies for grid-connected prosumers with distributed battery storages. Renew. Energy 178, 1261–1278. doi:10.1016/J.RENENE.2021.06.100

CrossRef Full Text | Google Scholar

Zheng, W., Xu, S., Lu, H., Wu, W., and Zhu, J. (2024). Trading mechanism for social welfare maximization in integrated electricity and heat systems with multiple self-interested stakeholders. Energy 306, 132267. doi:10.1016/J.ENERGY.2024.132267

CrossRef Full Text | Google Scholar

Zhu, X., Sun, Y., Yang, J., Dou, Z., Li, G., Xu, C., et al. (2022). Day-ahead energy pricing and management method for regional integrated energy systems considering multi-energy demand responses. Energy 251, 123914. doi:10.1016/J.ENERGY.2022.123914

CrossRef Full Text | Google Scholar