Optimal configuration strategy of energy storage considering flexible response of high energy-consuming industrial and mining loads in independent microgrid

The coordinated optimization of industrial and mining loads with energy storage (ES) is a critical approach to achieving power and energy balance in microgrids while promoting the new energy accommodation. Addressing the issue of insufficient flexibility in demand response from high-energy-consuming lithium mining loads, which may lead to conservative ES capacity allocation and underutilization of complementary flexibility potential, this paper proposes an ES optimization strategy for microgrids considering the participation of high-energy-consuming lithium mining loads in demand response. Firstly, considering the production process of extracting lithium from salt lakes brine and the electricity consumption characteristics of major energy-consuming equipment, a mathematical model is developed to quantify the flexibility adjustment potential of lithium mining loads under production behavior constraints. Based on this, incorporating the regulation boundaries of photovoltaic (PV) units, gas turbine units, concentrated solar power (CSP), ES system, and flexible lithium mining loads, an ES capacity optimization model is constructed to minimize the comprehensive system capital and operation costs in independent microgrid. The model is then linearized into a mixed-integer programming problem. Finally, through case study simulations of an actual microgrid in Southwest China, the feasibility and effectiveness of the proposed ES optimization strategy are verified. The results demonstrate that the proposed strategy can economically and effectively meet the power and energy balance of the independent microgrid and the electricity demands of high-energy-consuming loads, while promoting the improvement of new energy accommodation capacity.

1 Introduction

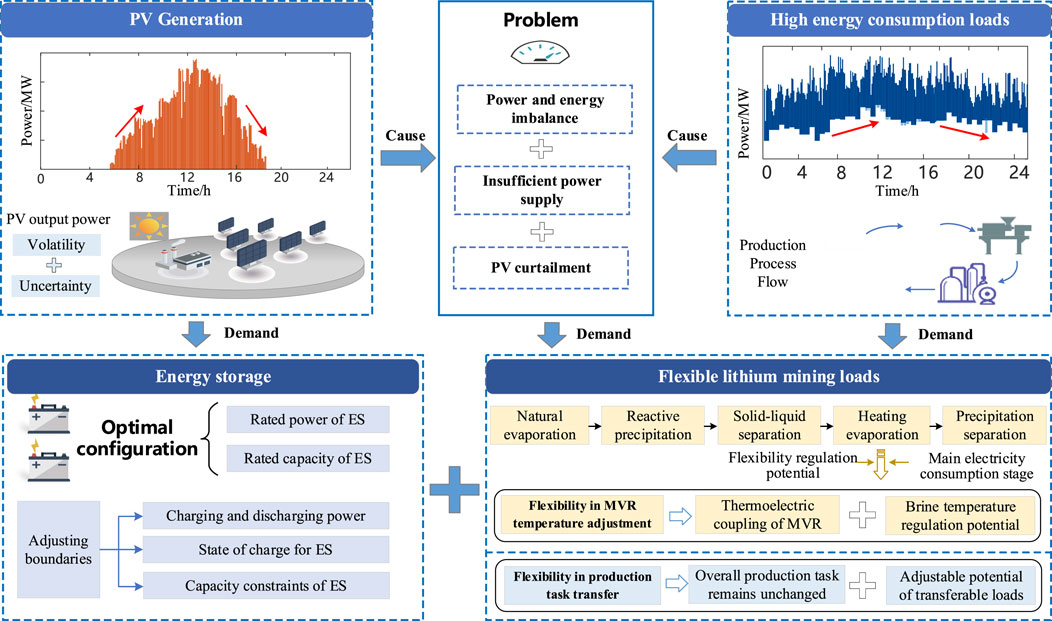
With the rapid development of new energy vehicles and lithium-ion ES, the demand for battery-grade lithium carbonate preparation continues to grow. However, the salt lakes lithium mines as a crucial raw material source are often located in remote areas, making it challenging to extend power transmission networks to meet the high energy demands of lithium mining operations. Therefore, it is necessary to develop localized microgrids for on-site power supply (Zhang et al., 2024)- (Wu et al., 2024). Under the dual-carbon goals and the new power system construction, the penetration of new energy in microgrids is increasing. However, the inherent seasonality, volatility, and uncertainty of new energy reduce the dispatchable capacity of traditional regulatory resources, making it difficult to ensure the balance of power and energy in microgrids. This highlights the urgent need to expand grid regulation resources and transition from the conventional “source-grid-load” model to the coordinated “source-grid-load-storage” interactive model (Liu et al., 2020). On one hand, high-energy-consuming lithium mining loads are characterized by high flexibility, fast dispatch response, and significant scalability potential. Leveraging their regulatory flexibility for demand response can alleviate the power supply pressure of microgrids (Nie et al., 2023). On the other hand, as an excellent regulatory resource for power and energy balance, the optimal configuration and coordinated operation of ES system are closely related to the operational performance and economic benefits of microgrids. Therefore, studying collaborative configuration strategies for ES under flexible lithium mining load responses is of great significance for maintaining power and energy balance in microgrids and meeting load power demands.

In recent years, some scholars have conducted research on the participation of high-energy-consuming industrial loads in optimizing grid operations, achieving notable results. For instance, Reference (Philipo et al., 2022) proposes a demand-side management strategy based on artificial neural networks that accounts for load-shifting behavior, effectively reducing load demand in standalone PV battery microgrids in East Africa. A novel flexible low-carbon optimal dispatch model is proposed for the distribution network, which coordinates the participation of heat storage industrial loads in demand response (Wang W. D. et al., 2024). In Reference (Xu et al., 2020), a method is proposed to involve the steam systems of industrial loads, such as paper mills and steel plants, as flexible loads in demand response. This approach approximated the flexibility boundaries under the influence of steam uncertainty. Furthermore, Reference (Cui and Zhou, 2018) summarizes the main methods for industrial load demand response, pointing out that modeling industrial processes using a production-buffer approach could yield more reasonable optimization results. Ramesh and Sofana utilize a resource-task network to represent refinery processes and implemented stochastic dynamic programming to shift the electricity usage of refineries, reducing energy costs (Reka and Ramesh, 2016). Additionally, Reference (Liao et al., 2024) analyzes production characteristics and regulation constraints to construct a demand response capability boundary, enhancing the flexibility of large-capacity electrolytic aluminum loads to interact bidirectionally with the grid. Reference (Golmohamadi et al., 2019) aggregates the flexibility of cement manufacturing, metal smelting, and residential loads using load aggregators, leveraging complementary characteristics among different loads to participate in demand response. These studies effectively improved the economic benefits of industrial enterprises and enhanced grid stability by tapping into the flexibility of industrial production processes. However, under the context of new energy standalone microgrids, the quantification and integration of lithium mining load flexibility in demand response remain insufficiently addressed, highlighting a gap in the current research landscape.

Relying solely on industrial and mining loads constrained by production processes is insufficient to effectively maintain the power and energy balance of the grid. Coordinated optimization of flexible loads and ES is a crucial solution. In Reference (Huang et al., 2021), A two-stage optimal scheduling method based on model predictive control is proposed for the energy management of the actual microgrid system containing ES and flexible loads, with improving the optimization control accuracy. Reference (Zeng et al., 2024) develops a refined demand response mechanism and shared ES optimization model for various building loads to achieve source-grid-load-storage synergistic interaction. In Reference (Wang D. et al., 2024), a joint optimization mechanism integrating electric and thermal energy storage with demand response is proposed, aiming to enhance the economic benefits of market participants while improving supply-demand coordination through interregional energy complementarity. Moreover, Reference (Karimianfard et al., 2022) proposes a large-scale ES coordination capacity and optimization strategy that considers load-side response behavior, improving the operational flexibility of smart grids and increasing economic returns for loads. Reference (Sun et al., 2022) treats flexible demand-side resources as virtual ES while employing conventional ES to mitigate load uncertainties. Additionally, Reference (Shen et al., 2022) proposes a multi-objective optimization model for multi-ES capacity planning in industrial park microgrids based on electricity-heat-gas coupled demand response, aiming to minimize economic costs and carbon emissions while enhancing energy supply reliability and economic performance. These studies construct models for load demand response and ES optimization from various perspectives, effectively maintaining grid power balance and ensuring reliable and economic system operation. However, research focusing on the coordinated optimization of ES and demand response for industrial and mining loads remains relatively scarce, leaving room for further exploration in this area.

This study addresses the power supply demands and flexibility regulation of high-energy-consuming lithium mining loads, focusing on independent industrial microgrid scenarios in remote areas. It proposes an optimized ES configuration and operational strategy for independent microgrids, incorporating the potential of mining load regulation to enhance system performance. The main contributions of this paper are summarized as follows:

• A flexibility regulation analysis and quantification model for lithium mining loads is developed, considering the specific production characteristics of lithium extraction. This model effectively enhances the bidirectional flexibility interaction capabilities with the microgrid.

• By considering the operational boundaries of PV units, CSP units, ES system, and lithium mining load regulation, an optimized ES configuration model is constructed to minimize the comprehensive construction and operational costs of the independent microgrid. Economically, this approach reduces the operating costs of the microgrid system, while technically, it enhances the renewable energy utilization rate and ensures reliable power supply for lithium mining loads.

The rest of the paper is organized as follows. In Section 2, the regulation potential of industrial and mining load is analyzed and modeled. In Section 3, the coordinated operation strategy of industrial and mining loads with ES is proposed, and the main objectives and constraints of the de-aggregation strategy are provided. Then, Section 4 presents results and discussion based on case studies. The conclusion and future work are drawn in Section 5.

2 Modeling of industrial and mining load regulation potential

Due to the volatility and uncertainty of its output, PV power generation is difficult to match the electricity demand of high-energy-consuming loads, which further leads to the imbalance of power and electricity in the microgrid and the lack of new energy accommodation capacity. By tapping the potential of flexible adjustment on the load side and cooperating with ES resources to participate in the optimal operation of the microgrid, it is helpful to alleviate the above problems, as shown in Figure 1. However, the load regulation potential of lithium ore is affected by its process production characteristics. How to consider this key factor and quantify modeling is an important difficulty and key point in the mining of industrial and mining load flexibility.

Figure 1

Figure 1. Coordinated operation framework of lithium mining loads and ES in microgrid.

The technologies for extracting lithium resources from salt lakes brine have reached a relatively mature stage both domestically and internationally. The primary methods include precipitation, solvent extraction, adsorption, calcination, and electrodialysis. Among these, the precipitation method has become the mainstream technology due to its mature process and wide application (Kong et al., 2024). The typical process flow involves natural evaporation and crystallization of the salt lakes, reaction precipitation, solid-liquid separation, heating and evaporative concentration, and precipitation separation. The heating and evaporative concentration stage primarily relies on MVR technology, which is also the most energy-intensive phase of the entire process (Xiao, 2014).

The flexibility potential of lithium mining loads is mainly reflected in two aspects: 1) Adjustability of the MVR system temperature (Zhou et al., 2022): The MVR evaporative concentration process operates within a temperature-adjustable range, where temperature regulation directly affects electricity consumption. 2) Flexibility in scheduling production tasks over time: The production process allows for adjustments in task timing to accommodate demand response requirements. Specifically, the MVR system provides an adjustable temperature range during the evaporative concentration stage. Temperature adjustments result in corresponding changes in power consumption. To evaluate the load regulation potential, a mathematical model based on thermal inertia can be developed. This model considers key factors such as the specific heat capacity of brine, the temperature range required to maintain process stability, heat transfer between the compression process and the environment, and the efficiency of heating loads, which contributes to offer theoretical support for assessing the flexibility potential of thermostatically-controlled lithium mining loads (TLMLs).

2.1 MVR temperature adjustable flexibility

2.1.1 Brine heating model

The heat required for heating and evaporating salt lakes brine is related to its mass, specific heat capacity, and temperature changes.

$Q=m{C}_b\Delta T(1)$

where Q represents the heat variation of brine heating; m is quality of brine; C_b represents the specific heat capacity of the brine; ∆T represents the temperature change of the brine.

2.1.2 Heat loss model

Due to the interaction between MVR and the external environment, a certain amount of heat loss is caused.

$Q_{loss}\left(t\right)=hA\left[T_{bri}\left(t\right)-T_{env}\left(t\right)\right](2)$

where Q_loss(t) represents heat loss due to environmental interaction at time t; h represents the heat transfer coefficient of environment and MVR; A represents the surface area of the MVR in contact with the external environment; T_bri(t) is brine temperature; T_env(t) is ambient temperature.

2.1.3 Regulation potential for lithium extraction from salt lakes

The process of isobaric evaporation to isobaric condensation of salt lakes brine meets the temperature, power and capacity adjustable range:

$T_{\min }\le T_{bri}\left(t\right)\le T_{\max }(3)$

$P_{Li}^{\min }\left(t\right)\le P_{Li}\left(t\right)\le P_{Li}^{\max }\left(t\right)(4)$

$Q_{\min }\le Q_{i,0}+\left[{\int }_0^T{P}_{Li}\left(t\right)dt-Q_{loss}\left(t\right)\right]\le Q_{\max }(5)$

where T_max represents the upper limit of brine temperature; T_min represents the lower limit of brine temperature; P_Li(t) is the operating power of TLMLs; P^max _Li(t) and P^min _Li(t) are the upper and lower limits of adjusted load power at time t, respectively; Q_min and Q_max are the upper and lower limits of thermal storage capacity, respectively.

2.1.4 Thermoelectric coupling characteristics

Considering environmental heat loss, there is a thermoelectric coupling characteristic between power consumption changes and MVR temperature variations.

$m{C}_b\left[T_{bri}\left(t+1\right)-T_{bri}\left(t\right)\right]=\eta P_{Li}\left(t\right)-Q_{loss}\left(t\right)(6)$

where η is coefficient of thermal efficiency.

2.1.5 MVR continuous regulation limits

The continuous adjustment of MVR will cause frequent fluctuations in evaporator temperature. To maintain production stability to the greatest extent possible, the continuous adjustment limit of lithium mining load power consumption is as follows:

$\left\{\begin{array}{l}{\mu }_{lu}^{dw}\left(t\right)v_{Li}^{-}\le P_{Li}\left(t\right)-P_{Li}\left(t-1\right)\le {\mu }_{lu}^{up}\left(t\right)v_{Li}^{+}\\ {\mu }_{lu}^{dw}\left(t\right)+{\mu }_{lu}^{up}\left(t\right)=1\\ \left[{\mu }_{lu}^{dw}\left(t\right)+{\mu }_{lu}^{up}\left(t\right)\right]+\left[{\mu }_{lu}^{dw}\left(t-1\right)+{\mu }_{lu}^{up}\left(t-1\right)\right]\le 1\end{array}\right.(7)$

where v- Li and v + Li are the lower and upper limits of the lithium mining load regulation rate; μdw lu and μup luare 0–1 state variables that characterize the downward and upward adjustment of the adjustment power.

2.1.6 Economic compensation for industrial and mining load regulation

The benefits of lithium mine load mainly come from two indicators: economic compensation and heat demand. The impact degree of heat demand is transformed into economic index, and the two are linearly summed:

$C_{Li}=c_{Li}\left|P_{Li}^{fr}-P_{Li}\left(t\right)\right|+c_{MVR}\left(\frac{T_{bri}\left(t\right)-T_{\min }}{T_{\max }-T_{\min }}\right)(8)$

where C_Li is the economic compensation for the temperature control adjustment of TLMLs; c_Li is the economic compensation cost per unit power for temperature regulation of TLMLs; P^fr_Li is the planned power consumption curve of TLMLs; c_MVR is the influence coefficient of temperature changes on the production efficiency of lithium mining loads.

2.2 Transferable flexibility of sequential production

The time-series transfer characteristics of production tasks can be equivalent to the modeling of transferable lithium mining loads. The specific mathematical modeling is as follows:

2.2.1 Load transferability feature

Ensuring the overall production task remains unchanged throughout the entire scheduling cycle, with only timing adjustments.

${\displaystyle \sum _{t=1}^T}\left[P_{tr}^{fr}\left(t\right)-P_{tr}\left(t\right)\right]=0(9)$

where P^fr_tr(t) and P_tr(t) are the power of transferable lithium mining loads before and after scheduling at time t, respectively; T is the scheduling period.

2.2.2 Adjustable potential of transferable loads

$P_{tr\_\min }\left(t\right)\le P_{tr}\left(t\right)\le P_{tr\_\max }\left(t\right)(10)$

where P_{tr_max}(t) and P_{tr_min}(t) are the upper and lower limits of power after lithium mining load transfer, respectively.

2.2.3 Transferable loads regulation rate

$v_{tr}^{-}\le P_{tr}\left(t\right)-P_{tr}\left(t-1\right)\le v_{tr}^{+}(11)$

where v-tr and v + tr are lower and upper limit on regulation rate of lithium mining transferable loads.

2.2.4 Economic compensation of transferable loads

When load power is transferred, appropriate economic compensation should be provided to the lithium mining enterprises, which is as Equation 12.

$C_{tr}={\displaystyle \sum _{t=1}^T}{c}_{tr}\left|P_{tr}^{fr}\left(t\right)-P_{tr}\left(t\right)\right|(12)$

where C_tr is economic compensation of lithium mining transferable loads; c_tr is the unit power compensation cost of lithium mining transferable loads.

3 Optimization model for coordinated operation of industrial and mining loads with ES

To fully exploit the flexibility potential of lithium mining loads and the adjustment capabilities of ES system, this study develops a coordinated optimization model for flexible lithium mining loads and ES configurations, as illustrated in Figure 2. The optimization model is implemented in MATLAB, utilizing the YALMIP toolbox to interface with the Gurobi solver for solution computation. Based on the mathematical model of lithium mining load flexibility and its regulatory boundaries, the optimization considers constraints from the grid side, generation side, load side, and storage side. The objective function is to minimize the operational cost of the microgrid system. This problem is formulated as a mixed-integer linear programming (MILP) problem and solved to derive the optimal ES configuration scheme for independent microgrids. This approach integrates flexibility from the lithium mining load and ES to enhance the operational efficiency and economic performance of microgrids, contributing to improved renewable energy utilization and reliable power supply.

Figure 2

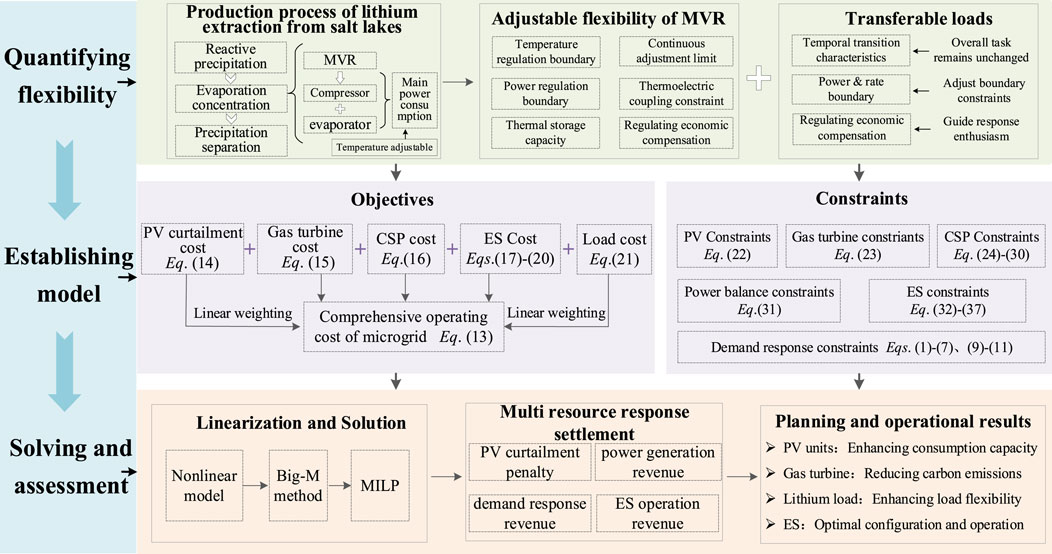
Figure 2. Block diagram of optimization configuration and operation model for ES in independent microgrid.

3.1 Objective function

Considering the new energy curtailment cost, gas turbine power generation and carbon reduction cost, CSP units cost, ES cost, industrial and mining load adjustment cost, the multi-objective is converted into single-objective comprehensive operation cost of microgrid by linear weighting method, which is as Equation 13.

$obj=ob{j}_{PV}+ob{j}_{GT}+ob{j}_{CSP}+ob{j}_{ES}+ob{j}_{load}(13)$

where obj is the comprehensive operating cost of microgrid; obj_PV is the penalty cost of PV curtailment; obj_GT is power generation and carbon emission penalty cost of gas turbine; obj_CSP is the operating cost of CSP units; obj_ES is the capital and operating cost of ES; obj_load is the adjustment cost of the flexible lithium mining loads.

3.1.1 PV curtailment penalty cost

The output power of PV units is used to supply load demand. To enhance the PV utilization rate, the PV curtailment is incorporated into the optimization objective and transformed into an economic objective of curtailment cost, which is as Equation 14.

$ob{j}_{PV}={\displaystyle \sum _t}{c}_{PV}\left[P_{PV}^{fr}\left(t\right)-P_{PV}\left(t\right)\right](14)$

where c_PV is the penalty cost per unit of curtailed PV power; P^fr_PV(t) is the predicted PV output power for the typical day; P_PV(t) indicates the PV actual operating power.

3.1.2 Gas turbine operating cost

Gas turbine operating costs include power generation costs and carbon emission penalty costs, which is as Equation 15.

$ob{j}_{GT}={\displaystyle \sum _t}\left(c_{GT}+c_{ca}\right)P_{GT}\left(t\right)(15)$

where c_GT and c_ca are the power generation cost and carbon emission penalty cost per unit power of gas turbine.; P_GT(t)is the operating power of the gas turbine.

3.1.3 CSP units operating cost

$ob{j}_{CSP}={\displaystyle \sum _t}{c}_{CSP}\left|P_{CSP}\left(t\right)\right|(16)$

where c_CSP is the operating cost per unit power of CSP; P_CSP(t) is the output power of the CSP unit at time t.

3.1.4 ES costs

The ES cost includes both capital and operation cost. The capital cost refers to the total investment cost of ES system, amortized into a fixed daily cost. The operation and maintenance cost covers the expenses required to keep the ES system in optimal standby condition, which is as Equations 17–20.

$ob{j}_{ES}=C_{inv}^{day}+C_{op}(17)$

$C_{inv}^{day}=\frac{R_{ES}}{365}{c}_E{E}_N(18)$

$R_{ES}=\frac{r{\left(1+r\right)}^{T_{ES}}}{{\left(1+\mathrm{r}\right)}^{T_{ES}}-1}(19)$

$C_{op}={\displaystyle \sum _t}{c}_{op}\left|P_{ES}\left(t\right)\right|(20)$

where Cday inv represents the capital cost converted on a typical day.; C_op is the operating cost of ES; R_ES is the annual investment recovery coefficient of ES; T_ES is the life of ES; r is the discount rate; c_E is the life-cycle capital cost of ES; E_N is the rated capacity of ES; P_ES(t) is the operating power of the ES at time t; c_op is the operation and maintenance cost factor of ES.

3.1.5 Lithium mining loads cost

$ob{j}_{laod}=C_{Li}+C_{tr}(21)$

3.2 Constraints

The optimal operation conditions of industrial microgrids include constraints on PV unit output, gas turbine output, CSP unit output, ES operation, and lithium mining load operation.

3.2.1 Power supply constraints

3.2.1.1 PV units constraint

PV output within the predicted output range to participate in the optimization of microgrid operation, which is as Equation 22.

$0\le P_{PV}\left(t\right)\le P_{PV}^{fr}\left(t\right)(22)$

3.2.1.2 Gas turbine constraint

${\mu }_{GT}{P}_{GT}^N\le P_{GT}\left(t\right)\le P_{GT}^N(23)$

where μ_GT is the minimum technical output coefficient of gas turbine; P^N_GT is rated power of gas turbine.

3.2.1.3 CSP units constraints

CSP utilizes photovoltaic power generation to heat molten salt, achieving the conversion of electrical energy into thermal energy, and stores the heat in high-temperature molten salt tanks. The process is subject to the following constraints.

The constraints on power generation output are as Equation 24:

$\left\{\begin{array}{l}{P}_{s,\min }\ast I_{CSP}\left(t\right)\le P_{CSP}\left(t\right)\le P_{s,\max }\ast I_{CSP}\left(t\right)\\ I_{CSP}\left(t\right)\in \left\{0,1\right\}\end{array}\right.(24)$

where I_CSP(t) represents the on/off status of the CSP units at time t, expressed as a binary variable; P_CSP(t) is the power output of the CSP at the time t; P_s,min, P_s,max are the lower and upper limit of the power output of CSP units, respectively.

The constraints on minimum on/off time period are as Equation 25:

$\left\{\begin{array}{l}\left[I_{CSP}\left(t-1\right)-I_{CSP}\left(t\right)\right]T_{s,off}+{\displaystyle \sum _{j=t-T_{s,on}}^{t-1}}\left(1-I_{j,s}\right)\ge 0\\ \left[I_{CSP}\left(t\right)-I_{t-1,s}\right]T_{s,on}+{\displaystyle \sum _{j=t-T_{s,on}}^{t-1}}{I}_{j,s}\ge 0\end{array}\right.(25)$

where T_s,off indicates the shutdown period of CSP units; T_s,on indicates the start period of the CSP units.

The constraints on output power are as Equations 26, 27:

$0\le P_{CHP}^{cha}\left(t\right)\le {\lambda }_{cha}{P}_{CSP}^{solar}\left(t\right)(26)$

$0\le P_{CSP}^{dis}\left(t\right)\le {\lambda }_{dis}{P}_{CSP}^N/{\eta }_{N,dis}(27)$

${\lambda }_{cha}+{\lambda }_{dis}\le 1(28)$

where P^cha_CHP(t) is the heat storage power of CSP at time t; P^dis_CSP(t) indicates the heat release power of CSP in time t; P^solar_CSP(t) is available solar thermal power at time t; P^N_CSP is the rated power of the CSP; η_N,dis is the efficiency of converting thermal power into electrical power; λ_cha and λ_dis represents the 0–1 state variable of the CSP thermal storage system, indicating whether it is in charging (heat storage) or discharging (heat release) mode at time t.

The constraints on the state of charge for thermal storage is as Equation 29:

$E_{CSP}\left(t\right)=E_{CSP}\left(t-1\right)+{\eta }_{CSP}{P}_{CHP}^{cha}\left(t\right)-P_{CSP}^{dis}\left(t\right)/{\eta }_{CSP}(29)$

where E_CSP(t) is the thermal energy stored in the CSP units at the time t; η_CSP is the efficiency coefficient of the thermal storage system.

The constraint on thermal storage capacity is as Equation 30:

$E_{s,\min }\le E_{CSP}\left(t\right)\le E_{s,\max }(30)$

where E_s,min, E_s,max are the lower and upper limit of the thermal ES capacity in the CSP untis, respectively.

3.2.2 Power balance constraint

The power on the supply side equals the power on the demand side, which is as Equation 31:

$P_{PV}\left(t\right)+P_{GT}\left(t\right)+P_{CSP}\left(t\right)+P_{ES}\left(t\right)=P_{Li}^{fr}\left(t\right)+P_{Li}\left(t\right)+P_{tr}^{fr}P\left(t\right)+P_{tr}\left(t\right)+P_{Net}\left(t\right)(31)$

where P_Net(t) is unbalanced power that cannot be fully absorbed at time t.

3.2.3 ES constraints

The constraints on capacity configuration and operation are as follows:

$\left\{\begin{array}{l}{P}_{ES,\min }\le {\lambda }_{ES}{P}_{ES,N}\le P_{ES,\max }\\ E_{ES,\min }\le {\lambda }_{ES}{E}_{ES,N}\le E_{ES,\max }\end{array}\right.(32)$

where P_ES,N is rated power of ES; E_ES,N is the rated capacity of ES; λ_ES is the 0–1 variable configured for ES; P_ES,min and P_ES,max are the minimum and maximum rated power of ES, respectively; E_ES,min and E_ES,max are the minimum and maximum rated capacity of ES respectively.

The constraint on ES operating is as Equation 33:

$-{\alpha }_{ch}{P}_{ES,N}\le P_{ES}\left(t\right)\le {\alpha }_{dis}{P}_{ES,N}(33)$

where P_ES(t)is the operating power of ES at time t; α_ch and α_dis are the maximum charging efficiency and the maximum discharge efficiency, respectively.

The constraints on response rate and time of ES are as Equation 34:

$\left\{\begin{array}{l}{v}_{ES}^{-}\le P_{ES}\left(t\right)-P_{ES}\left(t-1\right)\le v_{ES}^{+}\\ D\le \Delta t\end{array}\right.(34)$

where v- ES, v + ES are the upper limits of the downregulation and upregulation response rates of ES participating in microgrid regulation at time t, respectively; D is the minimum time period for ES to participate in microgrid regulation; Δt is the time period with ES actually participating in microgrid regulation.

The constraints on state of charge (SOC) for ES are as Equation 35:

$\left\{\begin{array}{l}SO{C}_{\min }\le SO{C}_0+\left[{\int }_{t_0}^{t_1}{P}_{ES}\left(t\right)dt\right]/E_{ES,N}\le SO{C}_{\max }\\ \forall t_1\in \left[t_0,t_{end}\right]\end{array}\right.(35)$

where SOC_min, SOC_max represents the ratio of the minimum and maximum capacity of ES; SOC₀ indicates the initial SOC of the ES; t₀, t_end represents the start time and end time of ES participation in microgrid regulation, respectively; t₁ represents any moment within the start time and end time of ES participation in microgrid regulation.

3.2.4 Load constraints

The load side constraints are shown in Equations 1–7 and Equations 8–11.

3.3 Model linearization based on Big-M method

Since the multiplication of 0–1 variable and continuous variable is non-linear, the Big-M method is used to linearize Equation 32, making it easy to solve using mature commercial optimization software Gurobi, which is as Equations 36, 37:

$\left\{\begin{array}{l}{P}_{MV}={\lambda }_{ES}{P}_{ES,N}\\ P_{MV}\le P_{ES,N}\\ P_{MV}\le P_{ES,N}-M\left(1-{\lambda }_{ES}\right)\\ {\lambda }_{ES}{P}_{ES,\min }\le P_{ES,N}\le {\lambda }_{ES}{P}_{ES,\max }\end{array}\right.(36)$

$\left\{\begin{array}{l}{E}_{MV}={\lambda }_{ES}{E}_{ES,N}\\ E_{MV}\le E_{ES,N}\\ E_{MV}\le E_{ES,N}-M\left(1-{\lambda }_{ES}\right)\\ {\lambda }_{ES}{E}_{ES,\min }\le E_{ES,N}\le {\lambda }_{ES}{E}_{ES,\max }\end{array}\right.(37)$

where P_MV and E_MV are the auxiliary variable that characterizes the ES state; M is relatively large constants.

4 Case study

4.1 Scene setting

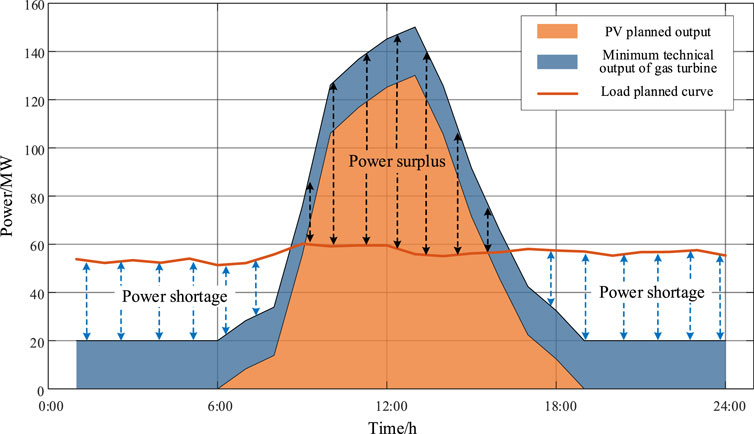
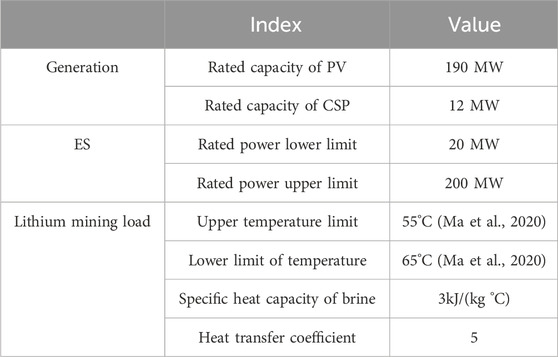
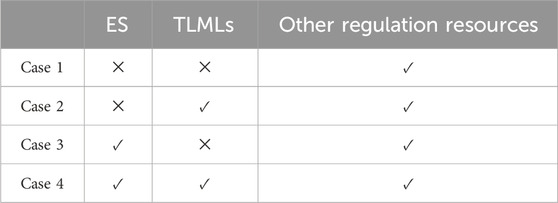
To validate the feasibility and effectiveness of the proposed strategy, this section conducts a simulation analysis based on an independent microgrid located in a remote area of Southwest China. The proposed optimization configuration model is solved using the linear solver Gurobi, with the simulation scheduling set for a 24-h period and a scheduling step size of 1 h. The predicted output of the PV unit and the planned load consumption curve are shown in Figure 3, and the basic operational parameters of the independent microgrid are listed in Table 1. Additionally, four cases are set up for comparative analysis, as detailed below. It should be noted that, for the sake of simplicity, other regulation resources below mainly include PV units, CSP units, gas turbines and transferable lithium mining loads.

Case 1: The regulation potential of TLMLs and ES is not considered. The power and energy balance of microgrid is managed solely by other regulation resources.

Case 2: The regulation potential of TLMLs is considered, but ES is not included. The power and energy balance of the microgrid is achieved through the participation of TLMLs and other regulation resources.

Case 3: The regulation potential of TLMLs is not considered, but ES is optimized. The power and energy balance of microgrid is managed through ES and other regulation resources.

Case 4: Both the regulation potential of TLMLs and the optimal configuration of ES are considered. The power and energy balance of the microgrid is achieved through the joint participation of TLMLs, ES, and other regulation resources.

Figure 3

Figure 3. Schematic diagram of operation baseline for independent microgrid.

Table 1

Table 1. Basic parameters of independent microgrid.

4.2 Analysis of ES optimization configuration results

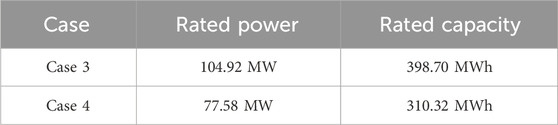
Considering the planned PV output, the minimum technical output of gas turbines, and the planned load consumption curve, the operational status of the independent microgrid is shown in Figure 3. The system exhibits a power surplus during the scheduling period of 9:00–16:00, while power deficits occur during 1:00–8:00 and 17:00–24:00. These highlight significant challenges in achieving system power balance. To address these challenges, the excellent characteristics of ES for power support and energy shifting are fully utilized. Combined with the proposed ES optimization strategy, ES system participates in the power and energy balance control of the microgrid. Furthermore, to effectively compare the impact of demand-side flexibility from lithium mining load regulation on microgrid ES configuration and operation, simulation analyses are conducted for Case 3 and Case 4 in Table 2, with the ES optimization results presented in Table 3. As shown in Table 3, when the flexibility of TLMLs is not considered in the grid optimization, the configured ES capacity is 104.92 MW/419.68 MWh. In contrast, when the flexibility of TLMLs is included in the optimization, the rated power and capacity of the optimized ES configuration are reduced by 26.06% and 22.17%, respectively, compared to Case 3.

Table 2

Table 2. Different operating scenarios in the microgrid.

Table 3

Table 3. Optimal configuration results of ES in independent microgrid.

By exploiting the temperature adjustability of the MVR system, the electricity flexibility of TLMLs can be effectively unlocked, achieving the following:

• During peak electricity demand periods when power supply is insufficient, the electricity demand of TLMLs is reduced to alleviate pressure on the power supply of microgrid.

• During low electricity demand periods and high PV generation periods, the electricity demand of TLMLs is increased to enhance the renewable energy utilization of the microgrid.

These results demonstrate that the flexible regulation capability of TLMLs effectively eliminates part of the system’s power imbalance, thereby reducing the ES configuration requirements.

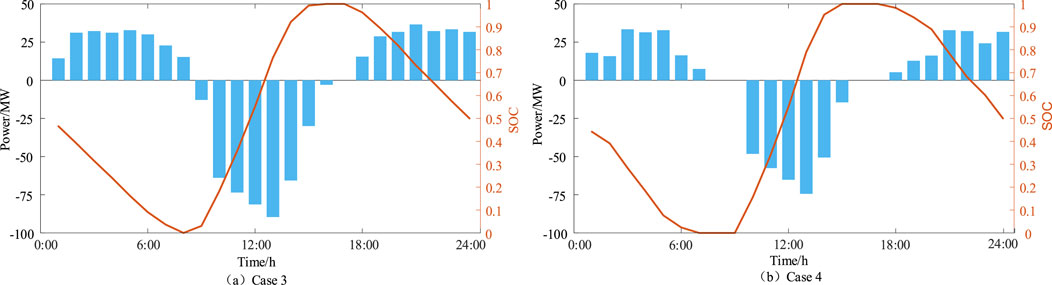
The operating power and SOC curves of the ES system configured in Cases 3 and 4 are shown in Figure 4. It can be observed that the ES system in both cases discharge during power deficit periods to meet load demands and charge during power surplus periods to absorb excess PV generation. This ensures sufficient energy is available for discharge during power deficit periods. Additionally, in Case 3, the configured ES system undergoes charge and discharge actions during all 24 scheduling periods of a typical day. In contrast, the number of charge-discharge cycles in Case 4 is reduced, which helps to minimize ES losses from frequent cycling and further extends the lifespan of the ES system.

Figure 4

Figure 4. Operating power and SOC operation curve of configured ES.

4.3 Technical analysis of optimal operation in independent microgrid

This section focuses on analyzing the optimal operation of different regulation resources in maintaining the power and energy balance of the microgrid. Figure 5 illustrates the optimized operation of the independent microgrid in Cases 1–4. In Case 1, the PV units, CSP units, gas turbines, and transferable loads collectively participate in system regulation. As shown in Figure 5A, some scheduling periods still experience power shortages, resulting in an unbalanced energy volume of 62.16 MWh. During periods of high PV generation, a significant amount of electricity is curtailed due to the limited accommodation capacity of the system, leading to a curtailment rate of 51.53%. This highlights the severe challenge to the microgrid’s renewable energy utilization capability. Compared with the regulation resources involved in Case 1, Case two incorporates flexible TLMLs by exploiting the temperature adjustability of MVR system to participate in the power and energy balance control of the microgrid. This approach further alleviates system imbalances and reduces the PV curtailment rate by 48.9% and 26.06%, respectively. However, due to the adjustment boundaries of lithium mining load power under the constraints of lithium extraction production efficiency, solely relying on the inclusion of flexible TLMLs is insufficient to both reduce the curtailment rate and improve the power and energy balance of the system.

Figure 5

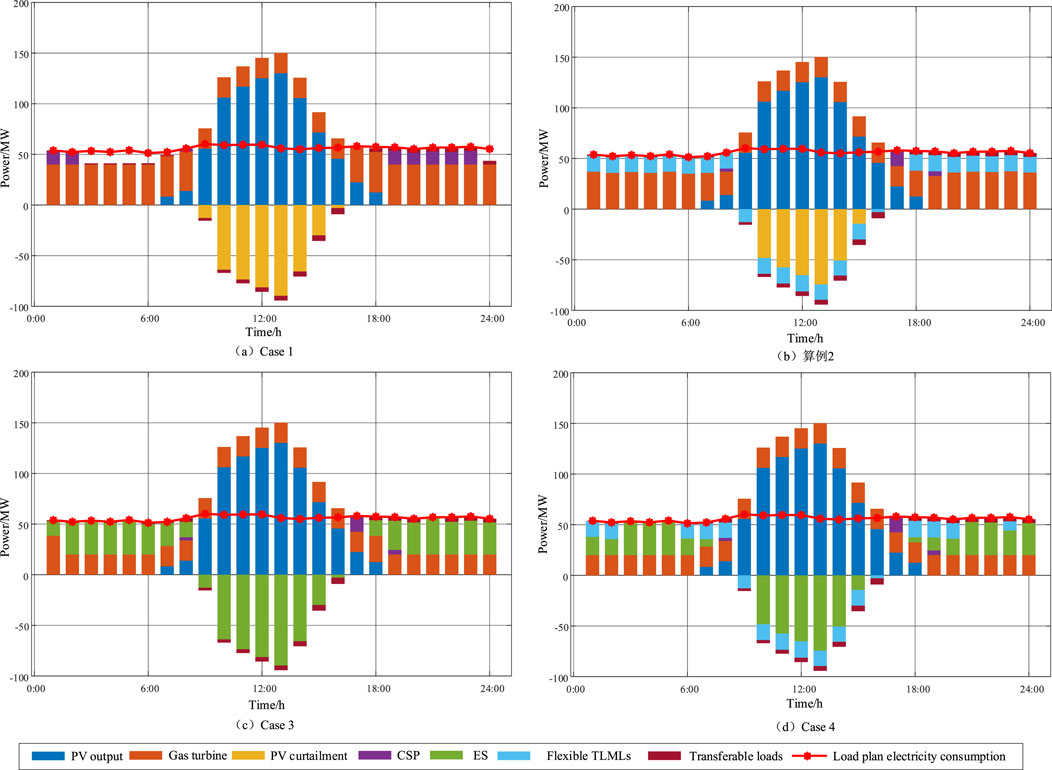
Figure 5. Coordinated optimization operation diagram of independent microgrid in cases 1–4. (A) Case 1. (B) Case 2. (C) Case 3. (D) Case 4.

Case 3 builds on Case 1 by considering ES configuration to enhance the stable operation of the microgrid. The results of ES optimization and charge-discharge operations were analyzed in detail in Section 4.2 and will not be repeated here. From the optimized operation of the microgrid in Case 3 shown in Figure 5C, it is evident that the PV output power is fully utilized by the microgrid.

Additionally, imbalanced power and gas turbine output power are reduced by 76.45% and 36.51%, respectively, compared with Case 1. Furthermore, despite achieving load demand satisfaction and significantly lowering the PV curtailment rate, the system incurs a high ES capacity cost—nearly twice the average load demand capacity. This highlights the need for further improvement in resource configuration and system flexibility. To address these issues, Case 4 integrates the flexible TLMLs from Case 2 and the ES system from Case 3 for joint participation in the power and energy balance control of the microgrid. The regulation resources in this case include PV units, CSP units, gas turbines, ES, and flexible TLMLs. Similarly, the ES configuration and operational performance, as well as a comparison with Case 3, were elaborated in Section 4.2 and are not repeated here. It is worth noting that, based on the ES capacity configuration in Case 4 and the optimized operation shown in Figure 5D, the microgrid achieves a significant improvement in stability by reducing system imbalances and PV curtailment to 2.12 MWh and 0 MWh, respectively, using only 74% of the ES capacity configured in Case 3.

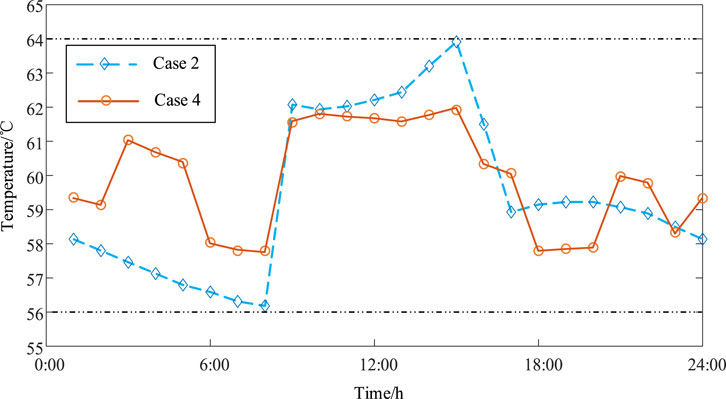
As indicated by the previous analysis, both Case 2 and Case 4 include flexible TLMLs as key regulation resources in microgrid operations. The main difference lies in the addition of ES regulation in Case 4 compared to Case 2. To compare the impact of ES on the temperature of the primary power-consuming equipment (MVR) in the lithium extraction process, the temperature regulation variation curves of TLMLs are shown in Figure 6. The MVR temperature represents the physical characteristics of lithium extraction from brine, while power quantifies its electricity consumption. These two parameters exhibit a thermo-electric coupling relationship. By analyzing temperature variations, the effect of power regulation on the production efficiency of TLMLs can be effectively reflected. The temperature variations shown in Figure 6 directly correspond to the power flexibility regulation of TLMLs in Figure 5. As observed in Figure 6, the MVR temperature fluctuates within the temperature control boundaries of 55°C–65°C in both Case 2 and Case 4, with similar trends. Specifically, as shown in Figures 3, 5, during power deficit periods (1:00–8:00 and 17:00–24:00), lowering the MVR temperature reduces the electricity demand of lithium mining loads to alleviate the supply pressure on the microgrid. Conversely, during power surplus periods (9:00–16:00), increasing the MVR temperature raises the electricity demand of lithium mining loads to absorb excess power. This effectively enables bidirectional flexible interaction between power supply and demand.

Figure 6

Figure 6. Temperature regulation diagram of TLMLs for Cases 2 and 4.

However, whether ES participates in microgrid operations significantly impacts the temperature variations of TLMLs, as evidenced by notable differences between Cases 2 and 4. Specifically, in Case 2, the temperature adjustment range is [56°C, 64°C], with a temperature difference of 8°C and a variance of 9.52°C². In comparison, Case 4 demonstrates a narrower temperature adjustment range of [57.8°C, 62°C], with the temperature difference and variance reduced by 47.5% and 25.87%, respectively. Combining Figures 5, 6, the collaboration of ES with flexible TLMLs in microgrid regulation effectively alleviates the pressure on flexible regulation, minimizing the impact of temperature variations on the production efficiency of the lithium extraction process.

4.4 Economic analysis of optimal operation in independent microgrid

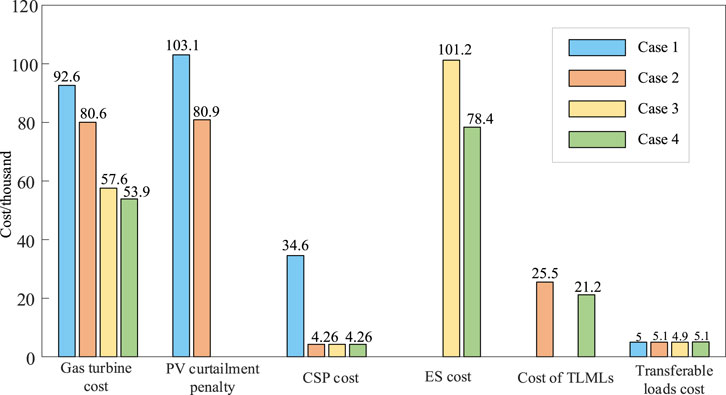
This section analyzes the economic costs of microgrid optimized operation. Based on the solution of the objective function in the optimization strategy for independent microgrids discussed in Section 3.1, the economic operation costs for Cases 1–4 are presented in Figure 7.

Figure 7

Figure 7. The comparison diagram of comprehensive operation cost in cases 1–4.

Specifically, the costs of thermal power generation and carbon emission penalties show a decreasing trend from Case 1 to Case 4, aligning with the technical analysis in Section 4.3. This is mainly due to the gradual inclusion of more flexible regulation resources in microgrid control, which reduces the reliance on costly thermal power generation, contributing to the achievement of “dual carbon” goals. The PV curtailment penalty cost in Case 2 decreases by 21.53% compared to Case 1, while Cases 3 and 4 fully utilize the PV output. This demonstrates that the participation of flexible TLMLs and ES in microgrid regulation continuously enhances the system’s renewable energy utilization capability. However, the regulation capacity of TLMLs is limited by the adjustment capacity and the production characteristics of lithium extraction processes, making their regulation capability less effective than that of ES. Nevertheless, the participation of flexible TLMLs in power and energy balance can further alleviate the need for conservative ES capacity configurations, effectively reducing the economic cost of ES. This conclusion is supported by the comparison of ES costs between Cases 3 and 4, where the total capital and operational cost of ES in Case 4 is 22.53% lower than in Case 3. Similarly, the regulation cost of TLMLs in Case 4 decreases from ¥25,500 in Case 2 to ¥21,200. The involvement of ES in power and energy balance also reduces the flexible regulation pressure on TLMLs, thereby mitigating the impact on lithium extraction production efficiency.

In addition, the total operating costs for Cases 1, 2, 3, and four are ¥359,600, ¥259,300, ¥197,300, and ¥167,000, respectively, showing a progressively decreasing trend. This demonstrates that, compared to considering the participation of flexible TLMLs or ES individually in microgrid optimization, their coordinated participation significantly reduces the overall operating costs of the system. ES participation in system regulation effectively reduces the temperature variation of TLMLs, thereby lowering the regulation costs of flexible TLMLs. Simultaneously, the participation of flexible TLMLs in system regulation further reduces the required ES capacity and charge-discharge power, effectively decreasing the capital and operating costs of ES. Therefore, combined with the previous technical analysis, the coordinated participation of flexible TLMLs and ES in microgrid regulation balances the technical and economic benefits of microgrid operation.

5 Conclusion

This study focuses on the power supply needs of high-energy-consuming industrial mining loads and the integration of new energy in an independent microgrid in a remote area of Southwest China. By analyzing the lithium extraction process from brine and exploring the regulation potential of lithium mining loads, it proposes an ES optimization configuration and operation strategy for independent microgrids, incorporating the flexible response of high-energy loads to jointly participate in the system’s power and energy balance regulation. The following conclusions are drawn:

1) Considering the flexibility of lithium mining loads is constrained by the production characteristics of the lithium extraction process, a mathematical model for the flexible regulation of lithium mining loads was developed. This model incorporates the adjustability of the MVR temperature of key power-consuming equipment and includes production behavior constraints.

2) By incorporating the regulation capacity boundaries of various resources in the microgrid, an optimal ES configuration model was developed to minimize the comprehensive operational cost of the system. The participation of ES in microgrid optimization reduced the system imbalance power and comprehensive operational cost by 93.32% and 35.6%, respectively, while effectively decreasing the temperature regulation variation of lithium mining loads by 47.5%.

3) By leveraging their demand-side regulation potential, the flexible lithium mining loads contribute to reducing the required ES capacity by 26.06%. Additionally, this approach effectively alleviates the power supply pressure on generation units, significantly enhancing the technical and economic performance of the microgrid.

This study aims to address the electricity challenges faced by high-energy-consuming loads in high-renewable-energy microgrids, providing valuable insights for the development of demand response. Future research will focus on characterizing the uncertainty in the response of flexible lithium mining loads and exploring multi-stakeholder benefit allocation within microgrid.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

CY: Conceptualization, Data curation, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. XL: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Writing–original draft, Writing–review and editing. YL: Conceptualization, Data curation, Funding acquisition, Investigation, Project administration, Resources, Supervision, Validation, Writing–original draft, Writing–review and editing. JT: Conceptualization, Data curation, Formal Analysis, Investigation, Resources, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. ZL: Conceptualization, Formal Analysis, Methodology, Resources, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. BD: Formal Analysis, Supervision, Writing–original draft, Writing–review and editing. LW: Formal Analysis, Methodology, Resources, Supervision, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the Science and Technology Major Project of Tibetan Autonomous Region of China (No. XZ202201ZD0003G).

Acknowledgments

The authors wish to thank the project funding from the Science and Technology Major Project of Tibetan Autonomous Region of China (NO. XZ202201ZD0003G).

Conflict of interest

Authors CY, XL, ZL, BD, and LW were employed by Economic and Technical Research Institute of State Grid Tibet Electric Power Co., Ltd. Authors YL and JT were employed by State Grid Tibet Electric Power Co., Ltd.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cui, H. B., and Zhou, K. L. (2018). Industrial power load scheduling considering demand response. J. Clean. Prod. 204, 447–460. doi:10.1016/j.jclepro.2018.08.270

CrossRef Full Text | Google Scholar

Golmohamadi, H., Keypour, R., Bak-Jensen, B., and Pillai, J. R. (2019). A multi-agent based optimization of residential and industrial demand response aggregators. Int. J. Electr. Power Energy Syst. 107, 472–485. doi:10.1016/j.ijepes.2018.12.020

CrossRef Full Text | Google Scholar

Huang, X. R., Yang, B., Yu, F. Y., Pan, J., Xu, Q., and Xu, W. X. (2021). Optimal dispatch of multi-energy integrated micro-energy grid: a model predictive control method. Front. Energy Res. 9, 2021. doi:10.3389/fenrg.2021.766012

CrossRef Full Text | Google Scholar

Karimianfard, H., Salehizadeh, M. R., and Siano, P. (2022). Economic profit enhancement of a demand response aggregator through investment of large-scale energy storage systems. CSEE J. Power Energy Syst. 8 (5), 1468–1476. doi:10.17775/CSEEJPES.2021.02650

CrossRef Full Text | Google Scholar

Kong, L. J., Li, G. B., Xie, J. H., Yang, X. H., and Bai, X. Q. (2024). Research progress of lithium extraction technology from salt lake brine. Inorg. Salt Ind., 1–15. doi:10.19964/j.issn.1006-4990.2024-0144

CrossRef Full Text | Google Scholar

Liao, S. Y., Bian, S. Q., Xu, J., Ke, D. P., and Sun, Y. Z. (2024). Evaluation of interactive adjustable capacity of electrolytic aluminum load grid considering energy flow optimization. Proc. CSEE, 1–12.

Google Scholar

Liu, C., Zhuo, J., and Zhao, D. (2020). A review on the utilization of ES system for the flexible and safe operation of renewable energy microgrids. Proc. CSEE 54 (10), 1–12. doi:10.1002/2050-7038.12934

CrossRef Full Text | Google Scholar

Ma, Y. H., Luo, Y. T., and Zhao, S. B. (2020). Process for preparing battery-grade lithium carbonate from salt lake brine Research on influencing factors. Yunnan Chem. Technol. 47 (6), 51–52. doi:10.3969/j.issn.1004-275X.2020.06.018

CrossRef Full Text | Google Scholar

Nie, Z., Wu, Q., Ding, T., Bu, L. Z., Wang, Y. S., Yu, J. J., et al. (2023). Research progress on industrialization technology of lithium extraction from salt lake brine in China. Inorg. Chem. Ind. 54 (10), 1–12. doi:10.19964/j.issn.1006-4990.2022-0542

CrossRef Full Text | Google Scholar

Philipo, G., Kakande, J., and Krauter, S. (2022). Neural network-based demand-side management in a stand-alone solar PV-battery microgrid using load-shifting and peak-clipping. Energies 15 (14), 5215. doi:10.3390/en15145215

CrossRef Full Text | Google Scholar

Reka, S. S., and Ramesh, V. (2016). Industrial demand side response modelling in smart grid using stochastic optimisation considering refinery process. Energy Build. 127, 84–94. doi:10.1016/j.enbuild.2016.05.070

CrossRef Full Text | Google Scholar

Shen, Y., Hu, W., Liu, M., Yang, M., Yang, F., and Kong, X. Y. (2022). Energy storage optimization method for microgrid considering multi-energy coupling demand response. J. Energy Storage 45, 103521. doi:10.10.1016/j.est.2021.103521

CrossRef Full Text | Google Scholar

Sun, W. Q., Liu, W., Xiang, W., and Zhang, J. (2022). Generalized energy storage allocation strategies for load aggregator in hierarchical electricity markets. J. Mod. Power Syst. Clean. Energy 10 (4), 1021–1031. doi:10.35833/MPCE.2020.000737

CrossRef Full Text | Google Scholar

Wang, D., Huang, D. Y., Hu, Q. E., Jia, H. J., Liu, B., and Yang, L. (2024b). Electricity-heat-based integrated demand response considering double auction energy market with multi-energy storage for interconnected areas. CSEE J. Power Energy Syst. 10 (4), 1688–1700. doi:10.17775/CSEEJPES.2022.02140

CrossRef Full Text | Google Scholar

Wang, W. D., Huang, H., Zhang, X. S., Tan, J., and Sun, S. B. (2024a). Flexible low carbon optimal dispatch of distribution networks considering the demand response of heat storage industrial loads. Front. Energy Res. 12. doi:10.3389/fenrg.2024.1507604

CrossRef Full Text | Google Scholar

Wu, M., Zhang, N. C., Liang, Y., Liu, H. T., and Ji, Y. (2024). Research and development of micropower system technology under the background of new power system. New Power Syst. 2 (03), 251–271. doi:10.20121/j.2097-2784.ntps.240049

CrossRef Full Text | Google Scholar

Xiao, L. H. (2014). Study on isothermal evaporation crystallization and ultrasonic heating crystallization process of brine in Zabye Salt Lake. Central South University.

Google Scholar

Xu, X. D., Sun, W. Q., Abeysekera, M., and Qadrdan, M. (2020). Quantifying the flexibility from industrial steam systems for supporting the power grid. IEEE Trans. Power Syst. 36 (1), 313–322. doi:10.1109/TPWRS.2020.3007720

CrossRef Full Text | Google Scholar

Zeng, L., Gong, Y. G., Xiao, H., Chen, T. J., Gao, W., Liang, J., et al. (2024). Research on interval optimization of power system considering shared energy storage and demand response. J. Energy Storage 86, 111273. doi:10.1016/j.est.2024.111273

CrossRef Full Text | Google Scholar

Zhang, Z. Z., Pan, Z. S., and Che, D. (2024). Analysis of lithium supply and demand situation based on lithium deposits and resources characteristics from 2024 to 2035, China. Chin. Min. Ind. 33 (06), 26–44. doi:10.12075/j.issn.1004-4051.20241183

CrossRef Full Text | Google Scholar

Zhou, D., Wen, X., Wang, J., Xiong, T., Sun, D. T., Dan, G. J., et al. (2022). Research on matching characteristics of centrifugal steam compressor and evaporator in MVR system. Chin. J. Eng. Des. 29 (05), 595–606. doi:10.3785/j.issn.1006-754X.2022.00.071

CrossRef Full Text | Google Scholar