Assessing the economic and technical feasibility of off-grid renewable hybrid energy systems through optimization

This research investigates the economic and environmental viability of a combined renewable energy system that incorporates solar photovoltaic, wind, and biomass power production with diesel generators and battery storage serving as backup options. The system is designed to optimize energy costs while ensuring high reliability, lower emissions, and greater renewable energy utilization. Various advanced optimization methods, including genetic algorithm, particle swarm optimization, artificial bee colony optimization, and teaching-learning-based optimization, are used to determine the most efficient system configuration. The combined energy system is evaluated under two operational strategies, load following and cycle charging, with a maximum power supply loss probability of 2% to maintain system dependability. The findings indicate that the teaching-learning-based optimization approach surpasses other methods in identifying the most cost-effective and environmentally friendly solution. This investigation centers on Barwani, a rural district in India, to evaluate the technical and economic feasibility of implementing such a combined energy system. Through comprehensive comparative analyses, the study emphasizes the superior performance of teaching-learning-based optimization in achieving optimal outcomes, showcasing its potential for practical applications in remote and energy-scarce regions.

1 Introduction

In this era of energy demand versus economics, a diesel generator (DG) is not a viable solution for electricity generation due to factors including fluctuations in fuel prices, high operational expenditures, safety, and theft of fuel. In addition to the depletion of fossil fuels and environmental concerns, renewable energy offers a superior choice for generating electricity that mitigates the emission of pollutants. The abundance of availability of renewable energy in the environment in distinct forms like solar, wind, and biomass can be configured with battery banks that enhance the hybrid system’s efficiency and dependability (Diaf et al., 2007). The optimized hybrid system is configured with a combination of batteries, PV panels, generators, PV panels, etc., and offers minimized total net present value (TNPC) and enhanced reliability. Various optimum approaches (quantitative, probabilistic, recursive, etc.) are employed to evaluate the hybrid system’s optimal solution. Dufo-Lopez et al. (Köprü et al., 2024) designed a multi-objective program for the optimal solution and control techniques by using a genetic algorithm (GA) and multi-objective evolutionary algorithm taking constraints as TNPC, unmet load, and emission. The standalone hybrid system is optimized and derived through the GA (Verma et al., 2024) PV panel, DG, and battery bank combination to meet the load demand of the customer by using HOMER software (Islam et al., 2024).

L. Prakash et al. (Shah et al., 2022) created an independent photovoltaic stimulated strong wind electrical generator for off-grid applications in India that reduces system costs and improves hybrid model system performance. Different strategies, including honey bee mating optimization, imperialist competition algorithm, linear programming, harmony search, simulated annealing, tabu search, and particle swarm optimization, are highlighted in various studies and are used to find the optimal combination of hybrid systems with minimal total net current value (Roy, 1997; Thirunavukkarasu and Yashwant, 2022; Zeng et al., 2025; Águila-León et al., 2024; Singh and Kumar, 2023; Jain et al., 2022a; Saha et al., 2023; Sawle et al., 2017; Deb et al., 2023). Deb et al. (2023) designed an ant lion optimization (ALO)-based approach for optimizing a smart local energy system (LES) with CHP, solar power, and lithium-ion battery storage. Validated on the University of Warwick’s energy system, the method effectively balances stochastic generation and demand, demonstrating high efficiency and reliability. Zeng et al. (2025) reported a novel constrained multi-objective optimization method for standalone microgrids, minimizing cost, reliability, and emissions. Using advanced techniques, it outperforms existing methods in achieving optimal planning with improved performance metrics. In a study on Hawai’i Island, Singh et al. (Jain et al., 2022a) use HOMER and MATLAB and show the effectiveness of combining diverse renewable energy sources with energy storage and demand management strategies. This approach results in a 62.62% decrease in net present cost, a 15.35% reduction in energy purchased from the grid, and a 42.98% increase in energy sales. The research demonstrates the viability of this integrated system for improving energy efficiency and cost-effectiveness. Zhou and Xu (2023) developed an optimal design framework for standalone renewable microgrids in Northeast China, finding that PV/wind/tidal/battery systems are the most viable. Sensitivity analysis highlights cost-effective, clean electrification solutions, supporting sustainable investment in rural power access. Loss of power supply probability (LPSP) plays a crucial role in the optimal sizing of hybrid systems involving photovoltaic (PV), wind, and battery storage. Recent studies focus on minimizing the LPSP while balancing costs and system efficiency (Emrani and Berrada, 2024).

Helpful design models and competent optimizing software platforms for studying suitable proposals and financial estimates for hybrid sustainable energy are scarcely available in the literature. A well-defined algorithm is needed to obtain an innovative study and effective utilization of sources of energy for the integration of renewable systems. In this study, an off-grid PV-wind-biomass hybrid model for the remote community of Barwani, Madhya Pradesh, India, is explored for the best solution and innovative proper evaluation with two alternative methods (demand flowing and cycle charging) using GA and particle swarm optimization (PSO). The analysis of comparative results uses PSO and GA based on different factors, for example, number of wind turbines (WIND), PV (NPV), LPSP, renewable factor, the cost of electricity (COE), wind power, pollutant emissions, reliability, biomass power, operating hours of DG, emissions penalty cost, PV power, DG power, and algorithm running time.

This paper is organized as follows:

Section 2 presents a comprehensive overview of component sizing fundamentals for hybrid renewable energy systems, encompassing load data and resource information such as solar radiation, wind velocity, and biomass availability. Section 3 explores various control strategies for standalone hybrid systems. Section 4 examines the optimization of hybrid system design, including mathematical models for different energy components. Section 5 offers a multifaceted comparison from technical, economic, environmental, and social standpoints, along with the identification of optimal system configurations. Section 6 delves into the results of the optimization process and provides a comparative analysis of the proposed research. Lastly, Section 7 concludes the study by summarizing the findings and discussing potential avenues for enhancing system performance in the future.

2 Unit sizing of a hybrid renewable energy system

The suggested integration of a renewable system is taken to develop a PV-wind-biomass hybrid renewable energy system (HRES) with a system of batteries to store energy and a DG to keep the supply and power system stable. The dump charge is used to discharge surplus power via an outer resistor. The goal of the dumped load is to preserve the reliability of the hybrid model and to intentionally discharge extra power when the DG’s constant power limit is lower than that established by the firm (Physical Progress Achievements, 2017; Nplindia, 2025). The hybridization system’s optimal size and tech-economic research are based on yearly daily average resource (wind/PV) data. Reliability assessment uses the loss of power supply probability (LPSP) technique. The system’s lower COE determines the best hybrid renewable energy system design. A dispatch strategy is needed to control the functioning of the battery system and the DG when there is sufficient renewable power to fulfill the load demands.

2.1 Load profile

The power load requirements are also reduced because there are fewer workers at the location implementing the planned renewable energy hybrid system. The average energy usage is estimated to be 110.6 kWh/day, with a peak load of 7.8 kW and an average of 4.61 kW. The statistics for the complete hourly rate daily load power situation of a load requirement for the Barwani district were estimated. Figure 1 depicts the load profile over a 24-hour period.

Figure 1

Figure 1. Load profile for 24 h.

2.2 Wind energy

Wind energy is plentiful in the atmosphere and is a source of energy that may be utilized to produce electricity. Wind energy capacity is greater in various parts of India, including the south, north, and west. These Indian areas now rank fourth in the world in terms of wind power generation, trailing only China, Germany, and the United States, having surpassed Spain in 2015. Wind power installed capacity in India is 27,441.15 MW as of 31/July/2016 (Author Anonymous, 2025). As of 03/2015, there are no grid-connected wind power plants in the East or Northeast. Figure 2 (Justus, 1978) depicts a rising number of wind energy installations in Indian states. A tiny wind turbine with a rated output of 1 kW is included in the planned work for the design of a solar hybrid renewable energy system (SHRES). Table 1 provides a full representation of a wind turbine. Equation 1 is used to determine wind energy (Gönül et al., 2024).

Figure 2

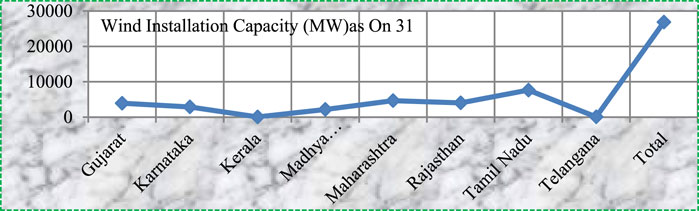
Figure 2. Wind energy installations across India (Government of India, (n.d.)).

Table 1

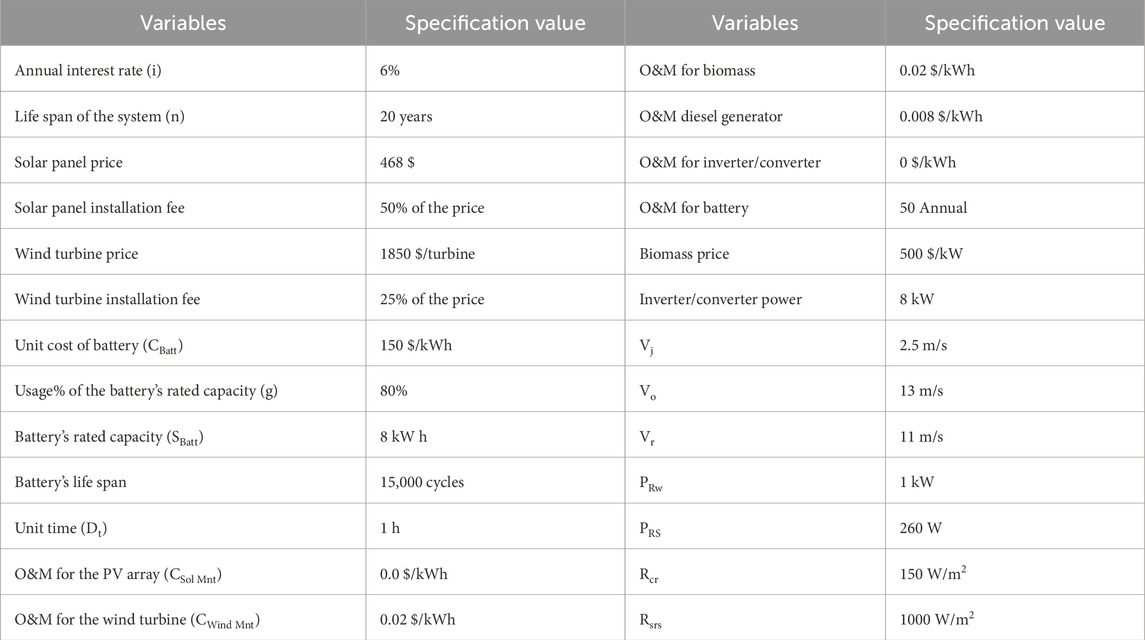
Table 1. Variables used in the hybrid system (Sawle, 2022; Akbar et al., 2015).

SHRES’s design site offers high availability in a wind system. The yearly average wind speed is 4.5 m/s. The wind’s speed changes constantly. It varies hourly and annually (Sawle, 2022). The wind speed is at a maximum in December, as shown in Figure 3, when wind turbine efficiency is at its peak and produces the most power (Physical Progress Achievements, 2017). The friction factor is also called the Hellmann exponent, the electricity exponent, or the airflow gradient. Terrain irregularity, height above ground, wind speed, region temperature, hourly statistics of the day, and seasonality influence the friction coefficient. The friction factor is often assumed to be approximately 1/7. The output power of wind turbines may be calculated using the calculations below.

$P_{WIND,each}^T=\left\{\begin{array}{l}0V\le v_{J}orV\ge v_o\\ P_{Rw}\left(\frac{V-v_J}{v_R-v_J}\right)v_J<V<v.\\ P_{Rw}{v}_r\le V<v_o\end{array}\right.(1)$

Figure 3

Figure 3. Hourly wind speed data.

2.3 PV energy

An SHRES is projected for Barwani, Madhya Pradesh, India (latitude 22.71 north, longitude 75.85 east) (Gupta, 2010). Solar radiation has a long-term annual capacity scalability of 5.531 kW/m². Summer solar activity is greater than winter solar irradiance, as shown in Figure 4.

Figure 4

Figure 4. Hourly solar radiation data.

The solar radiation output of a PV panel is estimated using Equation 2 (Sawle et al., 2018; Medghalchi and Taylan, 2023). Table 1 provides precise information on the PV panels used in the suggested work.

$P_{PV,each}=\left\{\begin{array}{l}{P}_{RS}\left(\frac{R^2}{R_{srs}{R}_{cr}}\right)0\le R<R_{CR}\\ P_{RS}\left(\frac{R}{R_{srs}}\right)R_{CR\le R}<R_{srs}\\ P_{RS}{R}_{srs}\le R\end{array}\right..(2)$

2.4 Biomass energy

In this research, rice husk is used as a renewable energy biomass source. In India, more than 40% of all grain is produced as rice, using 30% or more of all farmed land. India produces 21% of the world’s rice. The design site at Barwani produces 460 Kg of paddy rice each day. Various studies predict that the production of rice husks will represent 25% of paddy output, and the growth of an immature paddy will represent 3% of paddy production. As a consequence, rice husk produces 115 kg/d total biomass (Physical Progress Achievements, 2017). The calorific values of various agricultural wastes have been reported in the literature to be between 12.1 MJ/kg and 15.2 MJ/kg. Equation 3 (Koholé et al., 2024) can be used to compute the power output from biomass energy.

Total available energy for electricity:

$P_{BM}\left(\frac{kWh}{yr}\right)=\left(\frac{Totalricehuskavailable\left(\frac{t}{yr}\right)\times 1000\times {CB}_{BIO}\times {CV}_{BIO}}{860\times \left(operatinghours/day\right)}\right).(3)$

2.5 Battery bank

Batteries implemented for storage maintain a balance between the load profile and the electricity energy coming from the resource. Because of the charge/discharge process, the current battery power input might be negative or positive. Analysis, condition of charge, efficiency, and time consumed are as follows:

a) $P_{PV}^T+P_{WIND}^T+P_{BIO}^T=P_{DEMAND}^T$ In this battery state, the battery’s capacity is steady and does not vary.

b) $P_{PV}^T+P_{WIND}^T+P_{BIO}^T>P_{DEMAND}^T$ In this case, the total hybrid (PV + Bio + Wind) output of the device exceeds the load requirements. At this point, the batteries are in the recharging position, and the recharged amount at time (T) is represented by Equation 4 (Sawle and Gupta, 2015):

$E_{battery}^T{=E}_{battery}^{T-1}.\left(1-\tau \right)+\left[\left(P_{PV}^T{+P}_{WIND}^T+P_{BIO}^T\right)-\frac{P_l^T}{{\eta }_{inverter}}\right]{\eta }_{bc.}(4)$

c) $P_{PV}^T+P_{WIND}^T+P_{BIO}^T<P_{demand}^T$ In this case, the total electricity produced by the hybrid system (PV + Bio + Wind) is lower than the load requirement. At this moment, the power system is in the discharging position, and the charge quantity is included in the equation. The battery storage bank is configured to a notional capacity and only allows discharge within that capacity (Sawle and Gupta, 2015). Table 1 contains information on the battery bank. The following Equation 5 represents the discharging mode of the batteries (Thirunavukkarasu and Sawle, 2021).

${E_{battery}^T=E}_{battery}^{T-1}.\left(1-\tau \right)+\left[\frac{P_l^T}{{\eta }_{inverter}}-\left(P_{PV}^T{+P}_{WIND}^T+P_{BIO}^T\right)\right]{\eta }_{bf.}(5)$

2.6 Diesel generator

When the electricity generated by the hybrid system is insufficient to supply the required load, the DG serves as a source of backup power. The DG improves system dependability while also lowering system costs (Akbar et al., 2015). The DG’s hourly fuel usage and efficiency study can be determined using Equation 6 (Zhou and Xu, 2023):

$F_{dsl}\left(t\right)=A.P_R+B.P\left(t\right).(6)$

2.7 Converter/inverter

An electronic converter is required to regulate the energy transfer between the DC and AC components. At the correct frequency for the load, electrical energy is converted by inverters from one form to another (inverter DC to AC and converter AC to DC). The efficiency of the inverter is given by Equation 7 (Yadav et al., 2022):

${ƞ}_{imv}=\frac{P}{P+P_0+k{P}^2,}(7)$

where P0, P, and k are calculated using the formulas in Equation 8:

$P_0=1-99{\left(\frac{10}{{ƞ}_{10}}-\frac{1}{{ƞ}_{100}}-9\right)}^2,k=\frac{1}{{ƞ}_{100}}-P_0-1,\text{And\hspace{0.17em}}P=\frac{P_{out}}{P_n},(8)$

where ${ƞ}_{10}$ and ${ƞ}_{100}$ are the inverter’s reliability at 10% and 100% of its power rating, as defined by the manufacturer. Table 1 shows the cost and other characteristics of electronic conversion.

3 Dispatch strategies for an isolated HES

The appropriate functioning of a load-following system to fulfill load requirements is strongly related to the dispatch strategy and system management operation (Barley et al., 1995; Dsouza et al., 2024). The hybrid system is maintained by the battery bank and DG, which also solves the problem of unreliable and fluctuating power supply. The battery bank and DG operations are managed by a dispatch strategy. The dispatch mechanism is impacted by the kind of renewable source, fuel price, generator, and battery storage capacity, percentage of renewable energy in the hybrid model, and cost of fuel. Typically, two different dispatch techniques are employed while creating hybrid systems: a cycle-charging strategy or a load-following strategy. The following Equation 5 represents the discharging mode of the batteries.

3.1 Cycle-charging strategy

The generator is running at maximum efficiency in accordance with the cycle-charging schedule, with any additional power going toward charging the battery. The cycle-charging method aims to provide a perfect hybrid vehicle, with or without renewable energy sources, which can be calculate using Equation 9 for cyclic charge strategy of DG. The DG always supplies electricity to the prime load supply. The battery bank, electrolyzer, and deferrable load are all charged using the extra power generated. The Equation 9 represents the energy balance among total demand and hybrid energyn system.

$\begin{array}{ll}\hfill P_L& =\left(P_{WIND}+P_{PV}+P_{BIO}+P_{DIESEL}\right)\left(Chargewithfullcapacity\right)\hfill \\ \hfill & +P_{BATTERY\left(chargewithexcesspower\right).}\hfill \end{array}(9)$

3.2 Load-following strategy

The load monitoring approach asserts that the DG only provides electricity when it is needed. Lower-priority tasks, such as charging batteries or fulfilling postponed demand, are left to renewable sources of energy. The following Equations 10–12, represent the load-following strategy mode of the DG operation (Gupta et al., 2025).

$P_L=P_{WIND}+P_{PV}+P_{BIO}+P_{BATTRY}\left(P_{DIESEL}isoff\right)withBatterybank.(10)$

$P_L=P_{DIESEL}withoutbattery.(11)$

$P_{EXCESS}=P_{DUM,L}+P_{THERMAL.}(12)$

4 Optimization of hybrid system design issues

4.1 Minimization of cost

The goal function of the viable design issue in this suggested hybrid system design is to lower the cost of electricity (COE). It is computed as a percentage of the total yearly cost (the total annualized cost minus the cost of serving the thermal load). Equation 13 refers to the topic of hybrid model design and is handled using the fractional swarm optimization approach (Thirunavukkarasu et al., 2023a).

$M_{Totalannual}=M_{AIC}+M_{OM,}(13)$

where $M_{AIC}$ is the annual initial cost and $M_{OM}$ is the annual operations and maintenance (O&M) cost.

If the energy cost is low, a hybrid system is preferable (Bamisile et al., 2024). Energy costs are expressed as the unit cost of electricity or as a steady price per energy unit. Equation 14 (Solargis, 2013) is used to compute it:

$\text{Minimization\hspace{0.17em}of\hspace{0.17em}}COE=\frac{M_{Totalannual}}{{\sum }_{H-8760}^{H-1}{P}_L}\times C_{RF.}(14)$

The asset recovery factor is a proportion used to assess an annuity’s current value (a series of equal annual cash flows). The present value factor is calculated using Equation 15 (Singh et al., 2022; Thirunavukkarasu et al., 2023b):

$C_{RF}=\frac{{I\left(1+I\right)}^N}{{\left(1+I\right)}^N-1.}(15)$

The anticipated hybrid model project lifespan of 20 years is taken into account. The converter and battery have 10-year lifespans. Equation 16 is used to calculate the present value factor of the converter and battery (C&B):

$P_{CB}=C_{CB}\times \left(1+\frac{1}{{\left(1+J\right)}^{10}}\right).(16)$

4.2 Reliability model based on LPSP conception

Stability is the main issue with any viable hybrid approach. Reliability is used to evaluate the load supply’s standard. The likelihood of a power outage is used to describe the statistical component of dependability (Ji, 2025). LPSP refers to a supplied power that is unable to meet load demands because of a problem with technology or a lack of renewable energy sources. If the generated power supply satisfies the demanded load demand while the LPSP current is 0, the opposite is true when the LPSP value is one. Because renewable energy sources are erratic, LPSP assessment was analyzed with a probabilistic technique that eliminates the need for time information and chronological modeling (enumeration is time-consuming and necessitates access to data spanning a specific period of time) using Equation 17 (Koholé et al., 2023; Homerenergy, 2025).

$LPSP=\frac{\sum \left(P_{LOAD}-P_{PV}-P_{wind}-P_{BIo}+P_{{SOC}_M}+P_{DISEL}\right)}{\sum P_{LOAD}}.(17)$

4.3 Pollutant emissions

DG is a traditional energy source that emits hazardous gases. Carbon monoxide (g/L of fuel), nitrogen oxides (g/L of fuel), particulate matter (PM) (g/L of fuel), fraction of sulfur transformed to PM (%), unburned hydrocarbons (g/L of fuel), and carbon dioxide are all present in exhaust gases. In this research, a large amount of carbon dioxide is evaluated for emission price in the emission output (Sawle et al., 2017; Nplindia, 2025). The cost of marketable renewable certificates is used to compute the estimated value of carbon dioxide. A biomass generator uses rice husk as its input fuel because it has the largest calorific value of all the fuels used. While operating the diesel generator, carbon dioxide has been released, and carbon monoxide gas has been emitted by the biomass generator. The cost of biomass generator and DG emissions is calculated using Equations 18–20:

DG:

${Co}_{2_W}=\frac{C_C\times P_{DIESELG}}{1000}.(18)$

${CO}_{2_{TAX}}=\left(\frac{P_{TRC}}{C_C}\right)\times 1000.(19)$

${EMISSION}_C={CO}_{2_W}\times {CO}_{2_{TAX}.}(20)$

where ${EMISSION}_C$, $P_{DIESELG}$ are the cost of emissions, $C_C$ is the carbon regarded as 0.6078 Kg per KWh, and $P_{TRC}$ is the cost of marketable renewable certificates (US$/KWh). ${Co}_{2_W}$ is granted in tons, and ${CO}_{2_{TAX}}$ has been calculated in terms of US dollars per ton

The emissions of the biomass generator are determined using Equation 21:

${EMISSION}_{BIOMASS}=\left(\frac{{\propto }_1+{\propto }_2}{1000}\right)\times M\text{\hspace{0.17em}ton}/\text{day},(21)$

where ${\propto }_1{\propto }_2$ are the biomass emission coefficients and M is the biomass volume (Gupta et al., 2008). The emission factors are 0.00532 kg/kg and 0.082 kg/kg, respectively.

4.4 Renewable fraction

The renewable fraction is the portion of the energy supply that comes from renewable sources compared to the overall demand. The hybrid energy system’s sustainable percentage reveals the limit of the power supply compared to non-renewable energy sources. The ideal hybrid model has 100% renewable fractions. This shows that all of electricity produced to power the load is generated from renewable sources. The renewable percentage is calculated using Equation 20. If the renewable fraction is zero, it signifies that the overall demand has been fulfilled entirely by generators powered by non-renewable energy sources (Jain et al., 2022b; Thirunavukkarasu and Sawle, 2020).

$Renewablefraction=\left(1-\frac{\sum P_{diesel}}{\sum p_{pv}+\sum p_{wind}}\right)\times 100.(22)$

4.5 Optimization techniques

The ideal size of the HES was determined using a genetic algorithm (GA), artificial bee colony optimization (ABCO), particle swarm optimization (PSO), and teacher-learning-based optimization (TLBO). A well-known optimization strategy based on swarm population is the optimization of particle swarms. During the PSO, the particle circles a promising location in the search space. Particles are randomly positioned via the PSO technique, and they can alter their placements based on their own and neighboring particles’ optimal performance (Sawle et al., 2017; Sawle and Gupta, 2015; Lvshan et al., 2017). Figure 5 depicts the process flow for equipment sizing via PSO. The underlying premise behind genetic algorithms is “survival of the fittest” (Lvshan et al., 2017). The GA optimization procedure includes only one powerful solution that can survive while the others cannot. The GA can generate an initial population of likely optimal solutions. The significant measurements in GA are population size, crossover mechanism, fitness function evaluation, and mutation rate. The process flowchart for using GA to choose the appropriate location and size of DGs in various test systems is shown in Figure 6.

Figure 5

Figure 5. Flowchart for optimal sizing of a hybrid system using PSO.

Figure 6

Figure 6. Flowchart for optimal sizing of a hybrid system using GA.

The artificial bee colony optimization (ABCO) is based on bee honey extraction behavior. It is divided into three parts: employed bees, food sources, and unemployed bees, and it comprises two main behavior patterns: food resource collecting and food source abandonment (Verma et al., 2024). Figure 7 depicts the flow chart for ABCO equipment sizing. Optimization based on teacher learning (TLBO) is focused on a teacher’s influence on a certain set of pupils (beginners). The method’s primary idea may be divided into two parts: the teacher component and the learning part (Bacha et al., 2024). Figure 8 depicts the flow diagram for TLBO system sizing.

Figure 7

Figure 7. Flowchart for optimal sizing of a hybrid system using the ABCO algorithm.

Figure 8

Figure 8. Flowchart for optimal sizing of a hybrid system using TLBO.

5 Results and discussion

The ideal PV, biomass, and wind hybrid energy system (HES) schedule, together with DG backup and battery, is shown using PSO, GA, ABCO, and TLBO analysis. The specified job is carried out using MATLAB (2009a) on a computer running Windows 8 and equipped with an Intel(R) Core(TM) i7-3,370 processor operating at 3.40 GHz and 4.0 GB of RAM. The population, swarm, hive, and class sizes for PSO, GA, ABCO, and TLBO are all 30 in this sample research, and the number of iterations is 50. The design of the ideal HES size for remote rural electrification using GA, TLBO, PSO, and ABCO with two distinct dispatch algorithms is described. The research study was done in Barwani, India, to enhance the construction of the PV-wind-biomass hybrid model.

The PV-wind-biomass HES’s best scheduling is assessed using optimization techniques for dispatch systems that use load monitoring and cycle charging. The following factors affect the hybrid system’s optimal parameters. The outcomes of the best planning of a PV-wind-biomass hybrid system for base load approach using PSO, GA, ABCO, and TLBO are displayed in Figures 9–12 and Table 2. Figures 9–12 show how, for load-following and cycle-charging techniques, TLBO beats GA, PSO, and ABCO in terms of yearly PV output power, wind output power, DG output power, and dump load. Because there is some fluctuation on an hourly basis and better performance metrics are determined for a cycle-charging strategy using TLBO than PSO, the evaluation for additional parameters may be provided.

Figure 9

Figure 9. PV output power of hybrid system using TLBO: (a) load-following strategy; (b) cycle-charging strategy.

Figure 10

Figure 10. Wind output power of the hybrid system using TLBO: (a) load-following strategy; (b) cycle-charging strategy.

Figure 11

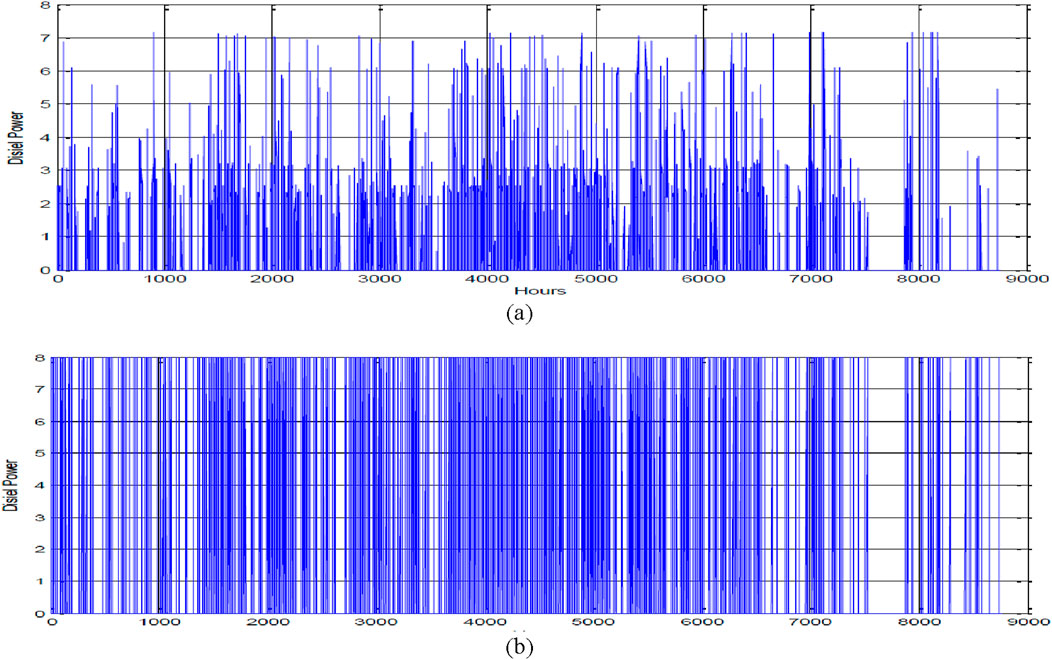
Figure 11. Diesel generator output power of hybrid system using TLBO: (a) load-following strategy; (b) cycle-charging strategy.

Figure 12

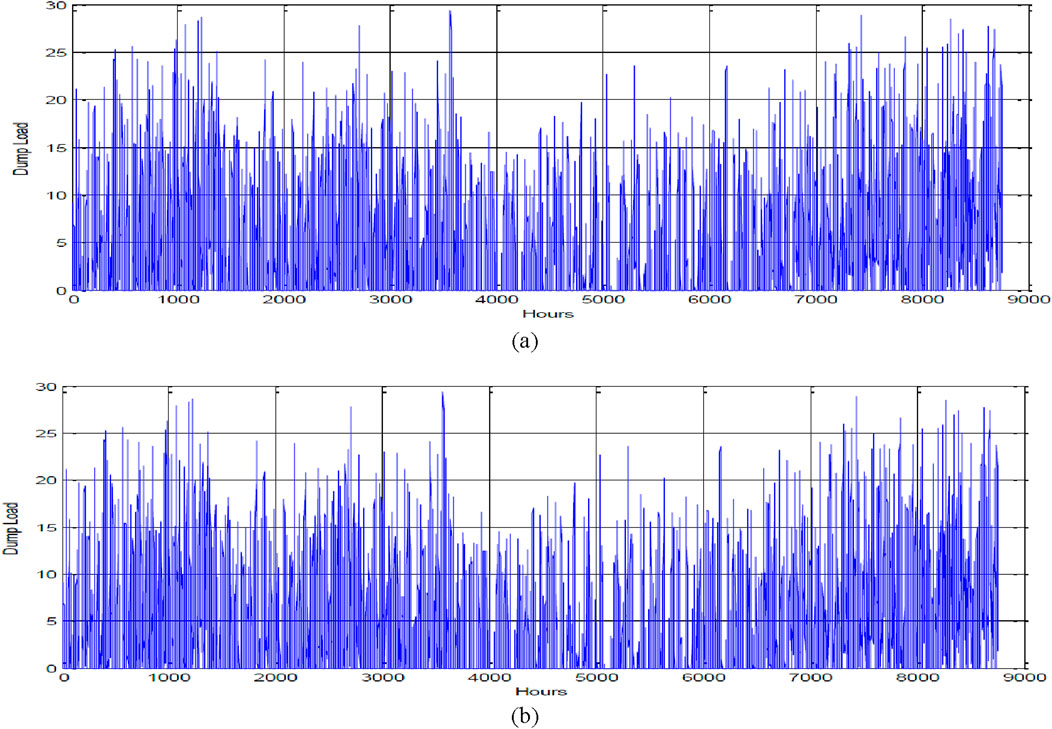
Figure 12. Dump load of a hybrid system using TLBO: (a) load-following strategy; (b) cycle-charging strategy.

Table 2

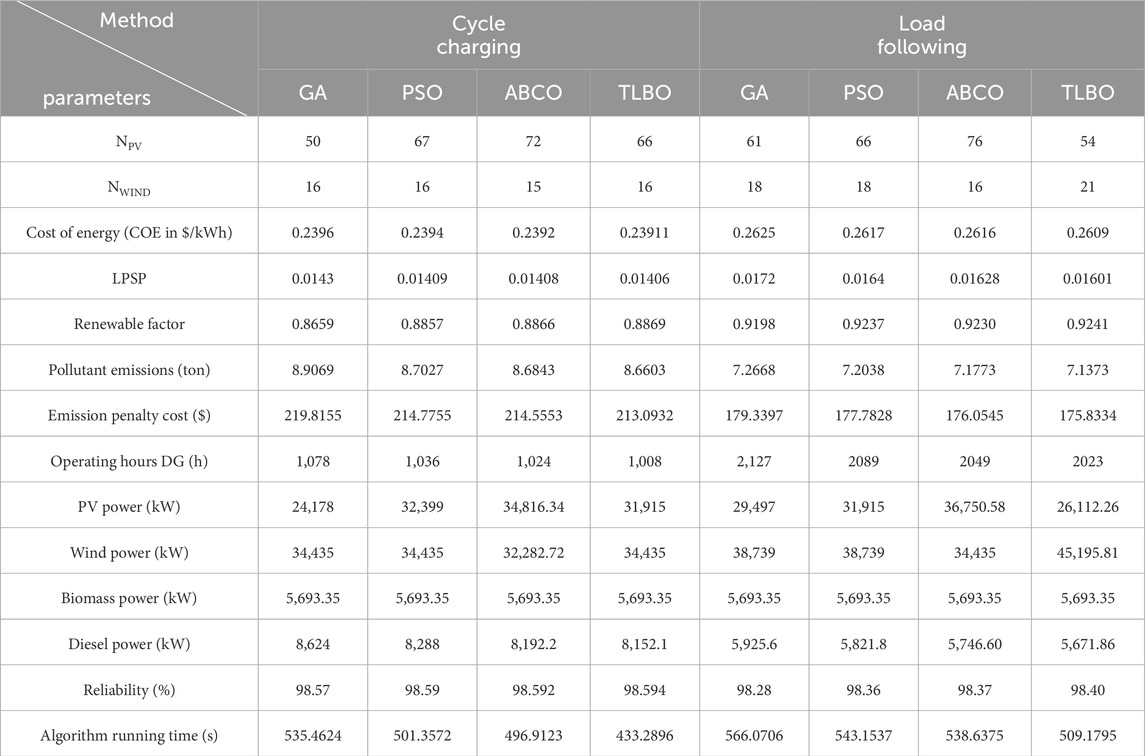
Table 2. Results for load-following and cycle-charging strategies using GA, PSO, ABCO, and TLBO with the hybrid system.

Table 2 lists several parameters, including NWIND, NPV, cost of electricity (COE), LPSP, pollutant emissions, renewable factor, cost, operating hours of DG, PV, wind, biomass, and DG power. Additionally, the reliability and algorithmic running time are listed for the cycle-charging method employing the load-following technique. The NPV and NWIND for a load-following strategy are 61 and 18, 66 and 18, 76 and 16, and 54 and 21, respectively, for GA, ABCO, PSO, and TLBO. Using GA, ABCO, PSO, and TLBO, the COE for the load-following approach is 0.2625 $/kWh, 0.2617 $/kWh, 0.2616 $/kWh, and 0.2609 $/kWh, respectively. Similarly, the load-following strategy’s LPSP values using PSO, GA, ABCO, and TLBO are 0.0172, 0.0164, 0.01628, and 0.01601, respectively. The following values are listed in order of PSO, GA, ABCO, and TLBO: sustainable factor, pollutants, penalty cost, operational hours of DG, biomass, wind, PV, and DG power, reliability, and algorithm running time. Sustainability factor values: 0.9198, 0.9237, 0.9230, and 0.9241; pollutants: 7.2668 ton, 7.2038 ton, 7.1773 ton, and 7.1373 ton; penalty cost: 179.3397 $, 177.7828 $, 176.0545 $, and 175.8334 $; operational hours: 2,127 h, 2,089 h, 2049h, and 2023 h; biomass power: 29,497 kW, 31,915 kW, 36,750.58 kW, and 26,112.26 kW; wind power: 38,739 kW, 38,739 kW, 34,435 kW, and 45,195.81 kW; PV power 5,693.3 kW, 5,693.3 kW, 5,693.35 kW, and 5,693.35 kW; DG power: 5,925.6 kW, 5,821.8 kW, 5,746.60 kW, and 5,671.86 kW; reliability: 98.28%, 98.36%, 98.37%, and 98.40%; and running time: 566.0706 s, 543.1537 s, 538.6375 s, and 509.1795 s, respectively.

Figures 9–12 and Table 2 show the findings for the best planning of a PV-wind-biomass hybrid model with a cycle-charging approach employing GA, PSO, ABCO, and TLBO, respectively. As demonstrated in Figures 13–15, it is more technologically and economically feasible to use TLBO than GA, PSO, and ABCO to use the output power from solar panels, wind turbines, DGs, and dump loads for cycle-charging strategies. Similar findings for other parameters are shown for the cycle-charging strategy. There is an equivalent hourly basis difference, and a cycle-charging strategy employing TLBO has superior performance characteristics than PSO, GA, and ABCO. The cycle-charging strategy’s NPV and NWIND values are 50 and 16 for GA, 67 and 16 for PSO, 72 and 15 for ABCO, and 66 and 16 for TLBO, respectively. When employing GA, PSO, ABCO, and TLBO, the cost of electricity (COE) for the cycle-charging method is 0.2396 $/kWh, 0.2394 $/kWh, 0.2392 $/kWh, and 0.23911 $/kWh, respectively. The following factors are listed in order of GA, PSO, ABCO, and TLBO: renewable factors, penalty cost, LPSP, pollutant emissions, DG operation hours, biomass, wind, PV, DG power, dependability, and algorithm running time. Renewable factors: 0.01430, 0.01409, 0.01408, and 0.01406; LPSP: 0.8659, 0.8857, 0.8866, and 0.8869; pollutant emissions: 8.9069 ton, 8.7027 ton, 8.6843 ton and 8.6603 ton; penalty cost: 219.8155 $, 214.7755 $, 214.5553 $ and 213.0932 $; DG operation hours: 1,078 h, 1,036 h, 1024 h, and 1008 h; biomass power: 24,178 kW, 32,399 kW, 34,816.34 kW and 31,915 kW; wind power: 34,435 kW, 34,435 kW, 32,282.72 kW, and 34,435 kW; PV power: 5,693.3 kW, 5,693.3 kW, 5,693.35 kW, and 5,693.35 kW; DG power: 8,624 kW, 8,288 kW, 8,192.2 kW and 8,152.1 kW; dependability: 98.57%, 98.59%, 98.592%, and 98.594 %; and running time: 535.4624 s, 501.3572 s, 496.9123 s and 433.2896 s, respectively. The research mentioned above clearly demonstrates that the PSO offers better outcomes for load-following and cyclic-charging approaches than hybrid systems in terms of performance measurements.

Figure 13

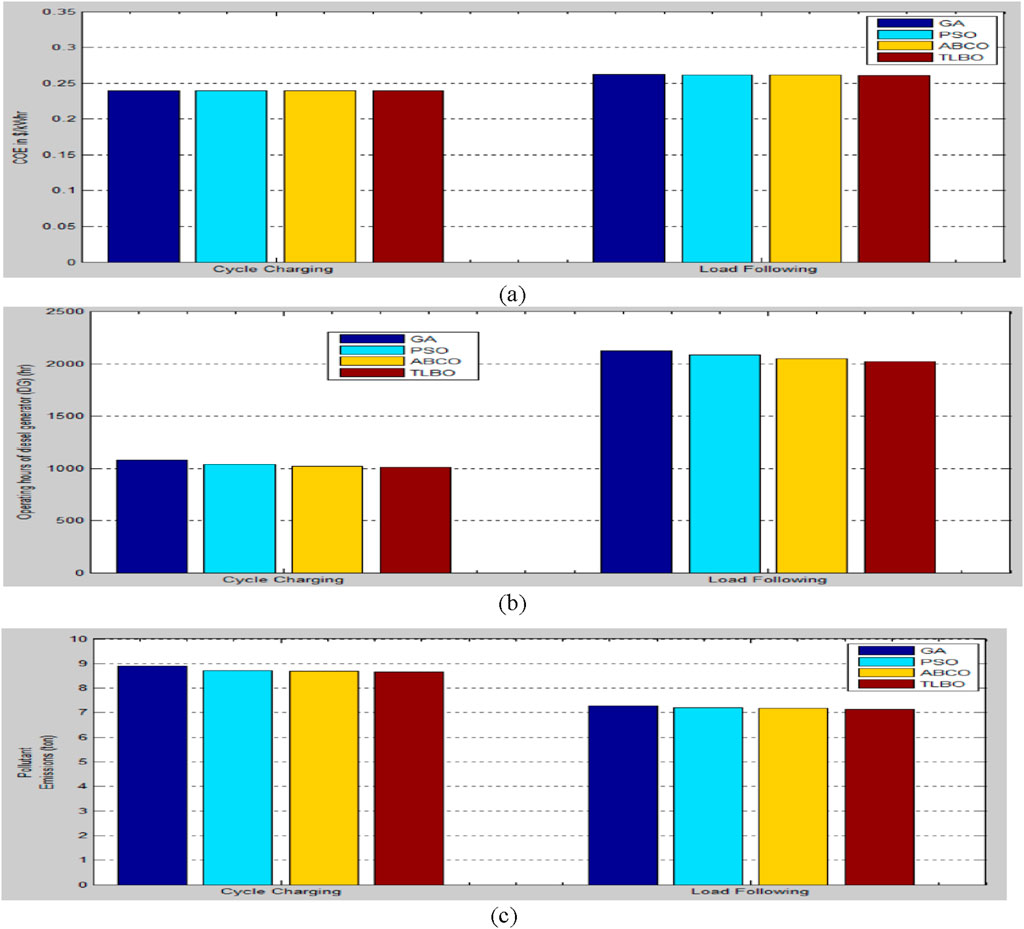
Figure 13. Comparison of load-following and cycle-charging strategy using GA, PSO, ABCO, and TLBO for a hybrid system: (a) COE, (b) operating hours of DG, and (c) Pollutant emissions.

Figure 14

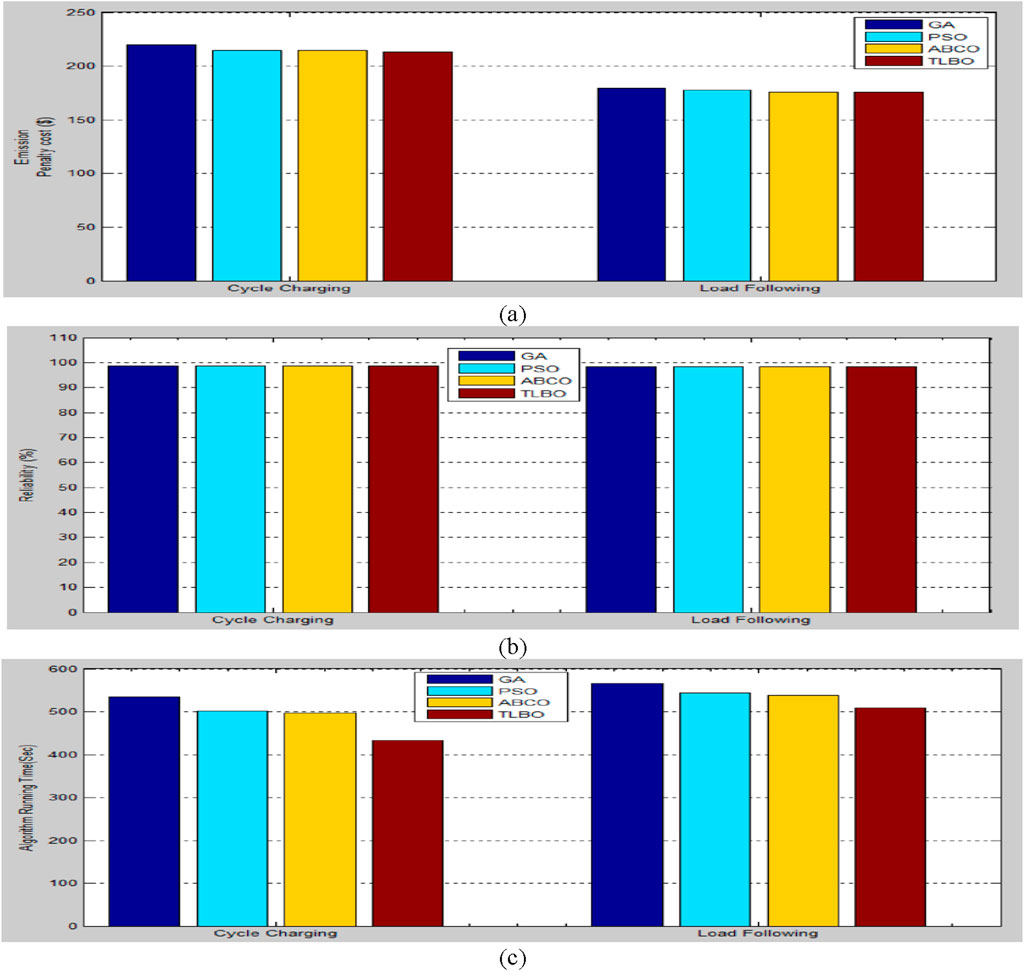
Figure 14. Comparison of load-following and cycle-charging strategies using GA, PSO, ABCO, and TLBO for a hybrid system: (a) emissions penalty cost, (b) reliability, and (c) algorithm running time.

Figure 15

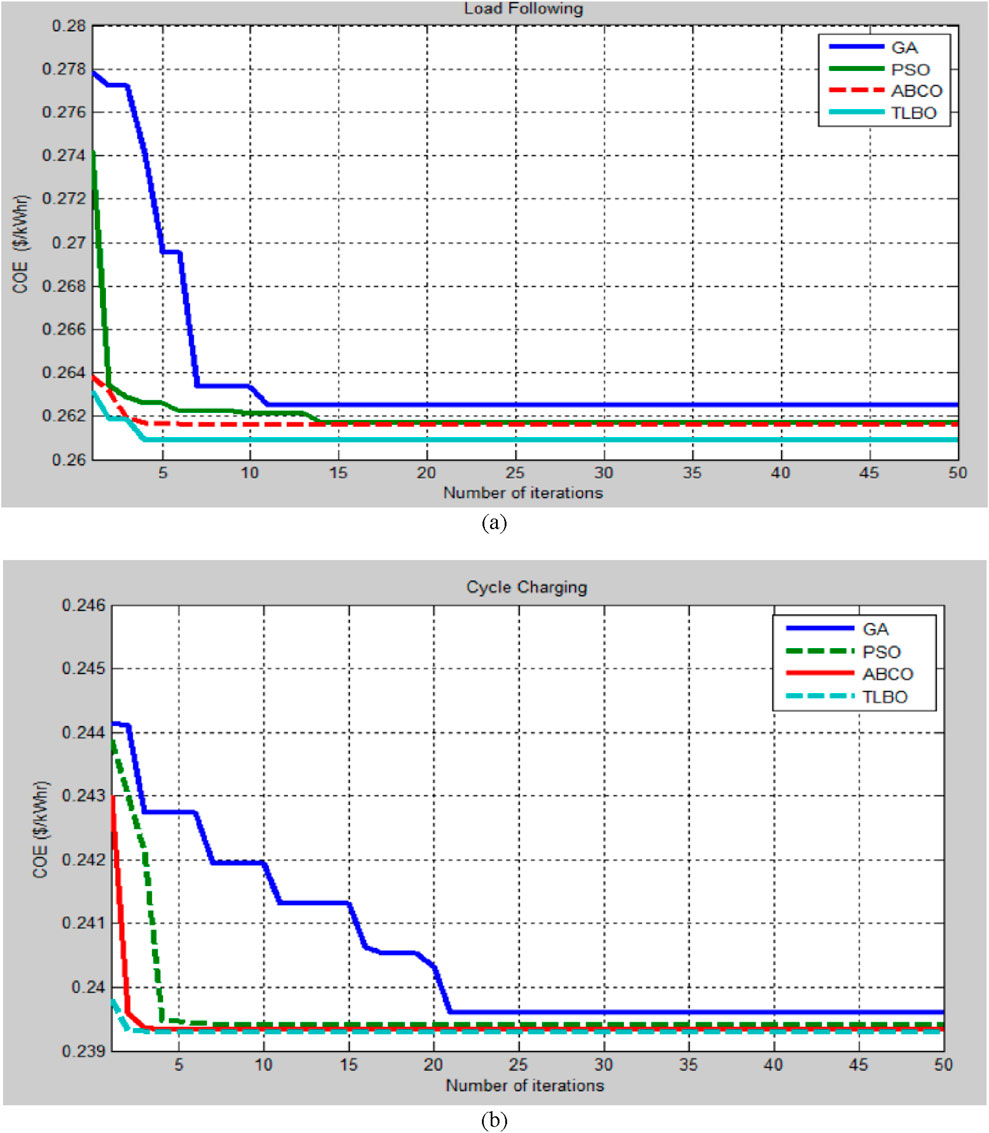
Figure 15. Comparison of the price of electricity (COE) using GA, PSO, ABCO, and TLBO in a (a) load-following strategy and (b) cycle-charging strategy.

Figures 13–15 display the comparison of the hybrid system results for DG, COE, pollutant emissions, reliability, load-following, algorithm running time, and cycle-charging methods using GA, PSO, ABCO, and TLBO. Figures 13, 14 demonstrate that TLBO performs better than GA, PSO, and ABCO for both load-following and cycle-charging methods in terms of COE, DG operation hours, pollutant emissions, emissions penalty cost, reliability, and algorithm running time. The load-following and cyclic charging techniques can be compared on the basis of the best outcomes attained by each method for COE, reliability, economy, and algorithm running time, as indicated in Table-2. These findings suggest that cycle-charging techniques using GA, PSO, ABCO, and TLBO have lower operation hours for COE, DG, algorithm running time, and greater dependability. As a result, cycle-charging solutions using TLBO have more effective overall results. The cycle-charging method is preferable for the best planning of the PV-wind-biomass hybrid power system employing TLBO because it is more dependable, efficient, and technologically affordable than the load-following strategy.

6 Conclusion

This study assesses the optimal design of a PV-wind-biomass hybrid energy system (HES) for a remote area in the Barwani region of India. It employs advanced optimization techniques, including teaching-learning-based optimization (TLBO), genetic algorithm (GA), particle swarm optimization (PSO), and artificial bee colony optimization (ABCO), under both cycle-charging and load-following strategies. The findings indicate that under the load-following approach, the cost of electricity (COE) ranges from $0.2609/kWh to $0.2625/kWh across the different optimization methods. In comparison, the cycle-charging strategy substantially reduces COE to between $0.23911/kWh and $0.2396/kWh. These results demonstrate the cycle-charging approach’s superior performance, with TLBO yielding the most economical and environmentally friendly outcomes. Further analysis reveals that the cycle-charging strategy surpasses load following in various performance indicators. These include loss of power supply probability (LPSP), pollutant emissions, renewable energy utilization factor, emissions penalty cost, diesel generator (DG) operational hours, and computational efficiency. Notably, TLBO excels in reducing pollutant emissions and emissions penalty costs, improving reliability, and decreasing DG operating hours and algorithm runtime compared to the other optimization techniques. Figures 13, 14 emphasize the technological and economic benefits of using the cycle-charging strategy with TLBO to achieve optimal configurations for a PV-wind-biomass HES. This approach not only enhances cost-effectiveness but also supports sustainability objectives by minimizing environmental impact and maximizing renewable energy use. The study concludes that the cycle-charging strategy using TLBO is the most efficient and techno-economically viable method for planning a PV-wind-biomass HES in remote areas. It outperforms the load-following approach across all major evaluation criteria, establishing a standard for future research in optimizing hybrid renewable energy systems for rural electrification and sustainable development.

6.1 Future possibilities and scope of the proposed work

Emerging trends in hybrid energy systems: Incorporating AI-driven methods to forecast energy requirements, renewable power generation, and system efficiency, facilitating more precise and anticipatory decision-making. Next-generation battery solutions: Creating more efficient, long-lasting, and economical batteries (e.g., solid-state and lithium-sulfur variants) to store surplus renewable energy for future use. Adoption of smart grid innovations: Deploying sophisticated monitoring systems to observe energy flows in real-time and enhance system performance. Energy management and demand response: Applying demand response tactics to equilibrate supply and demand, decrease peak loads, and boost system efficiency. Electric vehicle incorporation: Assimilating electric vehicle charging infrastructure into the energy network to optimize power consumption and grid stability. Regulatory and policy frameworks: Establishing supportive policies and incentives to encourage the adoption of renewable energy and energy-efficient measures. Community-centric energy systems: Enabling communities to engage in energy generation and consumption, promoting local economic growth and social equity. By concentrating on these areas, scientists and policymakers can collaborate to develop more sustainable, resilient, and cost-effective hybrid energy systems that contribute to a greener future.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

YS: writing – original draft, funding acquisition, investigation, resources, supervision, visualization, and writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The author extends their appreciation to the M.P. Council of Science & Technology R&D Project, Bhopal, India, entitled “Renewable Energy Empowerment for Rural Sustainable Development using Advanced Techniques” (Sanction Order 14446/CST/R&DIPhy and Engg. and Pharmacy/2023–24 Ref: File No_AIRLYR.P-2/370dated05.10.2023) for providing resources to carry out this research work.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Águila-León, J., Vargas-Salgado, C., Díaz-Bello, D., and Montagud-Montalvá, C. (2024). Optimizing photovoltaic systems: a meta-optimization approach with GWO-Enhanced PSO algorithm for improving MPPT controllers. Renew. Energy 230, 120892. doi:10.1016/j.renene.2024.120892

CrossRef Full Text | Google Scholar

Akbar, M., Mehran, A., and Farshid, K. (2015). Scrutiny of multifarious particle swarm optimization for finding the optimal size of a PV/wind/battery hybrid system. Renew. Energy 80, 552–563. doi:10.1016/j.renene.2015.02.045

CrossRef Full Text | Google Scholar

Author Anonymous (2025). Windpowerindia. Available online at: http://www.windpowerindia.com/state-year-wise.

Google Scholar

Bacha, B., Ghodbane, H., Dahmani, H., Betka, A., Toumi, A., and Chouder, A. (2024). Optimal sizing of a hybrid microgrid system using solar, wind, diesel, and battery energy storage to alleviate energy poverty in a rural area of Biskra, Algeria. J. Energy Storage 84, 110651. doi:10.1016/j.est.2024.110651

CrossRef Full Text | Google Scholar

Bamisile, O., Cai, D., Adun, H., Dagbasi, M., Ukwuoma, C. C., Huang, Q., et al. (2024). Towards renewables development: review of optimization techniques for energy storage and hybrid renewable energy systems. Heliyon 10, e37482. doi:10.1016/j.heliyon.2024.e37482

PubMed Abstract | CrossRef Full Text | Google Scholar

Barley, C. D., Winn, C., and Flowers, L. (1995). Optimal control of remote hybrid power systems. Part 1: simplified model. Golden, CO (United States): National Renewable Energy Lab. No. NREL/TP--441-7806; CONF-950309--3.

Google Scholar

Deb, S., Sachan, S., Sinha, S., and Malik, P. (2023). “Planning and operation of hybrid local energy system through Ant-Lion optimization,” in 2023 IEEE 3rd international conference on sustainable energy and future electric transportation (SEFET) USA, 9-12 Aug. 2023, (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Diaf, S., Diaf, D., Belhamel, M., Haddadi, M., and Louche, A. (2007). A methodology for optimal sizing of autonomous hybrid PV/wind system. Energy Policy 35 (11), 5708–5718. doi:10.1016/j.enpol.2007.06.020

CrossRef Full Text | Google Scholar

Dsouza, O. D., Shilpa, G., and Irusapparajan, G. (2024). Optimized energy management for hybrid renewable energy sources with Hybrid Energy Storage: an SMO-KNN approach. J. Energy Storage 96, 112152. doi:10.1016/j.est.2024.112152

CrossRef Full Text | Google Scholar

Emrani, A., and Berrada, A. (2024). Modeling and optimal capacity configuration of dry gravity energy storage integrated in off-grid hybrid PV/wind/biogas plant incorporating renewable power generation forecast. J. Energy Storage 97, 112698. doi:10.1016/j.est.2024.112698

CrossRef Full Text | Google Scholar

Gönül, Ö., Can Duman, A., and Güler, Ö. (2024). Multi-objective optimal sizing and techno-economic analysis of on-and off-grid hybrid renewable energy systems for EV charging stations. Sustain. Cities Soc. 115, 105846. doi:10.1016/j.scs.2024.105846

CrossRef Full Text | Google Scholar

Government of India (n.d.) Year End Review 2017 –MNRE. Gov.In. Available online at: https://pib.gov.in/newsite/PrintRelease.aspx?relid=174832 (Retrieved on April 6, 2025).

Google Scholar

Gupta, A. (2010). Modelling of HES. [Ph.D. thesis] (Roorkee: Alternate Hydro Energy Centre, Indian Institute of Technology).

Google Scholar

Gupta, S., Sawle, Y., Thakre, K., and Thirunavukkarasu, M. (2025). Hippopotamus based optimization for reliable and cost effective designing of stand-alone hybrid renewable system for a remote area. Front. Energy Res. 12, 1496070. doi:10.3389/fenrg.2024.1496070

CrossRef Full Text | Google Scholar

Gupta, S. C., Kumar, Y., and Agnihotri, G. (2008). Techno-economical design of an autonomous photovoltaic wind hybrid energy system. New Delhi, India: IEEE Power India Conference POWERCON.

Google Scholar

Homerenergy (2025). Homerenergy. Available online at: http://www.homerenergy.com.

Google Scholar

Islam, M. K., Hassan, N., Rasul, M., Emami, K., and Chowdhury, A. A. (2024). An off-grid hybrid renewable energy solution in remote Doomadgee of Far North Queensland, Australia: optimisation, techno-socio-enviro-economic analysis and multivariate polynomial regression. Renew. Energy 231, 120991. doi:10.1016/j.renene.2024.120991

CrossRef Full Text | Google Scholar

Jain, S., Babu, S., and Sawle, Y. (2022b). “Prefeasibility economic scrutiny of the off-grid hybrid renewable system for remote area electrification,” in Proceedings of the international conference on paradigms of communication, computing and data sciences: pccds 2021 (Singapore: Springer).

Google Scholar

Jain, S., Kulkarni, A., and Sawle, Y. (2022a). “Overview of energy management systems for microgrids and smart grid,” in Planning of hybrid renewable energy systems, electric vehicles and microgrid: modeling, control and optimization (Singapore: Springer Nature Singapore), 61–88.

CrossRef Full Text | Google Scholar

Ji, C. (2025). Design, techno-economic feasibility analysis, and sensitivity study of an off-grid hybrid microgrid for developing communities. Renew. Energy 239, 121956. doi:10.1016/j.renene.2024.121956

CrossRef Full Text | Google Scholar

Justus, C. G. (1978). Wind energy statistics for large arrays of wind turbines (New England and Central US Regions). Sol. Energy 20 (5), 379–386. doi:10.1016/0038-092x(78)90153-6

CrossRef Full Text | Google Scholar

Koholé, Y. W., Wankouo Ngouleu, C. A., Fohagui, F. C. V., and Tchuen, G. (2023). Quantitative techno-economic comparison of a photovoltaic/wind hybrid power system with different energy storage technologies for electrification of three remote areas in Cameroon using Cuckoo search algorithm. J. Energy Storage 68, 107783. doi:10.1016/j.est.2023.107783

CrossRef Full Text | Google Scholar

Koholé, Y. W., Wankouo Ngouleu, C. A., Fohagui, F. C. V., and Tchuen, G. (2024). Optimization of an off-grid hybrid photovoltaic/wind/diesel/fuel cell system for residential applications power generation employing evolutionary algorithms. Renew. Energy 224, 120131. doi:10.1016/j.renene.2024.120131

CrossRef Full Text | Google Scholar

Köprü, M. A., Öztürk, D., and Yildirim, B. (2024). Techno-economic analysis of a hybrid system for rural areas: electricity and heat generation with hydrogen and battery storage. Int. J. Hydrogen Energy. doi:10.1016/j.ijhydene.2024.11.394

CrossRef Full Text | Google Scholar

Lvshan, Ye, Yuan, D., and Yu, W. (2017). “Artificial bee colony algorithm with genetic algorithm for job shop scheduling problem,” in 2017 international symposium on intelligent signal processing and communication systems (ISPACS) (IEEE).

Google Scholar

Medghalchi, Z., and Taylan, O. (2023). A novel hybrid optimization framework for sizing renewable energy systems integrated with energy storage systems with solar photovoltaics, wind, battery and electrolyzer-fuel cell. Energy Convers. Manag. 294, 117594. doi:10.1016/j.enconman.2023.117594

CrossRef Full Text | Google Scholar

Nplindia (2025). NPL (national physical laboratory). Delhi, India. Available online at: http://www.nplindia.org/S.

Google Scholar

Physical Progress Achievements (2017). Ministry of New and Renewable Energy.

Google Scholar

Rodolfo, D.-L., and Bernal-Agustín, J. L. (2008). Multi-objective design of PV–wind–diesel–hydrogen–battery systems. Renew. Energy 33 (12), 2559–2572. doi:10.1016/j.renene.2008.02.027

CrossRef Full Text | Google Scholar

Roy, S. (1997). Optimal planning of wind energy conversion systems over an energy scenario. Energy Convers. IEEE Trans. 12, 248–254. doi:10.1109/60.629710

CrossRef Full Text | Google Scholar

Saha, S., Saini, G., Chauhan, A., Upadhyay, S., Madurai Elavarasan, R., and Hossain Lipu, M. (2023). Optimum design and techno-socio-economic analysis of a PV/biomass based hybrid energy system for a remote hilly area using discrete grey wolf optimization algorithm. Sustain. Energy Technol. Assessments 57, 103213. doi:10.1016/j.seta.2023.103213

CrossRef Full Text | Google Scholar

Sawle, Y. (2022). “Scrutiny of PV biomass stand-alone hybrid system for rice mill electrification,” in Deregulated electricity market (Apple Academic Press), 135–152.

CrossRef Full Text | Google Scholar

Sawle, Y., Gupta, S. C., and &Bohre, A. K. (2017). Optimal sizing of standalone PV/Wind/Biomass hybrid energy system using GA and PSO optimization technique. Energy Procedia 117, 690–698. doi:10.1016/j.egypro.2017.05.183

CrossRef Full Text | Google Scholar

Sawle, Y., Gupta, S. C., and Kumar Bohre, A. (2018). Techno-economic scrutiny of HRES through GA and PSO technique. Int. J. Renew. Energy Technol. 9 (1-2), 84–107. doi:10.1504/ijret.2018.090106

CrossRef Full Text | Google Scholar

Sawle, Y., and Gupta, S. C. (2015). A novel system optimization of a grid independent hybrid renewable energy system for telecom base station. Int. J. Soft Comput. Math. Control (IJSCMC) 4 (2), 49–57. doi:10.14810/ijscmc.2015.4204

CrossRef Full Text | Google Scholar

Shah, S., et al. (2022). “Optimal planning and design of an off-grid solar, wind, biomass, fuel cell hybrid energy system using HOMER pro,” in Recent advances in power systems: select proceedings of EPREC-2021. Singapore: Springer Nature Singapore, 255–275.

CrossRef Full Text | Google Scholar

Singh, B., and Kumar, A. (2023). Optimal energy management and feasibility analysis of hybrid renewable energy sources with BESS and impact of electric vehicle load with demand response program. Energy 278, 127867. doi:10.1016/j.energy.2023.127867

CrossRef Full Text | Google Scholar

Singh, P., Pandit, M., and Srivastava, L. (2022). Techno-socio-economic-environmental estimation of hybrid renewable energy system using two-phase swarm-evolutionary algorithm. Sustain. Energy Technol. Assessments 53, 102483. doi:10.1016/j.seta.2022.102483

CrossRef Full Text | Google Scholar

Solargis (2013). “Global horizontal irradiation (GHI),” in SolarGIS. GeoModel solar. Available online at: http://solargis.info/doc/71.

Google Scholar

Thirunavukkarasu, M., and Yashwant, S. (2022). An examination of the techno-economic viability of hybrid grid-integrated and stand-alone generation systems for an Indian tea plant. Front. Energy Res. 10, 806870. doi:10.3389/fenrg.2022.806870

CrossRef Full Text | Google Scholar

Thirunavukkarasu, M., Lala, H., and Sawle, Y. (2023a). Reliability index based optimal sizing and statistical performance analysis of stand-alone hybrid renewable energy system using metaheuristic algorithms. Alex. Eng. J. 74, 387–413. doi:10.1016/j.aej.2023.04.070

CrossRef Full Text | Google Scholar

Thirunavukkarasu, M., Lala, H., and Sawle, Y. (2023b). Techno-economic-environmental analysis of off-grid hybrid energy systems using honey badger optimizer. Renew. Energy 218, 119247. doi:10.1016/j.renene.2023.119247

CrossRef Full Text | Google Scholar

Thirunavukkarasu, M., and Sawle, Y. (2020). Design, analysis and optimal sizing of standalone PV/diesel/battery hybrid energy system using HOMER. IOP Conf. Ser. Mater. Sci. Eng. 937 (1), 012034.

CrossRef Full Text | Google Scholar

Thirunavukkarasu, M., and Sawle, Y. (2021). A comparative study of the optimal sizing and management of off-grid solar/wind/diesel and battery energy systems for remote areas. Front. Energy Res. 9. doi:10.3389/fenrg.2021.752043

CrossRef Full Text | Google Scholar

Verma, R., Bhatia, R., and Raghuwanshi, S. S. (2024). Optimization and performance enhancement of renewable energy microgrid energy system using pheasant bird optimization algorithm. Sustain. Energy Technol. Assessments 66, 103801. doi:10.1016/j.seta.2024.103801

CrossRef Full Text | Google Scholar

Yadav, N., Sawle, Y., Khan, B., and Miro, Y. (2022). Evaluating the technical and economic feasibility of a hybrid renewable energy system for off-grid. J. Aut. Intell. 5 (2), 13. doi:10.32629/jai.v5i2.540

CrossRef Full Text | Google Scholar

Zeng, G.-Q., Qin, Z., Lu, K. D., and Li, L. M. (2025). CMOPEO-OP: constrained multi-objective population extremal optimization-based optimal planning of standalone microgrids. Swarm Evol. Comput. 92, 101787. doi:10.1016/j.swevo.2024.101787

CrossRef Full Text | Google Scholar

Zhou, J., and Xu, Z. (2023). Optimal sizing design and integrated cost-benefit assessment of stand-alone microgrid system with different energy storage employing chameleon swarm algorithm: a rural case in Northeast China. Renew. Energy 202, 1110–1137. doi:10.1016/j.renene.2022.12.005

CrossRef Full Text | Google Scholar

Nomenclature

$P_{WIND,each}^T$ Power generated by the wind turbine

$v_r$ Nominal speed of the wind turbine

$V$ Windspeed

$v_o$ Cut out speed

$v_J$ Cut in speed

${\eta }_{BIO}$ Efficiency of the biomass

${CV}_{BIO}$ Calorific value of the rice husk

$F_{dsl}\left(t\right)$ Diesel fuel consumption L/h

$P\left(t\right)$ Diesel generator power (kW)

$P_R$ Rated power of the generator

$P_R$ Wind generator rated power

${SOC}_M$ Minimum state of charge

$P_L$ The hourly power consumption

N Number of years

I Real interest rate

$P_{CB}$ Worth of converter/battery components

$A,B$ Area costs and parameters (L/kW)

P^T_PV:each PV system-generated power.

P_RS Rated power by PV panel.

R Solar radiation factor.

R_cr Certain radiation at 150 W/m²

R_srs Standard solar radiation at 1000 W/m²

$T-1$and $T$ Charge times by battery bank.

$P_l^T$ Energy demand of a particular hour

$P_{WIND}^T$ Power generated by the wind turbine

$P_{PV}^T$ Power generated by the PV panel

$P_{BIO}^T$ Power generated by biomass

$P_l^T$ Energy demand for a particular hour

${\eta }_{bc}$ Charge efficiency of the battery bank

${\eta }_{inverter}$ Efficiency of the inverter

$\tau$ Hourly self-discharge rate

${\eta }_{bf}$ Discharging efficiency of batterybank

$C_{CB}$ Converter/inverter price

$E_{battery}^T$and $E_{battery}^{T-1}$ Charge quantities of the battery