Abstract
With the rapid development of integrated energy systems (IES), the extensive integration of dis-tributed energy and the increasing coupling of multiple energy systems need higher requirements for the coordinated control methods of IESs. This paper proposes a distributed emergency control method for integrated energy systems of industrial parks based on the alternating direction multiplier method (ADMM). Firstly, an optimization scheduling model is established for the integrated energy system in industrial parks. On the basis of minimizing operating costs, the model takes into account the operational constraints of each energy equipment. Secondly, considering the shortage of energy supply, in order to achieve energy transfer between users, a distributed optimization scheduling model for IES of the industrial park is established based on the typical energy structure of users. And a distributed optimization scheduling algorithm for the comprehensive energy system of the industrial park based on ADMM is proposed. Finally, the proposed emergency control method is verified under typical fault scenarios.
1 Introduction
The integrated energy system (IES) is a complex multi energy coupling system, mainly composed of energy networks sub system, energy production sub system, energy conversion sub system, energy storage sub system and energy consumption sub system. The energy networks sub system mainly includes power supply network, cooling supply network, heating supply network, natural gas supply network and other networks. The energy conversion subsystem mainly includes equipment such as combined cooling, heating and power (CCHP), heat pumps, refrigeration and air conditioning. The energy storage sub system mainly includes equipment for storing electricity, heat, cold, and natural gas. The energy consumption sub system mainly consists of multiple types of end users (Cheng et al., 2019). IES has been developing rapidly with its characteristics of high efficiency and environmental protection (Sun et al., 2021).
Therefore, there have been abundant research achievements in the field of IES. In terms of optimizing scheduling, in order to balance the interests of Integrated Energy Operators (IEOs) and users, Cheng et al. (2019) proposed a novel IES optimization framework based on the Stackelberg game of integrated demand response (IDR) to realize the IES optimizing scheduling with uncertain renewable energy generation. By fully utilizing the potential of regional heating networks, a regional heating network model considering time delay and thermal attenuation characteristics was established. Li et al. (2021a) proposed a scheduling model based on opportunity constrained planning for community IES (CIES), which was applied to achieve integrated demand response (IDR) in uncertain environments to minimize system operating costs. The proposed model was applied to explore the potential interaction capabilities of electricity, natural gas, thermal flexible loads, and electric vehicles. On this basis, Li et al. (2021b) analyzed the interactive response characteristics of multiple energy loads. Li et al. (2021b) introduced the horizontal complementary substitution and vertical time shift strategy of electric gas heating cooling, and considers the collaborative complementarity and flexible conversion of multiple energy sources. A stochastic robust optimization operation model of CIES based on comprehensive demand response was established Li et al. (2021a). In order to address the energy management and pricing issues of multi CIES (MCIES), a hierarchical stochastic optimization scheduling method in uncertain environments was proposed (Li et al., 2021).
In terms of reducing carbon emissions, Li et al. (2022) established a comprehensive energy system cooperative game model with cost and carbon emissions as objectives based on the cooperative game theory. And a profit distribution method that combines an improved Shapley value and kernel method was proposed. Wang et al. (2022) proposed an objective function and optimization strategy based on deviation satisfaction. The current carbon tax policy is not ideal in stimulating carbon emissions reduction in this IES. Wang et al. (2022) suggested to increase the current carbon tax threshold price. Zhou et al. (2021) transformed traditional thermal power plants into carbon capture power plants through carbon capture to achieve collaborative optimization of IES. In order to achieve the joint operation of wind power (WP), photovoltaics (PV), heating energy and energy storage, a regional IES (RIES) was constructed (Xuan et al., 2022). Based on carbon capture and carbon footprint tracking technology, effective conversion and utilization of carbon were achieved to meet the requirements of environmental protection, sustainability, and economic development.
In terms of emergency control, due to strong heating electric coupling limitations, uncontrollable renewable energy sources, and limited grid regulation capabilities, the operational performance of IES with a high proportion of renewable energy has deteriorated to increase the reduction of renewable energy. Saxena et al. (2023) pointed the problem of unavailable operating areas in traditional IES and its flexibility improvement mechanism combined with gas boilers, electric boilers, power to gas (P2G), electrical energy storage, and thermal energy storage. Based on the multi type, the flexibility of grid connection of P2G technology and the synergistic effect between different energy carriers were studied (Yan et al., 2023). The results showed that P2G technology can play a role in energy buffering and preventing unpredictable behavior interference. Marzi et al. (2023) proposed a reliability evaluation method for RIES based on intelligent agent communication, which determines the impact of equipment component failures on the system through intelligent agent communication. Li et al. (2016) proposed a reliability assessment method for RIES that includes P2G and gas turbines. Juanwei et al. (2019) constructed a reliability evaluation model for RIES. Based on the proposed model, Juanwei et al. (2019) proposed a topology simplification method for calculating the reliability index of natural gas systems. Lei et al. (2018) proposed a reliability evaluation method for RIES based on the incremental state enumeration method. Guelpa and Verda (2018) modeled and analyzed the impact of pipeline leakage and circulation pump failure on the heating system. And an optimization scheduling method was proposed for the heating system under fault conditions.
With the development of industrial park construction, industrial park construction pays more attention to improving the comprehensive utilization rate of energy Kaisong et al. (2021). Based on the analysis of the problems existing in the industrial park, Kaisong et al. (2021) applied the level comprehensive energy system optimization model to realize a more economic, environmental protection and reasonable energy utilization scheme for the industrial park. In order to provide important reference for designers select typical power load days, Chen et al. (2024) established a hybrid time series model of energy consuming equipment to realize energy consumption characteristics analysis based on data clustering. Considering the price transmission mechanism of multi type energy markets, Jintao and Yang. (2019) proposed the integrated demand response strategy of IES in industrial parks.
In summary, there has been sufficient research on IES in various aspects. There is still relatively little research on energy supply control in industrial park integrated energy systems. This study focuses on the integrated energy systems in industrial parks. The main contributions are as follows:
(1) A distributed emergency control model is proposed for integrated energy systems in industrial parks based on energy transfer. Firstly, a comprehensive energy system is established to optimize objectives, which take into account energy costs, maintenance costs, load loss costs, and user energy transfer costs. Then, establish multi energy bus power balance constraints and multi energy flow device constraints. Finally, the distributed emergency control model for the integrated energy system of industrial parks based on energy transfer is established.
(2) A distributed emergency control solution method is proposed for integrated energy systems in industrial parks based on the alternating direction multiplier method (ADMM). Firstly, an augmented Lagrange function is established. And the original objective function is decomposed into two optimization subproblems. The iterative solution of the subproblems is achieved by calculating the original residuals and dual residuals to realize the distributed emergency control solution method.
2 Distributed emergency control model for IES in industrial park
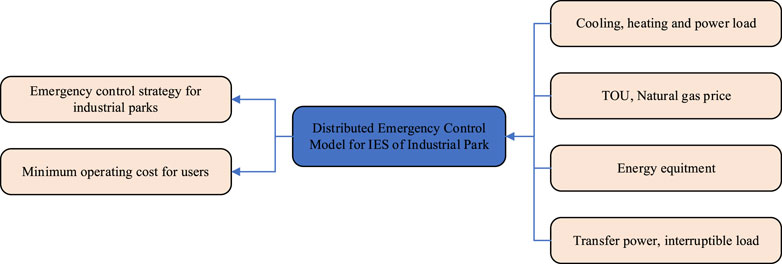
In this paper, based on the typical energy supply structure a distributed emergency control model for IES of the industrial park is establishing. The model framework is shown in Figure 1. The input of the model includes the market price of energy, the types and capacities of energy supply and storage equipment, and the cooling, heating, and electricity loads of users. The purpose of the model is to realize the emergency control to minimize operating costs for users.
FIGURE 1
The most common result of energy equipment failure is a shortage of energy supply for users. If energy supply is restored only after the equipment is repaired, it will have a certain impact on users’ production. In order to enhance the reliability of energy supply for users, it is possible to solve the problem by increasing the output of other energy devices or transferring energy between users after the energy equipment failure. If users arbitrarily change the external power purchase plan after formulating daily operation strategies, the gateway power may exceed the limit. So users should prioritize using their own energy equipment for regulation after a failure occurs. If it cannot be met, energy conversion between users should be considered. If the energy supply demand cannot be met, interruptible loads of users should be cut off. The ultimate guarantee is to solve the energy shortage caused by energy equipment failures without changing the external power purchase plan to ensure the normal operation of users.
2.1 Objective function
The distributed emergency control goal of IES in the park is to minimize the daily operating cost for users. The daily operating cost of the IES in the park mainly includes the following five aspects: fuel cost, power grid interaction cost, energy equipment operation and maintenance cost, interruptible load loss cost, and energy conversion cost between users:In Equation 1, is the total cost of purchasing natural gas for the system; represents the total cost of purchasing electrical energy for the system; represents the operating and maintenance costs of all energy supply and storage devices within the system; represents the cost of losses caused by interrupted loads; represents the cost of energy transfer between users.In Equation 2, , , and are the parameters obtained by fitting the consumption curve of the ith gas turbine with natural gas; is the electricity production power of the ith gas turbine during time .
The cost of purchasing electricity can be expressed as follows:In Equation 3, is the time of use electricity price at time ; is the purchasing power of the ith user at time .
The operation and maintenance costs of energy supply equipment and energy storage equipment can be expressed as follows:In Equation 4, is the operating and maintenance cost per unit power of the ith gas turbine; is the operating and maintenance cost per unit power of the ith waste heat boiler; is the operating and maintenance cost per unit power of the ith electric refrigeration air conditioner; is the operating and maintenance cost per unit power of the ith dual condition refrigeration unit; is the operating and maintenance cost per unit power of the ith energy storage device; is the electricity production power of the ith gas turbine at time ; is the heating production power of the ith waste heat boiler during time period ; is the cooling power of the ith electric refrigeration air conditioner during time period ; is the cooling power of the ith dual condition refrigeration unit during time period ; and are the charging and discharging power of the ith energy storage device during time .
The cost of losses caused by interruptible loads can be expressed as follows:In Equation 5, and are the cost coefficients corresponding to the ith interruptible load, which are related to the load characteristics of the user; is the power of the interruptible load of ith user that is cut off.
The cost of energy conversion between users can be summarized as follows:In Equation 6, is the cost price of interruptible loads; is the energy power transferred between users.
2.2 Constraints
2.2.1 Power balance constraints
Due to the consideration of interruptible loads and energy transfer between users, the constraints of the energy bus have changed.
The electrical bus power constraint is shown in Equation 7.
The heating bus balance constraint is shown in Equation 8.
The cooling bus balance constraint is shown in Equation 9.In Equations 7–9, is the interruptible electrical load power; is the power of the electrical load transferred to the user; is the power of the electrical load that the user transfers to the outside; is interruptible heat load power; is interruptible cooling load power.
2.2.2 Interruptible load constraints
In Equations 10–12, is the maximum interruptible power loads; is the maximum interruptible heating load power; is the maximum interruptible cooling load power.
2.2.3 Energy conversion constraints
In Equations 13–14, is the maximum electrical power transferred to the user; is the maximum electrical power that users can transfer externally.
2.2.4 Operation constraints of various energy equipments
Electric energy storage constraints:In Equation 15, is the capacity of electric energy storage equipment; and are the minimum allowable capacity and maximum allowable capacity of electrical energy storage equipment, respectively. In Equations 16, 17, is the rated storage capacity of electrical energy storage equipment; and are the charging power and discharging power of the electric energy storage equipment, respectively; and are the maximum charging multiple and maximum discharging multiple of the electric energy storage equipment, respectively. In Equation 18, and are the energy stored before and after charging or discharging of electrical energy storage equipment, respectively; is the self loss rate of energy storage devices; and are the charging efficiency and discharging efficiency of the electric energy storage device, respectively.
Cooling storage equipment constraints:In Equations 19–22, is a 0–1 variable that can only take on values of 0 or 1; is the electrical power consumed by the dual working condition refrigeration machine; is the ice making power of the dual working condition refrigeration machine; is the ice energy efficiency ratio of the dual working condition refrigeration machine; and are the minimum ice making power and maximum ice making power of the dual working condition refrigeration machine, respectively; and are respectively the minimum cooling power and maximum cooling power of the dual working condition refrigeration machine.
For ease of description, the above constraints are uniformly expressed as:In Equations 23, 24, is the equality constraints; is the inequality constraints; is the set of variables.
In summary, the distributed optimization scheduling model for IES can be obtained in Equation 25.
3 Solution method for distributed emergency control strategy of IES based on ADMM
3.1 Objection function
In this paper, the alternating direction multiplier method is applied to analyze the distributed emergency control solution method for IES in the industrial park. User 1 has the ability to transfer energy, while User 2 and User 3 can accept the energy transferred by User 1. The constraints are shown in Equations 26, 27. is the power load transferred from user 1 to user 2; is the electrical load power received by User 2 from User 1; is the power load transferred from user 1 to user 3; is the electrical load power received by User 3 from User 1.
Convert the objective function of User 1 into Equation 28. is the total daily operating cost of User 1; is the daily operating cost including the energy cost transferred from User 1 to User 2; is the daily operating cost that includes the energy cost transferred from User 1 to User 3.
An augmented Lagrange function is established based on the alternating direction multiplier method. And the objective function can be decomposed into two optimization problems to solve them.
Equation 29 is the augmented Lagrange function for distributed optimization scheduling of the integrated energy system in the industrial park. And it can be decomposed into the following optimization subproblems.
Transfer sub question 1–1 is shown in Equation 30:
Transfer sub question 1–2 is shown in Equation 31: is the Lagrange multiplier.
Transfer sub question 2–1 is shown in Equation 32:
Transfer sub question 2–2 is shown in Equation 33: is the Lagrange multiplier.
The specific solution process for the distributed emergency control problem of the integrated energy system in the park based on the alternating direction multiplier method is shown in
Figure 2.
Step 1: set the initial value of the variable. , , , ; Lagrange multiplier , ; iteration times .
Step 2: for iteration time , and can be updated based on Equations 30, 32.
Step 3: for iteration time , and can be updated based on Equations 31, 33.
Step 4: update Lagrange multipliers and based on Equations 34, 35.
Step 5: calculate the original residuals and dual residuals according to Equation 36. Judge whether the convergence conditions.
FIGURE 2
Where
and
are the original residuals and dual residuals of the transfer subproblem 1, respectively;
and
are the original residuals and dual residuals of the transfer subproblem 2, respectively.
Step 6: if the convergence condition is met, stop the iteration; otherwise update the iteration number and return to step 2 to continue the calculation.
4 Case study
In this paper, IES with three typical users within of the industrial park for calculation and analysis. The distributed emergency control schematic diagram of the integrated energy system of industrial park is shown in Figure 3.
FIGURE 3
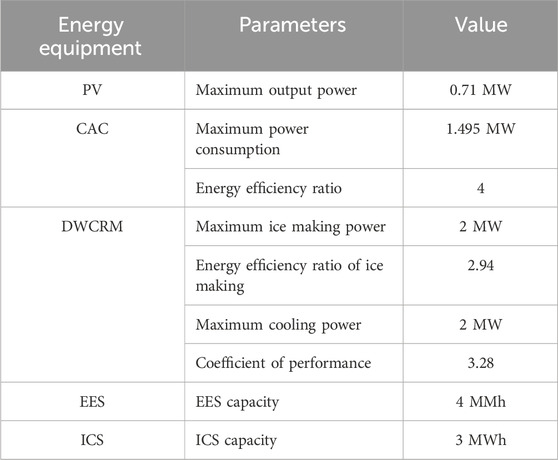
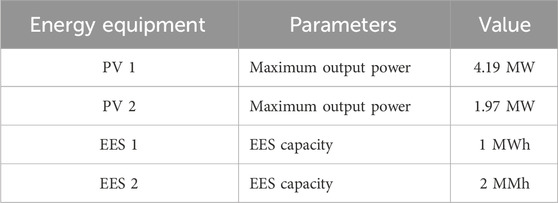
For user 1, IES includes central air conditioning (CAC), photovoltaics (PV), electric energy storage (EES), combined heat and power (CHP) and electrical loads (EL). For user 2, IES includes CAC, PV, EES, dual working condition refrigeration machine (DWCRM), ice cooling storge (ICS), interruptible cooling load (ICL), and EL. For user 3, IES includes PV, EES, interruptible electrical load (IEL) and EL.
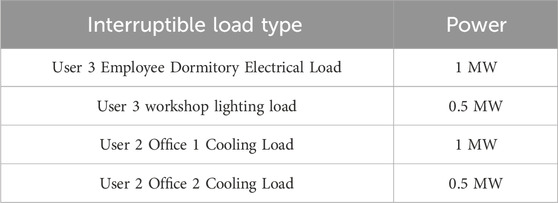
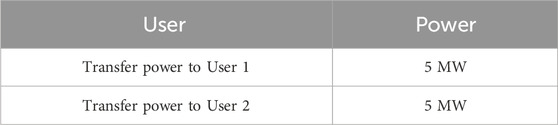
The interruptible load data of the industrial park is shown in Table 1. The upper limit of power transfer between users is shown in Table 2.
TABLE 1
| Interruptible load type | Power |
|---|---|
| User 3 Employee Dormitory Electrical Load | 1 MW |
| User 3 workshop lighting load | 0.5 MW |
| User 2 Office 1 Cooling Load | 1 MW |
| User 2 Office 2 Cooling Load | 0.5 MW |
User interruptible load.
TABLE 2
| User | Power |
|---|---|
| Transfer power to User 1 | 5 MW |
| Transfer power to User 2 | 5 MW |
User interruptible load.
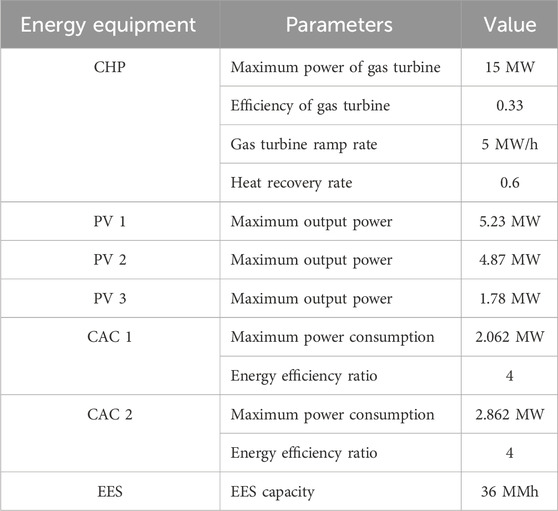
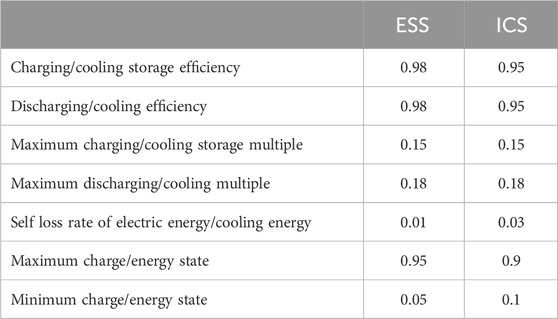
The configuration details of energy equipment for the three users are shown in Tables 3–5 respectively. The relevant parameters of energy storage equipment are shown in Table 6.
TABLE 3
| Energy equipment | Parameters | Value |
|---|---|---|
| CHP | Maximum power of gas turbine | 15 MW |
| Efficiency of gas turbine | 0.33 | |
| Gas turbine ramp rate | 5 MW/h | |
| Heat recovery rate | 0.6 | |
| PV 1 | Maximum output power | 5.23 MW |
| PV 2 | Maximum output power | 4.87 MW |
| PV 3 | Maximum output power | 1.78 MW |
| CAC 1 | Maximum power consumption | 2.062 MW |
| Energy efficiency ratio | 4 | |
| CAC 2 | Maximum power consumption | 2.862 MW |
| Energy efficiency ratio | 4 | |
| EES | EES capacity | 36 MMh |
Configuration of energy equipment of typical user 1.
TABLE 4
| Energy equipment | Parameters | Value |
|---|---|---|
| PV | Maximum output power | 0.71 MW |
| CAC | Maximum power consumption | 1.495 MW |
| Energy efficiency ratio | 4 | |
| DWCRM | Maximum ice making power | 2 MW |
| Energy efficiency ratio of ice making | 2.94 | |
| Maximum cooling power | 2 MW | |
| Coefficient of performance | 3.28 | |
| EES | EES capacity | 4 MMh |
| ICS | ICS capacity | 3 MWh |
Configuration of energy equipment of typical user 2.
TABLE 5
| Energy equipment | Parameters | Value |
|---|---|---|
| PV 1 | Maximum output power | 4.19 MW |
| PV 2 | Maximum output power | 1.97 MW |
| EES 1 | EES capacity | 1 MWh |
| EES 2 | EES capacity | 2 MMh |
Configuration of energy equipment of typical user 3.
TABLE 6
| ESS | ICS | |
|---|---|---|
| Charging/cooling storage efficiency | 0.98 | 0.95 |
| Discharging/cooling efficiency | 0.98 | 0.95 |
| Maximum charging/cooling storage multiple | 0.15 | 0.15 |
| Maximum discharging/cooling multiple | 0.18 | 0.18 |
| Self loss rate of electric energy/cooling energy | 0.01 | 0.03 |
| Maximum charge/energy state | 0.95 | 0.9 |
| Minimum charge/energy state | 0.05 | 0.1 |
Relevant parameters of energy storage equipment.
4.1 Scenario 1
In this scenario, User 1’s partial photovoltaic system experiences a sudden malfunction and requires off grid maintenance. If there is a shortage of energy supply for User 1, the first choice is to increase the output of User 1’s own energy equipment to solve it.
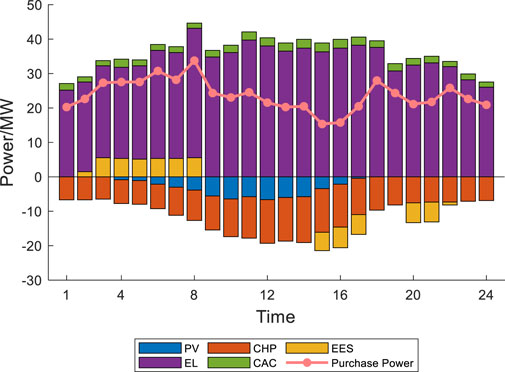
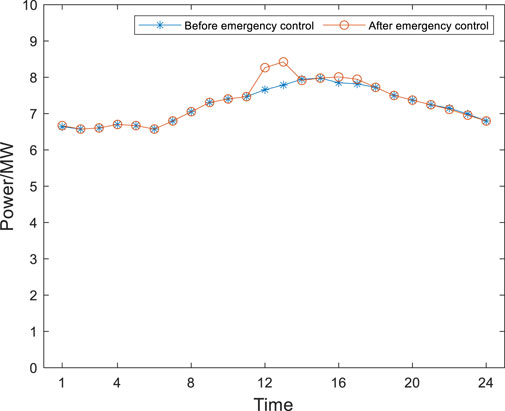
Through the distributed emergency control calculation of the comprehensive energy system in the park, the emergency control result of User 1 is shown in Figure 4, and the operating status of User 1’s CHP unit before and after emergency control is shown in Figure 5.
FIGURE 4
FIGURE 5
According to the analysis of the optimization scheduling results for User 1, it can be concluded that the CHP unit increases its power generation from 6:00 to 19:00, and the output of the CHP unit does not exceed the maximum power generation and ramp up power. Therefore, when conducting PV maintenance, User 1’s own CHP can increase the power supply to meet the energy shortage caused by PV maintenance. For the purchased electricity, it is the same before and after emergency control.
4.2 Scenario 2
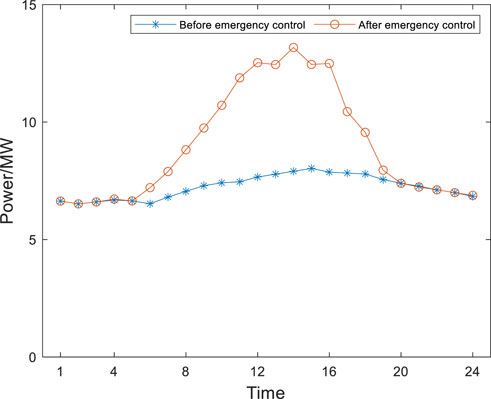
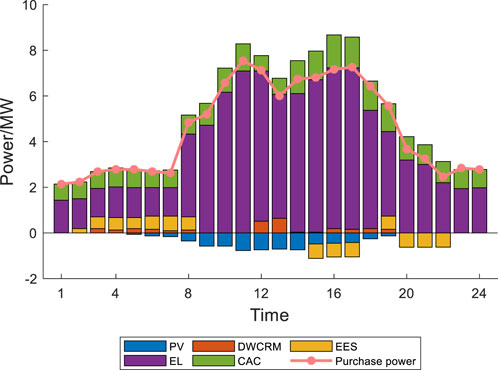
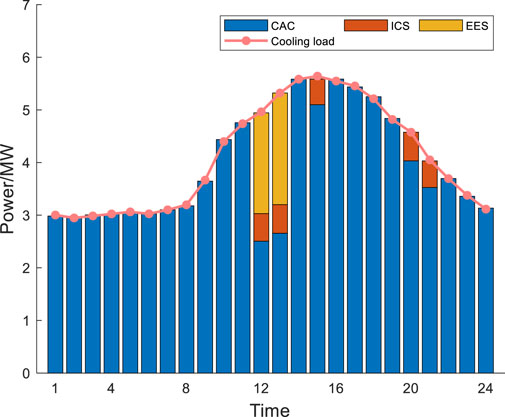
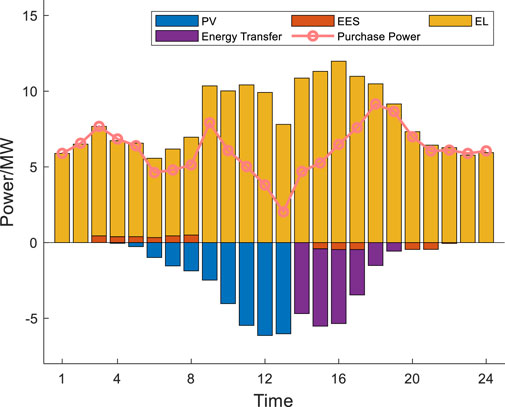
In this scenario, User 2’s CAC malfunctioned, resulting in a 50% reduction during the 12:00–13:00. If there is a shortage of cooling supply for User 2, the first consideration is to control User 2’s own energy equipment. If the shortage cannot be fully compensated by User 2 themselves, IES should transfer energy from User 1. If it is still not met, consider cutting off the interruptible cooling load. Through the distributed emergency control calculation of IES, the emergency control results of User 2 are shown in Figures 6, 7. The operating status of ICS before and after emergency control is shown in Figure 8, and the operating status of User 1’s CHP unit before and after emergency control is shown in Figure 9.
FIGURE 6
FIGURE 7
FIGURE 8
FIGURE 9
The cooling shortage caused by the malfunction of CAC between 12:00–13:00 is jointly provided by ICS and DWCRM. The ICS equipment releases cooling to compensate the cooling shortage during the period of 12:00–13:00. However, the maximum cooling power of the ICS during 12:00–13:00 cannot meet the cooling shortage. There-fore, the DWCRM is applied to compensate the remaining energy shortage. The electric power consumed by DWCRM is provided by the CHP of user 1. During the period of 16:00–17:00, the output of ICS cannot meet the cooling load, the CAC will increase its output to meet the cooling load. The increased power consumption of the CAC during this period will be provided by the CHP unit of user 1. The cooling shortage generated by User 2 can be compensated by User 2’s own energy equipment and the energy transferred by User 1. By the application of the proposed strategy, the cooling load can not be reduced.
4.3 Scenario 3
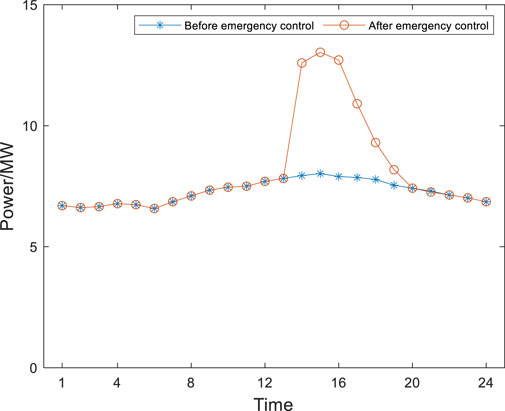
In this scenario, User 3’s PV malfunctioned. The PV output decrease to zero between 14:00–24:00. Through the proposed distributed emergency control method of the IES the emergency control results of user 3 are shown in Figure 10. The operating status of user 1’s CHP unit before and after emergency control is shown in Figure 11. And the interruptible power load cut off by user 3 is shown in Figure 12.
FIGURE 10
FIGURE 11
FIGURE 12
Due to PV failure, user 3 has a significant power shortage. Even if user 1’s CHP transfers electricity at maximum transfer power during the 14:00–16:00 period, it cannot meet user 3’s power shortage. By the application of the proposed emergency control method for user 3, the interruptible load of user 3 is cut off to ensure the power supply of important equipment for user 3. From 14:00 to 19:00, the CHP of User 1 will transfer power to User 3. And during 14:00. The employee dormitory interruptible load and the workshop lighting interruptible load will be cut off by 1.5 MW. From 15:00 to 16:00, the workshop lighting interruptible load will be cut off by 0.5 MW.
5 Conclusion
In this paper, a distributed emergency control method for IES of the industrial park based on the alternating direction multiplier method is proposed. The optimization objective function of the distributed emergency control method increases the cost of interruptible load loss and energy transfer between users. The interruptible load power and energy transfer power between users is considered. By the application of the alternating direction multiplier method, the emergency control problem is decomposed into two transfer sub problems. By solving the two transfer sub problems separately, the emergency control strategy is obtained. By analyzing three typical energy equipment failure scenarios, the proposed emergency control method is verified.
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
WL: Data curation, Formal Analysis, Methodology, Software, Writing–original draft, Writing–review and editing. LJ: Methodology, Project administration, Writing–original draft, Writing–review and editing. BX: Writing–original draft, Writing–review and editing. RL: Writing–original draft, Writing–review and editing. YH: Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
Authors WL, LJ, BX, and RL were employed by Guangdong Power Grid Energy Investment Co., Ltd. Author YH was employed by Chaozhou Power Supply Bureau of Guangdong Power Grid Co., Ltd.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
ChenD.CuiQ.RenP. (2024). Integrated energy system planning for a heavy equipment manufacturing industrial park. Front. Energy Res.12, 1448362. 10.3389/fenrg.2024.1448362
2
ChengY.ZhangN.ZhangB.KangC.XiW.FengM. (2019). Low-carbon operation of multiple energy systems based on energy-carbon integrated prices. IEEE Trans. Smart Grid11 (2), 1307–1318. 10.1109/tsg.2019.2935736
3
GuelpaE.VerdaV. (2018). Model for optimal malfunction management in extended district heating networks. Appl. energy230, 519–530. 10.1016/j.apenergy.2018.08.024
4
JintaoC.YangP. (2019). “Optimized operation of multi-energy system in the industrial park based on integrated demand response strategy,” in 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11-14 August 2019 (IEEE).
5
JuanweiC.TaoY.YueX.XiaohuaC.BoY.BaominZ. (2019). Fast analytical method for reliability evaluation of electricity-gas integrated energy system considering dispatch strategies. Appl. Energy242, 260–272. 10.1016/j.apenergy.2019.03.106
6
KaisongD.HuD.-G.LiS.MaX.CuiY.CuiQ.et al (2021). “Research on planning and operation of distributed integrated energy system in industrial park,” in 2021 China International Conference on Electricity Distribution (CICED), Shanghai, China, 07-09 April 2021 (IEEE).
7
LeiY.HouK.WangY.JiaH.ZhangP.MuY.et al (2018). A new reliability assessment approach for integrated energy systems: using hierarchical decoupling optimization framework and impact-increment based state enumeration method. Appl. Energy210, 1237–1250. 10.1016/j.apenergy.2017.08.099
8
LiG.BieZ.KouY.JiangJ.BettinelliM. (2016). Reliability evaluation of integrated energy systems based on smart agent communication. Appl. energy167, 397–406. 10.1016/j.apenergy.2015.11.033
9
LiP.WangZ.WangN.YangW.LiM.ZhouX.et al (2021). Stochastic robust optimal operation of community integrated energy system based on integrated demand response. Int. J. Electr. Power and Energy Syst.128, 106735. 10.1016/j.ijepes.2020.106735
10
LiY.WangB.YangZ.LiJ.ChenC. (2022). Hierarchical stochastic scheduling of multi-community integrated energy systems in uncertain environments via Stackelberg game. Appl. Energy308, 118392. 10.1016/j.apenergy.2021.118392
11
LiY.WangB.YangZ.LiJ.LiG. (2021b). Optimal scheduling of integrated demand response-enabled community-integrated energy systems in uncertain environments. IEEE Trans. Industry Appl.58 (2), 2640–2651. 10.1109/tia.2021.3106573
12
LiY.WangC.LiG.ChenC. (2021a). Optimal scheduling of integrated demand response-enabled integrated energy systems with uncertain renewable generations: a Stackelberg game approach. Energy Convers. Manag.235, 113996. 10.1016/j.enconman.2021.113996
13
MarziE.MoriniM.SalettiC.VourosS.ZaccariaV.KyprianidisK.et al (2023). Power-to-Gas for energy system flexibility under uncertainty in demand, production and price. Energy284, 129212. 10.1016/j.energy.2023.129212
14
SaxenaA.ChandelA.DashA. K.GuptaS. K.Kumar VS.PandeyJ. P. (2023). An effective optimal economic sustainable clean energy solution with reduced carbon capturing/carbon utilization/carbon footprint for grid integrated hybrid system. IEEE Trans. Sustain. Comput.8 (3), 385–399. 10.1109/tsusc.2023.3262982
15
SunJ.RuzeN.ZhangJ.ShiJ.ShenB. (2021). Capacity planning and optimization for integrated energy system in industrial park considering environmental externalities. Renew. Energy167, 56–65. 10.1016/j.renene.2020.11.045
16
WangY.LiuZ.CaiC.XueL.MaY.ShenH.et al (2022). Research on the optimization method of integrated energy system operation with multi-subject game. Energy245, 123305. 10.1016/j.energy.2022.123305
17
XuanA.ShenX.GuoQ.SunH. (2022). Two-stage planning for electricity-gas coupled integrated energy system with carbon capture, utilization, and storage considering carbon tax and price uncertainties. IEEE Trans. Power Syst.38 (3), 2553–2565. 10.1109/tpwrs.2022.3189273
18
YanR.WangJ.HuoS.QinY.ZhangJ.TangS.et al (2023). Flexibility improvement and stochastic multi-scenario hybrid optimization for an integrated energy system with high-proportion renewable energy. Energy263, 125779. 10.1016/j.energy.2022.125779
19
ZhouJ.WuY.ZhongZ.XuC.KeY.GaoJ. (2021). Modeling and configuration optimization of the natural gas-wind-photovoltaic-hydrogen integrated energy system: a novel deviation satisfaction strategy. Energy Convers. Manag.243, 114340. 10.1016/j.enconman.2021.114340
Summary
Keywords
integrated energy systems, emergency control, alternating direction multiplier method, distributed optimization scheduling, energy transfer
Citation
Li W, Jia L, Xu B, Lu R and Huang Y (2025) Distributed emergency control method for integrated energy system in industrial park based on alternating direction multiplier method. Front. Energy Res. 12:1534825. doi: 10.3389/fenrg.2024.1534825
Received
26 November 2024
Accepted
19 December 2024
Published
10 January 2025
Volume
12 - 2024
Edited by
Haifeng Qiu, Nanyang Technological University, Singapore
Reviewed by
Yuanyuan Chai, Hebei University of Technology, China
Qi Liu, Shandong University of Science and Technology, China
Haotian Ge, Hainan Normal University, China
Updates
Copyright
© 2025 Li, Jia, Xu, Lu and Huang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wenbin Li, leewenbin2024@163.com
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.