An evaluation method for power supply guarantee capability of multi-city interconnected power system based on security region

In the context of global climate change, the multi-city interconnected power system offers the potential for low-carbon and efficient energy utilization, addressing the challenge of ensuring safety, stability, and reduced carbon emissions while meeting diverse demands. This study proposes a security region-based method to evaluate the power supply guarantee capability of such systems, employing a collaborative support framework to characterize the low-carbon feasible space of each city system. A multi-dimensional piecewise linear approximation method and model transformation were applied to construct a scheduling and transformation model for the provincial power grid. The proposed approach enhances power supply security, achieving a 7.21% reduction in system operating costs and a 24.7% decrease in carbon emissions. These findings highlight the effectiveness of the security region approach in balancing safety, efficiency, and environmental objectives, providing a scalable solution for interconnected power grids.

1 Introduction

In recent years, the global renewable energy industry has witnessed remarkable growth, with a significant increase in the share of renewable energy in power systems (Al-Shetwi, 2022; Hassan et al., 2024). Following this trend, China’s renewable energy sector has also developed rapidly, with the proportion of renewable energy generation in its power system steadily rising (Zhang et al., 2017; Li et al., 2023). However, the high integration of renewables presents significant challenges for the safe and stable operation of the power system, making the issue of power supply assurance increasingly prominent (Ourahou et al., 2020). During the “13th Five-Year Plan” period, China’s renewable energy capacity grew by over 70 million kilowatts annually, and it is projected that during the “14th Five-Year Plan,” the average annual addition will exceed 100 million kilowatts, indicating a trend of exponential growth (Bensadi, 2024). By 2030, the installed capacity of wind, solar, and other renewable sources in China is expected to surpass that of coal power, making renewable energy the largest power source (He et al., 2023; Tian et al., 2023). Furthermore, by 2060, the share of renewable energy in power generation is anticipated to exceed 50%, positioning it as the primary energy supply source (Li et al., 2024). As the share of renewable energy continues to increase, the volatility and uncertainty of the power system grow, setting higher requirements for the system’s power supply capability (Baraa and El, 2024). To address this challenge, a multi-city interconnected power system has demonstrated significant potential for achieving the reliability of power supply and more efficient energy utilization.

In multi-city interconnected power systems, ensuring the reliability of power supply is essential for maintaining stable electricity provision across cities. Existing research on power supply guarantee capability primarily emphasizes network structure optimization (Miao et al., 2018; Li et al., 2022; Su et al., 2023) and emergency power solutions (Jiang et al., 2019; Han et al., 2021; Zhang et al., 2021; Wang et al., 2022; Yan et al., 2024), relying on conventional analytical methods to uphold system stability. For network structure optimization (Miao et al., 2018), investigated optimizing output capacity in large-scale power grids to enhance system security, proposing various interconnection schemes and evaluating their impacts on power transmission and transfer capacity. Regarding emergency power Jiang et al. (2019), analyzed the feasibility and benefits of replacing traditional diesel generators with electric emergency power vehicles, highlighting their technical, environmental, and economic advantages during outages. Additionally Yan et al. (2024), explored the integration of stationary and mobile energy storage systems to improve urban emergency power supply, focusing on strategies to bolster grid stability, optimize resource allocation, and ensure reliable power during outages. However, as the interconnections between urban power grids continue to expand, these traditional approaches face significant limitations in addressing the evolving demands for power supply assurance. They fail to comprehensively identify potential security risks in multi-city power networks, particularly given the increasing integration of renewable energy, making it difficult to effectively manage the system’s stability and safety boundaries.

Against this background, the security region method has gained attention for its ability to define the safe operating boundaries of complex systems and dynamically adjust them to enhance the stable operation of urban power grids under different conditions (Yang and Yu, 2021). Compared with traditional methods, the security region approach constructs multi-dimensional security boundaries for system operations, enabling more accurate identification and quantification of security risks while allowing rapid response in emergencies, thus offering greater practicality and reliability. However, there has yet to be any application of the security region method in the study of power supply guarantee capability for urban power grids. Therefore, this paper proposes a security region-based method to evaluate the power supply guarantee capability of multi-city interconnected power systems. By building a security region model, this method effectively integrates low-carbon operational objectives with low-carbon resources from collaborative multi-city support, achieving a more comprehensive assessment and optimization of power supply capability and advancing the green, low-carbon development of interconnected urban power systems.

In summary, despite the significant potential of multi-city interconnected power systems, ensuring power supply safety and stability while meeting diverse urban energy demands remains a critical challenge. This issue is compounded by the growing integration of renewable energy sources, which introduces uncertainties that traditional methods struggle to address effectively. To address the above issues, this paper proposes an Integrated Electricity-Hydrogen-Gas System (IEHGS) scheduling model based on security region theory, considering the collaborative support among multiple city systems. This model effectively utilizes the low-carbon resources of city systems to enhance the low-carbon operation of the IEHGS. The contributions of this work are:

1. A framework is established based on security regions, considering the collaborative support among multiple city systems. The security region is used to describe the low-carbon feasible space of each city system, taking into account the collaborative support provided by multiple city systems for the low-carbon operation of the provincial grid’s IEHGS. This framework employs regional methods to model the low-carbon flexible operation constraints of city systems, enabling the exploration of low-carbon resources within the city systems.

2. A low-carbon operation method for the IEHGS, considering the collaborative support of multiple city systems, is proposed. Using the distributed robust chance-constrained method and multi-dimensional piecewise linear approximation, the low-carbon feasible space of city systems is analyzed, and a scheduling model for the IEHGS that incorporates the collaborative support of multiple city systems is constructed. A model transformation method is also proposed. The heterogeneous energy auxiliary conversion and clean energy supply provided by the city systems are fully utilized, enhancing the low-carbon performance of the IEHGS.

The rest of the paper is organized as follows: Section 2 introduces the collaborative support among multiple city systems described using security regions. Section 3 discusses the provincial grid scheduling considering the collaborative support of multiple city systems. Section 4 presents case studies. Finally, Section 5 provides the conclusions.

2 Characterizing the collaborative support of multi-city systems based on security regions

The development of city-side power systems can provide support for the low-carbon operation of the provincial grid IEHGS, including carbon emission rights, multi-energy resources, flexibility, and various carbon reduction technologies. In this section, based on security region theory, the region method is employed to represent the support of city systems as a low-carbon feasible space, quantifying the support capacity of city systems to facilitate the low-carbon operation of the IEHGS.

2.1 Framework for considering the support of city systems based on security regions

Figure 1 illustrates the basic framework based on security regions, considering the collaborative support of multiple city systems. It is specifically divided into two parts: characterizing the low-carbon feasible space of each city system based on security regions, and the IEHGS scheduling model that accounts for the collaborative support of multiple city systems. Details are provided as follows:

Figure 1

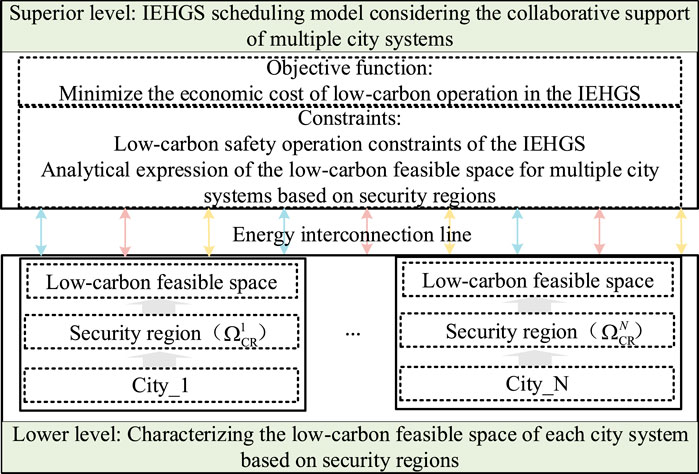
Figure 1. IEHGS scheduling framework considering the collaborative support of multiple city systems.

2.1.1 Characterizing the low-carbon feasible space of each city system based on security regions

Each city system first constructs a security region based on its own low-carbon flexible operation characteristics, renewable energy uncertainties, and carbon emission quotas, as shown in Equation 1. The security region envelope is used to characterize the support provided by city systems for the low-carbon operation of the provincial grid IEHGS, representing it as the low-carbon feasible space of each city system. Then, by projecting the heterogeneous energy interconnection line coupling the city system and the provincial grid IEHGS, the low-carbon feasible space of each city system is visualized and analytically represented, thereby achieving the transfer of the city system’s support to the provincial grid IEHGS.

${\mathrm{\Omega }}_{\text{CR}}^k=\left\{{\mathit{W}}_k\left|H_1\left({\mathit{W}}_k\right)\le 0,H_2\left({\mathit{W}}_k\right)\le E_k^{\text{car}\_\text{cap}}\right.\right\},k=1,2,\dots ,K(1)$

Where ${\mathrm{\Omega }}_{\text{CR}}^k$ represents the security region of the k-th city system; K is the number of city systems; $W_k={\left[w^{1k},w^{2k},\dots ,w^{Nk}\right]}^T$, where $w^{xk}$ denotes the energy interaction of the x-th interconnection line of the k-th city system. N_k is the number of interconnection lines coupling the k-th city system with the provincial grid IEHGS. H₁(W_k) ≤ 0 represents the simplified expression for the low-carbon safety operation constraints of the k-th city system, incorporating renewable energy uncertainties and low-carbon flexible operation characteristics. $H_2\left({\mathit{W}}_k\right)\le E_k^{\text{car}\_\text{cap}}$ is the simplified expression for the carbon emission constraints of the k-th city system.

2.1.2 IEHGS scheduling model considering the collaborative support of multiple city systems

Considering the analytical expressions of each city system’s low-carbon feasible space, an IEHGS scheduling model for the provincial grid is constructed, aggregating and coordinating the low-carbon feasible space sent by each city system. This approach leverages the support from individual city systems while also utilizing the collaborative support among multiple city systems. Based on this foundation, the model further incorporates the provincial grid IEHGS’s own low-carbon safety operation constraints and renewable energy uncertainties to create an operational scheduling model.

2.2 Security region model of city systems

To fully utilize energy, city systems are coupled with distributed renewable energy sources, combined heat and power units and micro gas turbines fueled by Hydrogen Enriched Compressed Natural Gas (HCNG), grid-connected electric vehicles, and various types of energy storage devices. Considering the low-carbon operation constraints and renewable energy uncertainties of city systems, a security region model is constructed to effectively quantify the low-carbon feasible space of city systems.

2.2.1 Power system balance constraints

$P_{t.k}^{\text{ELE}.\mathrm{L}}+P_{\text{ELE}.t.k}^{\text{LINE}}=E_{\text{ELE}.t.k}^{\text{Storage}}+P_{t.k}^{\text{CHP}}+P_{t.k}^{\text{HFC}}+P_{t.k}^{\text{MGT}}+P_{t.k}^{\mathrm{H}2\text{MG}}+P_{t.k}^{\text{RDG}}+{\xi }_{t.k}^{\text{RDG}}(2)$

Where t = 1, 2, … , T represents the scheduling periods. $P_{t.k}^{\text{ELE}.\mathrm{L}}$ denotes the load of the power system, $P_{t.k}^{\text{CHP}}$ is the electric power of the combined heat and power unit, and $P_{t.k}^{\text{HFC}}$ represents the power of the fuel cell. $P_{t.k}^{\text{RDG}}$ and ${\xi }_{t.k}^{\text{RDG}}$ are the predicted renewable energy output and the prediction error, respectively. $P_{t.k}^{\text{MGT}}$ and $P_{t.k}^{\mathrm{H}2\text{MG}}$ indicate the power of the micro gas turbine and the power from the grid-connected electric vehicle mode, respectively. $E_{\text{ELE}.t.k}^{\text{Storage}}$ represents the charging and discharging of electric storage in Equation 2, while $P_{\text{ELE}.t.k}^{\text{LINE}}$ denotes the energy interaction of the electrical interconnection line.

2.2.2 Energy storage device operation constraints

The operation constraints of energy storage are modeled uniformly by Equations 3–6. Among them, Equation 3 limits the storage capacity of the energy storage; Equation 4 prevents the charging and discharging of the storage from exceeding the rated values; Equation 5 ensures that the storage capacity at the beginning and end of the scheduling period remains unchanged; and Equation 6 represents the energy balance constraint of the energy storage.

$Q_{\text{ELE}/\text{Hy}/\text{NG}/\text{He}.k}^{\text{Storage}.\min }\le Q_{\text{ELE}/\text{Hy}/\text{NG}/\text{He}.t.k}^{\text{Storage}}\le Q_{\text{ELE}/\text{Hy}/\text{NG}/\text{He}.k}^{\text{Storage}.\max }(3)$

$-E_{\text{ELE}/\text{Hy}/\text{NG}/\text{He}.k}^{\text{Storage}.\max }\le E_{\text{ELE}/\text{Hy}/\text{NG}/\text{He}.t.k}^{\text{Storage}}\le E_{\text{ELE}/\text{Hy}/\text{NG}/\text{He}.k}^{\text{Storage}.\max }(4)$

$Q_{\text{ELE}/\text{Hy}/\text{NG}/\text{He}.T.k}^{\text{Storage}}=Q_{\text{ELE}/\text{Hy}/\text{NG}/\text{He}.0.k}^{\text{Storage}}(5)$

$Q_{\text{ELE}/\text{Hy}/\text{NG}/\text{He}.t.k}^{\text{Storage}}=Q_{\text{ELE}/\text{Hy}/\text{NG}/\text{He}.t-1.k}^{\text{Storage}}+E_{\text{ELE}/\text{Hy}/\text{NG}/\text{He}.t.k}^{\text{Storage}}(6)$

Where $Q_{ELE/Hy/NG/He.t.k}^{Storage}$ represents the storage capacity of the energy storage, $Q_{ELE/Hy/NG/He.k}^{Storage.\mathit{max}}$ and $Q_{ELE/Hy/NG/He.k}^{Storage.\mathit{min}}$ are the upper and lower capacity limits, respectively, and $E_{ELE/Hy/NG/He.k}^{Storage.\mathit{max}}$ is the maximum charging and discharging rate. $Q_{ELE/Hy/NG/He.0.k}^{Storage}$ and $Q_{ELE/Hy/NG/He.T.k}^{Storage}$ denote the storage capacities at the beginning and end of the scheduling period.

2.2.3 Grid-connected operation constraints of electric vehicles

The grid-connected operation mode of electric vehicles allows the onboard battery to generate power and feedback energy to the system through the discharger. This can be modeled by Equation 7, and Equation 8 constrains the electric power from the grid-connected electric vehicles to be less than the rated capacity of the discharger.

$P_{t.k}^{\mathrm{H}2\text{MG}}={\text{GHV}}_{\text{Hy}}{F}_{t.k}^{\mathrm{H}2\text{MG}}{\eta }_{\text{ELE}}^{\mathrm{H}2\text{MG}}(7)$

$0\le P_{t.k}^{\mathrm{H}2\text{MG}}\le P_{\text{nom}.k}^{\mathrm{H}2\text{MG}}(8)$

Where ${\eta }_{ELE}^{H2MG}$ represents the hydrogen-electric conversion efficiency of the H2MG mode, and $P_{\text{nom}.k}^{\mathrm{H}2\text{MG}}$ is the rated capacity of the discharger.

2.2.4 Interconnection line power exchange constraints

$P_{\text{ELE}.\min .k}^{\text{LINE}}\le P_{\text{ELE}.t.k}^{\text{LINE}}\le P_{\text{ELE}.\max .k}^{\text{LINE}}(9)$

Where $P_{\text{ELE}.\min .k}^{\text{LINE}}$ and $P_{\text{ELE}.\max .k}^{\text{LINE}}$ are the upper and lower limits of the electrical power exchanged between city systems.

2.2.5 Carbon emission constraints

$E_k^{\text{Car}\_\text{emi}}\le E_k^{\text{Car}\_\text{quota}}(10)$

Where $E_k^{\text{Car}\_\text{emi}}$ and $E_k^{\text{Car}\_\text{quota}}$ represent the total carbon emissions and the carbon emission quota of the city system, respectively.

Thus, the security region model of the k-th city system can be expressed as shown in Equation 11:

${\mathrm{\Omega }}_{\text{CR}}^k=\left\{{\mathit{W}}_k\left|\text{equations}\left(2\right)-\left(10\right)\right.\right\}(11)$

2.3 Analytical representation of the low-carbon feasible space of city systems

The security region model constructed above contains random variables, making it an uncertainty model that is difficult to solve directly. This section uses the distribution-ally robust chance-constrained method to handle the model, transforming the original uncertain security region model into a deterministic one. On this basis, based on the boundary points of the security region, the low-carbon feasible space of the city system is analytically represented using a multi-dimensional piecewise linear approximation method.

2.3.1 Deterministic conversion of the uncertain security region model

${\mathrm{\Omega }}_{\text{CR}}^k=\left\{{\mathit{W}}_k\left|\begin{array}{l}{\mathit{A}}_k{\mathit{X}}_k+{\mathit{B}}_k{\mathit{Y}}_k+{\mathit{C}}_k+{\mathit{M}}_k{\mathit{W}}_k\le 0\\ {\mathrm{Pr}}_{\sim p_k}\left\{P_{t.k}^{\mathrm{D}}\le P_{t.k}^{\text{RDG}}+{\xi }_{t.k}^{\text{RDG}}\right\}\ge 1-{\beta }_k\end{array}\right.\right\},P_k\in {\mathbb{R}}_k(12)$

Where ${\mathit{A}}_k{\mathit{X}}_k+{\mathit{B}}_k{\mathit{Y}}_k+{\mathit{C}}_k+{\mathit{M}}_k{\mathit{W}}_k\le 0$ represents the unified expression for the deterministic constraints in Equations 3–10. ${\mathit{X}}_k$ and ${\mathit{Y}}_k$ are the matrices of continuous and discrete decision variables, respectively, while A_k, B_k, C_k, and M_k are the corresponding coefficient matrices. P_k is the probability distribution function of ${\xi }_{t.k}^{\text{RDG}}$; ${\mathbb{R}}_k$ is the fuzzy set of P_k; 1-β_k is the confidence level; and $P_{t.k}^{\mathrm{D}}$ is an auxiliary variable, which can be expressed as:

$P_{t.k}^{\text{ELE}.\mathrm{L}}+P_{t.k}^{\mathrm{P}2\mathrm{G}}+P_{\text{ELE}.t.k}^{\text{LINE}}-E_{\text{ELE}.t.k}^{\text{Storage}}-P_{t.k}^{\text{CHP}}-P_{t.k}^{\text{HFC}}-P_{t.k}^{\text{GT}}-P_{t.k}^{\mathrm{H}2\text{MG}}=P_{t.k}^{\mathrm{D}}(13)$

Equation 13 ensures that ${\mathrm{\Omega }}_{\text{CR}}^k$ holds with a probability of at least $1-{\beta }_k$ under the worst-case probability distribution ${\mathbb{R}}_k$.

Based on the fuzzy chance-constrained security region model transformation method and the chance-constrained security region model transformation method, ${\mathrm{\Omega }}_{\text{CR}}^k$ in Equation 12 can be converted into the following deterministic security region model as shown in Equation 14:

${\mathrm{\Omega }}_{\text{CR}}^k=\left\{{\mathit{W}}_k\left|\begin{array}{l}{\mathit{A}}_k{\mathit{X}}_k+{\mathit{B}}_k{\mathit{Y}}_k+{\mathit{C}}_k+{\mathit{M}}_k{\mathit{W}}_k\le 0\\ P_{t.k}^{\mathrm{D}}-P_{t.k}^{\text{RDG}}-{\mu }_{t.k}^{\text{RDG}}+{\sigma }_{t.k}^{\text{RDG}}\sqrt{-2\text{In}{\overline{\beta }}_k}\le 0\end{array}\right.\right\}(14)$

Where ${\mu }_{t.k}^{\text{RDG}}$ and ${\sigma }_{t.k}^{\text{RDG}}$ represent the mean and standard deviation of the reference distribution within the fuzzy set, and ${\beta }_k$ is the reconstructed risk parameter.

2.3.2 Analytical expression of the low-carbon feasible space

Illustrates the principle of the analytical expression of the low-carbon feasible space using two-dimensional and three-dimensional security regions.

2.3.2.1 Two-dimensional

Firstly, the two-dimensional security region is calculated based on the security region solving method from reference (Ren et al., 2023). As shown in Figure 2A, the boundary points in Figure 2A are then used to construct the analytical expression of the boundary of the two-dimensional security region through the two-dimensional piecewise linear approximation method, as follows:

$\left\{\begin{array}{l}{\overline{S}}_1:{\overline{a}}_1{P}_i+{\overline{b}}_1{H}_j+{\overline{c}}_1=0\\ {\overline{S}}_2:{\overline{a}}_2{P}_i+{\overline{b}}_2{H}_j+{\overline{c}}_2=0\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ {\overline{S}}_n:{\overline{a}}_n{P}_i+{\overline{b}}_n{H}_j+{\overline{c}}_n=0\end{array}\right.(15)$

Where ${\overline{S}}_1$, ${\overline{S}}_2$, …, ${\overline{S}}_n$ are the segments of the boundary fitted from the boundary points of the security region, and n is the number of boundaries. $P_i$ and $H_j$ represent the energy exchange of electrical and hydrogen interconnections, respectively. ${\overline{a}}_1$, ${\overline{a}}_2$, …, ${\overline{a}}_n$ and ${\overline{b}}_1$, ${\overline{b}}_2$, …, ${\overline{b}}_n$ are the coefficients corresponding to each boundary, while ${\overline{c}}_1$, ${\overline{c}}_2$, …, ${\overline{c}}_n$ are the constants corresponding to each boundary, which can be obtained by the following formula as shown in Equation 16:

$\left\{\begin{array}{l}{\overline{a}}_x={\overline{H}}_{x.1}^{\text{bound}}-{\overline{H}}_{x.2}^{\text{bound}}\\ {\overline{b}}_x={\overline{P}}_{x.2}^{\text{bound}}-{\overline{P}}_{x.1}^{\text{bound}}\\ {\overline{c}}_x=-{\overline{H}}_{x.2}^{\text{bound}}{\overline{b}}_x-{\overline{P}}_{x.2}^{\text{bound}}{\overline{a}}_x\end{array}\right.(16)$

Where ${\overline{P}}_{x.1}^{\text{bound}}$ and ${\overline{P}}_{x.2}^{\text{bound}}$ represent the electrical quantities corresponding to the two boundary points of the x-th boundary (denoted as ${\overline{S}}_x$), and ${\overline{H}}_{x.1}^{\text{bound}}$ and ${\overline{H}}_{x.2}^{\text{bound}}$ represent the hydrogen quantities corresponding to the two boundary points of the boundary ${\overline{S}}_x$.

Figure 2

Figure 2. Diagram of analytical representation for constructing low-carbon feasible space.

Finally, select any feasible point within the region, such as point O in Figure 2A, and substitute it into Equation 15 to determine the position of point O relative to ${\overline{S}}_1$, ${\overline{S}}_2$, …, ${\overline{S}}_n$. Then, transform the boundary’s analytical expressions into inequality constraints, thereby constructing the analytical expression of the two-dimensional low-carbon feasible space depicted by the safety region as shown in Equation 17:

$\left\{\begin{array}{l}{\stackrel{\sim }{a}}_1{P}_i+{\stackrel{\sim }{b}}_1{H}_j+{\stackrel{\sim }{c}}_1\ge 0\\ {\stackrel{\sim }{a}}_2{P}_i+{\stackrel{\sim }{b}}_2{H}_j+{\stackrel{\sim }{c}}_2\ge 0\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ {\stackrel{\sim }{a}}_n{P}_i+{\stackrel{\sim }{b}}_n{H}_j+{\stackrel{\sim }{c}}_n\ge 0\end{array}\right.(17)$

Where ${\stackrel{\sim }{a}}_1$, ${\stackrel{\sim }{a}}_2$, …, ${\stackrel{\sim }{a}}_n$, ${\stackrel{\sim }{b}}_1$, ${\stackrel{\sim }{b}}_2$, …, ${\stackrel{\sim }{b}}_n$, and ${\stackrel{\sim }{c}}_1$, ${\stackrel{\sim }{c}}_2$, …, ${\stackrel{\sim }{c}}_n$ are the coefficients and constants corresponding to the boundary’s analytical expressions after converting them into inequality constraints.

2.3.2.2 Three-dimensional

Similarly, the three-dimensional security region is calculated, as shown in Figure 2B. Then, based on the boundary points in Figure 2B, the three-dimensional piecewise linear approximation method is used to establish the analytical expression of the hyperplane for the three-dimensional security region as follows:

$\left\{\begin{array}{l}{\underset{¯}{S}}_1:{\underset{¯}{a}}_1{P}_i+{\underset{¯}{b}}_1{H}_j+{\underset{¯}{c}}_1{F}_z+{\underset{¯}{d}}_1=0\\ {\underset{¯}{S}}_2:{\underset{¯}{a}}_2{P}_i+{\underset{¯}{b}}_2{H}_j+{\underset{¯}{c}}_2{F}_z+{\underset{¯}{d}}_2=0\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ {\underset{¯}{S}}_n:{\underset{¯}{a}}_n{P}_i+{\underset{¯}{b}}_n{H}_j+{\underset{¯}{c}}_n{F}_z+{\underset{¯}{d}}_n=0\end{array}\right.(18)$

Where ${\underset{\_}{S}}_1$, ${\underset{\_}{S}}_2$, …, ${\underset{\_}{S}}_n$ represent the piecewise-fitted hyperplanes; P_i, H_j, and F_z denote the energy exchange quantities for electric, hydrogen, and gas interconnection lines, respectively. ${\underset{\_}{a}}_x$, ${\underset{\_}{b}}_x$, ${\underset{\_}{c}}_x$ and ${\underset{\_}{d}}_x$ are the coefficients and constant terms corresponding to the x-th hyperplane, where $x=1,2,\dots ,n$, and they can be obtained from the following formula as shown in Equation 19:

$\left\{\begin{array}{l}{\underset{¯}{a}}_x=\left({\underset{¯}{H}}_{x.2}^{\text{bound}}-{\underset{¯}{H}}_{x.1}^{\text{bound}}\right)\left({\underset{¯}{F}}_{x.3}^{\text{bound}}-{\underset{¯}{F}}_{x.1}^{\text{bound}}\right)-\left({\underset{¯}{H}}_{x.3}^{\text{bound}}-{\underset{¯}{H}}_{x.1}^{\text{bound}}\right)\left({\underset{¯}{F}}_{x.2}^{\text{bound}}-{\underset{¯}{F}}_{x.1}^{\text{bound}}\right)\\ {\underset{¯}{b}}_x=\left({\underset{¯}{F}}_{x.2}^{\text{bound}}-{\underset{¯}{F}}_{x.1}^{\text{bound}}\right)\left({\underset{¯}{P}}_{x.3}^{\text{bound}}-{\underset{¯}{P}}_{x.1}^{\text{bound}}\right)-\left({\underset{¯}{F}}_{x.3}^{\text{bound}}-{\underset{¯}{F}}_{x.1}^{\text{bound}}\right)\left({\underset{¯}{P}}_{x.2}^{\text{bound}}-{\underset{¯}{P}}_{x.1}^{\text{bound}}\right)\\ {\underset{¯}{c}}_x=\left({\underset{¯}{P}}_{x.2}^{\text{bound}}-{\underset{¯}{P}}_{x.1}^{\text{bound}}\right)\left({\underset{¯}{H}}_{x.3}^{\text{bound}}-{\underset{¯}{H}}_{x.1}^{\text{bound}}\right)-\left({\underset{¯}{P}}_{x.3}^{\text{bound}}-{\underset{¯}{P}}_{x.1}^{\text{bound}}\right)\left({\underset{¯}{H}}_{x.2}^{\text{bound}}-{\underset{¯}{H}}_{x.1}^{\text{bound}}\right)\\ {\underset{¯}{d}}_x=-{\underset{¯}{a}}_x{\underset{¯}{P}}_{x.1}^{\text{bound}}-{\underset{¯}{b}}_x{\underset{¯}{H}}_{x.1}^{\text{bound}}-{\underset{¯}{c}}_x{\underset{¯}{F}}_{x.1}^{\text{bound}}\end{array}\right.(19)$

Where ${\underset{¯}{P}}_{x.1}^{\text{bound}}$, ${\underset{¯}{P}}_{x.2}^{\text{bound}}$ and ${\underset{¯}{P}}_{x.3}^{\text{bound}}$ are the electric quantities corresponding to the three boundary points of the x-th hyperplane (denoted as ${\underset{\_}{S}}_x$); ${\underset{\_}{H}}_{x.1}^{\text{bound}}$, ${\underset{\_}{H}}_{x.2}^{\text{bound}}$ and ${\underset{\_}{H}}_{x.3}^{\text{bound}}$ represent the hydrogen quantities at these boundary points, and ${\underset{\_}{F}}_{x.1}^{\text{bound}}$, ${\underset{\_}{F}}_{x.2}^{\text{bound}}$ and ${\underset{\_}{F}}_{x.3}^{\text{bound}}$ represent the natural gas quantities at the same points.

Finally, select any feasible point within the region, such as point Θ in Figure 2B, and substitute it into the analytical expressions of each hyperplane in Equation 18. Based on the position of point Θ relative to ${\underset{\_}{S}}_1,{\underset{\_}{S}}_2,\dots ,{\underset{\_}{S}}_n$, convert each hyperplane’s analytical expression into inequality constraints to construct the analytical expression of the three-dimensional low-carbon feasible space depicted by the security region as shown in Equation 20:

$\left\{\begin{array}{l}{\underset{\sim }{a}}_1{P}_i+{\underset{\sim }{b}}_1{H}_j+{\underset{\sim }{c}}_1{F}_z+{\underset{\sim }{d}}_1\ge 0\\ {\underset{\sim }{a}}_2{P}_i+{\underset{\sim }{b}}_2{H}_j+{\underset{\sim }{c}}_2{F}_z+{\underset{\sim }{d}}_2\ge 0\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ {\underset{\sim }{a}}_n{P}_i+{\underset{\sim }{b}}_n{H}_j+{\underset{\sim }{c}}_n{F}_z+{\underset{\sim }{d}}_n\ge 0\end{array}\right.(20)$

Where ${\underset{\sim }{a}}_x$, ${\underset{\sim }{b}}_x$, ${\underset{\sim }{c}}_x$, and ${\underset{\sim }{d}}_x$ are the coefficients and constant terms of the analytical expression for the low-carbon feasible space. Similar to the two-dimensional low-carbon feasible space analytical expression, these can be obtained by converting the analytical expression of the x-th hyperplane in Equation 18 into inequalities.

3 Provincial power grid dispatch considering multi-city system collaborative support

Based on the analytically derived low-carbon feasible space of urban systems using security regions, a provincial power grid IEHGS dispatch model is developed. Additionally, a transformation strategy for the proposed model is presented, utilizing distributionally robust chance constraints and linear transformation methods. This approach effectively leverages the collaborative support of multiple urban systems, enhancing the low-carbon operation level of the IEHGS.

3.1 Objective function

The model aims to minimize the total operating cost C of the provincial power grid IEHGS. The total cost C includes: the handling cost of renewable energy uncertainty $C_{\text{Uncer}}^{\text{deal}}$, electricity purchase cost $C_{\text{Power}}^{\text{buy}}$, compensation cost for city system support $C_{\text{LCFS}}^{\text{supp}}$, and carbon emission cost $C_{\text{CO}2}^{\text{emi}}$. The details are as follows:

$\min C=C_{\text{Uncer}}^{\text{deal}}+C_{\text{Power}}^{\text{buy}}+C_{\text{LCFS}}^{\text{supp}}+C_{\text{CO}2}^{\text{emi}}(21)$

Where each cost can be calculated using Equations 21–25.

$C_{\text{Uncer}}^{\text{deal}}={\displaystyle \sum _{t\in {\mathrm{\Omega }}_{\mathrm{T}}}}{\displaystyle \sum _{m\in {\mathrm{\Omega }}_{\text{GS}}}}\left(a_{\text{GS}}^{\mathrm{U}}{F}_{m.t}^{\text{GS}.\mathrm{U}}+a_{\text{GS}}^{\mathrm{D}}{F}_{m.t}^{\text{GS}.\mathrm{D}}\right)+{\displaystyle \sum _{t\in {\mathrm{\Omega }}_{\mathrm{T}}}}{\displaystyle \sum _{w\in {\mathrm{\Omega }}_{\text{GFU}}}}\left(a_{\text{GFU}}^{\mathrm{U}}{P}_{w.t}^{\text{GFU}.\mathrm{U}}+a_{\text{GFU}}^{\mathrm{D}}{P}_{w.t}^{\text{GFU}.\mathrm{D}}\right)(22)$

Where ${\mathrm{\Omega }}_{\mathrm{T}}$ represents the set of scheduling periods, ${\mathrm{\Omega }}_{GS}$ and ${\mathrm{\Omega }}_{GFU}$ refer to the sets of gas sources and gas turbines, respectively. m denotes the gas node, $F_{m.t}^{\text{GS}.\mathrm{U}}$ and $F_{m.t}^{\text{GS}.\mathrm{D}}$ represent the upper and lower control quantities of the gas source, respectively. $a_{\text{GS}}^{\mathrm{U}}$ and $a_{\text{GS}}^{\mathrm{D}}$ are the unit control costs, while www is the equipment index. $P_{w.t}^{\text{GFU}.\mathrm{U}}$ and $P_{w.t}^{\text{GFU}.\mathrm{D}}$ represent the upper and lower control quantities of the gas turbine, with $a_{\text{GFU}}^{\mathrm{U}}$ and $a_{\text{GFU}}^{\mathrm{D}}$ being the control costs.

$C_{\text{Power}}^{\text{buy}}={\displaystyle \sum _{w\in {\mathrm{\Omega }}_{\text{Rene}}}}{\displaystyle \sum _{t\in {\mathrm{\Omega }}_{\mathrm{T}}}}{a}_{\text{Rene}}^{\text{buy}}\left(P_{w.t}^{\text{Re}}+{\xi }_{w.t}^{\text{Re}}\right)+{\displaystyle \sum _{i\in {\mathrm{\Omega }}_{\text{slack}}}}{\displaystyle \sum _{t\in {\mathrm{\Omega }}_{\mathrm{T}}}}\left(a_{\text{UPG}}^{\text{buy}}{P}_{i.t}^{\text{UPG}+}-a_{\text{UPG}}^{\text{sell}}{P}_{i.t}^{\text{UPG}-}\right)(23)$

Where ${\mathrm{\Omega }}_{\text{Rene}}$ and ${\mathrm{\Omega }}_{slack}$ represent the sets of renewable energy stations and the slack node, respectively. $P_{w.t}^{\text{Re}}$ and ${\xi }_{w.t}^{\text{Re}}$ represent the predicted output and prediction error of the renewable energy stations, respectively. $P_{i.t}^{\text{UPG}+}$ and $P_{i.t}^{\text{UPG}-}$ represent the power purchased from and sold to the distribution network root node i and the upper-level grid, respectively. $a_{\text{Rene}}^{\text{buy}}$, $a_{\text{UPG}}^{\text{buy}}$, and $a_{\text{UPG}}^{\text{sell}}$ are the feed-in tariffs for renewable energy stations, and the purchase and sale of electricity prices for the distribution network and upper-level grid, respectively.

$C_{\text{LCFS}}^{\text{supp}}={\displaystyle \sum _{k\in {\mathrm{\Omega }}_{\text{Park}}}}\left(a_{\text{Ele}}^{\sup }{E}_{\text{Ele}.k}^{\sup }+a_{\mathrm{H}2}^{\sup }{E}_{\mathrm{H}2.k}^{\sup }+a_{\text{NG}}^{\sup }{E}_{\text{NG}.k}^{\sup }\right)(24)$

Where ${\mathrm{\Omega }}_{Park}$ represents the set of urban systems. $a_{\text{Ele}}^{\sup }$, $a_{\mathrm{H}2}^{\sup }$, and $a_{\text{NG}}^{\sup }$ are the compensation prices for the energy support provided by the urban systems in terms of electricity, hydrogen, and natural gas, respectively. $E_{\text{Ele}.k}^{\sup }$, $E_{\mathrm{H}2.k}^{\sup }$, and $E_{\text{NG}.k}^{\sup }$ represent the electricity, hydrogen, and natural gas support amounts provided by the urban systems, respectively.

$C_{\text{CO}2}^{\text{emi}}=a_{\text{CO}2}^{\text{ce}}\left(E_{\text{car}}^{\text{total}}-E_{\text{car}}^{\text{base}}\right)(25)$

Where $a_{\text{CO}2}^{\text{ce}}$ represents the carbon trading price, $E_{\text{car}}^{\text{total}}$ and $E_{\text{car}}^{\text{base}}$ are the total carbon emissions and the free carbon emission allowance for the regional IEHGS, respectively. $E_{\text{car}}^{\text{base}}$ can be further expressed as:

$E_{\text{car}}^{\text{total}}={\displaystyle \sum _{t\in {\mathrm{\Omega }}_{\mathrm{T}}}}\left[{\displaystyle \sum _{m\in {\mathrm{\Omega }}_{\text{GS}}}}{e}_{\text{car}}^{\text{Gas}}\left(F_{m.t}^{\text{GS}.\mathrm{E}}+{\eta }_{m-i}^{\text{GFU}}{\xi }_{i.t}^{\text{Re}}\right)+{\displaystyle \sum _{i\in {\mathrm{\Omega }}_{\text{slack}}}}{e}_{\text{car}}^{\text{UPG}}{P}_{i.t}^{\text{UPG}+}-{\displaystyle \sum _{i\in {\mathrm{\Omega }}_{\text{slack}}}}{e}_{\text{car}}^{\text{UPG}}{P}_{i.t}^{\text{UPG}-}\right](26)$

Where ${\eta }_{m-i}^{\text{GFU}}{\xi }_{i.t}^{\text{Re}}$ represents the additional output from the gas source to cope with the uncertainty of renewable energy, while $e_{\text{car}}^{\text{Gas}}$ and $e_{\text{car}}^{\text{UPG}}$ are the carbon emission intensities for the gas source and the upper-level grid, respectively.

3.2 Constraints

Based on the analytical expressions of the low-carbon feasible space of urban systems in Section 2.3, further consideration is given to the low-carbon safe operation constraints of the provincial-level IEHGS, as detailed below.

Gas turbines and gas sources can serve as flexible resources to address the uncertainty of renewable energy. Considering the impact of renewable energy uncertainty, the distributional robust chance constraints for the gas turbine power output and reserve capacity are constructed as Formulas 27, 28; similarly, the distributional robust chance constraints for the gas source’s gas output and reserve capacity are constructed as Formulas 29, 30.

${\mathrm{Pr}}_{\sim P_{\text{Re}}}\left(P_{i.\text{lo}}^{\text{GFU}}\le P_{i.t}^{\text{GFU}.\mathrm{E}}-{\xi }_{i.t}^{\text{Re}}\le P_{i.\text{up}}^{\text{GFU}}\right)\ge 1-{\beta }_{\text{Re}},\forall P_{\text{Re}}\in {\mathfrak{R}}_{\text{Re}}(27)$

${\mathrm{Pr}}_{\sim P_{\text{Re}}}\left(-P_{i.t}^{\text{GFU}.\mathrm{D}}\le -{\xi }_{i.t}^{\text{Re}}\le P_{i.t}^{\text{GFU}.\mathrm{U}}\right)\ge 1-{\beta }_{\text{Re}},\forall P_{\text{Re}}\in {\mathfrak{R}}_{\text{Re}}(28)$

${\mathrm{Pr}}_{\sim P_{\text{Re}}}\left(F_{m.\text{lo}}^{\text{GS}}\le F_{m.t}^{\text{GS}.\mathrm{E}}+{\eta }_{m-i}^{\text{GFU}}{\xi }_{i.t}^{\text{Re}}\le F_{m.\text{up}}^{\text{GS}}\right)\ge 1-{\beta }_{\text{Re}},\forall P_{\text{Re}}\in {\mathfrak{R}}_{\text{Re}}(29)$

${\mathrm{Pr}}_{\sim P_{\text{Re}}}\left(-F_{m.t}^{\text{GS}.\mathrm{D}}\le {\eta }_{m-i}^{\text{GFU}}{\xi }_{i.t}^{\text{Re}}\le F_{m.t}^{\text{GS}.\mathrm{U}}\right)\ge 1-{\beta }_{\text{Re}},\forall P_{\text{Re}}\in {\mathfrak{R}}_{\text{Re}}(30)$

Where $P_{\text{Re}}$ is the probability distribution function of the renewable energy uncertainty random variable ${\xi }_{i.t}^{\text{Re}}$, ${\mathfrak{R}}_{\text{Re}}$ is the fuzzy set of $P_{\text{Re}}$, $1-{\beta }_{\text{Re}}$ is the confidence level, $P_{i.t}^{\text{GFU}.\mathrm{E}}$ and ${\eta }_{m-i}^{\text{GFU}}$ are the planned active power and energy conversion coefficient of the gas turbine, respectively. $P_{i.t}^{\text{GFU}.\mathrm{E}}-{\xi }_{i.t}^{\text{Re}}$ and $F_{m.t}^{\text{GS}.\mathrm{E}}+{\eta }_{m-i}^{\text{GFU}}{\xi }_{i.t}^{\text{Re}}$ represent the actual outputs of the gas turbine and gas source point under the impact of uncertainty. $P_{i.\text{up}}^{\text{GFU}}$ and $P_{i.\text{lo}}^{\text{GFU}}$ are the power limits of the gas turbine, and $F_{m.\text{up}}^{\text{GS}}$ and $F_{m.\text{lo}}^{\text{GS}}$ are the gas output limits of the gas source point.

The node voltage constraint is shown in Equation 31, the upper grid interaction power constraint is shown in Equation 32, and the power flow and branch capacity constraints are shown in Equations 33–37. Considering the mitigation effect of gas turbines and gas sources on renewable energy uncertainty, the node power balance constraints are shown in Equations 38, 39.

$U_{i.\min }\le U_{i.t}\le U_{i.\max }(31)$

$\left\{\begin{array}{l}-P_{i.\text{up}}^{\text{grid}}⩽P_{i.t}^{\text{grid}}⩽P_{i.\text{up}}^{\text{grid}}\\ -Q_{i.\text{up}}^{\text{grid}}⩽Q_{i.t}^{\text{grid}}⩽Q_{i.\text{up}}^{\text{grid}}\end{array}\right.(32)$

$P_{i.t}^{\text{Grid}}+P_{i.t}^{\text{GFG}}+P_{i.t}^{\text{DG}}-P_{i.t}^{\text{Load}}-P_{i.t}^{\mathrm{P}2\mathrm{G}}={\displaystyle \sum _{j\in i}}{P}_{ij.t}(33)$

$Q_{i.t}^{\text{Grid}}+Q_{i.t}^{\text{GFG}}+Q_{i.t}^{\text{DG}}-Q_{i.t}^{\text{Load}}={\displaystyle \sum _{j\in i}}{Q}_{ij.t}(34)$

$P_{ij.t}=\left(U_{i.t}-U_{j.t}\right)r_{ij}/\left(r_{ij}^2+x_{ij}^2\right)+\left({\theta }_{i.t}-{\theta }_{j.t}\right)x_{ij}/\left(r_{ij}^2+x_{ij}^2\right)(35)$

$Q_{ij.t}=\left(U_{i.t}-U_{j.t}\right)x_{ij}/\left(r_{ij}^2+x_{ij}^2\right)-\left({\theta }_{i.t}-{\theta }_{j.t}\right)r_{ij}/\left(r_{ij}^2+x_{ij}^2\right)(36)$

$P_{ij.t}^2+Q_{ij.t}^2\le {\left(S_{ij}^{\text{cap}}\right)}^2(37)$

$P_{i.t}^{\text{UPG}}+P_{i.t}^{\text{Re}}+P_{i.t}^{\text{GFU}.\mathrm{E}}+{\displaystyle \sum _{k\in {\mathrm{\Omega }}_{i.\text{Park}}}}{P}_{\text{ELE}.t.k}^{\text{LINE}}-P_{i.t}^{\mathrm{P}2\mathrm{G}}-P_{i.t}^{\text{Load}}={\displaystyle \sum _{j\in {\mathrm{\Omega }}_{\text{bus}.i}}}{P}_{ij.t}(38)$

$Q_{i.t}^{\text{UPG}}+Q_{i.t}^{\text{Re}}+Q_{i.t}^{\text{GFU}}-Q_{i.t}^{\text{Load}}={\displaystyle \sum _{j\in {\mathrm{\Omega }}_{\text{bus}.i}}}{Q}_{ij.t}(39)$

Where ${\mathrm{\Omega }}_{bus.i}$ and ${\mathrm{\Omega }}_{i.Park}$ represent the set of distribution network nodes connected to node i and the set of city systems, respectively. $P_{ij.t}$ and $Q_{ij.t}$ are the active and reactive power transmitted through branch ij, respectively. $P_{i.t}^{\text{Load}}$ and $Q_{i.t}^{\text{Load}}$ are the active and reactive loads at the node, respectively. $P_{i.t}^{\text{UPG}}$ and $Q_{i.t}^{\text{UPG}}$ are the active and reactive power exchanged between the upper grid and node i, respectively. $P_{i.t}^{\mathrm{P}2\mathrm{G}}$ represents the electricity consumption of P2G. $Q_{i.t}^{\text{Re}}$ and $Q_{i.t}^{\text{GFU}}$ are the reactive power of renewable energy and gas turbines, respectively.

3.3 Model transformation

The IEHGS scheduling model established above can be written in the following form:

$\begin{array}{l}\underset{\mathit{x}\in \mathbb{X}}{\min }F\left(\mathit{x},\mathit{\xi }\right)\\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{c}\underset{Distributionally\mathrm{r}obust\mathrm{c}hance\mathrm{c}onstraints}{\underbrace{{\mathrm{Pr}}_{\sim p_{\text{Re}}}\left[f_1\left(\mathit{x},\mathit{\xi }\right)\le 0\right]\ge 1-{\beta }_{\text{Re}},\forall P_{\text{Re}}\in {\mathfrak{R}}_{\text{Re}}}}\\ \underset{Analyticalexpressionofthelow-carbonfeasiblespaceofurbansystems}{\underbrace{f_2\left(\mathit{x}\right)\le 0}},\underset{Deterministic\mathrm{c}onstraints}{\underbrace{f_3\left(\mathit{x}\right)\le 0}}\end{array}\right.\end{array}(40)$

Where x represents all decision variables, and $\mathbb{X}$ is the feasible region of x. $\mathit{\xi }$ is a random variable. $F\left(\mathit{x},\mathit{\xi }\right)$ is the unified expression of the objective function Formulas 21–26; the constraints involving random variables in the scheduling model (i.e., Formulas 27–30) are uniformly represented as distributionally robust chance constraints; the analytical expression of the low-carbon feasible space of the urban system in Section 2.3 is uniformly represented as $f_2\left(\mathit{x}\right)\le 0$; other remaining constraints (such as Formulas 38, 39) are uniformly represented as $f_3\left(\mathit{x}\right)\le 0$. $F\left(\mathit{x},\mathit{\xi }\right)$, $f_1\left(\mathit{x},\mathit{\xi }\right)$, and $f_3\left(\mathit{x}\right)\le 0$ contain random variables or nonlinear constraints, which increases the difficulty of solving the model. To address this, the following transformation method is proposed.

1) Deterministic transformation of the objective function $\underset{\mathit{x}\mathbb{\in }\mathbb{X}}{\min }F\left(\mathit{x},\mathit{\xi }\right)$

Based on distributionally robust chance constraints, the objective function in Equation 40 can be equivalently transformed into:

$\underset{\mathit{x}\in \mathbb{X}}{\min }F\left(\mathit{x},\mathit{\xi }\right)=\underset{\mathit{x}\in \mathbb{X}}{\min }\underset{P_{\text{Re}}\in {\mathfrak{R}}_{\text{Re}}}{\max }{\mathrm{E}}_P\left[F\left(\mathit{x},\mathit{\xi }\right)\right](41)$

Based on Theorem 4 from reference (Hu and Hong, 2012), Equation 41 can be equivalently transformed into as shown in Equation 42:

$\underset{\mathit{x}\in \mathbb{X},{\nu }_{\text{Re}}\ge 0}{\min }\left\{{\nu }_{\text{Re}}{\text{InE}}_{P_{\text{Re}.0}}\left[e^{F\left(\mathit{x},\mathit{\xi }\right)/{\nu }_{\text{Re}}}\right]+{\nu }_{\text{Re}}{\kappa }_{\text{Re}}\right\}(42)$

Where $P_{\text{Re}.0}$ is the reference distribution of the random variable, ${\kappa }_{\text{Re}}$ is the KL divergence tolerance, and ${\nu }_{\text{Re}}$ is the auxiliary variable.

Further, $F\left(\mathit{x},\mathit{\xi }\right)$ can be expressed as $F\left(x,\xi \right)=d^{T}x+h^{T}x+g$, where d and h are the coefficient vectors of x and ξ in Equations 21–26, and g is the constant term in Equations 21–26. Therefore, the following expression holds:

$\underset{\mathit{x}\in \mathbb{X},{\nu }_{\text{Re}}\ge 0}{\min }\left\{{\mathit{d}}^T\mathit{x}+g+{\displaystyle \sum _{i\in {\mathrm{\Omega }}_h}}{\displaystyle \sum _{t\in {\mathrm{\Omega }}_{\mathrm{T}}}}\left[\frac{{\left(h_i\right)}^2{\left({\sigma }_{i.t}^{\text{Re}}\right)}^2}{2{\nu }_{\text{Re}}}+h_i{\mu }_{i.t}^{\text{Re}}\right]+{\nu }_{\text{Re}}{\kappa }_{\text{Re}}\right\}(43)$

For the variable ${\nu }_{\text{Re}}$ in Equation 43, when

${\nu }_{\text{Re}}=\sqrt{\frac{{\displaystyle \sum _{i\in {\mathrm{\Omega }}_h}}{\displaystyle \sum _{t\in {\mathrm{\Omega }}_{\mathrm{T}}}}{\left(h_i\right)}^2{\left({\sigma }_{i.t}^{\text{Re}}\right)}^2}{2{\kappa }_{\text{Re}}}}(44)$

Then, the terms containing ${\nu }_{\text{Re}}$ in Equation 43 can attain their minimum value by Equation 44, which can be expressed as shown in Equation 45:

$\underset{{\nu }_{\text{Re}}\ge 0}{\min }\left[{\displaystyle \sum _{i\in {\mathrm{\Omega }}_h}}{\displaystyle \sum _{t\in {\mathrm{\Omega }}_{\mathrm{T}}}}\frac{{\left(h_i\right)}^2{\left({\sigma }_{i.t}^{\text{Re}}\right)}^2}{2{\nu }_{\text{Re}}}+{\nu }_{\text{Re}}{\kappa }_{\text{Re}}\right]=\sqrt{2{\kappa }_{\text{Re}}{\displaystyle \sum _{i\in {\mathrm{\Omega }}_h}}{\displaystyle \sum _{t\in {\mathrm{\Omega }}_{\mathrm{T}}}}{\left(h_i\right)}^2{\left({\sigma }_{i.t}^{\text{Re}}\right)}^2}(45)$

Based on this, Equation 43 can be further transformed into Equation 46:

$\underset{\mathit{x}\in \mathbb{X}}{\min }\left[{\mathit{d}}^T\mathit{x}+g+{\displaystyle \sum _{i\in {\mathrm{\Omega }}_h}}{\displaystyle \sum _{t\in {\mathrm{\Omega }}_{\mathrm{T}}}}\left(h_i{\mu }_{i.t}^{\text{Re}}\right)+\sqrt{2{\kappa }_{\text{Re}}{\displaystyle \sum _{i\in {\mathrm{\Omega }}_h}}{\displaystyle \sum _{t\in {\mathrm{\Omega }}_{\mathrm{T}}}}{\left(h_i\right)}^2{\left({\sigma }_{i.t}^{\text{Re}}\right)}^2}\right](46)$

2) Deterministic transformation of the distributionally robust chance constraint ${\mathrm{Pr}}_{\sim P_{\text{Re}}}\left[f_1\left(\mathit{x},\mathit{\xi }\right)\le 0\right]\ge 1-{\beta }_{\text{Re}},\forall P_{\text{Re}}\in {\mathfrak{R}}_{\text{Re}}$

The constraints represented by the distributionally robust chance constraint in Equation 40 can be further expressed as:

${\mathrm{Pr}}_{\sim P_{\text{Re}}}\left(a{x}_{\text{Re}}+b{\xi }_{i.t}^{\text{Re}}+c\le 0\right)\ge 1-{\beta }_{\text{Re}},\forall P_{\text{Re}}\in {\mathfrak{R}}_{\text{Re}}(47)$

Where $x_{\text{Re}}$ a, b, and c represent the decision variables, coefficients of the decision variables, coefficients of the random variables, and constant terms in Equations 27–30, respectively.

Based on the equivalent transformation method for fuzzy chance-constrained problems, adjusting the risk parameter ${\beta }_{\text{Re}}$ in Equation 47 allows the fuzzy chance constraint to be converted into the following chance constraint:

${\mathrm{Pr}}_{\sim P_{\text{Re}.0}}\left(a{x}_{\text{Re}}+b{\xi }_{i.t}^{\text{Re}}+c\le 0\right)\ge 1-{\overline{\beta }}_{\text{Re}}(48)$

Where ${\overline{\beta }}_{\text{Re}}$ is the adjusted risk parameter, which is associated with ${\beta }_{\text{Re}}$ and ${\kappa }_{\text{Re}}$ and can be obtained using a binary search algorithm.

Based on the Bernstein approximation method, Equation 48 can be further converted to Equation 49:

$\underset{{\alpha }_{\text{Re}}>0}{\inf }\left\{{\alpha }_{\text{Re}}\text{In}{E}_{P_{\text{Re}.0}}\left[e^{\left(a{x}_{\text{Re}}+b{\xi }_{i.t}^{\text{Re}}+c\right)/{\alpha }_{\text{Re}}}\right]-{\alpha }_{\text{Re}}\text{In}{\overline{\beta }}_{\text{Re}}\right\}\le 0(49)$

Where ${\alpha }_{\text{Re}}$ is an auxiliary variable.

3) Linearization of nonlinear constraint $f_3\left(\mathit{x}\right)\le 0$

The nonlinearity in $f_3\left(\mathit{x}\right)\le 0$ arises from branch capacity constraints, which can be handled using a piecewise linearization method to reduce the computational burden.

At this point, the original non-convex, nonlinear scheduling model with uncertainty has been transformed into a mixed-integer linear optimization model, which can be solved directly using commercial solvers.

4 Case studies analysis

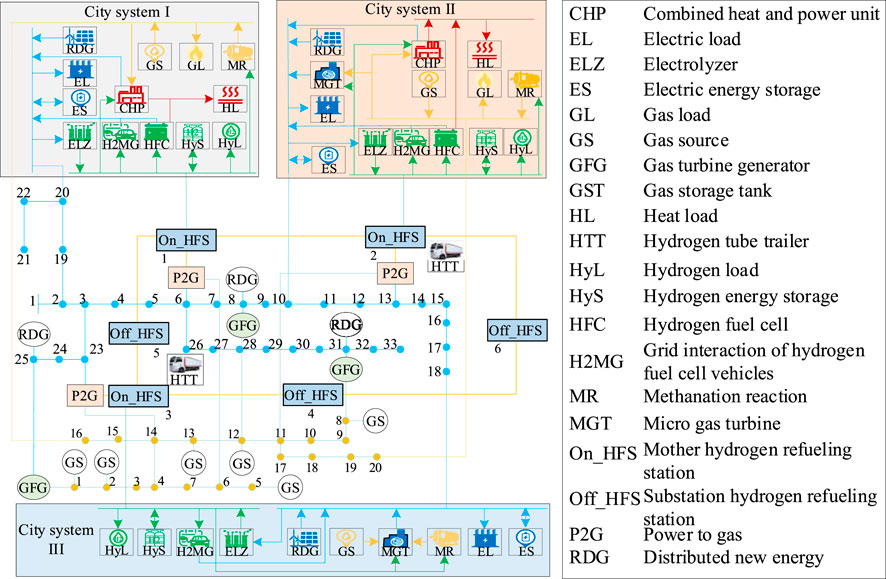
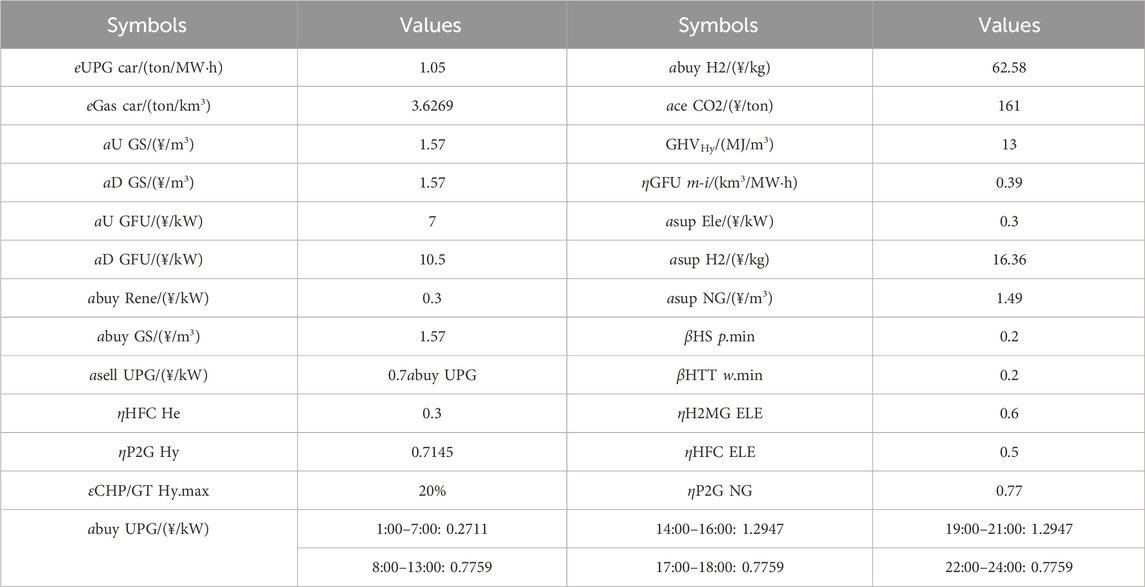
To verify the effectiveness and applicability of the model and method proposed in this paper, simulation analysis is conducted using IEHGS_1 as shown in Figure 3. IEHGS_1 consists of an IEEE 33-node distribution network, a 20-node gas network, a 6-node hydrogen energy system, and three coupled city systems. City systems I-III are coupled with IEHGS_1 through different electric, hydrogen, and gas interconnections. Assume that the prediction error of renewable energy follows a normal distribution with a mean of 0 and a standard deviation of 0.2. The confidence level is set to 0.95, the divergence tolerance is set to 0.5, and the scheduling period is T = 24 h. The technical and economic parameters of IEHGSs are detailed in Table 1.

Figure 3

Figure 3. Topology of IEHGS_1.

Table 1

Table 1. Technical and economic parameters of IEHGSs.

4.1 Analysis of the collaborative support function of multi-city systems

To investigate the impact of the collaborative support function of multi-city systems on the low-carbon operation of the IEHGS, the following two comparative cases are set up to analyze the collaborative support function of multiple city systems in IEHGS_1.

Case 1:. The IEHGS scheduling model proposed in this paper, formulates a low-carbon operation strategy for IEHGS_1 based on security regions and considers the collaborative support function of multi-city interconnected power systems.

Case 2:. The low-carbon operation strategy for IEHGS_1 without considering the support function of city systems (Hu et al., 2021).

The operating costs of IEHGS_1 in Cases 1, 2 are shown in Table 2. Compared to Case 2, the total operating cost of IEHGS_1 in Case 1 decreases by 7.21%. Specifically, the electricity purchase cost of IEHGS_1 is reduced by 60.78%, and no carbon emission costs are incurred, allowing the sale of surplus carbon allowances for profit. This result demonstrates that the proposed IEHGS low-carbon operation strategy (Case 1), which considers the collaborative support of multiple city systems, effectively reduces electricity purchase costs and carbon emission expenses, thereby lowering the total operating cost of IEHGS. This outcome validates the effectiveness of incorporating city system collaboration into IEHGS dispatching as proposed in this paper.

The optimal support points provided by each city system in Case 1 are located within their own low-carbon feasible space, as shown in Figure 4. This result indicates that each city can collaboratively utilize different low-carbon resources and system flexibility resources, effectively assisting in the heterogeneous energy conversion of IEHGS_1. This provides heterogeneous energy support for the low-carbon operation of IEHGS_1, thereby reducing its energy procurement costs.

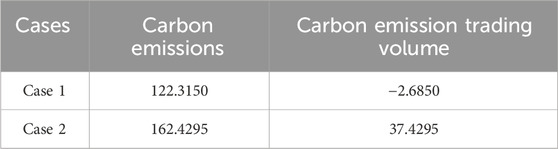
In addition, the provision of clean, heterogeneous energy from multiple cities to IEHGS_1 reduces its consumption of fossil fuel (natural gas), thereby contributing to lower carbon emissions and reducing the need for carbon allowance trading. As shown in Table 3, the carbon emissions of IEHGS_1 in Case 1 are reduced by 24.70%. Since there is no requirement for additional carbon allowances, the surplus allowances can be sold to make a profit. Therefore, considering the collaborative support of multiple city systems also effectively reduces the carbon emission costs of IEHGS_1.

Based on this, the various city systems of IEHGS_1 can be characterized by the low-carbon feasible space defined by security regions. While exploring the low-carbon operating potential of the city systems, they provide collaborative support for the low-carbon operation of IEHGS_1, enhancing its low-carbon performance and improving the supply guarantee capability of the multi-city interconnected power system.

Table 2

Table 2. Total Operation Cost of IEHGSs Under Case 1, 2 Unit: Ten thousand yuan.

Figure 4

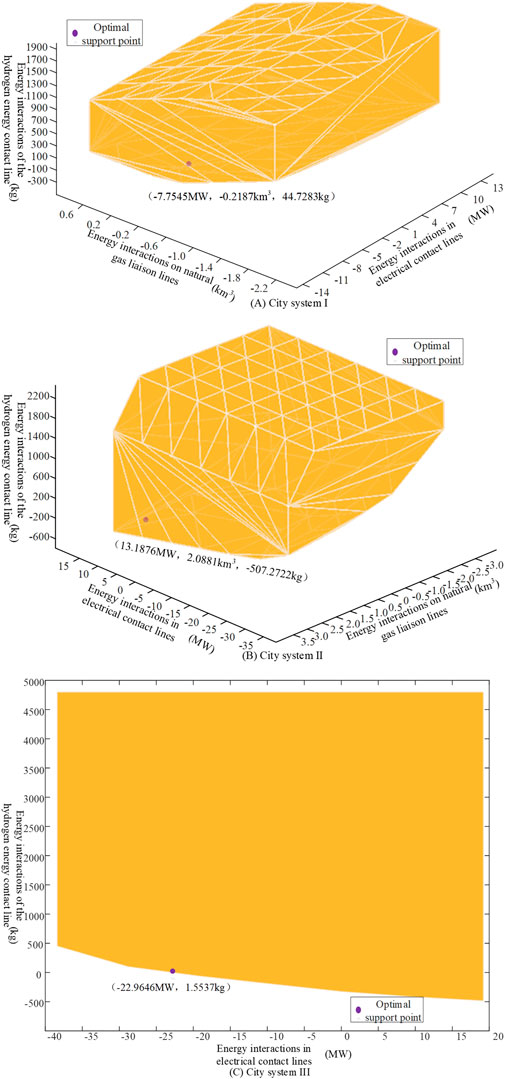
Figure 4. Optimal support point of each park system under Case 1.

Table 3

Table 3. Carbon Emissions and Carbon Trading of IEHGS_1 Under Cases 1, 2 Unit: ton.

4.2 Verifying the effectiveness of the support role considered by the security region

To verify the effectiveness of the security region in characterizing the low-carbon feasible space of city systems and providing support for the low-carbon operation of the provincial grid IEHGS, the following two case studies are set up for comparative analysis.

Case 3:. The low-carbon operation strategy of IEHGS_1 is developed based on the collaborative support role of the multi-city interconnected power system considered by the security region, as proposed in this paper.

Case 4:. The low-carbon operation strategy of IEHGS_1 is developed based on the collaborative support role of the multi-city system, considering the interconnection line energy exchange capacity, as proposed in reference (Yang and Liu, 2023).

The optimal support points provided by each city system in Case 4 are shown in Figure 5. It can be observed that the optimal support points in Case 4 are located outside the low-carbon feasible space, meaning these support points are infeasible. This is because Case 4 only considers the transmission capacity constraints of the interconnection lines and does not account for the internal security operation constraints of the city systems, resulting in the optimal support points being unsuitable for the city systems. However, the support points of each park system in Case 3 are all located within the low-carbon feasible space (as shown in Figure 4), which verifies the effectiveness of considering the collaborative support role of multi-city systems based on the security region.

Figure 5

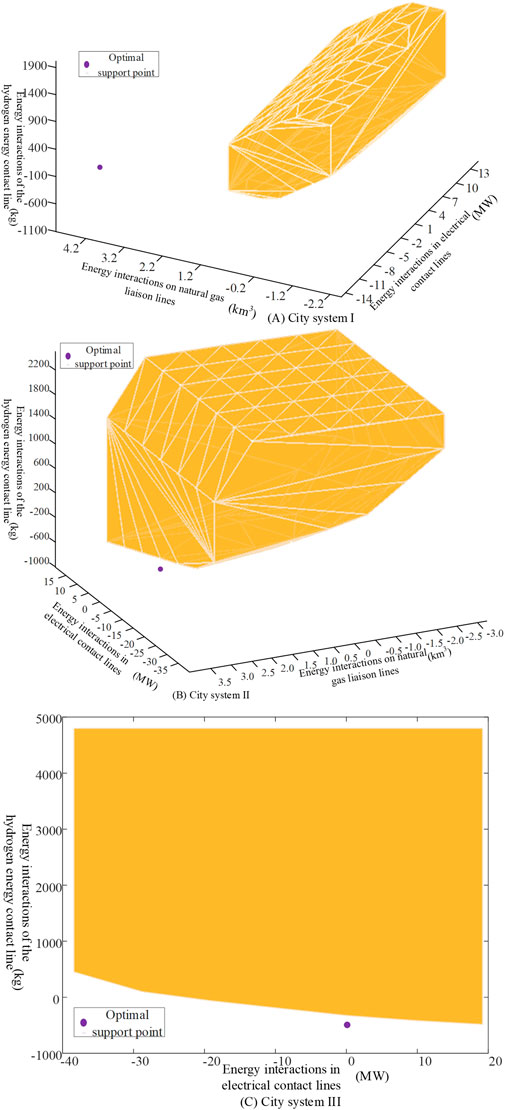
Figure 5. Optimal support point of each park system under Case 4.

5 Conclusion

To enhance the power supply guarantee capability of multi-city interconnected power systems, this paper proposes a low-carbon operation method for IEHGS that considers the collaborative support role of multi-city interconnected power systems based on the security region.

The low-carbon feasible space of city systems is characterized based on the security region, and an analytical expression for the low-carbon feasible space is constructed. A dispatch model for IEHGS that considers the collaborative support role of city systems is established, along with a model transformation method. Finally, the proposed model and methods are validated and applied using a test system. The case studies demonstrate the applicability and effectiveness of the proposed approach. Compared with conventional methods, the proposed method significantly reduces the total operating cost by 7.21% and carbon emissions by 24.7%. It also leverages collaborative support among multiple cities to improve power supply security. This research has the following features:

1) The security region characterizes the low-carbon feasible space of city systems, allowing for the visualization of the heterogeneous energy conversion capability that city systems provide to the provincial grid IEHGS in the entire quadrant space. This, in turn, enhances the supply guarantee capability of the interconnected power system.

2) The analytical formulation of the low-carbon feasible space of city systems uses the security region to equivalently represent the system’s low-carbon operational constraints. This allows for the exploration of low-carbon resources within city systems, providing collaborative support for the low-carbon operation of the provincial grid IEHGS. It not only ensures the feasibility of the optimal support points but also avoids the shortcomings of traditional distributed algorithms, such as poor convergence.

3) Each city system can utilize its own distributed renewable energy, low-carbon equipment, flexibility resources, and surplus carbon emission allowances to assist the heterogeneous energy conversion of the provincial grid IEHGS, supply clean energy, and enhance the performance of low-carbon operations, thereby improving the supply guarantee capability of the multi-city interconnected power system.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ZL: Conceptualization, Data curation, Investigation, Methodology, Software, Supervision, Writing–original draft, Writing–review and editing. YC: Data curation, Formal Analysis, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. YD: Data curation, Investigation, Methodology, Resources, Supervision, Writing–original draft, Writing–review and editing. YL: Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study received funding from the State Grid Tibet Electric Power Co., Ltd. Science and Technology Project (523153240003).

Conflict of interest

Authors ZL, YC, YD, and YL were employed by State Grid Tibet Electric Power Co., Ltd.

The authors declare that this study received funding from State Grid Tibet Electric Power Co., Ltd. The funder had the following involvement in the study: study design, data collection and analysis.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Shetwi, A. Q. (2022). Sustainable development of renewable energy integrated power sector: trends, environmental impacts, and recent challenges. Sci. Total Environ. 822, 153645. doi:10.1016/j.scitotenv.2022.153645

PubMed Abstract | CrossRef Full Text | Google Scholar

Baraa, M., and El, M. (2024). A Review of Power System Flexibility with High Penetration of Renewables, 2024 (IEEE) Available at: https://ieeexplore.ieee.org/abstract/document/8635327 (Accessed December 5, 2024). doi:10.1109/TPWRS.2019.2897727

CrossRef Full Text | Google Scholar

Bensadi, A. (2024). Assessing the impact of renewable energy integration on energy efficiency within the China-Pakistan economic corridor (CPEC). Sci. Rep. 14, 29374. doi:10.1038/s41598-024-81173-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, Z., Song, X., Li, M., and Xiaoxuan, Z. (2021). Experience and enlightenment of Japan’s emergency power supply guarantee mechanism. IOP Conf. Ser. Earth Environ. Sci. 680, 012048. doi:10.1088/1755-1315/680/1/012048

CrossRef Full Text | Google Scholar

Hassan, Q., Viktor, P., J. Al-Musawi, T., Mahmood Ali, B., Algburi, S., Alzoubi, H. M., et al. (2024). The renewable energy role in the global energy Transformations. Renew. Energy Focus 48, 100545. doi:10.1016/j.ref.2024.100545

CrossRef Full Text | Google Scholar

He, X., Lin, J., Xu, J., Huang, J., Wu, N., Zhang, Y., et al. (2023). Long-term planning of wind and solar power considering the technology readiness level under China’s decarbonization strategy. Appl. Energy 348, 121517. doi:10.1016/j.apenergy.2023.121517

CrossRef Full Text | Google Scholar

Hu, H., Wen, L., and Zheng, K. (2021). “Low carbon economic dispatch of multi-energy combined system considering carbon trading,” in 2021 11th international conference on power and energy systems (ICPES), 838–843. doi:10.1109/ICPES53652.2021.9683862

CrossRef Full Text | Google Scholar

Hu, Z., and Hong, L. (2012). Kullback-leibler divergence constrained distributionally robust optimization.

Google Scholar

Jiang, J., Chen, W., Wu, G., and Jiao, Y. (2019). “Power supply service: assessing the feasibility and merits of applying electric emergency power vehicles,” in 2019 4th international conference on control and robotics engineering (ICCRE), 60–64. doi:10.1109/ICCRE.2019.8724341

CrossRef Full Text | Google Scholar

Li, M., Hou, Y., Xie, Y., Jiang, S., Ye, D., and Zheng, G. (2022). “A selection method of the guaranteed power source for the provincial power grid,” in 2022 IEEE 5th advanced information management, communicates, electronic and automation control conference (IMCEC), 342–347. doi:10.1109/IMCEC55388.2022.10019852

CrossRef Full Text | Google Scholar

Li, R., Hu, Y., Wang, X., Zhang, B., and Chen, H. (2024). Estimating the impacts of a new power system on electricity prices under dual carbon targets. J. Clean. Prod. 438, 140583. doi:10.1016/j.jclepro.2024.140583

CrossRef Full Text | Google Scholar

Li, X., Pan, L., and Zhang, J. (2023). Development status evaluation and path analysis of regional clean energy power generation in China. Energy Strategy Rev. 49, 101139. doi:10.1016/j.esr.2023.101139

CrossRef Full Text | Google Scholar

Miao, M., Ping, J., Hai-tao, Y., Xin, Z., Xiang-cheng, Z., Yuan-yuan, L., et al. (2018). “Research on comprehensive optimization of power intensive UHV/EHV sending power grid,” in 2018 International Conference on Power System Technology (POWERCON), 266–271. doi:10.1109/POWERCON.2018.8602312

CrossRef Full Text | Google Scholar

Ourahou, M., Ayrir, W., EL Hassouni, B., and Haddi, A. (2020). Review on smart grid control and reliability in presence of renewable energies: challenges and prospects. Math. Comput. Simul. 167, 19–31. doi:10.1016/j.matcom.2018.11.009

CrossRef Full Text | Google Scholar

Ren, J., Zeng, Y., Qin, C., Li, B., Wang, Z., and Yuan, Q. (2023). “Steady-state security region boundary modification model: a hybrid physical model-driven and data-driven approach,” in 2023 IEEE power and energy society general meeting (PESGM), 1–5. doi:10.1109/PESGM52003.2023.10253053

CrossRef Full Text | Google Scholar

Su, Y., Shen, L., Li, A., Rong, J., Wang, Y., and Cheng, S. (2023). “Research on grid structure of backbone power transmission network,” in 2023 6th international conference on energy, electrical and power engineering (CEEPE), 459–462. doi:10.1109/CEEPE58418.2023.10165759

CrossRef Full Text | Google Scholar

Tian, J., Zhou, S., and Wang, Y. (2023). Assessing the technical and economic potential of wind and solar energy in China—a provincial-scale analysis. Environ. Impact Assess. Rev. 102, 107161. doi:10.1016/j.eiar.2023.107161

CrossRef Full Text | Google Scholar

Wang, P., Xue, Q., Yang, J., Ma, H., Li, Y., and Zhao, X. (2022). Energy security planning for hydrogen fuel cell vehicles in large-scale events: a case study of Beijing 2022 winter olympics. Automot. Innov. 5, 209–220. doi:10.1007/s42154-022-00183-3

CrossRef Full Text | Google Scholar

Yan, Z., Zhang, Y., and Yu, J. (2024). An allocative method of stationary and vehicle-mounted mobile energy storage for emergency power supply in urban areas. Energy Storage 6, e681. doi:10.1002/est2.681

CrossRef Full Text | Google Scholar

Yang, M., and Liu, Y. (2023). Research on multi-energy collaborative operation optimization of integrated energy system considering carbon trading and demand response. Energy 283, 129117. doi:10.1016/j.energy.2023.129117

CrossRef Full Text | Google Scholar

Yang, T., and Yu, Y. (2021). Security region-based laminar flow coordinated optimization of grids. Int. J. Electr. Power and Energy Syst. 124, 106406. doi:10.1016/j.ijepes.2020.106406

CrossRef Full Text | Google Scholar

Zhang, D., Wang, J., Lin, Y., Si, Y., Huang, C., Yang, J., et al. (2017). Present situation and future prospect of renewable energy in China. Renew. Sustain. Energy Rev. 76, 865–871. doi:10.1016/j.rser.2017.03.023

CrossRef Full Text | Google Scholar

Zhang, L., Yang, Y., Li, Q., Gao, W., Qian, F., and Song, L. (2021). Reliability and cost analysis of the integrated emergency power system in building complex. Energy Explor. and Exploitation 40, 501–527. doi:10.1177/01445987211036824

CrossRef Full Text | Google Scholar