- 1 State Grid Jiangsu Electric Power Co., Ltd. Research Institute, Nanjing, China
- 2 Standardization Management Center, China Electricity Council, Beijing, China
- 3 Department of Automation, Shanghai Jiao Tong University, Shanghai, China
The integration of a large number of electric vehicles (EVs) offers a new perspective for providing voltage regulation services for the operation of distribution networks. The flexible charging and discharging capabilities of EVs can help mitigate voltage fluctuations and improve grid stability. In this paper, we utilize EV clusters by controlling the discharging power to realize voltage regulation of distribution networks. We formulate a feedback-based optimization problem with the objectives of minimizing voltage mismatch as well as reducing the cost of voltage regulation services provided by EV clusters. Then we propose an algorithm with online resistance estimation to find the optimal solution without requiring complete information about distribution networks. The convergence of the proposed algorithm is guaranteed by the oretical proof. Numerical results in 33-bus system validate the performance of the algorithm. The results validate the applicability of the proposed approach in distribution networks, highlighting the potential of EV clusters as a flexible and cost-effective solution for voltage regulation.
1 Introduction
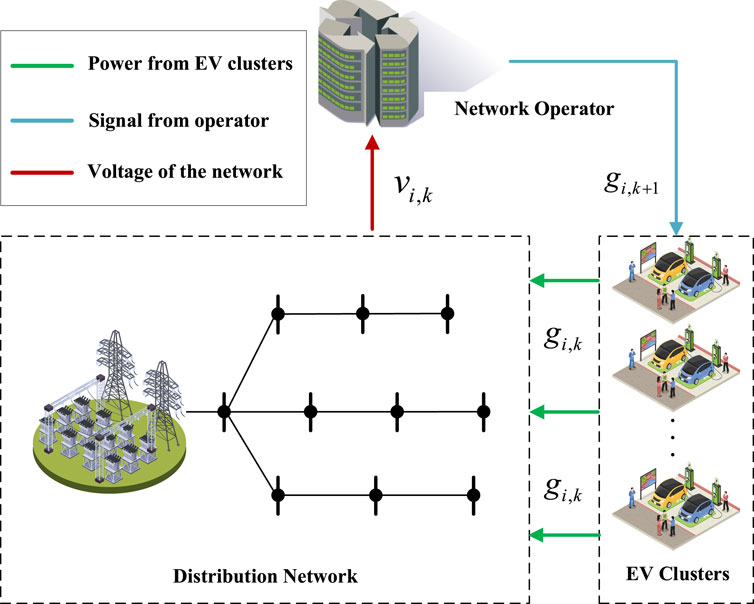
In recent years, a low-carbon society has become a common goal for many countries, which promotes energy transition (Wang et al., 2021b); (Qin et al., 2024b); (Sun et al., 2023). Moreover, large-scale renewable energy resources (RES) have been witnessed in distribution networks, such as wind power, solar power, hydropower, etc., (Qin et al., 2024c); (Jia et al., 2020); (Liu et al., 2022); (Qin et al., 2024a). These RES are much more variable and unpredictable than conventional generations and loads, posing a great challenge to the stable operation of the modern network (Guo et al., 2022); (Shuai et al., 2021). Improper regulation may lead to voltage fluctuation and instability, which will degrade the performance of the network, even resulting in potential danger (Li et al., 2017); (Wang Z. et al., 2020); (Zhang et al., 2024). To address the issue, there is a growing need for a flexible and responsive voltage regulation strategy. One promising approach is the utilization of electric vehicles (EVs) for voltage regulation (Yang et al., 2024); (Wang et al., 2024); (Yin et al., 2023); (Yang et al., 2023). The network operator compensates EVs for their participation in voltage regulation. In this paper, we investigate how to utilize EVs to realize voltage regulation in distribution networks at a relatively low cost.
Voltage regulation by EVs in distribution networks aims to minimize the voltage mismatch by regulating the charge/discharge power of EV clusters. Model predictive control (MPC) based methods are widely considered in this area (Li et al., 2019); (Wang et al., 2022); (Hu et al., 2022); (Feng and Liu, 2023). In reference (Li et al., 2019), a model predictive control (MPC) method is proposed to allow EVs to participate in the grid voltage regulation as a reactive power compensation device to maintain the grid voltage within a stable range. Authors in Wang et al. (2022) developed an MPC-based decentralized algorithm to solve the voltage-related problem using the respective PVs and EVs while ensuring that the EV charging demand is satisfied while contributing to the voltage regulation. Reference (Hu et al., 2022) established a distributed MPC strategy for EV chargers to exploit reactive power vehicle-to-grid (V2G) abilities and participate in real-time voltage regulation of both balanced and unbalanced distribution networks without intervening in the active power exchange. The adaptive primary control and the distributed MPC-based secondary control were combined in Feng and Liu (2023) to maintain accurate dynamic power sharing and stable frequency and voltage.
While MPC-based methods are powerful for voltage regulation, optimization-based methods may handle complex objectives and constraints and scale better with problem size. Many existing works have investigated optimization-based methods (Beaude et al., 2013); (Wu et al., 2016); (Wang S. et al., 2020); (Zhao et al., 2020); (Hu et al., 2021); (ur Rehman, 2022); Yumiki et al. (2022); (Wang et al., 2023). Authors in Beaude et al. (2013) investigated a decentralized optimization methodology to coordinate EV charging in order to contribute to the voltage control on a residential electrical distribution feeder. Reference Wu et al. (2016) used the EVs to regulate the voltage of the smart grid and propose an algorithm to maximize the revenue of the parking lot in a line distribution grid considering the EV users’ charging demand and the voltage fluctuations. A game-theoretic machine learning framework was proposed in Wang S. et al. (2020) to utilize EV charging stations and achieve decentralized Volt-Var control. Reference Zhao et al. (2020) studied an incentive mechanism based on Nash bargaining theory to solve the voltage regulation problem in a distributed network integrated with EVs. Reference Hu et al. (2021) proposed a distributed voltage regulation scheme for dominantly resistive distribution networks through a coordinated EV charging/discharging process. A novel and robust central aggregation hierarchical V2G optimization algorithm is proposed in ur Rehman (2022) to provide voltage and frequency regulation services to the grid. Reference Yumiki et al. (2022) developed a system-level design for the control of electric power grids by EVs to realize multi-objective ancillary service including primary frequency control and voltage amplitude regulation. Authors in Zhang et al. (2018) proposed a novel EV charging scheduling mechanism by controlling the active and reactive charging power of EVs to provide joint voltage and frequency regulation. They formulate a non-convex optimization problem and solve it by transforming the problem into a second-order cone program problem. Reference Wang et al. (2023) proposed an incentive-based control strategy to encourage EVs in desired locations to participate in grid voltage regulation.
In most aforementioned optimization-based works, the main focus is on problem formulation and modeling. The optimization problem is usually formulated with power flow constraints of the network model. Few works intend to investigate how to solve the problem effectively. Commonly, gradient-based methods to find the optimal solution are widely utilized. However, accurate model information is hard to obtain, e.g. resistance values of electrical lines, due to environmental influences. How to realize voltage regulation with EVs in distribution networks without accurate model information remains unsolved.
In this paper, we formulate a voltage regulation strategy in distribution networks provided by EV clusters with an online parameter estimation method. Our main contributions are as follows:
The rest of this paper is organized as follows. In Section 2, preliminaries are presented and the distribution network is built. Section 3 formulates the problem of voltage regulation with EV clusters in distribution networks. An optimal seeking algorithm with online parameter estimation is proposed in Section 4. The convergence proof of the algorithm is also given in this section. Numerical results are demonstrated in Section 5. Finally, Section 6 concludes the paper.
2 Preliminaries and modeling
2.1 Preliminaries
In this paper,
2.2 Distribution network model
We consider a radial distribution network with
Assumption 1. Each node in the distribution network is connected to one EV cluster which can charge and discharge within a certain power range except node 0. Node 0 does not have an EV cluster connected to it.
The active power generated by EV cluster
As for the reactive power, we use
From the DistFlow model proposed in Baran and Wu (1989), we have the following power flow equations of the distribution network.
where
The incidence matrix of the network
where
Since the network is connected,
where
3 Problem formulation
In this section, we formulate an optimization problem to realize voltage regulation in the distribution network by EV clusters. For EV cluster
where
When EV clusters discharge to help realize voltage regulation, we compensate for EV clusters according to their discharge power. The compensation function for EV cluster
where
To realize voltage regulation, we aim to maintain voltage at each node as a predetermined value. We use the node voltage as a feedback value and define the voltage mismatch as the following function:
The goal for the network operator is to lower voltage mismatch while reducing compensation costs, which is a combination of (Equation 7) and (Equation 8). Therefore, the regulation problem can be summarized as the following optimization problem:
where
Lemma 1. The cost function
Proof. The cost function
For a positive
Obviously,
Remark 1. For the optimization problem (Equation 9a–c), the cost function (Equation 9a) is a strictly convex function subject to
4 Algorithm
The optimization problem (Equation 9a–c) is a constrained convex optimization problem. One commonly used algorithm is the projected gradient descent (PGD) method, which is demonstrated in (Equation 10).
where
where the matrix
The key step in the iteration (Equation 10) is the gradient computation (Equation 11). Obviously, it relies on the network resistance parameter
For the RLS design, we first transform (Equation 5) into a simpler form. Let
Since we only need to estimate
To utilize RLS, we need to transform the matrix
Now we utilize the RLS method to obtain the recursive estimation of
where
To learn
Using the estimation parameter
Then the operator may use (Equation 16) to update
Algorithm 1.PGD-RLS.
Initialization for EV clusters:
Initialization for estimation:
Iteration at
Step 1: The operator measures the voltage
Step 2: EV clusters apply generation power in the network. The operator measures voltage difference
Recover
Next, we will analyze the performance of the proposed algorithm, which includes the estimation accuracy of RLS method (Equations 15a, b) and the convergence of decision variable
Theorem 1. For any initial estimation
for all
Following Lemma 2 and Theorem 3 in Brüggemann and Bitmead (2021), Theorem 1 is easy to prove, which is omitted here. With Theorem 1 guaranteeing the convergence of estimation error, we now intend to prove the convergence of the PGD-RLS Algorithm 1. First, we have a property about the gradient of the cost function (Equation 9a).
Lemma 2. The gradient of the cost function
Proof. For any
If we choose
With Theorem 1 and Lemma 1,2, we have the following theorem about the convergence of the PGD-RLS Algorithm 1.
Theorem 2. With step sizes chosen to satisfy
Proof.
The first inequality holds because the projection operator is nonexpansive while the second inequality holds because of the triangle inequality. For the term
where
For the second term
The inequality holds because
Therefore, we have proved that the decision variable
5 Case study
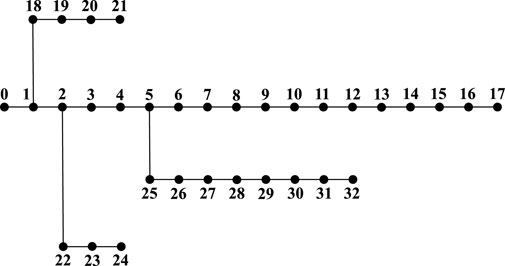
In this section, we validate the PGD-RLS algorithm through simulation results on the 33-bus distribution network shown in Figure 2.
5.1 Simulation setup
For the generation constraints of EV clusters, the lower bound of discharge power is
5.2 Case 1: single period
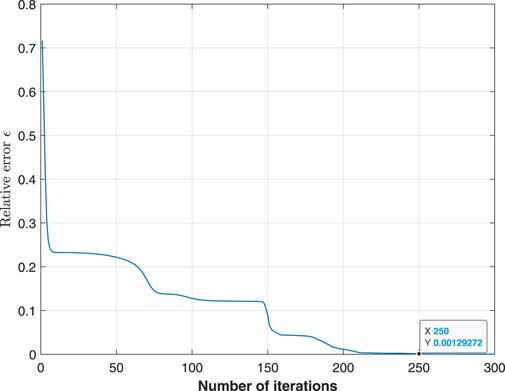
Initially, the distribution network is stable with each voltage within an acceptable range. Then the active load at every node increases by 2%, leading to a voltage drop. To address this, the operator applies our PGD-RLS Algorithm 1 to adjust the discharge power of each EV cluster, aiming to restore the voltage to the desired level.We first demonstrate the convergence of the estimation error, defined as
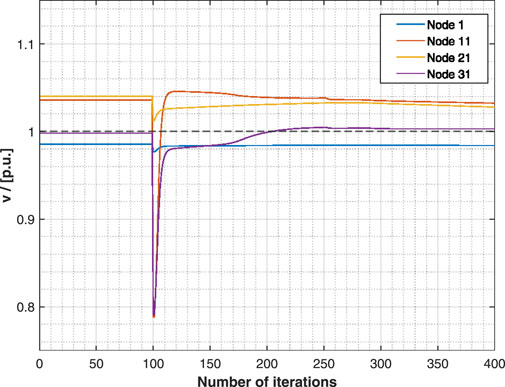
We take the voltage at Node 1, 11, 21, and 31, for example to illustrate the voltage variations during the iterations in Figure 4. When active loads increase, the voltage drops immediately, as shown in the 100th iteration in Figure 4. The operator then utilizes the PGD-RLS algorithm to iteratively adjust the generation power of EV clusters, which causes voltage variation. As seen in Figure 4, the voltage responds quickly to changes in active loads. BlueAfter about 250 iterations, which takes less than 7.5 s on a personal computer, all voltages return to the desired values, which demonstrates the effective regulation performance of our PGD-RLS algorithm 1.
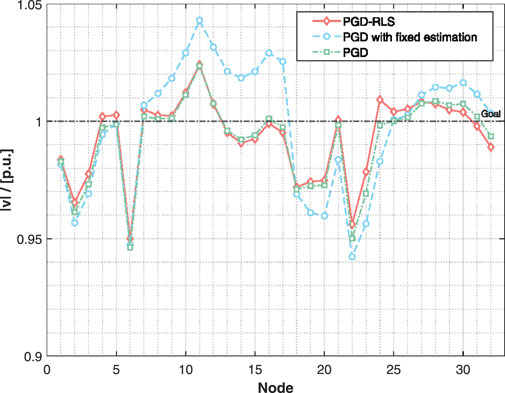
Next, we compare the regulation performance of different algorithms by showing the voltage at all nodes when the algorithms converge to their optimal solutions, as depicted in Figure 5. From Figure 5, we see that the results of the traditional PGD method (Equation 10) (green line with square dots) and the proposed PGD-RLS algorithm (red line with diamond dots) are quite similar with only minor differences. Although the regulation performance of the PGD-RLS algorithm is slightly inferior to that of PGD, it is more practical since it does not require much prior knowledge of the resistance of the distribution network. Additionally, we implement another test case using PGD with fixed estimation (blue line with round dot), i.e. offline estimation. Here the fixed estimation
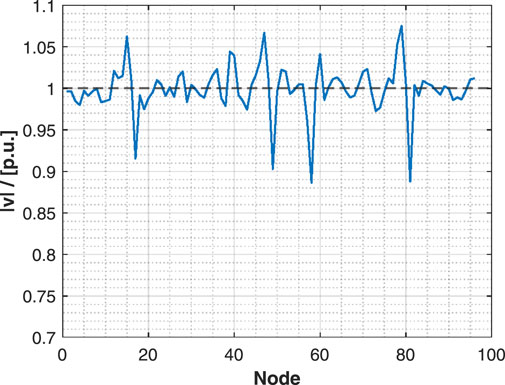
Moreover, we apply our algorithm in the network three times the size of the original one to show the scalability. The result is shown in Figure 6. The figure shows that the voltage of the vast majority of nodes is maintained near the target voltage, with only a few nodes having slightly larger offsets. However, compared to the on-load tap changers method, the voltage regulation performance is clearly better, which demonstrates the scalability of the algorithm.
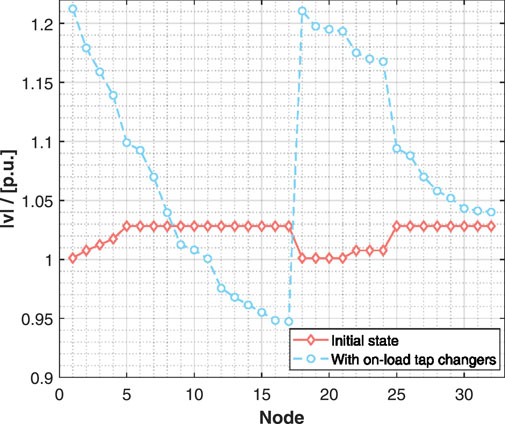
Finally, we add a test case of voltage regulation with on-load tap changers. The result is displayed in Figure 7. At the initial state, the voltage of all nodes is stable with acceptable values. Then the active loads increase by 2%. By utilizing on-load tap changers, we have the voltage of all nodes as shown in Figure 7. It is noticeable that the voltage at the node far away from the tap changer remains relatively low. If we adopt the tap changer to make the lowest voltage acceptable, the voltage of other closer nodes will be too high, as displayed in Figure 7. However, by using EV clusters to realize voltage regulation, we may overcome the drawback of the on-load tap changers method with relatively consistent voltage of all nodes.
5.3 Case 2: Real-life simulation
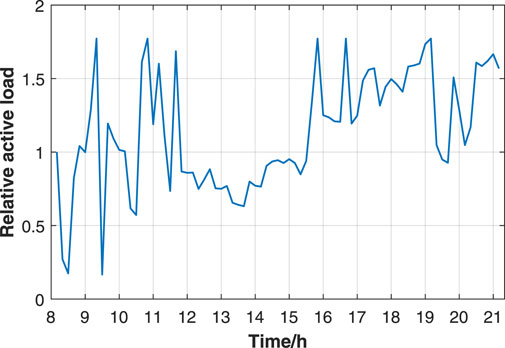
In case 2, we conduct a simulation based on the real-life trend of active load changes. The sampled profiles of active loads are from an online data repository (Hebrail and Berard, 2012). Here we set the active load at 8 a.m. as the reference value and the active load change is shown in Figure 8. The granularity is 10 min. We utilize the voltage loss
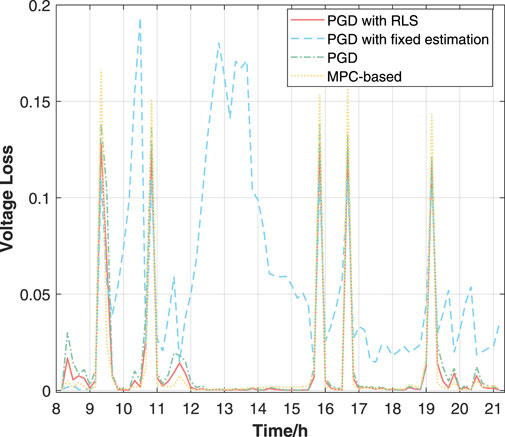
Similar to Case 1, the PGD-RLS Algorithm 1, PGD with fixed estimation algorithm, and the traditional PGD algorithm (10) are tested. The fixed estimation of the coefficient
As shown in Figure 9, in most of the moments, the voltage loss by PGD-RLS and PGD is maintained at less than 0.15 and the difference in the voltage loss is tiny. This further illustrates the effectiveness of the online estimation of parameters using RLS. However, when the active load rises quickly, the voltage loss of PGD-RLS is higher than that of PGD. This is because the estimation value of the coefficient
The PGD with fixed estimation algorithm shows poor regulation performance, as the voltage loss is much higher than that of the other two algorithms. Since the estimation is randomly selected without correction, the gap between the solution of PGD with fixed estimation algorithm and the optimal solution is huge, weakening the performance of voltage regulation badly. This result stresses the necessity of designing effective parameter estimation methods when seeking the optimal solution.
As for the performance of the MPC-based method, it has a similar result with our PGD-RLS algorithm, but with a higher loss. MPC-based methods may perform well if the model is accurate enough. However, the noise always exists in real practice and will decrease the performance of voltage regulation as shown in Figure 9. If the model is more complex, the result will become more unsatisfactory, which is inferior to our PGL-RLS algorithm in scenarios where model information is not precise.
5.4 Sensitivity analysis
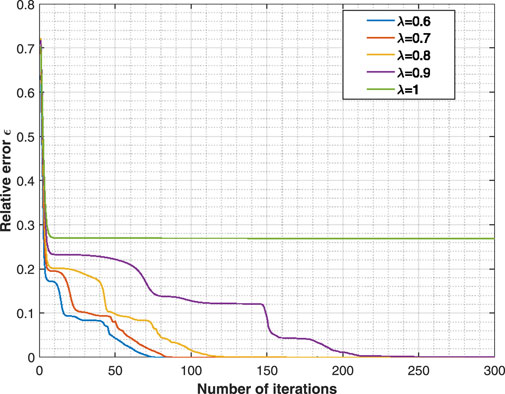
In this subsection, we will analyze the effect of the forgetting factor
We first analyze the impact of the forgetting factor
It is clear that the convergence rate slows as the value of
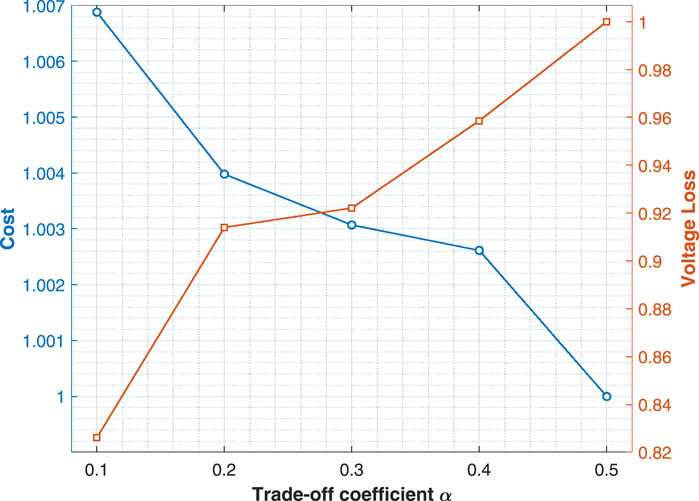
Next, we explore the effect of the trade-off coefficient
From Figure 11, we observe that the cost decreases as the value of
6 Conclusion
In this work, we investigate voltage regulation in distribution networks using EV clusters. By utilizing a feedback-based optimization approach, we formulate a voltage regulation problem to minimize voltage mismatch while keeping the cost of services provided by EV clusters relatively low. To find the optimal solution without precise knowledge of network resistance, we propose a PGD algorithm with an RLS method to enable online estimation of resistance. The accuracy of the RLS online estimation is proved. The convergence of the proposed PGD-RLS algorithm is rigorously guaranteed. Numerical results in the IEEE 33-bus verify the effectiveness of the proposed method for voltage regulation. Future research directions include the decentralization of the proposed framework to allow each EV cluster to individually implement the update of discharge power.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
SL: Conceptualization, Investigation, Methodology, Validation, Writing–original draft, Writing–review and editing. HH: Conceptualization, Resources, Software, Validation, Visualization, Writing–review and editing. JL: Validation, Writing–review and editing. XY: Funding acquisition, Project administration, Supervision, Writing–review and editing. WW: Data curation, Formal Analysis, Validation, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by National Key R&D Program of China (No. 2021YFB2501600) and Jiangsu Funding Program for Excellent Postdoctoral Talent (No. 2023ZB146).
Conflict of interest
Authors SL, HH, and XY were employed by State Grid Jiangsu Electric Power Co., Ltd. Research Institute.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Baran, M. E., and Wu, F. F. (1989). Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 4, 1401–1407. doi:10.1109/61.25627
Beaude, O., He, Y., and Hennebel, M. (2013). “Introducing decentralized ev charging coordination for the voltage regulation,” in IEEE PES ISGT europe 2013, 1–5.
Brüggemann, S., and Bitmead, R. R. (2021). Exponential convergence of recursive least squares with forgetting factor for multiple-output systems. Automatica 124, 109389. doi:10.1016/j.automatica.2020.109389
Farivar, M., Chen, L., and Low, S. (2013). “Equilibrium and dynamics of local voltage control in distribution systems,” in 52nd IEEE Conference on Decision and control (firenze, Italy), 4329–4334.
Feng, K., and Liu, C. (2023). Adaptive dmpc-based frequency and voltage control for microgrid deploying a novel ev-based virtual energy router. IEEE Trans. Transp. Electrification, 1. doi:10.1109/TTE.2023.3319109
Guo, Z., Wei, W., Shahidehpour, M., Wang, Z., and Mei, S. (2022). Optimisation methods for dispatch and control of energy storage with renewable integration. IET Smart Grid 5, 137–160. doi:10.1049/stg2.12063
Hebrail, G., and Berard, A. (2012). Individual household electric power consumption. UCI Mach. Learn. Repos. doi:10.24432/C58K54
Hu, J., Ye, C., Ding, Y., Tang, J., and Liu, S. (2022). A distributed mpc to exploit reactive power v2g for real-time voltage regulation in distribution networks. IEEE Trans. Smart Grid 13, 576–588. doi:10.1109/tsg.2021.3109453
Hu, Q., Bu, S., and Terzija, V. (2021). A distributed p and q provision-based voltage regulation scheme by incentivized ev fleet charging for resistive distribution networks. IEEE Trans. Transp. Electrification 7, 2376–2389. doi:10.1109/tte.2021.3068270
Jia, M., Shen, C., and Wang, Z. (2020). A distributed incremental update scheme for probability distribution of wind power forecast error. Int. J. Electr. Power and Energy Syst. 121, 106151. doi:10.1016/j.ijepes.2020.106151
Johnstone, R. M., Johnson, C. R., Bitmead, R. R., and O. Anderson, B. D. (1982). “Exponential convergence of recursive least squares with exponential forgetting factor,” in 1982 21st IEEE conference on decision and control, 994–997.
Kekatos, V., Zhang, L., Giannakis, G. B., and Baldick, R. (2015a). “Fast localized voltage regulation in single-phase distribution grids,” in 2015 IEEE international Conference on smart grid communications (SmartGridComm) (miami, FL, USA: IEEE), 725–730.
Kekatos, V., Zhang, L., Giannakis, G. B., and Baldick, R. (2015b). Voltage regulation algorithms for multiphase power distribution grids. IEEE Trans. Power Syst. 31, 3913–3923. doi:10.1109/tpwrs.2015.2493520
Li, Y., Li, L., Peng, C., and Zou, J. (2019). An mpc based optimized control approach for ev-based voltage regulation in distribution grid. Electr. Power Syst. Res. 172, 152–160. doi:10.1016/j.epsr.2019.03.003
Li, Y., Tian, X., Liu, C., Su, Y., Li, L., Zhang, L., et al. (2017). “Study on voltage control in distribution network with renewable energy integration,” in 2017 IEEE conference on energy internet and energy system integration (EI2), 1–5.
Liu, Q., Yang, B., Wang, Z., Zhu, D., Wang, X., Ma, K., et al. (2022). Asynchronous decentralized federated learning for collaborative fault diagnosis of pv stations. IEEE Trans. Netw. Sci. Eng. 9, 1680–1696. doi:10.1109/tnse.2022.3150182
Qin, B., Wang, H., Li, F., Liu, D., Liao, Y., and Li, H. (2024a). Towards zero carbon hydrogen: Co-production of photovoltaic electrolysis and natural gas reforming with ccs. Int. J. Hydrogen Energy 78, 604–609. doi:10.1016/j.ijhydene.2024.06.337
Qin, B., Wang, H., Liao, Y., Li, H., Ding, T., Wang, Z., et al. (2024b). Challenges and opportunities for long-distance renewable energy transmission in China. Sustain. Energy Technol. Assessments 69, 103925. doi:10.1016/j.seta.2024.103925
Qin, B., Wang, H., Liao, Y., Liu, D., Wang, Z., and Li, F. (2024c). Liquid hydrogen superconducting transmission based super energy pipeline for pacific rim in the context of global energy sustainable development. Int. J. Hydrogen Energy 56, 1391–1396. doi:10.1016/j.ijhydene.2023.12.289
Shuai, C., Deyou, Y., Weichun, G., Chuang, L., Guowei, C., and Lei, K. (2021). Global sensitivity analysis of voltage stability in the power system with correlated renewable energy. Electr. Power Syst. Res. 192, 106916. doi:10.1016/j.epsr.2020.106916
Sun, Z., Yuan, Z., Zhao, C., and Cortés, J. (2023). Learning decentralized frequency controllers for energy storage systems. IEEE Con. Sys. Let. 7, 3459–3464. doi:10.1109/LCSYS.2023.3332297
ur Rehman, U. (2022). RETRACTED: a robust vehicle to grid aggregation framework for electric vehicles charging cost minimization and for smart grid regulation. Int. J. Electr. Power and Energy Syst. 140, 108090. doi:10.1016/j.ijepes.2022.108090
Wang, J., Jacob, R. A., and Zhang, J. (2023). “Voltage regulation in distribution networks via fleet electric vehicles incentive service,” in 2023 19th international conference on the European energy market (EEM), 1–6.
Wang, J., Wang, Z., Yang, B., Liu, F., Wei, W., and Guan, X. (2024). V2g for frequency regulation service: a stackelberg game approach considering endogenous uncertainties. IEEE Trans. Transp. Electrification, 1. doi:10.1109/tte.2024.3392496
Wang, L., Dubey, A., Gebremedhin, A. H., Srivastava, A. K., and Schulz, N. (2022). Mpc-based decentralized voltage control in power distribution systems with ev and pv coordination. IEEE Trans. Smart Grid 13, 2908–2919. doi:10.1109/tsg.2022.3156115
Wang, S., Du, L., and Li, Y. (2020a). “Decentralized volt/var control of ev charging station inverters for voltage regulation,” in 2020 IEEE transportation electrification conference and expo (ITEC), 604–608.
Wang, Z., Liu, F., Ma, Z., Chen, Y., Jia, M., Wei, W., et al. (2021a). Distributed generalized nash equilibrium seeking for energy sharing games in prosumers. IEEE Trans. Power Syst. 36, 3973–3986. doi:10.1109/tpwrs.2021.3058675
Wang, Z., Liu, F., Su, Y., Yang, P., and Qin, B. (2020b). Asynchronous distributed voltage control in active distribution networks. Automatica 122, 109269. doi:10.1016/j.automatica.2020.109269
Wang, Z., Yang, B., Wei, W., Zhu, S., Guan, X., and Sun, D. (2021b). Multi-energy microgrids: designing, operation under new business models, and engineering practices in China. IEEE Electrification Mag. 9, 75–82. doi:10.1109/mele.2021.3093602
Wu, X., Li, L., Zou, J., and Zhang, G. (2016). “Ev-based voltage regulation in line distribution grid,” in 2016 IEEE international instrumentation and measurement technology conference proceedings (IEEE), 1–6.
Yang, X., Du, X., Lei, J., Zou, C., Zhang, H., Li, B., et al. (2023). “A voltage control method for electric vehicle charging in the new power system,” in 2023 5th international conference on electrical engineering and control technologies (CEECT), 80–84.
Yang, X., Yang, B., Wang, Z., Liu, S., Ma, K., Xu, X., et al. (2024). Online optimal scheduling for battery swapping charging systems with partial delivery. Electr. Power Syst. Res. 235, 110629. doi:10.1016/j.epsr.2024.110629
Yin, K., Tian, Y., Fang, J., Wang, H., Qin, Y., Chen, W., et al. (2023). “A new grid side inertia support control method for cascaded power converters in bi-directional ev chargers,” in 2023 3rd power system and green energy conference (PSGEC), 473–478.
Yumiki, S., Susuki, Y., Oshikubo, Y., Ota, Y., Masegi, R., Kawashima, A., et al. (2022). Autonomous vehicle-to-grid design for provision of frequency control ancillary service and distribution voltage regulation. Sustain. Energy, Grids Netw. 30, 100664. doi:10.1016/j.segan.2022.100664
Zhang, A., Sun, B., Liu, T., Tan, X., Wang, S., and Tsang, D. H. (2018). “Joint voltage and frequency regulation by ev charging scheduling in the distribution network,” in 2018 IEEE power and energy society innovative smart grid technologies conference (ISGT) (IEEE), 1–5.
Zhang, Z., Qin, B., Gao, X., Ding, T., Zhang, Y., and Wang, H. (2024). Se-cnn based emergency control coordination strategy against voltage instability in multi-infeed hybrid ac/dc systems. Int. J. Electr. Power and Energy Syst. 160, 110082. doi:10.1016/j.ijepes.2024.110082
Keywords: EV clusters, voltage regulation, feedback-based optimization, online estimation, recursive least squares
Citation: Lyu S, Han H, Li J, Yuan X and Wang W (2024) Voltage regulation in distribution networks by electrical vehicles with online parameter estimation. Front. Energy Res. 12:1506211. doi: 10.3389/fenrg.2024.1506211
Received: 04 October 2024; Accepted: 18 November 2024;
Published: 04 December 2024.
Edited by:
Ning Qi, Columbia University, United StatesCopyright © 2024 Lyu, Han, Li, Yuan and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaodong Yuan, bGFubnl5dWFuQGpzLnNnY2MuY29tLmNu
 Shukang Lyu1
Shukang Lyu1 Wenyue Wang
Wenyue Wang