- China Energy Engineering Group Jiangsu Power Design Institute Co., LTD., Nanjing, Jiangsu, China
Floating offshore wind turbines (FOWTs) often operate under turbulent wind conditions. However, to enhance computational efficiency, steady wind is sometimes used as an alternative to turbulent wind, potentially resulting in conservative estimates. Assessing FOWT motion and fatigue performance under both steady and turbulent wind conditions is therefore crucial. This study focuses on an enhanced steel semi-submersible FOWT, adapted from the LIFES50+ OO-Star concrete design. The FOWT is modeled using OPENFAST software under various load scenarios, including steady and turbulent winds with irregular waves, for time-domain analysis. The results reveal that the FOWT experiences reduce motion, tension response, blade root loads, and tower-top loads under steady winds combined with irregular waves, compared to turbulent winds with irregular waves. The blade root and tower top loads are lower under steady winds with irregular waves, indicating that steady wind analysis may yield unfavorable outcomes for FOWTs. The findings in this study offer valuable theoretical insights and technical support for the design and evaluation of FOWTs.
1 Introduction
Wind energy is a highly promising clean renewable energy resource, with offshore wind power gaining significant attention for its high wind energy density and consistent wind speeds. According to a report by the Global Wind Energy Council (Author Anonymous, 2024), offshore wind is projected to grow at a compound annual growth rate of 28% over the next 5 years. Offshore wind capacity of 138 GW is anticipated globally within 2024–2028. Offshore wind installations are expected to triple between 2023 and 2028, thereby increasing the share of offshore wind from 9% to 20% in the overall global capacity by 2028. The advancement of floating offshore wind turbines (FOWTs) minimizes land use, enhances energy industry structure, and mitigates energy supply challenges, playing a pivotal role in the optimization of the energy industry.
Wind loads are a critical design factor for FOWT. Three methods currently exist to simulate wind loads on FOWTs: 1) Using static wind force based on the rotor thrust curve; 2) Applying steady wind in the form of a time-domain to the rotor; 3) Simulating turbulent wind in the form of a time-domain according to the operational conditions outlined in IEC 61400–3. In engineering practice, the first two methods are relatively simple to use, while the third one is more complex and time-consuming. However, the last approach is ideal for detailed investigations and certification calculations during the final design process when sufficient design data are available. Nonetheless, the specified approach is incompatible with the iterative nature of early design stages. Therefore, substituting steady wind with turbulent wind is more practical for FOWT design analysis in the early stages. This study aims to compare the response characteristics of FOWTs and their mooring system under both turbulent and steady wind conditions, offering insights into the design of floating offshore wind turbine.
The strong inhomogeneity of the wind makes it crucial to consider the impact of turbulent wind on the kinematics and mooring fatigue performance of FOWTs. Neglecting this factor could lead to premature damage before reaching the maximum design wind speeds and service life. Consequently, it is crucial to investigate the motion and fatigue performance of FOWTs under high and sudden wind speed fluctuations. Previous scholars have explored FOWT motion and fatigue performance under various loads using numerical simulation tools. Yang et al. (2020) examined the effects of wind–wave coupling impacts and decoupling methods on platform motion and mooring cable fatigue, concluding that neglecting coupling effects would overestimate the fatigue damage and that the surge, pitch, and yaw motions of the platform were more sensitive to aerodynamic and hydrodynamic loads. Kvittem and Moan (2015) examined the loading conditions leading to significant fatigue damage in FOWTs, identifying blade resonance and longitudinal platform motion as major contributors to short-term fatigue. Accurately capturing resonant responses is critical when selecting load cases for fatigue analysis. It is also essential to choose load cases that minimize fatigue damage for a more realistic estimation of fatigue life. Bachynski and Eliassen (2019) analyzed the response differences of three 5 MW FOWT types, namely, semi-submersible, spar, and TLP, under Mann and Kaimal turbulent wind fields. The study revealed that floating wind turbines were more sensitive to low-frequency variations than bottom-fixed offshore wind turbines, with the most significant differences in motion response and mooring cable occurring at low frequencies below wave frequency. Antonutti et al. (2016) examined the coupling effects caused by changes in the hydrodynamic behavior of a floating wind turbine under a significant inclination angle due to wind loading. Time-domain simulations reveal that both the geometrically non-linear effects of the floater and the variations in viscous hydrodynamics considerably influence the dynamics of typical floating wind turbines in wave conditions. Li H. et al. (2024), Li Y. et al. (2024) studied the transient deformations of the tower and blades of a spar-type floating wind turbine in extreme wave conditions.
Taking a simulation time wind series length of 600 s as an example, For turbulent wind, it will take 15 min. For steady wind, it only need 50 s, less than 1 min. The simulation time required for turbulent wind is 18 times that for steady wind in one case. In engineering design, thousands of total cases need to be considered. Therefore, the total calculation time for turbulent wind is much longer than that for steady wind. However, at the early of the design process, a lot of parameters need to be iterative and optimized. In such situations it would be convenient to replace the steady wind with turbulent wind to carry out the parameter optimization and iteration. This will save a lot of time. Based on this, we studied Influence of Steady and turbulent wind on the motions, mooring tension and fatigue performance of floating offshore wind turbine.
This study introduces a novel methodology for load selection in the design and optimization of floating platforms and mooring systems for offshore wind turbines. Numerical simulations are conducted using the OpenFast software. The study examines the impact of steady and turbulent winds on the motion and fatigue performance of a new floating wind turbine, featuring an enhanced steel semi-submersible with a LIFES50+ OO-Star concrete structure, offering valuable theoretical guidance and technical support for the calculations of floating wind turbine design (Wang Shuaishuai et al., 2023).
The remainder of this paper is organized as follows. Section 2 presents the methodology. Section 3 discusses the research objective. Section 4 presents the results and discussion. Finally, Section 5 concludes the study.
2 Methodology
2.1 Numerical simulation tool
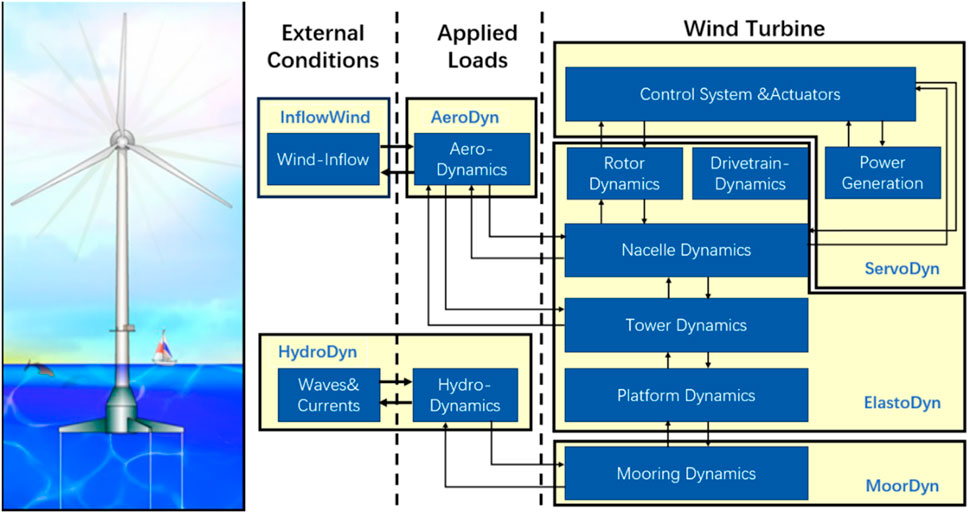
Recently, the National Renewable Energy Laboratory (NREL) has developed OpenFAST, a fully coupled aerodynamic-hydrodynamic-servoelastic tool, that utilizes the boundary element method and potential flow theory (Jonkman J. M., 2009). Figure 1 illustrates the time-domain coupling process of OpenFAST. In this study, the hydrodynamic coefficients of the platform were derived using ANSYS/AQWA, while the inflow wind module was used to derive the wind loads. The HydroDyn module calculates instantaneous substructure displacements based on the buoyancy at each time step. This module directly captures the hydrostatic restoring forces using strip theory, eliminating the need for an additional stiffness matrix (Jonkman et al., 2014). The Reference Open Source Controller (ROSCO), developed by Delft University of Technology, was selected as the control system (Abbas et al., 2020). Aerodynamic efficiency was optimized by adjusting the pitch angle. Within the wind speed range between the cut-in and rated wind speeds, the wind turbine operates at peak aerodynamic efficiency. Above the rated wind speed, the turbine limits output to the rated power to protect the blade structure.
2.2 Time domain equation of motion
FOWTs are commonly exposed to complex environmental loads, including wind, hydrodynamic, and mooring system loads. The time-domain coupled dynamic analysis model can be expressed in Equation 1:
where
2.3 Fatigue damage calculation
The impact of loading on fatigue damage was evaluated by calculating short-term fatigue damage, focusing on specific load components, including blades, towers, and mooring cables. A MATLAB-based program developed by NREL was used to compute the short-term fatigue damage equivalent load (DEL) for each component under various environmental conditions.
DEL represents a constant-amplitude fatigue load with a fixed mean and frequency, causing damage equivalent to variable-spectrum loading. MLife calculates short-term DELs for each input time series using the S–N curve method. The rainflow-counting algorithm identifies cycle counts for different mean loads and load ranges. Short-term DELs are determined in Equations 2–5 (Hayman, 2012):
where
3 Research objective
3.1 Wind turbine parameters
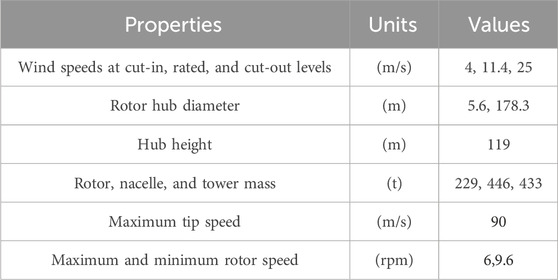
DTU, in collaboration with Vestas, developed a reference 10 MW wind turbine as part of the Light Rotor project (Bak et al., 2012). The specifications for the DTU 10 MW wind turbine are summarized in Table 1.
3.2 Platform parameters
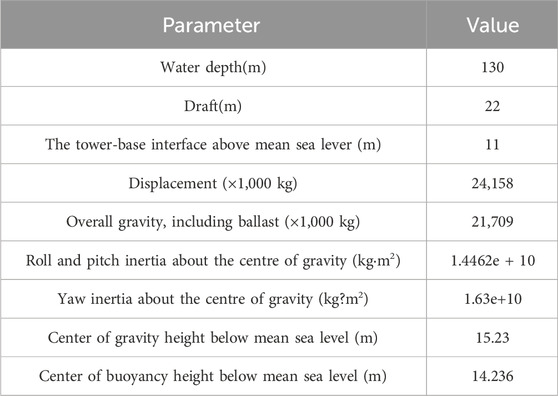
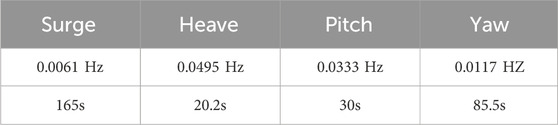
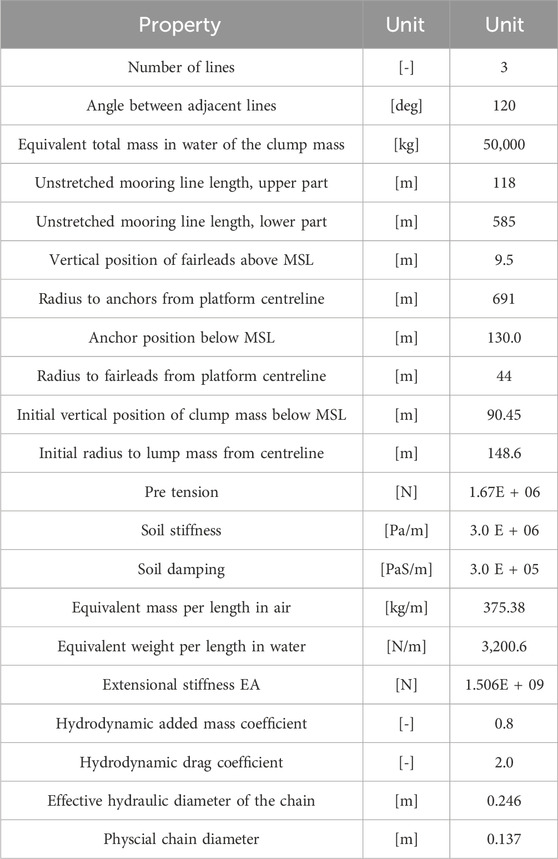
This study discusses a modified steel semi-submersible floating foundation, with a concrete structure, based on the LIFES50+ OO-Star design. The sketch and key dimensions of the 10 MW steel semi-submersible platform are shown in Figure 2 (Berthelsen, 2015), with detailed parameters of the platform provided in Table 2. The natural period of the platform is listed in Table 3.
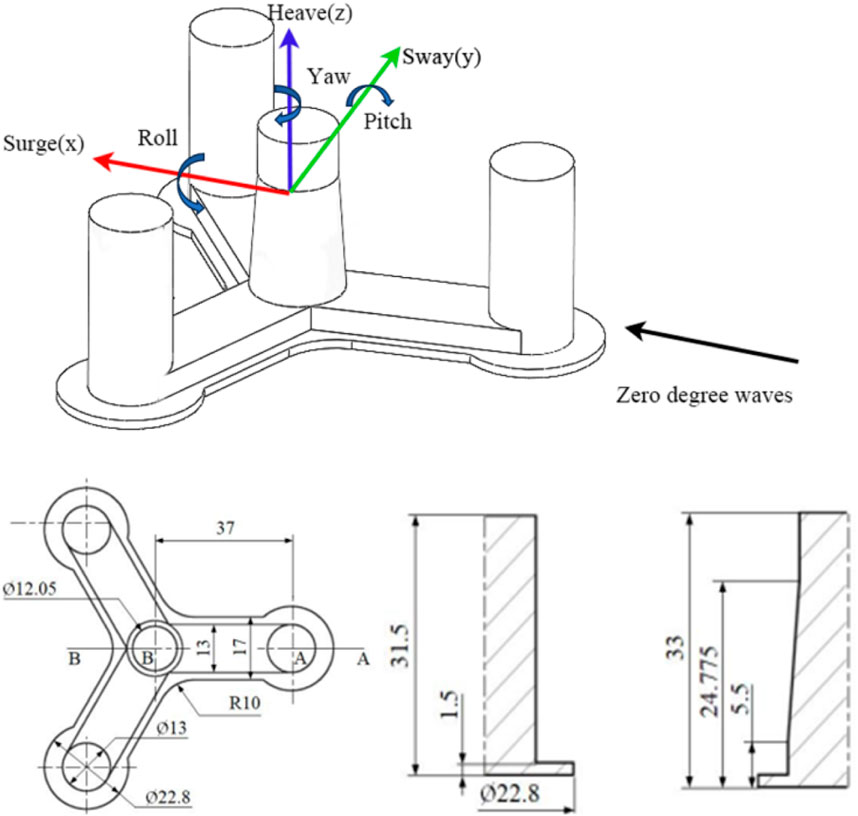
Figure 2. Overview and key dimensions of the 10 MW steel based on semi-submersible platform (Wang S. et al., 2023).
3.3 Mooring system parameters
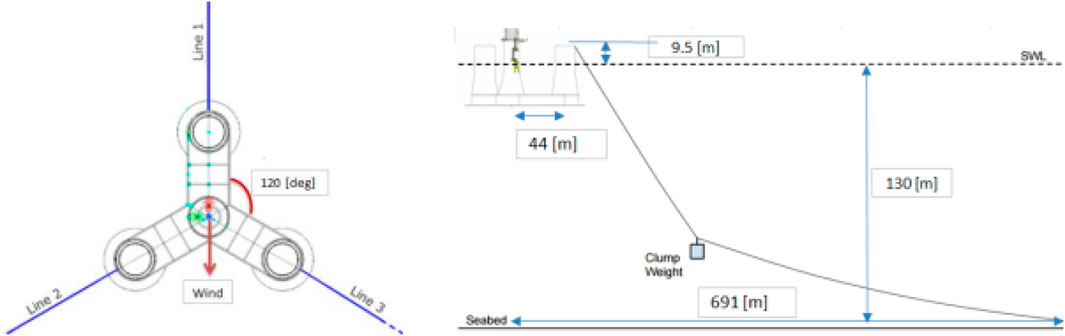
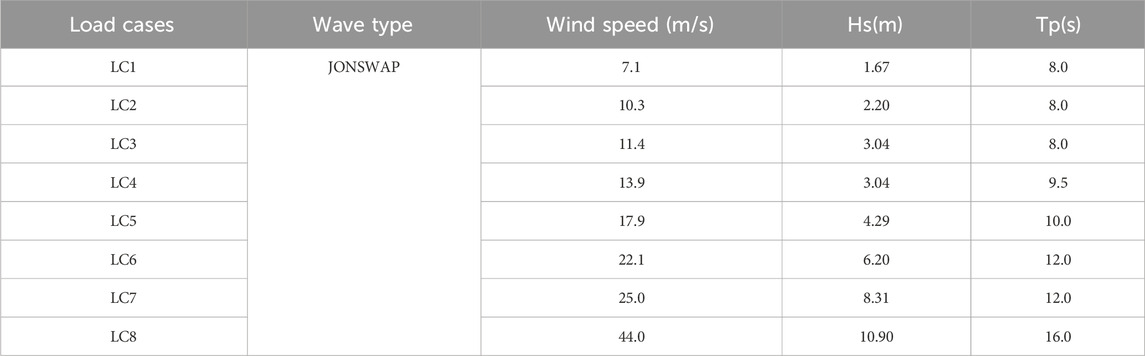
Figure 3 illustrates the mooring system layout, which includes three chains arranged at a horizontal angle of 120°. The blocks were attached to each line, dividing it into two segments. Both sections, lying above and below the bundled mass, have identical chain parameters, with the upper section connected to the cable guide, measuring 160 m long. The lower section measures 543 m. Key mooring system parameters are summarized in Table 4.
3.4 Environmental conditions
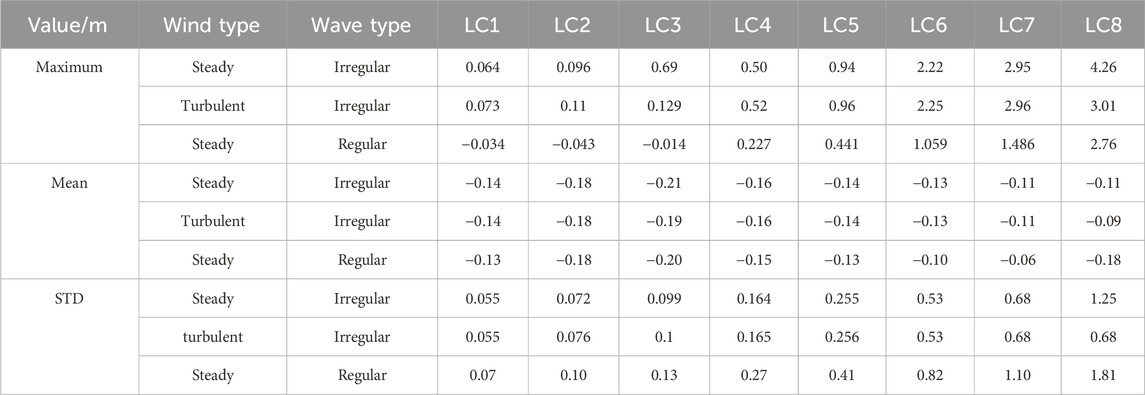
Table 5 presents the representative set of conditions based on the sea state in the Gulf of Maine, demonstrating the numerical model, with the wind turbulence set to level C (Pegalajar-Jurado et al., 2018). LC1–LC7 represent the FOWT operating conditions, while LC8 denotes the parked state.
The three-dimensional (3D) turbulent wind field was generated in TurbSim using IEC Kaimal spectra (Jonkman B. J., 2009). This model, outlined in IEC 61400–1 s (Author Anonymous, 1999) and third (Author Anonymous, 2005) editions, defines the wind components in three directions, represented by K = u, v, and w, in Equation 6:
where
where
The relationships between the STDs are defined in Equation 9:
where
We present a 3D representation of the wind field time history at Uref = 11.4 m/s to highlight wind field variations, as depicted in Figure 4. The figures provided in this section offer essential insights for analyzing platform motion and load.
The irregular waves used for the calculations were based on JONSWAP wave spectra. The wave heights and spectral peak periods for different wind speeds and sea states are provided in Table 5.
4 Results and discussion
4.1 Effect of different load coupling on FOWT motion
This section examines the influence of wave loads, turbulent wind, and steady wind loads on the motion of a floating platform. The specified platform is defined by the movement and rotation around its center of mass.
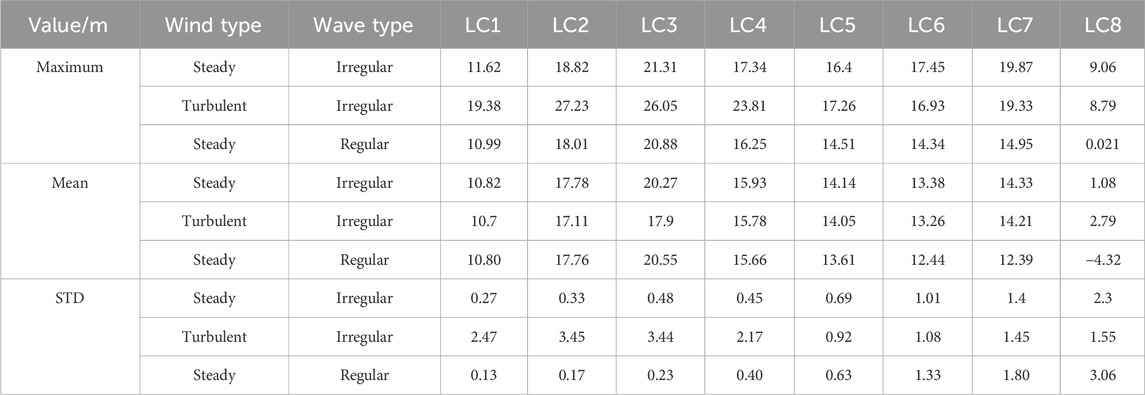
With a load incidence angle of 0° and platform symmetry, only the power spectral densities of heave, surge, and pitch are evaluated. Figure 5 presents the power spectral density response of the heave under turbulent, steady, and no wind conditions for all LCs in Table 5. As illustrated in Figure 5, the power spectral density peaks around 0.1 Hz, aligning with the wave frequency. The low-frequency response is concentrated near 0.05 Hz, corresponding to the heave natural frequency.
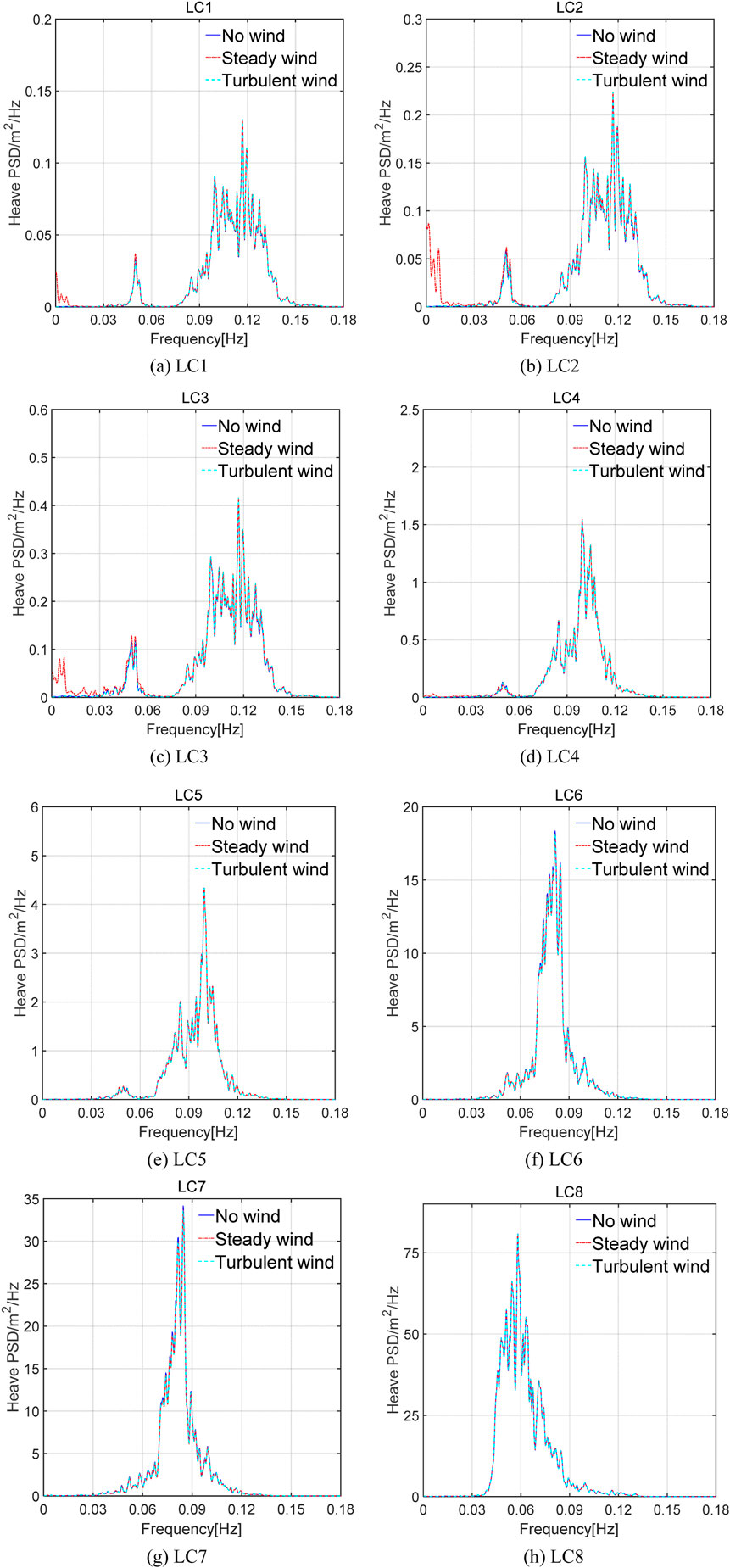
Figure 5. Power spectral distribution of the platform’s heave motion. (A) LC1. (B) LC2. (C) LC3. (D) LC4. (E) LC5. (F) LC6. (G) LC7. (H) LC8.
For all LCs, the power spectral density amplitude is predominantly influenced by the wave loads. Consequently, the heave motion of FOWT is largely governed by wave loads, with minimal influence from wind loads.
Figure 6 presents the power spectral density response of the platform surge motion under steady, turbulent, and no wind conditions. For LC5–LC8, the surge motion exhibits multiple peaks, corresponding to both wind and wave frequencies.
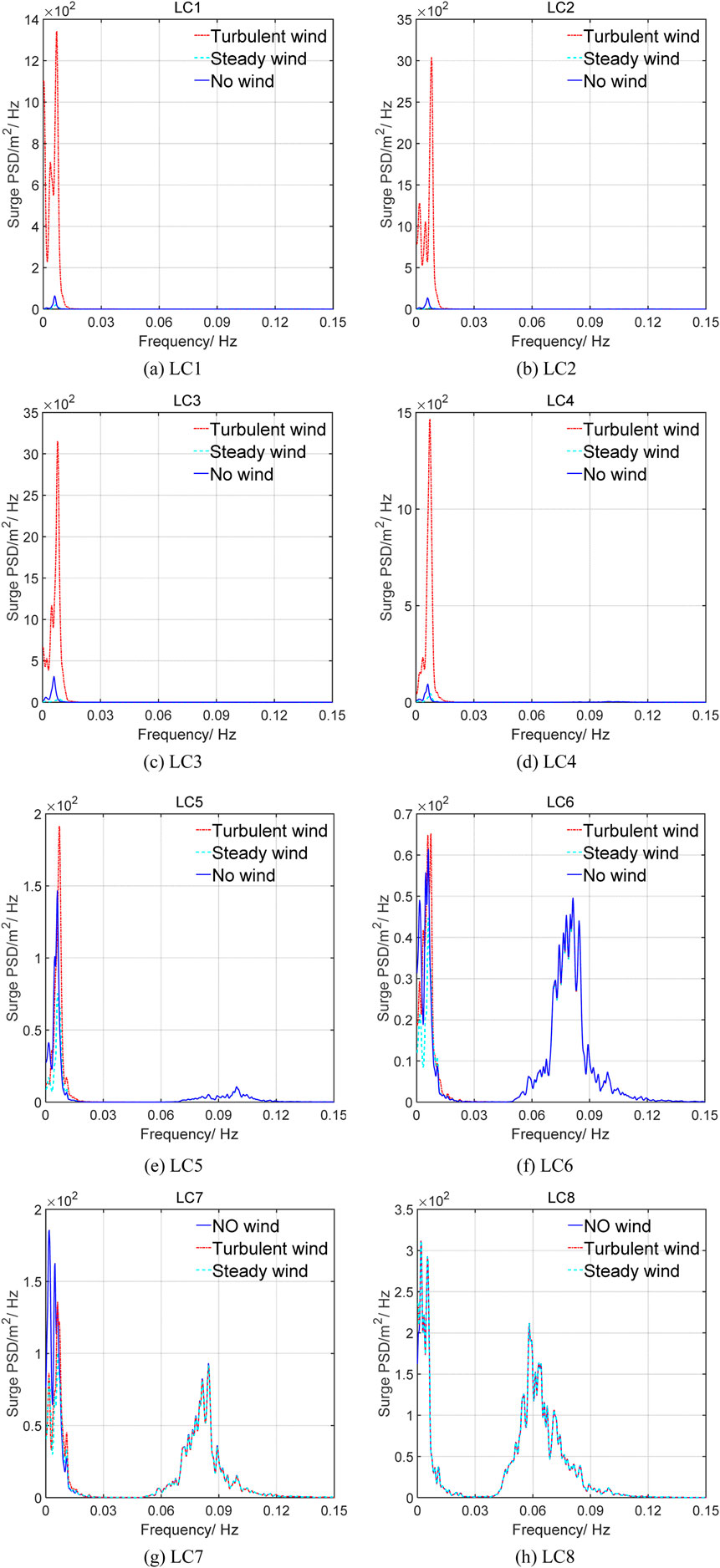
Figure 6. Power spectral distribution of the platform’s surge motion. (A) LC1. (B) LC2. (C) LC3. (D) LC4. (E) LC5. (F) LC6. (G) LC7. (H) LC8.
The surge motion is primarily driven by the wind and wave load. The power density spectrum under turbulent wind spans 0.0001–0.012 Hz, reflecting the low-frequency nature of turbulent wind. This phenomenon leads to an increased low-frequency response and an amplified response at the natural frequency of the platform. In the parked condition (LC8), the power density spectrum of the platform motion under the steady wind is similar to that under the no-wind condition. The coupling effect of turbulent wind and waves enhances the platform’s response at its natural frequency.
Figure 7 displays the pitch power density spectra under steady, turbulent, and no wind conditions, each exhibiting different characteristics. For LC1–LC5, the low-frequency response predominates, with wave frequency having minimal impact. In contrast, for LC8, wave frequency, corresponding to 0.0625 Hz, is the dominant factor. For LC6 and LC7, multi-peaks indicate that the pitch of FOWT is influenced by both wind and wave loads. Overall, turbulent wind has a more significant effect on the pitch of FOWT than that of steady wind.
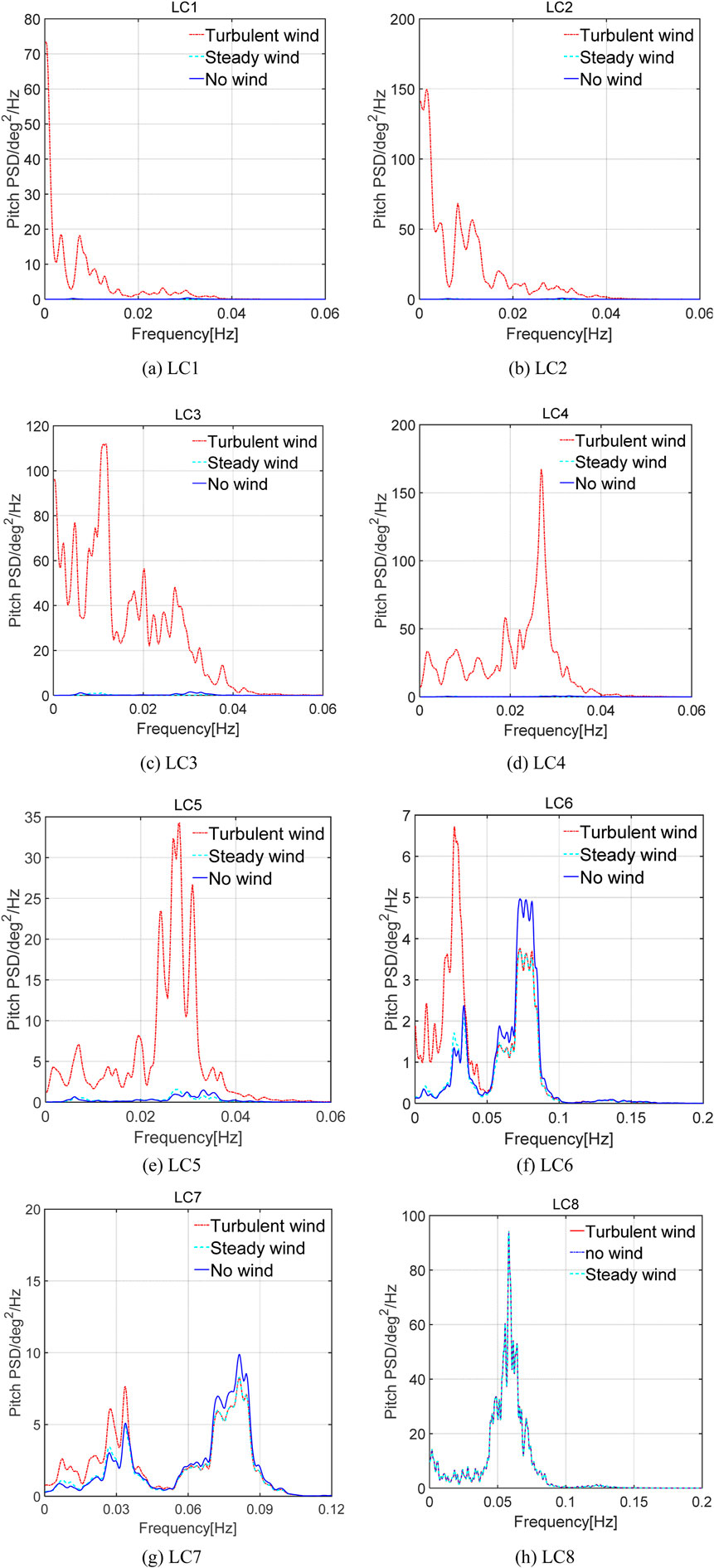
Figure 7. Power spectral distribution of the platform’s pitch motion. (A) LC1. (B) LC2. (C) LC3. (D) LC4. (E) LC5. (F) LC6. (G) LC7. (H) LC8.
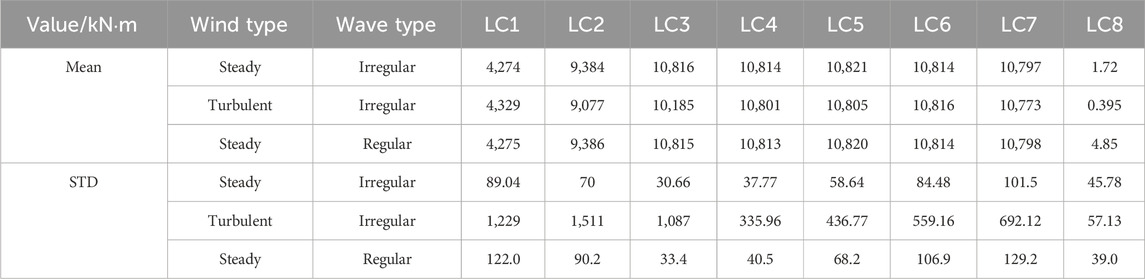
Tables 6–8 present the statistical values—maximum, mean, and variance—of the platform’s heave, surge, and pitch motions. Table 6 highlights that the maximum, mean, and STD of the heave motions are similar under turbulent and steady winds. This observation supports the conclusion depicted in Figure 5 that wave loads primarily govern heave motion. Tables 7 and 8 reveal that the maximum values of surge and pitch motions under turbulent winds occur at rated wind speeds. As low-frequency winds, turbulent winds cause variations in the maximum values and STDs of the platform motions, consistent with the power density spectral responses illustrated in Figures 6, 7. The mean surge and pitch values show minimal variations between turbulent and steady winds. Therefore, non-zero mean drift values of surge and pitch under wind–wave coupling can be derived using steady wind.
4.2 Effect of different load coupling on mooring line tension and fatigue performance
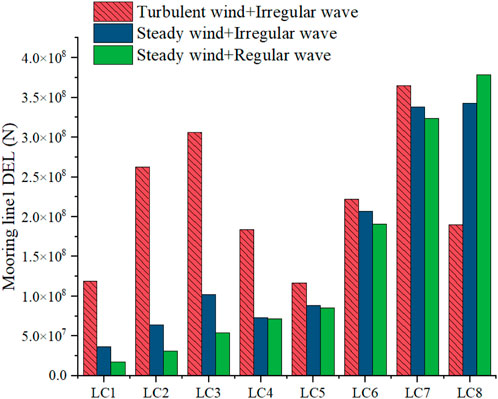
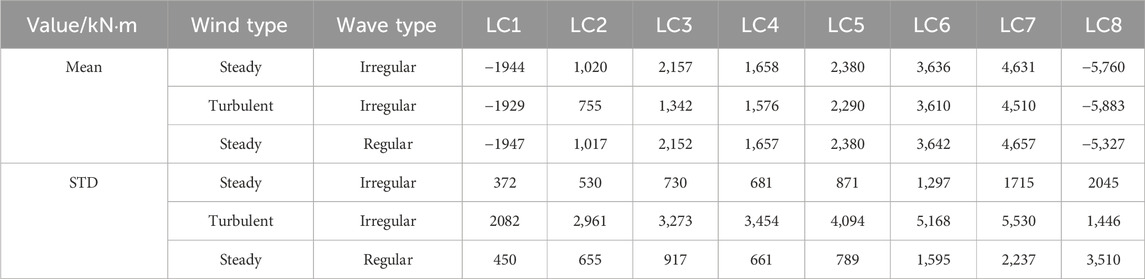
The layout of the mooring system is symmetrically aligned with the wind and wave directions, placing mooring line 1 upwind and mooring lines 2 and 3 downwind. These results indicate that mooring line 1 experiences greater tension than lines 2 and 3 under wind and wave conditions, exhibiting the greatest maximum and average tension values. Therefore, this study emphasizes the tension and fatigue performance of mooring line 1.
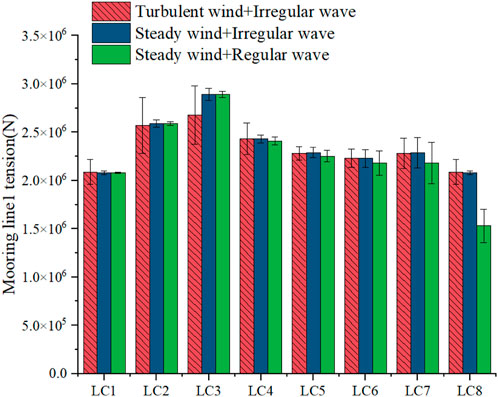
Wang and Xing (Li H. et al., 2024) found that the mean values of platform mooring line tension were nearly identical, while the STDs varied under different environmental conditions. This finding aligns with the conclusion reached in Figure 8. The study investigates the effects of turbulent and steady winds, coupled with waves, on the new FOWT mooring system. The tension in mooring line 1 was compared between steady and turbulent winds, both coupled with waves.
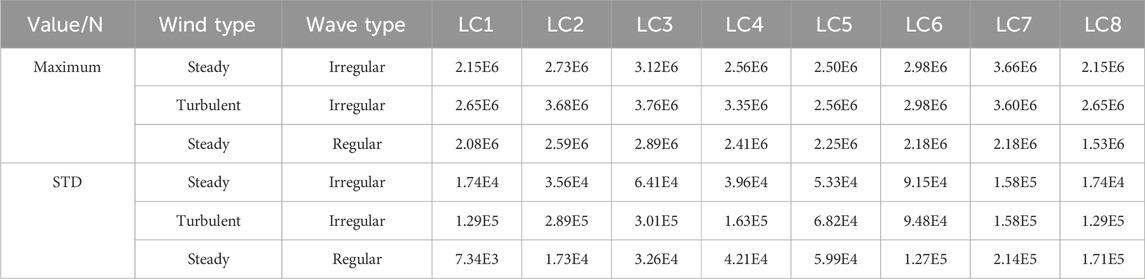
Table 9 presents the maximum and STD values of mooring tension under various operating conditions. For LC1–LC5, using steady winds for FOWT mooring analysis yields overly conservative results, with the maximum tension reduced by 2%–26%, and the STD of tension atop the mooring cable decreased by 22%–88%. This discrepancy significantly impacts the fatigue life of the mooring system. Figures 8, 9 presents the short-term DELs of the mooring system under various operating conditions to examine the impact of both load types on fatigue life. Under operating conditions, the short-term DELs derived from the steady wind analysis are 7%–76% lower, whereas under parked conditions, they are higher. When evaluating the fatigue life of the mooring system, steady state wind analysis under operating conditions presents a dangerous estimate, while steady wind analysis under parked conditions ensures higher safety levels.
4.3 Effect of different load coupling on the load and fatigue properties of blade roots and tower-top/yaw bearing
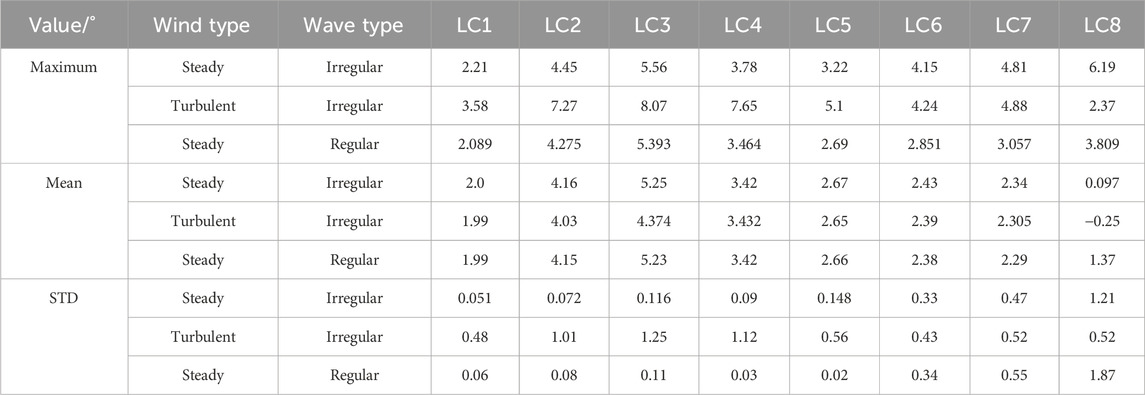
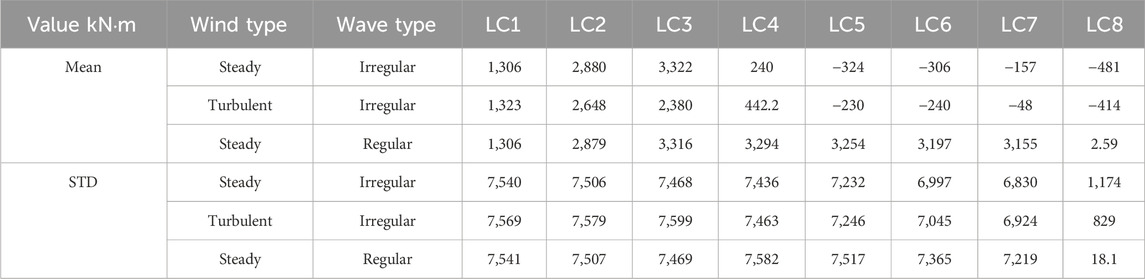
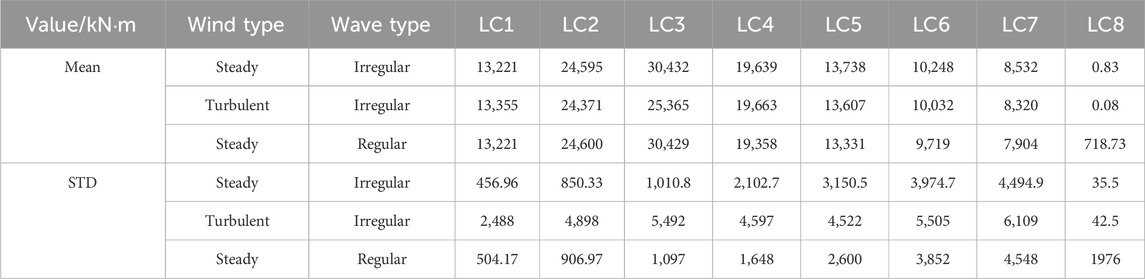
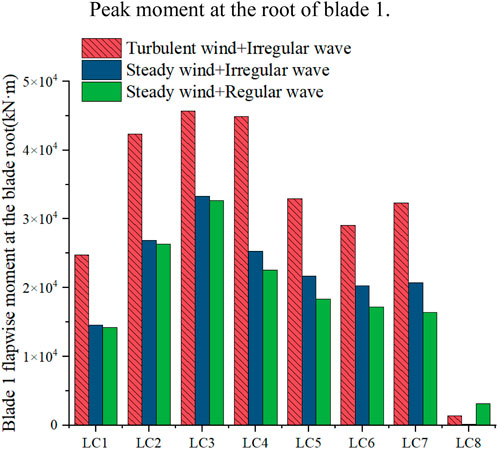
Tables 10 and 11 display the statistical values of the mean and STD of the edgewise and flapwise moments at the blade root. Figure 10 illustrates the maximum bending moment at the blade root. The maximum values of the edgewise and flapwise moments at the blade root, under turbulent winds, occur at rated wind speeds. The low-frequency response of turbulent winds causes variations in both the maximum values and STDs of these moments, significantly affecting the fatigue life of the blade root. Figure 11 presents the short-term DELs under different operating conditions to assess the impact of these load types affecting the blade root’s fatigue life. Under operating conditions, short-term DELs derived from steady wind analysis are 10%–27% lower, whereas they are higher under parked conditions. This finding indicates that when analyzing the fatigue life of the blade root, the steady wind analysis under operating conditions suggests a higher risk to fatigue life, while the steady wind analysis under parked conditions offers greater safety. The mean values of the blade root moment show no significant differences between turbulent and steady winds. This observation suggests that, although turbulent winds increase peak moments and variability, the overall average load remains unchanged across both wind conditions. Resultantly, the average load values of the blade root under wind–wave coupling can be derived using steady wind conditions.
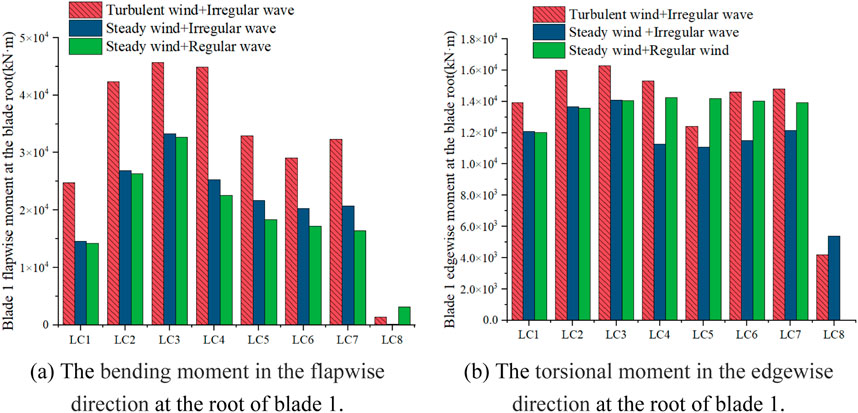
Figure 10. Peak moment at the root of blade 1. (A) The bending moment in the flapwise direction at the root of blade 1. (B) The torsional moment in the edgewise direction at the root of blade 1.
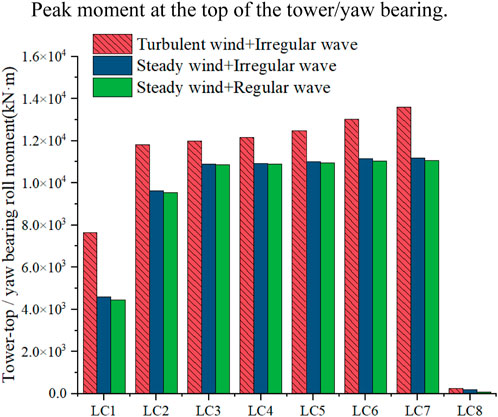
Tables 12 and 13 display the mean and STD of the roll and pitch moments at the tower top/yaw bearing. Figures 11, 12 shows the maximum bending moments at the tower top/yaw bearing for both roll and pitch. Under operating conditions, the maximum and STD values vary due to directional shifts of turbulent winds, significantly impacting the fatigue life of the tower top/yaw bearing. Figures 13–15 presents the short-term DELs under different conditions to assess the impact of these two load types on the fatigue life of the tower top/yaw bearing. During operation, the short-term DEL obtained from steady wind analysis is 70%–80% lower, while under parked conditions, it is higher. The mean moments at the tower top/yaw bearing exhibit no significant difference between turbulent and steady wind conditions. This observation suggests that, while turbulent winds increase peak moments and variability, the overall average load remains unchanged across both wind conditions. Consequently, steady winds can be used to determine the overall average load on the tower top/yaw bearing under wind–wave coupling conditions.
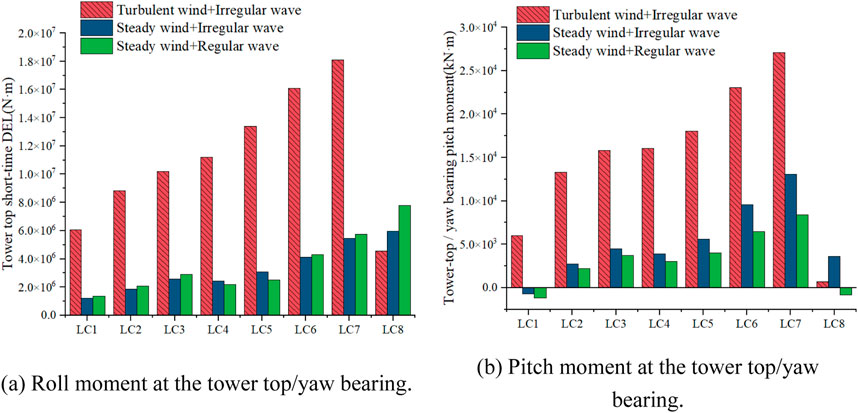
Figure 12. Peak moment at the top of the tower/yaw bearing. (A) Roll moment at the tower top/yaw bearing. (B) Pitch moment at the tower top/yaw bearing.
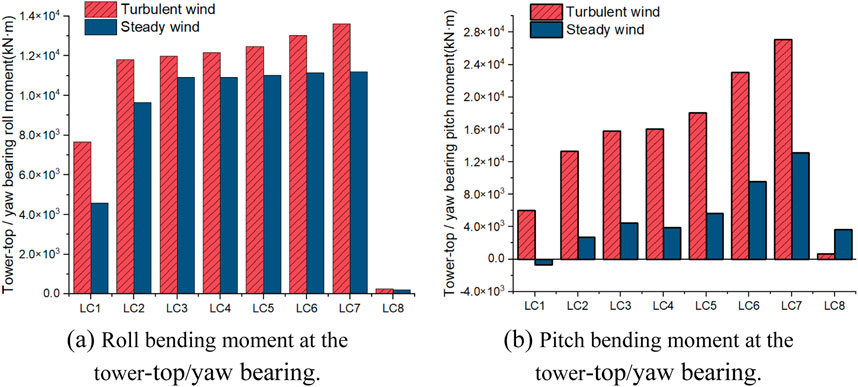
Figure 14. Peak bending moment at the tower-top/yaw bearing. (A) Roll bending moment at the tower-top/yaw bearing. (B) Pitch bending moment at the tower-top/yaw bearing.
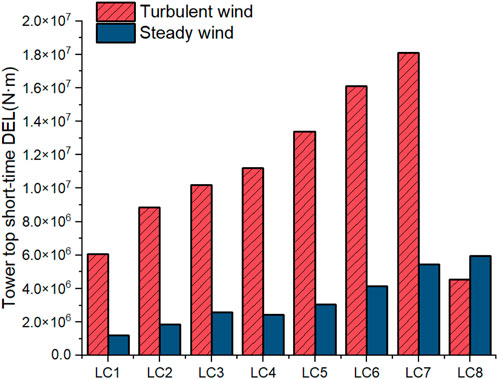
Figure 15. Comparison of the short-term DEL at the tower top under turbulent and constant wind conditions.
5 Conclusion
This study presents a fully coupled simulation of a 10 MW floating wind turbine subjected to varying wind and wave loads. The study examines the platform motion, dynamic response, and fatigue loading of the mooring system and blade root under turbulent and steady wind conditions. The key conclusions are as follows:
The mean motions of the FOWT, derived from steady winds, and the dynamic response of the mooring system do not significantly differ from those under turbulent winds. For LC1–LC5, using steady winds to analyze the floating wind turbine motion and mooring system dynamics reveals notable differences, with maximum tension reduced by 2%–26% and the STD decreased by 22%–88%. This discrepancy highlights the significant impact of turbulent winds on the motion performance and mooring tension of FOWTs.
The average values of blade root and tower-top/yaw bearing calculated under steady wind conditions exhibit little variation when compared to those computed under turbulent wind conditions. However, under operational conditions, the analysis of steady wind reveals significant differences between the maximum values and the STD of moments at both the blade root and the tower top. Consequently, the fatigue loads at the blade root and tower top are decreased by 10%–27% and 70%–80%, respectively. In contrast, under parked conditions, short-term fatigue loads at both the blade root and tower top increase, highlighting the significant effect of turbulent wind on fatigue durability. However, for the preliminary design phase, it is suggested to use steady wind simulations to improve computational efficiency.
Considering the requirements of practical design work, it is recommended to adopt different approaches for the design of floating wind turbine mooring systems at various design stages. During the initial design stage, the steady wind method can be employed to enhance efficiency. At the detail design stage, a turbulent wind model should be used to review critical operating conditions and adjust the design parameters accordingly.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
JS: Writing–original draft, Writing–review and editing. XG: Conceptualization, Data curation, Formal Analysis, Methodology, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
We thank LetPub (www.letpub.com.cn) for its linguistic assistance during the preparation of this manuscript.
Conflict of interest
Authors JS and XG were employed by China Energy Engineering Group Jiangsu Power Design Institute Co. LTD.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbas, N. J., Wright, A., and Pao, L. (2020). An update to the national renewable energy laboratory baseline wind turbine controller. J. Phys. Conf. Ser. IOP Pub. 1452 (1), 012002. doi:10.1088/1742-6596/1452/1/012002
Antonutti, R., Peyrard, C., Johanning, L., Incecik, A., and Ingram, D. (2016). The effects of wind-induced inclination on the dynamics of semi-submersible floating wind turbines in the time domain. Renew. Energy 88 (2016), 83–94. ISSN 0960-1481. doi:10.1016/j.renene.2015.11.020
Author Anonymous (1999). IEC 61400-1 “Wind turbine generator systems-Part 1: safety requirements.”. 2nd edition. Geneva, Switzerland: International Electrotechnical Commission.
Author Anonymous (2005). IEC 61400-1 “Wind turbines-Part 1: design requirements.”. 3rd edition. Geneva, Switzerland: International Electrotechnical Commission.
Bachynski, E. E., and Eliassen, L. (2019). The effects of coherent structures on the global response of floating offshore wind turbines. Wind Energy 22, 219–238. doi:10.1002/we.2280
Bak, C., Bitsche, R., Yde, A., Kim, T., Hansen, M., Zahle, F., et al. (2012). Light rotor: the 10-MW reference wind turbine. 1.
Berthelsen (2015). Petter A Qualification of innovative floating substructures for 10MW wind turbines and water depths greater than 50m.
Jonkman, B. J. (2009a). TurbSim user's guide: version 1.50. Golden, CO (United States): National Renewable Energy Lab. NREL.
Jonkman, J. M. (2009b). Dynamics of offshore floating wind turbines—model development and verification. Wind Energ 12, 459–492. doi:10.1002/we.347
Jonkman, J. M., Robertson, A. N., and Hayman, G. J. (2014). HydroDyn user’s guide and theory manual. National Renewable Energy Laboratory.
Kvittem, M. I., and Moan, T. (2015). Time domain analysis procedures for fatigue assessment of a semi-submersible wind turbine. Mar. Struct. 40, 38–59. ISSN 0951-8339. doi:10.1016/j.marstruc.2014.10.009
Li, H., Li, Y., Li, G., Zhu, Q., Wang, B., and Tang, Y. (2024a). Transient tower and blade deformations of a Spar-type floating wind turbine in freak waves. Ocean. Eng. 294, 116801. doi:10.1016/j.oceaneng.2024.116801
Li, Y., Li, H., Wang, B., Meng, H., Su, O., and Tang, Y. (2024b). Effects of various freak waves on dynamic responses of a Spar-buoy floating offshore wind turbine. Ocean. Eng. 311, 118837. doi:10.1016/j.oceaneng.2024.118837
Pegalajar-Jurado, A., Bredmose, H., Borg, M., Straume, J. G., Landbø, T., Andersen, H. S., et al. (2018). State-of-the-art model for the LIFES50+ OO-Star Wind Floater Semi 10MW floating wind turbine. J. Phys. Conf. Ser. 1104, 012024. doi:10.1088/1742-6596/1104/1/012024
Wang, S., Moan, T., and Gao, Z. (2023b). Methodology for global structural load effect analysis of the semi-submersible hull of floating wind turbines under still water, wind, and wave loads. Mar. Struct. 91, 103463. doi:10.1016/j.marstruc.2023.103463
Wang, S., Xing, Y., Balakrishna, R., Shi, W., and Xu, X. (2023a). Design, local structural stress, and global dynamic response analysis of a steel semi-submersible hull for a 10-MW floating wind turbine. Eng. Struct. 291, 116474. doi:10.1016/j.engstruct.2023.116474
Keywords: floating offshore wind turbine (FOWT), turbulent wind, steady wind, motion, mooring tension
Citation: Shu J and Gu X (2025) Influence of steady and turbulent wind on motions, mooring tension, and fatigue performance of a steel OO-Star floating offshore wind turbine. Front. Energy Res. 12:1505538. doi: 10.3389/fenrg.2024.1505538
Received: 03 October 2024; Accepted: 06 December 2024;
Published: 07 January 2025.
Edited by:
Renwei Ji, Jiangsu University of Science and Technology, ChinaReviewed by:
Yihan Xing, University of Stavanger, NorwayShuaishuai Wang, Norwegian University of Science and Technology, Norway
Yan Li, Tianjin University, China
Copyright © 2025 Shu and Gu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jiaqing Shu, c2h1amlhcWluZ0Bqc3BkaS5jb20uY24=
 Jiaqing Shu
Jiaqing Shu Xiaoqing Gu
Xiaoqing Gu