Hybrid MPPT control using hybrid pelican optimization algorithm with perturb and observe for PV connected grid

Introduction: Photovoltaic systems offer immense potential as a future energy source, yet maximizing their efficiency presents challenges, notably in achieving optimal voltage due to their nonlinear behavior. Operating current and voltage fluctuations, driven by temperature and radiation changes, significantly impact power output. Traditional Maximum Power Point Tracking (MPPT) methods struggle to adapt accurately to these dynamic environmental conditions. While Artificial Intelligence (AI) and optimization techniques show promise, their implementation complexity and longer attainment times for Maximum Power Point (MPP) hinder widespread adoption.

Method: This paper proposes a hybrid MPPT technique that integrates the Pelican Optimization algorithm (POA) with the Perturb and Observe algorithm (P&O) for a grid-connected photovoltaic system (PV). The proposed technique consists of two loops: PO as the reference point setting loop (inner loop) and POA as a fine-tuning (outer)loop. The combination of inner and outer loops minimizes oscillations by adjusting the perturbation direction and enhancing the convergence speed of the MPPT.

Results and Discussion: To validate the efficacy of the proposed MPPT technique for different environmental conditions, a comprehensive comparison is conducted between the proposed hybrid pelican and perturb and observe (HPPO) technique and other MPPT algorithms. The proposed technique has optimized PV and grid outputs with an MPPT efficiency of 99%, best tracking speed, and total harmonic distortion (THD) for all conditions below 5% agree with IEEE 519 standards.

1 Introduction

The integration of non-conventional energy sources, particularly photovoltaic (PV) systems, into the grid, has garnered considerable attention due to their capacity to alleviate environmental issues and meet the growing energy demand worldwide. Optimizing PV system energy output while guaranteeing effective power transfer to the grid is a crucial area of research (Dutta et al., 2018). The PV system’s power generation is subject to variations in weather-related factors, including load, solar irradiation, and PV cell temperature. In addition, the current against voltage and power against voltage curves illustrate a non-linear connection between the PV module and voltage. Consequently, the PV array should constantly operate at its maximum power point, or MPP, to maintain the PV system’s efficiency (Wang et al., 2016). The extreme MPP, often referred to as the Global Maximum Power Point, or GMPP, is suggested to be tracked by MPPT controllers (Chen et al., 2014).

Numerous Maximum Power Point Tracking (MPPT) solutions have been studied in the literature; these strategies were selected based on several factors, including needs, implementation, tracking capabilities, and accuracy. Conventional methods, such as the Perturb and Observe algorithm (P&O) and incremental Conductance (INC.), are simple to implement and the most used MPPTs but are unable to track GMPP during changing environmental conditions. Furthermore, they demonstrate oscillations close to MPP that exhibit sluggish convergence when the ambient circumstances alter (Ghasemi et al., 2016). Artificial Intelligence (AI) based MPPT methods like Neural network (NN) and Fuzzy Logic MPPT Controllers were extensively investigated to address the limitations of the conventional techniques however, the design, classification rules, and training were the main limitations. The limitations and advantages are summarized in (Seyedmahmoudian et al., 2016). In recent years, the emphasis has been on MPPT techniques that primarily use optimization algorithms and bio-inspired algorithms to track GMPP. To improve efficiency, MPPT techniques based on Artificial Bee Swarm Optimization (ABSO), Grey Wolf Optimization (GWO), Flower Pollination Algorithm (FPA), Ant colony Optimization (ACO), Cuckoo Search, and Particle Swarm Optimization (PSO) have been used recently (Kumar et al., 2023; Boubaker, 2023; Chang et al., 2023) provide a thorough analysis of the MPPT performance in comparison to optimization algorithm-based MPPT. In (Díaz Martínez et al., 2021), PSO was employed to determine the MPP by proposing convergence detection and change in solar insolation. A single-phase grid-linked solar method utilizing GMPP tracking based on the particle swarm optimization (PSO) approach is proposed by the authors (Grid-tied photovoltaic system based on). The goal of the PSO-based MPPT process is to address issues related to mismatching phenomena, including partial shadowing in photovoltaic arrays. The study suggests a current generator technique for calculating the grid-tied inverter’s reference current. This algorithm works in conjunction with a DC-bus controller and MPPT algorithms, and it is based on a synchronous reference frame. Furthermore, the energy processed by the PV system is managed by the current generator to prevent overpower rating of the inverter. The system’s performance and feasibility are evaluated through simulation and experimental results. Improvement-based PSO MPPT for PV inverters was proposed by the authors (Sangrody et al., 2024), and it was verified by an experiment in which the MPPT was used to solve problems including fluctuations AT GMPP, sluggish tracking time, and becoming stuck in LMPP. To track GMPP under partial shade situations, several changes are suggested that employ PSO in combination with the direct duty cycle (Hayder et al., 2020), (Koh et al., 2023).

In (Ahmed and Salam, 2014), the Authors introduced an MPPT approach for solar PV schemes utilizing the Cuckoo Search (CS) process. The concept of CS is detailed in the paper, emphasizing its advantages, including rapid convergence and increased efficiency, while requiring fewer tuning parameters. Comparative assessments between two recognized MPPT methods, P&O and PSO, are conducted under diverse environmental conditions. The results demonstrate CS’s superiority over P&O and PSO in tracing ability, transient behavior, and convergence. However, the levy flight methodology for tracking and composite mathematical modeling makes it more complex.

In (Prasanth Ram and Rajasekar, 2017), Authors proposed FPA-based MPPT for GMPP tacking. The proposed model was tested to track local MPP and Global MPP in a single stage. (Yousri et al., 2019)., presents a novel optimization algorithm, the Chaotic-Flower Pollination Algorithm (C-FPA), designed for peak power tracking in solar PV structures under partial shading conditions. This algorithm dynamically integrates chaos maps (including Logistic, sine, and tent maps) to adjust the fundamental procedure limits. The algorithm’s efficacy is demonstrated in various partial shading conditions. Statistical analysis indicates that the C-FPA enhances the reliability and stability of the flower pollination algorithm (FPA) and delivers improved tracking efficiency with fifty percent less tracking time than FPA. Nevertheless, the paper lacks a comprehensive comparison with other existing MPPT techniques. Furthermore, it does not discuss the implementation challenges or limitations of the C-FPA algorithm in real-world PV systems.

The Grey Wolf Optimization (GWO) peak tracking technique outperforms existing MPPT algorithms, such as P&O and PSO peak tracking methods, based on findings reported in the research (A New MPPT Design Using). The proposed method effectively monitors the global peak of a solar array under partial shade conditions, addressing the drawbacks of poor tracking efficiency and oscillations. In (Comparative analysis of MPPT algorithms), a comparative analysis demonstrates that all peak power tracking systems can reach the GMPP under various test conditions, including uniform solar irradiance, partial shading, and smooth irradiance transients. The main disadvantage is that because of the vast search space, it requires more calculation time. The implementation of fuzzy logic control (FLC) is divided into three parts (Abbadi et al., 2020): defuzzification, control rule evaluation, and fuzzification. The FLC tracks MPP quickly and in uniform conditions however, the main disadvantage is that non-uniform environmental conditions complicate the implementation. Defining the shape of membership rule tables affects the tracking speed depending on intuition and experience. The authors in (Jyothy and Sindhu, 2018) presented an MPPT based on neural networks (NNs). This method’s ability to monitor the GMPP depends on both the learning process and the structure. Because it relies on the PV characteristics, NN is mostly applied in uniform circumstances, according to the more precise number of data sets (VPV, IPV) presented in the literature. The primary drawback of the method is the requirement for PV system data, which makes it expensive to keep and complicated to adjust the parameters (Mellit and Pavan, 2010).

An Adaptive neuro-fuzzy inference system (ANFIS) based MPPT is proposed in (Belhachat and Larbes, 2017) to achieve GMPP.ANFIS are immune to variations in the training data since they include built-in adaptive learning capabilities. Due to the requirement for substantial computer resources and excellent training data, this approach has several drawbacks. Due to the chances of overfitting and scalability, the response time of ANFIS-based MPPT can be slower, and improvements were proposed as well by the authors (Savrun and İnci, 2021).

Developed by combining many MPPT techniques to improve overall performance and leverage the advantages of each algorithm, hybrid MPPT algorithms make up the third category. A hybrid usually combines one quasi-seeking strategy with one true-seeking technique. Two phases are involved in the tracking proven in these hybrid methods: first, the MPP is estimated, and then it is adjusted using the optimization technique (Mohapatra et al., 2017). Many MPPT approaches have been proposed recently. The authors in (Ram et al., 2020), proposed the FPA and P&O-based hybrid MPPT technique. FPA, a bio-inspired metaheuristic algorithm, demonstrates a favorable balance between exploration and exploitation capabilities. P&O, a simple and robust MPPT method, is integrated via a novel switching strategy, ensuring efficient exploitation of both algorithms. The suggested FPA and P&O method is compared with other MPPT methods, including Enhanced Leader Particle Swarm Optimization (ELPSO) and established PSO approaches. Notably, the paper lacks experimental results or validation using real-world PV systems. The findings are derived solely from simulation outcomes and compared with other MPPT methods.

In (Ge et al., 2020), simulation findings demonstrate the benefits of the BAT-Fuzzy approach in tracking the highest power point effectively and efficiently, even during sudden changes in solar irradiation. The program demonstrates exceptional skills in managing power transfer between the hybrid system and the electrical network, guaranteeing prompt transient response and enhanced stability. However, further research and experimentation are required to evaluate the viability and performance of the BAT-Fuzzy performance in practical applications. An entirely novel grid-integrated photovoltaic (PV) control system is shown in (Padmanaban et al., 2019). The system uses the Artificial Bee Colony (ABC) method and ANFIS to reduce the Root Mean Square Error and optimize the membership function, resulting in rapid PV power tracking. In (Meddour et al., 2019), PSO, FS-MPC (finite set model predictive controller) and a comparison with P&O are presented. To boost energy output and efficiency, the authors suggested an improved P&O-PI MPPT based on a Genetic Algorithm (GA) for both axis-tracking and stationary grid-linked solar systems (Zaghba et al., 2019). An improved P&O with ABC to track GMPP is proposed by the authors in (Restrepo et al., 2021), and the findings indicate greater efficiency with a quick payback period. Based on tracking speed, control strategy, complexity, stability, ability to track under non-uniform environmental conditions, and efficiency, the literature has compared several other hybrid MPPT techniques, including fuzzy particle swarm optimization (FSPO), ANFIS, GWO-P&O MPPT, PSO-P&O MPPT, and hill climb (HC)-ANFIS MPPT. The limitations of the majority of the hybrid techniques are intricate mathematical computations and design (Bollipo et al., 2021). Recent studies have proposed various optimization techniques for enhancing the efficiency of MPPT in photovoltaic (PV) systems, each addressing specific challenges such as partial shading, system stability, and improved power extraction. In (Ranjan et al., 2024), the authors explore adaptive strategies for Building Applied Photovoltaic (BAPV) systems under partial shading, addressing voltage imbalances and the trade-offs between static and dynamic MPPT algorithms to improve real-time performance. Bayesian optimization Extreme Gradient (BO-XG) Boost-based voltage/var optimization is proposed in (BO-XGBoost-based voltage), to improve XG Boost performance and reduce PV system levelized cost of energy (LCOE), validated on the PG&E 69-node system. In (A Dimension-Independent Array Relocation (DIAR) Approach for Partial Shading Losses Minimization in Asymmetrical Photovoltaic Arrays), a Dimension-Independent Array Relocation (DIAR) approach is introduced to reduce partial shading losses in asymmetrical PV arrays, achieving over 96% efficiency. An optimized method for determining PV-inverter power sizing ratio (PSR) is presented, balancing energy production and cost-effectiveness (Imad et al., 2024). A novel super-twisting sliding mode controller to enhance real-time power management in grid-connected PV systems proposed by authors in (Mohapatra et al., 2024), to improve efficiency under dynamic conditions. In (Aljafari et al., 2024),The ggorilla Troop reconfiguration-power line communication (GTR-PLC) approach enhances power output and monitoring under partial shading, achieving a 38.37% power increase with 98.99% efficiency. In (Smadi et al., 2024), artificial intelligence-based control using ANN optimizes energy flow and addresses grid connection delays in PV systems. In (Jiang, 2024), an African Vulture Optimization Algorithm with RNN was proposed for efficient MPPT, achieving 99.81% accuracy. In (Krishnaram et al., 2024), a hybrid GWO-MFTSMC algorithm was proposed to improve MPPT efficiency under partial shading, with 99.72% simulation and 96.15% hardware conversion efficiency. In (Satpathy et al., 2024), the Authors proposed a multi-string differential power processing (MS-DPP) voltage equalizer that improves power output under partial shading, achieving over 99% efficiency. In (Mariprasath et al., 2024), a high voltage gain boost converter with cuckoo search optimization enhances MPPT efficiency in PV systems is proposed. In (Refaat et al., 2024), a Horse herd Optimization -based MPPT controller outperforms other algorithms in tracking time and efficiency under varying conditions. In (Ranjan Satpathy et al., 2024), a Grouped String Voltage Balancing (GSVB) approach improves PV system performance under shading and multi-irradiance conditions. In (Sameera et al., 2024), the Authors compared all major soft computing and hybrid MPPT techniques, analyzing the performance of Cuckoo Search, JAYA, and PSO.

The Pelican Optimization Algorithm (POA) is a straightforward optimization technique that effectively addresses optimization issues, offering simplicity, adaptability, and ease of implementation. It is tested by authors for both unimodal and multimodal optimization problems (Trojovský and Dehghani, 2022). While POA often outperforms traditional MPPT algorithms in tracking the Global Maximum Power Point (GMPP), it may exhibit randomness and some unpredictability, leading to unwanted oscillations during the search process. On the other hand, the Perturb and Observe (P&O) method, known for its simplicity, continuously adjusts the operating point to track the MPP but may face oscillations around the MPP and slower convergence in dynamic conditions. Research suggests that hybrid approaches can leverage the strengths of both algorithms to improve MPPT performance (Gao et al., 2009). However, careful consideration of each method’s advantages and disadvantages is required to avoid slow convergence and local maxima (Batarseh and Za’ter, 2018). Many current MPPT techniques still struggle to adapt to varying environmental conditions, leading to reduced efficiency and energy production. To address this gap, this paper proposes a novel hybrid MPPT approach, combining P&O with POA, to optimize grid-connected PV systems. The novel proposed Hybrid HPPO MPPT aims to minimize oscillations and improve both local and global search capabilities, enhancing convergence and tracking precision. The paper also compares the proposed hybrid technique with existing techniques, including PSO, CUCKOO, FPA, GWO, FUZZY, ANFIS, and NN, to evaluate its performance, stability, and feasibility under various conditions.

The rest of the paper is structured as follows: Section 2 describes the problem statement, Section 3 describes the overview of the Proposed HPPO, Section 4 describes the modeling of the 5-level Neutral clamped inverter used and the operation of the proposed technique, Section 5 discusses the results, and Section 6 concludes the paper.

2 Research problem

The existing literature on Solar PV MPPT algorithms presents various methodologies to enhance efficiency, stability, and rapid response under varied environmental and grid conditions. Most MPPT methods are made to effectively search spaces and identify near-optimal or ideal answers to optimization problems. The POA achieves an appropriate balance between exploration and exploitation, making it useful for utilizing promising regions to converge toward the optimal level or solution.

The studied literature concentrated on unique aspects of PV systems, such as modeling approaches, oscillation mitigation, dynamic weather conditions, partial shading, grid integration, and specific algorithms like Hybrid ANFIS-PSO, CS, ANN, Fuzzy Logic Control (FLC), and NN-MPPT. However, this focused approach limits a holistic understanding and comparative analysis across multiple factors impacting MPPT efficiency and system stability.

The studies often lack direct comparative assessments with a broad range of MPPT techniques, especially across different environmental conditions or system sizes. The challenges of incorporating photovoltaic schemes into the grid include optimizing energy output and power transfer efficiency. Selecting the most effective Peak Power Point Tracking algorithm is critical in optimizing solar PV schemes. Although the PO MPPT method is extensively used due to its ability to continuously adjust the solar PV functional point for maximum power output, it can be further enhanced by integrating advanced optimization methods. The quest for improved efficiency, stability, and performance prompts exploration into hybrid approaches, such as the (HPPO), which syndicates the capabilities of the P&O MPPT with the adaptability and robustness of the Pelican Optimization (PO).

The main contributions are:

1. A novel hybrid HPPO MPPT is employed in the PV-connected grid to achieve maximum peak power from PV under varying solar irradiance and temperatures.

2. The proposed hybrid HPPO MPPT method is used to diminish steady-state oscillations and to prevent premature convergence due to perturbation direction with better tracking speed.

3. A 3-phase grid-connected PV model, suitable for power system dynamic analysis, is introduced to validate the proposed method via MATLAB/Simulink.

4. The proposed hybrid HPPO MPPT is integrated with a 5-level Neutral clamped inverter employing a feed-forward control strategy, demonstrating its to extract the peak power, enhance power quality, and support the grid functionality.

5. The proposed HPPO MPPT is contrasted with other optimization algorithm-based MPPT techniques. Performance in terms of output voltage, current, power, tracking speed, and THD show the benefits of the HPPO MPPT.

The novelty of this paper lies in implementing the Pelican Optimization Algorithm, inspired by the hunting behavior of pelicans to efficiently track prey, aiming to reduce tracking time. This algorithm is combined with the Perturb and Observe (P&O) MPPT method, which maximizes the output of grid-connected solar PV systems through systematic perturbation and observation of output levels. The integrated approach is designed to ensure that PV systems operate at maximum efficiency when connected to the grid, maintaining optimal performance even under varying environmental conditions.

3 Hybrid pelican optimization algorithm and perturb and observe MPPT

Figure 1 below shows the suggested hybrid POA and PO MPPT-controlled solar PV-connected grid configuration. A flyback converter, a 5-level 3-phase inverter, an inductor, a three-phase grid, and a solar module make up the system. The flyback converter is managed using the P&O MPPT algorithm and hybrid pelican optimization. A feed-forward decoupling controller is used to manage the three-phase inverter. In Figure 1, the various components are succinctly summarized.

Figure 1

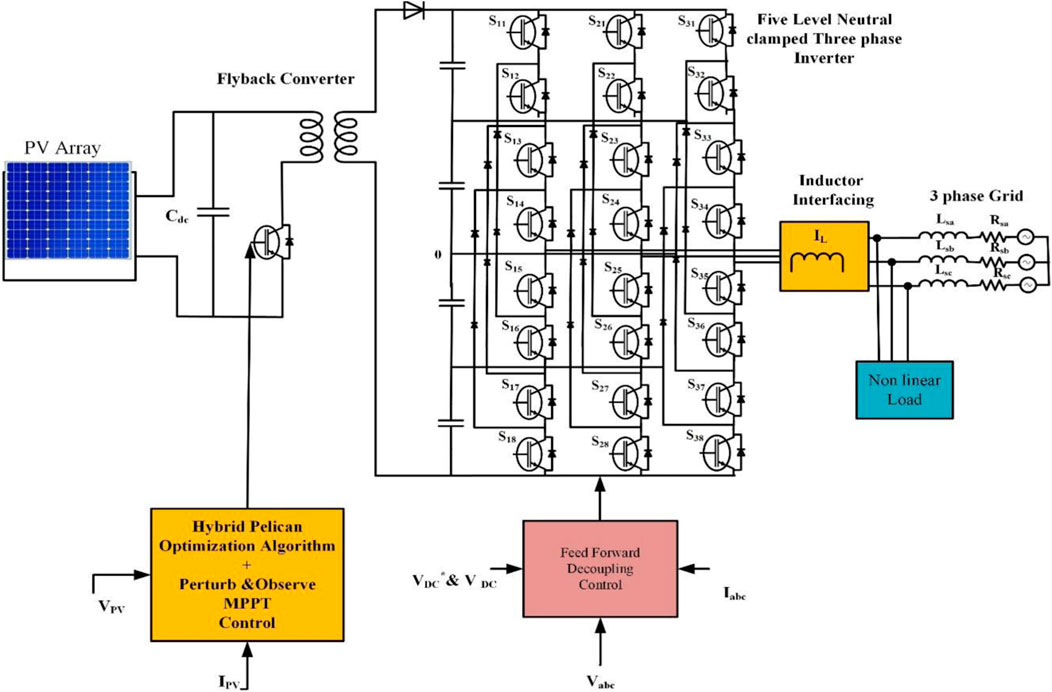
Figure 1. Block diagram of hybrid pelican optimization and PO MPPT for solar input to grid integration.

3.1 Perturbation and observation algorithm

The P&O technique in solar PV approaches has gained popularity since it is easy to install and reasonably priced. Using this method, the PV module’s voltage and current measurements are used to calculate PV power. Equation 1 illustrates how algorithmic changes and boost converter tweaks to improve the system’s performance based on comparative research.

$\mathit{D}\_\left(\mathit{k}+\mathbf{1}\right)=\mathit{D}\_\mathit{k}\pm ∆\mathit{D}(1)$

The optimal duty cycle is found using the P&O MPPT approach. The result is obtained by adding the previous perturbation (Dk+1) to the present perturbation (Dk) throughout each cycle. The computing procedure includes power, instantaneous voltage change (V), prior instant power (P), instantaneous current change (I), and analysis of the observed PV current and voltage. The next step is to assess V to determine whether P is more important than 0. If V is larger than 0, D lowers the duty cycle. Similarly, D increases the duty cycle if P is less than 0 and V is more than 0. On the other hand, if P is less than 0 and V is not greater than 0, the duty cycle is decreased by D.

Three main limitations of the P&O technique include drifting caused by abrupt variations in irradiance and partial shadow situations, long convergence times, and large oscillations around the peak power point. A critical component of the P&O MPPT is the perturbation step size (D). The perturbation step size in the Perturb and Observe (P&O) algorithm is a crucial parameter that directly impacts the speed and stability of convergence to achieve the maximum power point (MPP). A small step size minimizes oscillations around the MPP, allowing the system to stabilize more precisely once it reaches optimal conditions. However, if the step size is too small, it can slow down the algorithm’s response, especially during rapid changes in irradiance or temperature, potentially hindering the system’s ability to track the MPP accurately. Faster oscillation settling results from larger decay durations, which get stronger as they get closer to the peak power point. On the other hand, shorter decay durations postpone the steady state but provide smoother oscillations. The algorithm’s tracking of fluctuations in the peak power point is greatly influenced by the direction of the perturbation step size, which affects the P&O MPPT system’s efficiency, especially as irradiance increases.

To solve these problems, a modified P&O MPPT approach with a programmable step size has been suggested; however, it still requires refinement. Scholars have proposed the use of PV peak power point tracing-based soft computing technologies to counteract the drawbacks of the traditional P&OMPPT approach.

3.2 Pelican optimization algorithm

The mathematical concept and motivation for the recommended Pelican Optimization Algorithm (POA) are detailed in this section: (Trojovský and Dehghani, 2022).

3.2.1 Proposed POA mathematical model

The POA is an algorithm that relies on a population, with members of this population being represented by pelicans. Every member of the population represents each potential solution candidate in such algorithms. Using their relative positions in the search space, these members propose estimates for the variable quantity of the optimization problem. Beginning with the lowest and maximum bounds of the issue, the population elements are randomly initialized using Equation 2.

${\mathbf{x}}_{\mathbf{i},\mathbf{j}}={\mathbf{l}}_{\mathbf{j}}+\mathbf{\text{rand}}\left({\mathbf{u}}_{\mathbf{j}}-{\mathbf{l}}_{\mathbf{j}}\right),\mathbf{i}=\mathbf{1},\mathbf{2},\dots ,\mathbf{N},\mathbf{j}=\mathbf{1},\mathbf{2},\dots .,\mathbf{m}(2)$

x(i,j) represents the value of the jth variable via the ith candidate solution. N is the number of population members; represents problem variables; rand is a random number in the interval [0, 1]; lj is the jth lower limit of the problem variables; and u_j is the jth upper bound. The population matrix, denoted by Equation 3, is the matrix that arranges the pelican population membership in the POA. In this matrix, the variables for each choice are represented by the columns, and each row denotes a possible solution.

$\mathit{X}={\left[\begin{array}{c}{\mathit{X}}_{\mathbf{1}}\\ ⋮\\ {\mathit{X}}_{\mathit{i}}\\ ⋮\\ {\mathit{X}}_{\mathit{N}}\end{array}\right]}_{\mathit{N}\times \mathit{m}}={\left[\begin{array}{ccccc}{\mathit{x}}_{\mathbf{1},\mathbf{1}}& \cdots & {\mathit{x}}_{\mathbf{1},\mathit{j}}& \cdots & {\mathit{x}}_{\mathbf{1},\mathit{m}}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\mathit{x}}_{\mathit{i},\mathbf{1}}& \cdots & {\mathit{x}}_{\mathit{i},\mathit{j}}& \cdots & {\mathit{x}}_{\mathit{i},\mathit{m}}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\mathit{x}}_{\mathit{N},\mathbf{1}}& \cdots & {\mathit{x}}_{\mathit{N},\mathit{j}}& \cdots & {\mathit{x}}_{\mathit{N},\mathit{m}}\end{array}\right]}_{\mathit{N}\times \mathit{m}}(3)$

The Pelicans population matrix is denoted by X, where each X_i signifies the ith pelican in the population.

According to the POA, pelicans are distinct members of the population, and each one represents a potential fix for the given issue. As a result, each prospective solution’s objective function is evaluated. Equation 4 defines the vector that results from evaluating the objective function as the objective function vector.

$\mathit{F}={\left[\begin{array}{c}{\mathit{F}}_{\mathbf{1}}\\ ⋮\\ {\mathit{F}}_{\mathit{i}}\\ ⋮\\ {\mathit{F}}_{\mathit{N}}\end{array}\right]}_{\mathit{N}\times \mathbf{1}}={\left[\begin{array}{c}\mathit{F}\left({\mathit{X}}_{\mathbf{1}}\right)\\ ⋮\\ \mathit{F}\left({\mathit{X}}_{\mathit{i}}\right)\\ ⋮\\ \mathit{F}\left({\mathit{X}}_{\mathit{N}}\right)\end{array}\right]}_{\mathit{N}\times \mathbf{1}}(4)$

The neutral function parameters of each corresponding candidate solution are included in the objective function vector, denoted as F.

The POA strategy emulates the hunting tactics of pelicans in two distinct stages, involving the simulation of their behavior and approach during the pursuit and capture of prey:

1. Moving in the direction of the prey (exploration phase).

2. At the water’s surface, skimming (exploitation phase).

Phase 1: Advancing Towards The Prey (Exploration Stage).

Finding and approaching the prey is the initial step for the pelicans. The approach used by these birds is modeled in this phase of the POA in terms of exploration and search space scanning capabilities. The random creation of the prey position inside the search zone is essential to the POA. This randomness helps the POA become more adept at exploring and navigating the problem-solving domain. Equation 5 provides a mathematical description of these concepts and the pelican’s hunting strategy.

${\mathit{x}}_{\mathit{i},\mathit{j}}^{{\mathit{P}}_{\mathbf{1}}}=\left\{\begin{array}{l}{\mathit{x}}_{\mathit{i},\mathit{j}}+\mathit{ran}\mathit{d}.\left({\mathit{p}}_{\mathit{j}}-\mathit{I}.{\mathit{x}}_{\mathit{i},\mathit{j}}\right),{\mathit{F}}_{\mathit{p}}<{\mathit{F}}_{\mathit{i}};\\ {\mathit{x}}_{\mathit{i},\mathit{j}}+\mathit{r}\mathit{a}\mathit{n}\mathit{d}.\left({\mathit{x}}_{\mathit{i},\mathit{j}}-{\mathit{p}}_{\mathit{j}}\right),\mathit{e}\mathit{l}\mathit{s}\mathit{e},\end{array}\right.(5)$

In Equation 6, the parameters denote various aspects of the pelican’s movement and the adjustment of its position based on the exploration phase. This phase involves the pelican possibly relocating into uncharted spaces in the search area, influenced by a randomly chosen integer, I, which can either be one or two. The selection of I plays a role in the algorithm’s exploration capacity and ability to navigate the search space more precisely. If the pelican’s new position results in a better objective function value, it is accepted, which maintains the algorithm’s trajectory toward more optimal solutions. This kind of updating, known as adequate updating, allows the algorithm to converge into less optimal paths.

${\mathit{X}}_{\mathit{i}}=\left\{\begin{array}{l}{\mathit{X}}_{\mathit{i}}^{{\mathit{P}}_{\mathbf{1}}},{\mathit{F}}_{\mathit{i}}^{{\mathit{P}}_{\mathbf{1}}}<{\mathit{F}}_{\mathit{i}};\\ {\mathit{X}}_{\mathit{i}},\mathit{e}\mathit{l}\mathit{s}\mathit{e},\end{array}\right.(6)$

Based on data from the pelican’s objective function value through phase 1, shown as $F_i^{P_1}$ $X_i^{P_1}$. Following its exploring phase, the pelican’s position is updated and represented by its status.

Phase 2: At the Water’s Surface: Winging (Exploitation Phase).

The simulation involves modeling their wing-stretching behavior when the pelicans reach the water surface phase in the second stage. This action emulates their tactic to raise fish in that specific region, allowing the pelicans to capture more prey. Adapting this pelican behavior in the suggested POA leads to convergence towards more beneficial locations within the hunting zone. This strategy amplifies the algorithm’s potential for exploiting local areas and enhances its capacity for conducting local searches. Mathematically, Equation 7 represents the pelicans’ hunting technique.

${\mathit{x}}_{\mathit{i},\mathit{j}}^{{\mathit{P}}_{\mathbf{2}}}={\mathit{x}}_{\mathit{i},\mathit{j}}+\mathit{R}.\left(\mathbf{1}-\frac{\mathit{t}}{\mathit{T}}\right).\left(\mathbf{2}.\mathit{r}\mathit{a}\mathit{n}\mathit{d}-\mathbf{1}\right).{\mathit{x}}_{\mathit{i},\mathit{j}}(7)$

Hence, according to phase 2, ${\mathrm{x}}_{\mathrm{i},\mathrm{j}}^{{\mathrm{P}}_2}$ represents the ith pelican’s new location in the jth dimension. The constant R has a value of 0.2. The “R” stands for the neighborhood’s radius surrounding the population members. For local searches to converge toward more optimal solutions, the (1-t/T) coefficient is necessary. This parameter dynamically adjusts the search region around each member so that the Pelican Optimization Algorithm (POA) may effectively use and explore the search space.

A broader area surrounding each member is considered in the initial stages when the coefficient holds a higher value. As the iterations progress, this coefficient gradually diminishes, leading to a smaller neighborhood radius for each member, ensuring more precise local scanning. The POA can effectively converge toward global and optimal solutions by enabling smaller and more exact steps in exploring the vicinity around each population member. The pelican’s modified position is shown by Equation 8, which also indicates whether or not the new location is accepted at this time.

${\mathit{X}}_{\mathit{i}}=\left\{\begin{array}{l}{\mathit{X}}_{\mathit{i}}^{{\mathit{P}}_{\mathbf{2}}},{\mathit{F}}_{\mathit{i}}^{{\mathit{P}}_{\mathbf{2}}}<{\mathit{F}}_{\mathit{i}};\\ {\mathit{X}}_{\mathit{i}},\mathit{e}\mathit{l}\mathit{s}\mathit{e},\end{array}\right.(8)$

As the pelicans adjust their locations by the system, the new importance of the ith pelican, represented as ${\mathrm{X}}_{\mathrm{i}}^{{\mathrm{P}}_2}$, and its real function value based on phase 2, represented as ${\mathrm{F}}_{\mathrm{i}}^{{\mathrm{P}}_2}$, is ascertained.

The Pelican Optimization Algorithm (POA) is inspired by the natural hunting behavior of pelicans, where they alternate between exploring wide areas to locate prey and then focusing on specific movements to capture it effectively. In the context of MPPT, POA simulates this by balancing two phases: exploration and exploitation. During the exploration phase, the algorithm uses broad duty cycle adjustments to identify potential regions of high power on the PV curve. Once it detects a promising power region, POA switches to the exploitation phase, where it makes precise adjustments to fine-tune the duty cycle around the identified Maximum Power Point (MPP).

4 Modelling of 5-level neutral clamped inverter

The five-level, three-phase Neutral Point Clamped inverter is represented in Figure 1, showcasing a power circuit diagram. A standard n-level NPC configuration necessitates a single DC voltage source and (n−1) capacitors to establish (n−1) DC voltage levels. Within this framework, every leg encompasses 2 (n−1) two-quadrant switching devices and 2 (n−2) clamping diodes. This design results in ‘n’ switching states for each leg, establishing an n-level pole voltage related to the DC bus midpoint. For example, as displayed in Figure 1, there are five distinctive switching states for the power semiconductors of leg 1. A distinct combination of ON and OFF positions for the respective switches defines each state.

4.1 Flyback converter

The transformation of alternating current (AC) into direct current (DC) while preserving galvanic isolation between the inputs and outputs characterizes power converters known as flyback converters. Energy is accumulated in circuits during the current flow and discharged when the current is intersected. It works as an independent switching conversion for voltage transformers that can step up or decrease the output voltage using a mutually coupled inductor.

From a variety of input voltages, the flyback converter may regulate and control the output voltages. Compared to most other converting mode power supply circuits, this converter has fewer components. What distinguishes the design’s on/off functionality is “fly back.”

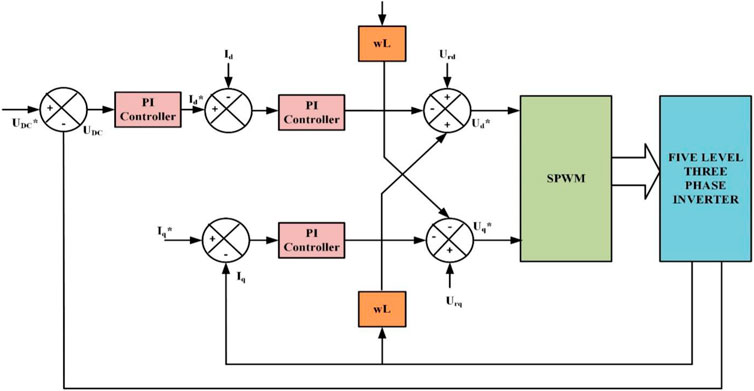
4.2 Control of feed-forward decoupling for three-phase grid-connected solar inverter

Deriving the equations involves an assumption considering a constant voltage across the three-phase electrical system and is written below as Equation 9, (Grid-tied photovoltaic system based on),Equation 11.

${\mathit{e}}_{\mathit{a}}=\mathit{E}\mathit{c}\mathit{o}\mathit{s}\mathit{\omega }\mathit{t}(9)$

${\mathit{e}}_{\mathit{a}}=\mathit{E}\mathit{cos}\left(\mathit{\omega }\mathit{t}-\mathbf{2}\mathit{\pi }/\mathbf{3}\right)(10)$

${\mathit{e}}_{\mathit{a}}=\mathit{E}\mathit{cos}\left(\mathit{\omega }\mathit{t}+\mathbf{2}\mathit{\pi }/\mathbf{3}\right)(11)$

The power grid’s angular frequency and maximum voltage on grid (E) are found in Equation 12.

$\left[\begin{array}{c}\frac{{\mathit{d}\mathit{i}}_{\mathit{a}}}{\mathit{d}\mathit{t}}\\ \frac{{\mathit{d}\mathit{i}}_{\mathit{b}}}{\mathit{d}\mathit{t}}\\ \frac{{\mathit{d}\mathit{i}}_{\mathit{c}}}{\mathit{d}\mathit{t}}\end{array}\right]=\left[\begin{array}{ccc}-\frac{\mathit{R}}{\mathit{L}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& -\frac{\mathit{R}}{\mathit{L}}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& -\frac{\mathit{R}}{\mathit{L}}\end{array}\right]\left[\begin{array}{c}{\mathit{i}}_{\mathit{a}}\\ {\mathit{i}}_{\mathit{b}}\\ {\mathit{i}}_{\mathit{c}}\end{array}\right]+\frac{\mathbf{1}}{\mathit{L}}\left[\begin{array}{c}{\mathit{u}}_{\mathit{a}}-{\mathit{e}}_{\mathit{a}}\\ {\mathit{u}}_{\mathit{b}}-{\mathit{e}}_{\mathit{b}}\\ {\mathit{u}}_{\mathit{c}}-{\mathit{e}}_{\mathit{c}}\end{array}\right](12)$

Equation 13 illustrates the coordinate transformation from the three-phase, fixed-frame abc to the two-phase, synchronously rotating d_q.

$\left[\begin{array}{c}\frac{{\mathit{d}\mathit{i}}_{\mathit{d}}}{\mathit{d}\mathit{t}}\\ \frac{{\mathit{d}\mathit{i}}_{\mathit{q}}}{\mathit{d}\mathit{t}}\end{array}\right]=\frac{\mathbf{1}}{\mathit{L}}\left[\begin{array}{cc}-\mathit{R}& \mathit{\omega }\mathit{L}\\ -\mathit{\omega }\mathit{L}& -\mathit{R}\end{array}\right]\left[\begin{array}{c}{\mathit{i}}_{\mathit{d}}\\ {\mathit{i}}_{\mathit{q}}\end{array}\right]-\frac{\mathbf{1}}{\mathit{L}}\left[\begin{array}{c}{\mathit{e}}_{\mathit{d}}\\ {\mathit{e}}_{\mathit{q}}\end{array}\right]+\frac{\mathbf{1}}{\mathit{L}}\left[\begin{array}{c}{\mathit{u}}_{\mathit{d}}\\ {\mathit{u}}_{\mathit{q}}\end{array}\right](13)$

The above equations show the d- and q-axes components for the three-phase system’s grid voltage (e_d and e_q) and grid current (u_d and u_q). They also represent the d and q-axis components (i_d and i_q) of the output current of the inverter. Equations 14, 15 are explained below.

${\mathit{u}}_{\mathit{d}}=\mathit{L}\frac{{\mathit{d}\mathit{i}}_{\mathit{d}}}{\mathit{d}\mathit{t}}+\mathit{R}{\mathit{i}}_{\mathit{d}}-\mathit{\omega }\mathit{L}{\mathit{i}}_{\mathit{q}}+{\mathit{e}}_{\mathit{q}}(14)$

${\mathit{u}}_{\mathit{q}}=\mathit{L}\frac{{\mathit{d}\mathit{i}}_{\mathit{q}}}{\mathit{d}\mathit{t}}+\mathit{R}{\mathit{i}}_{\mathit{q}}-\mathit{\omega }\mathit{L}{\mathit{i}}_{\mathit{q}}+{\mathit{e}}_{\mathit{q}}(15)$

The d and q-axis variables are interdependent, as the established d-q mathematical paradigm illustrates. The controller’s design is complex. The system may accomplish reliable closed-loop control by utilizing the feed-forward decoupling control approach in conjunction with the provided PI controller. The following are the outlined control Equations 16, 17.

${\mathit{u}}_{\mathit{d}}=\left({\mathit{K}}_{\mathit{p}}+\frac{{\mathit{K}}_{\mathit{i}}}{\mathit{s}}\right)\left({{\mathit{i}}_{\mathit{d}}}^{*}-{\mathit{i}}_{\mathit{d}}\right)-\mathit{\omega }\mathit{L}{\mathit{i}}_{\mathit{q}}+{\mathit{e}}_{\mathit{d}}(16)$

${\mathit{u}}_{\mathit{q}}=\left({\mathit{K}}_{\mathit{p}}+\frac{{\mathit{K}}_{\mathit{i}}}{\mathit{s}}\right)\left({{\mathit{i}}_{\mathit{q}}}^{*}-{\mathit{i}}_{\mathit{q}}\right)-\mathit{\omega }\mathit{L}{\mathit{i}}_{\mathit{d}}+{\mathit{e}}_{\mathit{q}}(17)$

A 3-phase solar grid inverter’s inner-loop current is independently controlled by a sinusoidal pulse width modulator (SPWM) for both reactive and active power using the feed-forward decoupling control approach, as shown in Figure 2.

Figure 2

Figure 2. Control strategy of feed-forward decoupling control.

5 Hybrid pelican and PO MPPT

Environmental factors like temperature and irradiance significantly influence the output of a solar PV scheme. The PV system must operate at maximum power despite these varying climatic conditions. To achieve this, a peak power tracker aids the PV array. The authors propose utilizing a novel MPPT technique, which integrates P&O MPPT with Pelican Optimization, aiming to maximize power generation.

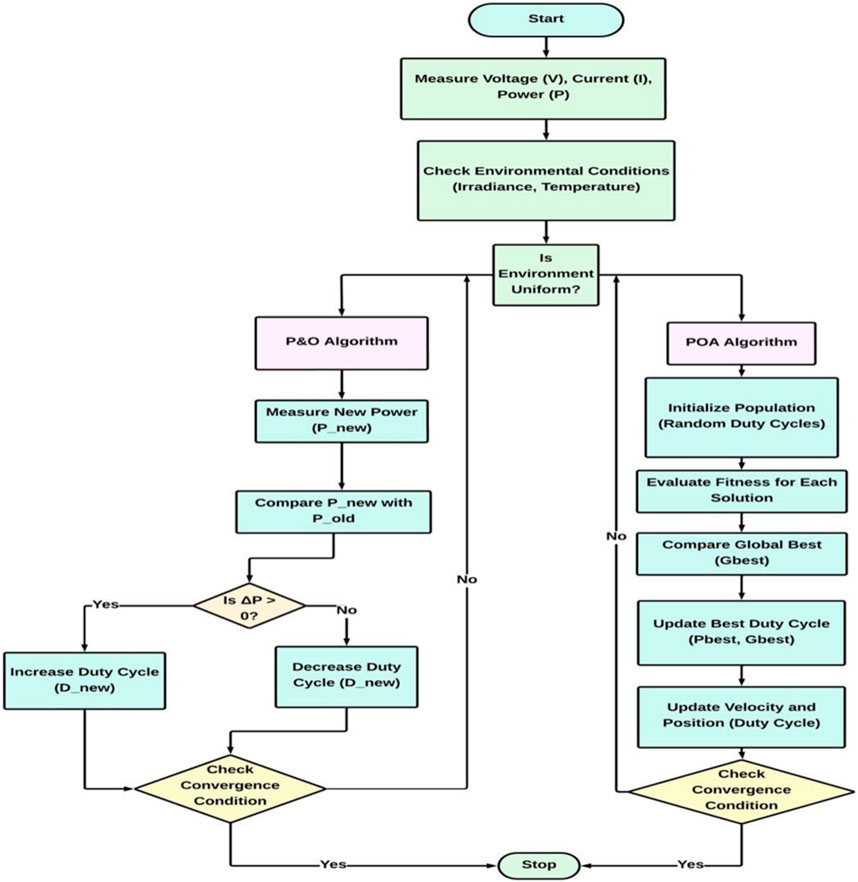
Conventional MPPT techniques, like the P&O algorithm, frequently encounter difficulties in variable environments, such as oscillations at the MPP, and can be trapped at local peaks, especially in situations with changeable irradiance. Similarly, while successful in complicated settings like partial shading, MPPT approaches based on optimization algorithms may have sluggish convergence and increased complexity. The advantages of both strategies are combined in the proposed novel hybrid MPPT technique. As seen in Figure 3’s flowchart, the hybrid strategy operates in two loops, utilizing the POA’s global search capabilities and the P&O method’s quick local search efficiency.

Figure 3

Figure 3. Flowchart of hybrid Pelican optimization algorithm and P&O MPPT.

In the first loop (inner loop), the P&O algorithm is employed to perform rapid local optimization under uniform conditions. This algorithm perturbs the duty cycle D by a small step $△D$ and observes a change in power output ($\left.\mathrm{V}*\mathrm{I}=\mathrm{P}\right)$. If the Power increases, perturbation is maintained, and if power decreases, the perturbation is updated, Duty cycle adjustment can be shown by Equations 18 below.

$\mathit{D}\mathit{n}\mathit{e}\mathit{w}=\mathit{D}\mathit{o}\mathit{l}\mathit{d}+△\mathit{D}\text{\hspace{1em}if\hspace{1em}dp}/\text{dv}>0(18)$

$\mathit{D}\mathit{n}\mathit{e}\mathit{w}=\mathit{D}\mathit{o}\mathit{l}\mathit{d}-△\mathit{D}\text{\hspace{1em}if\hspace{1em}dp}/\text{dv}<0(19)$

The value $△D$ in this stage is kept small to reduce the oscillations near MPP. The range of value from (0.005–0.01).

In the second loop (outer loop), The POA is activated by complex conditions like partial shading where multiple LMPP exists. POA evaluates a population of possible solutions, each representing a duty cycle. It then updates the best-known individual positions (p^best) and the global best position (g^best). The change in duty cycle (V_new) is calculated using Equation 20 below and the updated (new) duty cycle in Equation 21 below:

$\mathit{V}\mathit{n}\mathit{e}\mathit{w}=\mathit{V}\mathit{o}\mathit{l}\mathit{d}+\mathit{C}\mathbf{1}\times \mathit{r}\mathit{a}\mathit{n}\mathit{d}\left(\right)\times \left(\mathit{p}\mathit{b}\mathit{e}\mathit{s}\mathit{t}-\mathit{X}\right)+\mathit{C}\mathbf{2}\times \mathit{r}\mathit{a}\mathit{n}\mathit{d}\left(\right)\times \left(\mathit{g}\mathit{b}\mathit{e}\mathit{s}\mathit{t}-\mathit{X}\right)(20)$

Updated Duty Cycle can be written as,

$\mathit{X}\mathit{n}\mathit{e}\mathit{w}=\mathit{X}\mathit{o}\mathit{l}\mathit{d}+\mathit{V}\mathit{n}\mathit{e}\mathit{w}+△\mathit{D}(21)$

V_new = Velocity of a pelican (change in duty cycle).

X = Current position (Duty Cycle).

C₁ and C₂ = acceleration coefficients.

rand () = Stochasticity in the search process, allowing the algorithm to search space without getting trapped.

p^best = Distance between current position(X) and best position found by the pelican.

g^best = Distance between the global best position found by the pelican and the current position (x).

$△D$ = Perturbation step from the P&O method.

The equations for velocity (v) and position (x) updates in the POA are central to how the algorithm manages the step ΔD indirectly. During the exploratory phase, larger velocities correspond to larger step sizes, enabling the algorithm to explore the search space effectively. As the system converges on the global MPP, the step size decreases, allowing for more precise control and stability in the duty cycle adjustments. This dynamic adjustment helps the hybrid HPPO MPPT algorithm in tracking the MPP under uniform and varying environmental conditions.

A particular convergence rule, based on the ratio between the best and worst fitness values in the population, is implemented to guarantee efficient convergence. To ascertain if the algorithm has successfully converged to an ideal solution, this ratio is essential. The convergence requirement can be expressed analytically as:

$\left(Xbest-Xworst\right)/Xbest\le ϵ,flag=1(22)$

X_best = best duty cycle found by optimization algorithm so far.

X_worst = Worst duty cycle found by optimization algorithm so far.

$\in$ = Threshold for convergence.

Fl $=1$ , This is a convergence indicator flag.

When the above condition is met, the algorithm is considered to have converged. The flag is set to 1, indicating that the population has reached a state where further iterations may yield diminishing returns. However, environmental conditions such as irradiance are not constant and may vary due to factors like cloud cover or shading, causing the position of the MPP to shift. For changing environmental conditions, the previous convergence might no longer hold, and the algorithm needs to adapt quickly. The program detects that the conditions have changed and restarts itself if the difference ratio condition Equation 22 is broken. To guarantee that the duty cycle stays within reasonable bounds and that the search space is sufficiently covered, the method resets the starting duty cycle values into a new range.

After reinitialization, the algorithm resets key variables such as the g^best, X_best, and convergence flags. This ensures that the algorithm starts afresh, considering the new environmental conditions and the changed MPP, and starts the optimization process again.

The hybrid HPPO (Pelican Optimization and Perturb and Observe) algorithm combines the strengths of both POA and P&O but at the cost of higher computational complexity and resource requirements compared to the standalone approaches. The P&O algorithm is computationally simple, with linear complexity O (Dutta et al., 2018) requiring minimal memory and processing power, making it ideal for low-resource systems. In contrast, POA is more complex due to its population-based optimization process, with a quadratic or higher computational cost (O (n²)) and increased memory demands to store the population and their associated variables. The hybrid HPPO algorithm, while leveraging the fast convergence of P&O and the stability of POA, requires significantly more memory and processing power due to the need to manage both algorithms simultaneously. This makes HPPO more resource-intensive, demanding faster processors and more memory compared to standalone P&O, but it offers more precise tracking of the Maximum Power Point (MPP) under varying environmental conditions.

6 Simulation results

A detailed simulation study has been conducted to assess the performance of the HPPO MPPT algorithm, designed explicitly for grid-connected photovoltaic (PV) systems. Performance evaluation parameters (PEP) are the PV system’s voltage, current, and power response, the efficiency of PV MPPT, DC link voltage response, grid power response, and THD of grid current.

The simulation was implemented using MATLAB 2020 software on a computer with a 4.1 GHz processor and 16 GB RAM. In addition, a thorough comparison was conducted between the suggested HPPO algorithm and various existing MPPT techniques, such as NN MPPT, GWO MPPT, fuzzy MPPT, FPA MPPT, CUCKOO MPPT, PSO MPPT, and ANFIS MPPT. The following specific cases were used to conduct the comparative analysis:

Case 1:. To evaluate the ability of the algorithm to adapt to varying irradiance conditions, the panel’s temperature was maintained at 25°C. In contrast, the irradiance variation array was chosen as [1000,800,600,400] W/m² with a sampling period of 0.2 s.

Case 2:. To assess the algorithm’s robustness in responding to temperature fluctuations, the PV panel irradiance was fixed as 1000 W/m², and the temperature was varied from 35°C to 10°C after every 0.2 s.

The typical climatic conditions of grid-connected PV systems in most locations and seasons are characterized by the range of irradiance and temperature levels, which include 1,000 to 400 W/m² for irradiance and 10°C to 35°C for temperature in Case 1 and Case 2, respectively. Since the effectiveness and performance of PV and outputs fluctuate directly with solar intensity and temperature, these fluctuations are required to evaluate the hybrid HPPO algorithm’s adaptability when applied to real-world scenarios. Making use of the formula $P=\eta .G.A$, Where P is the output of the Photovoltaic system. $\eta$ is efficiency depending on temperature, G is irradiance, and A is the area of the PV panel (constant).

6.1 Simulation results for case 1

6.1.1 PV voltage response

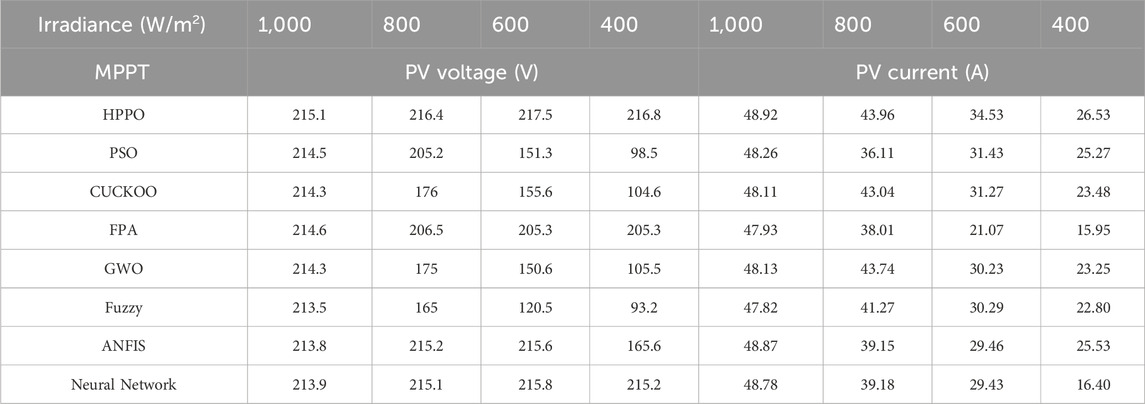
In the following section, the simulation results of the PV voltage and PV current of the HPPO MPPT algorithm, along with P&O MPPT, Cuckoo MPPT, FPA MPPT, GWO MPPT, Fuzzy MPPT, ANFIS MPPT, NN MPPT, are presented in Table 1. Based on the preferred evaluation, parameters were deliberated individually for the condition of case 1.

Table 1

Table 1. PV voltage details for case 1.

Notably, HPPO consistently demonstrates competitive PV voltage across varying irradiance levels. At 1000 W/m², the PV voltage for HPPO is 215.1 V, outperforming other algorithms. Similarly, at 400 W/m², HPPO maintains a high PV voltage of 216.8 V. In contrast, alternative MPPT algorithms exhibit varying performances and fluctuating PV voltage values under changing irradiance conditions. These quantitative results reveal the favorable performance of HPPO in sustaining stable and optimized PV voltage responses compared to alternative MPPT techniques.

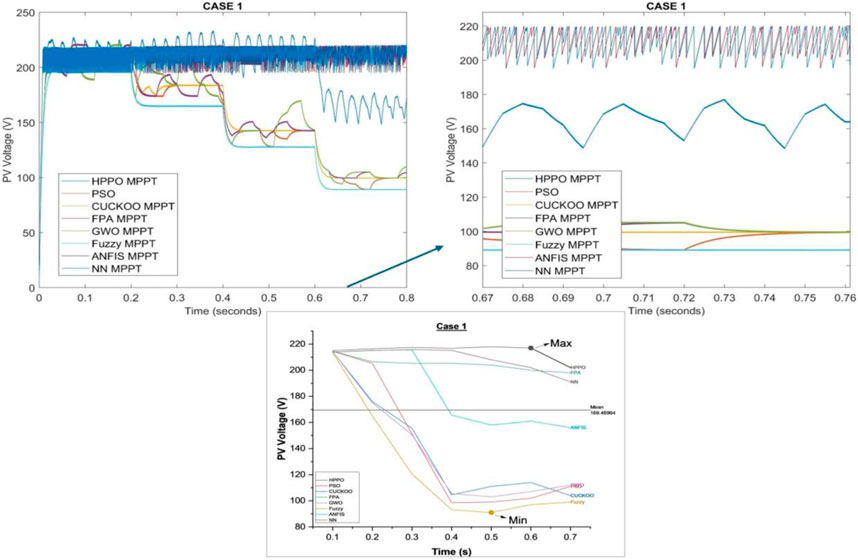
A graphical representation of the PV voltage response of HPPO and other MPPT algorithms has been presented in Figure 4 for comparison.

Figure 4

Figure 4. PV voltage response for Case 1.

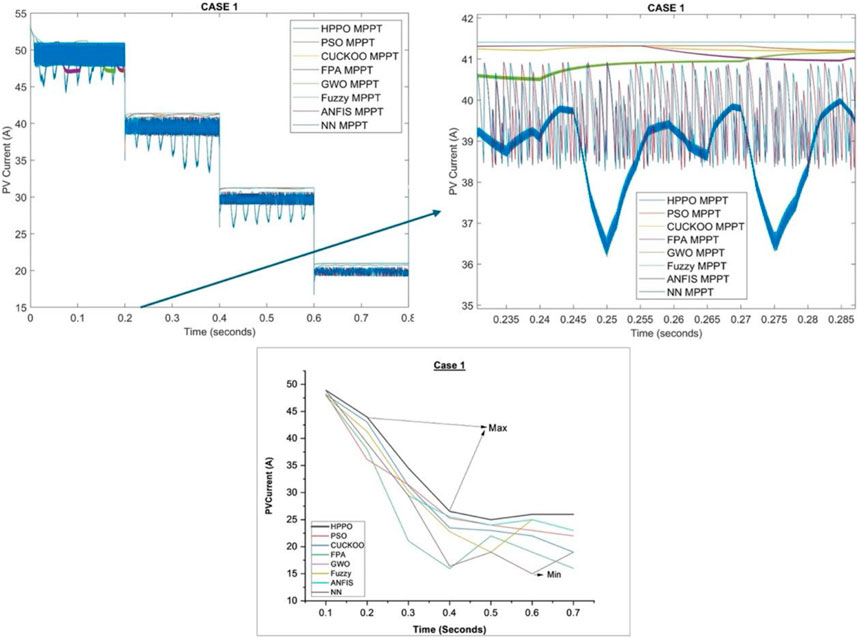
6.1.2 PV current response

Table 1 provided above compares the PV current values corresponding to various algorithms with reference HPPO under different irradiation conditions.

The table shows that HPPO consistently demonstrates competitive PV current values across varying irradiance levels. At 1000 W/m², the PV current for HPPO is 48.62A, outperforming other algorithms. Similarly, at 400 W/m², HPPO maintains a high PV current of 26.53A. In contrast, alternative MPPT algorithms exhibit varying performances and fluctuating PV current values under changing irradiance conditions. These results confirm the better performance of HPPO in sustaining stable and optimized PV current responses compared to alternative MPPT techniques.

The PV current response for case 1 has been presented in Figure 5.

Figure 5

Figure 5. PV Current response for Case 1.

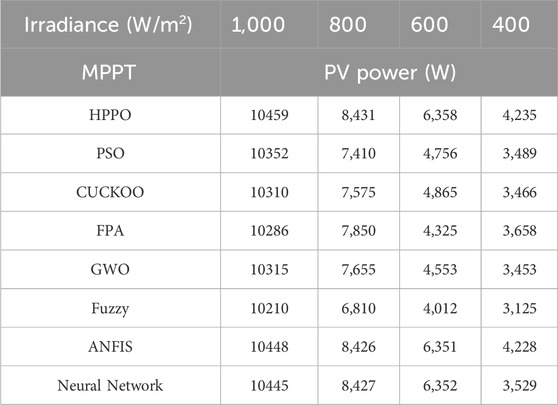
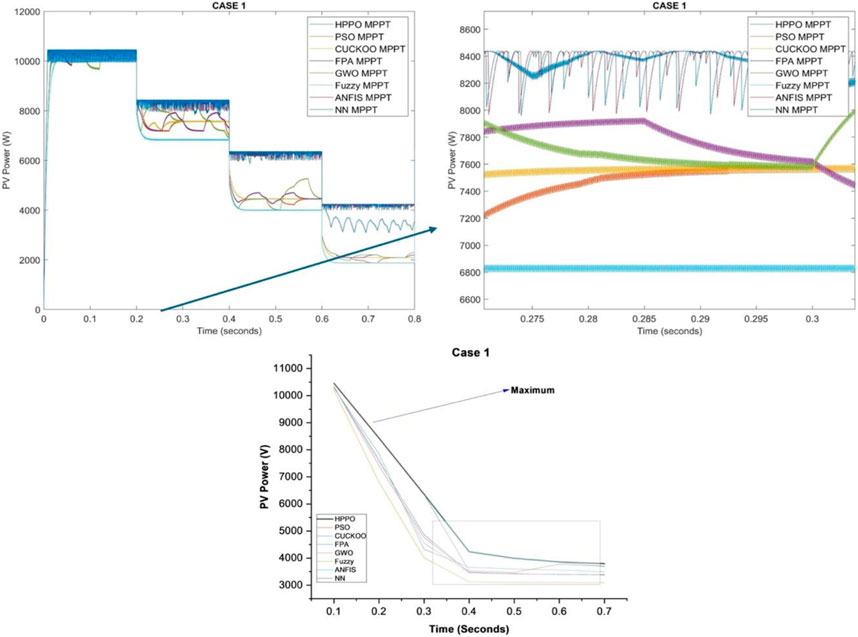
6.1.3 PV power response

Table 2 compares the PV output response of various algorithms with reference HPPO under different irradiation conditions.

Table 2

Table 2. PV power response for case 1.

Notably, HPPO consistently demonstrates competitive PV power across varying irradiance levels. At 1000 W/m², the PV voltage for HPPO is 10459W, the highest compared to other considered algorithms. Similarly, at 400 W/m², HPPO maintains a high PV voltage of 4235W. In contrast, alternative MPPT algorithms exhibit varying performances, with fluctuations in PV power values under changing irradiance conditions, confirming the supremacy of the HPPO algorithm for maintaining stable and optimized PV power response performance of HPPO in sustaining stable and optimized PV power responses in comparison with alternative MPPT techniques.

The PV power for case 1, has been presented in Figure 6.

Figure 6

Figure 6. PV Power response for Case 1.

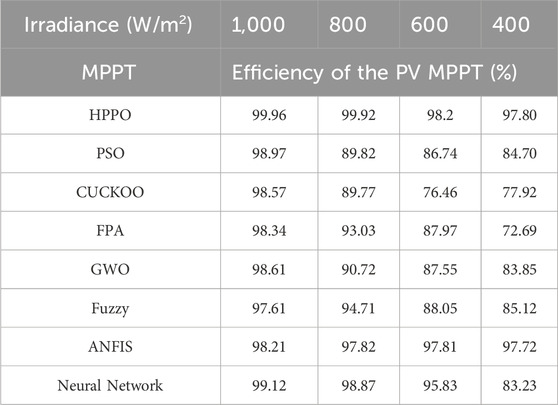
6.1.4 PV MPPT efficiency response

Table 3 compares the MPPT efficiency corresponding to various algorithms with reference HPPO under different irradiation conditions.

Table 3

Table 3. Efficiency of the PV MPPT for case 1.

The efficiency values are expressed as a percentage and reflect how effectively each MPPT algorithm optimizes the PV system’s operation at its maximum power point. From the table, it is observed for 1000 W/m², the PV efficiency is at its maximum power point for HPPO, which is 99.96%, outperforming other algorithms. Similarly, at 400 W/m², HPPO maintains a high efficiency of 99.80. In contrast, alternative MPPT algorithms exhibit varying performances, with fluctuations in inefficiencies under changing irradiance conditions. These results emphasize the superior efficiency of HPPO in optimizing the PV system across a range of irradiance conditions, establishing it as a robust and effective MPPT algorithm.

6.1.5 DC link voltage response

For all the MPPT algorithms, the simulation results for DC link voltage obtained at the output of the inverter have been tabulated in Table 4 to compare their performance.

Table 4

Table 4. DC link voltage details for case 1.

HPPO has demonstrated competitive DC link voltage when subjected to varying irradiance levels. From the values of the DC link voltage levels, HPPO is outperforming other MPPTS. At 1000 W/m², the DC link voltage for HPPO is 1056V, outperforming other algorithms. Similarly, at 400 W/m², HPPO maintains a high PV voltage of 1040 V. These quantitative results reveal the favorable performance of HPPO in sustaining stable and optimized DC link voltage compared with alternative MPPT techniques.

6.1.6 Grid power response

Table 4 provided above compares the grid power values of various algorithms with HPPO under different irradiation conditions.

The PV grid power for HPPO is 10302W for 1000 W/m², outperforming other algorithms. Similarly, at 400 W/m², HPPO maintains a high PV grid power of 4176W. In contrast, alternative MPPT algorithms exhibit varying performances and fluctuating PV grid power values under changing irradiance conditions. These quantitative results reveal the favorable performance of HPPO in sustaining stable and optimized grid power responses compared to alternative MPPT techniques.

6.1.7 Efficiency of overall system

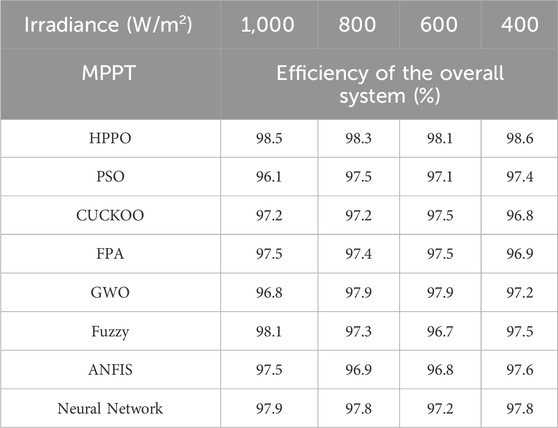
Table 5 presents the efficiency of the overall PV system, considering both the PV array and the Maximum Power Point Tracking (MPPT) algorithms.

Table 5

Table 5. Efficiency of the overall system for case 1.

Notably, HPPO consistently demonstrates competitive efficiency of the overall PV system values across varying irradiance levels. At 1000 W/m², the PV efficiency for HPPO is 98.5%, outperforming other algorithms. Similarly, at 400 W/m², HPPO maintains a high PV efficiency of 98.6%. In contrast, alternative MPPT algorithms exhibit varying performances and fluctuating PV efficiency values under changing irradiance conditions. These quantitative results reveal the favorable performance of HPPO in sustaining stable and optimized overall PV efficiency responses compared with alternative MPPT techniques.

6.1.8 Total harmonic distortion

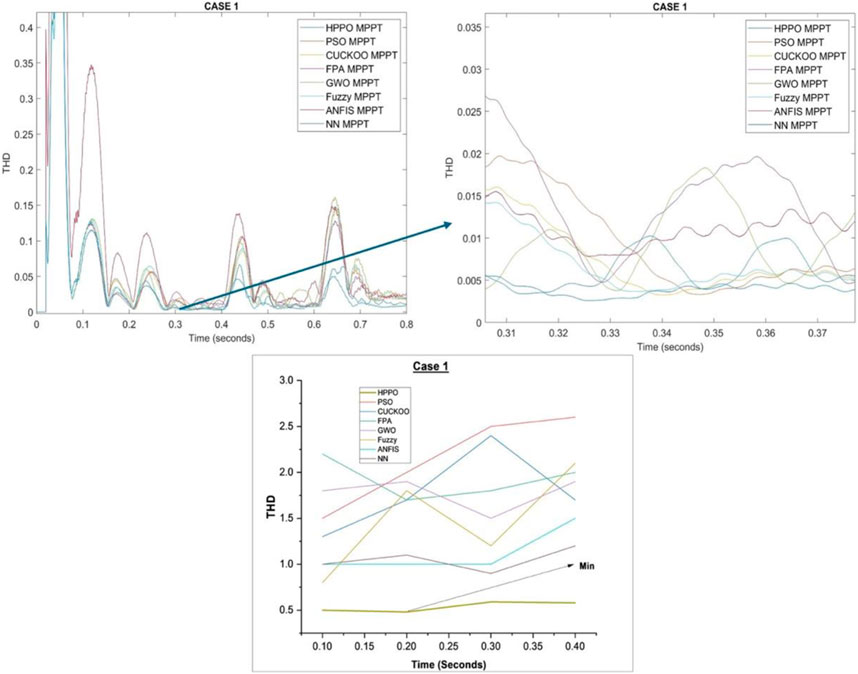
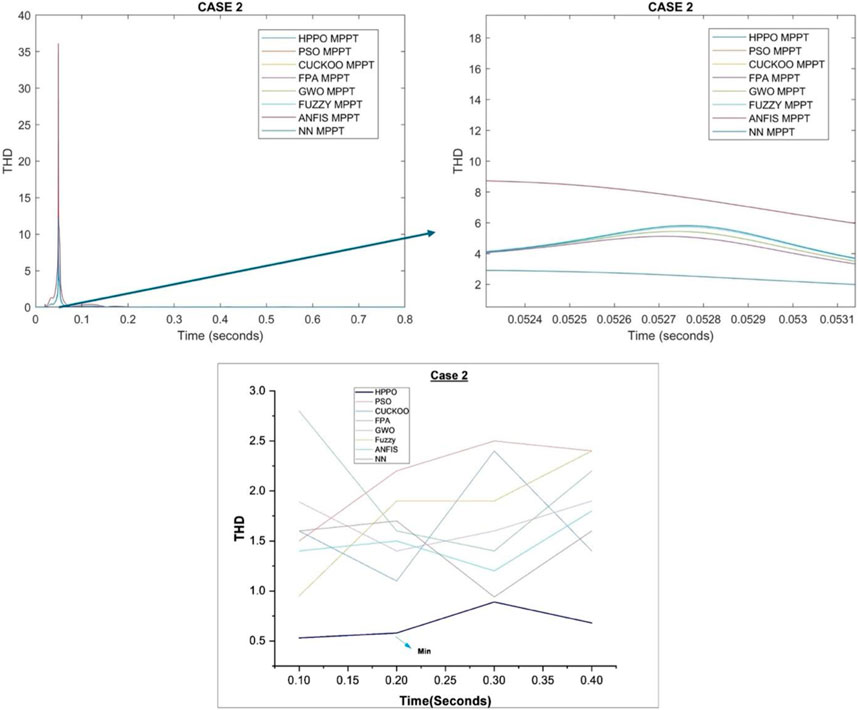
High THD affects grid stability due to distortion in voltage and current waveform since distorted waveforms lead to poor power quality that could damage the equipment, lower efficiency, and cause overheating. Some of the reasons for relevance include triggering resonances in the grid, amplifying currents, and potentially breaking grid operations, along with elevated THD thereby shortening equipment lifespan, increasing power losses and heat, and interfering with protective relay operation, risking unintentional disconnections and reliability loss. Table 6 compares the total harmonic distortion (THD) values corresponding to various algorithms with reference HPPO under different irradiation conditions, also called oscillations around MPP. THD is a measure of the distortion in the waveform of the grid current, reflecting the presence of harmonics.

Table 6

Table 6. Total Harmonic Distortion of the grid current for Case 1.

The PV THD for HPPO is 0.5% at 1000 W/m2, which is better than previous methods. Similarly, HPPO has the best PV THD of 0.58% at 400 W/m². As a result, HPPO continuously shows competitive PV THD values over a range of irradiance levels.

Figure 7 displays the THD of the grid current response for case 1.

Figure 7

Figure 7. Total Harmonic distortion of grid current response for Case 1.

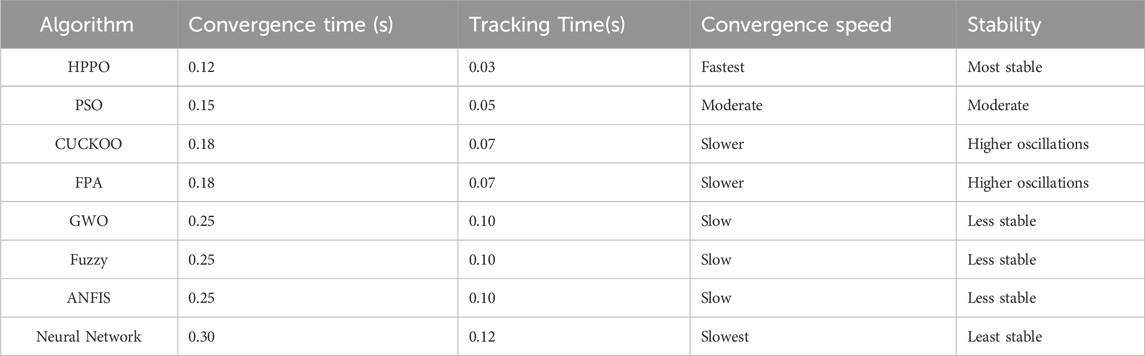
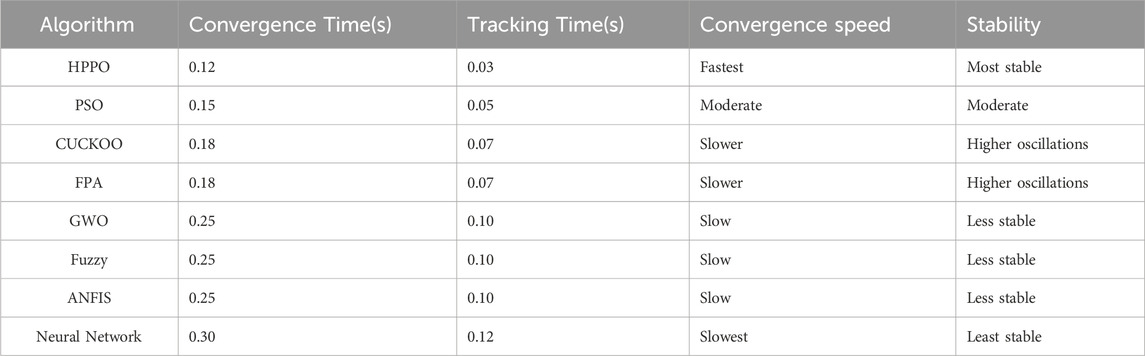
Table 7 compares the convergence time, tracking time, tracking speed, convergence speed, and stability of the proposed technique with other techniques for case 1.

Table 7

Table 7. Convergence time, tracking time for case 1.

The table compares several algorithms based on their convergence time, tracking time, convergence speed, and stability. The proposed HPPO emerges as the top performer, with the fastest convergence time of 0.12 s and the quickest tracking time of 0.03 s, and is the most stable algorithm, while the Neural Network algorithm performs the worst, with the slowest convergence and tracking times, making it the “least stable” technique.

6.2 Simulation results for case 2

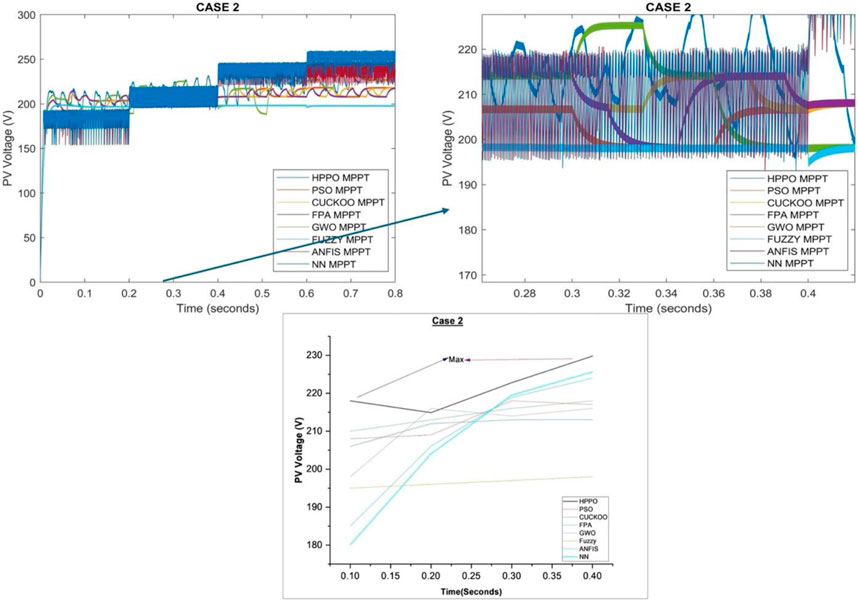
6.2.1 PV voltage response

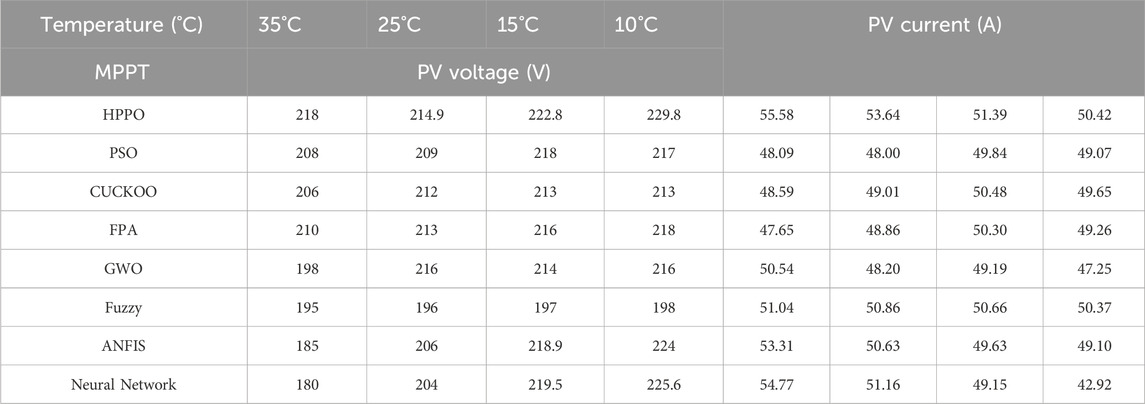
Table 8 compares the PV voltage values corresponding to various algorithms with reference HPPO under different temperature conditions.

Table 8

Table 8. PV Voltage details for Case 2.

Notably, HPPO consistently demonstrates competitive PV voltage values across varying temperature levels. At 35°C, the PV voltage for HPPO is 218 V, outperforming other algorithms. Similarly, at 10°C, HPPO maintains a high PV voltage of 229.8 V. In contrast, other algorithms such as PSO, CUCKOO, FPA, GWO, Fuzzy, ANFIS, and Neural Network record lower values ranging from 180 V to 220 V. These quantitative results reveal the favorable performance of HPPO in sustaining stable and optimized PV voltage responses in comparison with alternative MPPT techniques.

The graphical representation of PV output voltage for the HPPO algorithm and other techniques has been presented in Figure 8.

Figure 8

Figure 8. PV voltage response for case 2.

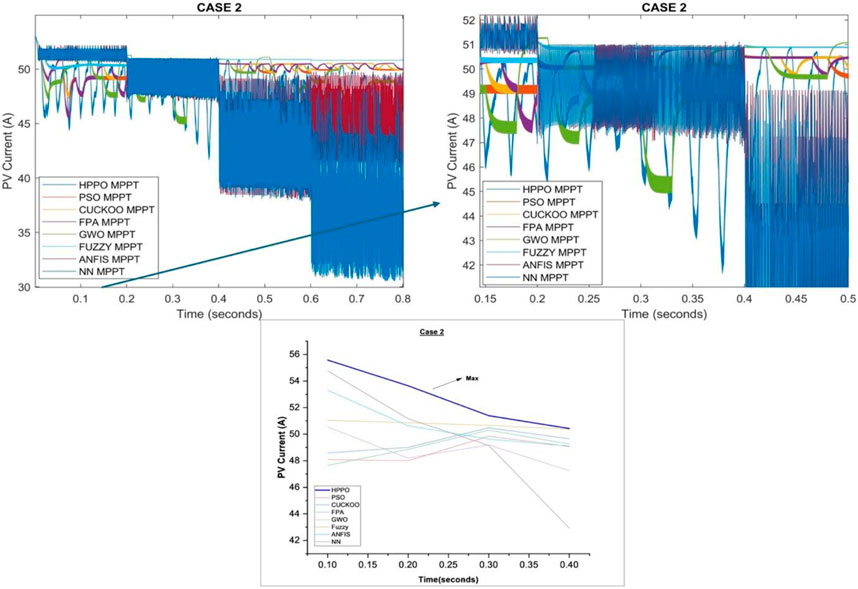
6.2.2 PV current response

Table 8 provided above compares the PV current values corresponding to various algorithms with reference HPPO under different Temperature conditions.

Notably, HPPO consistently demonstrates competitive PV current values across varying irradiance levels. At 35°C, the PV current for HPPO is 55.58A, outperforming other algorithms. Similarly, at 10°C, HPPO maintains a high PV current of 50.42 A. In contrast, alternative MPPT algorithms exhibit varying performances and fluctuating PV current values under changing temperature conditions. These quantitative results reveal the favorable performance of HPPO in sustaining stable and optimized PV current responses compared to alternative MPPT techniques.

The PV current for case 2 is presented in Figure 9.

Figure 9

Figure 9. PV current response for case 2.

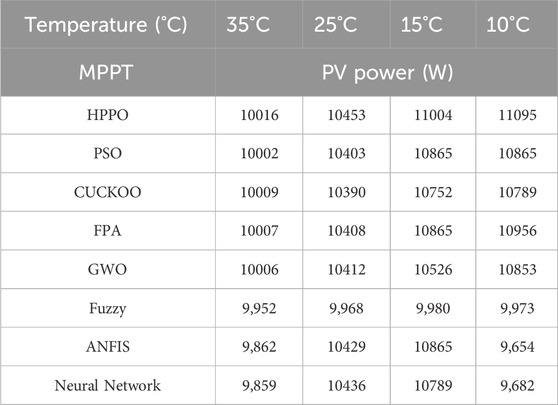
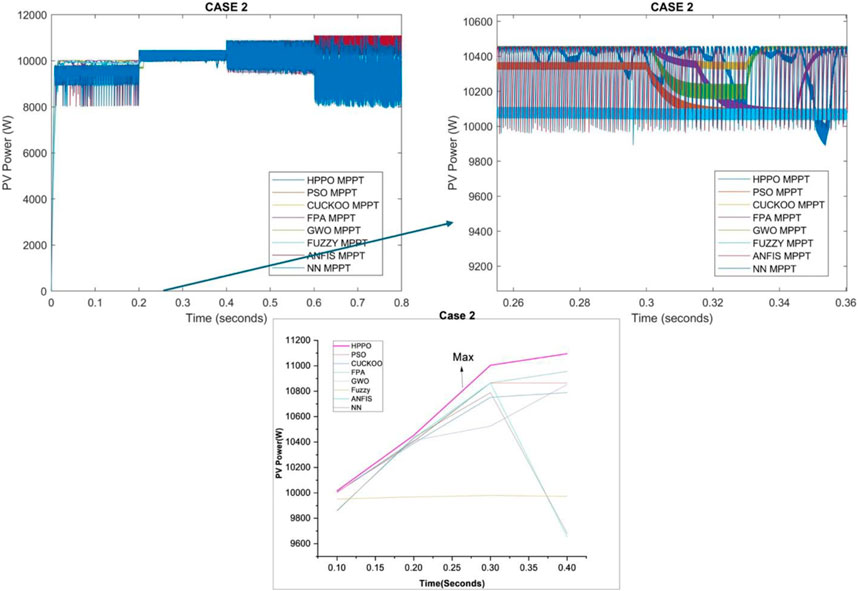
6.2.3 PV power response

Table 9 compares the PV power values corresponding to various algorithms with reference HPPO under different temperature conditions.

Table 9

Table 9. PV Power response for Case 2.

Notably, HPPO consistently demonstrates competitive PV power values across varying temperature levels. At 35°C, the PV power for HPPO is 10016W, outperforming other algorithms. Similarly, at 10°C, HPPO maintains a high PV power of 11095W. In contrast, alternative MPPT algorithms exhibit varying performances and fluctuating PV power values under changing temperature conditions. These quantitative results reveal the favorable performance of HPPO in sustaining stable and optimized PV power responses compared to alternative MPPT techniques.

The PV power for case 2 is presented in Figure 10.

Figure 10

Figure 10. PV Power response for Case 2.

6.2.4 The efficiency of PV MPPT response

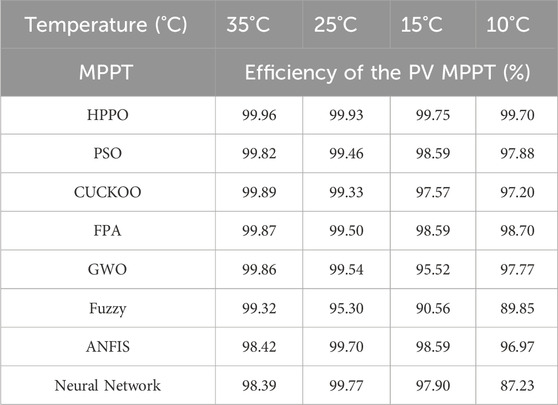
The efficiency values of PVMPPT are presented in Table 10.

Table 10

Table 10. Efficiency of the PV MPPT for case 2.

HPPO consistently demonstrates competitive PV MPPT efficiency values across varying irradiance levels. At 35°C, the PV MPPT efficiency for HPPO is 99.96%, outperforming other algorithms. Similarly, at 10°C, HPPO maintains a high PV MPPT efficiency of 99.70%. In contrast, alternative MPPT algorithms exhibit varying performances and fluctuating PV MPPT efficiency values under changing temperature conditions. These quantitative results reveal the favorable performance of HPPO in sustaining stable and optimized PV MPPT efficiency responses compared with alternative MPPT techniques.

6.2.5 DC link voltage response

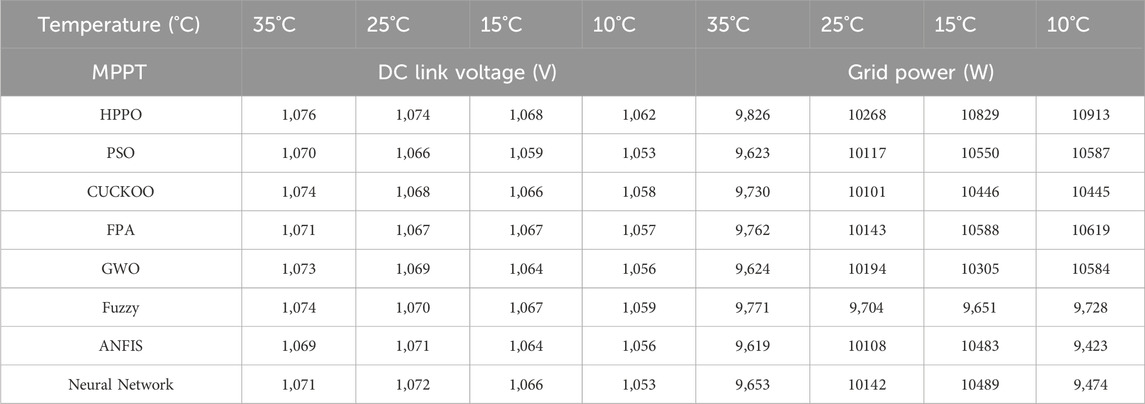
Table 11 compares the PV DC Link voltage values under case 2.

Table 11

Table 11. DC Link Voltage details for Case 2.

From the tabulated values, it was observed that for the HPPO algorithm at 35°C, the DC link voltage is 1073V. For 10°C, HPPO maintains a high PV voltage of 1062 V. These quantitative results reveal the favorable performance of HPPO in sustaining stable and optimized DC link voltage.

6.2.6 Grid power response

The grid response regarding grid power output for all MPPT algorithms has been tabulated in Table 11 under variable conditions.

The grid power output for HPPO is 9826W for 35°C,10268 for 25°C,10829W for 15°C, and 10913W for 10°C. Notably, HPPO consistently has the highest value of grid output voltage in all the temperature conditions considered.

6.2.7 Efficiency of the overall system

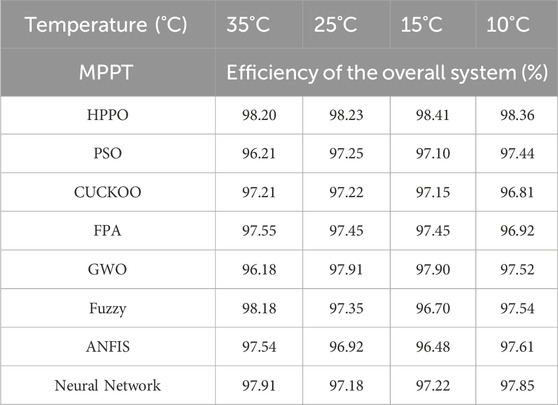
Table 12 compares the PV system efficiency values corresponding to various algorithms with reference HPPO under different temperature conditions.

Table 12

Table 12. Efficiency of the overall system for Case 2.

HPPO consistently demonstrates competitive PV system efficiency values across varying temperature levels. At 35°C, the PV system efficiency for HPPO is 98.20%, outperforming other algorithms. Similarly, at 10°C, HPPO maintains a high PV system efficiency of 98.36%. In contrast, alternative MPPT algorithms exhibit varying performances and fluctuating PV system efficiency values under changing temperature conditions. These quantitative results reveal the favorable performance of HPPO in sustaining stable and optimized PV system efficiency compared to alternative MPPT techniques.

6.2.7.1 THD response system

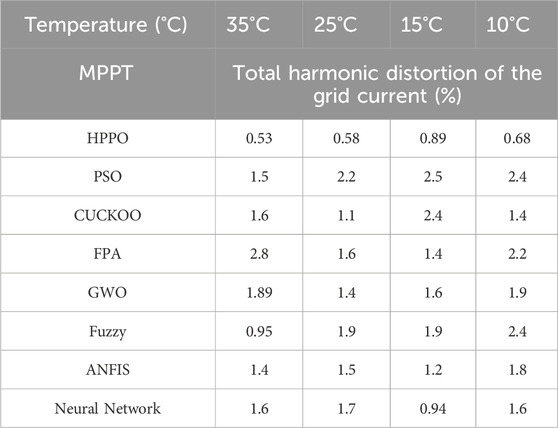
The simulation results of calculated THD values for the case 2 condition are in tabular form in Table 13 and graphically in Figure 11.

Table 13

Table 13. Total Harmonic Distortion of the grid current for Case 2.

Figure 11

Figure 11. Total harmonic distortion of grid current response for Case 2.

HPPO consistently demonstrates competitive PV THD response values across varying temperature levels. At 35°C, the PV THD response for HPPO is 0.53%, outperforming other algorithms. Similarly, at 10°C, HPPO maintains a high PV THD response of 216.8 V. In contrast, alternative MPPT algorithms exhibit varying performances and fluctuating PV THD response values under changing temperature conditions. These quantitative results reveal the favorable performance of HPPO in sustaining stable and optimized PV THD response compared with alternative MPPT techniques.

The PV THD response for case 2 is presented in Figure 11.

Table 14 below is a comparison of the proposed technique’s convergence time, tracking time, tracking speed, convergence speed, and stability with other techniques for case 2.

Table 14

Table 14. Convergence time, tracking time summary for case 2.

This table compares the performance of various algorithms based on how quickly and steadily they reach a stable state in a system. The proposed HPPO technique is the most responsive and reliable, with the fastest convergence time of 0.12 s, while the Neural Network-based MPPT is the slowest at 0.30 s, with the least stability among all methods.

7 Conclusion

This paper introduces a grid-interactive PV system utilizing the hybrid HPPO method for MPPT. The performance evaluation of this innovative technique was conducted by examining a range of parameters, including PV voltage, current, power, MPPT efficiency, grid voltage, current, inverter metrics, power factor, overall system efficiency, total harmonic distortion (THD), and convergence speed. Two distinct scenarios were analyzed: varying irradiance at a constant temperature and fluctuating temperature at steady irradiance.

In the first scenario, where irradiance varied while temperature remained constant at 25°C, the HPPO (Hybrid Particle Population Optimization) MPPT algorithm consistently outperformed other algorithms across all tested parameters. It achieved an MPPT efficiency exceeding 99.8% and maintained an overall system efficiency above 98%, demonstrating robust optimization of PV systems in dynamic conditions. The HPPO algorithm also demonstrated the fastest convergence and tracking times (0.12s and 0.03s, respectively) and the highest stability among tested algorithms. Unlike PSO and Cuckoo, which showed moderate to slower speeds and moderate to higher oscillations, HPPO minimized harmonic distortions effectively, making it exceptionally stable.

In the second scenario, where temperature changes occurred at fixed irradiance, HPPO continued to excel across all parameters, sustaining an MPPT efficiency above 99.8% and a PV system efficiency of 98.4%, outperforming all other techniques. THD analysis revealed that HPPO produced minimal harmonic distortion in grid current under 5% while delivering the best convergence and tracking speed, thus supporting a cleaner, more stable power output that aligns with IEEE 519 standards. Algorithms like GWO, Fuzzy, ANFIS, and Neural Networks were slower and less stable, with convergence times up to 0.30s and tracking times up to 0.12s, showing higher oscillations and reduced reliability. Overall, HPPO’s performance in both convergence speed and stability makes it ideal for precise, rapid tracking in dynamic conditions.

The simulation results confirm that the proposed HPPO method achieves efficiencies exceeding 99% across various scenarios, highlighting its superior performance compared to other approaches. This consistency in effectiveness under diverse conditions positions it as a promising solution for enhancing the efficiency and reliability of grid-connected PV systems. Future work will involve hardware testing of the MPPT to alleviate computational demands through the use of efficient microcontrollers or programmable arrays, as well as exploring a broader range of conditions to gain deeper insights into the method’s limitations and potential for further optimization.

Data availability statement

The datasets presented in this article are not readily available because the data will be public after PHD thesis submission. Requests to access the datasets should be directed to YnVyaGFuYWJkdWxsYWg2QGdtYWlsLmNvbQ==.

Author contributions

BA: Conceptualization, Formal Analysis, Methodology, Writing–original draft, Writing–review and editing. SD: Conceptualization, Methodology, Supervision, Writing–review and editing. SJ: Conceptualization, Formal Analysis, Writing–review and editing. MG: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Validation, Writing–review and editing. MA: Data curation, Formal Analysis, Funding acquisition, Validation, Visualization, Writing–review and editing. MK: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Resources, Software, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors would like to express their profound gratitude to King Abdullah City for Atomic and Renewable Energy (K.A.CARE) for their financial support in accomplishing this work at KFUPM, and the author MA also acknowledges the support by the Deanship of Scientific Research through King Khalid University, Saudi Arabia funded by the Large Group Research Project RGP2/392/45.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbadi, A., Hamidia, F., Morsli, A., Benbouabdellah, O., and Chiba, Y. (2020). “MPPT based fuzzy-logic controller for grid connected residential photovoltaic power system,” in Smart energy empowerment in smart and resilient cities. Editor M. Hatti (Cham: Springer International Publishing), 124–131. (Lecture Notes in Networks and Systems).

CrossRef Full Text | Google Scholar

A Dimension-Independent Array Relocation (DIAR) Approach for Partial Shading Losses Minimization in Asymmetrical Photovoltaic Arrays. IEEE Journals and Magazine | IEEE Xplore. Available at: https://ieeexplore.ieee.org/document/10158683.

Google Scholar

Ahmed, J., and Salam, Z. (2014). A maximum power point tracking (MPPT) for PV system using cuckoo search with partial shading capability. Appl. energy 119, 118–130. doi:10.1016/j.apenergy.2013.12.062

CrossRef Full Text | Google Scholar

Aljafari, B., Satpathy, P. R., Thanikanti, S. B., and Krishna Madeti, S. R. (2024). A reliable GTR-PLC approach for power enhancement and online monitoring of solar PV arrays during partial shading. Energy 303, 131839. doi:10.1016/j.energy.2024.131839

CrossRef Full Text | Google Scholar

A new MPPT design using grey wolf optimization technique for photovoltaic system under partial shading conditions | IEEE journals and magazine | IEEE Xplore Available at: https://ieeexplore.ieee.org/abstract/document/7305794.

Batarseh, M. G., and Za’ter, M. E. (2018). Hybrid maximum power point tracking techniques: a comparative survey, suggested classification and uninvestigated combinations. Sol. Energy 169, 535–555. doi:10.1016/j.solener.2018.04.045

CrossRef Full Text | Google Scholar

Belhachat, F., and Larbes, C. (2017). Global maximum power point tracking based on ANFIS approach for PV array configurations under partial shading conditions. Renew. Sustain. Energy Rev. 77, 875–889. doi:10.1016/j.rser.2017.02.056

CrossRef Full Text | Google Scholar

Bollipo, R. B., Mikkili, S., and Bonthagorla, P. K. (2021). Hybrid, optimal, intelligent and classical PV MPPT techniques: a review. CSEE J. Power Energy Syst. 7 (1), 9–33. doi:10.17775/CSEEJPES.2019.02720

CrossRef Full Text | Google Scholar

Boubaker, O. (2023). MPPT techniques for photovoltaic systems: a systematic review in current trends and recent advances in artificial intelligence. Discov. Energy 3 (1), 9. doi:10.1007/s43937-023-00024-2

CrossRef Full Text | Google Scholar

BO-XGBoost-based voltage/var optimization for distribution network considering the LCOE of PV system - zhang - 2024 - IET Renewable Power Generation - wiley Online Library Available at: https://ietresearch.onlinelibrary.wiley.com/doi/10.1049/rpg2.12868

Chang, C. C. W., Ding, T. J., Bhuiyan, M. A. S., Chao, K. C., Ariannejad, M., and Yian, H. C. (2023). Nature-inspired optimization algorithms in solving partial shading problems: a systematic review. Arch. Comput. Methods Eng. 30 (1), 223–249. doi:10.1007/s11831-022-09803-x

CrossRef Full Text | Google Scholar

Chen, K., Tian, S., Cheng, Y., and Bai, L. (2014). An improved MPPT controller for photovoltaic system under partial shading condition. IEEE Trans. Sustain. Energy 5 (3), 978–985. doi:10.1109/tste.2014.2315653

CrossRef Full Text | Google Scholar

Comparative analysis of MPPT algorithms bio-inspired by grey wolves employing a feed-forward control loop in a three-phase grid-connected photovoltaic system - poltronieri Sampaio - 2019 - IET Renewable Power Generation - Wiley Online Library Available at: https://ietresearch.onlinelibrary.wiley.com/doi/full/10.1049/iet-rpg.2018.5941.

Kumar, M., Panda, K. P., and Rosas-Caro, J. C. (2023). Comprehensive review of conventional and emerging maximum power point tracking algorithms for uniformly and partially shaded solar photovoltaic systems IEEE journals and magazine. IEEE Xplore. 11, 31778–31812. Available at: https://ieeexplore.ieee.org/document/10083133.

CrossRef Full Text | Google Scholar

Díaz Martínez, D., Trujillo Codorniu, R., Giral, R., and Vázquez Seisdedos, L. (2021). Evaluation of particle swarm optimization techniques applied to maximum power point tracking in photovoltaic systems. Int. J. Circuit Theory Appl. 49 (7), 1849–1867. doi:10.1002/cta.2978

CrossRef Full Text | Google Scholar

Dutta, S., Sadhu, P. K., Jaya Bharata Reddy, M., and Mohanta, D. K. (2018). Shifting of research trends in islanding detection method - a comprehensive survey. Prot. Control Mod. Power Syst. 3 (1), 1. doi:10.1186/s41601-017-0075-8

CrossRef Full Text | Google Scholar

Gao, L., Dougal, R. A., Liu, S., and Iotova, A. P. (2009). Parallel-connected solar PV system to address partial and rapidly fluctuating shadow conditions. IEEE Trans. Industrial Electron. 56 (5), 1548–1556. doi:10.1109/tie.2008.2011296

CrossRef Full Text | Google Scholar

Ge, X., Ahmed, F. W., and Rezvani, A. (2020). Implementation of a novel hybrid BAT-Fuzzy controller based MPPT for grid-connected PV-battery system - ScienceDirect. Available at: https://www.sciencedirect.com/science/article/abs/pii/S0967066120300496.

Google Scholar

Ghasemi, M. A., Foroushani, H. M., and Parniani, M. (2016). Partial shading detection and smooth maximum power point tracking of PV arrays under PSC. IEEE Trans. Power Electron. 31 (9), 6281–6292. doi:10.1109/tpel.2015.2504515

CrossRef Full Text | Google Scholar

Grid-tied photovoltaic system based on PSO MPPT technique with active power line conditioning - oliveira - 2016 - IET Power Electronics - Wiley Online Library Available at: https://ietresearch.onlinelibrary.wiley.com/doi/10.1049/iet-pel.2015.0655

Hayder, W., Ogliari, E., Dolara, A., Abid, A., Ben Hamed, M., Sbita, L., et al. (2020). Improved PSO: a comparative study in MPPT algorithm for PV system control under partial shading conditions. Energies 13 (8), 2035. doi:10.3390/en13082035

CrossRef Full Text | Google Scholar

Imad, H. H., Azmi Baharin, K., Kim Gan, C., and Sabry, A. H. (2024). Techno-economic optimization of photovoltaic (PV)-inverter power sizing ratio for grid-connected PV systems. Results Eng. 23, 102580. doi:10.1016/j.rineng.2024.102580

CrossRef Full Text | Google Scholar

Jiang, C. (2024). African vulture optimized RNN algorithm maximum power point tracking (MPPT) controller for photovoltaic (PV) system. Meas. Sensors 24, 101392. doi:10.1016/j.measen.2024.101392

CrossRef Full Text | Google Scholar

Jyothy, L. P. N., and Sindhu, M. R. (2018). “An artificial neural network based MPPT algorithm for solar PV system,” in 2018 4th international conference on electrical energy systems (ICEES), 375–380.

Google Scholar

Koh, J. S., Tan, R. H. G., Lim, W. H., and Tan, N. M. L. (2023). A modified particle swarm optimization for efficient maximum power point tracking under partial shading condition. IEEE Trans. Sustain. Energy 14, 1822–1834. doi:10.1109/tste.2023.3250710

CrossRef Full Text | Google Scholar

Krishnaram, K., Suresh Padmanabhan, T., Alsaif, F., and Senthilkumar, S. (2024). Development of grey wolf optimization based modified fast terminal sliding mode controller for three phase interleaved boost converter fed PV system. Sci. Rep. 14 (1), 9256. doi:10.1038/s41598-024-59900-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Mariprasath, T., Basha, C. H. H., Khan, B., and Ali, A. (2024). A novel on high voltage gain boost converter with cuckoo search optimization based MPPTController for solar PV system. Sci. Rep. 14 (1), 8545. doi:10.1038/s41598-024-58820-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Meddour, S., Rahem, D., Cherif, A. Y., Hachelfi, W., and Hichem, L. (2019). A novel approach for PV system based on metaheuristic algorithm connected to the grid using FS-MPC controller. Energy Procedia 162, 57–66. doi:10.1016/j.egypro.2019.04.007

CrossRef Full Text | Google Scholar

Mellit, A., and Pavan, A. M. (2010). A 24-h forecast of solar irradiance using artificial neural network: application for performance prediction of a grid-connected PV plant at Trieste, Italy. Sol. Energy 84 (5), 807–821. doi:10.1016/j.solener.2010.02.006

CrossRef Full Text | Google Scholar

Mohapatra, A., Nayak, B., Das, P., and Mohanty, K. B. (2017). A review on MPPT techniques of PV system under partial shading condition. Renew. Sustain. Energy Rev. 80, 854–867. doi:10.1016/j.rser.2017.05.083

CrossRef Full Text | Google Scholar

Mohapatra, B., Sahu, B. K., Pati, S., Bajaj, M., Blazek, V., Prokop, L., et al. (2024). Optimizing grid-connected PV systems with novel super-twisting sliding mode controllers for real-time power management. Sci. Rep. 14 (1), 4646. doi:10.1038/s41598-024-55380-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Padmanaban, S., Priyadarshi, N., Mbhaskar, M. S., Holm-Nielsen, J. B., Ramachandaramurthy, V. K., and Hossain, E. (2019). A hybrid ANFIS-ABC based MPPT controller for PV system with anti-islanding grid protection: experimental realization. IEEE Journals and Mag. IEEE Xplore 7, 103377–103389. doi:10.1109/access.2019.2931547

CrossRef Full Text | Google Scholar

Prasanth Ram, J., and Rajasekar, N. (2017). A novel flower pollination based global maximum power point method for solar maximum power point tracking. IEEE Trans. Power Electron. 32 (11), 8486–8499. doi:10.1109/tpel.2016.2645449

CrossRef Full Text | Google Scholar

Ram, J. P., Pillai, D. S., Ghias, AMYM, and Rajasekar, N. (2020). Performance enhancement of solar PV systems applying P&O assisted Flower Pollination Algorithm (FPA). Sol. Energy 199, 214–229. doi:10.1016/j.solener.2020.02.019

CrossRef Full Text | Google Scholar

Ranjan, S. P., Ramachandaramurthy, V. K., Roslan, M. F., and Motahhir, S. (2024). An adaptive architecture for strategic Enhancement of energy yield in shading sensitive Building-Applied Photovoltaic systems under Real-Time environments. Energy Build. 324, 114877. doi:10.1016/j.enbuild.2024.114877

CrossRef Full Text | Google Scholar

Ranjan Satpathy, P., Ramachandaramurthy, V. K., Radha Krishnan, T. R., Pulenthirarasa, S., and Padmanaban, S. (2024). Power and efficiency enhancement of solar photovoltaic power plants through grouped string voltage balancing approach. Energy Convers. Manag. X 24, 100711. doi:10.1016/j.ecmx.2024.100711

CrossRef Full Text | Google Scholar

Refaat, A., Ali, Q. A., Elsakka, M. M., Elhenawy, Y., Majozi, T., Korovkin, N. V., et al. (2024). Extraction of maximum power from PV system based on horse herd optimization MPPT technique under various weather conditions. Renew. Energy 220, 119718. doi:10.1016/j.renene.2023.119718

CrossRef Full Text | Google Scholar

Restrepo, C., Yanẽz-Monsalvez, N., González-Castaño, C., Kouro, S., and Rodriguez, J. (2021). A fast converging hybrid MPPT algorithm based on ABC and P&O techniques for a partially shaded PV system. Mathematics 9 (18), 2228. doi:10.3390/math9182228

CrossRef Full Text | Google Scholar

Sameera, T. M., Rihan, M., and Ayan, M. (2024). A comprehensive review on the application of recently introduced optimization techniques obtaining maximum power in the solar PV System. Renew. Energy Focus 49, 100564. doi:10.1016/j.ref.2024.100564

CrossRef Full Text | Google Scholar

Sangrody, R., Taheri, S., Cretu, A. M., and Pouresmaeil, E. (2024). An improved PSO-based MPPT technique using stability and steady state analyses under partial shading conditions. IEEE Trans. Sustain. Energy 15 (1), 136–145. doi:10.1109/tste.2023.3274939

CrossRef Full Text | Google Scholar

Satpathy, P. R., Aljafari, B., Thanikanti, S. B., Nwulu, N., and Sharma, R. (2024). A multi-string differential power processing based voltage equalizer for partial shading detection and mitigation in PV arrays. Alexandria Eng. J. 104, 12–30. doi:10.1016/j.aej.2024.05.105

CrossRef Full Text | Google Scholar

Savrun, M. M., and İnci, M. (2021). Adaptive neuro-fuzzy inference system combined with genetic algorithm to improve power extraction capability in fuel cell applications. J. Clean. Prod. 299, 126944. doi:10.1016/j.jclepro.2021.126944

CrossRef Full Text | Google Scholar

Seyedmahmoudian, M., Horan, B., Soon, T. K., Rahmani, R., Than Oo, A. M., Mekhilef, S., et al. (2016). State of the art artificial intelligence-based MPPT techniques for mitigating partial shading effects on PV systems – a review. Renew. Sustain. Energy Rev. 64, 435–455. doi:10.1016/j.rser.2016.06.053

CrossRef Full Text | Google Scholar

Smadi, T. A., Handam, A., Gaeid, K. S., Al-Smadi, A., Al-Husban, Y., and Khalid, A. smadi (2024). Artificial intelligent control of energy management PV system. Results Control Optim. 14, 100343. doi:10.1016/j.rico.2023.100343

CrossRef Full Text | Google Scholar

Trojovský, P., and Dehghani, M. (2022). Pelican optimization algorithm: a novel nature-inspired algorithm for engineering applications. Sensors 22 (3), 855. doi:10.3390/s22030855

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Li, Y., and Ruan, X. (2016). High-accuracy and fast-speed MPPT methods for PV string under partially shaded conditions. IEEE Trans. Industrial Electron. 63 (1), 235–245. doi:10.1109/tie.2015.2465897

CrossRef Full Text | Google Scholar

Yousri, D., Babu, T. S., Allam, D., Ramachandaramurthy, V. K., and Etiba, M. B. (2019). A novel chaotic flower pollination algorithm for global maximum power point tracking for photovoltaic system under partial shading conditions. IEEE Access 7, 121432–121445. doi:10.1109/access.2019.2937600

CrossRef Full Text | Google Scholar

Zaghba, L., Khennane, M., Borni, A., Fezzani, A., Bouchakour, A., Mahammed, I. H., et al. (2019). “A genetic algorithm based improve P&O-PI MPPT controller for stationary and tracking grid-connected photovoltaic system,” in 2019 7th international renewable and sustainable energy conference (IRSEC), 1–6. Available at: https://ieeexplore.ieee.org/document/9078304.

Google Scholar