Hippopotamus based optimization for reliable and cost-effective designing of stand-alone hybrid renewable system for a remote area

Energy is an important aspect of a country’s long-term growth, and to meet the increasing electrical demand for reliable manner, there is an urge to plan for future generations. In this study, metaheuristic optimization approaches that have recently been constructed, which include the coati optimization algorithm and hippopotamus optimization, were applied to determine the perfect dimensions for a grid-independent composite renewable energy infrastructure. The optimization problem attempts to reduce the total annual cost of the system while maintaining the reliability of the loss of power supply probability in an acceptable range. Three combinations of hybrid energy systems were designed and optimized, and the optimization findings point out that the system consisting of a photovoltaic module, wind turbine, storage battery, and battery is the most cost-effective optimal energy system. The lowest total annual cost of the PV/WT/SB/DG system obtained by using HOA is $24473, followed by PV/WT/DG at $ 26270 and PV/SB/DG at $35848. Also, the outcomes of the proposed algorithm were contrasted with those of the HOMER platform. When contrasting the effectiveness of optimization methods, the HOA is the optimal solution for resolving the sizing issue since it offers the most effective compromise among robustness, accuracy, and convergence rate.

1 Introduction

All the countries aim to install renewable energy projects, which will act as a solution to the problems encountered with the utilization of fossil fuels to generate energy. There are several clean energy sources available, such as solar PV energy, wind energy, biomass fuel energy, and geothermal sources, which have the merits of being reliable, clean, environmentally friendly, and sustainable. The level of energy generation from renewable-based plants is based on the readiness of sources, for example, solar radiation, wind speed, etc., which are all intermittent. Hence, to ensure regularity and reliable power supply from an environmentally friendly energy system, the combination of two or more energy production systems is recommended to complement their own intermittent (Thirunavukkarasu and Sawle, 2021a). The problem encountered while designing a composite renewable energy system is the inefficient design of the framework, which is not able to meet the load demand, increase energy expenditure, and decrease reliability and competence. Several years of research have been accomplished to design an optimal hybrid renewable system, and for this, various methods have been used that are based on software, mathematical programming, and metaheuristic algorithms (Mahmoudi et al., 2022).

In prior research, several authors have employed hybrid optimization of multiple energy resources (HOMER) to determine the superior design and feasible scrutiny of hybrid power systems. Riayatsyah et al. structured an on-grid hybrid energy system to provide vitality for Syiah Kaula University, which is located on Sumatra Island. Techno-economic and optimization analyses were conducted for the design of the system in the selected, tsunami-affected region. In Indonesia, where electricity availability is low, the integration of PV solar and wind systems was revealed to be viable for implementation (Riayatsyah et al., 2022). Wong and Li carried out research work to examine the feasibility analysis based on cost, energy production, and emission of different hybrid energy systems for the Xiamen University, Malaysia campus located in Malaysia. The comparative analysis of different scenarios concludes that the wind-biogas-hydrogen module-battery system seems to be the most optimal system to meet the load, sustain university operations, and curtail the dependency on the grid (Wong and Li, 2023). Also, a multitude of studies has been undertaken using HOMER to optimize the energy system for diverse countries and applications which includes rural areas, India (Kumar et al., 2019); Rural electrification (Ali et al., 2021), Pakistan; Agriculture well, Iran (Heydari and Askarzadeh, 2016); Household, United Kingdom (Miao et al., 2020); Household, Peru (Rinaldi et al., 2021); Nitric Acid plant, Africa (Anastasopoulou et al., 2016); Rural community, Ethiopia (Nigussie et al., 2017). The HOMER software tool has several demerits, such as the requirement of a long time to perform calculations and the lack of an option to perform optimization based on multi-objective tasks. However, several software tools, which include RETScreen, Hybrid2, RAPSIM, ARES, iHOGA, etc., are available to optimize hybrid energy systems. Several researchers state that the paramount commonly used tools to optimally design the hybrid energy system are HOMER and iHOGA.

Over the past years, a vast number of researchers have employed traditional, metaheuristic, and hybrid techniques to evaluate the optimal sizing and feasible analysis of grid-connected and off-grid hybrid renewable systems. The Improved Archimedes Optimization Algorithm was successfully used to create a hybrid renewable energy system (HRES) for a microgrid in Farafra, Egypt, by optimizing PV panels, wind turbines, diesel generators, and battery storage. The findings revealed that IAOA beats other algorithms, with a net present cost of $187,181 and a levelized cost of energy of 0.213 $/kWh. The system met all constraints and demonstrated the synergy of PV and wind systems, with batteries playing an important role in energy management (Kharrich et al., 2023). In Kaele, Cameroon, a hybrid system was developed to meet the energy requirements of houses, multimedia centers, and healthcare facilities. The system was optimized with four meta-heuristic algorithms: colliding body optimization, charged system search, teaching-learning-based optimization, and water evaporation optimization. The results show that the TLBO algorithm produced the best results for system sizing, with the PV/Wind/Battery/Diesel configuration being the most cost-effective (Koholé et al., 2024). The Leader Artificial Rabbits Optimization Algorithm has been used to design a hybrid microgrid for residential use in Guelmim City, Morocco. The LAROA findings were compared to those of various other algorithms, and the results show that the proposed approach beats the others in terms of convergence speed and solution correctness. The optimal microgrid structure, consisting of PV, wind, diesel, and battery systems, reaches a net present cost of $106,821, with an energy cost of around $0.11 per kWh (Kharrich et al., 2024). Incorporated a design of PV-BM-FC with a hydrogen storage system to reduce the system’s overall net present expense using a whale optimization technique with the consideration of component units and LPSP as a constraint. The outcomes revealed that the least NPC and lower LPSP were obtained from the proposed algorithm with higher accuracy and reliability than the PSO method. Furthermore, simulation findings show that while decreasing the availability of system unit sizes, the objective function increases and weakens the LPSP indices (Sun et al., 2022). Used the means of an improved harmonic search to solve the optimal design of an off-grid hybrid power system with the consideration of four different energy storage components and analyzed the effect of storage components on the production cost of energy, system reliability, and stabilization of power provision. The efficacy of the proposed algorithm is compared with the original harmonic search algorithm, and the results state that while using an improved harmony search, the total cost to achieve the optimal design has been reduced compared to the original harmony search. Also, the level of system operation cost and reliability have been investigated due to the impact of wind speed, load demands, project interest rate, battery life, and battery DOD (Sun et al., 2024).

Although several researchers employed a variety of algorithms for HRES optimal sizing, some of the algorithms may not be able to converge global optima and do not attain quick convergence. Also, to explore the future of several applications, several new algorithms have been developed, and not all algorithms have the skills to adapt to all optimization problems. Thus, it is important to use recent algorithms to check their effectiveness in the area of optimal sizing of HRES. The essence of this work is to design and optimize an off-grid hybrid energy system to ensure a reliable supply of power at a relatively low cost for a location in India. Many authors compared their results obtained from the metaheuristics algorithms with those of other metaheuristics algorithms, and their results have not been in-depth compared and analyzed with HOMER software. Widely used HOMER software to address the needs of optimal sizing for the applications includes residential (Thirunavukkarasu and Sawle, 2021b), (Thirunavukkarasu and Sawle, 2020), and tea factories (Thirunavukkarasu and Sawle, 2022) in India. Several prior studies have been carried out to model and optimize off-grid-connected hybrid renewable energy systems in various configurations. According to the authors, only a few have been conducted for some locations in Rajasthan’s Jaisalmer district. Saraswat and Rao (Saraswat and Rao, 2018) explore an off-grid PV/DG/SB hybrid design and perform an economic analysis for a location in Jaisalmer town, Rajasthan, India.

According to the literature, while much attention has been paid to the feasibility and resource examination of hybrid renewable energy systems, yet is still a lack of understanding of their technical and economic sustainability, particularly in rural areas. Despite the increased usage of renewable energy, hybrid systems that integrate several renewable resources are still underexplored. Furthermore, microgrid design and sizing pose major obstacles, which are worsened by energy price volatility, climate change, and technological limits. This study is motivated by the necessity to optimize HRES for rural areas in order to satisfy energy demands at the lowest possible cost. The objective function used to model the economic viability of each arrangement is the system’s total annual cost, subject to numerous constraints. The study’s aims include (i) modeling renewable energy systems for rural areas in India using various hybrid configurations, (ii) reducing CO₂ emissions, (iii) fulfilling electric load demands, and (iv) assuring enough energy storage capacity. Unlike previous research, which often rely on software tools such as HOMER for optimization, our approach uses a novel optimization algorithm to provide a more complete viable option for rural electrification in poor nations. Despite metaheuristic algorithms have been extensively used in microgrid design, their erratic convergence behavior frequently produces contradictory outcomes. As a result, our research presents a new coati optimization approach to overcome these discrepancies and enhance solution accuracy. The Hippopotamus optimization algorithm, another well-known optimization technique, is used to compare the results of the Coati optimization algorithm, and HOMER software is used to evaluate the results.

1.1 Identifying research gaps and formulating a pertinent research question by examining the current literature

➢ Comprehensive techno-economic-environmental analyses of Hybrid Renewable Energy Systems (HRES) using meteorological data for Bhopal, India, are lacking, according to a review of the literature. Despite Madhya Pradesh’s exploration of solar and wind energy, HRES is not given enough priority based on variables including emissions, energy production, costs (capital, operating, and maintenance), and the renewable fraction. The need for such an analysis is highlighted by the research gap that requires addressing the viability of HRES in Madhya Pradesh.

➢ The majority of research optimize using HOMER, although the study of novel constraints is limited by the difficulty of introducing additional constraints.

➢ Although metaheuristic approaches have been extensively researched for HRES optimization, their accuracy, exploration, exploitation, and convergence rates differ, necessitating a reliable and effective sizing optimization strategy.

1.2 A summary of this study’s main contributions is provided below

➢ In order to supply electricity to a metropolitan region in Madhya Pradesh, India, three distinct off-grid hybrid renewable energy system configurations underwent thorough technical, economic, and environmental studies.

➢ To ascertain the ideal sizing of off-grid hybrid renewable energy systems, this work presents a revolutionary coati optimization technique and hippopotamus optimization algorithm. The method ensures a reliability constraint, which is the tolerable loss of power supply, while minimizing the overall annual cost.

➢ The hippopotamus optimization algorithm was compared to the coati optimization algorithm in order to evaluate its robustness and effectiveness. The comparison was based on a number of performance indicators, such as the mean, standard deviation, degree of oscillations around the global optimum, pace of convergence, and the minimum and highest values of the system’s total annual cost.

➢ The proposed algorithms are optimized with MATLAB software, and the outcomes are verified by contrasting them with those from HOMER software.

2 Methodology

2.1 Geographical site

India is experiencing a power shortage due to the higher level of consumption. The impending coal issue will reduce power generation while increasing the number of hours of power outages. According to the progress report for April 2024, Madhya Pradesh has 50 villages without power (PMAGY, 2024). The role of electricity supply for villages, especially Adivasis, remains elusive. The villages of Koopgarh, Chervi, and Dhanjara do not have electricity, and the residents of Semli village have never witnessed electricity. For this study, Koopgarh village (24° 50.9 ‘N, 77° 60.0’ E) is located in Ashoknagar district in Madhya Pradesh, India, which is situated around 250 km away from the capital Bhopal has been selected. Out of Madhya Pradesh’s 72 million population, 22% are from scheduled tribes, who have been notably excluded from electrification facilities.

2.2 Load profile

In the selected location, the inhabitants continue to live without electricity, trekking through impenetrable forests to obtain firewood and drinking dirty water from streams. Students at a local government school study in the sunlight streaming through the windows, and the intense summer heat has also caused kids to avoid school since it is too hot for them to learn. The World Resources Institute, India claims that the key driver behind the failure of renewable energy projects in underserved areas is the lack of government investment in these areas. Figure 1 depicts the power crisis in the koopgarh village, Madhya Pradesh, India. Table 1 tabulates the basic need for electrical power for several application purposes.

Figure 1

Figure 1. Power crises in the selected location.

Table 1

Table 1. Basic needs of the electrical consumption.

2.3 Resource assessment

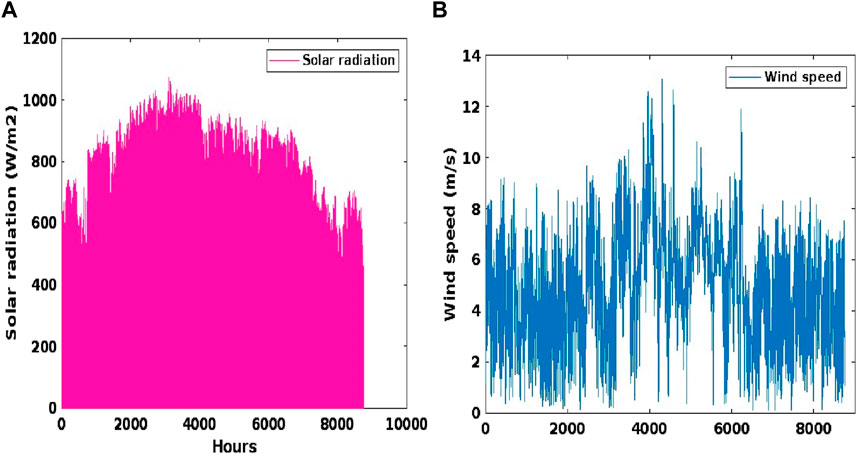
As input parameters for the study area, the National Renewable Energy Laboratory of India provides the hourly total solar radiation and wind speed data at Koppgarh. The software platforms HOMER and MATLAB are then used to process and evaluate these data. Figure 2 represent the availability of renewable sources.

Figure 2

Figure 2. Renewable energy resources. (A) Solar radiation. (B) Wind speed.

2.4 Modelling of system components

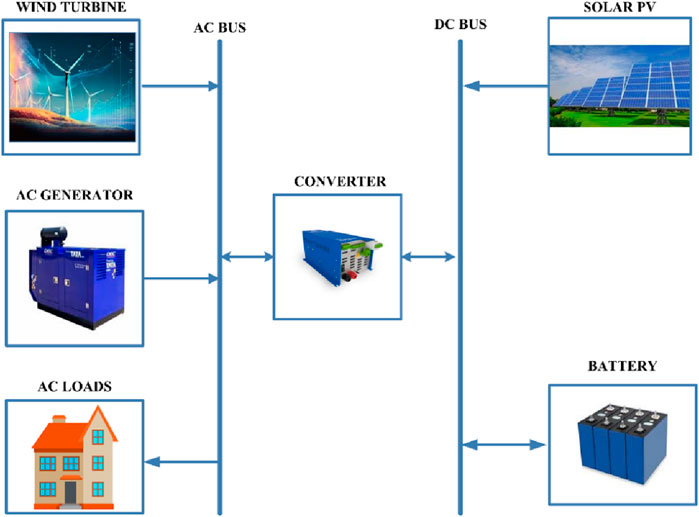
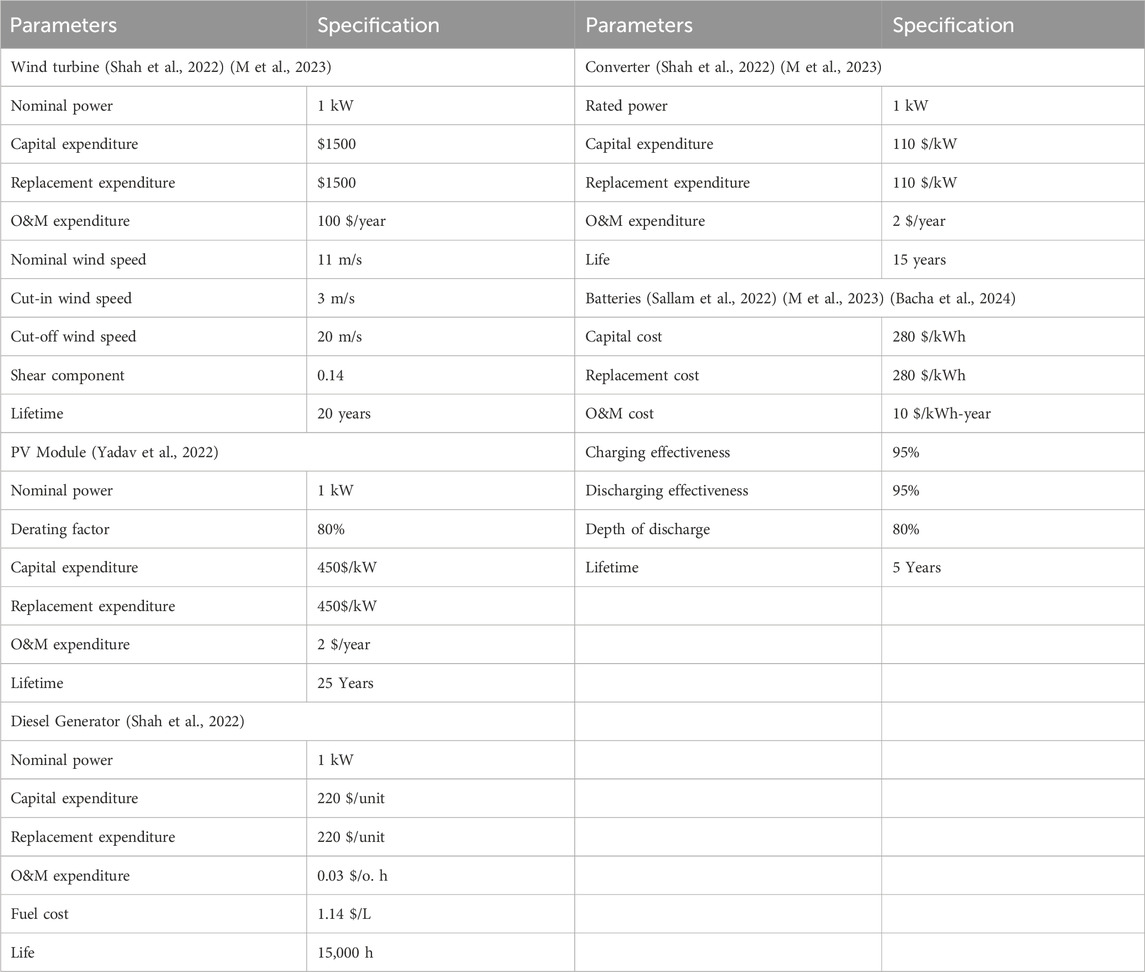
The feasibility of three different configurations of multi-source energy systems, which consist of a diverse fusion of solar PV modules, wind turbine systems, energy storage components, and diesel generators, has been analyzed using MATLAB and HOMER. Figure 3 illustrates the diagrammatic representation of a hybrid energy model with renewable energy sources, an energy storage system, and a diesel generator. Table 2 tabulates the economic and technical parameters of the utilized components.

Figure 3

Figure 3. Diagrammatic representation of hybrid energy model.

Table 2

Table 2. Indicators of technical and economic data.

2.4.1 Modelling of solar PV module

The electrical power generated from the solar PV modules depends on the level of solar irradiation, and the output of the PV modules is uncertain in nature as a result of changes in weather conditions, and the reliability of the solar PV modules to meet the demands is poor. The obtained DC output from the PV module may be computed using the formula that follows Equation 1 (Thirunavukkarasu et al., 2023).

${\mathrm{P}}_{\text{Sol}\_\text{PV}}\left(\mathrm{t}\right)={\mathrm{N}}_{\text{Sol}\_\text{PV}}{\mathrm{f}}_{\text{Sol}\_\text{PV}}{\mathrm{P}}_{{\text{Sol}\_\text{PV}\_\text{Rcap}}^{*}}\left(\frac{\mathrm{G}\left(\mathrm{t}\right)}{{\mathrm{G}}_{\text{Ref}}}\right)(1{+\mathrm{K}}_{\mathrm{t}}\left({\mathrm{T}}_{\text{Amb}}\left(\mathrm{t}\right)+\left({0.0256}^{*}\mathrm{G}\left(\mathrm{t}\right)\right){-\mathrm{T}}_{\text{Ref}}\right)(1)$

Where P_{Sol_PV} (t) denotes PV system generated energy; N_{Sol_PV} represents optimal number of solar PV sizes; f_{Sol_PV} represents % of solar_PV derating factor; P_{Sol_PV_Rcap} stands for the considered rated capacity of PV module; G (t) and G_Ref indicates the hour wise solar radiation (W/m²) and standard solar radiation (W/m²), respectively; K_t, T_Amb (t), and T_Ref stands for temperature coefficient, hour wise ambient temperature, and cell temperature at standard conditions (W/m²), respectively.

2.4.2 Modelling of wind turbine system

The wind speed and duration will have an impact on the electrical output power produced by the wind turbine system. At any desired hub height, the range of wind speed can be determined by exploiting the power law using Equation 2 (Thirunavukkarasu and Sawle, 2021b):

$\frac{{\mathrm{u}}_2}{{\mathrm{u}}_1}={\left(\frac{{\mathrm{z}}_2}{{\mathrm{z}}_1}\right)}^{\alpha }(2)$

Where u₂ signifies wind speed profile at hub height z₂, u₁ signifies wind speed profile at standard height z₁, and ὰ denotes shear coefficient. One may determine the wind turbine’s power output by using Equation 3 (Thirunavukkarasu et al., 2023):

${\mathrm{P}}_{\mathrm{e}\_\text{wt}}=\left\{\begin{array}{l}0\mathrm{f}\mathrm{o}\mathrm{r}{\mathrm{w}}_{\mathrm{s}}\le {\mathrm{v}}_{\text{cut}\_\text{in}}\text{\hspace{0.17em}or\hspace{0.5em}}{\mathrm{w}}_{\mathrm{s}}\ge {\mathrm{v}}_{\text{cut}\_\text{out}}\\ {\mathrm{P}}_{\text{rated}}*\frac{{\mathrm{w}}_{\mathrm{s}}\left(\mathrm{t}\right)-{\mathrm{v}}_{\text{cut}\_\text{in}}}{{\mathrm{v}}_{\text{rated}}-{\mathrm{v}}_{\text{cut}\_\mathrm{o}ut}}\text{\hspace{1em}for }{\mathrm{v}}_{\text{cut}\_\text{in}}\le {\mathrm{w}}_{\mathrm{s}}\le {\mathrm{v}}_{\text{rated}}\\ {\mathrm{p}}_{\text{rated}}\text{\hspace{1em}for }{\mathrm{v}}_{\text{rated}}\le {\mathrm{w}}_{\mathrm{s}}\le {\mathrm{v}}_{\text{cut}\_\text{out}}\end{array}\right\}(3)$

Where P_{e_wt} denotes the electrical output of the wind turbine, P_rated represents the wind turbine rated capacity, v_rated, v_cut-in and v_cut-out represent rated, cut in, and cut out the speed of the wind turbine, respectively.

2.4.3 Modelling of energy storage system

The proposed system energy storage unit is integrated to store the availability of excess electricity from renewable sources. Its charging and discharging rate represented by Equation 4, mainly depends on its storage capacity. Charging mode happens at an instant when the hybrid system’s power output surpasses the amount of energy required for the load (M et al., 2023; Sawle and Gupta, 2015).

${\mathrm{E}}_{\mathrm{s}}\left(\mathrm{t}\right)={\mathrm{E}}_{\mathrm{s}}\left(\mathrm{t}-1\right)+\left[{\mathrm{E}}_{\mathrm{g}}\left(\mathrm{t}\right)-{\mathrm{E}}_{\mathrm{d}}\left(\mathrm{t}\right)/{\mathrm{\eta }}_{\text{inv}}\right]*{\mathrm{S}}_{\mathrm{\eta }}(\mathrm{4a})$

${\mathrm{E}}_{\mathrm{s}}\left(\mathrm{t}\right)={\mathrm{E}}_{\mathrm{s}}\left(\mathrm{t}-1\right)+\left[{\mathrm{E}}_{\mathrm{d}}\left(\mathrm{t}\right)/{\mathrm{\eta }}_{\text{inv}}-{\mathrm{E}}_{\mathrm{g}}\left(\mathrm{t}\right)\right](\mathrm{4b})$

Where E_s (t) and E_s (t-1) denote energy stored at an hour, t and (t-1), respectively; E_g(t) and E_d (t) represent energy generated by renewables, and demand energy, respectively; whereas S_ή and ή_inv represent the efficiency of storage device and inverter, respectively.

2.4.4 Modelling of converter

A bidirectional converter converts power according to the requirements, and its range of selection depends on the peak load and its efficiency. Hence, the size of the converter can be formulated using the following Equation 5 (Singh et al., 2020).

${\mathrm{P}}_{\mathrm{S}}^{\mathrm{c}}=\frac{{\mathrm{P}}_{\text{peak}}^{\text{Demand}}}{{\mathrm{\eta }}_{\text{eff}}}(5)$

2.4.5 Modelling of diesel generator

When there is a lack of energy availability from renewable sources and the battery is not delivering the energy as it should, a diesel generator comes into play to meet load needs. The required amount of fuel can be calculated by using Equation 6. (Mouachi et al., 2020).

$\mathrm{F}\mathrm{u}\mathrm{e}\mathrm{l}\_\mathrm{D}\mathrm{G}={\mathrm{K}}_{\mathrm{a}}*\text{Pdg}+{\mathrm{K}}_{\mathrm{b}}*\text{Rdg}(6)$

Where the term Fuel_DG denotes the total fuel consumed by the generator to meet the load needs, K_a (0.246 L/kWh), P_dg represents the output power of the diesel generator, R_dg represents diesel generator rated power, and K_b (0.08145 L/kWh) are fuel consumption curve coefficients.

The fuel cost for the consumed fuel can be formulated by using Equation 7. (M et al., 2023).

${\mathrm{T}}_{\mathrm{F}\mathrm{P}}={\mathrm{F}}_{\mathrm{p}\mathrm{l}}*{\mathrm{T}}_{\mathrm{F}\mathrm{C}}(7)$

Where T_FP represents the total fuel price, F_pl represents the price of the fuel per liter, T_FC represents the total fuel utilized by the generator.

3 Formulation of objectives

It is essential to choose the intended objective function when executing the optimal scaling of HRES while considering factors such as variables, parameters, and other aspects. This study considers the total annual cost of the system as a criterion function for the designed system since economics is one of the most important factors for optimizing HRES. The total annual cost of the system has been evaluated with the consideration of various costs of the system components, capacity recovery factor, and single payment present worth factor. The system’s total annual cost is calculated by using Equation 8 (M et al., 2023):

$\mathrm{o}{\mathrm{s}}_{\text{Tac}}=\mathrm{o}{\mathrm{s}}_{\mathrm{n}\_\text{comp}}*\left\{\left(\mathrm{s}{\mathrm{c}}_{\text{cap}}+\left(\mathrm{s}{\mathrm{c}}_{\text{rep}}*\text{sppw}\right)\right)*\text{CRF}+\mathrm{s}{\mathrm{c}}_{\mathrm{O}\&\mathrm{M}}\right\}(8)$

Where OS_Tac: Total annual expenditure of the optimal system, os_ncomp is: Optimal size of the system components,

sc_cap: Capital expenditure of the system components, sc_ep: Replacement expenditure of the system components, sc_O&M: Operation and maintenance expenditure of the system components.

The single payment present worth (sppw) were calculated by using Equation 9.

$\mathrm{s}\mathrm{p}\mathrm{p}\mathrm{w}={\displaystyle \sum _{\mathrm{n}=1}^{r_{\text{nt}}}}\frac{1}{{\left(1+{\mathrm{i}}_{\mathrm{r}}\right)}^{{\mathrm{n}*\mathrm{c}}_{\text{ul}\mathrm{t}}}}(9)$

Where i_r: Real interest rate, r_nt: Number of times of replacement of components over the project lifetime, C_ult: useful lifetime.

The term capital recovery factor is used to transform the system’s initial investment expenses into annual capital outlay of the system, and is represented by Equation 10 (Thirunavukkarasu and Sawle, 2022):

$\mathrm{C}\mathrm{R}\mathrm{F}=\frac{{\mathrm{i}}_{\mathrm{r}}*{\left(1+{\mathrm{i}}_{\mathrm{r}}\right)}^{\mathrm{t}}}{{\left(1+{\mathrm{i}}_{\mathrm{r}}\right)}^{\mathrm{t}}-1}(10)$

The cost for the electricity generated in a hybrid system is determined by, as stated in Equation 11 (Sawle and Thirunavukkarasu, 2021).

$\text{LCOE}=\frac{\mathrm{o}{\mathrm{s}}_{\text{tac}}\left(\$/\text{yr}\right)}{\mathrm{e}{\mathrm{e}}_{\text{ts}}\left(\text{kWh}/\text{yr}\right)}(11)$

Where os_tac: Total annual cost of the optimal system, ee_ts: Total electrical energy served.

3.1 Minimization of loss of power supply probability

As the load and availability of renewable sources are dynamic, the reliability of the system is one of the important criteria that need to be considered while designing HRES. If the HRES does not satisfy the load due to the unavailability of renewable sources, sufficient storage requirements, or some other technical issue, a loss of power supply probability will occur. Hence, to maintain system reliability, the reliability constraint LPSP represented by Equation 12 must be at the desired level (M et al., 2023).

$\text{LPSP}=\frac{{\displaystyle \sum }{\mathrm{P}}_{\mathrm{L}}\left(\mathrm{t}\right)-({\mathrm{P}}_{\mathrm{P}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{W}}\left(\mathrm{t}\right)+\left({\mathrm{E}}_{\mathrm{b}}\left(\mathrm{t}-1\right)-{\mathrm{E}}_{\text{bmin}}+{\mathrm{P}}_{\text{diesel}}\right)}{{\displaystyle \sum }{\mathrm{P}}_{\mathrm{L}}\left(\mathrm{t}\right)}(12)$

Where: P_L(t) represents total demand.

P_p(t) represents the total demand satisfied by solar PV.

P_w(t) represents the total demand satisfied by wind turbine.

E_b (t - 1) represents the state of charge of the storage device.

E_bmin indicates the minimum state of the storage device.

P_diesel represents power met by the diesel generator.

3.2 Renewable fraction

The total amount of energy produced by sources of clean energy is expressed as a renewable fraction, and when this term is at its maximum, more energy has been supplied from renewable energy resources. This factor can be calculated from Equation 13 (M et al., 2023; Jain et al., 2022a).

$\text{RF}\left(\%\right)=\left(1-\frac{{\text{Pd}}_{\mathrm{g}}}{{\mathrm{P}}_{\mathrm{L}}}\right)*100(13)$

P_dg represents the amount of energy generated by a diesel generator.

P_L represents the total energy demand.

4 Optimal load following dispatch strategy employed for the operation of energy management

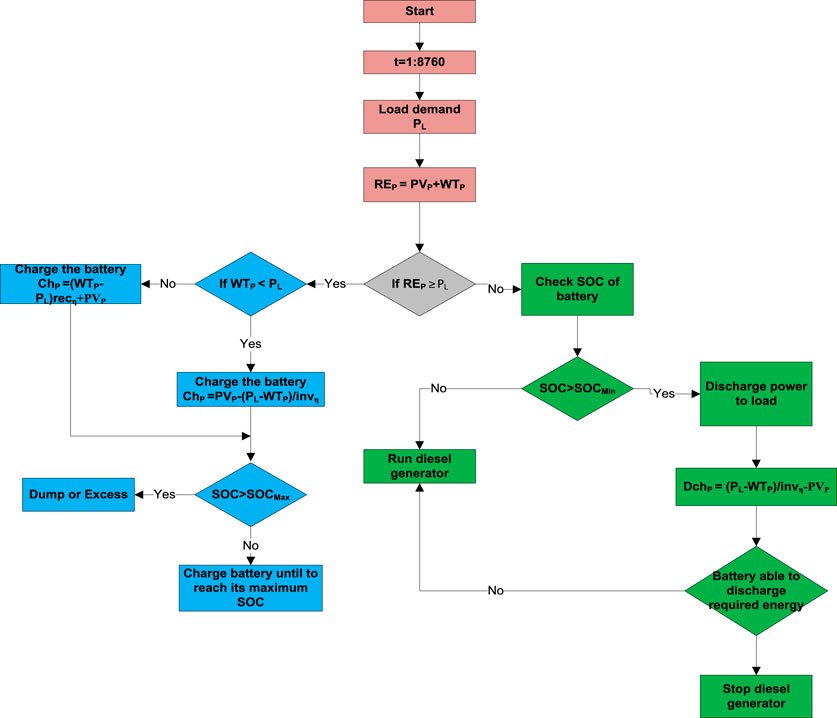
In situations where the load cannot be met by renewable resources, the dispatch strategy uses a set of rules to regulate the operation of the generator and the storage unit. The functioning of the diesel power generators and energy storage components in HRES has been regulated through the use of a dispatch strategy; a series of steps are required. In this study, the load-following dispatch strategy is implemented and assessed. The question of how the battery bank will be energized arises during system operation because the HRES consists of both energy storage and a diesel generator. In this strategy, the diesel generator generates only enough power to meet demand and does not energize the storage system, which means the battery will charge through a renewable energy generator. The operation of the energy management strategy with the load following strategies is rendered in Figure 4 (Thirunavukkarasu et al., 2023). The first stage in adopting a load-following control scheme is calculating hourly demand and renewable energy generation. When the renewable power output for 1 hour exceeds the demand, the battery bank’s state of charge (SOC) is determined. If the SOC falls below the maximum permitted level, the battery is charged. In contrast, if the SOC exceeds the maximum threshold, extra energy is routed to dump loads. In circumstances where renewable energy generation falls short of demand, the battery is discharged to keep the SOC from falling below the minimal value. If the battery charge is inadequate to satisfy demand, the diesel generator is turned on to fulfill the net demand without charging the battery.

Figure 4

Figure 4. Operating modes of the hybrid energy system.

5 Modern optimization algorithm

This section provides a brief outline of the metaheuristic optimization algorithms that have been applied to sizing; these algorithms have not yet been examined for the use of composite renewable energy systems sized optimally.

5.1 Coati optimization algorithm

The coati optimization algorithm is a novel bio-inspired algorithm population-based one, inspired by the two natural behaviors of coati, which are their behavior while hunting and attacking iguanas and their behavior of escaping from predators. Coatis, sometimes referred to as coatimundis, is a member of the Procyonidae family, namely, the Nasua and Nasuella genera. Native to Mexico, some regions in America, and the Southwest of the United States, they are diurnal animals. Figure 5 represents the photograph to visualize the coati omnivores. As omnivores, coatis consume both tiny vertebrates as well as invertebrates’ prey. Coatis hunt in groups because iguanas, which are huge reptiles, are frequently found in trees. While some of them swiftly attack the iguana, others scale trees and frighten it into jumping to the ground. However, coatis are vulnerable to attacks by predators, including maned wolves, anacondas, foxes, boa constrictors, jaguarundis, ocelots, etc. (Dehghani et al., 2023).

Figure 5

Figure 5. Photograph to visualize the coati omnivores.

The mathematical modeling of COA consists of two phases. In the first phase, the population of coati rising from the tree is updated in search space using the following Equation 14 (Dehghani et al., 2023).

${\mathrm{X}}_{\mathrm{p}1}^{\mathrm{i}}:{\mathrm{X}}_{\mathrm{p}1}^{\mathrm{i},\mathrm{j}}={\mathrm{X}}_{\mathrm{i},\mathrm{j}}+\mathrm{r}.\left(\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{a}\mathrm{n}{\mathrm{a}}^{\mathrm{j}}-\mathrm{I}.{\mathrm{X}}^{\mathrm{i},\mathrm{j}}\right)(14)$

For i = [1,2,…., (N/2)] and j = [1,2, … ,m]

Based on the random position of iguana on the ground, the coatis move in search space is updated using the following Equations 15–17 (Dehghani et al., 2023).

$\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{a}\mathrm{n}{\mathrm{a}}_{\mathrm{G}}:\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{a}\mathrm{n}{\mathrm{a}}_{\mathrm{G}}^{\mathrm{j}}=\mathrm{L}{\mathrm{B}}^{\mathrm{j}}+\mathrm{r}.\left(\mathrm{U}{\mathrm{B}}^{\mathrm{j}}-\mathrm{L}{\mathrm{B}}^{\mathrm{j}}\right)(15)$

For j = 1 2 …., m

${\mathrm{X}}_{\mathrm{p}1}^{\mathrm{i}}:{\mathrm{X}}_{\mathrm{p}1}^{\mathrm{i},\mathrm{j}}=\left\{{\mathrm{X}}^{\mathrm{i},\mathrm{j}}+\mathrm{r}.\left(\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{a}\mathrm{n}{\mathrm{a}}_{\mathrm{G}}^{\mathrm{j}}-\mathrm{I}.{\mathrm{X}}^{\mathrm{i},\mathrm{j}}\right)\right\}\text{for}{\mathrm{F}}_{\text{iguana},\mathrm{G}}<{\mathrm{F}}_{\mathrm{i}}(16)$

else

${\mathrm{X}}_{\mathrm{p}1}^{\mathrm{i}}:{\mathrm{X}}_{\mathrm{p}1}^{\mathrm{i},\mathrm{j}}=\left\{{\mathrm{X}}^{\mathrm{i},\mathrm{j}}+\mathrm{r}.\left({\mathrm{X}}^{\mathrm{i},\mathrm{j}}-\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{a}\mathrm{n}{\mathrm{a}}_{\mathrm{G}}^{\mathrm{j}}\right)\right\}(17)$

Coatis’ inherent behavior when interacting with and evading predators is the basis for a mathematical model used in the second segment of the procedure to update the position of coatis in the search space.

In order to replicate this behavior, a random position is created using Equations 18 and 19 (Dehghani et al., 2023). In the vicinity of each coati’s location.

$\mathrm{L}{\mathrm{B}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}^{\mathrm{j}}=\frac{\mathrm{L}{\mathrm{B}}^{\mathrm{j}}}{\mathrm{t}}(18)$

$\mathrm{U}{\mathrm{B}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}^{\mathrm{j}}=\frac{\mathrm{U}{\mathrm{B}}^{\mathrm{j}}}{\mathrm{t}}(19)$

Where t = [1 2 … , T]

${\mathrm{X}}_{\mathrm{p}2}^{\mathrm{i}}:{\mathrm{X}}_{\mathrm{p}2}^{\mathrm{i},\mathrm{j}}=\{{\mathrm{X}}^{\mathrm{i},\mathrm{j}}+(\left.1-2\mathrm{r}).(\mathrm{L}{\mathrm{B}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}^{\mathrm{j}}+\mathrm{r}.\left(\mathrm{U}{\mathrm{B}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}^{\mathrm{j}}-\mathrm{L}{\mathrm{B}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}^{\mathrm{j}}\right)\right\}(20)$

For i = 1,2, … N and j = 1,2 … ,m.

An iteration of a COA ends when every coati’s position in the search space has been updated based on the first and second phases, and until the algorithm reaches its final iteration, the population is updated by using Equation 20 (Dehghani et al., 2023).

5.2 Hippopotamus optimization algorithm

The technique known as “Hippopotamus Optimization” is a new kind of stochastic technique that was inspired by the natural behaviors of hippos as represented by Figure 6. A trinary-phase model that includes their position updating in ponds or rivers, defense mechanisms against predators, and evasion techniques is used to conceptually define this algorithm. A dominant male hippopotamus, numerous adult male hippopotamuses, hippopotamus calves, and several females make up a hippopotamus group. Owing to their natural curiosity, young and calves hippopotamuses frequently show signs of straying from the pack. They could consequently experience isolation and become prey for predators. Hippopotamuses have a defensive secondary behavioral pattern that is set off when they are attacked by predators or when other animals trespass into their domain. The initial position of all the hippopotamuses has been generated, and for this initial position, the objective function is evaluated. Phase I is an exploration phase in which the hippopotamus position in a river or pond is updated. Then the new position of the hippopotamus is determined and updated. In Phase II, the hippopotamus defends against predators, a random position for predators is created, and again, the new position is updated. Phase III is the exploitation phase in which hippopotamuses escape from their predators. In this phase, the new bonds of decision variables are determined, and once again, the new position and its update are formulated (Amiri et al., 2024).

Figure 6

Figure 6. Photograph to visualize the behavior of a hippopotamus.

6 Result and discussion

To alleviate the power crisis in a remote Adivasi village, we designed a standalone hybrid system and optimized its sizing to minimize total annual cost, minimize LPSP, and maximize the renewable fraction. Though the considered system looks simple, its modeling is complex due to the control strategy, energy storage system, managing constraints, selection, and implementation of the optimizing algorithm. Three recently developed optimization algorithms (COA, HOA, and HBO) have been utilized to optimize the desired objectives at the best rank. The effectiveness of these algorithms is compared to certain standard approaches from earlier research.

6.1 Scenario 1: solar PV/wind/battery/diesel generator

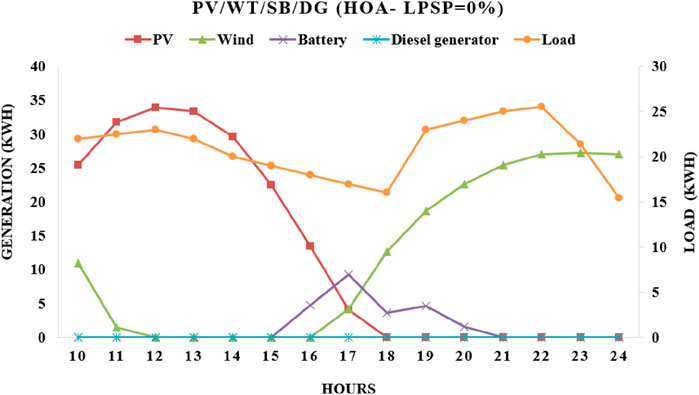
In this scenario, the required energy of the users has been obtained through the PV electric modules, wind turbine, battery bank, and diesel genset for 25 years. Table 3 tabulated the obtained optimal values using optimization algorithms with the consideration of different reliability indexes. For this, the optimal number of PV electric modules, wind turbines, storage batteries, and diesel gensets obtained by using HOA optimization techniques was 69 kW, 50 kW, 40 nos, and 26.8 kW, respectively. Hence, for this scenario, the total annual cost and electricity costs were $24473 and 0.1473 $/kWh, respectively. The behavior of each component of this scenario over a predetermined number of hours every year. The range of energy that each component shares for a specified number of hours is visualized in Figure 7. During hours 10 to 18, the required energy has been met by the solar PV system, while the generation from the wind turbine has increased from 16 to 24 h. The aggregate kWh of energy generated from the wind turbine, solar PV, and diesel generator is 120470, 119760, and 26100, respectively. As the total amount of energy discharged from the battery per year is 15468 kWh, which means most of the required energy has been met by renewables, Observations have shown that the diesel generator produces quite a bit of energy.

Table 3

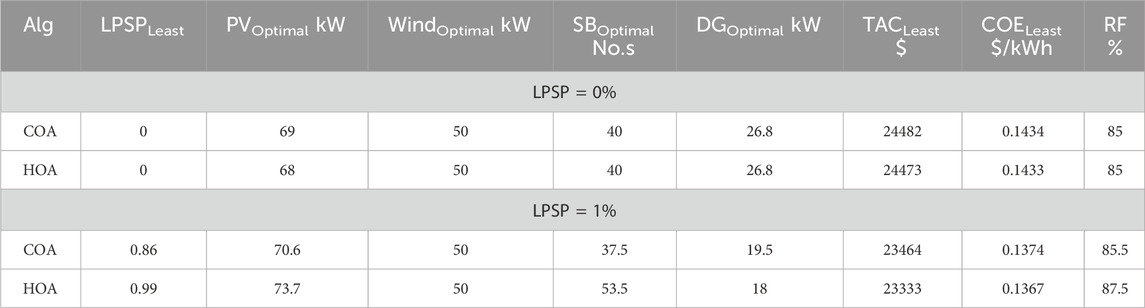
Table 3. Summary of the optimal values for the hybrid system (PV/Wind/Battery/DG) obtained from various optimization techniques.

Figure 7

Figure 7. Range of energy that each component shares for a specified number of hours.

6.2 Scenario II: PV/battery/diesel generator

The PV module, battery, and diesel generator generated the energy required for the users, and the components of this scenario obtained by using optimization techniques are illustrated in Table 4. The optimal sizing of the components obtained from both technologies is quite similar, ensuring a zero loss of power supply probability. But to ensure the loss of power supply of probability as one, the optimal sizing of the components obtained by using the HOA algorithm is less while compared to COA. Hence, the total annual loss obtained from the HOA is $34650, whereas the COA is $34714. It has been observed that the required number of system components is decreasing while increasing the level of loss of power supply probability. When compared with scenario I, the total annual cost of the system has increased by 48% (HBO-LPSP = 1%). The behavior of each component of this scenario obtained by using the HOA algorithm for a specific number of hours annually is shown in the figure for the constraint as LPSP = 1%. The amount of energy generated from the solar PV system is increased compared with scenario I owing to the void of a wind turbine system. To compensate for the fluctuation of energy from the solar PV system, the response from the battery and diesel generator is increased. The range of energy that each component shares for a specified number of hours is visualized in Figure 8.

Table 4

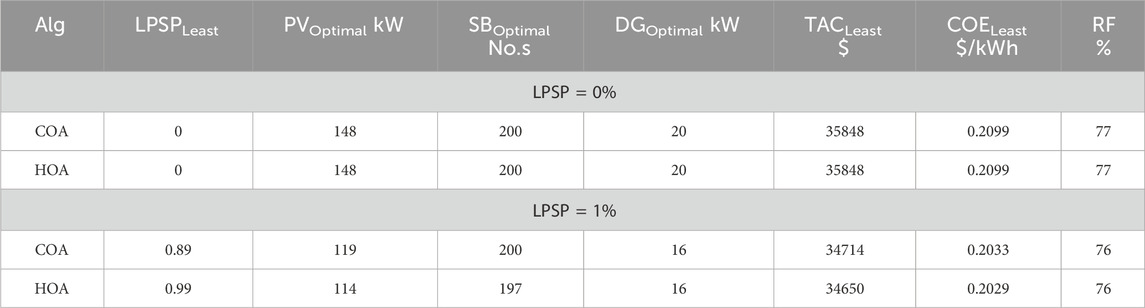
Table 4. Summary of the optimal values for the hybrid system (PV/Battery/DG) obtained from various optimization techniques.

Figure 8

Figure 8. Range of energy that each component shares for a specified number of hours.

6.3 Scenario III: PV/WT/DG

In this scenario, the sources of power supply are a solar PV electric module, a wind turbine, and a diesel genset. This has the disadvantage of the absence of energy storage units, which means there is no possibility to store surplus energy generated from renewables. Due to the non-consideration of battery storage, the question of agreement on energy sharing among the generation systems and energy pricing, including the total annual cost of the system, has to be discussed. A summary of the optimal values for the hybrid system (PV/Wind/DG) obtained from various optimization techniques is illustrated in Table 5. In this regard, the HOA algorithm has the advantage of meeting the required energy with the least annual cost for both values of reliability constraints. A higher total annual cost is reported in case II, whereas the obtained annual cost for this scenario is lower than scenario II. The behavior of each component of this scenario obtained by using the HOA algorithm for a set number of hours each year is shown in the figure for the constraint as LPSP = 1%. The total amount of kWh of energy generated from solar electric PV, wind turbines, and diesel genset is 131800, 120472, and 33000, respectively. The range of energy that each component shares for a specified number of hours is visualized in Figure 9.

Table 5

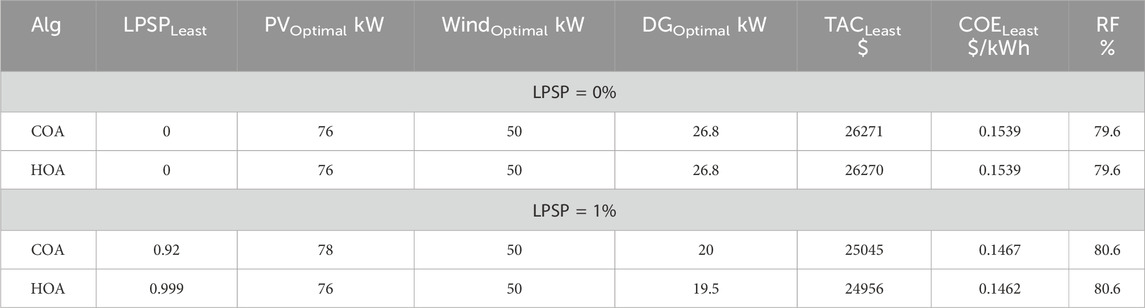
Table 5. Summary of the optimal values for the hybrid system (PV/Wind/DG) obtained from various optimization techniques.

Figure 9

Figure 9. Range of energy that each component shares for a specified number of hours.

6.4 Performance analysis for various scenarios

Based on the comparison of optimum values of the total annual cost of the system, it is concluded that the hybrid system involving a PV electric module, wind turbine, a storage battery, and a diesel genset is suitable for the selected location to serve the users. The simulation results indicated that the system consisting of solar PV electric, batteries, and a diesel genset shows a high increase in the total annual cost of the system. In light of the loss of power supply probability as a reliability constraint, the reliability of the system decreases while increasing the reliability constraint. By comparison, the combination of solar PV electric modules and wind turbine energy systems holds better future potential for the selected region, which leads to renewables as a promising alternative to fossil fuel-based power systems.

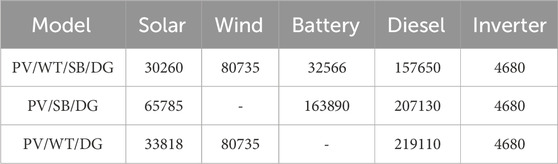
To analyze the difference that exists among the component costs, the cost distribution of various scenarios has been demonstrated in Table 6. It can be observed that while comparing the PV/WT/SB/DG scenarios, the solar PV cost increased by 4% and 10% for the scenarios PV/WT/DG and PV/SB/DG, respectively. Concerning PV/WT/SB/DG, the battery and diesel generator costs have increased by 403% and 31%, respectively. It happens that solar renewable energy is not adequate to satisfy the required load demand. Further, while comparing the PV/WT/SB/DG scenarios, the cost incurred by a diesel generator is very high due to the absence of a storage battery.

Table 6

Table 6. Annualized total cost of the system ($) obtained by using HOA for dissimilar scenarios.

6.5 Performance evaluation of optimization algorithms

Two different sizing methods such as COA and HOA have been implemented to determine the optimal system using the MATLAB environment. For each algorithm, the maximum number of iterations is set to 50, while the number of runs is set to 25. The performance of the optimization algorithm has been analyzed based on the minimal and maximum values of the system’s total annual cost, mean, and standard deviation of the obtained values. Both algorithms have obtained the optimal values, but HOA outperforms COA due to its minimum and maximum TNPC and low standard deviation. Figures 10A–C represents the analysis of the relationship between total annual cost and runs for the hybrid energy model. Most investigation focuses on the convergence capabilities of the sizing algorithm for the best-executed run, which may not provide a thorough examination of the algorithm’s convergence process as it can vary between runs.

Figure 10

Figure 10. Analysis of the relationship between total annual cost and runs for the hybrid energy model (A) PV/WT/SB/DG. (B) PV/SB/DG. (C) PV/WT/DG. Analysis of the relationship between total annual cost and iterations for the hybrid energy model. (D) PV/WT/SB/DG. (E) PV/SB/DG. (F) PV/WT/DG.

In this work, we recorded the convergence iterations for each algorithm throughout 25 runs. Regarding the convergence process, HOA outperforms COA, which achieves optimal solutions in early iterations. It is noticed that due to the mechanism and complication level of the optimization algorithm, there is a significant difference in accuracy and robustness. Figures 10D–F illustrates the convergence curve for 50 iterations with the proposed two algorithms (COA and HOA). Also, the statistical performance of the proposed algorithm is summarized in Table 7. The stability of the HOA is acceptable and comparable to that of the COA, which suggests the HOA provides a better optimal solution with fewer deviations and a superiority in solving optimization problems.

Table 7

Table 7. Summary of the statistical characteristics of the algorithms through the 25 runs.

Both the hippopotamus and coati optimization algorithms provide excellent ways to hybrid renewable energy system sizing. Their global search capability, adaptability, and robustness make them ideal for dealing with the inherent complexity, multimodality, and dynamism of HRES optimization issues. The HOA outperforms the COA in circumstances that require investigation and flexibility to changing conditions. HOA has more consistent convergence, whereas COA tends to converge to optimal solutions in the early iterations. The statistical examination of the optimization results shows that HOA has the lowest standard deviation, implying fewer solution volatility and a higher convergence rate than COA.

7 Prediction of renewable energy components cost

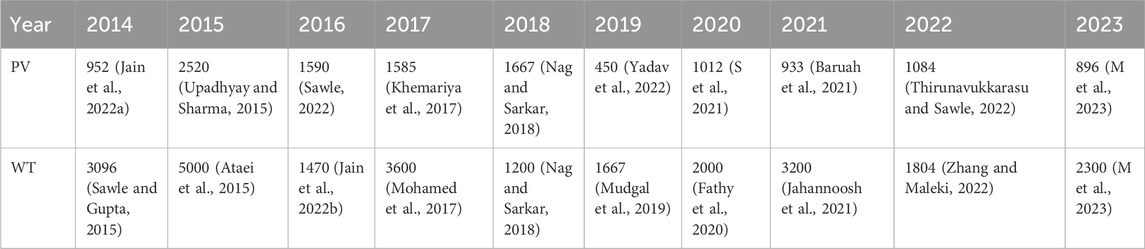
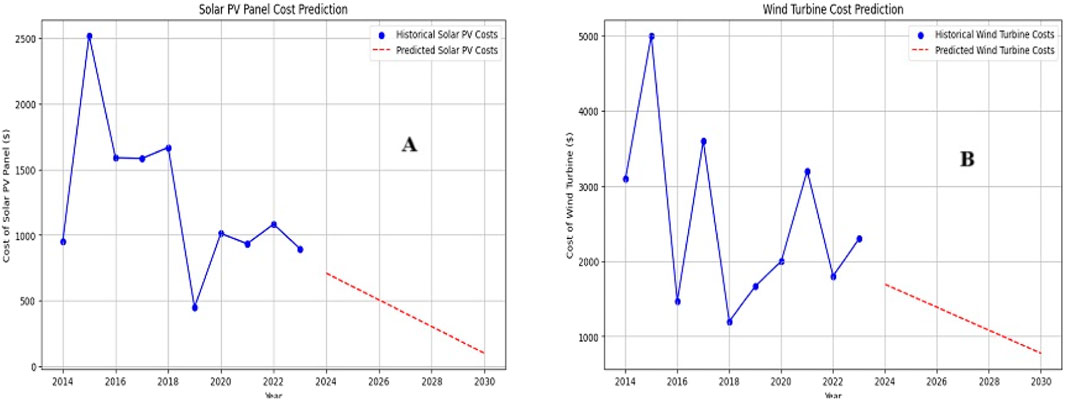
Over the past years of research handled by several researchers, we have noticed the initial capital cost considered for the renewable components has significantly varied. Hence, an accurate prediction of the cost of the cost of renewable components for future designs of hybrid renewable energy models would be a significant improvement. For this, a statistical linear regression method is used to estimate the cost of renewable components with consideration of the cost dataset for the last 10 years. The datasets considered for solar PV and wind turbine capital costs are listed in Tables 8, 9, respectively. The lower predicted initial cost will provide an effective decision for the implementation of an extensive hybrid renewable energy system framework. The predicted outcomes indicate much-inclined variation in the range of costs over the next few years, and the plotted graph summarizes the visually supported evidence of how well the predicted values decrease over the next 10 years. The predicted outcomes indicate much-inclined variation in the range of costs over the next few years, and the plotted graph in Figure 11 summarizes the visually supported evidence of how well the predicted values decrease over the next 10 years. Table 8 illustrates the divergence of capital costs among several researchers, whereas Table 9 represents the predicted cost for solar PV panels and wind turbines over the next 10 years.

Table 8

Table 8. Divergence of capital costs among several researchers.

Table 9

Table 9. Predicted cost over the next 10 years.

Figure 11

Figure 11. Prediction of cost. (A) PV panel. (B) Wind turbine.

8 Sensitivity analysis for the predicted cost of renewable components

Table 10 reveals that for the prediction of renewable energy components, the optimal results of COE decrease due to the reduction of energy components in the upcoming years. Figure 12 demonstrates the impact of the predicted cost of system components on the PV/WT/SB/DG hybrid systems NPC and TAC. This investigation demonstrates that the economic value of the system decreases due to the drop in the predicted cover over the next few years.

Table 10

Table 10. Cost of electricity obtained for the predicted value of renewable components.

Figure 12

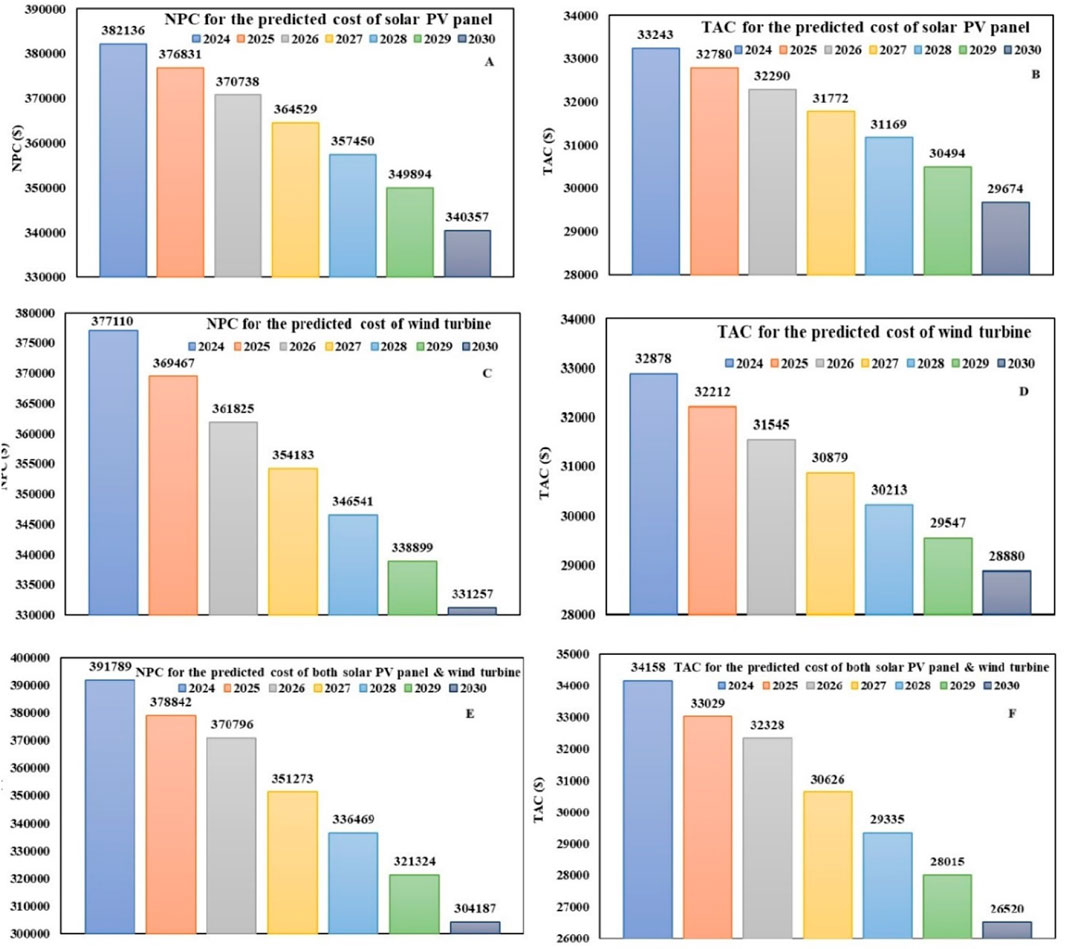
Figure 12. Impact of the predicted cost of system components on the PV/WT/SB/DG hybrid systems. (A) Comparison of system NPC for the predicted cost of solar PV panel. (B) Comparison of system TAC for the predicted cost of solar PV panel. (C) Comparison of system NPC for the predicted cost of wind turbine. (D) Comparison of system TAC for the predicted cost of wind turbine. (E) Comparison of system NPC for the predicted cost of both solar PV panel and wind turbine. (F) Comparison of system TAC for the predicted cost of both solar PV panel and wind turbine.

9 Comparative analysis with HOMER software and existing research

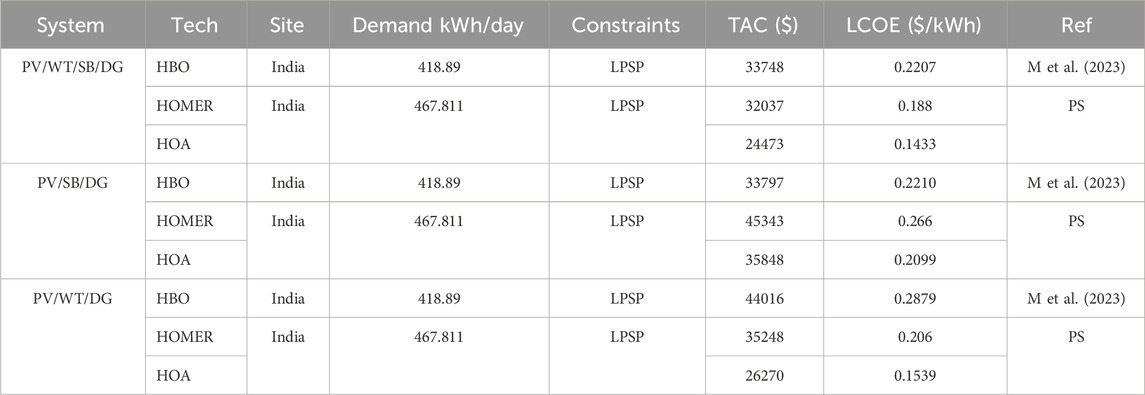
Different approaches were used in the reference to develop various scenarios and achieve the best possible outcomes. The authors have compared the performance analysis of some recently developed optimization approaches with a few traditional algorithms to achieve better and more promising outcomes. Ultimately, the authors concluded that the outcomes of the HBO algorithm represented a feasible and successful approach. Therefore, the proposed algorithm’s superiority was examined by comparing the acquired results with HBO. The comparison between the HBO findings and the HOA result, which the authors have utilized in the literature, is shown in Table 11. Additionally, HOMER software was used to compare the outcomes obtained using the proposed approach to validate the findings.

Table 11

Table 11. Comparison of the economic values with HOMER software and existing research.

10 Conclusion

This study investigates the feasibility of a hybrid system in light of two different clean renewable resources, solar and wind, to alleviate the power crisis in a rural area of northern Madhya Pradesh, India. We have performed the optimal sizing of three different scenarios using a recently developed metaheuristics optimization algorithm. To analyze the reliability of the hybrid system, the parameter loss of power supply probability has been regarded as a constraint. Using COA, HOA, and HOMER Pro software, three different scenarios, which include PV/WT/SB/DG, PV/DG/SB, and PC/WT/SB, have been assessed. The combination of PV/WT/SB/DG yields the lowest total annual cost and minimum cost of electricity of $24473 and $0.1433/kWh, respectively, by using the HOA optimization algorithm. By increasing the reliability constraint of LPSP from 0% to 1%, there is a decline in the size of the components, which in turn increases the system’s annual cost. While evaluating the performance of optimization methods, optimum results show that HOA-based optimization is more economical than COA, followed by HOMER Pro software. Also, the statistical analysis of the optimization algorithm reveals that HOA attains the least standard deviation, which implies less oscillation and a better convergence rate than the COA optimization technique. In conclusion, both algorithms can be effective tools for HRES size, but in order to overcome their drawbacks and improve performance in real-world applications, they might need to be fine tuning or hybridization with other optimization strategies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SG: Writing–original draft, Writing–review and editing. YS: Investigation, Supervision, Writing–review and editing. KT: Methodology, Writing–review and editing. MT: Visualization, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors extend their appreciation to the M.P. Council of Science & Technology R&D Project, Bhopal, India entitled “Renewable Energy Empowerment for Rural Sustainable Development using Advanced Techniques” (Sanction Order 14446/CST/R&DIPhy. and Engg. and Pharmacy/2023-24 Ref: File No_ AIRLYR. P-2/370 dated 05.10.2023) for providing support for carrying out this research work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

BM, Biomass; CR, Convergence rate; COA, Coati optimization algorithm; CRF, Capacity recovery factor; DG, Diesel Generator; DOD, Depth of discharge; FC, Fuel cell; GWO, Gray wolf algorithm; HBO, Honey badger optimizer; HOA, Horizontal axis continuous adjustment; HOMER, Hybrid Optimization of Multiple Energy Resources software; HRES, Hybrid renewable energy system; LCOE, Levelized cost of electricity; LPSP, Loss of power supply probability; PSO, Particle swarm optimization; PV, Photovoltaic; RF, Renewable fraction; SB, Storage battery; SD, Standard deviation; SPPW, Single payment present worth; TAC, Total annual cost; TNPC, Total net present cost; WT, Wind turbine.

References

Ali, F., Ahmar, M., Jiang, Y., and AlAhmad, M. (2021). A techno-economic assessment of hybrid energy systems in rural Pakistan. Energy 215, 119103. doi:10.1016/j.energy.2020.119103

CrossRef Full Text | Google Scholar

Amiri, M., Mehrabi Hashjin, N., Montazeri, M., Mirjalili, S., and Khodadadi, N. (2024). Hippopotamus optimization algorithm: a novel nature-inspired optimization algorithm. Sci. Rep. 14, 5032. doi:10.1038/s41598-024-54910-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Anastasopoulou, A., Butala, S., Patil, B., Suberu, J., Fregene, M., and Lang, J. (2016). Techno-economic feasibility study of renewable power systems for a small-scale plasma-assisted nitric Acid plant in Africa. Processes 4 (4), 54. doi:10.3390/pr4040054

CrossRef Full Text | Google Scholar

Ataei, A., Rashidi, R., Nedaei, M., and Kurdestani, E. (2015). Techno-economic viability of a hybrid wind and solar power system for electrification of a commercial building in Shiraz. Iran 3, 251–263. doi:10.12989/eri.2015.3.4.251

CrossRef Full Text | Google Scholar

Bacha, B., Ghodbane, H., Dahmani, H., Betka, A., Toumi, A., and Chouder, A. (2024). Optimal sizing of a hybrid microgrid system using solar, wind, diesel, and battery energy storage to alleviate energy poverty in a rural area of Biskra, Algeria. J. Energy Storage 84, 110651. doi:10.1016/j.est.2024.110651

CrossRef Full Text | Google Scholar

Baruah, A., Basu, M., and Amuley, D. (2021). Modeling of an autonomous hybrid renewable energy system for electrification of a township: a case study for Sikkim, India. Renew. Sustain. Energy Rev. 135, 110158. doi:10.1016/j.rser.2020.110158

CrossRef Full Text | Google Scholar

Dehghani, M., Montazeri, Z., Trojovska, E., and Trojovsky, P. (2023). Coati Optimization Algorithm: a new bio-inspired metaheuristic algorithm for solving optimization problems. Knowledge-Based Syst. 259, 110011. doi:10.1016/j.knosys.2022.110011

CrossRef Full Text | Google Scholar

Fathy, A., Kaaniche, K., and Alanazi, T. M. (2020). Recent approach based social spider optimizer for optimal sizing of hybrid PV/Wind/Battery/Diesel integrated microgrid in aljouf region. IEEE Access 8, 57630–57645. doi:10.1109/ACCESS.2020.2982805

CrossRef Full Text | Google Scholar

Heydari, A., and Askarzadeh, A. (2016). Techno-economic analysis of a PV/biomass/fuel cell energy system considering different fuel cell system initial capital costs. Sol. Energy 133, 409–420. doi:10.1016/j.solener.2016.04.018

CrossRef Full Text | Google Scholar

Jahannoosh, M., Nowdeh, S. A., Naderipour, A., Kamyab, H., Davoudkhani, I. F., and Klemeš, J. J. (2021). New hybrid meta-heuristic algorithm for reliable and cost-effective designing of photovoltaic/wind/fuel cell energy system considering load interruption probability. J. Clean. Prod. 278, 123406. doi:10.1016/j.jclepro.2020.123406

CrossRef Full Text | Google Scholar

Jain, S., Babu, S., and Sawle, Y. (2022a). “Prefeasibility economic scrutiny of the off-grid hybrid renewable system for remote area electrification,” in Proceedings of the international conference on paradigms of communication, computing and data sciences: pccds 2021. Singapore: Springer. doi:10.1007/978-981-16-5747-4_7

CrossRef Full Text | Google Scholar

Jain, S., Kulkarni, A., and Sawle, Y. (2022b). “Overview of energy management systems for microgrids and smart grid,” in Planning of hybrid renewable energy systems, electric vehicles and microgrid: modeling, control and optimization. Singapore: Springer Nature Singapore, 61–88.

CrossRef Full Text | Google Scholar

Kharrich, M., Hassan, M. H., Kamel, S., and Kim, J. (2024). Designing an optimal hybrid microgrid system using a leader artificial rabbits optimization algorithm for domestic load in Guelmim city, Morocco. Renew. Energy 223, 120011. doi:10.1016/j.renene.2024.120011

CrossRef Full Text | Google Scholar

Kharrich, M., Selim, A., Kamel, S., and Kim, J. (2023). An effective design of hybrid renewable energy system using an improved Archimedes Optimization Algorithm: a case study of Farafra, Egypt. Energy Convers. Manag. 283, 116907. doi:10.1016/j.enconman.2023.116907

CrossRef Full Text | Google Scholar

Khemariya, M., Mittal, A., Baredar, P., and Singh, A. (2017). Cost and size optimization of solar photovoltaic and fuel cell based integrated energy system for un-electrified village. J. Energy Storage 14, 62–70. doi:10.1016/j.est.2017.09.011

CrossRef Full Text | Google Scholar

Koholé, Y. W., Fohagui, F. C. V., Wankouo Ngouleu, C. A., and Tchuen, G. (2024). An effective sizing and sensitivity analysis of a hybrid renewable energy system for household, multi-media and rural healthcare centres power supply: a case study of Kaele, Cameroon. Int. J. Hydrogen Energy 49, 1321–1359. doi:10.1016/j.ijhydene.2023.09.093

CrossRef Full Text | Google Scholar

Kumar, J., V Suryakiran, B., Verma, A., and Bhatti, T. S. (2019). Analysis of techno-economic viability with demand response strategy of a grid-connected microgrid model for enhanced rural electrification in Uttar Pradesh state, India. Energy 178, 176–185. doi:10.1016/j.energy.2019.04.105

CrossRef Full Text | Google Scholar

Mahmoudi, S. M., Maleki, A., and Rezaei ochbelagh, D. (2022). A novel method based on fuzzy logic to evaluate the storage and backup systems in determining the optimal size of a hybrid renewable energy system. J. Energy Storage 49, 104015. doi:10.1016/j.est.2022.104015

CrossRef Full Text | Google Scholar

Miao, C., Teng, K., Wang, Y., and Jiang, L. (2020). Technoeconomic analysis on a hybrid power system for the UK household using renewable energy: a case study. A Case Study 13, 3231. doi:10.3390/en13123231

CrossRef Full Text | Google Scholar

Mohamed, M. A., Eltamaly, A. M., and Alolah, A. I. (2017). Swarm intelligence-based optimization of grid-dependent hybrid renewable energy systems. Renew. Sustain. Energy Rev. 77, 515–524. doi:10.1016/j.rser.2017.04.048

CrossRef Full Text | Google Scholar

Mouachi, R., Jallal, M. A., Gharnati, F., and Mustapha, R. (2020). Multiobjective sizing of an autonomous hybrid microgrid using a multimodal delayed PSO algorithm: a case study of a fishing village. Comput. Intell. Neurosci. 2020, 1–18. doi:10.1155/2020/8894094

PubMed Abstract | CrossRef Full Text | Google Scholar

M, T., Lala, H., and Sawle, Y. (2023). Techno-economic-environmental analysis of off-grid hybrid energy systems using honey badger optimizer. Renew. Energy 218, 119247. doi:10.1016/j.renene.2023.119247

CrossRef Full Text | Google Scholar

Mudgal, V., Reddy, S., and Mallick, T. (2019). Techno-economic analysis of standalone solar photovoltaic-wind-biogas hybrid renewable energy system for community energy requirement. Futur. Cities Environ. 5. doi:10.5334/fce.72

CrossRef Full Text | Google Scholar

Nag, A. K., and Sarkar, S. (2018). Modeling of hybrid energy system for futuristic energy demand of an Indian rural area and their optimal and sensitivity analysis. Renew. Energy 118, 477–488. doi:10.1016/j.renene.2017.11.047

CrossRef Full Text | Google Scholar

Nigussie, T., Bogale, W., Bekele, F., and Dribssa, E. (2017). Feasibility study for power generation using off-grid energy system from micro hydro-PV-diesel generator-battery for rural area of Ethiopia: the case of Melkey Hera village, Western Ethiopia. AIMS Energy 5, 667–690. doi:10.3934/energy.2017.4.667

CrossRef Full Text | Google Scholar

PMAGY (2024). Report: pradhan Mantri Adarsh gram ministry of social justice and empowerment government of India. Gov.in my village has never seen light: Madhya Pradesh’s adivasis wait for electricity.

Google Scholar

Riayatsyah, T. M. I., Geumpana, T. A., Fattah, I. M. R., Rizal, S., and Mahlia, T. M. I. (2022). Techno-economic analysis and optimisation of campus grid-connected hybrid renewable energy system using HOMER grid. Sustainability 14 (13), 7735. doi:10.3390/su14137735

CrossRef Full Text | Google Scholar

Rinaldi, F., Moghaddampoor, F., Najafi, B., and Marchesi, R. (2021). Economic feasibility analysis and optimization of hybrid renewable energy systems for rural electrification in Peru. Clean. Technol. Environ. Policy 23, 731–748. doi:10.1007/s10098-020-01906-y

CrossRef Full Text | Google Scholar

Sallam, M. E., Attia, M. A., Abdelaziz, A. Y., Sameh, M. A., and Yakout, A. H. (2022). Optimal sizing of different energy sources in an isolated hybrid microgrid using turbulent flow water-based optimization algorithm. IEEE Access 10, 61922–61936. doi:10.1109/ACCESS.2022.3182032

CrossRef Full Text | Google Scholar

Saraswat, S., and Rao, K. (2018). Optimization of 10 kW solar photovoltaic – diesel generator hybrid energy system for different load factors at Jaisalmer location of Rajasthan, India. IOP Conf. Ser. Mater. Sci. Eng. 330, 012099. doi:10.1088/1757-899X/330/1/012099

CrossRef Full Text | Google Scholar

Sawle, Y. (2022). “Scrutiny of PV biomass stand-alone hybrid system for rice mill electrification,” in Deregulated electricity market. Apple Academic Press, 135–152.

CrossRef Full Text | Google Scholar

Sawle, Y., and Gupta, S. C. (2015). A novel system optimization of a grid independent hybrid renewable energy system for telecom base station. Int. J. Soft Comput. Math. Control 4 (2), 49–57. doi:10.14810/ijscmc.2015.4204

CrossRef Full Text | Google Scholar

Sawle, Y., and Thirunavukkarasu, M. (2021). Techno-economic comparative assessment of an off-grid hybrid renewable energy system for electrification of remote area. Des. Analysis, Appl. Renew. Energy Syst., 199–247. doi:10.1016/B978-0-12-824555-2.00027-7

CrossRef Full Text | Google Scholar

Shah, S., Mahajan, D., Varun, R., and Jain, V. (2022). “Optimal planning and design of an off-grid solar, wind, biomass, fuel cell hybrid energy system using HOMER Pro,” in Recent advances in power systems: select proceedings of EPREC-2021. Singapore: Springer Nature Singapore, 255–275. doi:10.1007/978-981-16-6970-5_20

CrossRef Full Text | Google Scholar

Singh, S., Chauhan, P., and Singh, N. (2020). Capacity optimization of grid connected solar/fuel cell energy system using hybrid ABC-PSO algorithm. Int. J. Hydrogen Energy 45 (16), 10070–10088. doi:10.1016/j.ijhydene.2020.02.018

CrossRef Full Text | Google Scholar

S, J., Krishnamoorthy, M., Saisandeep, M., Balasubramanian, K., Srinivasan, S., and Thaniaknti, S. B. (2021). Techno economic performance analysis of hybrid renewable electrification system for remote villages of India. Int. Trans. Electr. Energy Syst. 31 (10), e12515. doi:10.1002/2050-7038.12515

CrossRef Full Text | Google Scholar

Sun, H., Ebadi, A., Toughani, M., Nowdeh, S., Naderipour, A., and Abdullah, A. (2022). Designing framework of hybrid photovoltaic-biowaste energy system with hydrogen storage considering economic and technical indices using whale optimization algorithm. Energy 238, 121555. doi:10.1016/j.energy.2021.121555

CrossRef Full Text | Google Scholar

Sun, X., He, H., and Ma, L. (2024). Harmony search meta-heuristic algorithm based on the optimal sizing of wind-battery hybrid micro-grid power system with different battery technologies. J. Energy Storage 75, 109582. doi:10.1016/j.est.2023.109582

CrossRef Full Text | Google Scholar

Thirunavukkarasu, M., Lala, H., and Sawle, Y. (2023). Reliability index based optimal sizing and statistical performance analysis of stand-alone hybrid renewable energy system using metaheuristic algorithms. Alex. Eng. J. 74, 387–413. doi:10.1016/j.aej.2023.04.070

CrossRef Full Text | Google Scholar

Thirunavukkarasu, M., and Sawle, Y. (2021a). “Smart microgrid integration and optimization,” in Active electrical distribution network (John Wiley and Sons, Ltd), 201–235. doi:10.1002/9781119599593.ch11

CrossRef Full Text | Google Scholar

Thirunavukkarasu, M., and Sawle, Y. (2021b). A comparative study of the optimal sizing and management of off-grid solar/wind/diesel and battery energy systems for remote areas. Front. Energy Res. 9. doi:10.3389/fenrg.2021.752043

CrossRef Full Text | Google Scholar

Thirunavukkarasu, M., and Sawle, Y. (2022). An examination of the techno-economic viability of hybrid grid-integrated and stand-alone generation systems for an Indian tea plant. Front. Energy Res. 10. doi:10.3389/fenrg.2022.806870

CrossRef Full Text | Google Scholar

Thirunavukkarasu, M., and Sawle, Y. (2020). Design, analysis and optimal sizing of standalone PV/diesel/battery hybrid energy system using HOMER. IOP Conf. Ser. Mater. Sci. Eng. 937 (1), 012034. doi:10.1088/1757-899X/937/1/012034

CrossRef Full Text | Google Scholar

Upadhyay, S., and Sharma, M. P. (2015). Development of hybrid energy system with cycle charging strategy using particle swarm optimization for a remote area in India. Renew. Energy 77, 586–598. doi:10.1016/j.renene.2014.12.051

CrossRef Full Text | Google Scholar

Wong, S. Y., and Li, C. (2023). Techno-economic analysis of optimal hybrid renewable energy systems – a case study for a campus microgrid. Energy Rep. 9, 134–138. doi:10.1016/j.egyr.2023.09.153

CrossRef Full Text | Google Scholar

Yadav, N., Sawle, Y., Khan, B., and Miro, Y. (2022). Evaluating the technical and economic feasibility of a hybrid renewable energy system for off-grid. J. Aut. Intell. 5 (2), 13. doi:10.32629/jai.v5i2.540

CrossRef Full Text | Google Scholar

Zhang, W., and Maleki, A. (2022). Modeling and optimization of a stand-alone desalination plant powered by solar/wind energies based on back-up systems using a hybrid algorithm. Energy 254, 124341. doi:10.1016/j.energy.2022.124341

CrossRef Full Text | Google Scholar