The phenomenon and suppression strategy of overvoltage caused by PV power reverse flow

In the current distribution network’s energy structure, photovoltaic (PV) occupies a high proportion. However, the access of a high proportion of PV will lead to the phenomenon of reverse power flow in the distribution network, and then the problem of line overvoltage. When the reverse power flow increases, the problem of line overvoltage also worsens, which endangers the normal operation of power system. To solve this problem, this paper starts with the voltage rise theory of distribution network lines. Firstly, through strict mathematical derivation, it compares the influence of main network line parameters and distribution network line parameters on the voltage rise, and summarizes a simple calculation equation for the voltage rise of the distribution network with high proportion PV. Then, according to the mechanism of voltage rise and the principle of inverter control, considering the economy and practicability of the overvoltage suppression strategy, a reverse power flow overvoltage suppression strategy of a system with high proportion PV is proposed. Finally, a PV system model simulating a small village is used to verify the effectiveness of the proposed overvoltage suppression strategy.

1 Introduction

The most widely used energy in the power system is fossil energy, but fossil energy has caused serious environmental pollution and energy loss. Under the pressure of the energy crisis and environmental degradation, most countries have increased their efforts to develop renewable energy. India has set a target of increasing the share of renewable energy in total power generation to 40% by 2030 (Elavarasan et al., 2020). Europe has enacted legislation to reduce EU (European Union)’s emissions by at least 55% by 2030 (Heubl, 2021). Among various renewable energies, photovoltaic (PV), which can be divided into centralized PV and distributed PV according to the installation method, is relatively mature. Distributed PV is favored because of its easy installation and small footprint. However, compared with the traditional power grid, there are many new problems in the distribution network with a high proportion of PV access. For example, after distributed PV access to the distribution network, it will lead to power factor reduction, grid-connected voltage increase, three-phase voltage imbalance increase, line loss changing, and other problems. Some papers have studied these problems (Fan et al., 2023; You et al., 2018; Tan et al., 2018; You et al., 2017; Quintero et al., 2014; Yan and Saha, 2012; Hung et al., 2014; Shah et al., 2015; Ding et al., 2016; Xie et al., 2024a; Xie et al., 2024b).

A large number of papers have studied the problem of voltage fluctuation in power systems with high PV permeability (Hernández et al., 2007; Le Dinh and Hayashi, 2013; Alam et al., 2012; Aramizu and Vieira, 2013). analyzed the problems of voltage rise, voltage imbalance, reverse power flow through simulation, and found that the voltage stability of the system became weaker and weaker with the increasing proportion of PV (Thomson and Infifield, 2007; Demirok et al., 2009). studied the effects of PV connection location, intermittency of solar radiation, and increased PV permeability on the reverse flow voltage. The results show that the high light-voltage permeability significantly changes the voltage distribution and increases the grid-connected voltage (Kawabe and Tanaka, 2015; Tamimi et al., 2013). suggest that the limited reactive power regulation capacity of photovoltaics is an important factor in causing voltage problems. Considering that PV would affect the power loss and voltage fluctuation of the distribution network (Olivier et al., 2016; Kumar and Bhimasingu, 2015; Liu et al., 2016; Zhan et al., 2016; Wang et al., 2022; Hasheminamin et al., 2015), proposed a strategy to accurately select and optimize the PV position (Kawabe et al., 2017; Islam et al., 2017; Islam et al., 2018; Tafti et al., 2020; Nasir et al., 2019; Anand et al., 2013; Rui et al., 2020), proposed common overvoltage suppression strategies, but these strategies are generally used to improve the voltage stability of the grid or suppress voltage fluctuation. There is no good solution to the problem of voltage rise caused by high proportion PV access.

Through the analysis of the above papers, it can be found that most papers use the simulation strategy to analyze the impact of the high proportion of distributed PV on the operation of the distribution network, and there are few relatively simple and economic strategies to solve the voltage rise caused by the high proportion of PV access. Although some papers employ mathematical derivation and theoretical analysis to investigate this problem, they fail to account for the difference in line parameters between the distribution network and the main network (whether X >> R or not?). In addition, most of the papers only discuss the influence of PV ratio on the operating characteristics of the system subjectively and do not investigate the effect of the change of PV permeability on the system operating indicators quantitatively.

Therefore, starting from the difference between the main network and the distribution network line parameters, this paper firstly proposes a new calculation method for the voltage rise level of the distribution network with a high-proportion PV access through strict mathematical derivation, and then specifically proposes the reverse power flow overvoltage suppression strategy for the system. The main contributions are as follows:

(1) According to the calculation equations of the main operation indicators of the power grid, a grid-connected voltage calculation deviation for the distribution network with high-proportion PV access is conducted based on the parameter conditions of distribution network line (X >> R is not valid).

(2) Aiming at the voltage rise caused by reverse power flow in the distribution network with high proportion PV, an overvoltage suppression strategy is proposed based on the control loop of the distributed PV system, which is guided by economy and practicability.

(3) Simulation scenario is set to verify the effectiveness of the overvoltage suppression strategy.

The main structure of this paper is as follows. Section 2 compares the influence of different line parameter conditions on the calculation of voltage deviation of distribution network with high-proportion PV access and puts forward the calculation strategy of voltage deviation under the condition of distribution network line parameters. The overvoltage suppression strategy is proposed in Section 3, and Section 4 sets a simulation model to verify the effectiveness of the overvoltage suppression strategy.

2 The calculation method of voltage deviation considering the parameters of distribution network lines

At present, the indicators of the power system are calculated according to the main network’s situation that is X >> R, so the resistance value can usually be omitted and approximate results can be obtained. However, this strategy is not suitable for the distribution network because X >> R is not valid. Ignoring the resistance will lead to serious calculation error. To solve this problem, this chapter analyzes the differences between the main network condition (X >> R) and the distribution network condition (X >> R is not valid) in the calculation of grid voltage parameters, summarizes the inapplicability of the main network condition (X >> R) in the calculation of distribution network indicators, and puts forward an accurate calculation strategy for the voltage of the junction point in the high-proportion PV access distribution network.

2.1 Voltage calculation in transmission network

Many papers have shown that a high proportion of grid-connected PV will lead to changes in voltage. Therefore, the research on voltage deviation mainly focuses on the voltage difference between the grid-connected side and the main network side. As shown in Figure 1, the difference between U_G and U_L is the voltage deviation. Since both voltages are vectors, the difference can be expressed by the longitudinal component ΔU and the transverse component δU, as follows:

$\Delta U=\frac{P_{L}R+Q_{L}X}{U_L}(1)$

$\delta U=\frac{P_{L}X-Q_{L}R}{U_L}(2)$

Figure 1

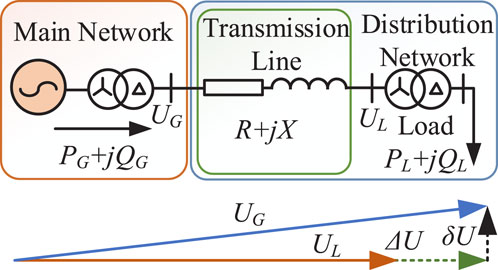
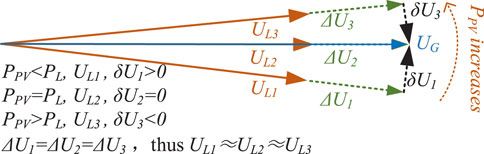
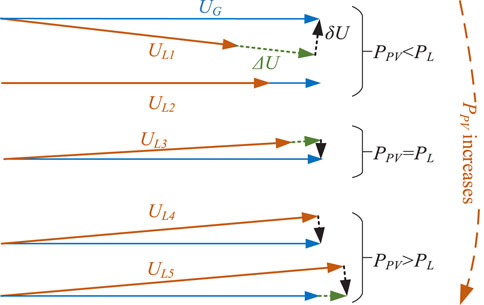
Figure 1. The voltage deviation, where U_G is the main network bus voltage, where U_L is the distribution network bus voltage, P_G + jQ_G is the active power and reactive power of the main network, and P_L + jQ_L is the active power and reactive power of the distribution network.

Figure 2

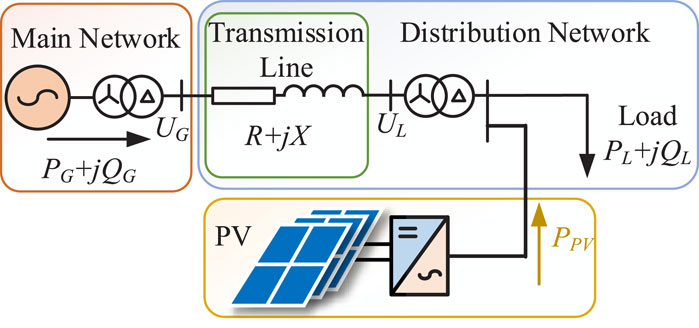
Figure 2. Distributed PV connected to the distribution network, where P_PV is power output by the PV.

According to the main network parameter conditions, X >> R, the resistance R can be omitted, and Equation 3 and Equation 4 are obtained. It can be concluded that the active power determines the voltage phase angle difference δU, and the reactive power determines the voltage amplitude difference ΔU. This conclusion is accurate and practical in the main network.

$\Delta U=\frac{Q_{L}X}{U_L}(3)$

$\delta U=\frac{P_{L}X}{U_L}(4)$

2.2 Voltage calculation in distribution network

Unlike the main network, the condition X >> R does not hold in the distribution network. Therefore, the distribution network’s voltage deviation can only be calculated by Equations 1, 2. There is no strict proportional relationship between active power and voltage amplitude difference, or reactive power and voltage phase angle difference, and the four indexes are coupled with each other. Therefore, the distribution network’s voltage deviation cannot be calculated simply by the main network condition.

Obviously, in the distribution network with a high proportion PV access, if the main network condition, X >> R, is still used, the calculation result will be seriously affected. The analysis is as follows.

After considering distributed PV access, the calculation equations of voltage deviation are as follows:

$\Delta U=\frac{\left(P_L-P_{PV}\right)R+Q_{L}X}{U_L}(5)$

$\delta U=\frac{\left(P_L-P_{PV}\right)X-Q_{L}R}{U_L}(6)$

It can be seen from Equation 5 and Equation 6 that the voltage deviation will change after distributed PV is integrated into the distribution network, and the calculation of voltage deviation is closely related to X/R. The calculation of voltage deviation under different line parameters will be analyzed below.

2.2.1 The analysis of main network conditions is adopted

If the main network condition X >> R is used, the resistance is ignored and the following equation is obtained:

$\Delta U=\frac{Q_{L}X}{U_L}(7)$

$\delta U=\frac{\left(P_L-P_{PV}\right)X}{U_L}(8)$

According to Equations 7, 8, when P_PV changes, the transverse component δU changes, which determines the voltage phase angle difference, while the longitudinal component ΔU does not change, which determines the voltage amplitude difference. Therefore, when the output power of PV changes, the distribution network does not have the problem of voltage rise at the PV junction point, or the voltage rise is very small. The relationship between voltage deviation and P_PV is shown in Figure 3. The voltage amplitude of the PV access point changes little (ΔU₁ = ΔU₂ = ΔU₃) with the increase of P_PV, while the phase difference changes significantly. When the PV ratio exceeds 100% (P_pv > P_L), the voltage phase difference, shown as the δU₃ in Figure 3, changes from positive to negative. This is contrary to actual voltage variation.

Figure 3

Figure 3. Diagram of voltage deviation change when X >> R.

2.2.2 The analysis of distribution network conditions is adopted

If X >> R do not hold, the longitudinal and transverse components of the voltage are coupled to the active and reactive power. Calculating the voltage deviation becomes more complicated. According to the definition of the longitudinal and transverse components of voltage, the following equations can be obtained.

${\left(U_L+\Delta U\right)}^2+{\left(\delta U\right)}^2=U_G^2(9)$

By introducing Equation 5 and Equation 6 into Equation 9, PV grid-connected voltage can be obtained as follows:

$\left\{\begin{array}{l}{U}_L^2=\frac{U_G^2-2\left(xR+Q_{L}X\right)+\sqrt{-{\left(2xX-2Q_{L}R\right)}^2+U_G^2\left[U_G^2-4\left(xR+Q_{L}X\right)\right]}}{2}\\ x=P_L-P_{PV}\end{array}\right.(10)$

As can be seen from Equation 10, the PV junction voltage U_L is a quantity that changes significantly with the change of PV output power P_PV. When the P_PV changes, not only the transverse component of the voltage deviation changes, but also the longitudinal component of the voltage deviation changes, which is different from the trend shown under the condition of X >> R. Therefore, in the subsequent theoretical calculation of the voltage deviation, the precise calculation strategy of the junction voltage in the high-proportion PV access distribution network, as shown in Equation 10, will be adopted.

As can be seen from Equation 10, with the gradual increase of the PV access ratio, the voltage at the grid-connected PV continues to rise. When P_PV is 0, U_L < U_G. When the proportion of PV is significantly larger, U_L > U_G. Figure 4 shows the changes of voltage deviation when X >> R is not valid with the increase of PV output. When P_PV is slightly less than P_L, the voltage phase difference changes from positive to negative. When P_PV is slightly greater than P_L, U_L = U_G. The grid-connected voltage increases with the increase of P_PV, with no upper limit. By comparing Figure 3 and Figure 4, it can be seen that there is a great difference obtained by whether applying X >> R or not. With a high proportion PV connected to the grid, the phenomenon of overvoltage always occurs at the connecting point, which will cause adverse effects on power system operation. Therefore, a corresponding overvoltage suppression strategy concerning the problem will be put forward in the next chapter.

Figure 4

Figure 4. Diagram of voltage deviation change without X >> R.

3 The suppression strategy of overvoltage caused by PV power reverse flow

There are many strategies to suppress overvoltage of the power system, and the common strategy is to set reactive power compensation. When reactive power compensation is added to a new energy system, it is inescapable to increase construction costs. In particular, the scenario considered in this paper is the distribution network, and the PV systems connected are all small-capacity and distributed. If a large number of reactive power compensation devices are installed, unnecessary economic losses will be caused. Therefore, this paper starts with the control link of the PV inverter, and realizes the inhibition effect of overvoltage by regulating the reactive power outer loop, so as to improve the economy under the premise of ensuring the safety of the power grid.

3.1 PV grid-connected inverter control link

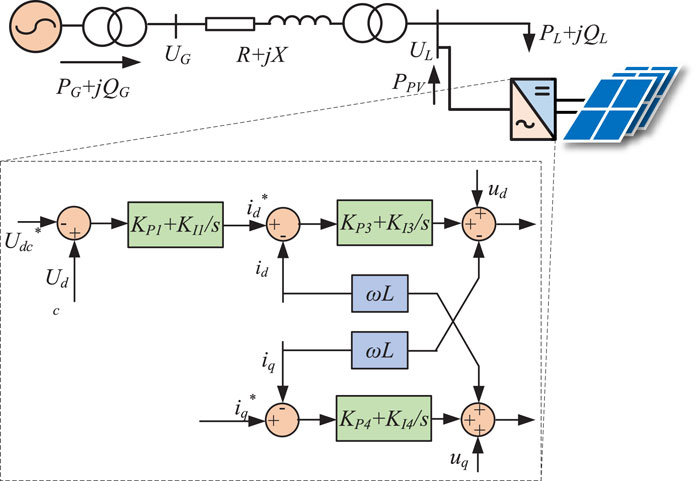
Figure 5 shows the structure of the inverter’s double closed-loop control system. The system consists of an outer loop for controlling DC voltage and an inner loop for controlling the active and reactive current of the three-phase inverter.

Figure 5

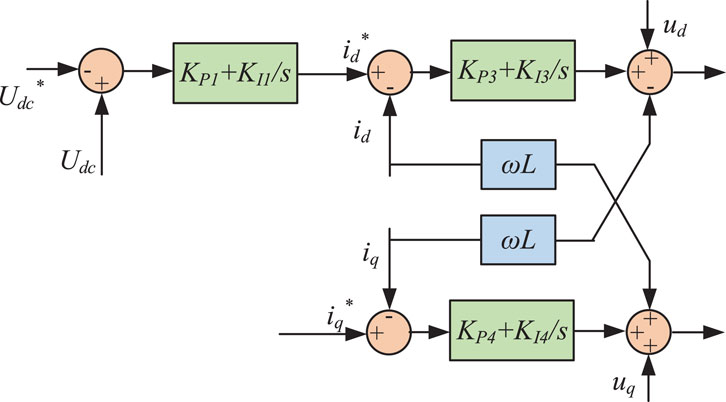
Figure 5. The double closed-loop control of the inverter, where U_dc is actual DC voltage of inverter, i_d is d-axis current, i_q is q-axis current, K_p is proportional parameter, K_i is integral parameter, u_d is d-axis voltage, u_q is q-axis voltage.

In the mathematical model of a three-phase inverter under the two-phase synchronous rotating coordinate system (d, q), the current component of the d-q axis is not only controlled by the corresponding variables but also affected by the cross-coupling quantities ωLi_q and ωLi_d, which increases the difficulty of controller design. The cross-coupling quantity can be eliminated by the strategy of feedforward decoupling control, and the current i_d and i_q can be adjusted without static difference by the PI regulator. Thus, the governing equation for the d-q component is:

$\left\{\begin{array}{l}{u}_d^{*}=-\left(K_P+\frac{K_I}{s}\right)\left(i_q^{*}-i_q\right)-\omega L{i}_d+e_q\\ u_q^{*}=-\left(K_P+\frac{K_I}{s}\right)\left(i_d^{*}-i_d\right)+\omega L{i}_q+e_d\end{array}\right.(11)$

As can be seen, MPPT in PV inverter generates reference DC voltage U_dc^*, which produces a difference compared with PV output DC voltage U_dc. This difference is controlled by PI and generates a reference current i_d^* on the d-axis. Similarly, i_q^* is generated by the difference between reactive power and reactive power reference value on the q-axis. The reference current i_q^* on the q-axis is usually set to 0. After the three-phase AC current flows through real-time sampling, it is converted into d-q axis components and compared with d and q-axis reference currents respectively. After the error is decoupled, it is controlled by the PI regulator. According to Equation 11, the reference voltage u_d^* and u_q^* of the d-q axis are obtained, and the inverter can adjust SVPWM according to the reference voltage.

3.2 Overvoltage suppression strategy

The control system, shown in Figure 5, is composed of an outer voltage loop and an inner current loop, and is divided into d-q axis, among which the q-axis is generally considered to achieve the function of controlling voltage. Therefore, we choose to control the reactive power by setting the reference current value of q-axis to suppress overvoltage. The overvoltage suppression strategy is described as follows:

(1) The inverter regularly monitors the voltage of the connecting point and compares it with rated voltage of the grid;

(2) When voltage of the connecting point is higher than rated voltage of the grid, reduce the reactive power by increasing the reference value of q-axis current, which can be supported by Equation 13 and Equation 10. Equation 13 can be obtained by putting (Q_L0-Q_PV) into the Q_L of Equation 10. Equation 13 is shown as follows:

$Q=-i_q\times u_d+i_d\times u_q\approx -i_q\times u_d(12)$

$\left\{\begin{array}{l}{U}_L^2=\frac{U_G^2-2\left(xR+yX\right)+\sqrt{-{\left(2xX-2yR\right)}^2+U_G^2\left[U_G^2-4\left(xR+yX\right)\right]}}{2}\\ \begin{array}{l}x=P_L-P_{PV}\\ y=Q_L-Q_{PV}\end{array}\end{array}\right.(13)$

Make U_L = U_G to obtain the reference value of reactive power Q_PV. Bring Q_PV into Equation 12, find the q-axis current i_q, make the q-axis current reference value i_q^* = i_q, and then achieve control;

(3) When the connecting point voltage is restored to rated voltage of the grid under the control of q-axis current, keep i_q^* = i_q;

(4) When the connecting point voltage is lower than the rated voltage of the power grid, Equation 13 can be applied to modify the q-axis current reference value as well.

It is worth noting that in practical applications, due to the interference of external reactive devices and the internal control of inverter, the effect of the modification of q-axis current reference value on the voltage is not as obvious as in theoretical calculations. Therefore, referring to the voltage control effect of the transformer variable tap, each change of the q-axis current reference value can be set to the constant Δi_q-c^*. Add step 5 as follows:

(5) After step (2), if the connecting point voltage is still higher than rated voltage of the grid, increase the q-axis current reference value to Δi_q-c^*. After the voltage is stabilized, the relationship between the connecting point voltage and rated voltage of the grid can be monitored again. If the two are similar, there is no need for further control; if there is still a large gap, the Δi_q-c^* will be adjusted again. The Δi_q-c^* will be adjusted n times until the voltage of connecting point returns to allowable value range.

4 Simulation verification

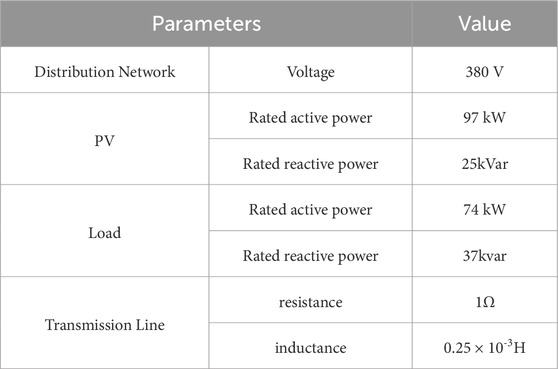
In order to verify the effectiveness of the overvoltage suppression strategy mentioned above, a simulation model is built in Simulink, as shown in the Figure 6. In the model, the PV inverter uses the control strategy shown in Figure 5, and applies the overvoltage suppression strategy proposed in Section 2.2. The construction of the model utilizes the actual data of a distribution network in a small village in Shandong province. By setting different PV output power, the model simulates the change of PV system output in a natural day, and then verifies the effectiveness of the proposed overvoltage suppression strategy. Table 1 lists the main parameters of the model.

Figure 6

Figure 6. The simulation model.

Table 1

Table 1. Parameters of the simulation model.

As can be seen from Table 1, when the rated power of the PV system is emitted, the PV power is higher than the load power, so the active power flow direction in the transmission line is from the distribution network to the main network, and U_L points to U_G in Figure 6, which is called reverse flow. Reactive power flows from the main network to the distribution network, with U_G pointing to U_L in Figure 6. According to the above theoretical analysis, the reverse flow of active power will lead the voltage of the distribution network to be higher than that of the main network. But due to the forward flow of reactive power, the voltage difference will be suppressed to some extent. To achieve the purpose of overvoltage suppression, we apply the strategy proposed in Section 2.2 and continue to increase the reactive power of the forward flow.

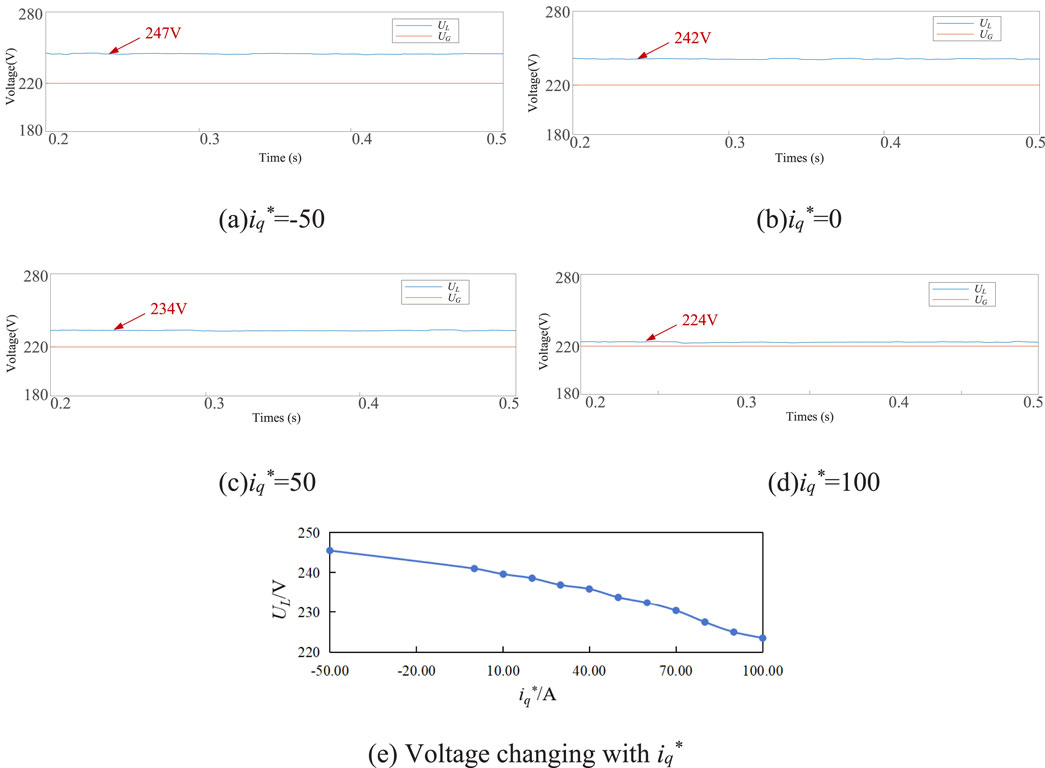
Figure 7 shows the effect diagram of overvoltage suppression with this strategy. Figures 7A–D is the voltage image under different values of q-axis current reference value i_q^*, and (e) is the voltage change trend diagram. When the q-axis current reference value i_q^* is −50A, it can be seen that the distribution network voltage U_L is 246 V at this time, which exceeds the rated phase voltage of the line by more than 10%, and overvoltage suppression is required. To better demonstrate the application effect of the strategy, the q-axis current reference value is first set to 0 when the strategy is applied, that is, the PV system does not output reactive power, and the voltage of the distribution network exceeds the rated phase voltage by 10%. Then let Δi_q-c^* = −10A, adjust the q-axis current reference value step by step, it can be seen that with the gradual increase of the q-axis current reference value, the distribution network voltage U_L gradually decreased, when i_q^* = 100A, U_L dropped to 223.5 V, the overvoltage can be ignored. Therefore, the overvoltage suppression strategy proposed in this paper is effective.

Figure 7

Figure 7. The application effect of the strategy.

5 Conclusion

In this paper, the reverse power flow phenomenon of a high proportion PV access system is deeply studied. Firstly, a new calculation strategy for the voltage rise, caused by the reverse power flow in the distribution network with a high proportion PV access, is proposed by doing strict mathematical derivation from the difference of line parameters between the main network and the distribution network. Then, according to the mechanism of voltage rise and the principle of inverter control, considering the economy and practicability, an overvoltage suppression strategy of a system with high proportion PV access is put forward. Finally, a PV system model simulating a small village is used to verify the effectiveness of the proposed overvoltage suppression strategy. The overvoltage caused by reverse power flow decreases from 10% above the rated voltage at the beginning to 1.5%, which indicates that the proposed overvoltage suppression strategy is practical and effective to the distribution network with a high proportion PV access.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YX: Writing–original draft. QL: Writing–original draft. LY: Writing–original draft. KY: Writing–original draft. ZW: Writing–original draft. JL: Writing–original draft. HF: Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study received funding from State Grid Shandong Electric Power Company Technology Project (520609230004). The funder had the following involvement in the study: 520609230004.

Conflict of interest

Authors YX, QL, LY, KY, and ZW were employed by State Grid Taian Power Supply Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from State Grid Shandong Electric Power Company Technology Project . The funder had the following involvement in the study: the study design, data collection and analysis, decision to publish, and preparation of the manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alam, M. J. E., Muttaqi, K. M., and Sutanto, D. (2012). “A comprehensive assessment tool for solar PV impacts on low voltage three phase distribution networks,” in Proc. 2nd IEEE int. Conf. Developments renewable energy technol, 1–5.

Google Scholar

Anand, S., Fernandes, B. G., and Guerrero, J. (2013). Distributed control to ensure proportional load sharing and improve voltage regulation in low-voltage DC microgrids. IEEE Trans. Power Electron. 28 (4), 1900–1913. doi:10.1109/tpel.2012.2215055

CrossRef Full Text | Google Scholar

Aramizu, J., and Vieira, J. C. (2013). “Analysis of PV generation impacts on voltage imbalance and on voltage regulation in distribution networks,” in Proc. IEEE power energy soc. General meeting, 1–5.

CrossRef Full Text | Google Scholar

Demirok, E., Sera, D., Teodorescu, R., Rodriguez, P., and Borup, U. (2009). “Clustered PV inverters in LV networks: an overview of impacts and comparison of voltage control strategies,” in 2009 IEEE electrical power and energy conference (EPEC), 1–6.

CrossRef Full Text | Google Scholar

Ding, M., Xu, Z., Wang, W., Wang, X., Song, Y., and Chen, D. (2016). A review on China’s large-scale PV integration: progress, challenges and recommendations. Renew. Sustain. Energy Rev. 53, 639–652. doi:10.1016/j.rser.2015.09.009

CrossRef Full Text | Google Scholar

Elavarasan, R. M., Shafiullah, G., Padmanaban, S., Kumar, N. M., Annam, A., Vetrichelvan, A. M., et al. (2020). A comprehensive review on renewable energy development, challenges, and policies of leading Indian States with an international perspective. IEEE Access 8, 74432–74457. doi:10.1109/access.2020.2988011

CrossRef Full Text | Google Scholar

Fan, H., Sun, K., Ning, D., Li, P., Zhu, F., and Dong, Y. (2023). A novel operating indexes calculation method for distribution network with high PV penetration. J. Phys. Conf. Ser. 2534 (1), 012014. doi:10.1088/1742-6596/2534/1/012014

CrossRef Full Text | Google Scholar

Hasheminamin, M., Agelidis, V. G., Salehi, V., Teodorescu, R., and Hredzak, B. (2015). Index-based assessment of voltage rise and reverse power flow phenomena in a distribution feeder under high PV penetration. IEEE J. Photovoltaics 5 (4), 1158–1168. doi:10.1109/jphotov.2015.2417753

CrossRef Full Text | Google Scholar

Hernández, J., Medina, A., and Jurado, F. (2007). Optimal allocation and sizing for profitability and voltage enhancement of PV systems on feeders. Renew. Energy 32 (10), 1768–1789. doi:10.1016/j.renene.2006.11.003

CrossRef Full Text | Google Scholar

Heubl, B. (2021). How hydrogen hype risks EU’s climate goals: the natural gas industry wants to secure its future in a net zero carbon world, but is the hydrogen economy it promotes all that it’s cracked up to be? Eng. and Technol. 16 (4), 1–7.

CrossRef Full Text | Google Scholar

Hung, D. Q., Mithulananthan, N., and Bansal, R. (2014). Integration of PV and BES units in commercial distribution systems considering energy loss and voltage stability. Appl. Energy 113, 1162–1170. doi:10.1016/j.apenergy.2013.08.069

CrossRef Full Text | Google Scholar

Islam, M., Mithulananthan, N., and Hossain, M. J. (2018). Dynamic voltage support by TL-PV systems to mitigate short-term voltage instability in residential DN. IEEE Trans. Power Syst. 33 (4), 4360–4370. doi:10.1109/tpwrs.2017.2765311

CrossRef Full Text | Google Scholar

Islam, M., Nadarajah, M., and Hossain, J. (2017). “Dynamic behavior of transformerless PV system on the short-term voltage stability of distribution network,” in 2017 IEEE power and energy society general meeting, 1–5.

CrossRef Full Text | Google Scholar

Kawabe, K., Ota, Y., Yokoyama, A., and Tanaka, K. (2017). Novel dynamic voltage support capability of photovoltaic systems for improvement of short-term voltage stability in power systems. IEEE Trans. Power Syst. 32 (3), 1796–1804. doi:10.1109/tpwrs.2016.2592970

CrossRef Full Text | Google Scholar

Kawabe, K., and Tanaka, K. (2015). Impact of dynamic behavior of photovoltaic power generation systems on short-term voltage stability. IEEE Trans. Power Syst. 30 (6), 3416–3424. doi:10.1109/tpwrs.2015.2390649

CrossRef Full Text | Google Scholar

Kumar, Y. V. P., and Bhimasingu, R. (2015). Renewable energy based microgrid system sizing and energy management for green buildings. J. Mod. Power Syst. Clean Energy 3 (1), 1–13. doi:10.1007/s40565-015-0101-7

CrossRef Full Text | Google Scholar

Le Dinh, K., and Hayashi, Y. (2013). “Coordinated BESS control for improving voltage stability of a PV-supplied microgrid,” in Power engineering conference (UPEC), 2013 48th international universities (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Liu, J., Miura, Y., and Ise, T. (2016). Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverterbased distributed generators. IEEE Trans. Power Electron. 31 (5), 3600–3611. doi:10.1109/tpel.2015.2465852

CrossRef Full Text | Google Scholar

Nasir, M., Anees, M., Khan, H. A., and Guerrero, J. M. (2019). Dual-loop control strategy applied to the cluster of multiple nanogrids for rural electrification applications. IET Smart Grid 2 (3), 327–335. doi:10.1049/iet-stg.2019.0098

CrossRef Full Text | Google Scholar

Olivier, F., Aristidou, P., Ernst, D., and Van Cutsem, T. (2016). Active management of low-voltage networks for mitigating overvoltages due to photovoltaic units. IEEE Trans. Smart Grid 7 (2), 926–936. doi:10.1109/tsg.2015.2410171

CrossRef Full Text | Google Scholar

Quintero, J., Vittal, V., Heydt, G. T., and Zhang, H. (2014). The impact of increased penetration of converter control-based generators on power system modes of oscillation. IEEE Trans. Power Syst. 29 (5), 2248–2256. doi:10.1109/tpwrs.2014.2303293

CrossRef Full Text | Google Scholar

Rui, W., Qiuye, S., Pinjia, Z., Yonghao, G., Dehao, Q., and Peng, W. (2020). Reduced-order transfer function model of the droop-controlled inverter via Jordan continued-fraction expansion. IEEE Trans. Energy Convers. 35 (3), 1585–1595. doi:10.1109/tec.2020.2980033

CrossRef Full Text | Google Scholar

Shah, R., Mithulananthan, N., Bansal, R. C., and Ramachandaramurthy, V. K. (2015). A review of key power system stability challenges for large-scale PV integration. Renew. Sustain. Energy Rev. 41, 1423–1436. doi:10.1016/j.rser.2014.09.027

CrossRef Full Text | Google Scholar

Tafti, H. D., Konstantinou, G., Townsend, C. D., Farivar, G. G., Sangwongwanich, A., Yang, Y., et al. (2020). Extended functionalities of photovoltaic systems with flexible power point tracking: recent advances. IEEE Trans. Power Electron. 35 (9), 9342–9356. doi:10.1109/tpel.2020.2970447

CrossRef Full Text | Google Scholar

Tamimi, B., Cañizares, C., and Bhattacharya, K. (2013). System stability impact of largescale and distributed solar photovoltaic generation: the case of Ontario, Canada. IEEE Trans. Sustain. energy 4 (3), 680–688. doi:10.1109/tste.2012.2235151

CrossRef Full Text | Google Scholar

Tan, J., Zhang, Y., You, S., Liu, Y., and Liu, Y. (2018). “Frequency response study of US western interconnection under extra-high photovoltaic generation penetrations,” in Power and energy society general meeting, 2018 IEEE (IEEE), 1–5.

CrossRef Full Text | Google Scholar

Thomson, M., and Infifield, D. G. (2007). Impact of widespread photovoltaics generation on distribution systems. IET Renew. Power Gener. 1 (1), 33–40. doi:10.1049/iet-rpg:20060009

CrossRef Full Text | Google Scholar

Wang, P., Liang, F., Song, J., Jiang, N., Zhang, X.-P., Guo, L., et al. (2022). Impact of the PV location in distribution networks on network power losses and voltage fluctuations with PSO analysis. CSEE J. Power Energy Syst. 8 (2), 523–534.

Google Scholar

Xie, X., Ding, Y., Sun, Y., Zhang, Z., and Fan, J. (2024a). A novel time-series probabilistic forecasting method for multi-energy loads. Energy 306, 132456. doi:10.1016/j.energy.2024.132456

CrossRef Full Text | Google Scholar

Xie, X., Zhang, J., Sun, Y., and Fan, J. (2024b). “A measurement-based dynamic harmonic model for single-phase diode bridge rectifier-type devices,” in IEEE Transactions on Instrumentation and Measurement 73, 1–13. doi:10.1109/TIM.2024.3370782

CrossRef Full Text | Google Scholar

Yan, R., and Saha, T. K. (2012). Investigation of voltage stability for residential customers due to high photovoltaic penetrations. IEEE Trans. power Syst. 27 (2), 651–662. doi:10.1109/tpwrs.2011.2180741

CrossRef Full Text | Google Scholar

You, S., Kou, G., Liu, Y., Zhang, X., Cui, Y., Till, M. J., et al. (2017). Impact of high PV penetration on the inter-area oscillations in the US eastern interconnection. IEEE Access 5, 4361–4369. doi:10.1109/access.2017.2682260

CrossRef Full Text | Google Scholar

You, S., Liu, Y., Kou, G., Zhang, X., Yao, W., Su, Y., et al. (2018). Non-invasive identification of inertia distribution change in high renewable systems using distribution level PMU. IEEE Trans. Power Syst. 33 (1), 1110–1112. doi:10.1109/tpwrs.2017.2713985

CrossRef Full Text | Google Scholar

Zhan, H. X., S Wang, C., Wang, Y., Yang, X. H., Zhang, X., Wu, C. J., et al. (2016). Relay protection coordination integrated optimal placement and sizing of distributed generation sources in distribution networks. IEEE Trans. Smart Grid 7 (1), 55–65. doi:10.1109/tsg.2015.2420667

CrossRef Full Text | Google Scholar