
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 17 October 2024
Sec. Smart Grids
Volume 12 - 2024 | https://doi.org/10.3389/fenrg.2024.1491846
This article is part of the Research Topic Advanced Data-Driven Uncertainty Optimization for Planning, Operation, and Analysis of Renewable Power Systems View all 16 articles
This paper proposes a novel two-stage transient stability assessment (TSA) model that integrates ensemble learning with cost sensitivity to address the challenges posed by the integration of renewable energy and load fluctuations. The model employs CNNs as positive and negative classifiers to initially evaluate samples, with consistent results output directly. In cases of inconsistency, the sample is evaluated by a fair classifier, specifically an ELM, trained on critical samples. This approach significantly enhances the classification performance and credibility of the fair classifier, especially under imbalanced conditions, thereby improving the overall efficiency and accuracy of TSA. The proposed model demonstrates superior performance compared to single-stage models and other two-stage models, achieving high accuracy and robustness in transient stability assessment, particularly for critical samples.
The development of modern power systems presents new challenges to the safety of these systems. In recent years, frequent blackouts worldwide have had significant economic impacts (Wei Zhang and Zhang, 202). Transient stability is crucial to the safe operation of power systems. Once a disturbance occurs in the power system, early assessment of transient stability and timely implementation of emergency control measures can protect the system’s stability (Guo et al., 2023; Meridji et al., 2023; Singh and Chauhan, 2023; Wang Y. et al., 2023; Zhu et al., 2023). Therefore, it is vital and necessary to design a TSA model that can quickly and accurately determine whether a power system will become unstable and infer the type of events that may cause instability.
Classical transient stability methods include time-domain simulation (TDS) and direct methods. TDS analyzes system stability through detailed modeling. As long as the component models and network structures are sufficiently accurate, the results are reliable. However, with the increasing complexity of power systems and rapid changes in electronic hardware, TDS-based models have become more complex, and their computational demands have increased, making TDS methods unsuitable for real-time transient stability assessment. The direct method, on the other hand, does not require numerical integration of dynamic processes and can quantitatively analyze system transient stability. However, direct method models are simple and may face applicability issues in complex power systems. Additionally, the evaluation results tend to be conservative. As a result, these methods currently cannot fully meet the practical needs of online transient stability assessment. To date, real-world power grids still require more advanced TSA solutions that can achieve high reliability and efficiency.
The rapid development of big data offers new ideas for transient stability assessment. TSA rules can be mined from large volumes of data using machine learning (ML) methods (Liu et al., 2023; Li et al., 2024; Shao et al., 2024). Once dynamic information is received, stability results can be output within milliseconds. After discovering underlying relationships offline through ML, they can be easily applied to online TSA. This data-driven approach almost eliminates online computation time and can effectively predict system stability.
Modern power systems usually remain stable after most disturbances due to their robustness. In practical applications, events causing power system instability are rare. These rare events lead to significant imbalances between stable (majority class) and unstable (minority class) transient data distributions. The imbalance in training data leads to high misclassification rates in TSA models. Moreover, misjudging the transient stability of power systems prevents timely responses and corresponding measures, leading to safety accidents and significant economic losses. Therefore, addressing the imbalance in training data is not only crucial for improving TSA accuracy but also has practical significance.
Existing methods for addressing class imbalance can be broadly categorized into data-driven and algorithm-driven approaches. Additionally, traditional data-driven methods attempt to oversample or undersample the data so that different classes appear in equal proportions in the training data. The main drawback of sampling-based methods is that they may lose important information in undersampling or overfit the training data in oversampling. Algorithm-driven methods primarily include cost-sensitive methods (Wang H. et al., 2023; Chen et al., 2022; Lin et al., 2022; Wang et al., 2020) and ensemble learning methods (Shen, 2023; Chen and Wang, 2021; Chen et al., 2021; Zhao et al., 2022; Wu et al., 2020). References (Wang H. et al., 2023) consider the imbalance in sample distribution in space by dividing samples into different levels of training sets and training the model using cost-sensitive approaches. Reference (Shen, 2023) proposes a comprehensive transient stability state assessment method for power systems based on machine learning, using multiple classifiers to alleviate the sample imbalance problem in transient stability samples. However, its drawbacks are also evident. The ensemble learning classifiers used are often weak classifiers with low resistance to interference and increased training time. Among these methods, the application of cost sensitivity in transient stability assessment is relatively limited. Although it helps mitigate sample imbalance, its blind use may lead to overfitting and increased misclassification rates. Applying ensemble learning alone to transient stability assessment can also mitigate sample imbalance, but due to the large number of ensemble classifiers, it may result in longer training times and weaker resistance to interference.
Recently, to mitigate the imbalance in transient stability samples, references (Chen and Wang, 2021; Wang et al., 2020) adopted a two-stage assessment approach combining cost sensitivity and ensemble learning. Specifically, three models are used, with two classifiers in the first stage, each biased towards one class of samples using cost-sensitive methods. A non-cost-sensitive classifier is then trained using the same training set as a fair classifier for second-stage evaluation. Although this approach combines the advantages of cost-sensitive learning and ensemble learning, it also overcomes some disadvantages. However, this method lacks credibility, mainly because the credibility of the fair classifier is low. This is because hard samples are evaluated by a non-cost-sensitive classifier, and the evaluation results are directly output. However, since the fair classifier is not selected based on the characteristics of the input samples, highly accurate and convincing evaluation results cannot be generated.
In transient stability assessment, what truly affects misclassification and missed judgments are the hard samples. In this study, we propose a two-stage transient stability assessment model based on the integration of ensemble learning and cost sensitivity. First, the initial sample set is input into positive and negative classifiers again, and samples with inconsistent evaluation results are collected to form a critical sample set. This critical sample set is used to train the ELM (fair classifier). The model combines the strengths of cost sensitivity and ensemble learning, greatly enhancing the credibility of the fair classifier while improving the overall reliability of the model.
The rest of this paper is structured as follows: Section 2 offers an overview of the transient stability assessment (TSA) problem and introduces the proposed two-stage TSA model. Section 3 details the implementation process of the model. Section 4 presents case studies and evaluates the model’s performance. Finally, Section 5 summarizes the conclusions of the paper.
Transient stability assessment (TSA) has become increasingly important in power systems, with the main challenge being how to overcome the inherent sample imbalance problem, which is determined by the robustness of power systems. To address the imbalance in transient stability samples, a two-stage assessment method combining cost sensitivity and ensemble learning has been widely adopted. However, due to the lack of optimization in the selection of the fair classifier, it is difficult to produce highly accurate and convincing evaluation results. The model proposed in this paper addresses the problem of transient stability assessment under imbalanced samples by considering the difficulty of classifying critical samples, combining cost sensitivity and ensemble learning, which greatly enhances the reliability of the fair classifier and the overall model reliability. Currently, the issue of sample imbalance in transient stability assessment cannot be ignored, as stable samples are the majority, unstable samples are fewer, and critical samples are even rarer. The training model must fully understand the characteristics of stable, unstable, and critical samples to classify them correctly. Therefore, solving the sample imbalance problem is crucial for transient stability assessment. The two-stage TSA model proposed in this paper aims to achieve accurate and reliable classification results even under imbalanced conditions.
Unlike most previous evaluation model designs, this paper designs a two-stage transient stability assessment model based on the integration of ensemble learning and cost sensitivity. The advantage of this approach is that it can combine the strengths of various models and effectively overcome the drawbacks of low accuracy, low effectiveness, and high cost caused by sample imbalance.
The positive and negative models are the foundational models in the entire two-stage framework; their results are only valid when they are consistent. Otherwise, if the results are inconsistent, the assessment will enter the next stage without directly outputting the results. Therefore, to maximize the role of the positive and negative models, cost sensitivity is applied to these models. The positive model is inclined to evaluate samples as stable, while the negative model is inclined to evaluate samples as unstable. Under this design, when the evaluation results of the positive and negative models are consistent, the input samples must be far from the boundary, indicating that the samples are either extremely stable or extremely unstable. In such cases, the positive and negative models require strong feature extraction capabilities to fully recognize samples beyond the boundary.
Convolutional Neural Networks (CNNs) possess strong nonlinear expression and pattern recognition capabilities, making them suitable for handling complex dynamic processes and nonlinear problems in power systems (Lee et al., 2023). This allows CNN-based TSA models to more accurately reflect the transient stability status of the power system based on input operational parameters. Compared to traditional time-domain and direct methods, CNN-based TSA methods offer higher assessment accuracy and faster computation speed. They can meet the requirements of online real-time prediction, providing timely and accurate power system stability analysis results for dispatchers (Gu et al., 2024). Additionally, CNN models can adapt to different power system scenarios and demands by adjusting the network structure and parameters, offering higher flexibility and scalability. In summary, applying CNNs to power system transient stability assessment has advantages such as automatic feature extraction, strong nonlinear processing capabilities, high accuracy, real-time performance, and applicability to complex systems, making it a vital tool in power system operation and control. Therefore, we select CNN as the positive and negative models. With CNN’s strong feature extraction capabilities, we can effectively handle the characteristics of stable and unstable sample regions, achieving initial simple classification. Furthermore, CNN-based methods can directly use low-level measurement data as input features, extracting multi-granularity information from measurement data through multi-size convolution kernels, thereby improving the accuracy of TSA in power systems (Jin et al., 2023).
For transient stability assessment, reasonable feature selection is needed to construct samples as input. This paper focuses on selecting steady-state quantities and fault characteristics for the forward-looking prediction of transient stability (Ji et al., 2022). Therefore, bus voltage, generator active and reactive power, and load active and reactive power are chosen as input features. Relevant data are obtained from measurements or time-domain simulations and input into the CNN model. The network structure of CNN is shown in Figure 1.
Based on the input electrical quantity matrix, the convolutional layer performs local learning through convolution kernels in the CNN model. The convolution operation for each convolution kernel is as Equation 1.
where
For the pooling layer, this paper adopts max pooling, as shown in Equation 2.
where
The calculation formula for the fully connected layer is as Equation 3.
In the fully connected layer,
The fully connected layer passes the output values to the output layer, and the expression of the sigmoid function in the output layer is as Equation 4.
where
Typically, the approach to solving quantity imbalance is to assign higher weights to unstable samples. However, the misclassification of critical samples still occurs. Another approach is to assign higher weights to both imbalances simultaneously: first, higher weights are given to unstable samples, and then higher weights are assigned to misclassified samples. This approach can lead to overfitting (Kesici et al., 2023).
In this study, the model is trained by optimizing parameters to improve the fit to the training samples. The loss function is used to measure the difference between the predicted and actual values, and the impact of training samples on evaluation rules can be assessed through the loss function. This cost-sensitive approach makes the positive model inclined to evaluate samples as stable and the negative model inclined to evaluate samples as unstable.
For the transient stability assessment problem, the weight correction coefficient for model parameters can be represented by Table 1.
Where
In different scenarios, the proportion of unstable samples to stable samples in the training set often differs, which causes the model trained under imbalanced samples to have a certain bias in its discriminative results. Therefore, this paper introduces a correction factor
where
By adjusting the weight correction coefficients during the evaluation model parameter correction process, the model’s loss function is as follows:
The model using Equation 7 is the positive model. After applying cost sensitivity, this model tends to evaluate input samples as stable. Conversely, if the model needs to incline toward evaluating input samples as unstable, an additional correction factor
When
The reorganized model’s loss function is shown in Equation 10.
The negative model applies the loss function from the above equation to tend toward evaluating input samples as unstable.
The fair classifier is used to classify hard samples, which are samples that the initial simple classification could not correctly categorize. Therefore, the sample set used to train the fair classifier is the critical sample set, and the model selection must consider this.
The fair classifier operates in the second stage of the assessment, requiring high accuracy and interpretability in its results. The sample set used to train the fair classifier is the critical sample set, which contains rich data information and high information entropy, requiring a suitable model to extract these features. For ELM training, the ideal sample should be data close to the stability boundary to obtain refined stability rules, allowing for effective learning of the critical region and a strong ability to correctly classify hard samples.
Given the above considerations, ELM is chosen as the fair classifier. Due to the distribution characteristics of the critical sample set, it matches the training requirements of the ELM model. If the training samples of ELM are from the critical region, the trained ELM will have a strong ability to correctly classify the critical sample set. ELM is used for training, but not with the original sample set; instead, it is trained using samples with conflicting evaluation results from two classifiers with opposing biases.
ELM can randomly select input layer parameters, and then use the Moore-Penrose generalized inverse to obtain the output layer weights with the smallest 2-norm. In ELM, only the number of hidden layer neuron nodes needs to be learned and adjusted, and the entire process does not require iteration. Figure 2 shows the ELM network structure.
Specifically, for a dataset
where
In ELM, the weight vector
After completing all the above designs, the framework for the proposed two-stage transient stability assessment model is established. Next, the overall evaluation process is designed.
The model proposed in this study is a two-stage evaluation model, where the second stage’s evaluation somewhat depends on the results of the first stage. Therefore, it is necessary to design scoring for the first-stage evaluation results to complete the evaluation logic of the first and second stages.
Define
To improve efficiency,
Define
According to the model logic proposed in this paper, the first-stage evaluation results are credible, and the evaluation results are directly output only when the positive and negative classifier outputs are consistent. This occurs when
The overall evaluation process can be simplified as shown in Table 3.
As shown in Table 3, when the total score is 1, the second-stage evaluation result is output as the model’s evaluation result. When the total score is 2, that is, when
After selecting a specific example system, transient stability simulations are performed to collect steady-state data and create the initial sample set.
Based on the obtained initial dataset, the positive and negative classifiers are trained separately. After training, the initial dataset is re-input into the trained positive and negative classifiers for evaluation, and the critical dataset is organized based on the differing evaluation results from the positive and negative classifiers.
Since the fair classifier needs to correctly classify critical samples, ELM is selected as the fair classifier. By training ELM using the critical sample set, the ability of ELM to correctly classify critical samples is greatly enhanced, meeting the requirements of the fair classifier. The construction of the integrated TSA model is then completed.
When evaluating real-time data obtained from the power system, the measured data is input into the positive and negative classifiers for evaluation. If the evaluation results are consistent, the results are output, completing the assessment; if the evaluation results are inconsistent, the measured data is input into the fair classifier, and the evaluation results from the fair classifier are output, completing the assessment. The specific implementation process is shown in Figure 3.
(1): Offline Training
(2): Online Application
Taking the New England 10-generator, 39-bus system as a case study, as shown in the Figure 4, the entire bus system is divided into four regions according to adjacent buses. Four different load levels, 80%, 90%, 110%, and 120%, are considered, and each region is assigned a different load level, resulting in 256 different power flows,256 different operating modes. The generator output is adjusted accordingly to ensure the convergence of power flow calculations. The fault is set as a three-phase short-circuit fault, and an N-1 scan is performed on the system by sequentially setting faults on different lines. The fault duration is set to 0.2 s on lines without transformers, with the fault point located at 50% of the line’s length. On lines with transformers, the fault point is set at the head section of the line.
The selection of input features including bus voltage, generator active power and reactive power, as well as load active power and reactive power, is indeed widely used in data-driven transient stability assessment (Li et al., 2021; Du et al., 2021). Bus voltage reflects the system’s voltage levels and can serve as an early warning for instability. Generator active power and reactive power respectively influence frequency stability and voltage regulation. Load active power affects the system’s energy balance, while load reactive power is crucial for voltage stability. These features provide a solid foundation for predictive transient stability assessment.
A total of 11,776 samples are generated. By sampling from these 11,776 simulated samples, the training set, testing set, and validation set are obtained in a ratio of 8:1:1.
Transient stability assessment in power systems includes two categories: stable and unstable. The criterion for stability is the transient stability index (TSI). The details are given in Equation 12.
When the maximum rotor angle difference among generators exceeds
The following indicators are set as in Equations 13–15 to evaluate the performance of the model:
After the training, the model is tested from the test set, and the performance test results of the model are obtained. At the same time, existing Two-Stage models (such as two-stage-LSTM, two-stage-GRU) are tested, which all use the same neural network (such as LSTM or GRU) for positive and negative sample classification and fair classification tasks. The weight coefficient matrix used for model parameter correction is shown in Table 4. Firstly, transient stability evaluation experiments were conducted on the single-stage model and the two-stage model, and the results were recorded and summarized as shown in Table 5.Vertical comparison shows that the two-stage method proposed in this paper outperforms the single-stage method in all indicators, with a significant reduction in misclassification rates and a marked improvement in classification accuracy. This validates the effectiveness of the two-stage model in complex tasks compared to a single model. Figure 5 shows the bar chart comparison of the performance between single-stage and two-stage models.Based on these findings, we further explored the effects of different neural network combinations within the two-stage framework. As such, this paper proposes the TCS-ELM model (Two-Stage Cost-Sensitive Ensemble Learning Model), using CNN for positive and negative sample classification in the first stage and ELM for fair classification in the second stage, fully leveraging CNN’s feature extraction strengths and ELM’s efficient classification capabilities. Table 6 shows the performance testing results of various two-stage models and the proposed TCS-ELM model.Results indicate that the proposed TCS-ELM model, by using CNN in the first stage for stronger feature extraction capabilities and ELM in the second stage for improved classification accuracy, outperforms other two-stage models (such as Two-Stage-LSTM and Two-Stage-GRU) in all indicators, particularly exhibiting higher accuracy and robustness when handling critical samples. This demonstrates that the TCS-ELM model combines the advantages of CNN and ELM in their respective stages, significantly enhancing overall performance. Figure 6 presents the bar chart comparison of the performance between TCS-ELM and other two-stage models.
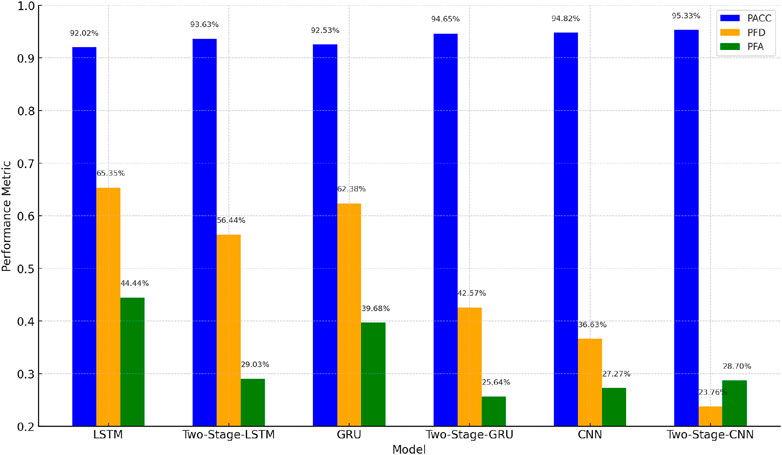
Figure 5. Comparison of performance between single-stage and two-stage models. Model performance improvement: two-stage vs. baseline (LSTM, GRU, CNN).
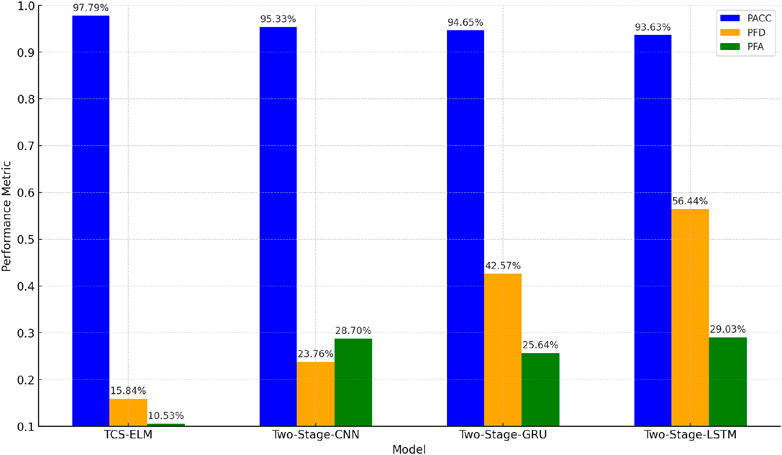
Figure 6. Comparison of performance between single-stage and two-stage models. Performance comparison of 4 deep learning models.
In conclusion, the two-stage transient stability assessment model proposed in this paper, which leverages a combination of cost sensitivity and ensemble learning, addresses the key challenge of sample imbalance while exhibiting robust classification capabilities, particularly for hard-to-classify samples. By integrating these advanced techniques, the model demonstrates exceptional performance, achieving high levels of accuracy without compromising the reliability and credibility of the evaluation results.
In contrast to widely used transient stability assessment methods, this model successfully overcomes several of their inherent limitations. Traditional models often struggle to balance speed, accuracy, and reliability, particularly in cases where the data distribution is uneven or where outliers skew the results. The proposed model not only mitigates these issues but also delivers rapid assessments, making it highly efficient for real-time or near-real-time applications. Its ability to provide convincing and trustworthy evaluations further strengthens its utility in practical scenarios where precise and timely decision-making is crucial, such as in power grid operations and other dynamic systems.
By offering a superior balance of speed, accuracy, and evaluation credibility, this model stands out as a significant advancement in the field of transient stability assessment, offering a practical solution that is both scalable and adaptable to diverse operating conditions.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
AL: Writing–original draft. YM: Writing–review and editing. DM: Writing–review and editing. ZL: Writing–review and editing. WT: Writing–review and editing. FH: Writing–original draft.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study received funding from the Science and Technology Project of China Southern Power Grid Co. Ltd. (ZDKJXM20210063).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors declare that this study received funding from the Science and Technology Project of China Southern Power Grid Co. Ltd. (ZDKJXM20210063). The funder had the following involvement with the study: the study design, the writing of this article.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Chen, Q., Lin, N., and Wang, H. (2021). Transient stability assessment model with parallel structure and data augmentation. Int. Trans. Electr. Energy Syst. 31, 12872. doi:10.1002/2050-7038.12872
Chen, Q., and Wang, H. (2021). Time-adaptive transient stability assessment based on gated recurrent unit. Int. J. Electr. Power and Energy Syst. 133, 107156. doi:10.1016/j.ijepes.2021.107156
Chen, Q., Wang, H., and Lin, N. (2022). Imbalance correction method based on ratio of loss function values for transient stability assessment. CSEE J. Power Energy Syst.
Du, Y., Hu, Z., and Wang, F. (2021). A hierarchical power system transient stability assessment method considering sample imbalance. Energy Rep. 7, 224–232. doi:10.1016/j.egyr.2021.08.052
Fuqiang, L., Shihua, T., Yan, Z., Xiaohui, S., Pengcheng, H., and Zhu, L. (2023). Application of ssa-bp neural network in uav point cloud hole repair. Bull. Surv. Mapp., 130.
Gu, T., Li, B., Xiao, L., Xu, Y., Mao, J., Yuan, M., et al. (2024). “Power system transient stability assessment based on svm-smote and one-dimensional convolutional neural network,” in 2024 IEEE 2nd international conference on power science and Technology (ICPST) (IEEE), 562–568.
Guo, W., Qureshi, N. M. F., Jarwar, M. A., Kim, J., and Shin, D. R. (2023). Ai-oriented smart power system transient stability: the rationality, applications, challenges and future opportunities. Sustain. Energy Technol. Assessments 56, 102990. doi:10.1016/j.seta.2022.102990
Ji, J., Wu, J., Wang, Y., Shi, F., and Li, B. (2022). Power system transient voltage stability assessment based on deep residual network. Power Syst. Technol. 46, 2500–2511.
Jin, W., Zhou, B., Althubiti, S. A., Alsenani, T. R., and Ghoneim, M. E. (2023). Transient stability assessment of power systems using support vector regressor and convolution neural network. Sustain. Comput. Inf. Syst. 37, 100826. doi:10.1016/j.suscom.2022.100826
Kesici, M., Mahdi, M., Yaslan, Y., Seker, S., and Genc, I. (2023). A novel integrated framework for real-time prediction of transient instabilities in power systems with their severity levels using deep learning. Sustain. Energy, Grids Netw. 36, 101221. doi:10.1016/j.segan.2023.101221
Lee, H., Kim, J., Park, J. H., and Chung, S.-H. (2023). Power system transient stability assessment using convolutional neural network and saliency map. Energies 16, 7743. doi:10.3390/en16237743
Li, J., Yang, H., Yan, L., Liu, D., Li, Z., and Xia, Y. (2021). Integrated assessment method for transient stability of power system under sample imbalance. Automation Electr. Power Syst. 45, 34–41.
Li, Y., Cao, J., Xu, Y., Zhu, L., and Dong, Z. Y. (2024). Deep learning based on transformer architecture for power system short-term voltage stability assessment with class imbalance. Renew. Sustain. Energy Rev. 189, 113913. doi:10.1016/j.rser.2023.113913
Lin, J., Cai, R., and Zheng, Z. (2022). A transient stability assessment model based on fault severity assignment. Front. Energy Res. 10, 822729. doi:10.3389/fenrg.2022.822729
Liu, F., Wang, X., Li, T., Huang, M., Hu, T., Wen, Y., et al. (2023). An automated and interpretable machine learning scheme for power system transient stability assessment. Energies 16, 1956. doi:10.3390/en16041956
Meridji, T., Joós, G., and Restrepo, J. (2023). A power system stability assessment framework using machine-learning. Electr. Power Syst. Res. 216, 108981. doi:10.1016/j.epsr.2022.108981
Shao, Z., Wang, Q., Cao, Y., Cai, D., You, Y., and Lu, R. (2024). A novel data-driven lstm-saf model for power systems transient stability assessment. IEEE Trans. Industrial Inf. 20, 9083–9097. doi:10.1109/tii.2024.3379629
Shen, J. (2023). Em-tsa: an ensemble machine learning-based transient stability assessment approach for operation of power systems. Math. Biosci. Eng. 20, 8226–8240. doi:10.3934/mbe.2023358
Singh, M., and Chauhan, S. (2023). A hybrid-extreme learning machine based ensemble method for online dynamic security assessment of power systems. Electr. Power Syst. Res. 214, 108923. doi:10.1016/j.epsr.2022.108923
Wang, H., Hu, L., and Zhang, Y. (2023a). Svm based imbalanced correction method for power systems transient stability evaluation. ISA Trans. 136, 245–253. doi:10.1016/j.isatra.2022.10.039
Wang, H., Wang, Q., and Chen, Q. (2020). Transient stability assessment model with improved cost-sensitive method based on the fault severity. IET Generation, Transm. and Distribution 14, 4605–4611. doi:10.1049/iet-gtd.2020.0967
Wang, Y., Sun, Y., Li, Y., Feng, C., and Chen, P. (2023b). Risk assessment of power imbalance for power systems with wind power integration considering governor ramp rate of conventional units. Electr. Power Syst. Res. 217, 109111. doi:10.1016/j.epsr.2022.109111
Wei Zhang, Q. Z., and Zhang, C. (2024). Spatial-temporal resilience assessment of distribution systems under typhoon coupled with rainstorm events. IEEE Trans. Industrial Inf. doi:10.1109/TII.2024.3450079
Wu, J., Zhang, R., Ji, J., and Li, B. (2020). Two-stage transient stability prediction method of power system considering cost of misdetection and false alarm. Automation Electr. Power Syst. 44, 44–56.
Zhang, L., Hu, X., Li, P., Shi, F., and Yu, Z. (2017). “Elm model for power system transient stability assessment,” in 2017 Chinese automation congress (CAC) (IEEE), 5740–5744.
Zhao, D., Xie, J., Wang, C., Wang, H., Jiang, W., and Wang, Y. (2022). On-line transient stability assessment of a power system based on bagging ensemble learning. Power Syst. Prot. control 50, 1–10.
Keywords: transient stability, cost sensitivity, critical sample, ensemble learning, sample imbalance
Citation: Lei A, Mei Y, Ma D, Liu Z, Tao W and Huang F (2024) Two-stage transient stability assessment using ensemble learning and cost sensitivity. Front. Energy Res. 12:1491846. doi: 10.3389/fenrg.2024.1491846
Received: 05 September 2024; Accepted: 25 September 2024;
Published: 17 October 2024.
Edited by:
Cong Zhang, Hunan University, ChinaReviewed by:
Weike Mo, Jinan University, ChinaCopyright © 2024 Lei, Mei, Ma, Liu, Tao and Huang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fangneng Huang, bGVpYXlAY3NnLmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.