- 1State Grid Wuhan Power Supply Co., Wuhan, Hubei, China
- 2School of Electrical Engineering and Automation, Wuhan University, Wuhan, Hubei, China
To address the challenge of identifying hidden faults in high-voltage power cables, this study proposes a fuzzy comprehensive evaluation method. The method aims to provide a comprehensive and effective means of fault identification for operation and maintenance personnel. The fuzzy comprehensive evaluation method involves several key steps. Firstly, relevant indices are selected from operation monitoring data of high-voltage cables to form a comprehensive evaluation factor set. This set is then matched with an evaluation set established according to corresponding operation guidelines. Secondly, membership functions are established using the triangular distribution function to calculate the cable fault evaluation set. Thirdly, the weights of the evaluation factors are quantified using the analytical hierarchy process. To demonstrate the effectiveness of the proposed method, a fault analysis of a city’s 220 kV double-circuit cable system is conducted. The results show that the fuzzy comprehensive evaluation method can accurately identify faults in the cable system. The proposed fuzzy comprehensive evaluation method provides a valuable reference for operation and maintenance personnel in identifying hidden faults in high-voltage power cables.
1 Introduction
With the continuous development of China’s economy, urbanization is accelerating which leading to an increasing demand for electricity consumption. Consequently, the scale of urban power cables, especially high-voltage power ones, is growing constantly. Because the cable tunnels occupy small area and are less affected by bad weather and other natural conditions, the high-voltage cables are gradually replacing overhead transmission lines and becoming the primary mode of urban power transmission. Ensuring the safe and stable operation of high-voltage cables has always been the most important work of the power grid (Song et al., 2022).
If the high-voltage cables are not replaced in time for long-term operation, it will cause hidden dangers. Some factors, such as insulation, operating temperature, tunnel temperature, and humidity, can impact the safety and stable operation of the power cables in tunnels. Currently, most of the operation and maintenance of cables and tunnels mainly rely on manual work, which has limitations both in terms of maintenance costs and the stable operation of power cables. For the stable and safe operation of cables and tunnels, real-time monitoring and analysis of working conditions must be carried out in order to discover and eliminate hidden dangers in time (Czapp and Dobrzynski, 2020; Huang et al., 2022; Zhang et al., 2022; Zhao et al., 2022; Nougain et al., 2023).
Various faults may occur during the operation of cables, including short-circuit faults, ground faults, disconnection faults, and faults such as cable fires and cable breaks due to cable aging, which may even lead to serious accidents (Akbal, 2020; Zhang et al., 2021; Duda, 2023). To assess the cable condition, Bindi et al. (2023) introduced and analyzed several methods to evaluate the cable insulation condition from both online and offline aspects. Su et al. (2019) and Chen et al. (2021) proposed a distribution network cable fault online monitoring and locating system, which could monitor the insulation status of cables online. Jahromi et al. (2020) and Lee et al. (2021) proposed a frequency domain dielectric spectrum (FDS) test method to evaluate the cable insulation condition. Meng et al. (2022) proposed a new cable assessment method based on the weight space Markov chain and Monte Carlo method (Markov chains Monte Carlo, MCMC), based on the analysis of the limitations of the cable operating condition assessment methods. Huang et al. (2021) proposed a multi-level fuzzy risk assessment method for cable lines based on fuzzy mathematics. Although all the above methods can assess the cable condition to some extent, they relied on a single data source. If multiple factors are considered comprehensively, more accurate results can be obtained.
In this paper, we address the challenges in identifying hidden cable faults by proposing an analytical approach based on various operating conditions of the tunnel high-voltage cables. An evaluation index set and evaluation framework have been built, which uses a fuzzy comprehensive evaluation method to analyze the likelihood of faults occurring during cable operation. By our proposed method, potential faults can be found in time and cable faults can be eliminated at the very early stage.
2 Introduction to the fuzzy comprehensive evaluation method
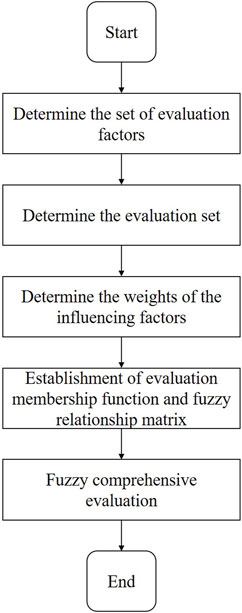
The fuzzy comprehensive evaluation method is a comprehensive bid evaluation approach grounded in the principles of fuzzy mathematics. It transforms qualitative evaluation into quantitative evaluation according to the affiliation theory of fuzzy mathematics. The fuzzy mathematics is used to make a comprehensive evaluation of things or objects constrained by multiple factors, hence it has the characteristics of clear results and strong systematicity, and it can better address fuzzy and hard-to-quantify problems (Huan et al., 2010; Hua et al., 2013), the flow chart is shown as Figure 1. The steps of the fuzzy comprehensive judgment method can be summarized as follows:
Step 1. Determine the set of evaluation factors
The factor set is a collection of factors that affect the object of the judgment as a collection of elements, it is denoted as U, as shown in Equation 1:
where n represents the number of indicator elements. Each element signifies a diverse factor that influences the object’s attributes or performance and reflects its comprehensive state collectively. Evaluation of the object is based on these factors.
Step 2. Determine the evaluation set
The judgment set is a set consisting of the various total possible judgment results on the object of judgment, and the evaluation set is denoted as V, as shown in Equation 2:
where m is the number of evaluation levels.
Step 3. Determine the weights of the influencing factors
Analyzes the indicators accordingly and determines the weights of the indicators, which are composed as follows:
where n is the number of indicator items and the weights satisfy the normalization condition, i.e.,
Step 4. Establishment of evaluation membership function and fuzzy relationship matrix
According to fuzzy set theory, elements no longer simply belong or do not belong to a set. Instead, their relationship is described by the degree of membership which is typically represented by a membership function. When an element belongs to a fuzzy set, the higher the value of the membership function, the greater the degree to which it belongs to the set, with the degree values ranging from 0 to 1. The degree of membership reflects how well an element fits into the set according to human knowledge, which is influenced by subjective experiences. So, it is very crucial to achieve consistency between subjective assessment and objective reality when we are determining the degree of membership. It needs to be adjusted constantly in practice to ensure that the assessment remains consistent with objective conditions.
The commonly used methods for determining the membership degree of an element to a fuzzy set include the boundary method, fuzzy statistical method, and fuzzy distribution method. The fuzzy distribution method relies on employing specific functions that can best represent the fuzzy set in question through reference comparisons. Generally, these functions include trapezoidal, parabolic, and normal distributions are categorized into biased small, biased large, and intermediate types according to their shapes and characteristics. The fuzzy distribution method facilitates a nuanced representation of membership degrees within fuzzy sets based on the chosen distribution function’s appropriateness to the context. Through the membership function, the fuzzy relation matrix R can be determined as Equation 4:
where
Step 5. fuzzy comprehensive evaluation
The comprehensive evaluation set B can be found using the fuzzy relationship matrix R and weights.
where “o” denotes the fuzzy operator to be chosen according to the actual problem. W is the weight vector of the influencing factors defined in Equation 3; R is the membership matrix of the evaluation index;
3 Fuzzy comprehensive evaluation for high voltage cable fault hazards
3.1 Evaluation indicators
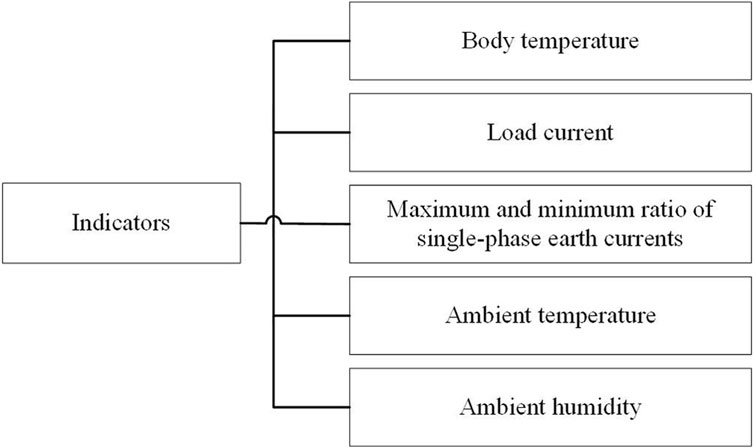
The high-voltage power cable performance indicators serve as quantitative representations of cable performance, guiding monitoring, analysis, and control efforts. In this study, based on field research of a local cable, five indicators including body temperature, load current, maximum-to-minimum ratio of single-phase grounding current, ambient temperature, and ambient humidity, are selected to form the evaluation factor set U. The cable body temperature refers to the temperature of the cable core, while the ambient temperature and humidity refer to those within the cable tunnel. These indicators are crucial for assessing and ensuring the operational efficiency and safety of high-voltage power cables. The content shown in Figure 2 analyses and evaluates the status of the cable (Tan et al., 2017; Hu et al., 2017; Shao and Bowler, 2019; Ding et al., 2022; Lee et al., 2023).
3.2 Establish fuzzy evaluation sets
The condition of the cable should be classified according to the condition of the high-voltage cable condition testing technology specification to achieve its specific performance. Accordingly, this paper classifies three conditions of the cable: normal, attention, and defective. The normal condition refers to when the cable tunnel operates normally. The attention condition indicates that it requires strengthened monitoring. The defective condition signifies that a defect is likely to occur with high probability, and thus requires close monitoring. Therefore, the evaluation set is composed, as shown in Equation 6:
3.3 Determination of evaluation factor weights
According to fuzzy judgment, the weight distribution of each factor significantly influences the judgment result; Therefore, determining a reasonable weight set becomes one of the key points and difficulties in fuzzy judgment.
We conduct empirical studies by utilizing expert opinions to assess the importance of each factor within its corresponding set, the importance values are rated on a scale from 1 to 9, and form a judgment matrix. Hierarchical analysis is then employed for pairwise comparisons of factors with different levels, ensuring test consistency. The weighting of factors in the preceding layer is reflected by the largest eigenvalue associated with the corresponding eigenvectors, following the methodologies discussed by Azadeh and Abdolhossein Zadeh (2016), Fang et al. (2018), and Sokolović et al. (2021).
3.3.1 Form a pairwise comparison matrix
According to experts’ judgment, we assign importance scores to each indicator within the respective criteria by adopting a 1–9 proportional scale to quantify their relative significance. It will yield a square matrix characterized by unity values along its diagonal, and reciprocals of each other for elements that are symmetric about this diagonal. This matrix is represented as Equation 7:
where n denotes the total number of indicators, aij ranges between 1 and 9, and indices i and j iterate from 1 to n.
To quantify the relationship accurately between the ith and jth evaluation indicators within a set of n indicators, we employ matrix A to construct a corresponding pairwise comparison matrix B, both matrices being of dimension n-by-n. The formula for determining the element bij in matrix B is provided as Equation 8:
where
3.3.2 Calculate the weights of the indicators
We employ the eigenvalue method as the primary approach to compute the weight vector of influencing factors. The specific steps are outlined as Equations 9–13:
1) Calculate the nth root of the product of all elements within the ith row
where Mi represents the nth root of the product of all elements in the ith row.
2) Calculate the weights
where Wi denotes the value of the ith element in the weight vector.
3) Calculate the largest eigenvalue of the pairwise comparison matrix
where λmax is the largest eigenvalue of matrix B.
4) Perform a consistency check on the results:
Firstly, the consistency index (CI) is computed, and the appropriate random index (RI) value is selected followingly, which is contingent upon the order of the pairwise comparison matrix B. Here Table 1 is as a reference. Finally, the consistency ratio (CR) is obtained by Equation 13. If the CR falls below 0.1, the pairwise comparison matrix is considered to have passed the consistency test. Conversely, the judgment matrix must be revised and the entire process reiterated until the consistency test is successfully passed.
3.4 Degree of deterioration of evaluation indicators
The performance state of a high-voltage cable can be represented by a set of state characteristic parameters such as
The condition parameters used to assess the state of the cable include various indicators. The cable operating parameters are shown in Figure 2, where the first four indicators typically indicate positive degradation—increasing values correlate with degradation. Conversely, ambient humidity is a negative degradation indicator, lower values contribute more to faults.
where
Considering the significant impact of air humidity on fire occurrence and the technical regulations for cable detection, the degradation of indicators such as conductor temperature, load current, ratios of maximum value and minimum value of single-phase ground current, ambient temperature, and humidity are calculated using Equations 15–19: they are borrowed from Equation 14. Some parameters in the following formulas can be obtained by querying relevant standards.
where
where
where
where,
The occurrence of fire is closely related to air humidity. Fire is less likely to occur when air humidity is more than 60%. In the range of 50%–60% humidity, fire can burn slowly but does not spread easily. With 40%–50% humidity, combustion can produce smoke but does not spread extensively. When humidity drops to 30%–40%, fire ignites more readily and can spread further. Humidity below 25% will significantly increase the risk of fire. The degree of air humidity contribution to cable failure can be expressed as:
where
3.5 Establishment of a fuzzy relationship matrix
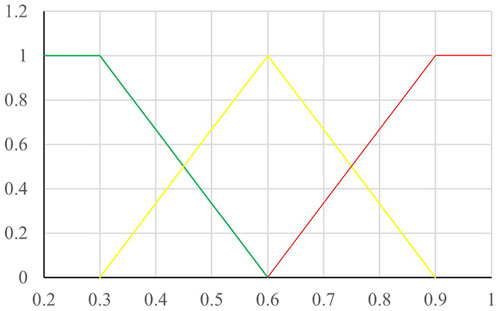
The fuzzy evaluation matrix represents the relationship between the factor set and the evaluation set. It utilizes cable indicators to gauge the degree of deterioration, which determines the degree of different states within the state space. The triangular distribution function categorizes objective entities into large, medium, and small groups. Evaluating sets across normal, attention-worthy, and defective classifications aligns perfectly with the triangular distribution function’s description, depicted in Figure 3. Therefore, we employ the indicator’s deterioration degree combined with the triangular distribution function to determine the membership function’s degree.
Based on the parameter ranges of each evaluation index of the cable, the degree of deterioration for each system factor can be calculated by Equations 20–22. By calculation, we can obtain these degrees of membership relative to the evaluation set, thereby we can construct R.
3.6 Fuzzy comprehensive evaluation
In fuzzy comprehensive evaluation, the “o” operator is applied in various ways, with the principle of maximum affiliation being the most commonly used method in practice. However, in certain cases, using only this method can lead to significant information loss and even produce unreasonable evaluation outcomes. In this paper, we propose a method that considers the weights of each evaluation factor of the cable system. It utilizes the fuzzy relationship matrix, which is formed based on the degree of affiliation of each factor. The approach involves using a weighted average as the fuzzy comprehensive evaluation operator which is expressed as follows:
The model takes into account the effects of all factors and retains all the information from the single-factor assessment, which makes it well-suited to engineering assessment.
3.7 Example analyses of a fuzzy comprehensive evaluation
This paper analyses a 220 kV double-circuit cable system in a city as an example. The cable length is 9.422 km, and the type of cable is YJLW03-220-1*1000. Both cable and its accessories were produced by one company. The double-circuit line was put into operation on 30 June 2008, it was equipped with 16 sets of intermediate connectors, one set of GIS terminals for the cable, and one set of outdoor terminals. Before the cable failure occurred in Joint No. 3, the cable was working normally. On 19 December 2019, the cable operation and inspection department conducted routine tests on this joint, including temperature measurement, circulating current measurement, partial discharge detection, etc. All the test results were normal. Table 2 shows the operating and environmental parameter measurements of Joint No. 3.
The analytical hierarchy process method was used to calculate the weight of each factor. Using the fuzzy comprehensive evaluation method, the corresponding deterioration degree was calculated based on the measured value, and the parameters and calculation results are shown in Table 3.
A comprehensive evaluation is conducted based on Equations 5, 23, the results of the comprehensive evaluation of the three phases A, B, and C were calculated as Equations 24–26:
According to the principle of maximum affiliation, the A and B phases should be categorized under the state of attention, while the C phase is in the state of defective. Theoretically, if our proposed method was applied it can suggest that monitoring efforts should be intensified for the A and B phases, whereas the C phase should be further inspection and investigation into the cause of its state. However, the test data on 19 December 2019 indicated that the cable was in normal condition; therefore, no further inspection has been done in accordance with the technical specifications. At 23:46 on 11 July 2020, a fault occurred in Joint No. 3 of the C phase of the 220 kV double-circuit cables, which led to severe rupture and burning of the joint, as shown in Figure 4.
The cable fault assessment method proposed in this paper demonstrates its ability to provide a very early warning, which is almost 6 months before the fault occurs. The assessment results can serve as valuable references for inspection and maintenance personnel.
4 Conclusion
Many current high-voltage cable fault assessment methods only consider a single factor. We proposed to use the analytic hierarchy process and fuzzy comprehensive evaluation method for evaluating potential faults in high-voltage power cables, with many specific factors taken into account. It constructs evaluation indices and degradation functions for cable fault diagnosis based on cable operational parameters. It uses the triangular distribution function to construct membership functions for calculating the cable fault evaluation set. The fuzzy comprehensive evaluation method is applied to identify potential cable faults. The example in the article demonstrates that the suggestions proposed by our method can serve as a valuable reference for inspection and maintenance. However, relying solely on one set of instances to validate the proposed method is insufficient, and subsequent verification using multiple sets of data is required. The proposed method integrates qualitative and quantitative approaches and can provide a very early warning before a fault occurs.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
HF: Conceptualization, Validation, Writing–original draft, Writing–review and editing. YuA: Conceptualization, Writing–review and editing. LQ: Methodology, Writing–review and editing. YoA: Validation, Writing–review and editing. BY: Investigation, Methodology, Supervision, Writing–review and editing. YS: Conceptualization, Funding acquisition, Investigation, Project administration, Supervision, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research presented in this paper was done with the financial support of the State Grid Hubei Electric Power Co Ltd Scienceand Technology (Project No. 5215A0230007).
Conflict of interest
Authors HF, LQ, YoA, BY, and YS were employed by State Grid Wuhan Power Supply Co.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors declare that this study received funding from the State Grid Hubei Electric Power Co Ltd. The funder had the following involvement in the study: the study design, collection, analysis, interpretation of data, the writing of this article, and the decision to submit it for publication.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akbal, B. (2020). High voltage underground cable bonding optimisation to prevent cable termination faults in mixed high-voltage lines. IET Gener. Transm. Amp Distrib. 14, 4331–4338. doi:10.1049/iet-gtd.2019.1559
Azadeh, A., and Abdolhossein Zadeh, S. (2016). An integrated fuzzy analytic hierarchy process and fuzzy multiple-criteria decision-making simulation approach for maintenance policy selection. Simulation 92, 3–18. doi:10.1177/0037549715616686
Bindi, M., Luchetta, A., Lozito, G. M., Carobbi, C. F. M., Grasso, F., and Piccirilli, M. C. (2023). Frequency characterization of medium voltage cables for fault prevention through multi-valued neural networks and power line communication technologies. IEEE Trans. Power Deliv. 38, 3227–3237. doi:10.1109/TPWRD.2023.3270128
Chen, J., Che, R., Zhang, M., Li, S., Che, B., Wang, N., et al. (2021). Exogenous spermine attenuates diabetic kidney injury in rats by inhibiting AMPK/mTOR signaling pathway. 3rd Asia Energy Electr. Eng. Symposium (AEEES) 47, 27–31. doi:10.3892/ijmm.2021.4860
Czapp, S., and Dobrzynski, K. (2020). Safety issues referred to induced sheath voltages in high-voltage power cables—case study. Appl. Sci. 10, 6706. doi:10.3390/app10196706
Ding, M., He, W., Wang, J., and Wang, J. (2022). Performance evaluation of cross-linked polyethylene insulation of operating 110 kV power cables. Polymers 14, 2282. doi:10.3390/polym14112282
Duda, D. (2023). Distance protection operation during earth-faults in high voltage networks with cable inserts. Electrotech. Rev. 1, 99–103. doi:10.15199/48.2023.06.19
Fang, Y., Sun, T., He, W., Wang, S., Wang, H., and Liu, B. (2018). Condition assessment of power cable based on fuzzy analytic hierarchy process and set pair analysis approach. 2nd IEEE Conf. Energy Internet Energy Syst. Integration EI2, 1–4. doi:10.1109/EI2.2018.8582487
Hu, R., Jing, Z. X., Wu, Q. H., Yan, R. B., and Cao, Z. C. (2017). Life cycle assessment of environmental impacts and total cost of power cable. Appl. Mech. Mater. 872, 412–419. doi:10.4028/www.scientific.net/AMM.872.412
Hua, Y. T., Hua, Z. Q., and Yang, W. (2013). Fuzzy comprehensive assessment of urban underground power cable infrastructure safety risk. Adv. Mater. Res. 860–863, 2544–2548. doi:10.4028/www.scientific.net/amr.860-863.2544
Huan, J., Wang, G., Li, H., and Sun, Z. (2010). Risk assessment of XLPE power cables based on fuzzy comprehensive evaluation method. Chengdu, China: IEEE Publications. doi:10.1109/APPEEC.2010.5448712
Huang, X., Wu, M., Zhu, Y., Wang, N., Liu, C., and Ma, Y. (2021). Research on risk assessment model of cable line based on fuzzy mathematics. High. Volt. Appar. 57, 19–25. doi:10.13296/j.1001-1609.hva.2021.09.003
Huang, Z., Lu, F., Tong, Y., and Shi, T. (2022). Technology for the detection of ablation defects in buffer layers of high-voltage cables. IEEE Access 10, 92843–92853. doi:10.1109/ACCESS.2022.3203054
Jahromi, A. N., Pattabi, P., Densley, J., and Lamarre, L. (2020). Medium voltage XLPE cable condition assessment using frequency domain spectroscopy. IEEE Electr. Insul. Mag. 36, 9–18. doi:10.1109/MEI.2020.9165695
Lee, H. M., Lee, G. S., Kwon, G.-Y., Bang, S. S., and Shin, Y.-J. (2021). Industrial applications of cable diagnostics and monitoring cables via time-frequency domain reflectometry. IEEE Sens. J. 21, 1082–1091. doi:10.1109/JSEN.2020.2997696
Lee, S.-W., Choe, J.-W., Kwon, I.-S., Park, B.-B., and Kim, H.-J. (2023). Precision and performance evaluation of accelerated aging system for DC TP power cables. IEEE Access 11, 43424–43434. doi:10.1109/ACCESS.2023.3269799
Meng, X.-K., Jia, Y.-B., Liu, Z.-H., Yu, Z.-Q., Han, P.-J., Lu, Z.-M., et al. (2022). High-voltage cable condition assessment method based on multi-source data analysis. Energies 15, 1369. doi:10.3390/en15041369
Nougain, V., Mishra, S., Nag, S. S., and Lekić, A. (2023). Fault location algorithm for multi-terminal radial medium voltage DC microgrid. IEEE Trans. Power Deliv. 38, 4476–4488. doi:10.1109/TPWRD.2023.3318689
Seguchi, T., Tamura, K., Kudoh, H., Shimada, A., and Sugimoto, M. (2015). Degradation of cable insulation material by accelerated thermal radiation combined ageing. IEEE Trans. Dielect. Electr. Insul. Trans. Ieee. 22, 3197–3206. doi:10.1109/TDEI.2015.004880
Shao, Z. H., and Bowler, N. (2019). “Capacitive nondestructive evaluation of aged cross-linked polyethylene (XLPE) cable insulation material,” in Proceedings of the 18th international conference on environmental degradation of materials in nuclear power systems – water reactors. Editors J. H. Jackson, D. Paraventi, and M. Wright (Cham: Springer International Publishing), 1303–1313. doi:10.1007/978-3-030-04639-2_84
Sokolović, J., Stanujkić, D., and Štirbanović, Z. (2021). Selection of process for aluminium separation from waste cables by TOPSIS and WASPAS methods. Min. Eng. 173, 107186. doi:10.1016/J.MINENG.2021.107186
Song, Y., Chen, W., Wan, F., Zhang, Z., Du, L., Wang, P., et al. (2022). Online multi-parameter sensing and condition assessment technology for power cables: a review. Electr. Power Syst. Res. 210, 108140. doi:10.1016/j.epsr.2022.108140
Su, Y., Liu, Y., and Zhong, L. (2019). Evaluation of voltage endurance characteristics for new and aged XLPE cable insulation by electrical treeing test. IEEE Trans. Dielect. Electr. Insul. Trans. IEEE 26, 72–80. doi:10.1109/TDEI.2018.007442
Tan, Z. J., Chen, G. Y., Luan, L., Yu, Z. Y., Zhang, R., and Tang, W. H. (2017). A novel life evaluation algorithm of XLPE power cables based on biclustering. 2017 IEEE Electrical Power and Energy Conference (EPEC), 1–5. doi:10.1109/EPEC.2017.8286144
Zhang, M., Zhao, K., Yan, Y., Lu, Y., Yang, S., Wang, L., et al. (2021). A double-terminal traveling-wave-based method using novel noncontact sensors for fault location in transmission cable lines. IEEE Access 9, 80797–80805. doi:10.1109/ACCESS.2021.3085298
Zhang, Y., Yu, F., Ma, Z., Li, J., Qian, J., Liang, X., et al. (2022). Conductor temperature monitoring of high-voltage cables based on electromagnetic-thermal coupling temperature analysis. Energies 15, 525. doi:10.3390/en15020525
Keywords: high-voltage power cable, fuzzy comprehensive evaluation, fault identification, analytical hierarchy process, state evaluation
Citation: Fu H, Ai Y, Qiu L, Ai Y, Yang B and Shi Y (2024) Application of fuzzy comprehensive evaluation method in the identification of potential faults of high-voltage power cables. Front. Energy Res. 12:1490524. doi: 10.3389/fenrg.2024.1490524
Received: 03 September 2024; Accepted: 11 November 2024;
Published: 21 November 2024.
Edited by:
Feng Liu, Nanjing Tech University, ChinaReviewed by:
Vassiliki T. Kontargyri, University of West Attica, GreeceElena Helerea, Transilvania University of Brașov, Romania
Copyright © 2024 Fu, Ai, Qiu, Ai, Yang and Shi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuhao Ai, MjAyMzI4MjA3MDE1MEB3aHUuZWR1LmNu
 Han Fu1
Han Fu1 Yuhao Ai
Yuhao Ai