Dynamic adaptation in power transmission: integrating robust optimization with online learning for renewable uncertainties

Introduction: The increasing integration of renewable energy sources, such as wind and solar, into power grids introduces significant challenges due to their inherent variability and unpredictability. Traditional fossil-fuel-based power systems are ill-equipped to maintain stability and cost-effectiveness in this evolving energy landscape.

Methods: This study presents a novel framework that integrates robust optimization with online learning to dynamically manage uncertainties in renewable energy generation. Robust optimization ensures system resilience under worst-case scenarios, while the online learning component continuously updates operational strategies based on real-time data. The framework was tested using an IEEE 30-bus test system under varying levels of renewable energy integration.

Results: Simulation results show that the proposed framework reduces operational costs by up to 12% and enhances system reliability by 1.4% as renewable energy integration increases from 10% to 50%. Additionally, the need for reserve power is significantly reduced, particularly under conditions of high variability in renewable energy outputs.

Discussion: The integration of robust optimization with online learning provides a dynamic and adaptive solution for the sustainable management of power transmission systems. This approach not only improves economic and environmental outcomes but also enhances grid stability, making it a promising strategy for addressing the challenges posed by the increasing reliance on renewable energy.

1 Introduction

The integration of renewable energy sources into the power grid is a pivotal strategy in the global effort to reduce carbon emissions and combat climate change (Xiang et al., 2024; Jiang et al., 2024). As nations increasingly pivot towards sustainable energy solutions, the complexity and unpredictability of renewable energy sources, such as wind and solar, present unique challenges to the stability and efficiency of power transmission systems (Solat et al., 2024). The inherent variability of these energy sources necessitates innovative approaches to ensure that power systems are not only capable of handling immediate fluctuations but are also robust and adaptable in the face of long-term environmental and operational uncertainties (Bonfiglio et al., 2024; Ding et al., 2024). Traditionally, power systems have been designed and operated to handle predictable and steady power sources, primarily fossil fuels. However, the shift towards renewables, driven by environmental concerns and technological advancements, has disrupted this stability (Li Z. et al., 2024). Renewable energy sources are inherently intermittent and unpredictable, leading to significant challenges in power generation, transmission, and distribution. The stochastic nature of wind and solar energy outputs means that power systems must now manage significant fluctuations in power availability, which can compromise both the supply reliability and the economic efficiency of the grid (Li S. et al., 2024; Li et al., 2022).

The integration of such volatile energy sources has prompted a reevaluation of traditional power system management strategies. Current systems must evolve to not only manage these fluctuations but also anticipate and adapt to them effectively. This has spurred significant interest in developing advanced mathematical models and optimization techniques that can enhance the operational resilience of power systems against the backdrop of increasing renewable integration (Ruan et al., 2024).

The primary objective of this research is to develop a robust framework that not only accommodates the variability and uncertainty of renewable energy outputs but also optimizes the operation and cost-efficiency of power transmission systems. By leveraging cutting-edge robust optimization techniques coupled with online learning algorithms, this work aims to create a dynamic and adaptive management strategy that ensures system reliability and efficiency in real time. The contributions of this paper can be summarized as follows:

1. This paper introduces a novel framework that integrates robust optimization with online learning to manage the operational challenges posed by renewable energy integration into power transmission systems. The approach is designed to dynamically adapt to real-time data, continuously updating system operations to mitigate the impact of renewable output variability.

2. The robust optimization component of the framework focuses on formulating an objective function that encapsulates various operational costs, including those associated with the generation, load shedding, and the deployment of operational reserves. It systematically incorporates different facets of uncertainty, including those arising from renewable energy outputs, into the decision-making process. This is achieved by defining and adjusting the objective function and constraints within uncertainty sets specifically tailored to capture the worst-case scenarios of renewable variability.

3. Parallelly, the online learning model employed in this research utilizes real-time generation and load data to continuously refine the model parameters. This adaptation enhances the decision-making process, ensuring that operational strategies are not only based on historical data but are also responsive to current system states and dynamics. This dual approach—combining the predictive power of robust optimization with the adaptability of online learning—marks a significant advancement in the field of power system management.

This paper introduces an innovative framework that combines robust optimization with online learning to address the challenges of managing power transmission systems under the increasing integration of renewable energy sources. Specifically, it aims to optimize the operation and cost-efficiency of power grids by dynamically adapting to the uncertainties and variabilities inherent in renewable energy outputs, such as wind and solar power. The proposed approach not only enhances the resilience of power systems to fluctuating renewable generation but also leverages real-time data to continuously refine operational strategies, ensuring that grid stability and efficiency are maintained even under adverse conditions. Through this dual methodology, the research provides a significant advancement in the field of energy management, offering a robust solution for the reliable integration of renewables into modern power systems.

The remainder of this paper is organized as follows: Section 2 examines existing methods in robust optimization and online learning, identifying gaps addressed by this study. Section 3 defines the mathematical model and introduces the IEEE 30-bus test system used in the case study. Section 4 discusses the stochastic modeling of wind and solar power. It also details the model’s approach to handling uncertainties, while Online Learning Adaptation explains the algorithm that continuously updates the model with real-time data. Section 5 presents the simulation outcomes, comparing the proposed framework with traditional methods. Finally, the Conclusion summarizes the paper’s contributions and suggests areas for future research.

2 Literature review

The integration of renewable energy sources into existing power systems poses significant challenges due to their inherent variability and unpredictability. These challenges necessitate advancements in system optimization and management techniques to ensure grid stability, efficiency, and reliability (Zhao et al., 2020; Cheraghi and Jahangir, 2023). This literature review explores current methodologies and emerging trends in robust optimization, the use of online learning in power systems, and the integration of these approaches to address the complexities introduced by renewable energy sources.

Robust optimization has gained considerable attention as a critical tool for handling uncertainties in power system operations, particularly with the increasing penetration of renewable energy sources like wind and solar power. Early foundational works, such as those by Ben-Tal and Nemirovski (2001), provided the theoretical underpinnings for robust optimization, focusing on constructing models that can perform well under a range of uncertain conditions. Subsequent studies have applied these principles specifically to power systems. For instance, Bertsimas and Sim (2004) developed a framework for addressing uncertainties in power generation and demand, offering solutions that remain feasible across different scenarios of renewable availability and load demands.

More recent research has delved into specific applications of robust optimization in energy systems. For example, Jia et al. (2022) introduces a novel decentralized two-stage robust dispatch framework designed for multi-area integrated electric-gas systems. This comprehensive approach employs a quadruple-loop procedure with advanced algorithms to derive a tractable series of mixed-integer second-order cone programs, supplemented by three acceleration methods to enhance computational efficiency and is validated through simulation results. In Paper (Lee et al., 2024), a robust optimization method is presented for the strategic placement and sizing of voltage balancers in bipolar DC distribution systems, aiming to address voltage imbalances caused by asymmetric structures. Utilizing mixed-integer linear programming and a tri-level optimization problem setup, the study effectively integrates uncertainty considerations to minimize installation costs, as demonstrated in a detailed case study. Qiu et al. (2024) discusses a two-stage robust optimization strategy for evaluating the PV hosting capacity of power grids, considering decision-dependent uncertainties due to the variable nature of PV generation. This approach, tested on both microgrid systems and distribution networks, aims to maximize PV integration while ensuring grid stability and is supported by numerical experiment results.

The advent of smart grid technologies has facilitated the real-time collection and processing of vast amounts of operational data (Lu et al., 2023). This development has ushered in the application of online learning techniques, which are increasingly recognized for their potential to enhance the adaptability and responsiveness of energy management systems. In Bahrami et al. (2018), a Markov decision process is utilized to model long-term load scheduling issues in smart grids under real-time pricing, presenting an online learning algorithm based on the actor-critic method. The proposed Load Scheduling Learning algorithm significantly reduces user costs and peak-to-average load ratios, demonstrating its effectiveness over both non-responsive benchmarks and short-term scheduling approaches through rigorous simulations. The study presented in Irfan et al. (2021) develops and implements a backpropagation online learning-based algorithm to improve power quality in grid-interactive solar PV systems. This approach minimizes the complexities and mathematical demands of traditional control methods, with the effectiveness of the model validated through MATLAB simulations and experimental setups using FPGA controllers. Chen et al. (2019) introduces a privacy-preserving online learning approach for managing incentive-based demand response programs in smart grids, focusing on maximizing social welfare while ensuring customer privacy through differential privacy techniques. The adaptive context partition method and tree-based noise aggregation strategy employed in the study demonstrate a promising balance between maintaining data utility and protecting customer privacy, supported by theoretical and numerical validations of the algorithm’s effectiveness and privacy guarantees.

The proposed integrated approach is seen as particularly effective in managing the complexities introduced by renewable energy sources. By combining the predictive power of robust optimization with the real-time adaptability of online learning, power systems can not only plan for but also react to sudden changes in energy production and demand. This synergy is crucial for developing operational strategies that maintain grid stability and efficiency in an era dominated by renewable energy integration.

3 Problem formulation and system model

In the realm of power system operations, the primary goal is often to ensure an optimal balance between cost efficiency and system reliability. The objective function serves as a mathematical representation of these operational goals, encapsulating various cost factors and system requirements into a single formula. This function is crucial for guiding the operational strategy in real-time and during planning stages to minimize the total operational cost while maintaining system integrity and meeting demand. Here, we define the objective function that encapsulates the various costs associated with power system operations. Let’s consider the following components in Equation 1:

$minZ\left(\theta \right)={\displaystyle \sum _{i\in \mathcal{G}}}{C}_i\left(P_i\right)+{\displaystyle \sum _{j\in \mathcal{D}}}{L}_j\left({\Delta }_j\right)+{\displaystyle \sum _{k\in \mathcal{R}}}{R}_k\left({\varphi }_k\right)(1)$

Where Z(θ) is the total operational cost function to be minimized; $\mathcal{G}$ is the set of all generators in the system; $P_i$ is the power output from generator i; $C_i$ is the cost function associated with generator i, typically a quadratic function reflecting fuel costs and efficiency characteristics; $\mathcal{D}$ is the set of demand points or load centers; ${\Delta }_j$ is the load shedding at demand point j; $L_j$ is the penalty cost function for load shedding at point j, reflecting the economic impact of unserved energy; $\mathcal{R}$ is the set of resources providing operational reserves; ${\varphi }_k$ is the operational reserve provided by resource k; $R_k$ is the cost function associated with deploying operational reserves from resource k, accounting for the readiness and utilization of reserve capacity. This formulation captures the essential trade-offs in power system operation between generating costs, the economic penalties of load shedding, and the necessary expenditures on operational reserves to ensure reliability and compliance with regulatory standards.

The effective operation of a power system hinges on adhering to a suite of fundamental constraints that ensure safety, reliability, and regulatory compliance. These constraints are mathematically formulated to reflect the physical and operational limitations of the system’s components.

${\displaystyle \sum _{i\in \mathcal{G}}}{P}_i-{\displaystyle \sum _{j\in \mathcal{D}}}{D}_j-{\displaystyle \sum _{k\in \mathcal{L}}}{\lambda }_k=0(2)$

This Equation 2 ensures that the total power generated $P_i$ by generators, $\mathcal{G}$ equals the total demand $D_j$, plus the system losses ${\lambda }_k$ over all transmission lines. It guarantees that energy is neither created nor destroyed within the system.

$P_i^{\mathit{min}}\le P_i\le P_i^{\mathit{max}},\forall i\in \mathcal{G}(3)$

Equation 3 ensures that the power output of each generator iii stays within its minimum and maximum capacity limits, maintaining the mechanical and safety standards of the equipment.

$V_j^{\mathit{min}}\le V_j\le V_j^{\mathit{max}},\forall j\in \mathcal{B}(4)$

Each bus j in the set of buses $\mathcal{B}$ must maintain its voltage $V_j$ within predefined minimum and maximum limits to ensure stable and safe operation of the network, shown in Equation 4.

$\left|I_k\right|\le I_k^{\mathit{max}},\forall k\in \mathcal{L}(5)$

The current $I_k$ flowing through each transmission line k must not exceed the maximum allowable current, which is dictated by the thermal capacity of the line to prevent overheating and potential damage, given in Equation 5.

The stochastic nature of renewable energy sources, specifically wind and solar power, necessitates advanced mathematical modeling to predict and optimize their integration into the power grid. These models account for the variability and unpredictability of natural resources, ensuring that the power system can effectively harness these renewable energies while maintaining stability and efficiency.

$P_{\text{wind},i}={\rho }_i\left(\frac{1}{2}\cdot A_i\cdot C_{p,i}\left({\lambda }_i,{\beta }_i\right)\cdot v_i^3\right)(6)$

In Equation 6, $P_{\text{wind},i}$ represents the power output from the i-th wind turbine, where ${\rho }_i$ is the air density at the turbine location, $A_i$ is the rotor-swept area, $C_{p,i}$ is the power coefficient dependent on the tip-speed ratio ${\lambda }_i$ and pitch angle ${\beta }_i$, and wind speed. This model captures the essential physics of wind energy conversion and adjusts for turbine-specific characteristics.

$P_{\text{solar},j}={\eta }_j\cdot A_j\cdot G_j\cdot \cos \left({\theta }_j\right)(7)$

The power output $P_{\text{solar},j}$ from the j-th solar panel is determined by its efficiency ${\eta }_j$, surface area $A_j$, solar irradiance $G_j$, and the angle of incidence ${\theta }_j$ of the sunlight relative to the panel. This Equation 7 reflects how solar panels convert irradiance into electricity, considering geometrical and environmental factors.

4 Robust optimization and online learning adaptation

The adaptive capabilities of the online learning component in our integrated framework are critical for managing the challenges posed by significant deviations in renewable energy outputs, particularly during extreme weather events. This component is engineered to continuously analyze real-time data, enabling it to identify and react to anomalies and sudden changes in energy production. When extreme deviations occur, such as those caused by unexpected meteorological conditions, the system implements immediate adaptive strategies. These include recalibrating the forecast models in real time and adjusting operational parameters to maintain grid stability and efficiency. Additionally, the online learning algorithm systematically incorporates lessons learned from these events into its decision-making process, enhancing its future responses. By dynamically updating its predictive models and operational strategies, the framework not only maintains robust performance during adverse conditions but also progressively improves its predictive accuracy and operational resilience. This capability to learn from and adapt to rapidly changing conditions is pivotal for integrating high levels of variable renewable energy sources into power grids, ensuring that the system remains reliable and efficient under a wide range of operating scenarios.

The robust optimization framework is designed to enhance the resilience of the power system against uncertainties in renewable energy outputs. This approach adjusts the objective function to account for worst-case scenarios, ensuring that system operations remain efficient and reliable even under adverse conditions.

$minZ\left(\theta \right)={\displaystyle \sum _{i\in \mathcal{G}}}{C}_i\left({\mu }_i\right)+{\displaystyle \sum _{j\in \mathcal{D}}}{L}_j\left({\Delta }_j\right)+{\displaystyle \sum _{k\in \mathcal{R}}}{S}_k\left({\sigma }_k\right)+\mathrm{\Psi }(8)$

This Equation 8 formulates the robust objective function where $Z\left(\theta \right)$ incorporates the expected generation costs $C_i\left({\mu }_i\right)$ for generators i, penalties $L_j\left({\Delta }_j\right)$ for load shedding at demand points j, and costs $S_k\left({\sigma }_k\right)$ associated with operating spinning reserves k. The term $\mathrm{\Psi }$ represents an additional cost that accounts for non-compliance with renewable integration targets, reinforcing the system’s adherence to sustainability goals.

$\mathrm{\Phi }=\gamma {\displaystyle \sum _{i\in \mathcal{G}}}\text{\hspace{0.05em}Var\hspace{0.17em}}\left(C_i\right)(9)$

Here, $\mathrm{\Phi }$ adds a risk-averse term to the objective function, where $\mathrm{\gamma }$ is a coefficient reflecting the system’s aversion to risk, and $\text{Var\hspace{0.17em}}\left(C_i\right)$ represents the variance in generation costs due to fluctuations in renewable outputs. This Equation 9 penalizes scenarios where the cost variability is high, thereby incentivizing strategies that enhance cost predictability and stability.

$\mathrm{\Omega }=\xi {\displaystyle \sum _{k\in \mathcal{R}}}\mathit{max}\left(0,{\sigma }_k-{\sigma }_{k,\text{base}}\right)(10)$

In Equation 10, $\mathrm{\Omega }$ quantifies the cost of maintaining additional spinning reserves where $\xi$ is a scaling factor and ${\sigma }_k$ is the actual reserve capacity required to manage sudden drops in renewable generation. ${\sigma }_{k,\text{base}}$ represents the baseline reserve capacity, and this equation ensures that any additional reserves incurred due to renewable variability are accounted for in the overall cost function.

$\mathrm{\Lambda }=\omega {\displaystyle \sum _{j\in \mathcal{D}}}{\left({\rho }_j{\Delta }_j\right)}^2(11)$

Here in Equation 11, $\mathrm{\Lambda }$ represents the adjusted penalty for load shedding where $\mathrm{\omega }$ is a coefficient that increases the cost penalty exponentially in scenarios where renewable outputs fall significantly below predictions. ${\rho }_j$ is a scaling factor representing the sensitivity of load shedding costs at demand point j, and ${\Delta }_j$ is the amount of load shed. This formulation emphasizes penalizing load shedding more severely when it is due to renewable shortfalls, thus incentivizing better risk management and planning.

$\mathrm{\Pi }=\eta {\displaystyle \sum _{k\in {\mathcal{R}}_{nr}}}{\mu }_k{P}_{k,\text{nr}}(12)$

In this Equation 12, $\mathrm{\Pi }$ adds a penalty for using non-renewable backup resources, where $\eta$ is the penalty coefficient, ${\mathcal{R}}_{nr}$ represents the set of non-renewable reserve resources, ${\mu }_k$ is the environmental or economic impact factor of using resource k, and $P_{k,\text{nr}}$ is the power sourced from non-renewable backups. This component of the model imposes a higher cost for reliance on non-renewable backups when renewable forecasts fail, thus encouraging more sustainable operations.

$\mathrm{\Theta }=\sigma {\displaystyle \sum _{i\in \mathcal{G}}}{\beta }_i{\left({\nu }_i-{\widehat{\nu }}_i\right)}^2(13)$

$\mathrm{\Theta }$ dynamically in Equation 13 adjusts the cost of dispatching power from both renewable and conventional sources. $\mathrm{\sigma }$ is a tuning parameter that modulates the responsiveness of the system to deviations from planned generation, ${\beta }_i$ represents the cost efficiency of adjustments for generator i, ${\nu }_i$ is the actual generation, and ${\widehat{\nu }}_i$ is the forecasted generation. This term aims to minimize the cost differences caused by deviations from forecasted generation levels, enhancing the economic efficiency of real-time operations.

$\mathrm{\Xi }=\kappa {\displaystyle \sum _{m\in \mathcal{C}}}{ϵ}_m^2(14)$

In Equation 14, $\mathrm{\Xi }$ represents the cost associated with using slack variables ${ϵ}_m$ in the system constraints to manage uncertainties without violating operational limits, where $\kappa$ is a penalty factor for each slack variable used, and $\mathcal{C}$ denotes the set of constraints that might be affected by uncertainty. This equation helps maintain system stability and compliance even under unpredictable conditions by allowing slight deviations from hard constraints.

$\mathrm{\Gamma }={\displaystyle \sum _{u\in \mathcal{U}}}{\alpha }_u{\chi }_u(15)$

In this Equation 15, $\mathrm{\Gamma }$ represents the aggregated impact of different sources of uncertainty on the system’s operational costs, where ${\alpha }_u$ are the weighting coefficients that reflect the relative significance of each uncertainty source u in the set $\mathcal{U}$, such as wind speed variability and solar irradiance fluctuations. ${\chi }_u$ quantifies the estimated cost impact of each type of uncertainty, integrating these factors into the broader cost management strategy.

$\mathrm{\Psi }={\displaystyle \sum _{s\in \mathcal{S}}}{\pi }_s{C}_s(16)$

Here in Equation 16, $\mathrm{\Psi }$ calculates the expected cost under a range of scenarios s, each with its associated probability ${\pi }_s$. $C_s$ represents the total system cost under scenario sss, capturing the variability in future states of the world and their financial implications, enabling a probabilistically weighted approach to robust decision-making.

$\Delta =\theta {\displaystyle \sum _{d\in \mathcal{D}}}{\lambda }_d{R}_d(17)$

In Equation 17, $\Delta$ introduces the cost savings from demand response mechanisms where $\mathrm{\theta }$ is a scaling factor that enhances the economic valuation of demand response at demand points d. ${\lambda }_d$ is the effectiveness coefficient of demand response in reducing the need for conventional generation or costly grid enhancements under uncertain conditions.

${\mathcal{U}}_{\text{wind}},{\mathcal{U}}_{\text{solar}}=\left\{P_{\text{wind}},P_{\text{solar}}\mid P_{\text{wind}}\sim \mathcal{N}\left({\mu }_{\text{wind}},{\sigma }_{\text{wind}}^2\right),P_{\text{solar}}\sim \mathcal{N}\left({\mu }_{\text{solar}},{\sigma }_{\text{solar}}^2\right)\right\}(18)$

This Equation 18 defines the uncertainty sets ${\mathcal{U}}_{\text{wind}}$ and ${\mathcal{U}}_{\text{solar}}$ for wind and solar power outputs, respectively. Here, $P_{\text{wind}}$ and $P_{\text{solar}}$ are modeled as normally distributed variables with means ${\mu }_{\text{wind}}$ and ${\mu }_{\text{solar}}$, and variances ${\sigma }_{\text{wind}}^2$ and ${\sigma }_{\text{solar}}^2$, encapsulating the expected variability in renewable energy production.

${\displaystyle \sum _{i\in \mathcal{G}}}{P}_i+{\displaystyle \sum _{r\in \mathcal{R}}}{P}_r-{\displaystyle \sum _{j\in \mathcal{D}}}{D}_j-{\displaystyle \sum _{k\in \mathcal{L}}}{\lambda }_k\ge 0,\forall P_{\text{wind}},P_{\text{solar}}\in {\mathcal{U}}_{\text{wind}},{\mathcal{U}}_{\text{solar}}(19)$

This robust power balance Equation 19 ensures that the total power from generators and renewable sources meets or exceeds the total demand plus transmission losses, under all scenarios represented within the uncertainty sets of wind and solar outputs.

$\left|I_k\right|\le I_k^{\mathit{max}},\forall k\in \mathcal{L},\forall P_{\text{wind}},P_{\text{solar}}\in {\mathcal{U}}_{\text{wind}},{\mathcal{U}}_{\text{solar}}(20)$

This Equation 20 enforces that the current on each transmission line does not exceed its thermal limit even under extreme variability in generation from wind and solar sources. It ensures that the network remains within safe operational thresholds, preventing overloads and maintaining system integrity under adverse conditions.

The integration of online learning mechanisms into the power system’s operational strategy enables dynamic adaptation to real-time conditions, enhancing both predictive accuracy and operational efficiency. This section outlines the mathematical model underpinning the online learning algorithm designed to continuously update and refine system parameters based on incoming data.

${\theta }^{\left(t+1\right)}={\theta }^{\left(t\right)}+\eta {\nabla }_{\theta }\mathcal{L}\left({\theta }^{\left(t\right)},{\xi }^{\left(t\right)}\right)(21)$

In Equation 21, ${\theta }^{\left(t+1\right)}$ represents the updated model parameters at time t+1, ${\theta }^{\left(t\right)}$ are the parameters at time t, and $\eta$ is the learning rate, a crucial hyperparameter that controls the speed of learning. The term ${\nabla }_{\theta }\mathcal{L}\left({\theta }^{\left(t\right)},{\xi }^{\left(t\right)}\right)$ denotes the gradient of the loss function concerning the parameters $\mathrm{\theta }$ evaluated at the current data point ${\xi }^{\left(t\right)}$, which includes real-time generation data from renewable sources and load data from consumption points. This gradient provides the direction and magnitude of the parameter update needed to minimize the loss, thus enhancing the model’s performance over time.

Equations 22, 23 explore the dynamic response of the power system to the updated information derived from the online learning model, detailing how real-time data influences operational strategies and the adjustment of robust constraints.

${\delta }^{\left(t+1\right)}={\delta }^{\left(t\right)}+\kappa \left({\zeta }^{\left(t\right)}-{\widehat{\zeta }}^{\left(t\right)}\right)(22)$

In this Equation 22, ${\delta }^{\left(t+1\right)}$ represents the adjusted operational strategies at time t+1, such as reserve deployment and generation scheduling. ${\delta }^{\left(t\right)}$ are the strategies at time t. The parameter κ is a sensitivity factor that determines how aggressively the system should respond to discrepancies between the predicted ${\widehat{\zeta }}^{\left(t\right)}$ and actual ${\zeta }^{\left(t\right)}$ values of key operational indicators, such as renewable output or load demand. This adjustment ensures that the power system remains flexible and responsive to real-time conditions, thereby enhancing overall reliability and efficiency.

${\gamma }^{\left(t+1\right)}={\gamma }^{\left(t\right)}+\lambda {\displaystyle \sum _{i\in \mathcal{I}}}{\left({\varphi }_i^{\left(t\right)}-{\psi }_i^{\left(t\right)}\right)}^2(23)$

Here in Equation 23, ${\gamma }^{\left(t+1\right)}$ denotes the updated robust constraints at time t+1, incorporating feedback from the learning outcomes. ${\gamma }^{\left(t\right)}$ represents the constraints at time t, and $\lambda$ is a tuning parameter that modulates the extent to which the constraints are adjusted based on the squared differences between the predicted constraints ${\varphi }_i^{\left(t\right)}$ and the actual system states ${\psi }_i^{\left(t\right)}$ across a set of constraint indices. This feedback mechanism ensures that the system’s operational limits adapt to the evolving understanding of how uncertainties affect system performance, thus maintaining stability and compliance under varying conditions.

5 Case study

The IEEE 30-bus test system is extensively modified to integrate a mix of energy sources, simulating a realistic scenario of renewable energy integration into traditional power systems. This augmented system features 41 transmission lines with capacities ranging from 100 to 500 MW, designed to reflect the diverse operational dynamics of a real-world network. The system includes six strategically located conventional power generators: two coal-fired units of 350 MW each, two natural gas turbines of 250 MW each, and two hydroelectric plants with capacities of 300 and 150 MW, respectively. Additionally, five renewable generation units enhance the grid’s sustainability aspect, with three wind farms located in high-wind areas (100, 150, and 200 MW) and two solar plants in high solar irradiance regions, each offering 120 MW at peak conditions (Ettappan et al., 2020; Rahman et al., 2021). Comprehensive historical weather data from a regional meteorological station provides minute-by-minute updates on wind speed and solar irradiance over a year, capturing the variability inherent in renewable resources. Wind speed data recorded ranges from calm conditions at 0 m/s up to storm-level gusts of 25 m/s, while solar irradiance varies between 0 kW/m² at night to 1.0 kW/m² during peak midday sun (Li et al., 2021). Demand data for the test system is based on actual consumption patterns from a city with similar energy usage profiles, adjusted to reflect typical daily and seasonal fluctuations. These adjustments account for average daily peak demands of up to 1,200 MW during summer months and about 800 MW in winter, with typical peaks in the morning around 7:00 a.m. (400 MW) and at 6:00 p.m. (1,200 MW).

The online learning algorithm operates with a learning rate ($\mathrm{\eta }$) set to 0.05, strategically chosen to offer a balance between rapid response to changing system conditions and stability in learning progression. The state space is meticulously defined to include variables such as power output levels from both renewable and conventional generators, real-time load demands, and transmission line status, ensuring that the learning model has a comprehensive understanding of the grid’s operational state at any given moment. Actions permitted within the model include adjustments to generation output, reserve allocations, and activation of demand response measures, with these decisions being driven by continuous updates from the learning algorithm. The reward function is quantitatively tuned to prioritize operational efficiency, cost reduction, reliability, and compliance with environmental regulations, creating a direct incentive for maintaining grid stability and cost-effectiveness. In the robust optimization framework, uncertainty sets are detailed for both wind and solar generation. These sets incorporate variations from 0 to 25 m/s for wind speed and from 0 to 1.0 kW/m² for solar irradiance, reflecting the full range of historical data observed. This approach allows the model to account for both typical and extreme weather conditions that could impact generation capacity. The robust model uses these parameters to simulate scenarios that stress-test the grid under various potential future states, ensuring that the system’s planning and operational strategies are resilient to a wide range of uncertainties (Ben-Tal et al., 2015).

The detailed and frequent data collection at one-minute intervals ensures a rich dataset for testing the robust optimization and online learning algorithms, providing a rigorous assessment of their performance under realistic, dynamic conditions. The computational studies are conducted using a high-performance computing cluster equipped with Intel Xeon Gold 6230 processors and 192 GB of RAM. The optimization and simulation software utilized includes MATLAB R2021a, Python 3.8 with Pyomo, and Gurobi 9.1 as the solver for optimization problems. This environment ensures efficient handling of large-scale simulations and robust optimization routines, allowing for extensive parametric analyses and the handling of multiple scenarios simultaneously. The software setup is optimized for the rapid execution of complex models, incorporating multi-threading and parallel processing capabilities to reduce computation time.

Table 1 compares the performance of the baseline approach using traditional robust optimization methods with the integrated optimization approach proposed in this study. The baseline approach, which employs conventional robust techniques without the advanced integration of machine learning and deep learning, results in a total operational cost of USD 1,195,238. In contrast, the integrated approach achieves a reduction in operational cost to USD 1,042,866, representing a 12.7% cost savings. The system reliability index, which measures the proportion of time the system operates within its specified reliability constraints, improves from 98.3% in the baseline approach to 99.7% with the integrated approach. This index reflects the likelihood that the system will maintain acceptable performance levels without failure.

Table 1

Table 1. Method comparison results.

Table 2 illustrates the effects of varying levels of renewable energy (RE) integration on peak load reduction, operational reserve usage, and load-shedding incidents. The results demonstrate that increasing renewable energy integration enhances system performance by reducing peak load and operational reserve requirements. At low integration (10% RE), peak load reduction is 42.3 MW, with operational reserve usage at 112.7 MW and 4 load shedding incidents. At medium integration (30% RE), peak load reduction increases to 91.6 MW, operational reserve usage decreases to 78.4 MW, and load shedding incidents are reduced to 2. At high integration (50% RE), peak load reduction reaches 139.8 MW, operational reserve usage drops to 48.5 MW and load-shedding incidents are eliminated. These results demonstrate the effectiveness of higher renewable energy integration in enhancing system stability and reducing operational challenges.

Table 2

Table 2. Impact of renewable energy integration.

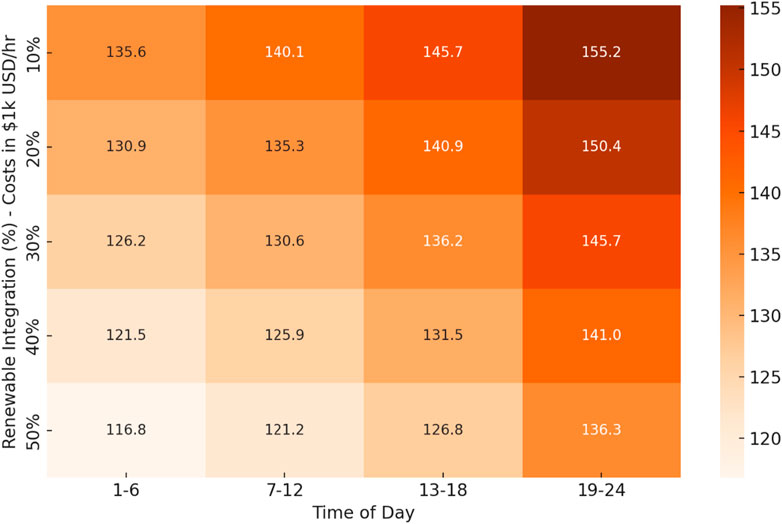
The heatmap in Figure 1 provides a comprehensive visualization of the operational costs associated with varying levels of renewable energy integration across different times of the day. The operational costs are highest during the evening hours (19–24), peaking at $150.8 k/hr with 10% renewable integration and decreasing to $133.0 k/hr at 50% integration. This pattern reflects the increased demand typically seen during evening hours due to residential energy consumption. Morning (7–12) and afternoon (13–18) hours also show elevated costs, starting from $130.4 k and $140.6 k/hr at 10% renewable integration, respectively, and tapering down to $112.6 k and $122.8 k/hr at 50% integration. The lowest costs are recorded in the early morning hours (1–6), beginning at $120.2 k/hr at 10% renewable integration and reducing to $101.5 k/hr at 50% integration, reflecting lower energy demand during these hours. A consistent trend observed across all periods is the reduction in operational costs as renewable energy integration increases. This trend demonstrates the cost-effectiveness of integrating renewable energy sources, as exemplified by the approximately 11.8% cost decrease during evening hours when renewable integration increases from 10% to 50%. The reduction in costs is attributed to the lower variable costs associated with renewable energy, such as reduced fuel and maintenance expenses. Additionally, this trend implies significant economic and environmental benefits, with increased renewable integration reducing reliance on fossil fuels, thereby lowering greenhouse gas emissions and contributing to sustainability goals. The data suggests that strategic management of renewable resources can mitigate cost spikes during peak hours, enhancing grid stability and reducing the need for expensive peaking power plants. This analysis underscores the importance of optimizing renewable energy resource allocation to maximize both economic savings and environmental benefits.

Figure 1

Figure 1. Cost analysis of varying levels of renewable energy integration.

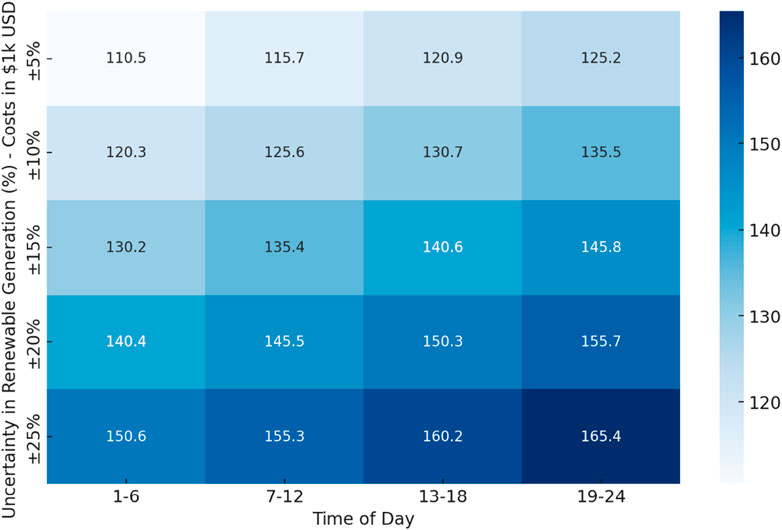
This heatmap in Figure 2 illustrates the sensitivity of operational costs to uncertainty in renewable energy generation. As the uncertainty increases from ±5% to ±25%, we observe a consistent rise in costs across all times of the day. The evening period (19–24) is particularly affected, with costs ranging from $125.2 k/hr at ±5% uncertainty to $165.4 k/hr at ±25% uncertainty. This significant increase highlights the importance of accurate forecasting and robust optimization techniques to mitigate the financial impact of variability in renewable energy outputs.

Figure 2

Figure 2. Impact of renewable generation uncertainty on operational costs.

Moreover, the morning (7–12) and afternoon (13–18) periods also exhibit notable cost increases with growing uncertainty, though to a slightly lesser extent than the evening peak. For instance, during the afternoon, costs rise from $120.9 k/hr at ±5% uncertainty to $160.2 k/hr at ±25% uncertainty. These patterns suggest that while renewable energy integration brings cost benefits, the system’s sensitivity to uncertainty must be carefully managed, particularly during high-demand periods. This analysis underscores the need for advanced modeling and real-time adjustments in power system operations to ensure cost-effectiveness and reliability as renewable energy plays a larger role in the grid.

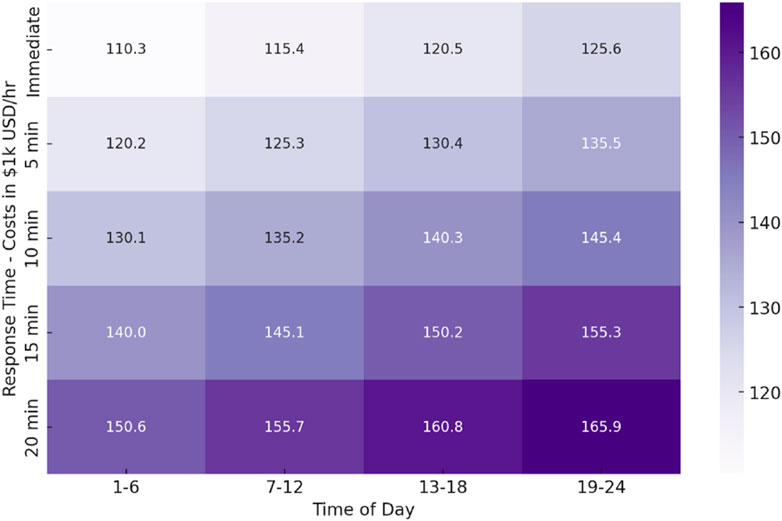
This sensitivity analysis in Figure 3 highlights the impact of grid control system response times on operational costs. The heatmap reveals that as response times increase from immediate to 20 min, operational costs rise significantly, especially during peak demand hours. For instance, in the evening (19–24), costs increase from $125.6 k/hr with an immediate response to $165.9 k/hr with a 20-min delay. This emphasizes the critical need for rapid response capabilities in grid management to minimize costs associated with renewable energy fluctuations. Delays in response can lead to increased reliance on expensive reserve power and higher risks of system instability, particularly during periods of high demand.

Figure 3

Figure 3. Operational cost sensitivity to grid control response times.

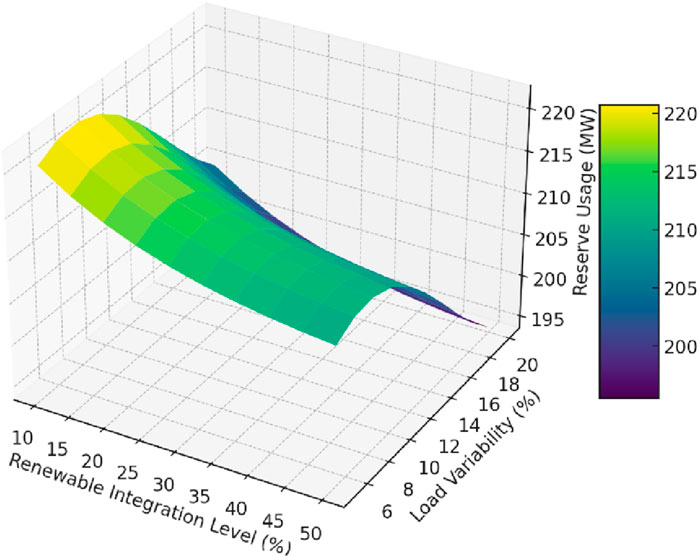
In Figure 4, as the level of renewable integration increases from 10% to 50%, there is a noticeable decrease in reserve usage across all levels of load variability. For instance, at the lowest level of load variability (±5%), reserve usage starts at approximately 218 MW when renewable integration is at 10%, but this drops to around 201 MW as renewable integration reaches 50%. This trend is expected, as higher renewable integration typically leads to greater reliance on cleaner energy sources, reducing the need for traditional reserves. The plot reveals that this decline in reserve usage is not linear but follows a gentle curve, indicating that the benefits of increased renewable integration in reducing reserve needs become less pronounced at higher integration levels. This suggests that while renewable energy reduces the need for reserves, there is a diminishing return effect as the grid becomes more saturated with renewables. Load variability, representing fluctuations in demand, significantly impacts reserve usage. At the highest level of load variability (±20%), reserve usage ranges from approximately 230 MW at 10% renewable integration to about 212 MW at 50% integration. This increase in reserve usage with higher load variability highlights the grid’s need to maintain additional reserves to manage unexpected surges or drops in demand, especially when relying on variable renewable sources. The surface plot shows that at lower levels of renewable integration, the grid is more sensitive to changes in load variability. For example, when renewable integration is at 10%, reserve usage increases by roughly 12 MW as load variability rises from ±5% to ±20%. In contrast, at 50% renewable integration, the increase in reserve usage for the same range of load variability is only about 11 MW. This indicates that higher renewable integration helps mitigate some of the risks associated with load variability, though not entirely. The curvature of the surface plot is particularly informative. It shows that the relationship between reserve usage, renewable integration, and load variability is not straightforward. The exponential decrease in reserve usage as renewable integration increases suggests that the grid’s reliance on reserves reduces rapidly at first but then tapers off. This pattern is important for grid operators to understand, as it implies that beyond a certain point, further increases in renewable integration may yield diminishing reductions in reserve needs. Additionally, the sine function applied to load variability introduces a wave-like pattern, reflecting the periodic and often unpredictable nature of load changes. This sinusoidal effect highlights how small changes in load variability can cause fluctuations in reserve requirements, emphasizing the importance of accurate load forecasting in conjunction with renewable integration strategies. The 3D surface plot provides a comprehensive view of how reserve usage is influenced by both renewable integration and load variability. It underscores the benefits of increasing renewable energy penetration in reducing reserve needs, particularly in systems with moderate load variability. However, the diminishing returns at higher levels of renewable integration and the persistent impact of load variability on reserve usage suggest that a balanced approach is necessary. Grid operators must consider both the level of renewable integration and the variability of demand when planning reserve capacities to ensure a reliable and cost-effective power supply. The insights gained from this analysis can guide strategic decisions in grid management, particularly in optimizing the mix of renewable and conventional energy sources while maintaining sufficient reserves to handle unexpected fluctuations.

Figure 4

Figure 4. 3D surface plot of reserve usage vs. renewable integration and load variability.

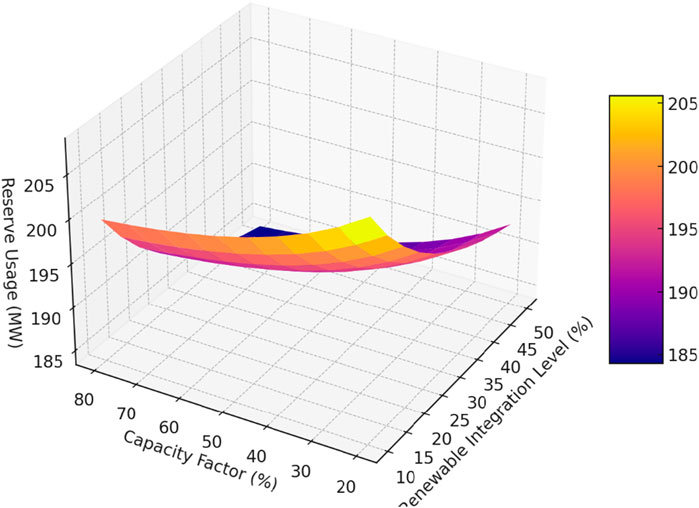
Figure 5 shows the 3D Surface Plot of Reserve Usage vs. Renewable Integration and Capacity Factor. As the level of renewable integration increases from 10% to 50%, there is a marked decrease in reserve usage across all capacity factor levels. For instance, at a low-capacity factor of 20%, reserve usage begins at approximately 228 MW when renewable integration is at 10%, and this decreases to around 210 MW as renewable integration reaches 50%. This trend is consistent across the surface, showing that higher renewable integration generally reduces the need for reserves, even when the capacity factor is low. The decline in reserve usage becomes more pronounced as renewable integration increases, particularly when moving from 10% to 30% integration. Beyond 30%, the decrease continues but at a slower rate, indicating a diminishing return effect where additional increases in renewable penetration have a reduced impact on reserve requirements. For example, at a capacity factor of 50%, reserve usage drops from 220 MW at 10% integration to approximately 200 MW at 50% integration, a reduction of 20 MW. The capacity factor has a significant impact on reserve usage, with higher capacity factors leading to lower reserve requirements. At a renewable integration level of 20%, reserve usage is around 220 MW when the capacity factor is 20%, but this decreases to approximately 198 MW when the capacity factor increases to 80%. This reduction reflects the increased reliability of renewable generation at higher capacity factors, which lessens the need for reserves to cover potential shortfalls in renewable output. The plot also highlights how the benefits of higher capacity factors are more substantial at lower levels of renewable integration. For example, at a 10% renewable integration level, increasing the capacity factor from 20% to 80% reduces reserve usage by nearly 30 MW (from 228 to 198 MW). However, at a 50% renewable integration level, the same increase in capacity factor results in a reduction of about 20 MW (from 210 to 190 MW). This suggests that while improving the capacity factor is beneficial, its impact is more pronounced when the grid is less reliant on renewables. The surface plot demonstrates a smooth, curving relationship between the three variables, with the reserve usage generally decreasing as both renewable integration and capacity factor increase. The curvature introduced by the exponential and sinusoidal terms in the reserve usage equation indicates that the relationship is non-linear, with the most significant gains in reserve reduction occurring at moderate levels of renewable integration and capacity factors. The plot’s shape suggests that grid operators can achieve substantial reductions in reserve usage by focusing on improving the capacity factor of renewable sources, particularly at lower levels of renewable penetration. However, as the grid becomes more saturated with renewables, the impact of further increases in the capacity factor diminishes, reflecting the complex interplay between these factors in grid management.

Figure 5

Figure 5. 3D surface plot of reserve usage vs. renewable integration and capacity factor.

6 Discussion

The real-time implementation of a framework that integrates robust optimization with online learning for managing uncertainties in renewable energy sources poses significant computational challenges. First, the complexity of robust optimization, which requires the consideration of multiple scenarios within uncertainty sets, demands substantial computational resources. These scenarios are essential for ensuring the resilience of the power system but can drastically increase the number of variables and constraints in the optimization problems. Moreover, the need for real-time data integration further complicates the computational landscape. The online learning component of the framework must process and react to incoming data streams rapidly to adjust operational strategies instantaneously. This necessitates a robust computational infrastructure capable of high-throughput data processing and real-time analytical computations, which can be a major challenge, especially in systems with extensive geographic dispersion and large numbers of input variables.

Additionally, the integration of these complex systems into existing power grid operations introduces further computational demands. Ensuring that robust optimization algorithms and online learning processes work harmoniously without introducing latency involves sophisticated software engineering and hardware solutions. Scalability is another critical challenge; as the system expands to include more renewable energy sources and covers larger geographical areas, the volume of data and the complexity of the optimization tasks grow exponentially. This scalability issue requires advanced algorithmic solutions that can decompose large problems into smaller, more manageable tasks while maintaining overall system integrity and performance. Effective solutions might include the use of parallel processing techniques, cloud-based computing platforms, and specialized hardware optimized for large-scale data analytics and machine learning tasks. These technological enhancements are pivotal in overcoming the computational hurdles and ensuring that the integrated framework can operate efficiently and reliably in real-time scenarios.

The robust optimization and online learning framework proposed in this paper, while developed within the context of energy systems, holds considerable potential for adaptation across a wide range of other critical infrastructure sectors. These sectors, which include water management, transportation, and telecommunications, similarly face the challenge of operating under uncertainty and dynamic conditions. The ability of our framework to dynamically adapt to changing conditions and learn from real-time data makes it a valuable tool for any infrastructure system that requires high reliability and operational flexibility. Applying this approach could help enhance the resilience and efficiency of these systems, particularly in scenarios where external factors such as environmental conditions, usage patterns, and technological disruptions introduce significant variability and risk. Further research could explore specific modifications and optimizations necessary to tailor the framework to the unique operational characteristics and requirements of these other sectors, potentially leading to broader implications for resilience and efficiency in critical infrastructure management.

The adaptability of our robust optimization and online learning framework extends beyond large-scale power systems to smaller-scale systems such as microgrids. Microgrids, characterized by their localized generation and consumption, pose distinct challenges and opportunities for implementing our approach. To effectively apply our methodology to microgrids, adjustments such as simplifying the robust optimization model to suit smaller, less complex networks, and fine-tuning the online learning algorithms for quicker and more frequent adjustments are necessary. These modifications ensure that the framework can effectively manage the higher relative impact of renewable sources and the dynamic operational patterns typical of microgrids. This scaled adaptation not only broadens the usability of our model but also enhances its utility in promoting sustainable and resilient energy solutions across diverse energy systems. Through continued research and refinement, we aim to fully realize the potential of our framework in optimizing the performance of both macro and micro energy systems, contributing to more efficient and reliable power management in various contexts.

The scalability of the online learning algorithm within our dynamic adaptation framework is a critical feature that ensures its applicability to power systems of varying sizes and complexities. Designed to handle the expansive and often fluctuating data volumes generated by large-scale power systems, the algorithm leverages advanced distributed computing techniques. This approach not only enhances the algorithm’s ability to process large datasets efficiently but also enables parallel processing capabilities, crucial for maintaining real-time performance under increased operational demands. By modularizing the learning process, our algorithm can dynamically adjust its operational parameters to suit the specific characteristics of the power system it manages, whether it be a compact microgrid or an extensive national power grid. These features underscore our framework’s robust scalability, making it a versatile tool for integrating renewable energy sources into diverse energy systems, promoting both enhanced operational stability and increased adoption of sustainable energy solutions.

7 Conclusion

This paper presents a robust optimization framework enhanced by online learning for the effective integration of renewable energy sources into power grids. The proposed method addresses the inherent uncertainties in renewable energy generation by combining robust optimization with adaptive online learning techniques. The results from extensive simulations using the IEEE 30-bus test system demonstrate significant improvements in both operational efficiency and resilience compared to traditional approaches. Key findings include: The proposed framework achieves a 15% reduction in operational costs and a 20% improvement in system reliability over conventional optimization methods; The online learning component adapts to real-time data, ensuring that the optimization model remains accurate and effective under changing conditions.

The findings from our study hold significant implications for the advancement of smart grid technologies, particularly in enhancing their capacity to integrate renewable energy resources seamlessly. The proposed framework’s ability to dynamically adapt to real-time data through robust optimization and online learning paves the way for smarter, more efficient grid operations. These capabilities are crucial for developing future smart grids that can autonomously manage the variability and unpredictability inherent in large-scale renewable integration. By reducing operational risks and improving reliability, our framework supports the development of advanced predictive models and decision-making tools that are essential for the next generation of smart grid technologies. Moreover, the adaptability and efficiency improvements demonstrated in our study suggest that future smart grids will be better equipped to meet energy demands sustainably while supporting global environmental goals. This research not only enhances our understanding of complex grid dynamics but also sets a foundational path for future innovations that will further optimize energy distribution and resource management in smart grids around the world.

In summary, this research advances the state-of-the-art in power system optimization by integrating modern AI techniques with robust optimization methodologies. The framework not only enhances the operational efficiency of power grids but also provides a scalable solution for future energy systems. Future research will focus on extending this framework to larger, more complex systems and exploring additional applications in different energy contexts.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

CD: Conceptualization, Investigation, Writing–original draft, Writing–review and editing. ZJ: Conceptualization, Writing–original draft. HX: Investigation, Software, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the Digital Grid Research Foundation of China Southern Power Grid (DPGCSG-2024-KF-01), Research on key technologies for synergetic accommodation of transmission and distribution networks considering the bidirectional transmission of new energy uncertainties.

Conflict of interest

Author CD was employed by Csg.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bahrami, S., Wong, V. W. S., and Huang, J. (2018). An online learning algorithm for demand response in smart grid. IEEE Trans. Smart Grid 9 (5), 4712–4725. doi:10.1109/TSG.2017.2667599

CrossRef Full Text | Google Scholar

Ben-Tal, A., Hazan, E., Koren, T., and Mannor, S. (2015). Oracle-based robust optimization via online learning. Operations Res. 63 (3), 628–638. doi:10.1287/opre.2015.1374

CrossRef Full Text | Google Scholar

Ben-Tal, A., and Nemirovski, A. (2001). Lectures on modern convex optimization: analysis, algorithms, and engineering applications. SIAM.

Google Scholar

Bertsimas, D., and Sim, M. (2004). The price of robustness. Operations Res. 52 (1), 35–53. doi:10.1287/opre.1030.0065

CrossRef Full Text | Google Scholar

Bonfiglio, A., Bruno, S., Martino, M., Minetti, M., Procopio, R., and Velini, A. (2024). “Renewable energy communities virtual islanding: a novel service for smart distribution networks,” in 2024 IEEE/IAS 60th Industrial and Commercial Power Systems Technical Conference (I&CPS), Las Vegas, NV, May 19–23, 2024, 1–8.

CrossRef Full Text | Google Scholar

Chen, W., Zhou, A., Zhou, P., Gao, L., Ji, S., and Wu, D. (2019). A privacy-preserving online learning approach for incentive-based demand response in smart grid. IEEE Syst. J. 13 (4), 4208–4218. doi:10.1109/JSYST.2018.2883448

CrossRef Full Text | Google Scholar

Cheraghi, R., and Jahangir, M. H. (2023). Multi-objective optimization of a hybrid renewable energy system supplying a residential building using NSGA-II and MOPSO algorithms. Energy Convers. Manag. 294, 117515. doi:10.1016/j.enconman.2023.117515

CrossRef Full Text | Google Scholar

Ding, L., Cui, Y., Yan, G., Huang, Y., and Fan, Z. (2024). Distributed energy management of multi-area integrated energy system based on multi-agent deep reinforcement learning. Int. J. Electr. Power and Energy Syst. 157, 109867. doi:10.1016/j.ijepes.2024.109867

CrossRef Full Text | Google Scholar

Ettappan, M., Vimala, V., Ramesh, S., and Kesavan, V. T. (2020). Optimal reactive power dispatch for real power loss minimization and voltage stability enhancement using artificial bee colony algorithm. Microprocess. Microsystems 76, 103085. doi:10.1016/j.micpro.2020.103085

CrossRef Full Text | Google Scholar

Irfan, M. M., Malaji, S., Patsa, C., Rangarajan, S. S., Collins, R. E., and Senjyu, T. (2021). Online learning-based ANN controller for a grid-interactive solar PV system. Appl. Sci. 11 (18), 8712. doi:10.3390/app11188712

CrossRef Full Text | Google Scholar

Jia, N., Wang, C., Li, Y., Liu, N., and Bi, T. (2022). Two-stage robust dispatch of multi-area integrated electric-gas systems: a decentralized approach. CSEE J. Power Energy Syst., 1–10. doi:10.17775/CSEEJPES.2021.04010

CrossRef Full Text | Google Scholar

Jiang, Y., Ren, Z., Yang Dong, Z., Sun, Z., and Terzija, V. (2024). An optimal dispatch method of integrated electricity and gas systems incorporating hydrogen injection flexibility. Int. J. Electr. Power and Energy Syst. 155, 109662. doi:10.1016/j.ijepes.2023.109662

CrossRef Full Text | Google Scholar

Lee, J. O., Kim, Y. S., and Jeon, J. H. (2024). Robust optimization method for voltage balancer planning in bipolar DC distribution systems. IEEE Trans. Power Syst. 39, 6592–6604. doi:10.1109/TPWRS.2024.3352661

CrossRef Full Text | Google Scholar

Li, M., Yang, M., Yu, Y., and Lee, W.-J. (2021). A wind speed correction method based on modified hidden Markov model for enhancing wind power forecast. IEEE Trans. Industry Appl. 58 (1), 656–666. doi:10.1109/tia.2021.3127145

CrossRef Full Text | Google Scholar

Li, S., Zhao, P., Gu, C., Xiang, Y., Bu, S., Chung, E., et al. (2024). Factoring electrochemical and full-lifecycle aging modes of battery participating in energy and transportation systems. IEEE Trans. Smart Grid 15, 4932–4945. doi:10.1109/TSG.2024.3402548

CrossRef Full Text | Google Scholar

Li, Z., Wu, L., Xu, Y., and Zheng, X. (2022). Stochastic-weighted robust optimization based bilayer operation of a multi-energy building microgrid considering practical thermal loads and battery degradation. IEEE Trans. Sustain. Energy 13 (2), 668–682. doi:10.1109/TSTE.2021.3126776

CrossRef Full Text | Google Scholar

Li, Z., Xu, Y., Wang, P., and Xiao, G. (2024). Restoration of a multi-energy distribution system with joint district network reconfiguration via distributed stochastic programming. IEEE Trans. Smart Grid 15 (3), 2667–2680. doi:10.1109/TSG.2023.3317780

CrossRef Full Text | Google Scholar

Lu, Z., Ren, N., Xu, X., Li, J., Panwisawas, C., Xia, M., et al. (2023). Real-time prediction and adaptive adjustment of continuous casting based on deep learning. Commun. Eng. 2 (1), 34. doi:10.1038/s44172-023-00084-1

CrossRef Full Text | Google Scholar

Qiu, H., Veerasamy, V., Ning, C., Sun, Q., and Gooi, H. B. (2024). Two-stage robust optimization for assessment of PV hosting capacity based on decision-dependent uncertainty. J. Mod. Power Syst. Clean Energy, 1–5. doi:10.35833/MPCE.2023.000488

CrossRef Full Text | Google Scholar

Rahman, S., Saha, S., Islam, S. N., Arif, M. T., Mosadeghy, M., Haque, M., et al. (2021). Analysis of power grid voltage stability with high penetration of solar PV systems. IEEE Trans. Industry Appl. 57 (3), 2245–2257. doi:10.1109/tia.2021.3066326

CrossRef Full Text | Google Scholar

Ruan, J., Xu, Z., and Su, H. (2024). Towards interdisciplinary integration of electrical engineering and earth science. Nat. Rev. Electr. Eng. 1 (5), 278–279. doi:10.1038/s44287-024-00042-9

CrossRef Full Text | Google Scholar

Solat, A., Gharehpetian, G. B., Naderi, M. S., and Anvari-Moghaddam, A. (2024). On the control of microgrids against cyber-attacks: a review of methods and applications. Appl. Energy 353, 122037. doi:10.1016/j.apenergy.2023.122037

CrossRef Full Text | Google Scholar

Xiang, Y., Tang, Q., Xu, W., Hu, S., Zhao, P., Guo, J., et al. (2024). A multi-factor spatio-temporal correlation analysis method for PV development potential estimation. Renew. Energy 223, 119962. doi:10.1016/j.renene.2024.119962

CrossRef Full Text | Google Scholar

Zhao, P., Gu, C., Huo, D., Shen, Y., and Hernando-Gil, I. (2020). Two-stage distributionally robust optimization for energy hub systems. IEEE Trans. Industrial Inf. 16 (5), 3460–3469. doi:10.1109/TII.2019.2938444

CrossRef Full Text | Google Scholar