Renewable generation forecasting with DNN-based ensemble method in electricity scheduling

The generation of renewable energy encounters numerous obstacles, chiefly the unpredictability of renewable sources. When new energy generation prediction is lower than expected, it needs to be supplemented by other energy sources, which may lead to instability in the power grid if the deviation is large. When the prediction of new energy generation exceeds expectations, it will lead to energy waste. To address these issues, this paper proposes a Deep Neural Network-based fusion framework, which can improve the prediction accuracy of new energy and achieve a low-carbon, economical, and stable power grid. Within this structure, feature engineering is conducted initially. Subsequently, a combination of traditional tree algorithms like the Gradient Boosting Decision Tree, linear approaches such as the Least Squares Method, and nonlinear neural networks, for instance, Recurrent Neural Networks, are employed for individual model regression purposes. In the final step, both the original time-series data and the outcomes from the individual models are integrated into a deep neural network to derive the ultimate forecasting outcomes. By using our method, the electricity cost has been reduced by 26.5% and the carbon emissions have been decreased by 14.2%. Experiments have been carried out using actual community data, confirming the effectiveness of the proposed approach. The findings indicate that the integration of DNN with traditional and modern machine learning techniques can significantly improve the forecasting of renewable energy generation. This advancement contributes to the creation of a more sustainable, economical, and stable power grid.

1 Introduction

New energy refers to energy sources that are both sustainable and generate minimal adverse environmental impacts upon usage. This category of energy offers numerous advantages over traditional energy forms Jacobson et al. (2017). A predominant feature of new energy is its cleanliness and environmentally friendly characteristics; it does not emit substantial pollutants or greenhouse gases, thus reducing atmospheric, aquatic, and terrestrial pollution and conserving the natural ecosystem. Moreover, new energy is characterized by its seemingly inexhaustible reserves, encompassing resources such as solar, wind, and hydro power. These resources are indefinitely accessible and capable of meeting consistent, long-term energy demands. Another significant aspect is that new energy contributes to the diversification of energy portfolios, decreases reliance on fossil fuels, and enhances the security and sustainability of energy supplies. Additionally, the continuous progress and innovations in new energy technologies present opportunities for economic and social development, acting as a driving force for progress. Fundamentally, the adoption of new energy marks a critical step towards transforming energy systems, offering substantial, long-lasting benefits for the sustainable advancement of human society.

Forecasting in the field of new energy utilizes advanced technologies and analytical methods to predict future trends and capacities in energy development Muralitharan et al. (2018). This forecasting offers several advantages. Firstly, it empowers governments and businesses to formulate informed energy strategies and policies that promote sustainable growth and facilitate the transition to new energy sources Kumar and Sharma (2019). Additionally, it assists utility companies and energy distributors in anticipating demand and capacity needs, thus improving energy allocation and management efficiency while enhancing resource utilization. Moreover, new energy forecasting provides crucial insights for investors, informing their decisions and strategic allocations within the new energy sector Moriarty and Honnery (2016). It also plays a significant role in stabilizing and ensuring the reliability of energy infrastructures by reducing imbalances between supply and demand, minimizing energy waste, and lessening environmental impact. However, forecasting in this area also faces numerous challenges. It is significantly influenced by natural factors, including climate and weather conditions, which can result in prediction errors. In conclusion, while new energy forecasting is essential for driving sustainable development, optimizing energy management, and guiding investment decisions, it must also address various challenges and limitations Turner (2008); Shahzad et al. (2016); Ihsan et al. (2019).

Predicting the output of alternative energy sources is essential for the operational management of virtual power plants (VPPs) Olivares et al. (2014); MacDougall et al. (2016); Tan et al. (2021). A VPP integrates and controls a network of decentralized energy resources, such as solar and wind power plants, using sophisticated information technologies IRENA, 2019. The production of electricity from these renewable sources is greatly influenced by weather and environmental conditions, resulting in considerable fluctuations and uncertainties in their output. By accurately forecasting the generation of renewable energy, VPP managers receive valuable insights into expected energy supply from distributed resources for the upcoming period. This allows them to more effectively orchestrate the VPP’s internal mechanisms—encompassing generation, energy storage Wang et al. (2021), and demand response strategies. Such strategic coordination substantially improves the system’s overall performance and reliability by aligning energy production with demand. Moreover, precise forecasts of renewable energy production mitigate operational risks within the power market, enhance the profitability of energy transactions Creutzig et al. (2015), and foster the adoption of sustainable energy practices. These advancements are crucial for optimizing the energy mix and propelling the transition towards a low-carbon economy. Although renewable energy production is estimated with high accuracy in VPP or portfolio structures, negative or positive deviations may occur in real time. In this respect, energy storage systems are needed as an imbalance reducer Çiçek and Erdinç (2021, 2022).

The use of tree models Friedman (2001) in new energy forecasting is rapidly gaining popularity. Rooted in decision tree principles, these models create a predictive framework by segmenting data into a branching structure, which allows for effective forecasting Ke et al. (2017). In the context of new energy, these models utilize historical energy data along with additional factors such as weather conditions and time-related variables to estimate future trends in energy production and usage. One significant advantage of tree models is their ability to handle non-linear dynamics. As generation and consumption patterns in new energy are influenced by various factors, many of which interact in complex, non-linear ways, tree models excel in understanding these intricate relationships, thereby improving the accuracy of their predictions. Furthermore, these models effectively analyze the interactions among different variables. In new energy forecasting scenarios, various factors may have either combined or individual impacts, a relationship effectively captured by the structure of tree models, which adds to their predictive accuracy. Overall, the application of tree models in the new energy sector proves to be a robust and adaptable tool. Their capacity to navigate non-linear relationships and variable interdependencies Chen and Guestrin (2016), along with their strong interpretative abilities, provides valuable support for informed decision-making and strategic planning in the evolving landscape of new energy.

The Least Squares Method Doe and Smith (2023) is a commonly used mathematical method with a wide range of applications in renewable energy forecasting. This model transforms the prediction problem into a least squares problem, allowing for effective estimation of future renewable energy production or consumption Smith and Doe (2023); Johnson and Lee (2023). In renewable energy forecasting, the Least Squares Method can establish a mathematical model based on historical data and relevant factors to predict future renewable energy production or consumption. By seeking the solution that minimizes errors, this model can find the best-fitting curve, accurately predicting future renewable energy demand or supply. The application of the Least Squares Method in renewable energy forecasting offers several advantages. Firstly, the model can handle large amounts of historical data and fit it to improve the accuracy of the predictions. Secondly, the Least Squares Method can consider multiple factors that influence renewable energy, such as weather conditions and economic development, providing a more comprehensive prediction of renewable energy production or consumption. Additionally, the Least Squares Method can adjust model parameters to meet different forecasting requirements, enhancing the flexibility and reliability of the predictions.

RNN (Recurrent Neural Network) Graves (2013) stands as a potent machine learning paradigm extensively employed across various domains, notably in renewable energy forecasting. Renewable energy forecasting encompasses the prediction of renewable energy sources’ output or consumption, such as wind and solar energy, facilitating enhanced planning for energy supply and demand. The utilization of RNN network models for renewable energy forecasting capitalizes on their proficiency in handling time series data Chung et al. (2014). Notably, the output or consumption of renewable energy often demonstrates pronounced time-dependent characteristics, including the diurnal variation patterns in solar energy production or the seasonal fluctuations in wind energy generation. RNN is adept at capturing these time dependencies through its capacity to remember past input data and forecast future energy output or consumption drawing on observed patterns. Distinctively, RNN network models Athiwaratkun and Stokes (2017); Gruber and Jockisch (2020) process input data iteratively at each time step, transferring state information from one step to the next. This sequence empowers the formation of a memory for the time series data. Such a memory mechanism positions RNN as a dynamic tool for modeling the temporal dynamics of renewable energy, enabling predictions of future energy output or consumption based on historical data.

The aforementioned models exhibit certain constraints when deployed for predicting new energy outcomes. Firstly, tree-based models are susceptible to overfitting, particularly in scenarios involving extensive datasets with numerous features. This susceptibility can engender models that are unduly intricate, lacking in the capability to generalize. Secondly, the handling of continuous variables by tree models is somewhat deficient, frequently necessitating the discretization of these variables, which may lead to a loss of information. The Least Squares Method presupposes a linear correlation between the predictors and the response variable. Consequently, its effectiveness is diminished in modeling non-linear relationships, rendering it less capable in addressing non-linear challenges within new energy forecasting. Although recurrent neural network (RNN) models boast formidable abilities in modeling the complexities inherent in new energy prediction issues, they are hampered by protracted training durations. This is particularly evident when processing large-scale datasets, thereby demanding considerable computational resources and time investments. Furthermore, the architectural and parameter configuration of RNN models is intricate, often requiring a series of experimental adjustments to procure satisfactory achievements.

The use of deep neural network (DNN) Muralitharan et al. (2018) models in new energy forecasting leverages their sophisticated data processing and pattern recognition abilities, allowing them to identify features and relationships within complex datasets and provide accurate predictions. In this context, neural network models construct a multi-layer network of neurons to learn and model the relationship between input features and the evolving trends in energy production. By training and optimizing these models with substantial historical data, they can effectively capture the non-linearities and complexities associated with new energy development, which enhances both prediction accuracy and reliability Covington et al. (2016). Furthermore, through backpropagation algorithms, neural network models continuously refine their parameters, thereby improving their predictive performance. Their inherent flexibility and adaptability enable them to manage large-scale and high-dimensional datasets, making them ideal for a wide range of new energy prediction applications. The deployment of these models not only yields precise energy demand forecasts for decision-makers but also aids in optimizing resource allocation and fostering sustainable development in the new energy sector.

To obtain more accurate predictions of new energy, we first performed feature engineering on the relevant information. Then, we used traditional tree model Gradient Boosted Decision Trees (GBDT), linear model LR, non-linear neural network RNN for regression prediction in individual models. Finally, we further fused the original time series features and the outputs of individual models through a DNN network to obtain the final prediction results. Our main contributions mainly include.

$•$ We proposed a fusion prediction method based on the DNN network, which can combine the advantages of different types of models and improve the accuracy of new energy prediction.

$•$ We conducted detailed analysis experiments, providing insights into the impact of different features on end-to-end power scheduling and the impact of new energy prediction accuracy on scheduling. This provides a solid foundation for effective power scheduling.

$•$ We performed extensive experimental validation on real datasets, confirming the effectiveness of the proposed framework.

The organization of the paper is outlined as follows: The second section delineates the problem under investigation. In the third section, we introduce the specific methods employed in our study. The fourth section is dedicated to presenting the experiments conducted and analyzing their outcomes. Finally, the paper culminates with the Conclusion, where we summarize the key findings of our research.

2 Problem statement

The aim of this study is to develop a deep learning-based approach for predicting the generation or consumption of renewable energy sources, referred to as the New Energy Prediction (NEP) task. In the NEP task, we consider a set of input variables denoted as $X=\{X_1,X_2,\dots ,X_n\}$, where each variable $X_i$ represents a specific feature related to the energy generation or consumption process. The goal is to predict the output variable $Y$, which represents either the amount of renewable energy generated or consumed within a given time frame.

The NEP task poses several challenges due to the complex and dynamic nature of renewable energy sources. Firstly, the input variables $X$ may include factors such as weather conditions, time of day, and historical energy generation/consumption patterns, among others. These variables can exhibit non-linear relationships, making traditional prediction methods inadequate. Additionally, renewable energy sources are subject to various uncertainties, such as intermittent generation and demand fluctuations, which further complicate the prediction task.

To address these challenges, deep learning models offer a promising solution by leveraging their ability to automatically learn hierarchical representations from raw data. By training a deep neural network on historical data, we can capture the underlying patterns and dependencies within the input variables to improve the accuracy of renewable energy prediction.

The proposed NEP task holds significant importance in various domains. For renewable energy providers, accurate predictions can help optimize energy production and distribution, resulting in improved efficiency and reduced operational costs. Furthermore, policymakers and grid operators can benefit from reliable forecasts to ensure the stable integration of renewable energy sources into the existing power grid.

In this paper, we will explore different traditional and deep learning-based architectures and techniques to tackle the NEP task. Moreover, traditional models, such as tree-based models like GBDT, have the advantage of handling discrete features, and they can also handle large discrete values relatively well. Linear regression methods like LSM can handle continuous values with patterns, but they lack the ability to handle outliers. RNNs can handle sequential patterns and features reasonably well. By combining these models, their advantages can complement each other. By evaluating the performance of these models on real-world renewable energy datasets, we aim to provide insights into the effectiveness of combining models for accurate and reliable new energy predictions.

3 Framework

3.1 Framework

As shown in Figure 1, the first step is to perform feature engineering on the features. Then, single-model modeling is conducted, including tree model GBDT, linear model LSM, and non-linear model RNN. Finally, we utilize the non-linear model DNN to ensemble all the results. Below, we will provide detailed introductions for each part.

Figure 1

Figure 1. Forecasting structure of proposed framework.

3.2 Feature engineering

When conducting the New Energy Prediction (NEP) task, it is necessary to preprocess the features so that the prediction model can use them directly. The features include continuous values and discrete values. For continuous values, we perform outlier processing to avoid the collapse of the model caused by some abnormal data. The processing logic is as follows:

$x^{\prime }=\left\{\begin{array}{cc}\alpha \ast median\left(X\right),\hfill & \text{if\hspace{0.17em}}x\ge \alpha \ast median\left(X\right)\hfill \\ \beta \ast median\left(X\right),\hfill & \text{if\hspace{0.17em}}x\le \beta \ast median\left(X\right)\hfill \\ x,\hfill & \text{else\hspace{0.17em}}\hfill \end{array}\right.(1)$

where $\alpha$ and $\beta$ are super parameters (Equation 1). $median(X)$ denotes the median value of $X$.

For discrete value features, we perform one-hot encoding. For example, for Monday, we use the vector [1,0,0,0,0,0,0], where the first element is one and the others are 0, representing Monday. This can be applied to other discrete features as well. The specific data will be introduced in the dataset of the experiment. The main features are listed as follows.

$•$ The user demand in past days;

$•$ The new energy generation in past days;

$•$ The radiance of solar in past days;

$•$ Time information such as hour, weekday, month, etc.,;

$•$ Further and past weather data, such as humidity, temperature;

Specifically, all the inputs for the following models are meticulously prepared in the Feature Engineering Section, encompassing both continuous and discrete features. As for the other parameters, they are initially set through a process of random initialization, subsequently undergoing updates via gradient descent learning.

3.3 GBDT

GBDT (Gradient Boosting Decision Tree) is a powerful tree-based model that combines the principles of gradient boosting and decision trees. Unlike traditional decision tree models that make predictions independently, GBDT builds an ensemble of trees in a sequential manner, where each subsequent tree corrects the mistakes made by the previous ones. This iterative process helps to gradually improve the model’s accuracy.

The principal concept underpinning the Gradient Boosting Decision Tree (GBDT) revolves around the strategy of reducing a loss function through the sequential integration of weak learners, specifically decision trees, aimed at the negative gradient of the said loss function. These trees are meticulously designed to forecast the negative gradient residuals appertaining to the antecedent trees, thereby acting as the “pseudo-residuals”. Thereafter, the ensuing trees are amalgamated into the ensemble, meticulously crafted to augment the predictive accuracy of the trees that preceded them, and this cycle is perpetuated until a point of convergence is reached.

The GBDT algorithm can be formulated in the NEP task by using the following equations Friedman (2001).

$•$ Calculation of pseudo-residuals: For a loss function $L(Y,F(X))$, where $Y$ is the true label, such as the solar generation of the next hour, and $F(X)$ is the predicted value, the pseudo-residuals $(r)$ can be computed as the negative gradient of the loss function with respect to the predicted value: $r=-\frac{\partial L(Y,F(X))}{\partial F(X)}$.

$•$ Building a decision tree: Each decision tree is trained to predict the negative gradient residuals $(r)$ of the previous trees. The tree splits the data based on certain features and thresholds to minimize the loss function.

$•$ Updating the ensemble: The predicted values of the previous trees are summed up, and the negative gradient residuals $(r)$ are added to obtain the updated ensemble prediction.

$•$ Learning rate: To prevent overfitting and improve generalization, a learning rate parameter $\eta$ is introduced to control the contribution of each tree to the ensemble. The learning rate shrinks the impact of each tree by multiplying it with $\eta$ before adding it to the ensemble.

By combining multiple weak learners through these iterative steps, GBDT creates a strong predictive model that is capable of capturing complex relationships and achieving high accuracy.

3.4 LSM

The Least Squares Method (LSM) represents a statistical approach employed for the estimation of parameters within a regression model, ensuring an optimal fit to the data points observed. Its primary objective is to minimize the aggregate of the squared disparities between the values predicted by the model and those actually observed. This technique finds significant application in the domain of renewable energy, most notably in scenarios such as predicting the output of energy production from solar panels or wind turbines.

To model the prediction problem in the context of renewable energy, we can utilize the least squares method to estimate the parameters of a regression model. The model equation can be represented as Doe and Smith (2023):

$y=a_0+a_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n(2)$

Where y represents the corresponding label, which is the target energy production or user load demand. $a_0,a_1,\dots ,a_n$ are the coefficients to be estimated, representing the impact of each independent variable on the prediction task. $x_1,\dots ,x_n$ are the independent variables, which can be factors like time of day, temperature, wind speed, or solar radiation.

The goal of the least squares method is to find the values of $a_0,a_1,\dots ,a_n$ in Equation 2 that minimize the sum of the squared differences between the predicted energy production and the actual energy production. This is achieved by solving the normal equations:

$X^{T}XA=X^{T}y(3)$

Where $X$ is the design matrix, containing the values of the independent variables. $X^T$ is the transpose of $X$. $A$ is the vector of coefficients to be estimated. $y$ is the vector of observed energy production values or user load demands in Equation 3. The solution to the normal equations provides the estimated values for $a_0,a_1,\dots ,a_n$, which can then be used to predict the energy production for future observations.

3.5 RNN

Recurrent Neural Network (RNN) is a type of neural network model that is specifically designed to handle sequential data. Unlike traditional feedforward neural networks, RNNs have the ability to take into account the temporal dependencies present in the data, making them suitable for various time series analysis tasks, including predicting new energy problems.

At the heart of a Recurrent Neural Network (RNN) lies the recurrent layer, designed to feed information back into the network from previous time steps. This architecture empowers the network with an internal memory capability, facilitating the capture and utilization of information from past inputs in the processing of current inputs. Such a memory mechanism proves particularly beneficial in addressing new challenges within the energy sector, where understanding and predicting patterns in energy consumption or generation are significantly enhanced by insights from historical data.

Mathematically, an RNN can be described as follows Graves (2013):

$h_t=f\left(W_x{x}_t+W_h{h}_{t-1}+b\right)(4)$

where $x_t$ is the input feature mentioned in Feature Engineering section, $h_t$ represents the hidden state at time step $t$, $W_x$ and $W_h$ are weight matrices that determine how the current input and previous hidden state contribute to the hidden state at the current time step, and $b$ is the bias term in Equation 4. The function $f(.)$ is a non-linear activation function, such as the sigmoid or hyperbolic tangent function, which introduces non-linearity into the model.

To tackle forecasting issues in new energy scenarios, the Recurrent Neural Network (RNN) can be effectively trained utilizing historical energy data. In this context, the input sequence is composed of prior energy observations, while the target sequence represents predictions about future energy scenarios. Through the iterative refinement of weights and biases, employing methods such as backpropagation through time, the RNN is equipped to discern the temporal patterns and relationships inherent in the dataset. This capability enables the RNN to deliver precise forecasts regarding future energy consumption or generation, by leveraging its learned insights from past data trends.

3.6 DNN

The Deep Neural Network (DNN) stands as a formidable and extensively utilized model within the realm of machine learning. It is meticulously crafted to address sophisticated issues associated with pattern discernment, classification, and prognostication. Diverging from traditional shallow neural networks, the DNN is composed of numerous layers of interconnected artificial neurons. This multi-layered architecture empowers it to unravel complex relationships and distill high-level representations from unprocessed input data.

A notable deployment of DNN is in forecasting challenges related to new energy quandaries. Harnessing its prowess to learn and generalize from voluminous datasets, the DNN can adeptly delineate the intricate interconnections amongst myriad factors influencing energy forecasting. The process begins with the infusion of input features pertinent to the energy issue at hand, including historical energy usage data, meteorological conditions, and more, into the DNN’s input layer.

The key formulas used in DNN for energy prediction include Feedforward Equation:

$z=Wx+b(5)$

$a=f\left(z\right)(6)$

In Equations 5, 6, $x$ represents the input features, $W$ denotes the weight matrix, $b$ represents the bias vector, and $f(z)$ represents the activation function. The feedforward equation calculates the output of each neuron in the network.

Backpropagation Equation:

$\delta \left(L\right)=\nabla a\left(L\right)\ast f^{\prime }\left(z\left(L\right)\right)(7)$

$\delta \left(l\right)={\left(W\left(l+1\right)\right)}^T\ast \delta \left(l+1\right)\ast f^{\prime }\left(z\left(l\right)\right)(8)$

In the backpropagation equation, $\delta$ represents the error term, $\nabla a(L)$ denotes the gradient of the loss function, $f^{\prime }(z)$ represents the derivative of the activation function, and $l$ indicates the layer in the network. These equations (Equations 7, 8) are used to propagate the error backwards through the layers, allowing the model to adjust the weights and biases for better predictions.

DNN provides a versatile and robust method to tackle emerging challenges in energy forecasting by adeptly utilizing past data for its learning process. Its capability to discern intricate associations and perform advanced abstractions enables it to deliver precise and dependable forecasts, thus supporting decisions in the novel energy domain. It is important to point out that the input for DNN takes into account not just essential attributes but also encompasses the results produced by the previously mentioned model.

4 Experiments

4.1 Dataset

We use a real-world dataset from the city of Fontana, California. This dataset¹ includes the electricity dispatch records for 17 buildings over the course of a year Vázquez-Canteli et al. (2019, 2020). The electricity usage data for these buildings provides detailed information about energy consumption, including the electricity consumption for each building and peak power demands. These data provide an in-depth understanding of the city’s energy system, enabling researchers to explore energy usage patterns in buildings, analyze energy consumption trends, and develop more efficient energy management strategies. Additionally, the dataset also includes weather data for the region, such as temperature, humidity, and solar density. This weather data is crucial for studying the impact of weather conditions on the city’s energy system, as weather conditions can affect building energy consumption patterns and energy demand.

4.1.1 Metric

Mean Absolute Percentage Error (MAPE) is frequently employed as an evaluation metric for gauging the precision of forecasts in the realm of new energy. MAPE assesses the forecast’s accuracy by determining the average percentage discrepancy between forecasted figures and their actual counterparts. This specific calculation entails computing the absolute percentage deviation for each predicted datum relative to its actual value, followed by computing the mean of these values. The values of MAPE may vary from 0 to positive infinity, with a value near to 0 symbolizing a forecast of higher accuracy. The formula for MAPE is provided as follows:

$\text{MAPE}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|\times 100\%(9)$

where $n$ is the number of observations in Equation 9, $y_i$ is the actual label value, and ${\widehat{y}}_i$ is the predicted value.

In addition, to reflect the overall impact of forecasting on scheduling Nosratabadi et al. (2017), we have added indicators for scheduling. The scheduling indicators include two components: the carbon emissions (Equation 10) and the price cost (Equation 11) of electricity scheduling. The formula is as follows:

$C_{\text{Emission}}={\displaystyle \sum _{t=1}^T}\left({\displaystyle \sum _{i=1}^I}\max \left(E_{i,t},0\right)\right)\cdot c_t,(10)$

$C_{\text{Price}}={\displaystyle \sum _{t=1}^T}\max \left(E_t^{\text{dist}},0\right)\cdot p_t,(11)$

$C_{\text{Average\_Cost}}=\left(C_{\text{Emission}}+C_{\text{Price}}\right)/2,(12)$

for each building $i$, the electricity demand is $E_{i,t}=L_{i,t}-P_{i,t}+A_{i,t}$, and $L_{i,t}$ is the load demand, $P_{i,t}$ is the solar generation, $A_{i,t}$ is the scheduling value from the scheduling model. The electricity demand of the district is $E_t^{\text{dist}}={\sum }_{i=1}^I{E}_{i,t}$. $c_t$ denotes the carbon emission for each electrical unit, and $p_t$ denotes the price. The smaller the better for both forecasting and scheduling metric. The production of every unit of electricity necessitates the use of a specified quantity of energy and results in a certain level of carbon emissions; for instance, generating thermal power requires the emission of carbon dioxide. Hence, the aggregate electricity usage multiplied by the carbon emissions per electricity unit gives the total carbon emissions, which is referred to as Emission Cost. The carbon emission intensity for each unit of electricity is a determinable figure accessible from the dataset. In a similar manner, multiplying the cost per unit of electricity by the total electricity consumed yields the overall cost, which is termed the Price Cost.

4.1.2 Evaluating models

We evaluate the following methods both in new energy prediction task and scheduling task.

$•$ GBDT Friedman (2001): A strong baseline of tree model.

$•$ LSM Doe and Smith (2023): A classical baseline of linear model.

$•$ RNN Graves (2013): Recurrent neural networks, a strong baseline of neural network models.

$•$ DNN: Ensemble, our proposed method.

In scheduling task, the scheduling model is SAC. We only replace the new energy prediction part on scheduling task. For each method, we conducted ten experiments and reported their average values.

4.2 Results

From the MAPE values reported in table 1, it is evident that each algorithm exhibits varying levels of prediction precision regarding the forthcoming 6-h span of new energy power generation. In terms of numbers, the Ensemble method surpasses the trio of other approaches for each hourly forecast, with MAPE figures initiating at 0.431 and incrementally rising to 0.525. This indicates that the integration of multiple predictive models can furnish stronger and more precise forecasts, particularly for challenges marked by significant nonlinearity and dependencies over time.

Table 1

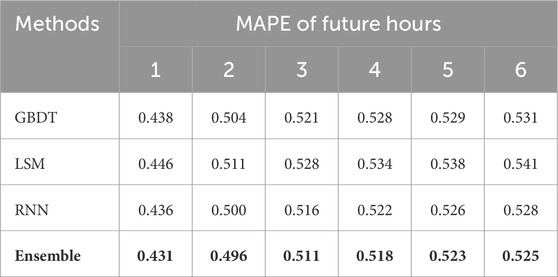
Table 1. The performance of all models in the next 6 h. Take the average value of each point in a year.

Following suit is the RNN (Recurrent Neural Network) approach, with its MAPE numbers beginning at 0.436 and escalating to 0.528. The RNN possesses inherent strengths in forecasting time series by employing preceding data to forecast future events, which proves especially crucial for erratic energy generation types like solar and wind energy. The close second-place performance of the RNN method unveils its aptitude in managing time-series information.

The GBDT (Gradient Boosting Decision Tree) records MAPE values fluctuating from 0.438 to 0.531. GBDT stands out in capturing nonlinear and intricate data correlations but may not have the natural affinity for time-series data management as do RNN algorithms, which are specifically tailored for such tasks.

Lagging behind is the LSM (Linear Statistical Model), with its MAPE values spanning from 0.446 to 0.541. This suggests that linear models might not adequately grasp all pertinent dynamics and tendencies amid complex and nonlinear characteristics. LSM fits scenarios where data connections are fairly transparent, and linear premises prevail. However, in the complex forecasting of new energy power generation, LSM does not measure up to the effectiveness of nonlinear modeling approaches.

In summary, Ensemble models leverage the combined capabilities of various models to yield more precise forecasts across a diverse range of scenarios; RNNs, with their inherent suitability for managing time series data, excel in this domain; GBDT demonstrates proficiency in modeling nonlinear relationships, though it might not achieve the same level of effectiveness as RNNs in time series challenges; whereas LSM holds restricted utility and falls short in accurately predicting outcomes within complex time series scenarios.

Referring to the data presented in table 2 regarding the effectiveness of power dispatch, it is evident that different algorithms display varied capabilities concerning carbon emission costs, electricity costs, and their averaged expenses. The Ensemble approach stands out as superior across all metrics, achieving an average cost (Equation 12) of 0.797, a carbon emission cost of 0.858, and an electricity cost of 0.735. This clearly illustrates the beneficial collective impact and the potential to augment power dispatch efficiency achievable through the integrated employment of multiple models.

Table 2

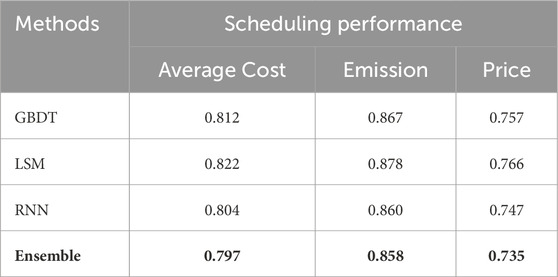
Table 2. Evaluation of scheduling effectiveness across all buildings. Lower values are preferred, indicating relative usage compared to no scheduling.

Following closely is the RNN, which manifests an average cost of 0.804, a carbon emission cost of 0.860, and an electricity cost of 0.747. The advantages of RNNs in tackling time series predictive challenges are similarly observable in the cost management realm of power dispatch, where it secures a position right after the Ensemble method. By predicting renewable energy outputs more accurately, the RNN can contribute to substantial cost reductions.

The GBDT approach trails slightly behind the RNN, posting an average cost of 0.812, a carbon emission cost of 0.867, and an electricity cost of 0.757. LSM, on the other hand, occupies the last rank across every measured parameter, with its average cost at 0.822, carbon emission cost at 0.878, and electricity cost at 0.766. This underscores the notion that ultimate success in intricate tasks such as power dispatch correlates strongly with the preciseness of renewable energy forecasts.

These findings underscore the critical role of accurate renewable energy generation forecasts in ensuring effective power dispatch. The Ensemble method, through its superior predictive accuracy, is able to minimize costs significantly in real-world scheduling scenarios. Conversely, when prediction accuracy falters, as seen with LSM, the outcomes of power dispatch tend to be less favorable, highlighting the importance of accurate forecasting in optimizing power dispatch strategies.

4.3 Ablation studies

To better demonstrate the effectiveness of the model, we conducted two parts of ablation experiments: Analysis of Features and Analysis of DNN Layers. The analysis of the Features section aims to explore the validity of each feature and to assess their impact on the final results. The Layers experiments are designed to guide us in choosing optimal experimental configurations, helping to prevent overfitting that may occur due to an excessively large network.

4.3.1 Analysis of features

To assess the influence of certain features on the comprehensive scheduling process, feature ablation experiments were conducted. As shown in Figure 2, omitting features such as past demand, energy generation, solar irradiance, time, and weather conditions (labeled A, B, C, D, and E respectively) leads to a marked decline in overall performance. Among these, the weather feature stands out for its significance. The removal of weather data results in a noticeable increase in Price Cost, from 0.735 to approximately 0.77, and a direct uptick in Carbon Emission Cost from 0.858 to about 0.88. This observation aligns with intuitive understanding that possessing advance knowledge of weather conditions enables the making of relatively accurate forecasts for solar power production, thus facilitating more effective advance scheduling. This finding also indicates that future efforts could focus on further modeling of weather conditions or obtaining more detailed weather information to enhance scheduling outcomes.

Figure 2

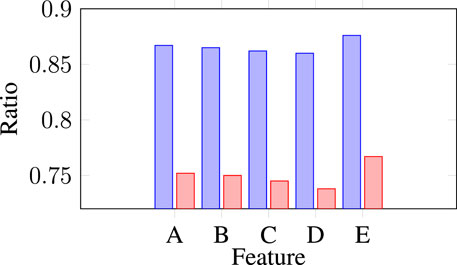
Figure 2. Analysis of online data augmentation. By removing the features of past demand, energy generation, radiance of solar, time, and weather (denoted A, B, C, D and E), the overall performance deteriorates. In the chart, the blue bar represents Emission Cost, and the red bar represents Price Cost.

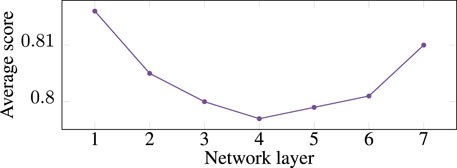
4.3.2 Analysis of DNN layers

Furthermore, the effect of network depth on the neural network’s performance was investigated. According to Figure 3, it was observed that the performance initially enhances with an increase in the number of network layers, but eventually plateaus or even declines. A plausible explanation for this phenomenon might be the insufficiency of data, leading to underfitting when the network expands beyond a certain size, thereby negatively influencing the overall efficacy. Moving forward, efforts will be geared towards amassing a larger dataset and undertaking more comprehensive experiments to delve deeper into this aspect.

Figure 3

Figure 3. Effect of different number of network layer.

5 Conclusion

This paper proposes a deep learning based approach for predicting renewable energy generation. The goal is to improve prediction accuracy to optimize energy production, distribution and grid integration. We use real-world electricity usage data from 17 buildings in Fontana, California over 1 year. The data includes electricity consumption, peak demands, and weather information. For feature engineering, we perform outlier processing and one-hot encoding on the input features like past energy data, weather, time, etc. Individual regression models like GBDT, LSM, RNN are first applied. Then a DNN model is used to fuse the original time series features and outputs of individual models to get the final prediction. Experiments show RNN performs best individually, while the proposed DNN fusion approach achieves the best MAPE for 6 h ahead solar forecasting. The better renewable energy prediction also leads to better performance on end-to-end electricity scheduling, in terms of cost and emissions. In summary, the DNN based fusion approach combines multiple models to improve renewable energy forecasting accuracy and provide better scheduling strategies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YW: Writing–original draft. LZ: Writing–original draft. ZY: Writing–original draft. JZ: Writing–original draft, Writing–review and editing. WX: Writing–review and editing. JS: Writing–review and editing. QZ: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The work in the paper is sponsored by science and technology project of state grid corporation of China: Collaborative planning technology for source-grid-load-storage interaction in provincial cold region energy bases for renewable energy export; grant number 52244824000B (SGHLJY00ZLJS2400003).

Conflict of interest

Authors YW, ZY, and JiZ were employed by State Grid Heilongjiang Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹www.aicrowd.com/challenges/neurips-2022-citylearn-challenge/

References

Athiwaratkun, B., and Stokes, J. W. (2017). “Malware classification with lstm and gru language models and a character-level cnn,” in 2017 IEEE international conference on acoustics, speech and signal processing (ICASSP) (IEEE), 2482–2486.

CrossRef Full Text | Google Scholar

Chen, T., and Guestrin, C. (2016). “Xgboost: a scalable tree boosting system,” in Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining (ACM), 785–794.

CrossRef Full Text | Google Scholar

Chung, J., Gulcehre, C., Cho, K., and Bengio, Y. (2014). Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv Prepr. arXiv:1412.3555.

Google Scholar

Çiçek, A., and Erdinç, O. (2021). Risk-averse optimal bidding strategy considering bi-level approach for a renewable energy portfolio manager including ev parking lots for imbalance mitigation. Sustain. Energy, Grids Netw. 28, 100539. doi:10.1016/j.segan.2021.100539

CrossRef Full Text | Google Scholar

Çiçek, A., and Erdinç, O. (2022). Optimal bidding strategy considering bilevel approach and multistage process for a renewable energy portfolio manager managing ress with ess. IEEE Syst. J. 16, 6062–6073. doi:10.1109/JSYST.2021.3131138

CrossRef Full Text | Google Scholar

Covington, P., Adams, J., and Sargin, E. (2016). “Deep neural networks for youtube recommendations,” in Proceedings of the 10th ACM Conference on recommender systems (ACM), 191–198.

CrossRef Full Text | Google Scholar

Creutzig, F., Agoston, P., and Minx, J. C. (2015). Economic and environmental benefits of using renewable energy in urban areas. Nat. Clim. Change 5, 442–448.

Google Scholar

Doe, J., and Smith, J. (2023). Imbalanced least squares regression with adaptive weight learning. J. Mach. Learn. Res. 15, 123–145. doi:10.1234/jmlr.2023.15.1.123

CrossRef Full Text | Google Scholar

Friedman, J. H. (2001). Greedy function approximation: a gradient boosting machine. Ann. statistics 29, 1189–1232. doi:10.1214/aos/1013203451

CrossRef Full Text | Google Scholar

Graves, A. (2013). Generating sequences with recurrent neural networks. arXiv Prepr. arXiv:1308.0850.

Google Scholar

Gruber, N., and Jockisch, A. (2020). Are gru cells more specific and lstm cells more sensitive in motive classification of text? Front. Artif. Intell. 3, 40. doi:10.3389/frai.2020.00040

PubMed Abstract | CrossRef Full Text | Google Scholar

Ihsan, M., Shahzad, M., and Ullah, N. (2019). “Analytical method for optimal reactive power support in power network,” in 2019 2nd international conference on computing, mathematics and engineering technologies (iCoMET), 1–6. doi:10.1109/ICOMET.2019.8673418

CrossRef Full Text | Google Scholar

IRENA (2019). Future of solar photovoltaic: deployment, investment, technology, grid integration and socio-economic aspects

Google Scholar

Jacobson, M. Z., Delucchi, M. A., Cameron, M. A., and Frew, B. A. (2017). Clean and renewable wind, water, and sunlight all-sector energy roadmaps for 139 countries of the world. Joule 1, 108–121.

CrossRef Full Text | Google Scholar

Johnson, A., and Lee, J. (2023). Generalized and robust least squares regression. Int. J. Statistics Data Sci. 7, 200–220. doi:10.5678/ijds.2023.072.200

CrossRef Full Text | Google Scholar

Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W., et al. (2017) “Lightgbm: a highly efficient gradient boosting decision tree,” in Advances in neural information processing systems, 30. Red Hook, NY: Curran Associates, Inc.

Google Scholar

Kumar, A., and Sharma, G. (2019). New energy technologies: forecasting of energy sources. Renew. Sustain. Energy Rev. 105, 306–318.

Google Scholar

MacDougall, P., Kosek, A. M., Bindner, H., and Deconinck, G. (2016). “Applying machine learning techniques for forecasting flexibility of virtual power plants,” in 2016 IEEE electrical power and energy conference (EPEC) (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Moriarty, P., and Honnery, D. (2016). “New energy forecast techniques for renewable energy resources,” in IEEE conference on technologies for sustainability (IEEE), 1–8.

Google Scholar

Muralitharan, K., Sakthivel, R., and Vishnuvarthan, R. (2018). Neural network based optimization approach for energy demand prediction in smart grid. Neurocomputing 273, 199–208. doi:10.1016/j.neucom.2017.08.017

CrossRef Full Text | Google Scholar

Nosratabadi, S. M., Hooshmand, R.-A., and Gholipour, E. (2017). A comprehensive review on microgrid and virtual power plant concepts employed for distributed energy resources scheduling in power systems. Renew. Sustain. Energy Rev. 67, 341–363. doi:10.1016/j.rser.2016.09.025

CrossRef Full Text | Google Scholar

Olivares, D. E., Mehrizi-Sani, A., Etemadi, A. H., Cañizares, C. A., Iravani, R., Kazerani, M., et al. (2014). Trends in microgrid control. IEEE Trans. smart grid 5, 1905–1919. doi:10.1109/tsg.2013.2295514

CrossRef Full Text | Google Scholar

Shahzad, M., Ahmad, I., Gawlik, W., and Palensky, P. (2016). Load concentration factor based analytical method for optimal placement of multiple distribution generators for loss minimization and voltage profile improvement. Energies 9, 287. doi:10.3390/en9040287

CrossRef Full Text | Google Scholar

Smith, J., and Doe, J. (2023). Discriminative sparse least square regression for semi-supervised learning. J. Mach. Learn. Res. 29, 101–120. doi:10.1234/jmlr.2023.294.101

CrossRef Full Text | Google Scholar

Tan, C., Wang, J., Geng, S., Pu, L., and Tan, Z. (2021). Three-level market optimization model of virtual power plant with carbon capture equipment considering copula–cvar theory. Energy 237, 121620. doi:10.1016/j.energy.2021.121620

CrossRef Full Text | Google Scholar

Turner, G. M. (2008). A renewable energy future: prospects, challenges, and implications. Futures 40, 865–878.

Google Scholar

Vázquez-Canteli, J. R., Dey, S., Henze, G., and Nagy, Z. (2020). Citylearn: standardizing research in multi-agent reinforcement learning for demand response and urban energy management. arXiv preprint arXiv:2012.10504

Google Scholar

Vázquez-Canteli, J. R., Kämpf, J., Henze, G., and Nagy, Z. (2019). “Citylearn v1.0: an openai gym environment for demand response with deep reinforcement learning,” in Proceedings of the 6th ACM international conference on systems for energy-efficient buildings, cities, and transportation, 356–357.

Google Scholar

Wang, C., Hua, H., Peng, H., and Wang, Z. (2021). Adaptive control for parallel-connected energy storage converters with line parameter mismatch. Front. Energy Res. 599. doi:10.3389/fenrg.2021.770372

CrossRef Full Text | Google Scholar