Optimization model for distributed energy trading based on a market value allocation mechanism in the electricity spot market

This study proposes a novel distributed energy trading market model with a value distribution mechanism to optimize the allocation and transactions of distributed energy resources (DERs). The framework incorporates a direct load management approach via an electricity aggregator agent, simplifying market processes and reducing transaction costs. A Nash bargaining model is employed to design a fair and efficient value distribution mechanism, promoting equitable benefit allocation among participants. The model integrates stochastic programming to account for uncertainties in real-time load and DER output, enhancing its robustness and applicability in real-world scenarios. The proposed mechanism quantifies each DER’s contribution using a market value contribution rate, serving as a foundation for the Nash bargaining model. This approach ensures individual rationality for both the aggregator and DERs while maximizing overall system benefits. Case studies validate the model’s effectiveness, demonstrating improvements in resource utilization and fair benefit allocation. This research contributes to the advancement of distributed energy markets, offering valuable insights for designing efficient and equitable market structures, ultimately promoting grid stability, renewable energy adoption, and the development of more sustainable and flexible energy systems.

1 Introduction

The rapid development of distributed energy resources (DERs) has brought new challenges and opportunities to the energy sector. DERs, including distributed generation, energy storage, and flexible loads, have the potential to enhance system efficiency, reliability, and sustainability (Ackermann et al., 2001). However, the integration of these resources into existing power systems requires innovative market mechanisms and operational strategies. Despite the growing adoption of DERs, existing market structures and pricing mechanisms often fail to effectively incentivize their optimal utilization and integration. Traditional fixed-price mechanisms and net metering schemes do not accurately reflect the real-time value of DERs, leading to suboptimal resource allocation and missed opportunities for system-wide efficiency improvements (Parag and Sovacool, 2016). Furthermore, the lack of appropriate market models hinders the ability of DER owners to fully capitalize on the flexibility of their assets and potential contributions to grid stability (Burger et al., 2017). This situation calls for innovative market designs that can facilitate efficient transactions, properly value DER services, and equitably distribute benefits among market participants. Without such advancements, the full potential of DERs in enhancing grid resilience, reducing costs, and supporting the transition to a low-carbon energy system remains unrealized (Zhou et al., 2018).

Existing approaches to DER integration face challenges including scalability issues in peer-to-peer (P2P) models, suboptimal resource allocation in aggregator-based systems, inaccurate valuation of DER contributions, and implementation difficulties due to regulatory barriers and integration complexities. Additionally, current methods often struggle with fair benefit allocation, effective coordination of numerous small-scale resources, and adequate consideration of real-time uncertainties in load and energy output.

Recent research has explored various approaches to address the challenges of integrating DERs into existing power systems. These approaches can be categorized into peer-to-peer energy trading models, aggregator-based approaches, value distribution mechanisms, and market design challenges for DERs. Peer-to-peer energy trading models have gained significant attention as a means to facilitate direct energy transactions between prosumers. Tushar et al. (2021) provided a comprehensive review of peer-to-peer energy systems for connected communities, highlighting their potential to enhance local energy autonomy and system efficiency. They discussed various market designs, including bilateral contracts and auction-based mechanisms, emphasizing the need for scalable and fair trading platforms. Morstyn et al. (2018) introduced a cooperative game theory approach for peer-to-peer energy trading, aiming to ensure stable and fair outcomes for all participants and potentially increase the adoption of such trading schemes.

Aggregator-based approaches have emerged as a promising solution to manage the complexity of coordinating numerous small-scale DERs. Burger et al. (2017) reviewed the value of aggregators in electricity systems, discussing how they can create value by optimizing DER portfolios and providing services to both DER owners and system operators. Their work underscored the importance of appropriate market designs to unlock the full potential of aggregation services. Wang et al. (2014) explored the concept of transactive energy systems, proposing a distributed optimization framework for coordinating DERs in distribution networks. Their approach showed promise in reducing system operational costs and enhancing the integration of renewable energy sources. Burger et al. (2019) conducted a critical review of the trade-offs between centralized and decentralized resources, highlighting the importance of proper value assessment and distribution in DER integration. Their analysis emphasized the need for market structures that accurately reflect the contributions of individual DERs to system-wide benefits.

Value distribution mechanisms are crucial for ensuring fair benefit allocation among market participants. In P2P energy trading frameworks, such as the Brooklyn Microgrid, the value allocation mechanism can be adapted to determine fair compensation for prosumers based on their contributions to the local energy market. This adaptation could replace traditional fixed pricing models with dynamic pricing that reflects real-time supply and demand, enhancing the economic viability of P2P transactions (Soto et al., 2021). In community energy systems, particularly those emerging under the European Union’s Clean Energy Package, the value allocation mechanism could be utilized by community energy managers to optimize local energy exchanges. This approach would ensure that benefits are distributed fairly among community members, thereby fostering participation and promoting local energy resilience (Inês et al., 2020). Furthermore, the mechanism can be integrated into ancillary service markets, allowing aggregators to participate in larger electricity markets while ensuring that the contributions of DERs are accurately valued. For instance, in the Power Responsive program in the United Kingdom, the value allocation mechanism could facilitate the participation of aggregators in providing demand response services, ensuring that all participants receive compensation commensurate with their contributions to grid stability (National Grid ESO, 2021).

Market design challenges for DERs remain a significant area of research. Parag and Sovacool (2016) examined the electricity market design for the prosumer era, identifying key challenges in integrating DERs into existing market structures. They emphasized the need for new market models that can accommodate the unique characteristics of DERs. Mengelkamp et al. (2018) investigated local electricity markets, proposing a blockchain-based microgrid energy market. Their work demonstrated the potential for decentralized market structures to facilitate efficient energy trading among prosumers while also highlighting the technical and regulatory challenges in implementing such systems.

A novel distributed energy market model based on a value distribution mechanism is proposed in this article, addressing key challenges in the optimization of DER allocation and market transactions. The framework integrates a direct load management approach through an electricity aggregator agent, aiming to simplify market transactions and reduce costs. The proposed model uses a Nash bargaining approach to design a fair and efficient value-distribution mechanism, promoting equitable benefit allocation among market participants. Additionally, stochastic programming is incorporated in this model to account for uncertainties in real-time load and distributed energy output, enhancing its robustness and applicability in real-world scenarios. This integrated approach offers a comprehensive solution that optimizes resource allocation, facilitates efficient market transactions, and ensures fair benefit distribution among participants. The proposed framework contributes to the ongoing development of effective distributed energy markets, addressing the need for scalable, fair, and efficient solutions in the evolving energy landscape.

The main contributions of this paper can be summarized as follows:

1. A novel distributed energy trading market model based on a value allocation mechanism is proposed in this article, which optimizes allocation and market transactions for DERs.

2. We design a value allocation mechanism using a Nash bargaining model, which incentivizes market participation and enhances overall system benefits.

3. The model is validated through case studies demonstrating the improved utilization of distributed resources and fair benefit allocation, contributing to the design of efficient and equitable distributed energy markets.

2 System model

It is essential to establish optimization models for distributed energy systems (DESs) under both independent operation and shared operation modes. This analysis elucidates the fundamental mechanism by which the shared operation mode incentivizes DESs to participate in the spot market, thereby enhancing social welfare. To streamline the bidding process and protect user privacy, we propose a direct load management model where electricity aggregators act as agents for DESs in distributed energy transactions. Following market optimization and clearing, we introduce the concept of a market value contribution ratio to quantitatively assess the contributions of different DESs. This ratio serves as the basis for allocating and settling system benefits according to the contribution of each DES, thereby ensuring sufficient incentives and willingness for DESs to participate in the distributed energy trading market.

2.1 Distributed energy trading market model

Considering the numerous DESs in the distribution network, we assume that DESs are price takers, meaning that the distributed system will not strategically alter its electricity consumption behavior to influence the benefits of participating in distributed energy transactions. Due to the relatively small electricity volumes of DESs in the distribution network, this model does not consider the impact of DES load behavior changes on transmission network nodal prices, treating nodal prices as predetermined constants. To simplify the market transaction model, the models in this section do not account for the distribution network topology or network losses.

2.1.1 Distributed energy trading market process

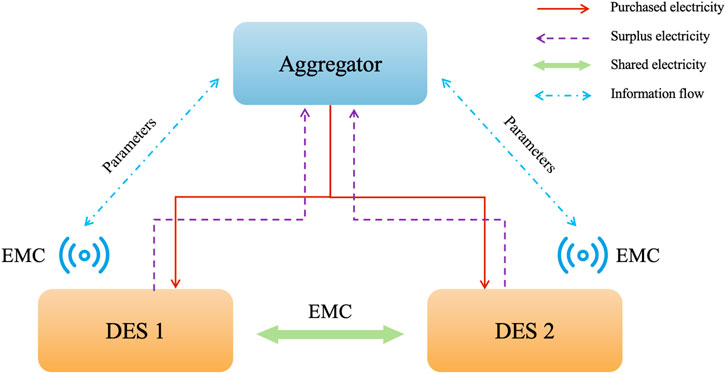
To streamline the bidding process and simplify market transactions, a market process adapted for distributed energy trading is designed in this section. Given that electricity is a homogeneous commodity, we consider an electricity aggregator operating a unified distributed energy trading platform, acting as an agent for all DESs. On this platform, DESs can share surplus electricity from their photovoltaic (PV) systems and energy storage or utilize surplus energy from other DESs. The energy consumption behavior of DESs is guided by the aggregator through coordinated pricing. After market clearing, the aggregator pays the corresponding fees based on the cleared trading volume of each DES in the distributed energy transactions. The specific process is as follows:

1. All DESs sign agreements with the aggregator, allowing them to participate in the aggregator-operated distributed energy trading platform and stipulating payment and settlement rules for distributed energy transactions.

2. Each DES optimizes its distributed energy resources and load based on the coordinated price issued by the aggregator and decides on its trading volume in the platform.

3. The aggregator collects net load information from all DESs, participates in wholesale market electricity purchases and sales, and maintains power supply and demand balance.

4. The aggregator settles accounts with all DESs: settling net loads at the retail electricity price, surplus electricity at the net metering price, and distributed energy market transactions according to the agreement.

Figure 1 shows the market framework of the DESs and aggregator. Compared to traditional models without a distributed energy trading market, energy sharing provides DESs with a win–win trading platform and business model. The distributed energy trading market forms a coalition of the aggregator and all DESs, aiming to maximize social welfare in response to price signals from the main grid.

Figure 1

Figure 1. Distributed energy trading market model based on the aggregator agency.

It should be noted that maximizing the overall benefits of the aggregator and all DESs requires all DESs to report their private information to the aggregator, including utility functions, load demands and adjustment ranges, and distributed energy parameters. However, in reality, it is challenging for the aggregator to require all DESs to report their private information, making it difficult to implement a centralized quotation-based market trading model. Therefore, the concept of direct load management is adopted in this section by the aggregator acting as an agent for DESs, proposing a distributed market trading model to simplify the transaction process and protect DES privacy.

Each DES is equipped with an energy management controller (EMC) to optimize and control the hourly power of energy storage, electrical appliances, and other equipment within the DES. The EMC communicates with the electricity aggregator, sending cost information, adjustment ranges, and other parameters of distributed energy resources to the aggregator while receiving control signals issued by the aggregator. Consequently, the aggregator acts as an agent for all DESs to participate in distributed energy trading, implementing direct load management. It is worth noting that under the direct load management mode, DESs only need to entrust their distributed energy resources to the aggregator. The aggregator then decides on the operation mode of the distributed energy resources and allocates value based on the benefits created by these resources.

2.1.2 Aggregator model

The aggregator acts as an intermediary connecting the DESs and the main grid. It purchases electricity from the main grid at nodal marginal prices and sells it to DESs at retail prices or buys distributed energy from DESs at net metering prices and feeds it back to the main grid at nodal marginal prices.

The aggregator acting as an agent is considered in this section for $N$ DESs participating in the day-ahead market. To account for the uncertainties in real-time load and distributed energy output, we use a scenario-based stochastic programming approach. Specifically, we use scenario sets to characterize possible real-time loads and distributed energy outputs. The net revenue model for the aggregator is as follows:

$r^A={\displaystyle \sum _{s\in {\mathrm{\Phi }}^S}}{\displaystyle \sum _{t\in {\mathrm{\Phi }}^T}}{\gamma }_s\left[{\lambda }_{s,t}^{\mathit{out}}{P}_{s,t}^{NS}-{\lambda }_{s,t}^{in}{P}_{s,t}^{NL}+{\lambda }_t^R{\displaystyle \sum _{i\in {\mathrm{\Phi }}^U}}{P}_{i,s,t}^{NL}-{\lambda }_t^S{\displaystyle \sum _{i\in {\mathrm{\Phi }}^U}}{P}_{i,s,t}^{NS}\right],(1)$

where $r^A$ is the net revenue of the aggregator; ${\mathrm{\Phi }}^S$, ${\mathrm{\Phi }}^T$, and ${\mathrm{\Phi }}^U$ represent the sets of scenarios, time periods, and DESs, respectively; ${\gamma }_s$ is the probability of scenario $s$; ${\lambda }_{s,t}^{\mathit{out}}$ and ${\lambda }_{s,t}^{in}$ are the prices for the aggregator to sell electricity to and buy electricity from the main grid, respectively; ${\lambda }_t^R$ and ${\lambda }_t^S$ are the retail price and net metering price offered by the aggregator to DESs, respectively; $P_{i,s,t}^{NS}$ and $P_{i,s,t}^{NL}$ are the net surplus power and net load, respectively, of $i^{\text{th}}$ DESs in scenario $s$ and time period $t$; $P_{s,t}^{NS}$ and $P_{s,t}^{NL}$ are the total net surplus power and net load of all DESs, respectively, in scenario $s$ and time period $t$, which are represented as follows:

$P_{s,t}^{NL}={\left[{\displaystyle \sum _{i\in {\mathrm{\Phi }}^U}}\left(P_{i,s,t}^{NL}-P_{i,s,t}^{NS}\right)\right]}_{+},\forall s,t,(2)$

$P_{s,t}^{NS}={\left[{\displaystyle \sum _{i\in {\mathrm{\Phi }}^U}}\left(P_{i,s,t}^{NS}-P_{i,s,t}^{NL}\right)\right]}_{+},\forall s,t.(3)$

The buying and selling prices between the aggregator and the main grid are related to nodal marginal prices. In reality, due to factors such as transmission fees and tax rates, the purchase price ${\lambda }_{s,t}^{in}$ is often not equal to the selling price ${\lambda }_{s,t}^{\mathit{out}}$. Purchase and sale ratio coefficients ${\omega }^{in}$ and ${\omega }^{\mathit{out}}$, respectively, are introduced in this section to reflect the relationship between nodal marginal prices and the aggregator buying and selling prices:

${\lambda }_{s,t}^{in}={\omega }^{in}{\lambda }_{s,t}^{\mathit{LMP}},{\lambda }_{s,t}^{\mathit{out}}={\omega }^{\mathit{out}}{\lambda }_{s,t}^{\mathit{LMP}},\forall s,t.(4)$

2.1.3 Distributed energy system management model

Let us assume that each distributed energy system is equipped with one rooftop PV system, one battery energy storage system, and several electrical devices. The energy management system of each DES is responsible for optimizing and controlling distributed energy resources and controllable loads. The optimization model is as follows. The objective function is

$\arg \underset{{\mathbf{X}}_i}{\min }{c}_i^U={\displaystyle \sum _{s\in {\mathrm{\Phi }}^S}}{\displaystyle \sum _{t\in {\mathrm{\Phi }}^T}}{\gamma }_s\left[{\lambda }_t^R{P}_{i,s,t}^{NL}-{\lambda }_t^S{P}_{i,s,t}^{NS}-U_i\left(P_{i,s,t}^L\right)\right],(5)$

where the optimization decision variable ${\mathbf{X}}_i$ includes the net surplus power $P_{i,s,t}^{NS}$, net load $P_{i,s,t}^{NL}$, controllable load $P_{i,s,t}^L$, PV power $P_{i,s,t}^{PV}$, energy storage charge and discharge power $P_{i,s,t,\alpha /\beta }^{\mathit{ESS}}$, and stored energy of the $i^{\text{th}}$ DES $E_{i,s,t}^{\mathit{ESS}}$. $c_i^U$ is the net cost of the $i^{\text{th}}$ DES. $U_i(\cdot )$ is the utility function of the $i^{\text{th}}$ DES, which is assumed to be a concave quadratic function in this paper.

The optimization model includes the following constraints.

2.1.3.1 Power balance constraint

$P_{i,s,t}^{NL}-P_{i,s,t}^{NS}=P_{i,s,t}^L-P_{i,s,t}^{PV}+P_{i,s,t,\alpha }^{\mathit{ESS}}-P_{i,s,t,\beta }^{\mathit{ESS}},\forall s,t,(6)$

which indicates that the net load of a DES equals the difference between its total load and distributed energy output. Note that as the retail electricity price $Ph{i}^R$ is higher than the net metering price $Ph{i}^S$, the objective function (Equation 5) ensures that at least one of the net surplus power and net load is 0. When the DES net load is positive, $P_{i,s,t}^{NL}>0$ and $P_{i,s,t}^{NS}=0$; when the DES net load is negative, $P_{i,s,t}^{NL}=0$ and $P_{i,s,t}^{NS}>0$.

2.1.3.2 Net load constraint

$0\le P_{i,s,t}^{NL},P_{i,s,t}^{NS}\le P_{i,\max }^C,\forall s,t.(7)$

2.1.3.3 PV power constraint

$0\le P_{i,s,t}^{PV}\le P_{i,s,t}^{\mathit{FPV}},\forall s,t.(8)$

2.1.3.4 Controllable load constraints

$P_{i,s,t,\min }^L\le P_{i,s,t}^L\le P_{i,s,t,\max }^L,\forall s,t.(9)$

${\displaystyle \sum _{t\in {\mathrm{\Phi }}^T}}{P}_{i,s,t}^L\ge Q_{i,s}^L,\forall s,(10)$

where $P_{i,s,t,\min }$ and $P_{i,s,t,\max }$, respectively, represent the lower and upper limits of controllable load for the $i^{\text{th}}$ DES, and $Q_{i,s}^L$ is the minimum daily electricity consumption of the $i^{\text{th}}$ DES.

2.1.3.5 Energy storage operation constraints

$0\le P_{i,s,t,a}^{\mathit{ESS}}\le P_{i,\alpha ,\max }^{\mathit{ESS}},\forall s,t,(11)$

$0\le P_{i,s,t,\beta }^{\mathit{ESS}}\le P_{i,\beta ,\max }^{\mathit{ESS}},\forall s,t,(12)$

$E_{i,s,t}^{\mathit{ESS}}=E_{i,s,t-1}^{\mathit{ESS}}+{\eta }_i^{\mathit{ESS}}{P}_{i,s,t,a}^{\mathit{ESS}}-P_{i,s,t,\beta }^{\mathit{ESS}}/{\eta }_i^{\mathit{ESS}},\forall s,t,(13)$

$E_{i,\min }^{\mathit{ESS}}\le E_{i,s,t}^{\mathit{ESS}}\le E_{i,\max }^{\mathit{ESS}},\forall s,t,(14)$

$E_{i,s,N^T}^{\mathit{ESS}}=E_{i,s,0}^{\mathit{ESS}},\forall s.(15)$

Equations 11, 12 represent the power constraints of energy storage charging and discharging, respectively, and $P_{i,\alpha ,\max }^{\mathit{ESS}}$ represents the maximum charging and discharging power. Equation 13 represents the dynamic change process of stored energy, Equation 14 limits the stored energy, and $E_{i,\min }^{\mathit{ESS}}$ and $E_{i,\max }^{\mathit{ESS}}$ are the lower and upper limits of stored energy, respectively. Equation 15 sets the final state of energy storage to be the same as the initial state, ensuring continuous operation of energy storage.

So far, we established the mathematical models for DESs operating independently without participating in the market. Optimizing and solving the above model can obtain the optimal operating state ${\mathbf{X}}_i^{*}$ of DESs when operating independently. At this time, the net cost of the DES is recorded as $c_i^{U,0}$ and the net income of the aggregator when DESs operate independently is recorded as $r^{A,0}$. At this point, the cost vector $[-r^{A,0},c_1^{U,0},\dots ,c_N^{U,0}]$ composed of DESs and the aggregator is called the non-cooperative state (disagreement point).

2.1.4 Distributed energy trading market model

As analyzed previously, the establishment of a distributed energy trading market by the aggregator is equivalent to organizing all DESs with the objective of maximizing social welfare or minimizing system operating costs as a market clearing model. When DESs participate in distributed energy trading, sharing their own distributed energy resources with other systems, it may lead to increased operating costs compared to their independent operation state. Therefore, the aggregator, as the market organizer, needs to pay fees to the DESs to incentivize their active participation in market optimization. Let the fee paid by the aggregator to the $i^{\text{th}}$ DES be ${\pi }_i^{ES}$, then the net cost of the DES becomes $c_i^U-{\pi }_i^{ES}$, whereas the net income of the aggregator becomes . The distributed energy trading market model is established as follows, with the objective function:

$\arg \underset{\mathbf{x}}{\min }-r^A+{\displaystyle \sum _i}{\pi }_i^{ES}+{\displaystyle \sum _i}\left(c_i^U-{\pi }_i^{ES}\right)=-r^A+{\displaystyle \sum _{i\in {\mathrm{\Phi }}^U}}{c}_i^U,(16)$

In Equation 16, the optimization decision variables $\mathbf{x}$ include all optimization decision variables of distributed energy systems, the total net surplus power and net load variables of the aggregator, and the electricity volume of distributed energy systems participating in distributed energy trading. The objective function represents minimizing the costs of the aggregator and all distributed energy systems. Note that as $p{i}_i^{ES}$ is the benefit settlement between the aggregator and distributed energy systems, it cancels out in the objective function. The model includes the following constraints.

2.1.4.1 Power balance constraint for distributed energy systems

$P_{i,s,t}^{NL}-P_{i,s,t}^{NS}-P_{i,s,t}^{ES}=P_{i,s,t}^L-P_{i,s,t}^{PV}+P_{i,s,t,\alpha }^{\mathit{ESS}}-P_{i,s,t,\beta }^{\mathit{ESS}},\forall i,s,t.(17)$

Compared to the power balance constraint Equation 6, when DESs operate independently, the electricity volume of DESs participating in market trading is introduced into the constraint condition.

2.1.4.2 Distributed energy trading balance constraint

${\displaystyle \sum _{i\in {\mathrm{\Phi }}^U}}{P}_{i,s,t}^{ES}=0:{\lambda }_{s,t}^{ES},\forall s,t.(18)$

The above equation indicates that the sum of the trading volumes of all distributed energy systems in each scenario and time period is zero. ${\lambda }_{s,t}^{ES}$ represents the marginal price of distributed energy market clearing.

2.1.4.3 Distributed energy trading volume constraint for DESs

$-P_{i,\max }^C\le P_{i,s,t}^{ES}\le P_{i,\max }^C,\forall i,s,t.(19)$

The above equation indicates that the trading volume of distributed energy systems can be positive or negative. A positive value means the distributed energy system is a supplier in the market, whereas a negative value means it is a consumer.

In addition, the distributed energy trading market model also includes individual constraints (Equations 6–15) for all distributed energy systems, as well as constraints (Equations 1–4) for the aggregator. Optimizing the above model yields the optimal operating state $\widehat{\mathrm{x}}$ when DESs participate in market trading. At this time, the net cost of distributed energy systems is represented as $c_i^{U,1}$, and the net income of the aggregator is recorded as $r_i^{A,1}$. The cost vector composed of distributed energy systems and the aggregator $[-r^{A,1},c_1^{U,1},\dots ,c_N^{U,1}]$ is called the cooperative state (agreement point). As the distributed energy market maximizes the benefits of the aggregator and distributed energy systems, the cooperative state has lower costs than the non-cooperative state. The difference is called the cooperative surplus, which is defined in Equation 20:

$\mathrm{\Delta }=\left(-r^{A,0}+{\displaystyle \sum _{i\in {\mathrm{\Phi }}^U}}{c}_i^{U,0}\right)-\left(-r^{A,1}+{\displaystyle \sum _{i\in {\mathrm{\Phi }}^U}}{c}_i^{U,1}\right)\ge 0.(20)$

After market optimization scheduling, distributed energy systems share distributed power sources, causing their operation to deviate from individual optimum, which may lead to an increase in their own electricity purchase costs, that is, $c_i^{U,1}>c_i^{U,0}$. For this reason, the aggregator needs to identify the contributions and values of different distributed energy systems in the distributed energy market and allocate benefits to ensure that all distributed energy systems have the willingness and incentive to actively participate in the distributed energy market, that is, ${}^{1}c_i^{U,1}-{\pi }_i^{ES}\le c_i^{U,0}$. As ${\pi }_i^{ES}$ cancels out in the distributed energy market clearing model, a value allocation mechanism to calculate ${\pi }_i^{ES}$ is proposed in this paper.

2.2 Value allocation mechanism for the distributed energy trading market

Nash bargaining theory is a method to study how market participants share cooperative surplus. By maximizing the product of utility differences before and after cooperation for all market participants, subject to a series of constraints, optimizing the Nash bargaining model can yield the benefit allocation results among market participants. The optimal solution of the Nash bargaining model satisfies properties such as individual rationality, balance of payments, and social welfare maximization.

First, a market value contribution rate is proposed in this section to quantify and identify the contributions and values of different DESs in distributed energy market transactions. Then, a Nash bargaining model is established considering the market value contribution rate, the benefit settlement between the aggregator and DESs is optimized, and the corresponding value allocation mechanism is derived theoretically to promote DES participation in the spot market.

2.2.1 Market value contribution rate

First, the contribution of a DES to distributed energy market transactions is defined as the economic value of its market participation volume. In scenario $s$ and time period $t$, the contribution $C_{i,s,t}^U$ of a DES is defined in Equation 21:

$C_{i,s,t}^U={\lambda }_{s,t}^{ES}\left|P_{i,s,t}^{E{S}^{*}}\right|,\forall i,s,t.(21)$

That is, the product of the distributed energy market clearing price and the DES market participation volume. Note that as the DES market participation volume $P_{i,s,t}^{E{S}^{*}}$ can be positive or negative, the absolute value of the volume is taken in the above equation. It is considered that both supply and demand generate value for the distributed energy market.

Therefore, the market value contribution rate of a DES is the ratio of its total contribution to market transactions to the contributions of all DESs, which is defined in Equation 22:

$SC{R}_i=\left(1-{\tau }^A\right)\frac{{{\displaystyle \sum }}_{s,t}{\gamma }_s{C}_{i,s,t}^U}{{{\displaystyle \sum }}_{j,s,t}{\gamma }_s{C}_{j,s,t}^U},(22)$

where ${\tau }^A\in (\mathrm{0,1})$ is the profit rate of the aggregator, which is assumed to be a constant in this section. In practice, this profit rate can be controlled by relevant government departments to limit the earnings of the aggregator. Note that for DESs not participating in the distributed energy market, $P_{i,s,t}^{ES*}$ is always 0, so their contribution is 0, and their market value contribution rate is also 0.

2.2.2 Value allocation mechanism

The settlement rules between the aggregator and DESs can be obtained by optimizing the following Nash bargaining model:

$\underset{\mathbf{X},\mathbf{\Pi }}{\max }{f}^{NB}={\left(-r^{A,0}+r^A-{\displaystyle \sum _{i\in {\mathrm{\Phi }}^{ES}}}{\pi }_i^{ES}\right)}^{T^A}{\displaystyle \prod _{i\in {\mathrm{\Phi }}^{ES}}}{\left(c_i^{U,0}-c_i^U+{\pi }_i^{ES}\right)}^{SC{R}_i},(23)$

Equation 23 is subjected to all DES individual constraints, aggregator constraints, and distributed energy market constraints (Equations 17–19), and the following individual rationality constraints:

$-r^{A,0}+r^A-{\displaystyle \sum _{i\in {\mathrm{\Phi }}^{ES}}}{\pi }_i^{ES}\ge 0,(24)$

$c_i^{U,0}-c_i^U+{\pi }_i^{ES}\ge 0,\forall i\in {\mathrm{\Phi }}^{ES}.(25)$

In this model, the optimization decision variables are $\mathrm{X}$ and the payment $\mathbf{\Pi }$ fees from the aggregator to DESs. The objective function is a Cobb–Douglas function, where the first term represents the utility difference of the aggregator before and after organizing the distributed energy market and the second term represents the utility difference of DESs before and after participating in the distributed energy market. Constraints (Equations 24, 25) represent the individual rationality of the aggregator and DESs, respectively, ensuring that costs decrease after participating in the distributed energy market, thus guaranteeing the willingness of market participants. Note that ${\mathrm{\Phi }}^{ES}$ represents the set of DESs with market value contribution rates greater than 0, excluding DESs not participating in the market from the DES set ${\mathrm{\Phi }}^U$.

The above Nash bargaining model has the following analytical solution:

${\pi }_i^{E{S}^{*}}=SC{R}_i\cdot \mathrm{\Delta }+c_i^{U,1}-c_i^{U,0},\forall i,(26)$

In Equation 26, $\mathrm{\Delta }$ is the cooperative surplus, that is, the total system cost reduction or total social welfare increase. The value allocation mechanism stipulates that the payment received by DESs consists of two parts: the first part is the increase in individual operating costs after DESs participate in the distributed trading market; $SC{R}_i\cdot \mathrm{\Delta }$ is the benefit obtained from the cooperative surplus according to the energy contribution rate.

Therefore, the economic connotation of the value allocation mechanism is as follows: first, pay each DES for the additional operating costs incurred by sharing distributed energy, to ensure that the operating costs of each DES do not increase after participating in market transactions; then, share the jointly created social welfare according to the contribution of each DES. Note that this settlement rule also applies to DESs not participating in market transactions, whose contribution rate is 0, and the individual operating cost change is 0, resulting in zero payment from the aggregator to these DESs.

From the value allocation mechanism, the net benefits of DESs and the aggregator after participating in the distributed trading market are defined in Equations 27, 28:

$-r^{A,0}+\left(r^{A,1}-{\displaystyle \sum _{i\in {\mathrm{\Phi }}^U}}{\pi }_i^{E{S}^{*}}\right)={\tau }^A\mathrm{\Delta },(27)$

$c_i^{U,0}-\left(c_i^{U,1}-{\pi }_i^{E{S}^{*}}\right)=SC{R}_i\mathrm{\Delta },\forall i.(28)$

Thus, it can be observed that the net benefits of all DESs and the aggregator in the distributed trading market are non-negative, ensuring the willingness of market participants to participate.

3 Simulations

3.1 Dataset

The effectiveness of the value allocation mechanism is verified in this section through a system of 10 DESs. The data used in this simulation include 1 aggregator and 10 DESs. The load and rooftop PV data for the DESs are sourced from Austin, Texas, United States. The quadratic and linear coefficients of the DES utility functions are drawn from U[−0.5, −0.1] and U[20, 50], respectively. The adjustable range of the DES load is 0.8–1.2 times the baseline, and the daily minimum electricity consumption requirement for each DES is its actual load. The parameters of the DES battery energy storage are shown in Table 1.

Table 1

Table 1. Parameters for the ESS.

The aggregator provides time-of-use electricity prices for DESs, that is, 0.212 $/kWh from 1:00 a.m. to 8:00 a.m. and 22:00 p.m. to 24:00 p.m.; 0.238 $/kWh from 8:00 a.m. to 12:00 p.m. and 18:00 p.m. to 22:00 p.m.; and 0.263 $/kWh from 12:00 p.m. to 18:00 p.m. The net metering price is 0.03 $/kWh. Locational marginal price data are taken from an annual price of a bus in the US PJM market. The coefficients are set to ${\mathit{\omega }}^{in}=2$ and ${\mathit{\omega }}^{in}=2$.

To verify the effectiveness of organizing the distributed energy market and the value allocation mechanism, three operation modes are adopted in this section, as shown in Table 2.

Table 2

Table 2. Comparison of three different operation modes for DESs.

Among them, M1 represents the independent operation mode of DESs, which does not consider the distributed energy trading market. DESs only trade and settle with the aggregator at given retail and net metering price levels. M2 represents market trading and benefit sharing settlement, which allows DESs to participate in the distributed energy trading market while using the traditional symmetric Nash bargaining model for average benefit sharing. Symmetric Nash bargaining requires equal weights for all DESs, that is,

$SC{R}_i=\frac{1-{\tau }^A}{N},\forall i.(29)$

The aggregator profit rate is set to ${\tau }^A=0.2$. Therefore, the traditional symmetric Nash bargaining model does not distinguish the value and contribution created by different DESs in market transactions, and the social welfare brought by market transactions is evenly distributed among all DESs.

M3 represents market trading and value allocation settlement, which allows DESs to participate in the distributed energy trading market and uses the value allocation mechanism proposed in this paper, that is, “market value contribution rate + Nash bargaining,” for benefit sharing. The market value contribution rate defines the bargaining power of DESs in the Nash bargaining model proposed in this paper:

$SC{R}_i=\left(1-{\tau }^A\right)\frac{{{\displaystyle \sum }}_{s,t}{\gamma }_s{C}_{i,s,t}^U}{{{\displaystyle \sum }}_{j,s,t}{\gamma }_s{C}_{j,s,t}^U}.(30)$

By comparing M1 and M3, we can verify the role of the distributed energy market and analyze the effects of different settlement mechanisms. It is worth noting that both M2 and M3 consider the distributed energy market, and their market trading results are consistent, with only the settlement results being different as indicated in Equations 29, 30.

3.2 Results of distributed energy market trading

Figures 2A, B compare the power curves of a DES with and without the distributed energy market. It shows that without a distributed energy market, DESs have no incentive or willingness to arbitrage through energy storage under peak–valley retail prices. Therefore, energy storage is only used to store excess photovoltaic electricity during the day and discharge at night to meet part of the load. Due to the low net metering price level, DESs tend to minimize their own net load rather than feed electricity back to the aggregator. After the aggregator organizes the distributed energy market, DESs will significantly increase the utilization of battery storage, shifting daytime loads to nighttime. The net load curve of the DES shows that the DES can even provide power during the day. Moreover, comparing the load curves with and without the market shows that the DES load curve itself also shows some degree of peak shaving and valley filling.

Figure 2

Figure 2. Power curves of a DES with and without the distributed energy market: (A) without energy sharing and (B) with energy sharing.

The marginal price of the 10 DESs is compared with market and without market, as shown in Figure 3. In the distributed energy market, the aggregator aggregates all DESs to respond to the main grid price. Therefore, during the peak load period from 8:00 to 20:00, the aggregated net load decreases by 101.56 kW h, which is equivalent to providing power support for the main grid, alleviating the main grid supply pressure, and demonstrating the grid-friendly benefits of distributed energy resources.

Figure 3

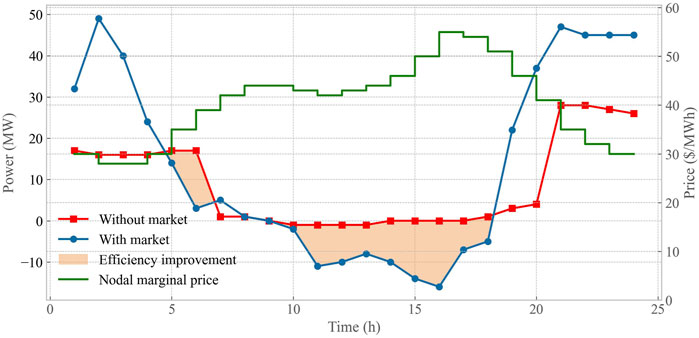
Figure 3. Comparison of the aggregated net load vs. nodal marginal price of the 10 DESs with and without a market.

Table 3 shows the load, energy storage charge/discharge amount, and photovoltaic consumption for all DESs. The distributed energy market allows DESs to share surplus electricity from PVs and ESSs, or purchase shared electricity from other DESs, thus providing a more cost-effective way of electricity consumption. DESs tend to use more electricity to increase their utility level, with the distributed energy market effectively increasing the load by 3.12%. Additionally, the energy storage utilization rate increased by 73.45%. Due to the zero marginal cost of photovoltaic generation, PV electricity is fully consumed under both market and non-market conditions.

Table 3

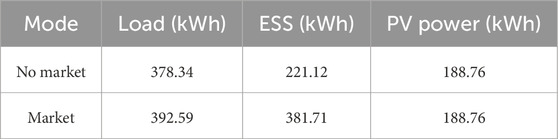
Table 3. Load, energy storage charge/discharge, and consumption of PV electricity for all smart buildings.

Table 4 compares the costs and benefits of the aggregator and DESs under three operation modes. Note that negative costs indicate positive benefits. Compared to M1, which has no distributed energy market, the costs of DESs significantly increase after participating in the market. This is because DESs need to deviate from their individually optimal operating states when sharing distributed energy or responding to main grid prices. However, the aggregator can profit from this. To incentivize DESs to participate in the distributed energy market, the aggregator needs to share the benefits generated from market operation with the DESs. Both M2 and M3 settlement methods can reduce the operating costs of DESs and improve their benefit levels. M2 evenly distributes the total fees the aggregator allocates to DESs among different DESs, whereas M3 distributes them according to the contribution rate of DESs. Under the M3 operation mode, the aggregator benefit can increase by 3.46%, and the cost reduction for different DESs ranges from 0.36 to 0.44 dollars.

Table 4

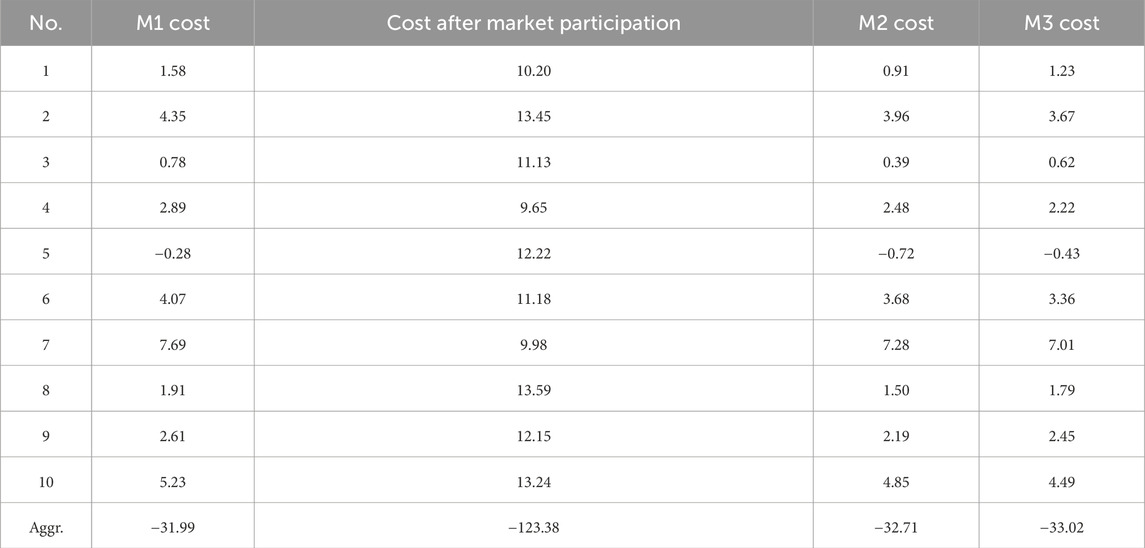
Table 4. Cost benefit of electricity retailers and smart buildings under three operation modes (unit: USD).

3.3 Results of the value allocation mechanism

As previously analyzed, symmetric Nash bargaining evenly distributes the total fees allocated by the aggregator among different DESs, resulting in equal contribution rates for each DES. However, in reality, different DESs contribute differently to distributed energy market transactions. A DES sharing 1 kW h of electricity and one sharing 10 kW h should be paid different fees and receive different benefits. The value allocation mechanism proposed in this paper can effectively identify the value and contribution of different DESs and allocate benefits according to their contribution rates.

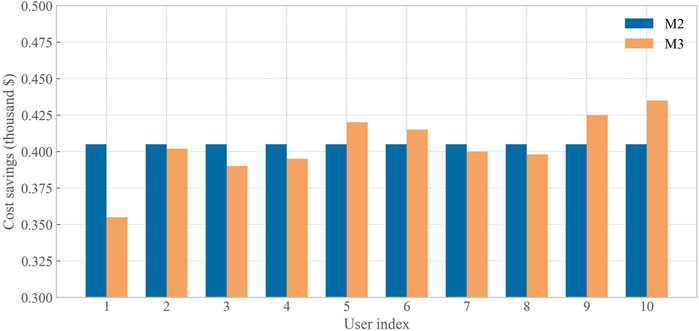
Figure 4 shows the cost reduction for different DESs under M2 and M3 settlements. Under the M2 settlement, all DESs have the same cost reduction of $0.41. However, under the M3 settlement, the cost reductions for all DESs range from $0.36 to $0.44. The difference in cost reductions among DESs stems from their contributions to the distributed energy market, that is, the value of surplus electricity shared or consumed by the DESs.

Figure 4

Figure 4. Cost reduction for different DESs under M2 and M3 settlements.

Under the M3 settlement, a significant positive correlation exists between the market value contribution rates of all DESs and the surplus electricity contributed or consumed. This indicates that the more a DES participates in market transactions, the higher its contribution and value to the market; therefore, it should receive a higher level of benefits. In contrast, under the M2 settlement, the contribution rates of all DESs are unrelated to their market participation levels and are all equal to 0.08.

Therefore, the distributed energy market model proposed in this paper can significantly improve the overall benefits of the aggregator and DESs. The value allocation mechanism can effectively identify the value and contribution of DESs and allocate corresponding benefits.

3.4 Analysis of the profit rate impact of the aggregator

The impact of the aggregator profit rate on the operation, clearing, and settlement of the distributed energy market is explored in this section. In the value allocation mechanism proposed in this paper, the aggregator profit rate affects its income level. Simultaneously, as the total benefit of the distributed energy market is fixed, the aggregator profit rate also affects the cost reduction of DESs.

Figure 5 shows the net benefits of the aggregator and DESs settled according to M3 as the aggregator profit rate increases. As the aggregator profit rate increases, the aggregator obtains higher benefits, whereas the cost reduction for DESs after participating in the market gradually decreases. The market value contribution rate of DESs can be directly derived from the slope of the cost reduction for different DESs.

Figure 5

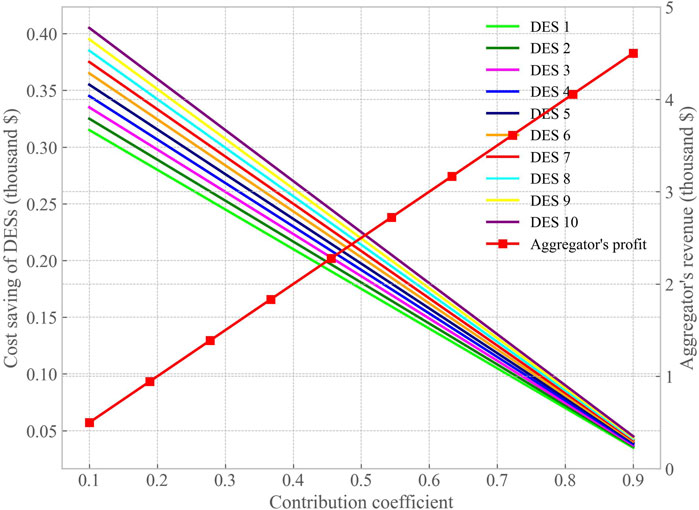
Figure 5. Net benefits of the aggregator and DESs settled according to M3 as the aggregator profit rate increases.

Furthermore, under different profit rates, the total benefit generated by the distributed energy market remains constant at $5.13. This verifies that the different settlement methods (M2 and M3) only affect the allocation of benefits among DESs and do not affect the operation of the distributed energy market.

The proposed distributed energy trading market model and value allocation mechanism have the potential to significantly impact grid stability and renewable energy adoption in the long term. By incentivizing the efficient use of DERs and promoting load shifting, the model could enhance grid stability and reliability over time. The fair value allocation mechanism may accelerate renewable energy adoption by encouraging investment in distributed resources like rooftop solar and small-scale wind turbines. Improved energy efficiency and increased use of energy storage systems could facilitate the higher penetration of variable renewable energy sources. As the market evolves, it could lead to more sophisticated products and services, potentially improving the overall system resilience.

4 Conclusion

In conclusion, a novel market value allocation mechanism designed to incentivize the active participation of DERs within smart buildings in market operations is presented in this study. The proposed framework, orchestrated by an aggregator, integrates independent operation and market trading models for DERs. The distributed energy market clearing model is fundamentally an optimization problem aimed at minimizing costs for both the aggregator and all DERs, subject to power balance, market clearing, and DER operational constraints. The introduction of the market value contribution rate concept provides a quantitative assessment of the contribution of each DER, defining it as the proportion of economic value created by an individual DER relative to the total value generated by all market participants. This metric serves as a foundation for a Nash bargaining model, culminating in a market value allocation mechanism that ensures individual rationality for both the aggregator and DERs. An empirical analysis based on a system of 10 DERs demonstrates the mechanism efficacy in identifying and quantifying the contributions of different market participants, leading to a fair distribution of social welfare. By reducing transaction costs and eliminating the need for DER bidding, this mechanism significantly enhances the market operational efficiency. Furthermore, the aggregator-led response to main-grid price signals enables DERs to provide substantial power support during peak load periods, thereby improving grid stability and resource utilization. This research contributes to the advancement of distributed energy markets and offers valuable insights for policymakers and market operators in designing effective and equitable market structures for the integration of DERs.

In future works, the research will focus on developing dynamic pricing mechanisms, assessing long-term impacts on grid stability and renewable energy adoption, integrating blockchain technology for enhanced security, and exploring machine learning applications for market optimization. Additionally, scalability studies will be conducted to ensure the model applicability in larger, more complex energy systems.

Data availability statement

The original contributions presented in the study are publicly available. This data can be found here: https://www.pecanstreet.org/dataport.

Author contributions

BH: conceptualization, funding acquisition, writing–original draft, and writing–review and editing. SD: investigation, methodology, writing–original draft, and writing–review and editing. ZX: resources, software, writing–review and editing, and writing–original draft. XC: methodology, validation, and writing–review and editing. LZ: validation, visualization, and writing–review and editing. YB: validation, writing–review and editing, and methodology. KW: project administration and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This paper is funded by the State Grid Corporation of China Headquarters Science and Technology Project (project number: 5400-202315229A-1-1-ZN). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Acknowledgments

This article was polished using Claude 3.5 Sonnet, an AI language model developed by Anthropic, PBC.

Conflict of interest

Authors BH, SD, ZX, LZ, and KW were employed by the State Grid Electric Power Research Institute Wuhan Efficiency Evaluation Company Limited.

Authors XC and YB were employed by the State Grid Shanxi Electric Power Company.

Authors XC and YB were employed by the State Grid Shanxi Electric Power Company Electric Power Research Institute.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ackermann, T., Andersson, G., and Söder, L. (2001). Distributed generation: a definition. Electr. power Syst. Res. 57, 195–204. doi:10.1016/s0378-7796(01)00101-8

CrossRef Full Text | Google Scholar

Burger, S., Chaves-Ávila, J. P., Batlle, C., and Pérez-Arriaga, I. J. (2017). A review of the value of aggregators in electricity systems. Renew. Sustain. Energy Rev. 77, 395–405. doi:10.1016/j.rser.2017.04.014

CrossRef Full Text | Google Scholar

Burger, S. P., Jenkins, J. D., Huntington, S. C., and Perez-Arriaga, I. J. (2019). Why distributed? a critical review of the tradeoffs between centralized and decentralized resources. IEEE Power Energy Mag. 17, 16–24. doi:10.1109/mpe.2018.2885203

CrossRef Full Text | Google Scholar

Inês, C., Guilherme, P. L., Esther, M.-G., Swantje, G., Stephen, H., and Lars, H. (2020). Regulatory challenges and opportunities for collective renewable energy prosumers in the eu. Energy policy 138, 111212. doi:10.1016/j.enpol.2019.111212

CrossRef Full Text | Google Scholar

Mengelkamp, E., Gärttner, J., Rock, K., Kessler, S., Orsini, L., and Weinhardt, C. (2018). Designing microgrid energy markets: a case study: the brooklyn microgrid. Appl. energy 210, 870–880. doi:10.1016/j.apenergy.2017.06.054

CrossRef Full Text | Google Scholar

Morstyn, T., Teytelboym, A., and McCulloch, M. D. (2018). Bilateral contract networks for peer-to-peer energy trading. IEEE Trans. Smart Grid 10, 2026–2035. doi:10.1109/tsg.2017.2786668

CrossRef Full Text | Google Scholar

National Grid ESO (2021) “Power responsive annual report 2020,”. London: National Grid ESO.

Google Scholar

Parag, Y., and Sovacool, B. K. (2016). Electricity market design for the prosumer era. Nat. energy 1, 16032–16036. doi:10.1038/nenergy.2016.32

CrossRef Full Text | Google Scholar

Soto, E. A., Bosman, L. B., Wollega, E., and Leon-Salas, W. D. (2021). Peer-to-peer energy trading: a review of the literature. Appl. Energy 283, 116268. doi:10.1016/j.apenergy.2020.116268

CrossRef Full Text | Google Scholar

Tushar, W., Yuen, C., Saha, T. K., Morstyn, T., Chapman, A. C., Alam, M. J. E., et al. (2021). Peer-to-peer energy systems for connected communities: a review of recent advances and emerging challenges. Appl. energy 282, 116131. doi:10.1016/j.apenergy.2020.116131

CrossRef Full Text | Google Scholar

Wang, Z., Chen, B., Wang, J., Begovic, M. M., and Chen, C. (2014). Coordinated energy management of networked microgrids in distribution systems. IEEE Trans. Smart Grid 6, 45–53. doi:10.1109/tsg.2014.2329846

CrossRef Full Text | Google Scholar

Zhou, Y., Wu, J., and Long, C. (2018). Evaluation of peer-to-peer energy sharing mechanisms based on a multiagent simulation framework. Appl. energy 222, 993–1022. doi:10.1016/j.apenergy.2018.02.089

CrossRef Full Text | Google Scholar