- 1College of Electrical and Information Engineering, Hunan University, Changsha, China
- 2Industrial Training Centre, Shenzhen Polytechnic University, Shenzhen, China
- 3College of Electrical and Information Engineering, Hunan University of Technology, Zhuzhou, China
In the current model, the unclear and unreasonable method of revenue sharing among wind-solar-storage hybrid energy plants may a lso hinder the effective measurement of energy storage power station costs. This lack of clarity discourages energy storage from effectively collaborating with renewable energy stations for greenpower trading and spot trading.Therefore, this study proposes an optimal revenue sharing model of wind-solar-storage hybrid energy plant under medium and long-term green power trading market to facilitate the coordinated operation and equitable revenue allocation. Firstly, a method for decomposing transaction volume of green power is introduced by considering the uncertainty of spot market prices and physical delivery characteristics of green power trading. Then, a coordinated scheduling strategy of hybrid renewable energy plant is proposed to maximize revenues generated from both the green power and spot markets. Consequently, a cost-benefit contribution index system is developed to quantify the contribution of energy storage in the wind-solar-storage hybrid power plant. The revenue sharing model based on the minimum cost-remaining savings (MCRS) method can significantly increase overall revenue for renewable energy plants by reducing deviation penalties. It also enhances the operating revenue of energy storage power stations by considering the contributions of both energy storage and renewable energy plant in the green power market. The superiority of the proposed cooperation revenue sharing m odel for profitability enhancement of energy storage is v alidated through comparative case studies.
1 Introduction
As a flexible resource with rapid response ability, an energy storage system can assist a renewable energy power plant to complete its power trading by tracking the scheduling plan (Guo et al., 2023) and power time shift (Abdelrazek and Kamalasadan, 2016; Castro and Espinoza-Trejo, 2023). Since green power trading also delivers the environmental values of renewable energy compared with conventional electricity trading, the particularity of the green electricity market and its coupling relationship with the spot market should be considered further in formulating the operational strategy of energy storage for renewable energy (Li et al., 2024; Yang et al., 2024). With the determination of the independent dominant position of energy storage in the electricity market, the existing research focuses on the mechanism design of the energy market (Akhavan-Hejazi and Mohsenian-Rad, 2014; Krishnamurthy et al., 2018; Xu et al., 2018) and the auxiliary market that adapt to the physical characteristics of energy storage (He et al., 2017; Yang et al., 2023). However, few studies considered the impact of green electricity trading on wind–solar-storage hybrid power plants (Ju et al., 2024). Furthermore, the revenue sharing method in existing research cannot guarantee that the energy storage would be fully able to obtain the return in promoting the realization of the green values of renewable energy (González-Garrido et al., 2020). Therefore, it is necessary to study a scheduling strategy coordinated by an energy storage power station for participating in multiple power markets at the same time and establishing a revenue sharing model for wind–solar-storage hybrid power plants by considering green power trading.
The main contributions of this work are two-fold: (1) a green power trading volume decomposition method considering the uncertainty of spot electricity prices is proposed. Furthermore, a coordinated scheduling strategy of a hybrid renewable energy plant is established with the goal of maximizing revenue from the green power and spot market, and (2) a cost–benefit contribution index system is developed to quantify the contribution of energy storage in the wind–solar-storage hybrid energy plant. Furthermore, a revenue sharing model with contribution degree correction based on the minimum cost-remaining saving (MCRS) method is proposed to enhance the competitive vitality of energy storage in the electricity market.
2 Coordinated scheduling of the hybrid renewable energy plant under the green power market
Although the revenue from a portion of renewable energy can be determined through the green power trading contract, the overall revenue in the green power and spot markets can be improved by adjusting the decomposition curve of the green power transaction volume (Wu et al., 2019). Since it is difficult to predict the electricity price in the spot market, a multi-scenario approach is usually used to describe the uncertainty associated with the day-ahead clearing electricity prices. In view of the day-ahead market clearing price uncertainty, a series of electricity price scenarios are generated by the Latin hypercube sampling (LHS) method. Subsequently, a fast scene reduction method based on Kantorovich probability distance is used to reduce the initial scene to obtain a suitable number of representative day-ahead clearing price scenarios (Roustaee and Kazemi, 2021; Yang et al., 2023), aiming to retain scenarios with the smallest probability distance from the initial scene. Then, a green power trading volume decomposition model is constructed by considering the uncertainty of spot electricity price, the objective function is presented as Equations 1–4:
where
In order to ensure the smooth progress of electricity trading in the medium- and long-term markets, it is stipulated that the sum of green power consumption in each period equals the decomposed green power output for the scheduling cycle (Fan et al., 2020). Therefore, the constraints Equations 5–10 of the hybrid renewable energy plant are as follows (Cao et al., 2024a):
where
To minimize the operational cost of the energy storage system, it is necessary to consider the physical constraints of the energy storage power station (Cao et al., 2024b), including charging and discharging power constraints and the state of charge constraints (Zhong et al., 2023), as shown below:
where
After determining the output for each time period, the execution of green power and spot trading requires the cooperative control of an energy storage power station to mitigate the adverse effects caused by the stochasticity and volatility of wind power and photovoltaic output (McPherson et al., 2007; He et al., 2017; Krishnamurthy et al., 2018). An energy storage power station scheduling model is constructed for the participation of the wind–solar-storage plant in green power and spot trading. The objective function is presented as Equation 15:
where
where
where
where
3 Revenue sharing model of the wind–solar-storage hybrid renewable energy plant
A shared energy storage power station under the leasing mode obtains fixed funds through its capacity, and it is difficult to give full play to the competitive vitality of energy storage in the electricity market (Tang et al., 2018). In the cooperative alliance mode, the unclear and unreasonable method of revenue sharing among various subjects may also lead to difficulties in effectively measuring the cost of the energy storage power station, which makes energy storage cooperate with renewable energy stations to complete the green power trading and spot trading with insufficient enthusiasm (Liu et al., 2022). In order to develop a scientific and reasonable revenue sharing scheme, this section constructs the energy storage contribution index system from the two levels of cost and benefit in order to comprehensively measure the contribution of energy storage in the wind–solar-storage plant.
The revenue from the storage capacity generated by the peak and valley arbitrage in the intraday real-time electricity market used by wind and solar renewable energy sources is considered the opportunity cost of the energy storage power station (Silva-Monroy and Watson, 2014). The equivalent power generation of the energy storage power station is the amount of electricity that the energy storage power station stores beyond the power generation plant during the period of wind power and photovoltaic curtailment. The marginal revenue contribution degree of each subject in the wind–solar-storage plants is the ratio of the marginal revenue to the total revenue of the hybrid energy plant. The higher marginal revenue contribution degree indicates the higher importance of the participants in the plants. The improvement degree of the green power trading deviation indicates increased transaction cost due to low green power performance under bilateral negotiation transactions. The Equations 28–32 for calculating the above indicators are shown below:
where
The root mean square error and maximum tracking planned output error (Wei et al., 2023) are utilized as tracking performance evaluation indicators to compare the accuracy rate of renewable energy output with and without energy storage participation (Zhang et al., 2023). The calculation Equations 34, 35 of the accuracy improvement indicator of power output prediction are shown as follows:
where
In order to ensure the effective cost allocation of the energy storage power station and stimulate active participation of the energy storage power station in a hybrid renewable energy plant, the benefits of energy storage and renewable energy are calculated using the MCRS method based on the cooperative game theory (Zhang et al., 2020), and then, revenues are shared according to the modified contribution degree. The MCRS method will distribute cooperation gains depending on the proportion of the difference between the marginal gain
where
4 Case studies
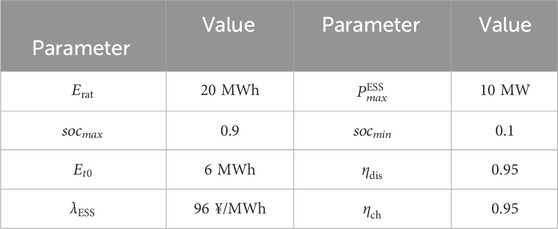
The wind–solar-storage hybrid energy plant in a western province of China is used as an example to validate the effectiveness of the proposed revenue sharing model. The specific operating parameters of the energy storage power station are shown in Table 1. The installed capacity of both the wind farm and photovoltaic power station is 30 MW. Each signed a green power trading contract with consumers stipulating that the output of green electricity will be 280 MWh and 120 MWh on the delivery day, respectively. The permitted power deviation range of the hybrid renewable energy plant is set to be 10%. The deviation assessment coefficient of renewable energy output is set to be 400 ¥/MWh (Jiang and Zhen, 2022). Based on the trading situation in the pilot area of the green power market, the green power price is set at 506.6 ¥/MWh, and the environmental premium is set at 91.3 ¥/MWh (Zhang et al., 2022). According to the historical clearing price data on the day-ahead electricity market, 10 sets of typical day-ahead clearing price scenarios are shown in Figure 1A. The predicted and actual output powers of the wind farm and photovoltaic power station and the clearing price in the electricity market are shown in Figure 1B.

Figure 1. (A) Typical scenarios for clearing price in day-ahead electricity market. (B) Wind power and photovoltaic output and electricity market price.
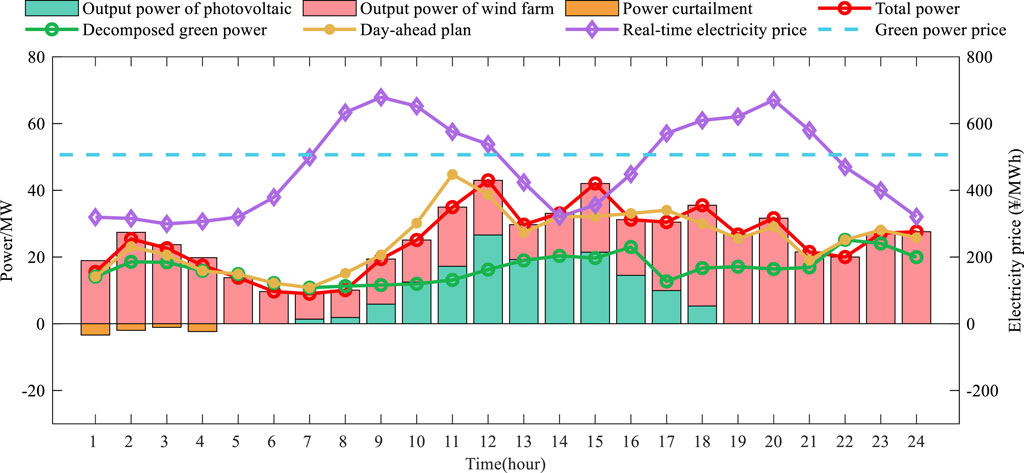
In the intra-day scheduling stage, the wind power and photovoltaic output has a certain deviation from the day-ahead plan. Within the permitted range of deviation, the excess power of renewable energy can be sold in the real-time market, while any shortfall must be procured from that market. When the deviation is outside the permitted range, the wind farm and photovoltaic power station need to pay the deviation fee. The green power trading curve and bidding status of the wind–solar-storage hybrid energy plant in the day-ahead market are shown in Figure 2A, and the actual operation scheduling results of the hybrid renewable energy plant are shown in Figure 2B.

Figure 2. (A) Green power decomposition curve and day-ahead outputs. (B) Coordinated scheduling results of the wind-solar-storage hybrid energy plant.
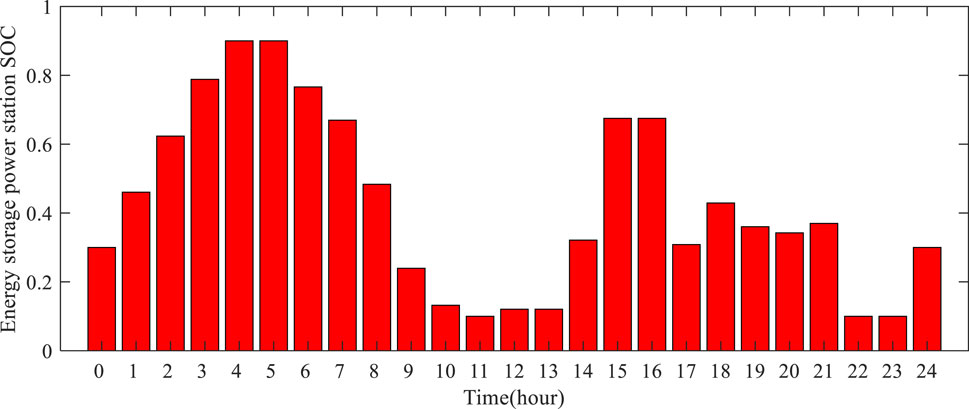
Figure 2 shows that the wind–solar-storage hybrid energy plant will decompose the green power into periods of off-peak price within a limited decomposition area according to day-ahead price prediction, resulting in the final green power decomposition curve being negatively correlated with the predicted day-ahead price. For example, the hybrid renewable energy plant tends to decompose more green power into the off-peak pricing times, such as 2–3 h and 12–16 h. Conversely, during the peak pricing times of 8–11 h and 17–21 h, the decomposed green power falls into the lower limit set by consumers. In addition, the scheduling strategy of the energy storage power station is more conservative, owing to the consideration of the uncertainty of electricity price and loss cost of energy storage during the day-ahead stage. The energy storage system plans to absorb only a portion of the electricity during the off-peak pricing time and resell it during the peak pricing time. Furthermore, the wind–solar-storage hybrid energy plant will release the stored power during the peak pricing times to obtain excess profit, such as in 19–20 h. Although the real-time price is not the highest in 6–7 h and 22 h, the hybrid energy plant still chooses to discharge the stored power to compensate for deviations in the green power output. The energy storage power station can compensate for deviations with its flexible adjustment capacity, thereby reducing deviation assessment cost and increasing profitability in real-time markets. The real-time scheduling result of the energy storage power station is shown in Figure 3.
When surplus electricity is available in the combined system, the energy storage power station chooses whether to charge or not based on the real-time electricity price. For example, in 1 h–4 h, the energy storage power station chooses to absorb the surplus power up to its capacity as the night-time price is lower than the deviation penalty cost. In contrast, when the real-time price is higher than the deviation penalty cost, such as in 12 and 20 h, the combined system sells the surplus electricity directly without using the energy storage power station. To further explore the contribution of energy storage power stations in hybrid renewable energy plants, the revenue model proposed in this paper is considered scheme 1, and the revenue model for the hybrid plant without energy storage participating in the green electricity market is considered scheme 2. The simulation results of scheme 2 are shown in Figure 4. The comparison of economic benefits between schemes 1 and 2 is shown in Table 2.
Figure 4 shows that the hybrid renewable energy plant can reduce the power deviation to a certain extent through complementary operation. However, the compensation to deviation under this scheme is stochastic in nature. Excess energy is curtailed proactively to partially mitigate deviation penalties when there is surplus wind and solar power. Passive acceptance of the penalty for deviation is unavoidable to compensate for the shortfall power of wind and solar. The comparison results in Table 2 show that the deviation penalty of scheme 1 is much smaller than that of scheme 2. The deviation penalty in the green power market and spot market of the wind–solar-storage hybrid energy plant is only 11.92% and 4.38% of the wind–solar plant, respectively. The market revenue increased by 14.50%, and the completion rate of the green power transaction increased by 5.93%. The net profit exceeds by 12.33%, considering the operational costs of the energy storage power station. Moreover, the incremental revenue of the wind–solar-storage hybrid energy plant is allocated according to the proposed cooperative revenue sharing method and MCRS method, as shown in Table 3.
Table 3 shows that the revenue sharing method proposed in this paper takes into account the contribution degree of the wind farm, photovoltaic power station, and energy storage power station to the combination system. Energy storage power station participation in renewable energy plants can mitigate their power deviations and enhance competitiveness in the green power market. Therefore, both the wind farm and photovoltaic power station are inclined to provide incentives for the energy storage power station, resulting in a 28.19% increase in energy storage power station revenue after adjusting for the contribution factor.
5 Conclusion
In this paper, a revenue sharing model of the wind–solar-storage hybrid energy plant under medium- and long-term green power trading markets is proposed to facilitate their coordinated scheduling and reasonable revenue allocation. The key findings of this study are as follows: 1) the proposed coordinated scheduling strategy for the hybrid renewable energy plant can significantly reduce the deviation penalty of green power and increase the completion rate of transactions and net income in the green power and spot trading market and 2) the revenue sharing model proposed in this paper effectively enhances the operating revenue of energy storage power stations by considering the contribution of the energy storage power station and renewable energy in the green power market.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
ZZ: writing–original draft and writing–review and editing. XG: conceptualization, data curation, and writing–review and editing. BF: visualization and writing–review and editing. TZ: formal analysis and writing–review and editing. YZ: formal analysis and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Guangdong Basic and Applied Basic Research Foundation (2023A1515110105) and the Scientific Research Startup Fund for Shenzhen High-Caliber Personnel of SZPT (6022310042k).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdelrazek, S. A., and Kamalasadan, S. (2016). Integrated PV capacity firming and energy time shift battery energy storage management using energy-oriented optimization. IEEE Trans. Industry Appl. 52, 2607–2617. doi:10.1109/TIA.2016.2531639
Akhavan-Hejazi, H., and Mohsenian-Rad, H. (2014). Optimal operation of independent storage systems in energy and reserve markets with high wind penetration. IEEE Trans. Smart Grid 5, 1088–1097. doi:10.1109/TSG.2013.2273800
Cao, Y., Zhou, B., Chung, C. Y., Wu, T., Ling, Z., and Shuai, Z. (2024b). A coordinated emergency response scheme for electricity and watershed networks considering spatio-temporal heterogeneity and volatility of rainstorm disasters. IEEE Trans. Smart Grid 15 (4), 3528–3541. doi:10.1109/TSG.2024.3362344
Cao, Y., Zhou, B., Chung, C. Y., Zhou, K., Zhu, L., and Shuai, Z. (2024a). Resilience-oriented coordinated topology reconfiguration of electricity and drainage networks with distributed mobile emergency resources. IEEE Trans. Smart Grid, 1. doi:10.1109/TSG.2024.3419086
Castro, L. M., and Espinoza-Trejo, D. R. (2023). Optimal placement of battery energy storage systems with energy time shift strategy in power networks with high penetration of photovoltaic plants. Sustain. Energy, Grids Netw. 35, 101093. doi:10.1016/j.segan.2023.101093
Fan, H., Yu, K., Zhang, S., Xing, H., Li, Z., and Shahidehpour, M. (2020). Medium and long-term electricity trading considering renewable energy participation. IEEE Access 8, 35290–35298. doi:10.1109/ACCESS.2020.2972560
Gan, L., Eskeland, G. S., and Kolshus, H. H. (2022). Green electricity market development: lessons from Europe and the US. J. Clean. Prod. doi:10.1016/j.jclepro.2022.134540
González-Garrido, A., Gaztañaga, H., Saez-de-Ibarra, A., Miloa, A., and Eguia, P. (2020). Electricity and reserve market bidding strategy including sizing evaluation and a novel renewable complementarity-based centralized control for storage lifetime enhancement. Appl. Energy 262, 114591. doi:10.1016/j.apenergy.2020.114591
Guo, M., Ren, M., Chen, J., Cheng, L., and Yang, Z. (2023). Tracking photovoltaic power output schedule of the energy storage system based on reinforcement learning. Energies 16, 5840. doi:10.3390/en16155840
He, G., Chen, Q., Kang, C., Xia, Q., and Poolla, K. (2017). Cooperation of wind power and battery storage to provide frequency regulation in power markets. IEEE Trans. Power Syst. 32, 3559–3568. doi:10.1109/TPWRS.2016.2644642
Jiang, Y., and Zhen, C. (2022). Two-stage operation optimization for grid-connected wind farm cluster with shared energy storage. Power Syst. Technol. doi:10.13335/j.1000-3673.pst.2022.0217
Ju, L., Bai, X., Li, G., Gan, W., Qi, X., and Ye, F. (2024). Two-stage robust transaction optimization model and benefit allocation strategy for new energy power stations with shared energy storage considering green certificate and virtual energy storage mode. Appl. Energy 362, 122996. doi:10.1016/j.apenergy.2024.122996
Krishnamurthy, D., Uckun, C., Zhou, Z., Thimmapuram, P. R., and Botterud, A. (2018). Energy storage arbitrage under day-ahead and real-time price uncertainty. IEEE Trans. Power Syst. 33, 84–93. doi:10.1109/TPWRS.2017.2685347
Li, J., He, X., Niu, W., and Liu, X. (2024). Analysis of the joint trading of local green power certificates, carbon emissions rights, and electricity considering demand flexibility. Int. J. Electr. Power and Energy Syst. 155, 109653. doi:10.1016/j.ijepes.2023.109653
Liu, Y., Xu, Q., Xia, Y., Fang, J., and Tang, L. (2022). Distribution network power flow constrained shared energy storage configuration for industrial consumers based on generalized NashBargaining theory. Power Syst. 38 (1), 1–14. doi:10.13335/j.1000-3673.pst.2022.1035
McPherson, M., McBennett, B., Sigler, D., and Denholm, P. (2007). Impacts of storage dispatch on revenue in electricity markets. Energy Policy. doi:10.1016/j.enpol.2005.10.008
Roustaee, M., and Kazemi, A. (2021). Multi-objective stochastic operation of multi-microgrids constrained to system reliability and clean energy based on energy management system. Electr. Power Syst. Res. 194, 106970. doi:10.1016/j.epsr.2020.106970.1016/j.epsr.2020.106970
Silva-Monroy, C. A., and Watson, J.-P. (2014). Integrating energy storage devices into market management systems. Proc. IEEE 102, 1084–1093. doi:10.1109/JPROC.2014.2327378
Tang, Y., Zhang, Q., Mclellan, B., and Li, H. (2018). Study on the impacts of sharing business models on economic performance of distributed PV-Battery systems. Energy 161, 544–558. doi:10.1016/j.energy.2018.07.096
Wei, S., Xu, C., Yan, J., and Zhao, Z. (2023). Wake control of wind farm based on model predictive control considering propagation delay. Proc. CSEE. doi:10.13334/j.0258-8013.pcsee.222696
Wu, Z., Zhou, M., Yao, S., Li, G., Zhang, Y., and Liu, X. (2019). Optimization operation strategy of wind-storage coalition in spot market based on cooperative game theory. Power Syst. Technol. doi:10.13335/j.1000-3673.pst.2019.0534
Xu, B., Zhao, J., Zheng, T., Litvinov, E., and Kirschen, D. S. (2018). Factoring the cycle aging cost of batteries participating in electricity markets. IEEE Trans. Power Syst. 33, 2248–2259. doi:10.1109/TPWRS.2017.2733339
Yang, X., Fan, L., Li, X., and Meng, L. (2023). Day-ahead and real-time market bidding and scheduling strategy for wind power participation based on shared energy storage. Electr. Power Syst. Res. 214, 108903. doi:10.1016/j.epsr.2022.108903
Yang, Y., Xie, B., and Tan, X. (2024). Impact of green power trading mechanism on power generation and interregional transmission in China. Energy Policy 189, 114088. doi:10.1016/j.enpol.2024.114088
Zhang, C., Liu, Q., Zhou, B., Chung, C. Y., Li, J., Zhu, L., et al. (2023). A central limit theorem-based method for dc and ac power flow analysis under interval uncertainty of renewable power generation. IEEE Trans. Sustain. Energy 14 (1), 563–575. doi:10.1109/TSTE.2022.3220567
Zhang, L., Xie, J., Chen, X., Zhan, Y., and Zhou, L. (2020). Cooperative game-based synergistic gains allocation methods for wind-solar-hydro hybrid generation system with cascade hydropower. Energies 13 (15), 3890. doi:10.3390/en13153890
Zhang, Y., Qiao, S., Xu, Q., and Yu, J. (2022). “Analysis of distributed green power transaction optimization based on nash bargaining theory,” in Electric power. doi:10.11930/j.issn.1004-9649.202209094
Keywords: renewable energy, energy storage, electricity market, green power trading, hybrid energy plant
Citation: Zeng Z, Gao X, Fang B, Zhang T and Zhu Y (2024) Optimal revenue sharing model of a wind–solar-storage hybrid energy plant under the green power trading market. Front. Energy Res. 12:1459090. doi: 10.3389/fenrg.2024.1459090
Received: 03 July 2024; Accepted: 30 July 2024;
Published: 13 August 2024.
Edited by:
Yuanxing Xia, Hohai University, ChinaReviewed by:
Qin Wang, Electric Power Research Institute (EPRI), United StatesManyun Huang, Hohai University, China
Copyright © 2024 Zeng, Gao, Fang, Zhang and Zhu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiang Gao, Z2FveGlhbmdAc3pwdS5lZHUuY24=
 Zhuo Zeng
Zhuo Zeng Xiang Gao
Xiang Gao Baling Fang
Baling Fang Tao Zhang
Tao Zhang Ying Zhu
Ying Zhu