Two-layer optimal scheduling of distribution network-multi-microgrids based on master–slave game

With the increase in the number of microgrids in the same distribution area usually belong to different subjects of interest, forming a multi-subject game pattern. Considering the interests of distribution networks and microgrids, a distribution network-multi-microgrid master–slave game model is established by selecting distribution networks as game masters and microgrids as game slaves. A master–slave game equilibrium algorithm based on a Kriging metamodel is proposed. The method replaces the microgrid energy internal management model with a proposed Kriging metamodel. In the iterative optimization process, the particle swarm optimization algorithm is used to generate new sampling points and modify the model in a targeted way so as to quickly and accurately obtain the transaction price and output plan of each microgrid. The algorithm does not need all the parameters of the microgrid, which both achieves the purpose of protecting the privacy of the microgrid and avoids a large number of calls to the lower optimization model, effectively reducing the amount of computation and improving the efficiency of the solution. The results show that the overall operating costs of the three microgrids used in the case study are reduced by 1.4%, 4.6%, and 1.6%, respectively, which effectively balances the interests of multiple parties in the microgrid system; the revenue of the distribution network is increased by 50.6%.

1 Introduction

Microgrids covering wind turbines, photovoltaics, and fuel cells face multiple complexities due to the massive increase in renewable energy sources (Chen et al., 2021). The current power grid dispatch system faces numerous challenges, including intermittent supply from conventional sources, increasing demand for reliable and sustainable energy, and the need for flexible grid operations. Incorporating renewable energy into microgrids presents a compelling solution. It mitigates the reliance on fossil fuels, reducing greenhouse gas emissions, and enhances grid resilience by enabling localized energy generation and distribution. Microgrids, powered by renewable sources like solar and wind, can island themselves during grid failures, ensuring critical services remain uninterrupted, thereby addressing the issues of reliability and sustainability in modern power systems. Microgrids should fulfill all the constraints in order to operate in the grid-connected mode, a mode in which they also interact with the electricity market (Zare et al., 2016; Uddin et al., 2021).

Most existing studies address the participation of microgrids in the electricity market while meeting operational and reliability constraints, thus minimizing the total cost. Khalid et al. (2018) planned for wind turbines and energy storage and predicted electricity prices to maximize the total profit. Xiao et al. (2017) investigated the impact of renewable energy sources on the electricity market through the concept of a microgrid. Wang et al. (2023a) and Wei et al. (2023) investigated the feasibility of renewable energy-based consumer participation in the electricity market. Mehrabadi et al. (2020) modeled electricity production from renewable sources in the electricity market and studied China as an example. Similar studies have assessed the impact of renewable energy participation in electricity markets on reducing CO₂ emissions (Piao et al., 2021).

Various algorithms for day-ahead scheduling problems have been proposed, considering multiple environmental, economic, and reliability constraints. Bakhtiari and Naghizadeh (2018) proposed a multi-objective-based optimal capacity management algorithm for wind turbines, photovoltaics, fuel cells, hydrogen storage tanks, and electrolyzers to reduce the annual cost and optimize the integration of renewable resources into microgrids based on pollution, economic, and reliability constraints. Jafari et al. (2020) proposed a management algorithm to address the bidding strategy of demand response aggregators in the electricity market. A similar study explored dynamic demand response and its impact on the electricity market (Abapour et al., 2020). Ren et al. (2021) proposed a multi-objective optimization algorithm to find the optimal operation of combined cooling, heating, and power (CCHP) systems as well as photovoltaic (PV) units and geothermal resources. Karimi and Jadid (2020) proposed an optimal stochastic energy management algorithm for multi-microgrid structures, which takes into account resource and demand uncertainties to optimize total cost and carbon emissions.

However, the studies mentioned above examine microgrid scheduling under the premise of a given tariff; if more renewable energy subjects participate in the electricity market, each microgrid will belong to different subjects with different interests, and each subject will pursue the maximization of interests. Applying the optimal scheduling method based on the given tariff will take more work. The game theory provides a new idea for analyzing the relationship between the interests of different subjects (Li et al., 2018; Li et al., 2021). In this article, we introduce a one-master-many-slave game optimization model between distribution network operators and multi-microgrids to realize the energy management of multiple microgrids.

The master–slave game model is a class of equilibrium constrained equilibrium optimization problems in which the lower game problem is a constraint of the upper optimization problem. Hence, the model is complex, non-linear, and non-convex (Mei and Wei, 2014). Currently, numerical optimization methods based on Karush–Kuhn–Tucker (KKT) conditions (Yu and Hong, 2016; Liu et al., 2017; Qin et al., 2019) and heuristic intelligent algorithms (HIAR) (Guo et al., 2020; Liu et al., 2021) can simplify the model. The lower-level model is a convex programming problem, and the upper level needs all the parameter information of the lower level, which involves privacy issues. The heuristic intelligent algorithm only needs to exchange a small amount of information between the upper and lower layers, which can protect the privacy of the lower layer. However, this approach requires many calls to the lower-layer game model, which could be more computationally complicated and efficient.

In order to deal with the above problems, this article proposes a metamodel-based optimization algorithm that introduces the Kriging metamodel into the equilibrium solution of the master–slave game for the first time to improve the computational efficiency while protecting the privacy of microgrids. The metamodel-based optimization algorithm is a kind of optimization mechanism based on historical data to drive the addition of sample points to approximate the local or global optimal solution, which can improve the defects of traditional heuristic intelligence algorithms that require complicated numerical simulation. The algorithm is most widely used in aerospace fields such as aircraft design (Gu et al., 2019). There are also preliminary applications in power systems. Paudel et al. (2019) used a Kriging metamodel to fit the stochastic wind speed and the stochastic response of power system transient simulation. Tang et al. (2018) and Xiao et al. (2018) used a Kriging metamodel instead of the current calculation to study the optimal economic operation and reactive power optimization of active distribution networks, respectively.

Therefore, considering that the distribution network and each microgrid have different interests, this article proposes a particle swarm-based game equilibrium algorithm that establishes a multi-microgrid optimal scheduling model based on the master–slave game during the solution process. The model searches for excellent sampling points using the particle swarm optimization algorithm to update and correct the model, avoiding the tedious computation of the lower game model and improving the efficiency of finding the optimal.

As a result, this article considers that the distribution network and each microgrid have different interests. The novelty of this study is as follows: 1) establish a dynamic pricing and energy management model for multiple microgrids based on master–slave games, 2) propose a particle swarm-based game equilibrium algorithm that establishes a multi-microgrid optimal scheduling model based on the master–slave game during the solution process, and 3) search for excellent sampling points using the particle swarm optimization algorithm to update and correct the model, avoiding the tedious computation of the lower game model.

The rest of this article is organized as follows: Section 2 introduces the multi-microgrid pricing mechanism based on a master–slave game. The multi-microgrid optimized scheduling model is introduced in Section 3. In Section 4, the metamodel-based solution method is presented. Section 5 studies simulated cases to investigate the effectiveness of the proposed strategy. Finally, Section 6 concludes.

2 Multi-microgrid pricing mechanism based on master–slave game

2.1 Master–slave game theory

The decisions of the participants in the master–slave game are sequential. The second decision maker may formulate its strategy based on the strategy developed by the first decision maker. At the same time, the strategy developed by the second decision maker may also impact the strategy formulated by the first decision maker. The master-slave game model can be expressed as Equation 1:

$Y=\left\{N;P_t;\left\{P_i\right\};F_t;\left\{F_i\right\}\right\},(1)$

where N denotes the set of participants, P_t denotes the set of feasible solutions to the game master’s strategy, P_i denotes the set of feasible solutions to the ith game slave’s strategy, F_t denotes the payment of the game master, and F_i denotes the payment of the ith game slave. The game reaches a Stackelberg equilibrium when all game slaves respond optimally according to the game master’s strategy, and the game master accepts that response.

If ($P_t^{*}$, $P_1^{*}$, $P_2^{*}$,…, $P_n^{*}$) is an equilibrium solution to the master–slave response, it needs to satisfy:

$\left\{\begin{array}{l}{F}_t\left(P_t^{*},P_1^{*},P_2^{*},...P_n^{*}\right)\le F_t\left(P_t,P_1^{*},P_2^{*},...P_n^{*}\right)\\ F_1\left(P_t^{*},P_1^{*},P_2^{*},...P_n^{*}\right)\le F_1\left(P_t^{*},P_1,P_2^{*},...P_n^{*}\right)\\ F_2\left(P_t^{*},P_1^{*},P_2^{*},...P_n^{*}\right)\le F_2\left(P_t^{*},P_1^{*},P_2^{*},...P_n^{*}\right)\\ ⋮\\ F_n\left(P_t^{*},P_1^{*},P_2^{*},...P_n^{*}\right)\le F_n\left(P_t^{*},P_1^{*},P_2^{*},...P_n\right)\end{array}\right..(2)$

Equation 2 shows that in the Stackelberg equilibrium solution, it is impossible for any participant to obtain a smaller cost by unilaterally changing its strategy.

2.2 Multi-microgrid pricing mechanisms in an electricity market environment

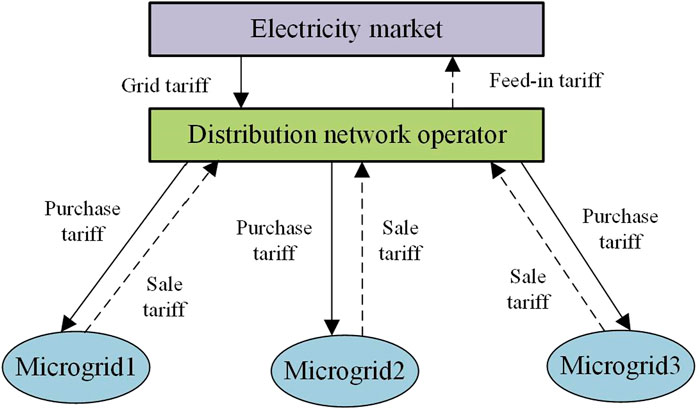
This article proposes a trading mechanism for solving the power trading problem between the distribution grid and multiple microgrids. Specifically, the distribution grid sets the purchase and sale prices, and the excess electricity is sold to the distribution grid at the sales price by the multiple microgrids, while the shortfall is purchased by the few microgrids at the purchase price from the distribution grid. Depending on the microgrid power interactions, the distribution grid trades with the electricity market and utilizes the difference in price between the two to generate revenue. The relationship between the exchanged energy is shown in Figure 1.

Figure 1

Figure 1. Relationship of exchange energy.

3 Multi-microgrid optimized scheduling model

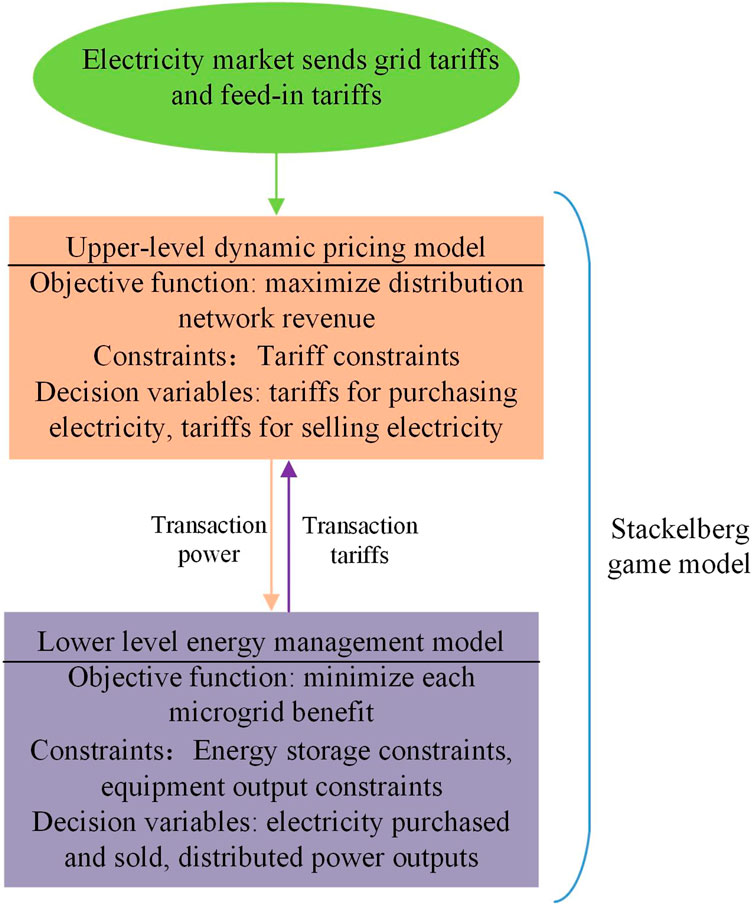
The microgrid, renewable energy (wind and photovoltaic), energy storage, and load are selected as game participants. To ensure safe, stable, and economic operation of the system, the whole microgrid system is selected as the game master, and renewable energy, energy storage, and loads are selected as game slaves. The dispatching model is shown in Figure 2.

Figure 2

Figure 2. Distribution network-multi-microgrid scheduling model.

3.1 Upper layer model

The microgrid gaming parties want to minimize the operating costs while ensuring the safe and stable operation of the microgrid system. Therefore, the optimization objective of the game is to maximize the total profit of the distribution network:

$\max C^{\text{DSO}}={\displaystyle \sum _{t=1}^T}\left({\lambda }_{\iota }^{\mathrm{W},\mathrm{s}}{P}_{\iota }^{\text{DSO},\mathrm{s}}-{\lambda }_{\iota }^{\mathrm{W},\mathrm{b}}{P}_{\iota }^{\text{DSO},\mathrm{b}}+{\lambda }_{\iota }^{\text{DA},\mathrm{b}}{\displaystyle \sum _{j=1}^N}{P}_{j,\iota }^{\text{MG},\mathrm{b}}-{\lambda }_{\iota }^{\text{DA},\mathrm{s}}{\displaystyle \sum _{j=1}^N}{P}_{j,\iota }^{\text{MG},\mathrm{s}}\right),(3)$

where ${\lambda }_t^{\mathrm{W},\mathrm{s}}$ and ${\lambda }_t^{\mathrm{W},\mathrm{b}}$ are the feed-in tariff and the grid tariff in the electricity market at time t, respectively; ${\lambda }_t^{\text{DA},\mathrm{b}}$ and ${\lambda }_t^{\text{DA},\mathrm{s}}$ are the purchase tariff and the sale tariff assigned to the microgrid by the distribution network operator (DSO) at time t, respectively; $P_{j,t}^{\text{MG},\mathrm{s}}$ and $P_{j,t}^{\text{MG},\mathrm{b}}$ denote the amount of electricity sold and purchased by microgrid (MG) j to the distribution network, respectively; $P_t^{\text{DSO},\mathrm{s}}$ and $P_t^{\text{DSO},\mathrm{b}}$ are the amount of electricity sold and purchased by the operator to the electricity market, respectively; and N is the total number of microgrids.

To ensure that each microgrid conducts normal transactions with the distribution network, the tariffs specified by the distribution network shall be met in Equation 4:

${{\lambda }_t}^{\mathrm{W},\mathrm{s}}\le {{\lambda }_t}^{\text{DA},\mathrm{s}}\le {{\lambda }_t}^{\text{DA},\mathrm{b}}\le {{\lambda }_t}^{\mathrm{W},\mathrm{b}}.(4)$

To ensure the balance of supply and demand between the microgrids, the expressions for $P_t^{\text{DSO},\mathrm{s}}$ and c $P_t^{\text{DSO},\mathrm{b}}$ are as follows:

$\left\{\begin{array}{l}{P}_t^{\text{DSO}}={\displaystyle \sum _{j=1}^N}\left(P_{j,t}^{\text{MG},\mathrm{b}}-P_{j,t}^{\text{MG},\mathrm{s}}\right)\\ P_t^{\text{DSO},\mathrm{b}}=\left\{\begin{array}{ccc}{P}_t^{\text{DSO}}& ,& P_t^{\text{DSO}}\ge 0\\ 0& ,& P_t^{\text{DSO}}<0\end{array}\right.\\ P_t^{\text{DSO},\mathrm{s}}=\left\{\begin{array}{ccc}-P_t^{\text{DSO}}& ,& P_t^{\text{DSO}}<0\\ 0& ,& P_t^{\text{DSO}}\ge 0\end{array}\right.\end{array}\right.,(5)$

where $P_t^{\text{DSO}}$ is the total electricity traded with the electricity market after the operator has aggregated the electricity purchased and sold by each microgrid. $P_t^{\text{DSO}}$ > 0 indicates that electricity is purchased from the electricity market, and $P_t^{\text{DSO}}$ < 0 indicates that electricity is sold to the electricity market.

3.2 Lower-layer model

Each microgrid aims to minimize the operating cost $C_j^{\text{MG}}$, which includes the cost of purchased power, the cost of operating the microfueling unit $C_t^{\text{MT}}$, and the cost of energy storage $C_t^{\text{ES}}$. This is shown below in Equations 6–8:

$\min C_j^{\text{MG}}={\displaystyle \sum _{t=1}^T}\left[\left({\lambda }_t^{\text{DA},\mathrm{b}}{P}_{j,t}^{\text{MG},\mathrm{b}}-{\lambda }_t^{\text{DA},\mathrm{s}}{P}_{j,t}^{\text{MG},\mathrm{s}}\right)+C_t^{\text{MT}}+C_t^{\text{ES}}\right],(6)$

$C_t^{\text{MT}}=a_i{\left(P_t^{\text{MT}}\right)}^2+b_i{P}_t^{\text{MT}}+c_{i,}(7)$

$C_t^{\text{ES}}={\lambda }_i^{\text{ES}}{\left(P_t^{\text{ES}}\right)}^2,(8)$

where $P_{j,t}^{\text{MG},\mathrm{b}}$ and $P_{j,t}^{\text{MG},\mathrm{s}}$ are the power purchased by the microgrid from the distribution grid and the power sold to the distribution grid, respectively; $P_t^{\text{MT}}$ is the output power of the micro gas turbine unit; $P_t^{\text{ES}}$ is the charging and discharging power of the energy storage, which is greater than o to indicate discharging and less than 0 to indicate charging; $a_i$, $b_i$, and $c_i$ are the cost coefficients of the micro gas turbine unit; and ${\lambda }_i^{\text{ES}}$ is the cost coefficient of the scheduling of the energy storage.

$P_{j,\mathrm{t}}^{\text{MG}}=P_{j,\mathrm{t}}^{\text{MG},\mathrm{b}}-P_{j,\mathrm{t}}^{\text{MG},\mathrm{s}}.(9)$

$P_{j,t}^{\text{MG}}+P_t^{\text{MT}}+P_t^{\text{ES}}=P_t^{\text{LD}}.(10)$

$0\le P_{j,t}^{\text{MG},\mathrm{s}}\le {\theta }_{j,t}{P}_{j,\max }^{\text{MG}}.(11)$

$0\le P_{j,t}^{\text{MG},\mathrm{b}}\le \left(1-{\theta }_{j,t}\right)P_{j,\max .}^{\text{MG}}(12)$

$0\le P_t^{\text{MT}}\le P_{\max }^{\text{MT}}.(13)$

$P_{\text{down}}^{\text{MT}}\le P_t^{\text{MT}}-P_{t-1}^{\text{MT}}\le P_{\text{up}}^{\text{MT}}.(14)$

$P_{\min }^{\text{ES}}\le P_t^{\text{ES}}\le P_{\max }^{\text{ES}}.(15)$

$S_t^{\text{ES}}=S_{t-1}^{\text{ES}}-\frac{\Delta t}{E_{\max }}{P}_t^{\text{ES}}(16)$

$S_{\min }^{\text{ES}}\le S_t^{\text{ES}}\le S_{\max .}^{\text{ES}}(17)$

$S_0^{\text{ES}}=S_T^{\text{ES}},(18)$

where $P_t^{\text{LD}}$ is the predicted value of the load at time t; ${\theta }_{j,t}$ is a Boolean variable that takes the value of 1 to indicate that microgrid j sells power to the operator at time t and takes the value of 0 to indicate that microgrid j purchases power from the operator; $P_{j,\max }^{\text{MG}}$ denotes the maximum amount of power traded between microgrid j and the operator; $P_{\max }^{\text{MT}}$ denotes the maximum output power of the micro gas turbine unit; $P_{\text{down}}^{\text{MT}}$ and $P_{\text{up}}^{\text{MT}}$ denote the upward and downward climbing power of the micro gas turbine unit, respectively; $S_t^{\text{ES}}$ is the charging state of the energy storage; $S_{\min }^{\text{ES}}$ and $S_{\max }^{\text{ES}}$ denote the upper and lower limit values of the charging state; $P_{\min }^{\text{ES}}$ and $P_{\max }^{\text{ES}}$ denote the upper and lower limits of charging and discharging power of the energy storage, respectively; and $E_{\max }$ denotes the maximum capacity value of the energy storage. Equations 9–18 constitute the strategy space of MG, denoted as ${\mathrm{\Omega }}_j^{\text{MG}}$.

3.3 Master-slave game modeling for distribution networks and multi-microgrids

Based on Sections 3.1, 3.2, the master–slave game for distribution networks and multiple microgrids is modeled as follows:

$\begin{array}{l}\underset{{\lambda }^{\text{DA}.\mathrm{s}},{\lambda }^{\text{DA}.\mathrm{b}},p}{\max }{C}^{\text{DSO}}\left({\lambda }^{\text{DA},\mathrm{s}},{\lambda }^{\text{DA},\mathrm{b}},p\right)\\ \left.\mathrm{s}.\mathrm{t}.\left\{\begin{array}{l}\left({\lambda }^{\text{DA},\mathrm{s}},{\lambda }^{\text{DA},\mathrm{b}}\right)\in {\mathrm{\Omega }}^{\text{DSO}}\\ p_j=\arg \underset{{\widehat{p}}_j}{\min }{C}_j^{\text{MG}}\left({\lambda }^{\text{DA},\mathrm{s}},{\lambda }^{\text{DA},\mathrm{b}},\widehat{p}\right)\\ {\widehat{p}}_j\in {\mathrm{\Omega }}_j^{\text{MG}}\end{array}\right.\right]\forall j,\end{array}(19)$

where $p={\left(p_1,p_2,...,p_N\right)}^{\mathrm{T}}$.

In Equation 19, the distribution system operator (DSO) and the microgrid (MG) formulate their strategies with the objectives of maximizing the revenue and minimizing the operating costs, respectively. The revenue of the DSO is related to the set tariff for the purchase and sale of electricity as well as the amount of electricity traded by the MG: the larger the difference between the purchase and sale tariffs, the larger the amount of electricity shared by the MG, and the larger the revenue of the DSO is. However, the MG’s behavior in response to the tariff also affects the DSO’s returns: the larger the purchase tariff, the smaller the amount of power purchased by the MG, and the smaller the sale tariff, the smaller the amount of power sold by the MG, leading to a reduction in the amount of power shared between the MG and the DSO. An interesting game between the DSO and the MG can be seen. In order to maximize their own benefits, the DSO needs to consider the MG’s response behavior to the price as the best tariff strategy by finding the Nash equilibrium solution.

4 Metamodel-based solution method

In the master–slave game model established in Section 3, the lower energy management game model contains 0–1 variables. It is impossible to derive the equivalent KKT condition. At the same time, the intelligent algorithm faces the problem of tedious computation. For this reason, this article proposes a solution algorithm based on the Kriging metamodel, which adopts the Kriging metamodel with small computation to fit and replace the internal management model of the energy of the microgrid and effectively avoids the above problems.

4.1 Kriging metamodel

A metamodel is a simplified mathematical model that can be used as an approximate substitute for a complex simulation model. The Kriging model is one of the many metamodels. Because of its good approximation ability and unique error estimation function for non-linear models, the Kriging model is chosen to simulate the lower-level energy management model, which displays the implicit mapping relationship between the traded tariff and traded electricity.

The Kriging model is constructed using the sale tariff ${\lambda }_t^{\text{DA},\mathrm{s}}$ and the purchase tariff ${\lambda }_t^{\text{DA},\mathrm{b}}$ for 24 time periods as inputs and the transaction power $P_{j,t}^{\text{MG}}$ of each microgrid for 24 time periods as outputs, as follows:

$P_j^{\text{MG}}=F_j\left({\lambda }^{\text{DA},\mathrm{s}},{\lambda }^{\text{DA},\mathrm{b}}\right),(20)$

where $P_j^{\text{MG}}={\left(P_{j,1}^{\text{MG}},P_{j,2}^{\text{MG}},...,P_{j,T}^{\text{MG}}\right)}^{\mathrm{T}}$.

Then, the master–slave game model of Equation 19 can be transformed into

$\begin{array}{l}\underset{{\lambda }^{\text{DA},\mathrm{s}},{\lambda }^{\text{DA},\mathrm{b}}}{\max }{C}^{\text{DSO}}\left({\lambda }^{\text{DA},\mathrm{s}},{\lambda }^{\text{DA},\mathrm{b}},P_1^{\text{MG}},\dots ,P_N^{\text{MG}}\right)\\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{l}\left({\lambda }^{\text{DA},\mathrm{s}},{\lambda }^{\text{DA},\mathrm{b}}\right)\in {\mathrm{\Omega }}^{\text{DSO}}\\ P_j^{\text{MG}}=F_j\left({\mathit{\lambda }}^{\text{DA},\mathrm{s}},{\mathit{\lambda }}^{\text{DA},\mathrm{b}}\right),j=1,\dots ,N\end{array}\right.\end{array}.(21)$

4.2 Master–slave game equilibrium algorithm based on the Kriging metamodel

Suppose the Kriging model is not updated and corrected. In that case, the optimization results are largely dependent on the fitting accuracy of the original Kriging model: when the known sample data set is small, the fitting accuracy is low, and the real optimal solution cannot be obtained; when the known sample data is large, the fitting accuracy is high, but the calculation is extremely time-consuming.

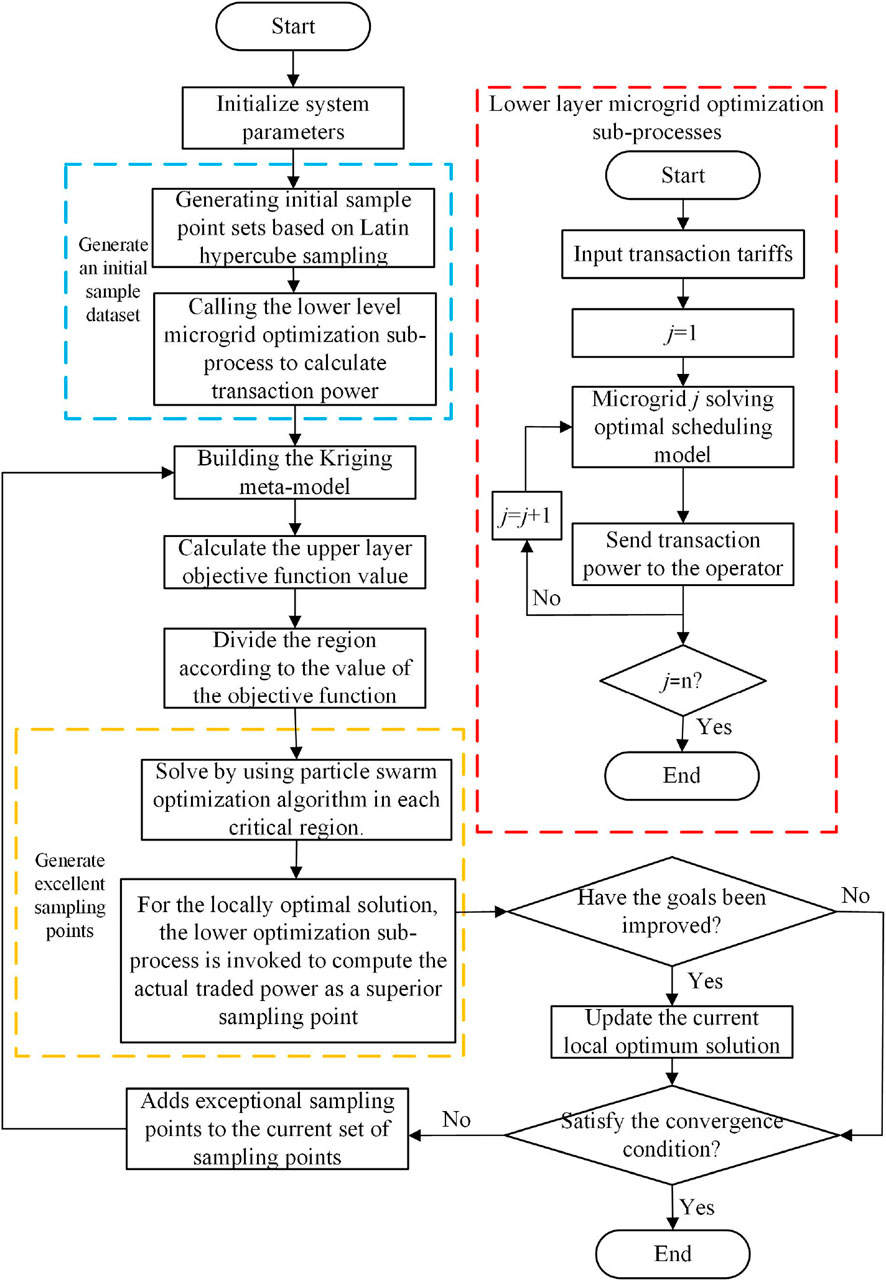
Therefore, this article proposes a dynamic Kriging metamodel equilibrium solution-solving algorithm. The algorithm first establishes an initial Kriging model based on a suitable amount of sample data and then splits the strategy space into multiple key regions according to the upper objective function value of each sample point. In each region, the particle swarm algorithm and the fitted Kriging model are used to find the optimization of the upper model quickly, and only the optimization result in the lower model is called to compute the true power and the value of the upper objective function, add it to the original sample point set, and update the modified Kriging metamodel to solve the equilibrium solution. The original sample point set is updated to correct the Kriging model and iterated until the optimal solution is obtained.

4.2.1 Kriging model construction

A Kriging model is constructed for each MG using the transaction tariff as input and the transaction electricity of the MG as output.

To ensure the uniformity and reasonableness of sampling, this article adopts Latin hypercube sampling (LHS) to generate n initial sample points. The coordinates of each sample point represent a set of transaction tariffs, including the selling price and the purchasing price of electricity, which is recorded as ${\lambda }_i^{\text{DA}}=\left({\lambda }_{i1}^{\text{DA},\mathrm{s}},{\lambda }_{i2}^{\text{DA},\mathrm{s}},...,{\lambda }_{iT}^{\text{DA},\mathrm{s}},{\lambda }_{i1}^{\text{DA},\mathrm{b}},{\lambda }_{i2}^{\text{DA},\mathrm{b}},...,{\lambda }_{iT}^{\text{DA},\mathrm{b}}\right)$, where ${\lambda }_i^{\text{DA}}$ in the policy space of the DSO satisfies the constraint of Equation 4. The initial sampling points are generally taken as 9–10 times the number of variables.

Each group of tariffs is brought into the lower-layer model in Section 3.2, and the transaction power $P_{j,i}^{\text{MG}}$ for each MG corresponding to each group of transaction tariffs can be obtained by calculation. The Kriging model of each MG can be constructed by taking the initial sample data sets of transaction tariffs ${\lambda }_i^{\text{DA}}$ and the transaction power $P_{j,i}^{\text{MG}}$.

4.2.2 Modified Kriging model

Due to the poor fitting accuracy of the initial Kriging model, an effective correction mechanism is needed to generate a superior set of sampling points, and new sampling points are added in the iterative process to continually correct the model to improve the accuracy.

4.2.2.1 Critical region segmentation

The current sample data set is brought into Equation 3, and the upper-level objective function value corresponding to each set of traded tariffs $C^{\text{DSO}}$ is calculated. According to $C^{\text{DSO}}$, the operator’s strategy space is divided into multiple key regions so as to eliminate regions containing a low probability of the optimal solution, narrow the sampling range of the excellent sampling points, and improve the efficiency of the optimization search.

4.2.2.2 Generate superior sampling points

On each key region, the particle swarm algorithm is used to find the optimization of Equation 21, and the Kriging model is used to quickly lock in the locally optimal transaction tariff and transaction power. However, at this time, the transaction power is not the real value, so it is necessary to carry out optimization calculations on the original lower model to get the real transaction power under the transaction tariff and add it to the original sample data set to correct the Kriging model.

The specific steps are as follows:

Step 1. Initialize system parameters. This includes the feed-in tariffs and grid tariffs in the power market, microgrid-related parameters, Kriging model-related parameters, and particle swarm algorithm-related parameters.

Step 2. Generate the initial sample point ${\lambda }_i^{\text{DA}}$ based on LHS.

Step 3. For the sample points generated in Step 2, the lower-level game model is invoked to calculate the transaction power $P_{j,i}^{\text{MG}}$ for each MG, constituting the sample data set B.

Step 4. Construct a Kriging metamodel for each MG based on the current sample data set, that is, Equation 20.

Step 5. Calculate the objective function value $C_i^{\text{DSO}}$ corresponding to each group of sample points and determine the key regions according to $C_i^{\text{DSO}}$. There are Nl in total, and the optimal value of each region is $C_{l,\text{best}}^{\text{DSO}}$.

Step 6. A particle swarm algorithm is used on each key region to solve the local optimal tariff ${\lambda }_{l,\text{opt}}^{\text{DA}}$.

Step 7. The lower-layer game model is invoked to compute the true transaction power $P_{j,l,\text{opt}}^{\text{MG}}$, which is added to the original set of sampling points as a superior sampling point. The true value $C_{l,\text{opt}}^{\text{DSO}}$ of the objective function of the upper layer model is calculated and compared with $C_{l,\text{opt}}^{\text{DSO}}$. If $C_{i,\text{best}}^{\text{DSO}}<C_{i,\text{opt}}^{\text{DSO}}$, then make $C_{i,\text{best}}^{\text{DSO}}=C_{i,\text{opt}}^{\text{DSO}}$.

Step 8. The global optimal solution for the current iteration step is obtained by comparing all regional optimal solutions as follows in Equation 22:

$C_{\text{best}}^{\text{DSO}}=\max \left\{C_{i,\text{best}}^{\text{DSO}}|l=1,2,...,N_l\right\}.(22)$

Step 9. Determine whether the convergence condition is satisfied; if so, stop the iteration and output the equilibrium solution; otherwise, return to Step 4.

4.2.3 Solution process

The solution flow is shown in Figure 3. In the lower level of each microgrid optimization sub-flow, the scheduling model of each microgrid is optimally solved using YALMIP + Gurobi in the MATLAB environment.

Figure 3

Figure 3. Flow chart of the complete methodology.

5 Case analysis

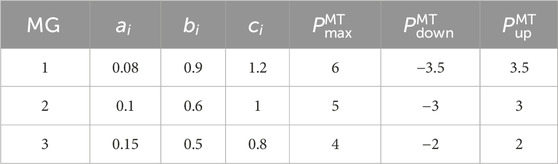
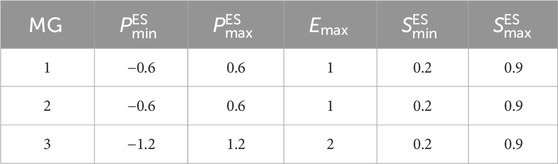
A distribution network with three typical microgrids is analyzed as an example (Liu et al., 2017; Qin et al., 2019), where each microgrid includes one wind turbine, one microfuel unit, and one energy storage. Demand response is also considered, and the model is referenced from the literature (Wang et al., 2023b; Yang et al., 2024). The parameters of the micro gas turbine unit and energy storage are shown in Tables 1, 2.

Table 1

Table 1. The parameters of a micro gas turbine.

Table 2

Table 2. Energy storage parameters.

The following two operation schemes are set up to verify the effectiveness of the proposed master–slave game-based distribution-multi-microgrid two-layer optimization strategy:

(1) The distribution network does not set the purchase and sale tariffs; the feed-in tariffs and grid tariffs of the big grid are used as the purchase and sale tariffs of each microgrid, and each microgrid operates independently and optimizes with the goal of minimizing its own cost;

(2) The distribution network sets the purchase and sale tariffs and establishes a two-layer optimization scheduling model based on the master–slave game for the distribution network-multi-microgrids.

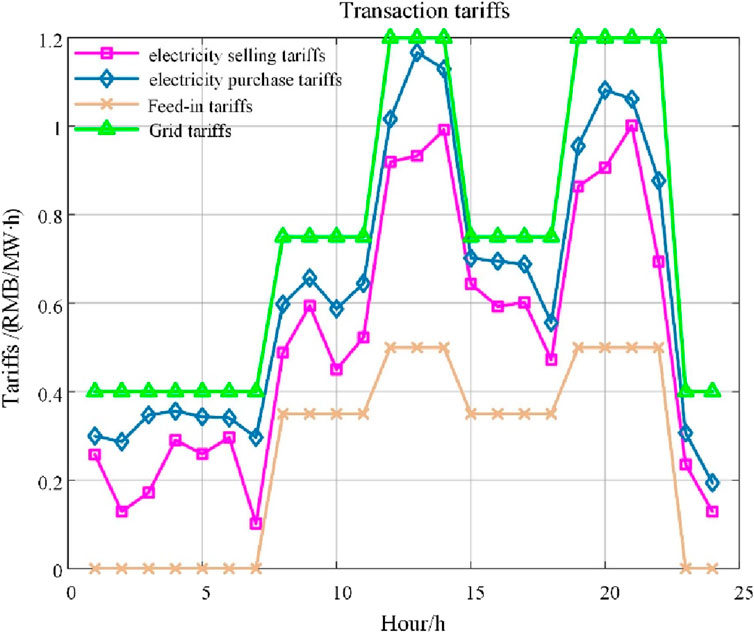
The tariffs specified by the operator for the purchase and sale are shown in Figure 4, which shows that the tariffs set by the distribution network operator are between the large grids, ensuring that the microgrids are willing to trade with the distribution network.

Figure 4

Figure 4. Transaction tariffs set by the distribution network operator.

The benefits of the distribution network operator and each microgrid under different strategies are shown in Table 3. Under operation scheme 2, the distribution grid effectively improves the benefits by optimizing the tariff, and the cost of the microgrid decreases.

Table 3

Table 3. The costs of the distribution network and microgrid under different operation schemes.

The second operation scheme is used for analysis:

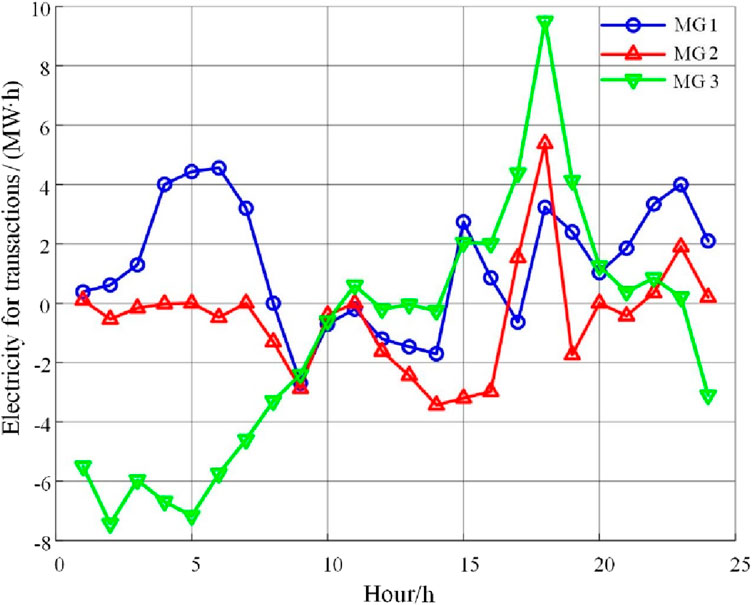
The result of the total power transaction between the multi-microgrid and the distribution grid is shown in Figure 5: if the power transaction volume is greater than 0, it means that the microgrid purchases power from the distribution grid operator. If the power transaction volume is less than 0, it means that the microgrid sells power to the distribution grid operator. If the traded power volume is equal to 0, the supply and demand within the microgrid are balanced.

Figure 5

Figure 5. Electricity trading results between the multi-microgrid and the distribution network.

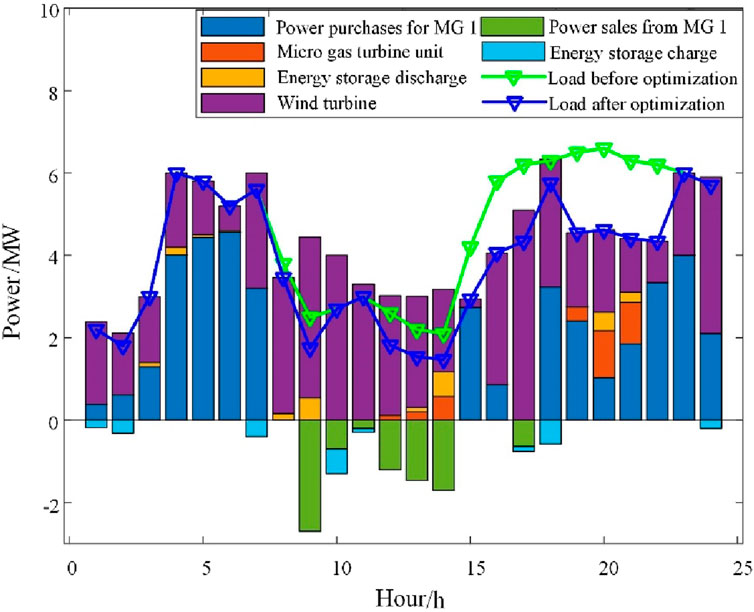
Figure 6 shows the results of the scheduling of microgrid 1 and the distribution grid. It can be seen that the turbines are always out of power. In periods 1–7, 15–16, and 18–24, microgrid 1 is in short supply and purchases power from the distribution grid to meet the loads. In periods 9–14, and 17, microgrid 1 is in greater supply than the loads, and sells power to the distribution grid. In periods 12–14 and 19–21, the micro gas turbine units are out to meet the load, and demand response plays the role of load “peak shaving and valley filling.”

Figure 6

Figure 6. The scheduling results of MG 1.

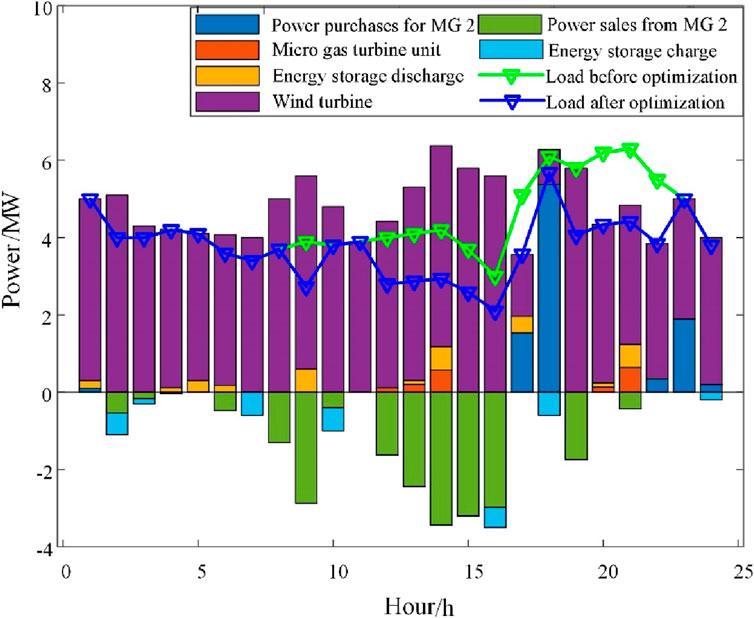
Figure 7 represents the results of scheduling microgrid 2 with the distribution grid. It can be seen that the wind turbines are always out of power, and in periods 17–18 and 22–24, microgrid 1 is in short supply and purchases power from the distribution grid to satisfy the loads. In periods 2–4, 6, 8–10, 12–16, 19, and 21, microgrid 2 has more supply than demand and sells power to the distribution grid.

Figure 7

Figure 7. The scheduling results of MG 2.

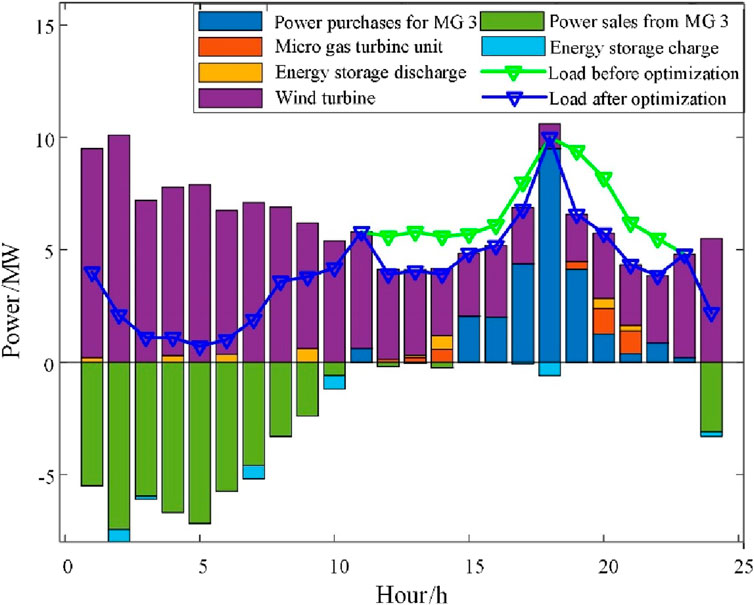
Figure 8 represents the results of the microgrid 3 and distribution grid scheduling. It can be seen that the wind turbines are always out of power, and in periods 11, 15–23, the microgrid 3 is in short supply and buys power from the distribution grid to satisfy the loads. In periods 1–10, 14, and 24, microgrid 3 has more supply than demand and sells power to the distribution grid.

Figure 8

Figure 8. The scheduling results of MG 3.

In order to verify the effectiveness of the proposed Kriging metamodel-based solution algorithm, it is compared with the genetic algorithm (GA) and particle swarm algorithm (PSO). Each algorithm is calculated 10 times independently, and the statistical results of each algorithm are shown in Table 4. The statistical results of each algorithm are shown in Table 4.

Table 4

Table 4. Performance comparison of various algorithms.

The above simulation results show that when using the proposed algorithm to solve the equilibrium solution of the master–slave game, the operator’s gain is greater, the convergence speed is faster, and it can achieve good solving accuracy and computational efficiency. The proposed algorithm generates a Kriging model for trading tariffs and trading electricity by fitting a computationally complex lower optimization model with reasonable sampling. In each iteration, the PSO and Kriging models are used for each region to quickly lock in the local solutions, and the lower-level optimization is invoked only for the local solutions. Therefore, the number of calls to the lower optimization program is significantly reduced, which effectively improves the computation speed. In addition, dividing the region according to the region division based on the sample point set can realize parallel operation, which further improves the computation speed and accuracy.

6 Conclusion

Considering that the distribution network and each microgrid have different interest demands, this article proposes a Kriging metamodel-based solution algorithm, in which a multi-microgrid optimal scheduling model based on a master–slave game is established in the solution process.

(1) After using the proposed master–slave game method, the operating cost of the microgrid system under the model of each game participant is reduced, and the Stackelberg equilibrium between the master of the distribution network game and the slave of the microgrid game is realized. After reaching the Stackelberg equilibrium, the overall operating cost of each of the three microgrids used in the case study decreases by 1.4%, 4.6%, and 1.6%, respectively, which effectively balances the interests of multiple parties in the microgrid system; the revenue of the distribution network increases by 50.6%.

(2) The Kriging metamodel is used to fit the price response behavior of the microgrids to replace the lower energy management model to obtain the equilibrium solution, which eliminates the need for repeated and significant calls to the lower optimization model compared with the traditional intelligent optimization algorithm. It dramatically improves the search efficiency of the equilibrium solution while protecting the privacy of each microgrid.

(3) The microgrid operation scheme under the multi-master coexistence mode optimized based on the proposed master–slave game method can ensure the safe and stable operation of the system. It can provide a feasible optimization technology route for potential microgrids/power systems in future multi-master mode.

The structure of the multi-microgrid composition considered in this article is fixed. However, in the future, with the further opening of the electricity market, each distribution network will have the power to choose microgrids according to its own interests, and the structure of multi-microgrids will change dynamically. Therefore, how to combine distribution grids and microgrids according to their needs to be further studied.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

ZC: writing–original draft. RJ: methodology and writing–original draft. SW: conceptualization and writing–original draft. HN: conceptualization and writing–original draft. LZ: supervision and writing–original draft. XZ: supervision and writing–original draft. SH: writing–review and editing. QX: supervision and writing–original draft.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Xinjiang Autonomous Region Key R&D Special Project “R&D of Key Technology of Large-capacity Hybrid Combined Shared Energy Storage for Regional New Energy Consumption,” grant number 2022B01019-5.

Conflict of interest

Authors ZC, SW, LZ, SH, and QX were employed by TBEA Sunoasis Co., Ltd. Author XZ was employed by TBEA Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abapour, S., Mohammadi-Ivatloo, B., and Hagh, M. T. (2020). A Bayesian game theoretic based bidding strategy for demand response aggregators in electricity markets. Sustain. Cities Soc. 54, 101787. doi:10.1016/j.scs.2019.101787

CrossRef Full Text | Google Scholar

Bakhtiari, H., and Naghizadeh, R. A. (2018). Multi-criteria optimal sizing of hybrid renewable energy systems including wind, photovoltaic, battery, and hydrogen storage with ɛ-constraint method. IET Renew. power Gener. 12 (8), 883–892. doi:10.1049/iet-rpg.2017.0706

CrossRef Full Text | Google Scholar

Chen, J., Qi, B., Rong, Z., Zhao, Y., and Zhang, X. (2021). Multi-energy coordinated microgrid scheduling with integrated demand response for flexibility improvement. Energy 217, 119387. doi:10.1016/j.energy.2020.119387

CrossRef Full Text | Google Scholar

Gu, J., Bai, K., and Shi, Y. (2019). Optimized operation of regional integrated energy system based on multi-agent master-slave game optimization interaction mechanism. Power Syst. Technol. 43 (9), 3119–3134. doi:10.13335/j.1000-3673.pst.2019.0717

CrossRef Full Text | Google Scholar

Guo, K., Gao, C., Lin, G., et al. (2020). Optimization stra tegy of incentive based demand response for electricity retailer in spot market environment. Automation Electr. Power Syst. 44 (15), 28–37.

Google Scholar

Jafari, A., Khalili, T., Ganjehlou, H. G., and Bidram, A. (2020). Optimal integration of renewable energy sources, diesel generators, and demand response program from pollution, financial, and reliability viewpoints: a multi-objective approach. J. Clean. Prod. 247, 119100. doi:10.1016/j.jclepro.2019.119100

CrossRef Full Text | Google Scholar

Karimi, H., and Jadid, S. (2020). Optimal energy management for multi-microgrid considering demand response programs: a stochastic multi-objective framework. Energy 195, 116992. doi:10.1016/j.energy.2020.116992

CrossRef Full Text | Google Scholar

Khalid, M., Aguilera, R. P., Savkin, A. V., and Agelidis, V. G. (2018). On maximizing profit of wind-battery supported power station based on wind power and energy price forecasting. Appl. Energy 211, 764–773. doi:10.1016/j.apenergy.2017.11.061

CrossRef Full Text | Google Scholar

Li, P., Wu, D., Li, Y., et al. (2021). Optimal dispatch of multi-microgrids integrated energy system based on integrated demand response and stackelberg game. Proc. CSEE 41 (4), 1307–1321. doi:10.13334/j.0258-8013.pcsee.201845

CrossRef Full Text | Google Scholar

Li, Y., Zhao, T., Wang, P., Gooi, H. B., Wu, L., Liu, Y., et al. (2018). Optimal operation of multimicrogrids via cooperative energy and reserve scheduling. IEEE Trans. Industrial Inf. 14 (8), 3459–3468. doi:10.1109/tii.2018.2792441

CrossRef Full Text | Google Scholar

Liu, N., Yu, X., Wang, C., and Wang, J. (2017). Energy sharing management for microgrids with PV prosumers: a Stackelberg game approach. IEEE Trans. Industrial Inf. 13 (3), 1088–1098. doi:10.1109/tii.2017.2654302

CrossRef Full Text | Google Scholar

Liu, Z., Liu, R., and Liang, N. (2021). Energy trading method of multi-microgrids based on game theory. Power Syst. Technol. 45 (2), 587–595. doi:10.13335/j.1000-3673.pst.2020.0175

CrossRef Full Text | Google Scholar

Mehrabadi, R. A., Moghaddam, M. P., and Sheikh-El-Eslami, M. K. (2020). Regulatory-intervented sustainable generation expansion planning in multi-electricity markets. Sustain. Cities Soc. 52, 101794. doi:10.1016/j.scs.2019.101794

CrossRef Full Text | Google Scholar

Mei, S., and Wei, W. (2014). Hierarchal game and its applications in the smart grid. J. Syst. Sci. Math. Sci. 34 (11), 1331–1344. doi:10.13335/j.1000-3673.pst.2014.0175

CrossRef Full Text | Google Scholar

Paudel, A., Chaudhari, K., Long, C., and Gooi, H. B. (2019). Peer-to-peer energy trading in a prosumer-based community microgrid: a game-theoretic model. IEEE Trans. Industrial Electron. 66 (8), 6087–6097. doi:10.1109/tie.2018.2874578

CrossRef Full Text | Google Scholar

Piao, L., DeVries, L., Weerdt, M., and Yorke-Smith, N. (2021). Electricity markets for DC distribution systems: locational pricing trumps wholesale pricing. Energy 214, 118876. doi:10.1016/j.energy.2020.118876

CrossRef Full Text | Google Scholar

Qin, T., Liu, H., Wang, J., et al. (2019). Profit allocation model of cooperative distributed energy resources based on bargaining game theory. Electr. Power Autom. Equip. Ment. 39 (1), 134–140. doi:10.16081/j.issn.1006-6047.2019.01.020

CrossRef Full Text | Google Scholar

Ren, F., Wei, Z., and Zhai, X. (2021). Multi-objective optimization and evaluation of hybrid CCHP systems for different building types. Energy 215, 119096. doi:10.1016/j.energy.2020.119096

CrossRef Full Text | Google Scholar

Tang, J., Wang, D., Jia, H., et al. (2018). Optimal economic operation of active distribution networks based on hybrid algorithm of surrogate model and particle swarm optimization. Automation Electr. Power Syst. 42 (4), 95–103. doi:10.7500/AEPS20170630006

CrossRef Full Text | Google Scholar

Uddin, M., Romlie, M., Abdullah, M., Tan, Ch, Shafiullah, G. M., and Bakar, A. (2021). A novel peak shaving algorithm for islanded microgrid using battery energy storage system. Energy 196, 117084. doi:10.1016/j.energy.2020.117084

CrossRef Full Text | Google Scholar

Wang, K., Liang, Y., Jia, R., et al. (2023a). Two-stage optimal scheduling of nash negotiation-based integrated energy multi-microgrids with hydrogen-doped gas under uncertain environment. Power Syst. Technol. 47 (08), 3141–3159. doi:10.13335/j.1000-3673.pst.2023.0156

CrossRef Full Text | Google Scholar

Wang, K., Liang, Y., Jia, R., Wu, X., Wang, X., and Dang, P. (2023b). Two-stage stochastic optimal scheduling for multi-microgrid networks with natural gas blending with hydrogen and low carbon incentive under uncertain envinronments. J. Energy Storage 72, 108319. doi:10.1016/j.est.2023.108319

CrossRef Full Text | Google Scholar

Wei, C., Wang, Y., Xu, J., et al. (2023). Optimization of available transfer capability for regional power grids in inter-provincial electricity spot markets. Power Syst. Technol. 47 (10), 4255–4264. doi:10.13335/j.1000-3673.pst.2023.0396

CrossRef Full Text | Google Scholar

Xiao, H., Pei, W., Dong, Z., et al. (2018). Reactive power optimization of distribution network with distributed generation using metamodel-based global optimization method. Proc. CSEE 38 (19), 5751–5762+5931. doi:10.13334/j.0258-8013.pcsee.171768

CrossRef Full Text | Google Scholar

Xiao, Y., Wang, X., Wang, X., Wu, Z., and Liu, W. (2017). The coordinated development path of renewable energy and national economy in China considering risks of electricity market and energy policy. IEEE Trans. industrial Inf. 13 (5), 2566–2575. doi:10.1109/tii.2017.2676814

CrossRef Full Text | Google Scholar

Yang, M., Liu, Y., Guo, L., Wang, Z., Zhu, J., Zhang, Y., et al. (2024). Hierarchical distributed chance-constrained voltage control for HV and MV DNs based on nonlinearity-adaptive data-driven method. IEEE Trans. Power Syst., 1–14. doi:10.1109/tpwrs.2024.3413680

CrossRef Full Text | Google Scholar

Yu, M., and Hong, S. H. (2016). A real-time demand-response algorithm for smart grids:a Stackelberg game approach. IEEE Trans. Smart Grid 7 (2), 879–888. doi:10.1109/TSG.2015.2413813

CrossRef Full Text | Google Scholar

Zare, M., Niknam, T., Azizipanah-Abarghooee, R., and Ostadi, A. (2016). New stochastic bi objective optimal cost and chance of operation management approach for smart microgrid. IEEE Trans. Ind. Inf. 12 (6), 2031–2040. doi:10.1109/tii.2016.2585379

CrossRef Full Text | Google Scholar

Nomenclature