A time-variant power distribution network voltage sag identification method based on the concept of inheritance

The present paper introduces a novel method for identifying voltage sags in time-variant power distribution networks, effectively addressing the challenges arising from the temporal variability of network topology and data. The proposed method is founded on the concept of inheritance, which is bifurcated into breadth and depth inheritance strategies. The breadth inheritance strategy employs transfer learning to manage topological temporality, utilizing the Euclidean distance between samples to ascertain the sequence of sample migration, and implements multitask learning to share feature representations across different tasks. The depth inheritance strategy, on the other hand, utilizes incremental learning to handle data temporality, building upon the initial model parameters to learn new sample features, which in turn reduces the time required for model updates and enhances the accuracy of target tasks. Case study findings validate the suitability of the proposed methods for reconstructing fault identification models in scenarios characterized by topological temporal variability and for rapidly updating fault identification models in scenarios with data temporal variability. The approach presented herein holds significant implications for the enhancement of power supply reliability and the adaptability of electrical grids.

1 Introduction

Power quality is a paramount concern within the electrical power industry, defining the conformity of voltage and current to the standards required for the reliable operation of electrical equipment and the execution of industrial processes. It encompasses critical aspects such as voltage magnitude, frequency, waveform integrity, and the presence of harmonic distortions. Voltage sags, also known as dips or momentary interruptions, are a prevalent power quality disturbance, characterized by a transient reduction in voltage between 10% and 90% of the nominal value for a brief interval, typically lasting from a few power cycles to several seconds. These sags can lead to significant operational disruptions, equipment failures, and economic losses in industrial and commercial sectors, emphasizing the importance of their detection and mitigation to ensure a stable and reliable power supply. For readers who may be less familiar with voltage sags, this introduction will provide a foundational understanding of their impact on power quality.

Based on actual operational statistical data of power distribution networks, voltage sag sources include faults, the start-up of large induction motors, and the operation of large capacity transformers (Bastos et al., 2019; Waqar et al., 2024). The latter two types of transient sources primarily affect a limited number of loads and are considerably less harmful in terms of both the frequency of occurrence and the severity of impact compared to faults (Zhang et al., 2024a). Therefore, this paper focuses on the identification of fault-type transient sources, conducting research from two aspects: fault discrimination and transition resistance estimation.

With the increasing integration of new energy sources into power distribution networks year by year, the operational data of power distribution networks evolve dynamically under the new paradigm of the power system (Shareef et al., 2013; Zhang et al., 2024b). To ensure the power quality of the distribution network and meet the energy needs of some sensitive users, the topological structure of the power distribution network must be adjusted in a timely manner, and the characteristics of voltage sags change accordingly, exhibiting strong topological temporal characteristics (Turizo et al., 2022). With the advancement of advanced measurement and communication technologies, the proliferation of Distribution Automation Systems (DAS) in power distribution networks is increasing, and monitoring equipment represented by DAS terminals and Power Quality Monitors (PQM) has gradually achieved comprehensive monitoring and data collection of voltage sag data in power distribution networks. The distribution network, with its wide distribution and numerous nodes, accumulates voltage sag data over time, forming a massive data pool that demonstrates significant data temporal characteristics (Liao et al., 2015).Machine learning methods have proven superior in many fields, with classification and regression being the two most widely applied tasks (Sun et al., 2024). The fault type discrimination and transition resistance estimation of transient sources studied in this paper belong to the classification and regression tasks within the field of machine learning, respectively (Alipoor et al., 2014). The performance of machine learning models is highly dependent on the quantity and stable distribution of samples; the more samples a model has, the better its predictive performance. However, an excessive amount of samples can affect the timeliness of model training (Liu J. et al., 2023; Chen et al., 2023). The dynamic changes in power distribution networks intensify the evolution of sample data, making it difficult to build high-performance models. Moreover, as data accumulates, the updating and optimization of models may take longer, affecting real-time performance (Liu et al., 2022). The concept of inheritance is a method of establishing cross-task, cross-dataset external associations between multiple models or datasets, aiming to achieve efficient use of existing models and datasets (Tang et al., 2017). The concept of inheritance can be divided into two methods: deep inheritance and breadth inheritance (Liu M. et al., 2023). The former focuses on how to deeply transfer the knowledge of existing models into the incremental sample training process to continuously optimize the model; the latter aims to reduce the model’s demand for a large number of samples by establishing associations between different tasks or datasets, providing more sample resources (Caicedo et al., 2023; Balouji and McKelvey, 2022). The concept of inheritance can make more efficient use of existing computing resources and can also improve the model’s generalization ability on specific data and tasks. When facing scenarios with strong temporal variability, large amounts of data, and frequent updates, the concept of inheritance enables the model to quickly adapt and make accurate predictions through deep and breadth dimensions of inheritance.

In response to the data evolution scenario of power distribution networks, this paper proposes a voltage sag source identification method based on the concept of inheritance. The concept of inheritance includes two dimensions:breadth inheritance and depth inheritance (Yalman et al., 2022; Yikun et al., 2022; Khetarpal et al., 2023). The former uses transfer learning (TL) to overcome the topological temporality of power distribution networks, and the latter adapts to the data temporality of power distribution networks through incremental learning (IL). Transfer learning establishes a migration channel between the target and source topological structures, inheriting their sample sets, and constructing models for identifying and predicting the type and transition resistance of voltage sag sources in power distribution networks under scenarios with a small number of samples (Sha et al., 2019). Incremental learning enables continuous optimization of the model in the face of constantly changing data and tasks, reducing model update time and improving the real-time performance of transient source identification tasks.

2 Inheritance concept based on transfer and incremental learning

In addressing the challenges in training predictive models for time-variant power distribution networks, such as the scarcity of sample data in the target system due to topological variability and the lengthy model update times due to data variability, this section proposes an inheritance learning approach based on incremental learning and transfer learning. To illustrate the practical application of these concepts, we introduce the voltage sag data that serves as the foundation for our model training and validation.

Voltage sag data is crucial for identifying and predicting the type and transition resistance of voltage sag sources in power distribution networks. These data are collected from advanced measurement and communication technologies, such as Distribution Automation Systems (DAS) and Power Quality Monitors (PQM), which provide comprehensive monitoring and data collection of voltage sag events. The characteristics of this data, including its temporal and topological variability, are integral to understanding the proposed breadth and depth inheritance methods.

2.1 Framework for fault identification based on inheritance concept

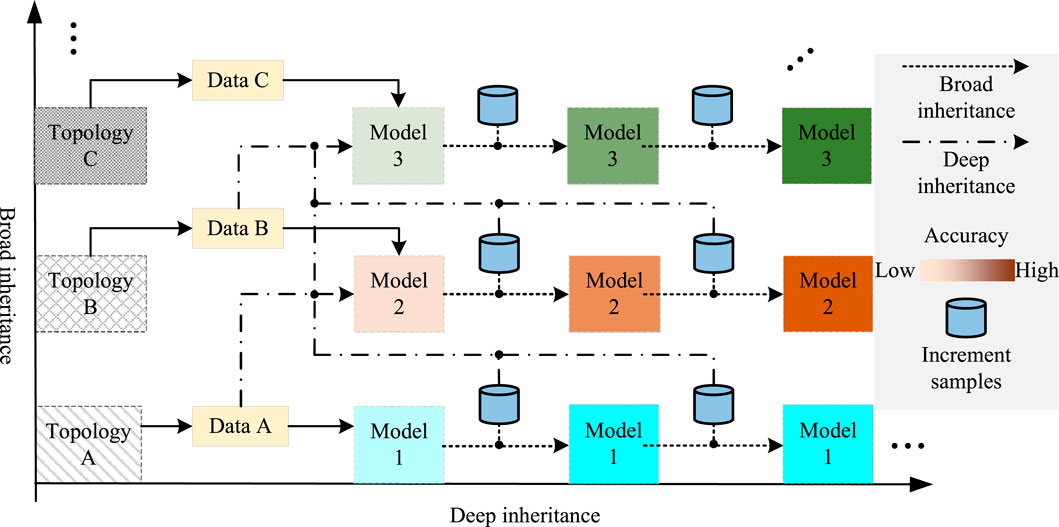
As shown in Figure 1, the illustration of the inheritance concept, through deep model inheritance and broad sample inheritance, the approach adapts to the temporal variability of power distribution networks.

Figure 1

Figure 1. Framework for voltage sag source identification based on inheritance concept.

In Figure 1, the horizontal axis represents a strategic approach to improve the predictive precision of the model through the acquisition of new knowledge from incremental samples and the deep inheritance of old knowledge from existing samples. Along this axis, the topological structure and the subject of the study remain constant, with incremental data continuously introduced over time to update the predictive model, resulting in a model with improved predictive accuracy.

The vertical axis captures the changes in the topological structure of the power distribution network, where the target system’s topology engages in breadth inheritance from the source system’s topology. This process involves migrating multiple sample sets from the source system, including incremental ones, to the target system, constructing a predictive model for voltage sag sources within the power distribution network under conditions of small sample sizes. This approach is crucial for initializing a robust predictive model, even when sample availability is limited.

Depth inheritance plays a critical role in the continuous optimization of the predictive model by integrating existing model parameters and knowledge into the incremental sample update process. This strategy achieves full-life-cycle knowledge depth inheritance within the predictive model, equipping it to adapt to the temporal variability inherent in power distribution network data.

Breadth inheritance, on the other hand, addresses the challenge of initial model construction by migrating a subset of samples from various source systems to the initial training phase of the target system’s model. This lateral knowledge transfer strategy enables the new system to leverage the accumulated insights from the old systems, promoting a synergistic exchange of knowledge that is essential for laying a solid foundation for the predictive model. This approach is crucial for adapting to the topological variability of the power distribution network, ensuring the model’s relevance and efficacy amidst structural transformations.

In summary, the framework depicted in Figure 1 adeptly employs a combination of breadth and depth inheritance to navigate the complexities and dynamics of power distribution networks. This method not only bolsters the model’s predictive accuracy but also ensures its durability and adaptability in response to evolving data and topological configurations.

2.2 Breadth inheritance

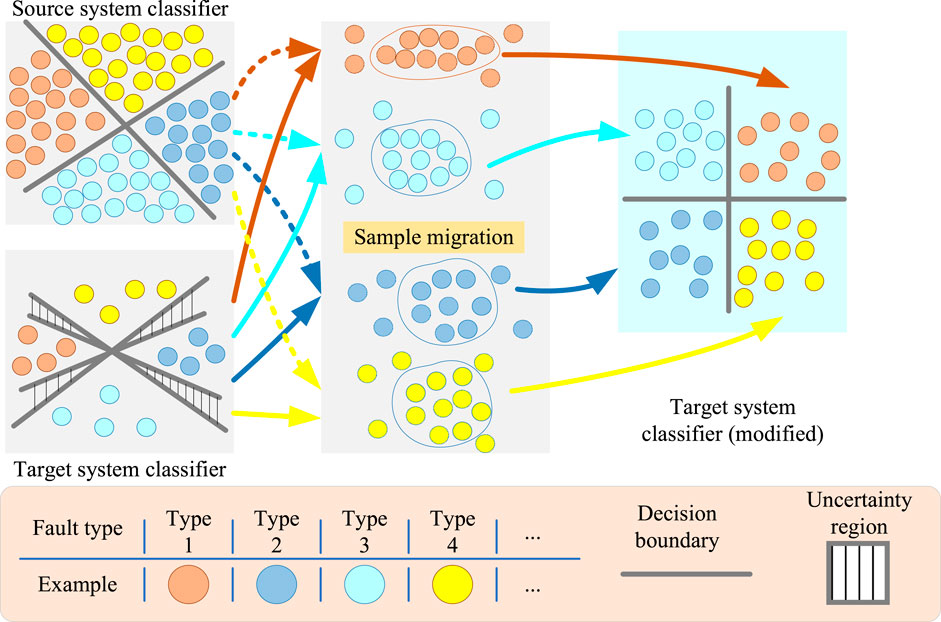
The concept of “breadth inheritance” within the framework of transfer learning emphasizes establishing connections from a source system to a target system, creating a channel for the inheritance of samples and features. This is particularly relevant in the domain of power distribution networks, where the strong variability of topological structures often results in a lack of sufficient steady-state operating samples for training identification models. Meanwhile, a wealth of voltage sag data has been accumulated in the source system through online monitoring and software simulation. This section utilizes a sample migration method to appropriately process the aforementioned voltage sag data, transforming it into data applicable for voltage sag source identification in the target system. Through this method, the dependence of the predictive model on the sample size of voltage sags in the target system is reduced, enabling the construction of a voltage sag identification model under conditions of limited samples.

Target systems are typically those with a short operation time and a small sample size. In contrast, source systems have the advantage of a long operation time and a large accumulation of sample data. By migrating samples, the rich sample data from the source system can be applied to the target system, thereby enhancing the identification accuracy of the target system to a certain extent. This process can be expressed as an optimization problem of sample distance in physical terms as follows:

$\left\{{\mathbf{S}}_T|\min \left(D_E\left(\mathbf{x},\mathbf{y},\mathbf{S}\right)\right)<\theta ,\left(\mathbf{x},\mathbf{y}\right)\in {\mathbf{S}}_T\right\}(1)$

In Equation 1, $\mathbf{S}$ represents the sample set of the source system, ${\mathbf{S}}_T$ represents the set of migratable samples, $\mathbf{x}$ and $\mathbf{y}$ are the input features and labels of ${\mathbf{S}}_T$, respectively, and $\theta$ is the threshold value for sample migration based on the Euclidean distance.

The figure (Figure 2) illustrates the process of sample migration, which can be summarized as follows: 1) According to the classification objectives of the identification model, samples corresponding to different labels in the source and target systems are classified by label; 2) All sample data are standardized to transform all data into the range of 0–1, using the Euclidean distance to measure the differences between samples of each class in the systems; 3) The Euclidean distance between systems is compared with the preset threshold $\theta$, and samples from the source system that are less than the preset threshold are migrated to the target system.

Figure 2

Figure 2. Schematic diagram of the sample migration process.

The target task is generally set for a new requirement and requires the joint action of data features, sample sets, and models. With the data features and samples determined, a source model with some similarity to the target task is selected. By transferring the model, the parameters of the source model that have been trained in other fields are transferred to the target model, which can greatly improve training efficiency. When the source task and the target task have similarity in the form of sample representation, the target model can inherit the parameters of the source model and continue training based on these model parameters and target samples.

2.3 Depth inheritance

Depth inheritance primarily addresses the issue of new data in time-variant power distribution networks and the update of predictive models. Therefore, this section replaces the existing full-scale training with incremental model training. Based on the pre-trained model, the predictive model is updated using incremental samples, inheriting the depth of the original model’s data, and enhancing the predictive model’s adaptability to temporal variability in data. Through the aforementioned method, the training time for updating the identification model is reduced, saving a significant amount of computational resources.

The more voltage sag data samples available, the higher the reliability of the output results of the voltage sag source predictive model. Most existing studies generate some time-domain data through simulation software to compensate for the shortcomings in the sample distribution of DAS monitoring data. During the dynamic growth of samples, new samples generated in later stages will gradually cover the sample space. As shown in Figure 3, the incremental learning process for voltage sag type identification starts with few samples at stage $t_1$, resulting in a larger confidence interval for the constructed voltage sag source classifier. At stage $t_2$, with the addition of incremental samples, the confidence interval of the classifier is gradually compressed to a smaller range. By stage $t_3$, when the full set of samples is used for training, the model has essentially achieved an ideal classification effect, with the confidence interval being extremely narrowed. In the above process, incremental learning corrects the classifier of the existing identification model with each new round of samples, which can be understood as the following parameter optimization problem:

$\beta =\mathrm{arg\; min}{\displaystyle \sum _{t\in \left\{\mathbf{A},\mathbf{I}\right\}}}{\displaystyle \sum _{i=1}^{n_t}}L\left(y_{t_i},f\left(\beta ,x_{t_i}\right)\right)(2)$

In Equation 2, $\mathbf{A}$ and $\mathbf{I}$ represent the existing and incremental samples, respectively, $n_t$ is the total number of samples in the set $\{\mathbf{A},\mathbf{I}\}$. $f$ is the classification model, $x_{t_i}$ and $y_{t_i}$ are the input features and output labels of a single sample, respectively, $L$ is the loss function of the model $f$, and $\beta$ is the output matrix of the identification model $f$.

Figure 3

Figure 3. Schematic diagram of the incremental learning process.

The incremental learning process, as shown in Equation 3, updates the output matrix $\beta$ of the model with new samples $\mathbf{I}$ to improve the recognition accuracy of the identification model $f$.

${\beta }_{i+1}={\beta }_i+{\mathbf{P}}_{i+1}{\mathbf{H}}_{i+1}^T\left(y_{i+1}^T-{\mathbf{H}}_{i+1}{\beta }_i\right)(3)$

In the equation, ${\beta }_{i+1}$ is the output matrix of the classification model after incremental learning (IL), ${\mathbf{H}}_{i+1}$ is the hidden layer output vector during model training using both existing $\mathbf{A}$ and incremental samples $\mathbf{I}$, $y_{i+1}$ is the sample label vector used for IL. ${\mathbf{P}}_{i+1}$ is the transition matrix, the calculation process of which is shown in Equation 4.

$\left\{\begin{array}{c}{\mathbf{P}}_{i+1}=\mathbf{P}-{\mathbf{P}\mathbf{H}}_i^T{\left(\mathbf{I}+{\mathbf{H}}_i^T{\mathbf{P}\mathbf{H}}_i^T\right)}^{-1}{\mathbf{H}}_i^{T}P\hfill \\ {\mathbf{P}}_1={\left({\mathbf{H}}_1^T{\mathbf{H}}_1\right)}^{-1}\hfill \end{array}\right.(4)$

In the equations, ${\mathbf{H}}_1$ is the first column of the output matrix ${\beta }_{i+1}$.

2.4 Multi-task learning

Multi-task Learning (MTL) is often considered a special case of transfer learning. Compared to Single-task Learning (STL), MTL has the following advantages: The MTL model learns and solves multiple related tasks simultaneously, improving performance by sharing knowledge and features; The shared module of MTL needs to balance different tasks to obtain a superior feature representation, equivalent to implicit data augmentation, which to some extent avoids the overfitting problem of a single task; Each task in MTL can selectively benefit from the hidden features learned in other tasks, thereby enhancing the performance of its own task. The voltage sag source identification task includes fault type classification and fault transition resistance prediction, the former being a classification problem and the latter a regression problem. There is a certain correlation between the two, making them suitable for processing with a multi-task learning model.

2.4.1 Multi-task learning framework

Deep Neural Networks (DNNs) are widely used for classification and regression problems, capable of handling complex nonlinear relationships, automatically learning sample features, and capturing the complexity of data at multiple levels with high robustness on large-scale datasets. Compared to other deep learning frameworks, TensorFlow has a broader application field, more powerful distributed computing capabilities, and richer support for advanced APIs, offering extremely high modeling efficiency. Based on this, this section constructs a multi-task learning model for voltage sag source identification as shown in Figure 4 using the TensorFlow deep learning framework. The voltage sag source identification task leverages the efficient data processing and feature extraction capabilities of DNNs. The DNN model adopts a multi-layer architecture, including an input layer, several hidden layers, and an output layer. The input layer is responsible for receiving multi-dimensional data related to voltage sags, and the hidden layers process the raw data through multiple levels of nonlinear transformation, achieving deep feature extraction. These hidden layers form a complex network of data abstractions, enabling the DNN to recognize subtle patterns and key features in the input data, laying the foundation for subsequent fault classification and transition resistance prediction tasks.

Figure 4

Figure 4. Schematic diagram of the voltage sag source identification multi-task learning model.

The multi-task learning strategy of this model allows for the simultaneous processing of fault classification and transition resistance prediction tasks. For fault classification, the output layer of the model is designed with multiple neurons, each representing a specific type of fault, enabling the network to effectively map the features extracted from the hidden layers to each fault category. For transition resistance prediction, the network uses a separate output neuron to estimate the resistance value associated with a specific sag event. The input features and shared hidden layers constitute the shared space of multi-task learning, where the model shares knowledge and features to improve the expressive performance of each task. This parallel task processing structure allows the model to learn and optimize specifically for different output requirements while sharing feature extraction layers, thereby improving overall analysis efficiency and predictive accuracy.

2.4.2 Sample feature settings

The sequence component method, a common method for analyzing power system faults, decomposes three-phase AC voltage or current signals into positive, negative, and zero sequences, often used for short-circuit analysis and imbalance detection. The values of sequence components can characterize the degree of imbalance in a three-phase system. The most common unbalanced states in power distribution networks, such as single-phase grounding and inter-phase short circuits, are characterized by significant fluctuations in sequence components. In the case of symmetrical faults, the positive sequence component fluctuates much more than the other sequence components. Therefore, this paper extracts the sequence components before and after the fault as the sample feature quantities for the aforementioned multi-task learning model.

The positive sequence component before the fault reflects the operating conditions of the system. During the fault, the positive, negative, and zero sequence components collectively characterize the type and transition resistance value features of the fault. Since the electrical characteristics closer to the location of the voltage sag source are more effective for voltage sag source identification. Therefore, this paper selects the sequence components of the bus voltage in the sag segment, the upstream and downstream current to construct the sample feature vector as follows:

$\left\{\begin{array}{c}\mathbf{F}=\left[\mathbf{S},{\mathbf{F}}^0,{\mathbf{F}}^1,{\mathbf{F}}^2\right]\hfill \\ \mathbf{S}=\left[U_s^1,{\varphi }_{U_s}^1,I_{su}^1,{\varphi }_{I_{su}}^1,I_{sd}^1,{\varphi }_{I_{sd}}^1\right]\hfill \\ {\mathbf{F}}^0=\left[U_f^0,{\varphi }_{U_f}^0,I_{fu}^0,{\varphi }_{I_{fu}}^0,I_{fd}^0,{\varphi }_{I_{fd}}^0\right]\hfill \\ {\mathbf{F}}^1=\left[U_f^1,{\varphi }_{U_f}^1,I_{fu}^1,{\varphi }_{I_{fu}}^1,I_{fd}^1,{\varphi }_{I_{fd}}^1\right]\hfill \\ {\mathbf{F}}^2=\left[U_f^2,{\varphi }_{U_f}^2,I_{fu}^2,{\varphi }_{I_{fu}}^2,I_{fd}^2,{\varphi }_{I_{fd}}^2\right]\hfill \end{array}\right.(5)$

In the equation, $\mathbf{F}$ is the sample feature vector, $\mathbf{S}$ represents the pre-fault characteristics, ${\mathbf{F}}^x$ ($x$ = 0, 1, 2) represents the zero-sequence, positive-sequence, and negative-sequence characteristics, respectively. $U$ and $I$ represent voltage and current, $\varphi$ represents the corresponding phase angle. The subscripts $s$ and $f$ represent pre-fault and during-fault, respectively, and $u$ and $d$ represent the relative upstream and downstream directions of the voltage with respect to the fault segment.

Under normal operating conditions of the power distribution network, the content of negative and zero sequence components is very low. Therefore, the pre-fault characteristics in Equation 5 only use the positive sequence component. To unify the sample phase angle features, the fundamental frequency phase at $\pm$0.5 cycles before the sag initiation moment is used as the phase before and after the fault. When a voltage sag event is detected, the wavelet decomposition is used to obtain the fault start time $t_0$, the pre-fault phase is taken at $t_0-0.5T$, and the phase during the fault process is taken at $t_0+0.5T$.

3 Case study

3.1 Setup

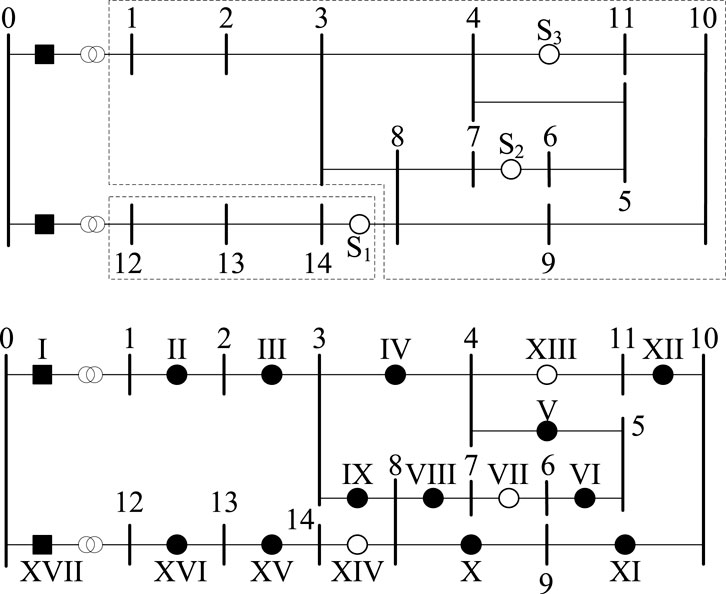
The case study employs the CIGRE 14-bus medium voltage distribution system pre-set in the RSCAD software, with its topology structure shown in Figure 5. A set of DAS remote measurements, including bus voltage and line current connected to the bus, is used. To simulate the temporal variability of the distribution network, the following settings are made based on the pre-set model: three tie switches are randomly switched on and off to simulate line topology changes, with a maximum of one tie switch being closed at a time; the load model’s load shedding ratio is adjusted to simulate load fluctuations, with a random value between −0.2 and 0.2; photovoltaic and wind turbines with a rated capacity of 1500 kW are installed on buses 3 and 10, respectively, with temperature, illumination, and wind speed fluctuating randomly within the preset range of the model. The tests are conducted on the deep learning open-source framework TensorFlow developed by Google, using the Python-based open-source machine learning toolkit Scikit-Learn. The computer platform used in the experiments is equipped with an Intel(R) Xeon(R) CPU E5-1620 v4 @ 3.50 GHz processor, 16.0 GB of RAM, and an NVIDIA Quadro P620 graphics card.

$P\left(x\right)=\left\{\begin{array}{c}0.65,x=LG\hfill \\ 0.09,x=LL\hfill \\ 0.2,x=LLG\hfill \\ 0.06,x=LLL\hfill \end{array}\right.(6)$

Figure 5

Figure 5. Topology structure of the CIGRE 14-bus medium voltage distribution system.

Voltage sag events are simulated by combining phase-to-ground and interphase faults using a setting module. The probability distribution of the fault types follows Equation 6. The resistances of phase-to-ground and inter-phase faults both follow a Gaussian distribution, with the same mean $\mu$ and standard deviation $\sigma$, taken as 10 and 3.5, respectively. When the effective value of the voltage sag source is between 0.1 and 0.9, it is considered a valid simulation, and the DAS remote measurements are saved.

In our study, the sampling process was designed to accurately capture the voltage quality during and after the switching of circuit breakers, which is a critical factor in assessing the impact on the power distribution network. The switching time of the circuit breaker, defined as the interval from the initiation of the switching action to the completion of the circuit interruption, was set to 50 milliseconds. This value is based on industry standards and typical operational parameters of modern circuit breakers, ensuring a realistic simulation of the switching process.

To simulate the effect of this switching time on voltage quality, we employed a high-resolution simulation with a time step of 1 millisecond. This allowed us to capture the transient voltage changes with precision, providing a detailed analysis of the voltage sag characteristics. The simulation was conducted over a period of 10 cycles (20 milliseconds) of the power frequency to ensure that we captured the complete response of the network to the switching event.

During the sampling process, we collected voltage and current data at each bus and line of the distribution network. The data were recorded at 100 Hz, providing a comprehensive dataset for analyzing the voltage quality and the performance of our proposed voltage sag identification method. The sampling interval was chosen to balance the need for detailed data with the computational efficiency of the simulation.

Using the aforementioned case study setup, 3,209 sets of valid voltage sag samples are generated, and the statistics of each sample generation condition are shown in Table 1. Among them, $LG$ represents single-phase grounding $(L=A,B,C)$, $LL$ represents inter-phase short circuits, $LLG$ represents inter-phase short circuits grounded, and $LLL$ represents three-phase symmetrical faults, resulting in a total of 11 classification labels. When marking the transition resistance labels of the samples, the fault sample labels of type $LLG$ take the smaller of the inter-phase and phase-to-ground values. Open Loop 0 represents the topology formed when all three tie switches are open, and Ring Network $i(i=\mathrm{1,2,3})$ represents the ring topology formed when tie switch $i$ is closed. A multi-task learning model is constructed and the hyperparameters of the model are given in Table 2.

Table 1

Table 1. RTDS-generated valid sample condition statistics list.

Table 2

Table 2. Hyperparameter list for the multi-task learning model.

3.2 Adaptability to topological temporality

3.2.1 Changes in power grid topology

From the sample generation conditions, it can be known that the three tie switches can construct one open-loop network and three ring networks. The above four networks are considered as different research systems, and when the topological state transitions from one system to another, the former is called the source system, and the latter is called the target system. The four networks can switch with each other, serving as source and target systems for each other.

For each target system, all samples in Table 1 are used to construct the model. For ease of statistics, the samples of the source system are migrated to the target system in steps of 200 according to the Euclidean distance from small to large. If the number of samples in the source system is insufficient, all samples of the source system are migrated. As shown in Table 3 is the sample migration process between each system and the type classification accuracy and transition resistance prediction loss before and after migration.

Table 3

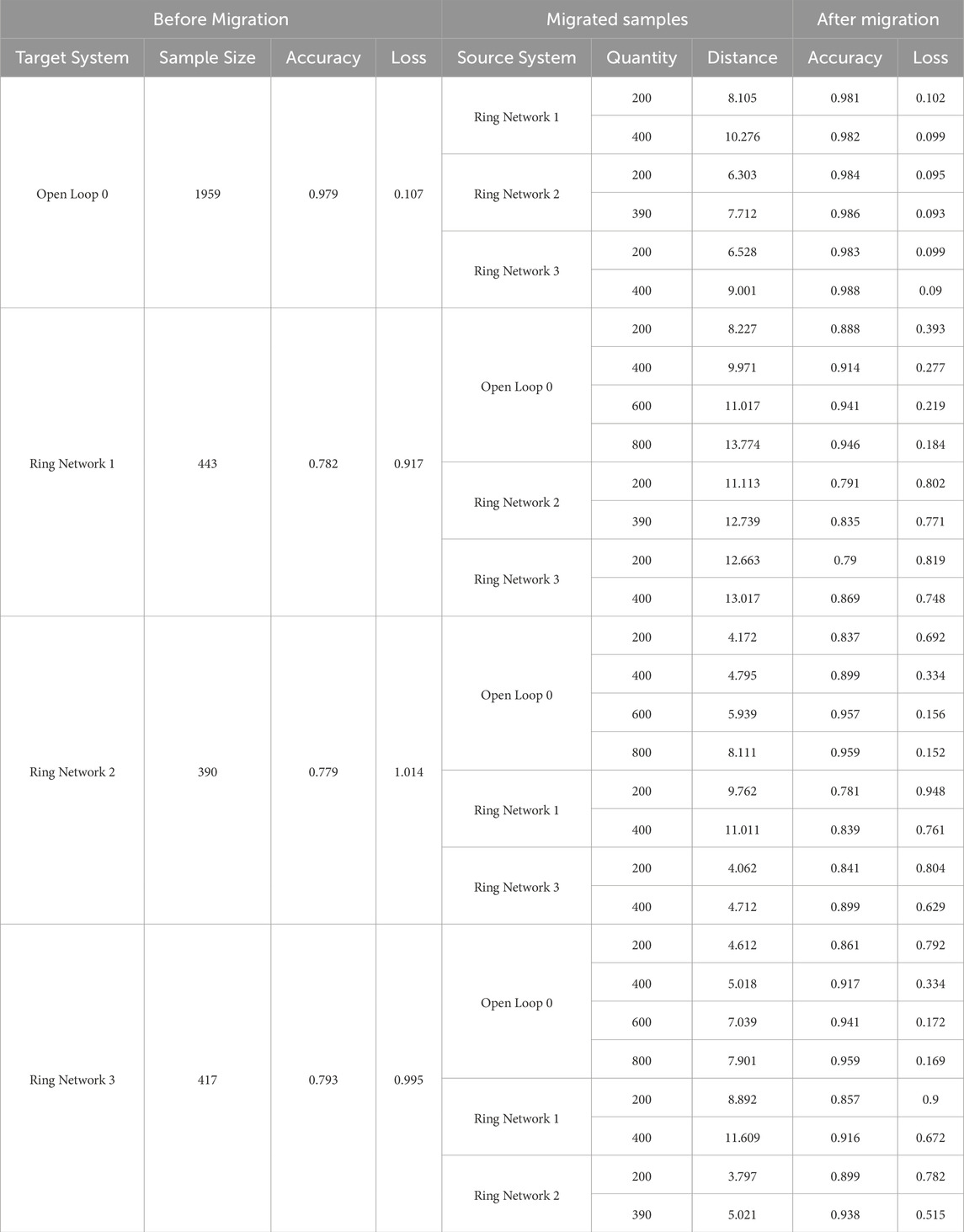
Table 3. Statistics of inheritance results caused by topological temporality due to tie switch position change.

The results in Table 3 can be observed as follows:

1) The sample size of Open Loop 0 significantly exceeds other systems. The model prediction effect before and after sample migration is better than other target systems, confirming the positive impact of sample size on model performance;

2) As the number of migratable samples increases, the model prediction effect of the target system gradually optimizes, indicating that sample migration is crucial for enhancing model performance, especially in the early stages of the target system’s operation;

3) When the same number of samples is migrated to the same target system, the contribution of samples from Ring Network 1 to the prediction model is lower than that of other source systems. Considering that Ring Network 1 is connected to two transformers, forming a larger ring network, this indicates that the quality of samples is closely related to the topological structure between the source and target systems;

4) The performance improvement of the Ring Network models is attributed to new features in the migrated samples, which may not have appeared or appeared less frequently in the target system samples, emphasizing the importance of sample migration when the target system has an insufficient number of samples;

5) With the increase in the number of migrated samples from the source system, the performance of the target system’s model gradually stabilizes, and the rate of improvement in prediction accuracy gradually slows down. Compared with other source systems, the contribution of samples from Ring Network 1 to the target system model performance is smaller. This phenomenon is closely related to the Euclidean distance between the source system and target system samples, and the impact of sample Euclidean distance will be introduced in detail in the following text.

As the number of migrated samples from the source system increases, the performance of the target system’s model gradually stabilizes, and the rate of improvement in prediction accuracy gradually slows down. Compared with other source systems, the contribution of samples from Ring Network 1 to the target system model performance is smaller. This phenomenon is closely related to the Euclidean distance between the source system and target system samples, and the impact of sample Euclidean distance will be introduced in detail in the following text.

3.2.2 Variation of migrated sample distance

Considering the actual operating conditions, the topologies before and after the integration of new energy in the case study are defined as the source system and the target system, respectively. Given that the previous analysis has detailed the significant effect of sample size on breadth inheritance, this section briefly analyzes the impact of excessive migration of a large number of samples and focuses on an in-depth discussion from the perspective of the Euclidean distance of the migrated samples.

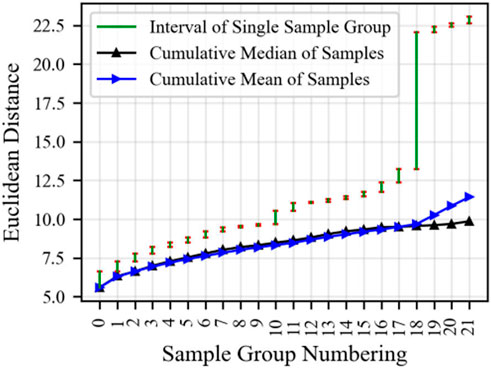
The source system and target system samples generated in the case study are 2,218 and 991, respectively. The Euclidean distance between the samples of the source system and the target system is calculated. The samples of the source system are divided into 22 groups according to the Euclidean distance from small to large, with a minimum migration unit of 100. The statistical Euclidean distance between each group of samples and the target system samples is shown in Figure 6. A single group of samples $i$ refers to the 100 samples in the $i$-th group of the source system, and the cumulative samples $i$ are the sample set composed of the first $i$ groups of samples, with a quantity of $i\times 100$.

Figure 6

Figure 6. Euclidean distance distribution of source system samples.

The single group of samples and cumulative samples from the source system are merged with the samples of the target system to form a new training set. The target system samples are used for training, and the obtained prediction results serve as the control group. Figure 7 shows the fault type and transition resistance prediction results of the target system for non-migrated samples, single group samples, and cumulative samples.

Figure 7

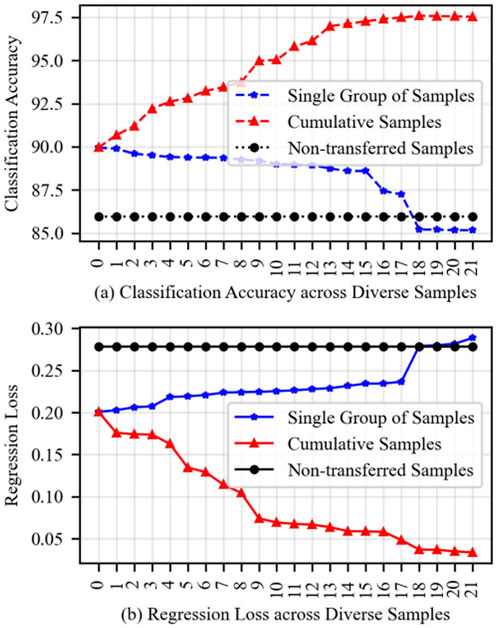
Figure 7. Prediction results of fault types and transition resistances in the target system for non-migrated samples, single group samples, and cumulative samples. (A) Classification accuracy across diverse samples (B) Regression loss acroass diverse samples.

Comparing Figures 6, 7, it can be observed that the smaller the Euclidean distance between the single group of samples and the target system samples, the better the prediction effect. The model performance of the cumulative samples is better than that of the single group of samples, proving the positive impact of sample quantity on model performance. The samples from the 18th group and beyond have a larger Euclidean distance with the target system samples, resulting in a situation where the migration effect of the single group of samples is lower than that of non-migrated samples.

The performance improvement of migration starting from the 18th group of cumulative samples also gradually stops. Considering that the model training time is positively correlated with the number of samples, it is timely to stop migrating samples with too large Euclidean distance. Overall, the model performance is negatively correlated with the Euclidean distance between samples: the smaller the Euclidean distance between the migrated samples and the target system samples, the better the migration effect.

With the increase in the number of migrated samples from the source system, the performance of the target system’s model gradually stabilizes, and the rate of improvement in prediction accuracy gradually slows down. Compared with other source systems, the contribution of Ring Network 1 samples to the performance of the target system model is smaller. This phenomenon is closely related to the Euclidean distance between the source system and target system samples, and the impact of sample Euclidean distance will be introduced in detail in the following text.

3.3 Adaptability to data temporality

As the system’s operational time progresses, the target system’s samples gradually accumulate, and the time cost of model training also increases. Incremental learning updates the model parameters based on the original model using incremental samples, which can significantly improve the timeliness of model updates while ensuring model performance. To verify the response of the depth inheritance method based on incremental learning in dealing with data variability, 1538 samples of Open Loop 0 without new energy access from Table 1 were data-augmented by adding random perturbations, as shown in Equations 7–9.

$\bar{\mathbf{F}}=\frac{\mathbf{F}-\min \left(\mathbf{F}\right)}{\max \left(\mathbf{F}\right)-\min \left(\mathbf{F}\right)}(7)$

$Noise=\text{np.random.normal}\left(\mu ,\sigma ,\left(n,24\right)\right)(8)$

$\tilde{\mathbf{F}}=\text{np.random.choice}\left(\bar{\mathbf{F}},n\right)+Noise(9)$

In the equations, $\mathbf{F}$ represents the original sample features, and $\min (\cdot )$ and $\max (\cdot )$ are the operations of taking the minimum and maximum values, respectively. The function $\text{np.random.normal}(\cdot )$ generates random numbers following a normal distribution with $n$ rows and 24 columns, where $\mu$ and $\sigma$ are the mean and standard deviation of the normal distribution, taken as 0 and 0.035, respectively. The function $\text{np.random.choice}(\cdot )$ randomly selects $n$ samples from the given samples, where $n$ is taken as 1,624. $\tilde{\mathbf{F}}$ and $\bar{\mathbf{F}}$ together form a new set of samples, with the former having the same labels as the extracted samples.

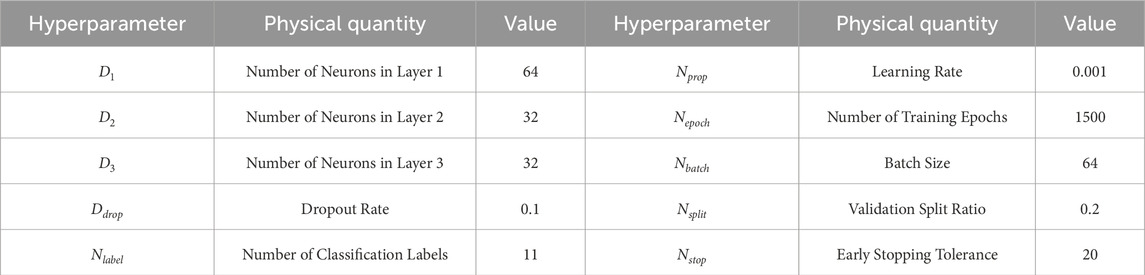
The above 3,000 samples were randomly divided into 15 groups, each containing 200 samples. Classification and regression models based on STL were constructed using the parameters in Table 2, and model training was performed using both full-scale and incremental learning. The classification task simultaneously monitored its accuracy and loss function values, while the regression task only monitored its loss function values.

It can be observed from the figures that after each update with new samples, the performance of the classification and regression task models has improved based on the original model. After four incremental training sessions, the loss value of the classification model decreased from 1.86 to 0.04, and the classification accuracy increased from below 0.2 to 0.9975. After the fourth update, the classification accuracy is basically maintained at 1, while the training and validation loss values continue to decrease, indicating that the performance of the classification model is still improving. The loss value of the regression model decreased from 20 to 0.05 after three updates. From the fourth update, the model’s performance has basically stabilized, with training and validation loss values changing within a very small range.

The above samples were divided into five groups, each containing 600 samples, and incremental and full-scale learning were restarted. Figure 8 shows the performance and training time of the transition resistance value prediction model for voltage sag sources under the two grouping methods, with the loss function value as the evaluation index. During the first group of model training, the performance and time consumption of full-scale learning and incremental learning models were quite close. As incremental samples continued to be added, the training time for full-scale learning increased dramatically, while the training time for incremental learning remained essentially unchanged. After each model update, the performance of the two learning methods was basically equivalent. For the application of voltage sag source type and transition resistance identification, the above models fully meet the prediction accuracy requirements.

Figure 8

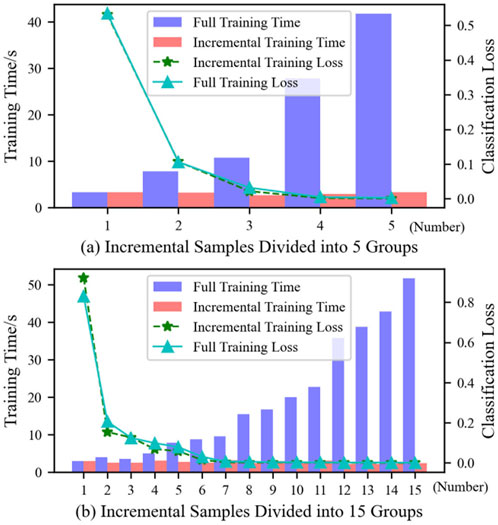
Figure 8. The impact of data update cycles on depth inheritance learning. (A) Incremental samples divided into 5 groups (B) Incremental samples divided into 15 groups.

The time difference between the end of the current model update and the end of the previous model update is called the model update latency, and the difference in loss values after two updates is called performance improvement. By comparing Figures 8A, B, it can be seen that the higher the sample update frequency, the more obvious the advantage of incremental learning in model update latency, and the better the timeliness of performance improvement. Therefore, incremental learning is more suitable for quasi-online prediction scenarios with higher real-time requirements.

3.4 Discussion

3.4.1 Implications of the study

This study presents a novel approach to identifying voltage sag sources in power distribution networks by leveraging the concept of inheritance, which includes breadth and depth inheritance strategies. The integration of transfer learning and incremental learning within this framework allows for adaptability to the dynamic nature of power distribution networks, which are subject to both topological and data temporal variability.

3.4.2 Comparison with existing method

The proposed method offers several advantages over traditional voltage sag identification techniques. Unlike methods that require a significant amount of data for model training, our breadth inheritance strategy enables the model to be constructed with a limited sample size, which is particularly beneficial during the initial stages of network operation or after significant topological changes. Furthermore, our depth inheritance strategy ensures that the model remains up-to-date with the latest data, reducing the time required for model updates and maintaining high accuracy in fault identification tasks.

3.4.3 Performance and accuracy

The case study results demonstrate the effectiveness of our proposed methods in scenarios with topological temporal variability and the rapid update of fault identification models in scenarios with data temporal variability. The multi-task learning model, which simultaneously handles fault type classification and transition resistance prediction, shows improved performance compared to single-task models. This improvement is attributed to the shared feature extraction layers, which enhance the model’s ability to capture complex patterns in the data.

3.4.4 Practical applications

The practical application of our method is significant, particularly in modern power distribution networks that are increasingly integrating renewable energy sources and facing frequent topological changes. Our method provides a tool for grid operators to quickly and accurately identify the sources of voltage sags, allowing for timely maintenance and mitigation strategies to be implemented, thereby improving power supply reliability.

3.4.5 Limitations and future work

While our study has shown promising results, there are limitations that should be acknowledged. The proposed method is tailored to the specific characteristics of the power distribution network studied and may require adjustments for different network configurations or operational conditions. Future work will focus on testing the method across a variety of network topologies and exploring the integration of additional data sources, such as weather data and real-time monitoring feeds, to further enhance the model’s robustness and accuracy.

4 Conclusion

This paper proposes a voltage-sag source identification method for power distribution networks based on the concept of inheritance, aiming at the rapid evolution characteristics of the distribution system. The proposed method is applicable to the reconstruction of voltage sag source identification models in topologically variant scenarios and the rapid update of voltage sag source identification models in data variant scenarios.

Firstly, sources of topological and data variability in power distribution networks were introduced, and the impact of temporal characteristics was analyzed in conjunction with the voltage sag source identification task. Based on the concept of inheritance learning, breadth inheritance methods for topological variability and depth inheritance methods for data variability were proposed.

Then, combined with the fault type discrimination and transition resistance estimation tasks of voltage sag source identification, breadth inheritance paths based on transfer learning and depth inheritance paths based on incremental learning were proposed. According to the special scenarios of power distribution network faults, sequence components were used as sample features to construct a multitask learning model.

Finally, case study analysis verified the effectiveness of the inheritance concept in dealing with the topological and data variability of power distribution networks. Transfer learning focuses on using existing knowledge to adapt to new tasks or datasets, overcoming the topological variability of power distribution networks. Incremental learning enhances the model’s adaptability to data variability, enabling the model to continuously and quickly update in the face of changing data.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

KL: Conceptualization, Investigation, Software, Writing–original draft, Writing–review and editing. XY: Data curation, Methodology, Supervision, Writing–review and editing. SO: Writing–review and editing. JP: Funding acquisition, Resources, Visualization, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

Research on rapid fault processing technology of distribution network under multienergy coupling scenario based on coordination between master station and distribution terminal: GXKJXM20222165.

Conflict of interest

Authors KL, XY and SO were employed by Institute of Guangxi Power Grid Co., Ltd.

Author JP was employed by Nanning Hengzhou Power Supply Bureau of Guangxi Power Grid Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alipoor, J., Doroudi, A., and Hosseinian, S. H. (2014). Identification of the critical characteristics of different types of voltage sags for synchronous machine torque oscillations. Electr. power components syst. 42, 1347–1355. doi:10.1080/15325008.2014.933376

CrossRef Full Text | Google Scholar

Balouji, E., Salor, , and McKelvey, T. (2022). Deep learning based predictive compensation of flicker, voltage dips, harmonics and interharmonics in electric arc furnaces. IEEE Trans. Industry Appl. 58, 4214–4224. doi:10.1109/TIA.2022.3160135

CrossRef Full Text | Google Scholar

Bastos, A. F., Lao, K.-W., Todeschini, G., and Santoso, S. (2019). Accurate identification of point-on-wave inception and recovery instants of voltage sags and swells. IEEE Trans. Power Deliv. 34, 551–560. doi:10.1109/TPWRD.2018.2876682

CrossRef Full Text | Google Scholar

Caicedo, J. E., Agudelo-Martínez, D., Rivas-Trujillo, E., and Meyer, J. (2023). A systematic review of real-time detection and classification of power quality disturbances. Prot. Control Mod. Power Syst. 8, 3–37. doi:10.1186/s41601-023-00277-y

CrossRef Full Text | Google Scholar

Chen, Y.-T., Chuang, Y.-C., Chang, L.-S., and Wu, A.-Y. (2023). S-qrd-elm: scalable qr-decomposition-based extreme learning machine engine supporting online class-incremental learning for ecg-based user identification. IEEE Trans. Circuits Syst. I-Regular Pap. 70, 2342–2355. doi:10.1109/TCSI.2023.3253705

CrossRef Full Text | Google Scholar

Khetarpal, P., Nagpal, N., Al-Numay, M. S., Siano, P., Arya, Y., and Kassarwani, N. (2023). Power quality disturbances detection and classification based on deep convolution auto-encoder networks. IEEE Access 11, 46026–46038. doi:10.1109/ACCESS.2023.3274732

CrossRef Full Text | Google Scholar

Liao, H., Abdelrahman, S., Guo, Y., and Milanovic, J. V. (2015). Identification of weak areas of power network based on exposure to voltage sags-part i: development of sag severity index for single-event characterization. IEEE Trans. Power Deliv. 30, 2392–2400. doi:10.1109/TPWRD.2014.2362965

CrossRef Full Text | Google Scholar

Liu, J., Wang, J., Yan, T., Qi, F., and Chen, G. (2023a). Unknown traffic recognition based on multi-feature fusion and incremental learning. Appl. Sciences-Basel 13, 7649. doi:10.3390/app13137649

CrossRef Full Text | Google Scholar

Liu, M., Chen, Y., Zhang, Z., and Deng, S. (2023b). Classification of power quality disturbance using segmented and modified s-transform and dcnn-msvm hybrid model. IEEE Access 11, 890–899. doi:10.1109/ACCESS.2022.3233767

CrossRef Full Text | Google Scholar

Liu, Y., Zhang, J., Jia, H., Yuan, L., and Zhou, M. (2022). Retracted: identification of voltage sag sources in the electrified railway power supply system based on cnns (retracted article). Wirel. Commun. and Mob. Comput. 2022, 1–7. doi:10.1155/2022/4602187

CrossRef Full Text | Google Scholar

Sha, H., Mei, F., Zhang, C., Pan, Y., and Zheng, J. (2019). Identification method for voltage sags based on k-means-singular value decomposition and least squares support vector machine. ENERGIES 12, 1137. doi:10.3390/en12061137

CrossRef Full Text | Google Scholar

Shareef, H., Mohamed, A., and Ibrahim, A. A. (2013). Identification of voltage sag source location using s and tt transformed disturbance power. J. Central South Univ. 20, 83–97. doi:10.1007/s11771-013-1463-5

CrossRef Full Text | Google Scholar

Sun, C., Han, H., Wu, X., and Yang, H. (2024). Antiforgetting incremental learning algorithm for interval type-2 fuzzy neural network. IEEE Trans. Fuzzy Syst. 32, 1938–1950. doi:10.1109/TFUZZ.2023.3336325

CrossRef Full Text | Google Scholar

Tang, Y., Wei, R., Chen, K., and Fang, Y. (2017). Voltage sag source identification based on the sign of internal resistance in a “thevenin’s equivalent circuit”. Int. Trans. Electr. ENERGY Syst. 27. doi:10.1002/etep.2461

CrossRef Full Text | Google Scholar

Turizo, S., Ramos, G., and Celeita, D. (2022). Voltage sags characterization using fault analysis and deep convolutional neural networks. IEEE Trans. Industry Appl. 58, 3333–3341. doi:10.1109/TIA.2022.3162569

CrossRef Full Text | Google Scholar

Waqar, H., Bukhari, S. B. A., Wadood, A., Albalawi, H., and Mehmood, K. K. (2024). Fault identification, classification, and localization in microgrids using superimposed components and wigner distribution function. Front. Energy Res. 12. doi:10.3389/fenrg.2024.1379475

CrossRef Full Text | Google Scholar

Yalman, Y., Uyanik, T., Tan, A., Bayindir, K. C., Terriche, Y., Su, C.-L., et al. (2022). Implementation of voltage sag relative location and fault type identification algorithm using real-time distribution system data. Mathematics 10, 3537. doi:10.3390/math10193537

CrossRef Full Text | Google Scholar

Yikun, Z., Yingjie, H., Haixiao, Z., Jiahao, L., Yijin, L., and Jinjun, L. (2022). Classification method of voltage sag sources based on sequential trajectory feature learning algorithm. IEEE Access 10, 38502–38510. doi:10.1109/ACCESS.2022.3164675

CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, L., Liu, B., Chen, J., and Yao, W. (2024a). Voltage sag sensitive load type identification based on power quality monitoring data. Int. J. Electr. Power and Energy Syst. 158, 109936. doi:10.1016/j.ijepes.2024.109936

CrossRef Full Text | Google Scholar

Zhang, Y., Zhu, Z., Deng, Z., and Wang, M. (2024b). A novel cause identification method of voltage sag for auxiliary power quality monitoring. Electr. POWER Syst. Res. 226, 109937. doi:10.1016/j.epsr.2023.109937

CrossRef Full Text | Google Scholar