- 1Measurement Center of Guangxi Power Grid Co., Ltd., Nanning, China
- 2NARI Group (State Grid Electric Power Research Institute) Co., Ltd., Nanning, China
In this paper, the maximal information coefficient method-variational mode decomposition-bidirectional long short term memory network-adaptive boosting (MIC-VMD-Bi-LSTM-Adaboost) algorithm is used to forecast the power load. Firstly, MIC is used to determine the correlation degree of meteorological parameters influencing power load. Features having a high correlation degree are then chosen to be input vectors. Secondly, the input characteristics are decomposed using VMD, and five distinct IMF components are retrieved in order to remove unnecessary information. Lastly, different assessment indices are computed and the power load is predicted using the Bi-LSTM-Adaboost method. In order to determine the benefit of the approach used in this work, the outcomes of LSTM, Bi-LSTM, and LSTM-Adaboost are compared concurrently.
1 Introduction
Power load forecasting is a key step in power industry planning. It comprehensively predicts and calculates future power load, power consumption situation, power demand and power consumption based on historical power load data and other relevant interfering factors (such as weather changes, human activities, industrial process types, time and seasonal characteristics, etc.) (Habbak et al., 2023). Accurate forecast and rapid response to power demand are critical to the safety, stability and efficiency of power system operation (Kumar, 2024). Electric vehicles, renewable energy, flexible loads and other unpredictable loads are being added to the modern power grid. It also enhances the accuracy of load forecasting (Kumar et al., 2013).
Existing load prediction approaches can be categorized into two types: conventional mathematical statistics and machine learning (Chen et al., 2023). Traditional mathematical statistics approaches include regression analysis, kalman filtering, load derivation, and exponential smoothing (Kumar et al., 2016). These approaches are basic in structure, operate and forecast quickly, and may be scaled. However, they rely on statistical law characteristics, and the results of nonlinear data processing are poor, with low precision (Kumar et al., 2020).
Machine learning methods for load forecasting, including neural network (NN), support vector machine (SVM), and long short term memory network (LSTM), have been developed with advancements in computer technology (Cordeiro-Costas et al., 2023). These strategies improve prediction accuracy and overcome the limitations of nonlinear data (Kumar et al., 2023b). In the actual prediction process, two or more algorithms are generally used to complement each other, and other meteorological factors are included, to make the forecast findings more realistic (Kumar et al., 2023a).
Currently, researchers have employed a combination of multiple techniques to anticipate load. Tian et al. (2022) Neural networks (NN) were integrated with type-2 fuzzy systems (T2FSs), and feedback was introduced to the fuzzy neural networks. This approach achieved an accuracy of 98
The above literature uses MIC, LSTM and XGBoost algorithms for load forecasting, but does not combine the algorithms, and does not consider the impact of various feature vectors on load forecasting. Considering the large amount of data, the direct prediction calculation is large and the data is redundant, which will also reduce the prediction accuracy. Therefore, a VMD of various meteorological factors affecting power load is proposed in this paper, and the Bi-LSTM combined with Adaboost algorithm is used to predict power load. Firstly, MIC is used to analyze the relevance of input factors affecting prediction, and the features with high correlation coefficient are extracted as input. Secondly, the input factors are decomposed by VMD to eliminate noise and avoid redundant data. Finally, Bi-LSTM combined with Adaboost algorithm is used to predict urban power load, and root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE) and coefficient of determination (
2 Feature processing
2.1 Maximal information coefficient method
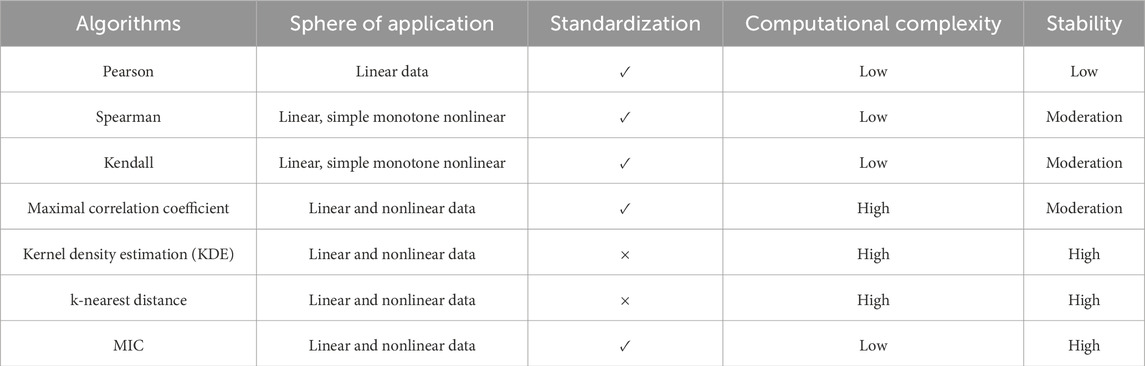
The MIC is used to assess the extent of significance between variables, linear or nonlinear strength, and is frequently employed in feature selection. It has good universality, fairness, and symmetry (Lin et al., 2022). Table 1 presents a comparison of commonly used methods. It can be seen that MIC has minimal computing complexity, great stability, and apparent advantages.
The theory of MIC is according to the concept of mutual information. Mutual information refers to the measure of interdependence between variables, that is, the degree of uncertainty reduction of random variable X to Y, which is expressed by Equation 1. The larger the value, the stronger the correlation between the two variables; conversely, the weaker the correlation. When I (X; Y) = 0, X and Y are independent.
Here,
The idea of MIC is as follows: according to the relationship between the two variables, the scatter plot is used to distribute in the two-dimensional space, and a certain interval is divided in the x and y directions respectively, and the distribution of all scatters in each interval is checked (Surapunt and Wang, 2024). Formula 2 is the calculation of MIC.
In the formula,
According to Equations 1, 2, MIC can be divided into three steps:
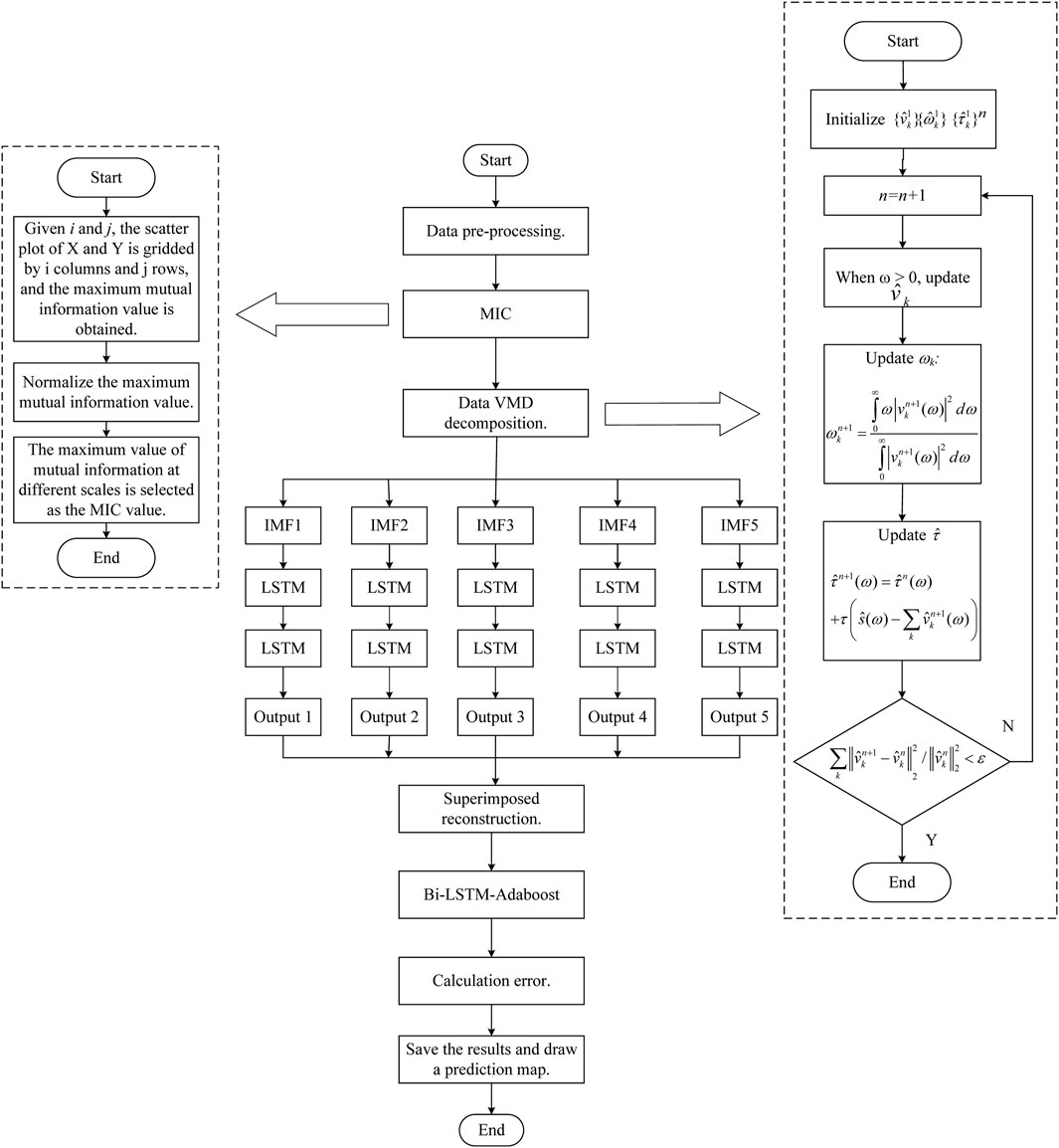
1. Given i and j, the scatter plot composed of XY is gridded by i columns and j rows, and the maximum mutual information value is obtained;
2. Normalize the maximum mutual information value;
3. The maximum value of mutual information at different scales is selected as the MIC value.
2.2 Feature extraction
MIC analyzes the degree of correlation between each feature and the load size since it is uncertain how much each affecting factor will effect the load (Sukanya Satapathy and Kumar, 2020; Satapathy and Kumar, 2019). The correlation is higher the greater the value’s absolute value. The correlation degree corresponding to various correlation coefficients is displayed in Table 2.
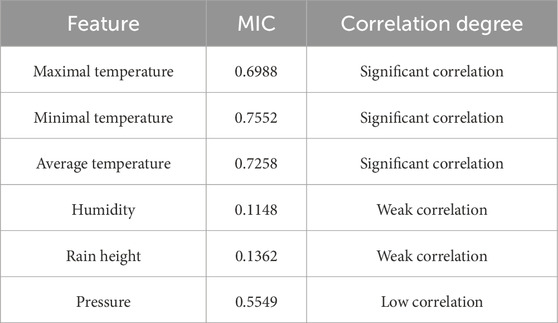
The correlation between the seven meteorological factors affecting the power load and the power value are obtained by MIC, and the outcomes are presented in Table 3.
Table 3 shows significant correlations between highest temperature, lowest temperature, average temperature, and power load. However, humidity, rain height, and pressure show weak and low correlations, which can be ignored. Therefore, the first three are used as inputs.
2.3 VMD decomposition
VMD enables the simultaneous extraction of decomposition modes. The model looks for a group of modes and their respective center frequencies so that they can replay the input signal together, and each mode is smooth after demodulation to the baseband. The algorithm’s essence is to expand the conventional Wiener filter to multiple adaptive bands, giving it a solid theoretical foundation while remaining simple to understand. The alternate direction multiplier method is utilized to successfully improve the variational model, increasing its robustness to sampling noise. The adaptability of VMD refers to the effective decomposition of intrinsic mode function (IMF) components and frequency domain section of signals by adaptively matching the optimal central frequency and bandwidth of every pattern while performing pattern decomposition on a given sequence, in order to obtain effective signal decomposition components and get the suitable results of the variational problem (Zhao et al., 2023; Wang et al., 2023). The following Equations 3–6 are the solution formulas of VMD decomposition (Geng et al., 2023). The VMD decomposition of highest temperature, lowest temperature and average temperature is shown in (Figures 1A–C).
In these formulas,
3 Forecasting model
3.1 LSTM network
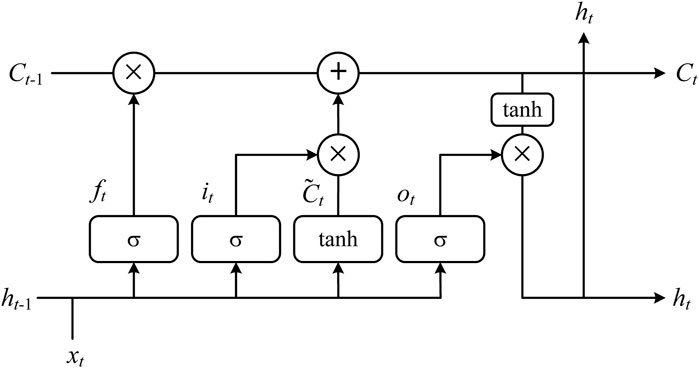
As a peculiar recurrent neural network, LSTM is primarily applied to predict time series (Abumohsen et al., 2023). The Figure 2 is a typical LSTM structure diagram. Bi-LSTM is an improved version of LSTM. The prediction process mainly includes three stages: forgetting stage, selective memory stage and output stage.
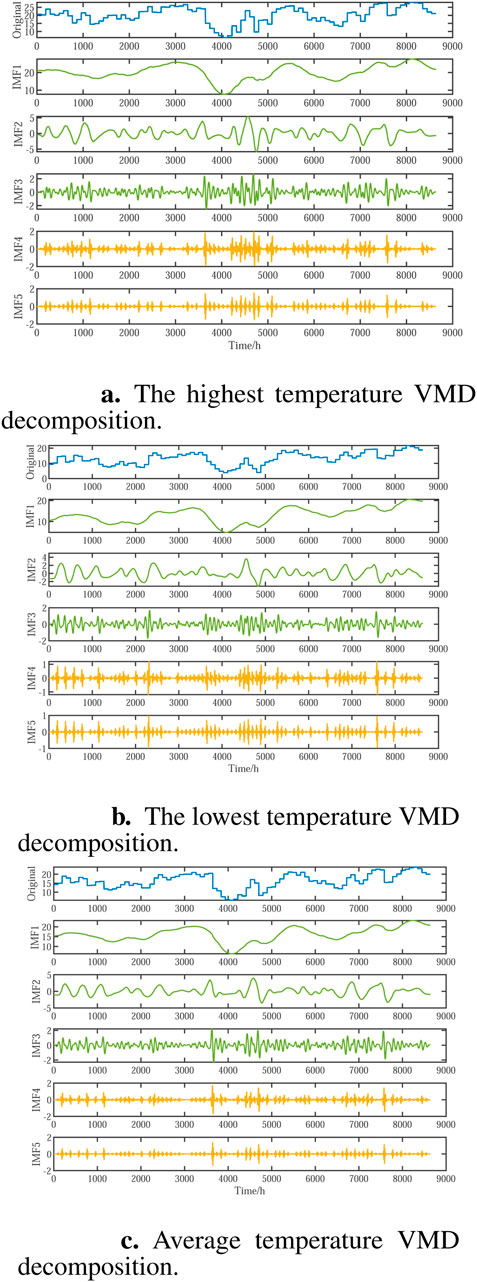
Figure 1. Feature decomposition. (A) The highest temperature VMD decomposition. (B) The lowest temperature VMD decomposition. (C) Average temperature VMD decomposition.
The following Formula 7–11 is the calculation of LSTM network (Madhukumar et al., 2022; Jailani et al., 2023).
Among them,
3.2 Adaboost algorithm
Boost is also known as reinforcement learning, which is an important ensemble learning strategy. It can help weak learners become strong learners with excellent predicting accuracy (Huang et al., 2022). The Adaboost (adaptive boosting) algorithm is self-adaptive in that it increases the weight of samples incorrectly classified by the prior fundamental classifier while decreasing the weight of correctly classified samples, which are reused for training the next basic classifier (Park and Son, 2023). Meanwhile, in each iteration, a new weak classifier is added when a low enough error rate or a certain maximum number of iterations is reached, confirming the final strong classification.
3.3 MIC-VMD-Bi-LSTM-Adaboost model
In this study, the MIC-VMD-Bi-LSTM-Adaboost fusion algorithm is applied to forecast urban power demand. To begin, MIC is used to calculate the correlation degree of each meteorological element to power load, and the meteorological parameters with a high correlation degree are selected as input. Second, the VMD technique is used to breakdown the input object, removing superfluous data and improving accuracy. Finally, the Bi-LSTM fusion Adaboost solver is utilized to perform the final predicting, and the results are produced. Figure 3 depicts the prediction flow chart.
4 Example analysis
4.1 Data pre-processing
Firstly, the data is cleaned, that is, the wrong data and missing data are eliminated; then, the data is normalized to make the data in the same order of magnitude, which is also used in the subsequent prediction. The normalized calculation formula is shown in Equation 12:
In the formula, x, is the processed data,
After the prediction, the normalized data is denormalized, as shown in Equation 13.
4.2 Evaluating indicator
The MAE, MAPE, RMSE and
4.2.1 Results and analysis of prediction
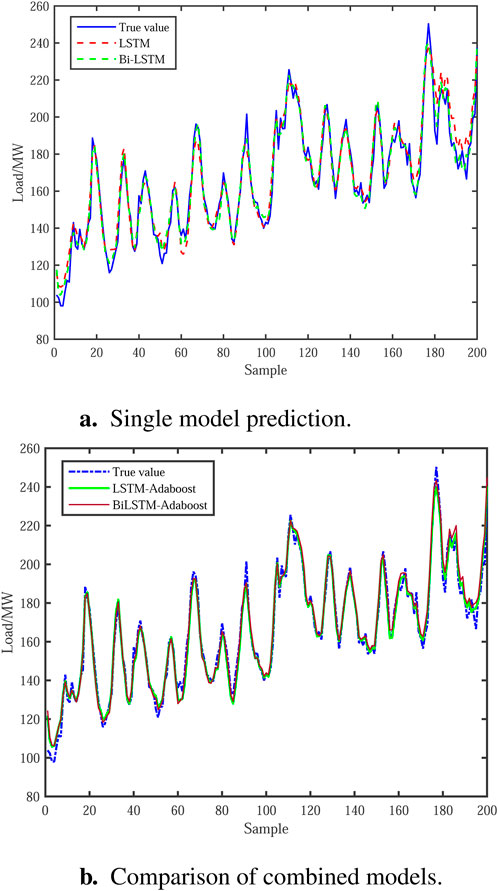
The MIC-VMD-Bi-LSTM-Adaboost algorithm is used to forecast power load. Figure 4A displays the prediction results, Figure 4B depicts the prediction error, and Table 4 displays the evaluation index.

Figure 4. Prediction results. (A) MIC-VMD-Bi-LSTM-Adaboost prediction results. (B) Prediction error.
As shown in Figure 4A, the forecast curve is nearly identical to the original curve, and the prediction accuracy is excellent, but there are minor differences at the start of the prediction. The error curve in Figure 4B similarly shows a considerable mistake.
Table 4 shows that the suggested technique has MAE, MAPE, RMSE, and
5 Comparison of prediction results
5.1 Prediction results
Figure 5 compares the viability of the hybrid forecasting method using a single and combined model. Figure 5A shows that in a single model, both the LSTM model and the Bi-LSTM model may fit loads. Bi-LSTM is more accurate than LSTM. When the load varies abruptly, resulting in a peak or peak valley, the single model cannot adequately anticipate; the inaccuracy is considerable, and there is some lag. Figure 5B shows that LSTM-Adaboost and Bi-LSTM-Adaboost models outperform other models in fitting load curves with peaks and valleys. At the same time, the combined model’s fitting curve is closer to the actual load at all times, demonstrating that the suggested method can better exploit the law and time aspects of load data. However, the effect of the two combined models is not significantly different, implying that the improved method’s optimization effect on LSTM and Bi-LSTM is comparable.
The models are assessed using MAE, MAPE, RMSE, and
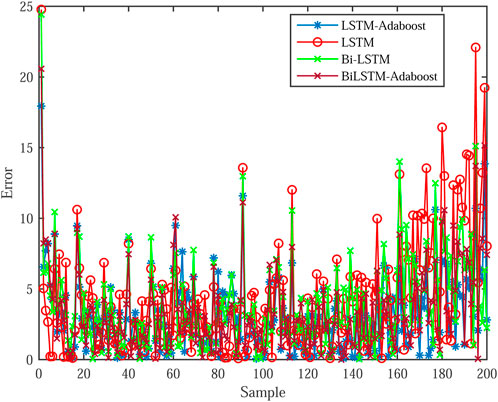
Figure 6 displays the relative absolute error distribution for each model. Figure 6 shows that this method has a lower relative absolute error and more steady load forecasting results than previous models. This is because the method presented in this paper employs VMD to decompose the sequence, remove the noise term, reduce the randomness of the sequence, and ensure that the sequence’s time characteristics are not discarded, allowing the Bi-LSTM model to be better used for error correction, resulting in a more detailed load forecasting process and improved load forecasting accuracy.
5.2 Ablation experiment
The ablation experiment of the method is equivalent to the control variable method. MIC, VMD, and Adaboost are used as the “variables” to be controlled, which are divided into the following three cases:
1. M1: MIC-Bi-LSTM-Adaboost was used and VMD was removed;
2. M2: VMD-Bi-LSTM-Aadboost was used and MIC was removed;
3. M3: MIC-VMD-Bi-LSTM was used and Adaboost was removed.
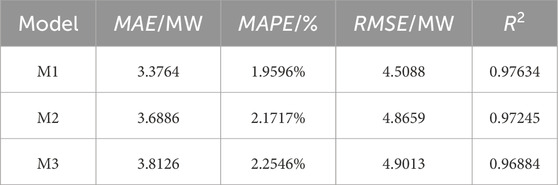
The results are shown in Table 6.
The table shows that all three techniques can enhance forecast accuracy. In comparison to M1, M2, and M3, Adaboost contributes the most to improving prediction accuracy. Compared to M1 and M2, selecting data meteorological elements can increase the prediction impact to some level, and removing factors with low correlation can minimize the number of principal components, simplify the method, and speed up prediction time. VMD primarily decomposes data and removes superfluous data, resulting in reduced algorithm complexity and improved prediction accuracy.
6 Conclusion
In this paper, a hybrid forecasting model according to MIC-VMD-Bi-LSTM-Adaboost is built by integrating the advantages of MIC, VMD, LSTM, Bi-LSTM and Adaboost. Firstly, the correlation analysis of meteorological factors influencing power load is ontained by using MIC, and the factors with higher correlation degree are extracted as input. Secondly, the input vector is decomposed by VMD to eliminate redundant data and extract features. Then, the Bi-LSTM-Adaboost fusion algorithm is applied to forecast the power load, calculate the error, and evaluate the model. Finally, the model is compared with two single algorithms of LSTM and Bi-LSTM and LSTM-Adaboost combination algorithm, so as to reflect the advantage of the algorithm in this paper. The following conclusions were reached:
1. MIC outperforms other correlation analysis functions in terms of computational complexity and robustness, providing significant advantages in correlation analysis. MIC chooses meteorological factors with high correlation as the input feature vector, which increases prediction accuracy in the subsequent combination process.
2. The Bi-LSTM network compensates for the LSTM network’s limitation of processing features in only one direction and outperforms it in terms of prediction effect.
3. Adaboost’s self-adaptability enhances the prediction accuracy of LSTM and Bi-LSTM, resulting in a more precise combined model than the individual models. The ablation experiment demonstrates that Adaboost contributes the most to the optimization algorithm in this research. The reason for this is that Adaboost may adaptively alter the anticipated error rate based on the weak classifier’s feedback, resulting in great execution efficiency.
4. The forecasting accuracy of the LSTM-Adaboost and Bi-LSTM-Adaboost algorithms is nearly same, showing that the Adaboost method has a similar influence on LSTM and Bi-LSTM optimization. Because of the lengthy prediction time of Bi-LSTM, LSTM can be combined directly in practical applications.
5. The combined approach suggested in this study outperforms the single algorithm in terms of accuracy, although there is still a significant inaccuracy at the start of the prediction. The evaluation coefficient is 0.97965, and there is still plenty of space for improvement. Future research will examine several aspects of the algorithm, including enhancing the attention mechanism, swapping out the GRU (Bi-GRU) algorithm, Transformer, and more.
Data availability statement
The datasets presented in this article are not readily available because the data set is urban power load, which is not disclosed in principle. Requests to access the datasets should be directed to ZY, MTkxMTI4NzQ4NTJAMTYzLmNvbQ==.
Author contributions
ZZ: Data curation, Formal Analysis, Writing–original draft, Writing–review and editing. CJ: Investigation, Methodology, Software, Writing–review and editing. YZ: Methodology, Supervision, Writing–review and editing. WW: Methodology, Supervision, Writing–review and editing. DH: Supervision, Validation, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
Authors sincerely acknowledge Measurement Center of Guangxi Power Grid Co., Ltd and NARI Group (State Grid Electric Power Research Institute) Co., Ltd.
Conflict of interest
Authors ZZ, CJ, and YZ were employed by Measurement Center of Guangxi Power Grid Co., Ltd. Authors WW and DH were employed by NARI Group (State Grid Electric Power Research Institute) Co., Ltd.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abumohsen, M., Owda, A. Y., and Owda, M. (2023). Electrical load forecasting using lstm, gru, and rnn algorithms. Energies 16, 2283. doi:10.3390/en16052283
Aguilar Madrid, E., and Antonio, N. (2021). Short-term electricity load forecasting with machine learning. Information 12, 50. doi:10.3390/info12020050
Álvarez, V., Mazuelas, S., and Lozano, J. A. (2021). Probabilistic load forecasting based on adaptive online learning. IEEE Trans. Power Syst. 36, 3668–3680. doi:10.1109/tpwrs.2021.3050837
Bareth, R., Yadav, A., Gupta, S., and Pazoki, M. (2024). Daily average load demand forecasting using lstm model based on historical load trends. IET Generation, Transm. and Distribution 18, 952–962. doi:10.1049/gtd2.13132
Chen, H., Wu, H., Kan, T., Zhang, J., and Li, H. (2023). Low-carbon economic dispatch of integrated energy system containing electric hydrogen production based on vmd-gru short-term wind power prediction. Int. J. Electr. Power and Energy Syst. 154, 109420. doi:10.1016/j.ijepes.2023.109420
Cordeiro-Costas, M., Villanueva, D., Eguía-Oller, P., Martínez-Comesaña, M., and Ramos, S. (2023). Load forecasting with machine learning and deep learning methods. Appl. Sci. 13, 7933. doi:10.3390/app13137933
Deng, S., Chen, F., Dong, X., Gao, G., and Wu, X. (2021). Short-term load forecasting by using improved gep and abnormal load recognition. ACM Trans. Internet Technol. (TOIT) 21, 1–28. doi:10.1145/3447513
Deng, S., Chen, F., Wu, D., He, Y., Ge, H., and Ge, Y. (2022). Quantitative combination load forecasting model based on forecasting error optimization. Comput. Electr. Eng. 101, 108125. doi:10.1016/j.compeleceng.2022.108125
Du, J., Cheng, Y., Zhou, Q., Zhang, J., Zhang, X., and Li, G. (2020). “Power load forecasting using bilstm-attention. IOP Conf. Ser. Earth Environ. Sci. 440, 032115. doi:10.1088/1755-1315/440/3/032115
Ge, Q., Guo, C., Jiang, H., Lu, Z., Yao, G., Zhang, J., et al. (2020). Industrial power load forecasting method based on reinforcement learning and pso-lssvm. IEEE Trans. Cybern. 52, 1112–1124. doi:10.1109/tcyb.2020.2983871
Geng, G., He, Y., Zhang, J., Qin, T., and Yang, B. (2023). Short-term power load forecasting based on pso-optimized vmd-tcn-attention mechanism. Energies 16, 4616. doi:10.3390/en16124616
Guo, Y., Li, Y., Qiao, X., Zhang, Z., Zhou, W., Mei, Y., et al. (2022). Bilstm multitask learning-based combined load forecasting considering the loads coupling relationship for multienergy system. IEEE Trans. Smart Grid 13, 3481–3492. doi:10.1109/tsg.2022.3173964
Habbak, H., Mahmoud, M., Metwally, K., Fouda, M. M., and Ibrahem, M. I. (2023). Load forecasting techniques and their applications in smart grids. Energies 16, 1480. doi:10.3390/en16031480
Huang, X., Li, Z., Jin, Y., and Zhang, W. (2022). Fair-adaboost: extending adaboost method to achieve fair classification. Expert Syst. Appl. 202, 117240. doi:10.1016/j.eswa.2022.117240
Jailani, N. L. M., Dhanasegaran, J. K., Alkawsi, G., Alkahtani, A. A., Phing, C. C., Baashar, Y., et al. (2023). Investigating the power of lstm-based models in solar energy forecasting. Processes 11, 1382. doi:10.3390/pr11051382
Kumar, N. (2024). Ev charging adapter to operate with isolated pillar top solar panels in remote locations. IEEE Trans. Energy Convers. 39, 29–36. doi:10.1109/tec.2023.3298817
Kumar, N., Mulo, T., and Verma, V. P. (2013). “Application of computer and modern automation system for protection and optimum use of high voltage power transformer,” in 2013 international conference on computer communication and informatics, 1–5.
Kumar, N., Panigrahi, B. K., and Singh, B. (2016). A solution to the ramp rate and prohibited operating zone constrained unit commitment by ghs-jgt evolutionary algorithm. Int. J. Electr. Power and Energy Syst. 81, 193–203. doi:10.1016/j.ijepes.2016.02.024
Kumar, N., Saxena, V., Singh, B., and Panigrahi, B. K. (2020). Intuitive control technique for grid connected partially shaded solar pv-based distributed generating system. IET Renew. Power Gener. 14, 600–607. doi:10.1049/iet-rpg.2018.6034
Kumar, N., Saxena, V., Singh, B., and Panigrahi, B. K. (2023a). Power quality improved grid-interfaced pv assisted onboard ev charging infrastructure for smart households consumers. IEEE Trans. Consumer Electron. 69, 1091–1100. doi:10.1109/tce.2023.3296480
Kumar, N., Singh, H. K., and Niwareeba, R. (2023b). Adaptive control technique for portable solar powered ev charging adapter to operate in remote location. IEEE Open J. Circuits Syst. 4, 115–125. doi:10.1109/ojcas.2023.3247573
Lin, G., Lin, A., and Gu, D. (2022). Using support vector regression and k-nearest neighbors for short-term traffic flow prediction based on maximal information coefficient. Inf. Sci. 608, 517–531. doi:10.1016/j.ins.2022.06.090
Madhukumar, M., Sebastian, A., Liang, X., Jamil, M., and Shabbir, M. N. S. K. (2022). Regression model-based short-term load forecasting for university campus load. IEEE Access 10, 8891–8905. doi:10.1109/access.2022.3144206
Moreira-Júnior, J. R., Abreu, T., Minussi, C. R., and Lopes, M. L. (2022). Using aggregated electrical loads for the multinodal load forecasting. J. Control, Automation Electr. Syst. 33, 1592–1600. doi:10.1007/s40313-022-00906-1
Nie, Y., Jiang, P., and Zhang, H. (2020). A novel hybrid model based on combined preprocessing method and advanced optimization algorithm for power load forecasting. Appl. Soft Comput. 97, 106809. doi:10.1016/j.asoc.2020.106809
Park, K.-J., and Son, S.-Y. (2023). Residential load forecasting using modified federated learning algorithm. IEEE Access 11, 40675–40691. doi:10.1109/access.2023.3268530
Rafi, S. H., Deeba, S. R., and Hossain, E. (2021). A short-term load forecasting method using integrated cnn and lstm network. IEEE access 9, 32436–32448. doi:10.1109/access.2021.3060654
Satapathy, S. S., and Kumar, N. (2019). “Modulated perturb and observe maximum power point tracking algorithm for solar pv energy conversion system,” in 2019 3rd international conference on recent developments in control, automation and power engineering (RDCAPE) (IEEE), 345–350.
Sukanya Satapathy, S., and Kumar, N. (2020). Framework of maximum power point tracking for solar pv panel using wsps technique. IET Renew. Power Gener. 14, 1668–1676. doi:10.1049/iet-rpg.2019.1132
Surapunt, T., and Wang, S. (2024). Ensemble modeling with a bayesian maximal information coefficient-based model of bayesian predictions on uncertainty data. Information 15, 228. doi:10.3390/info15040228
Tian, M.-W., Alattas, K., El-Sousy, F., Alanazi, A., Mohammadzadeh, A., Tavoosi, J., et al. (2022). A new short term electrical load forecasting by type-2 fuzzy neural networks. Energies 15, 3034. doi:10.3390/en15093034
Wan, A., Chang, Q., Khalil, A.-B., and He, J. (2023). Short-term power load forecasting for combined heat and power using cnn-lstm enhanced by attention mechanism. Energy 282, 128274. doi:10.1016/j.energy.2023.128274
Wang, Z., Wang, Q., and Wu, T. (2023). A novel hybrid model for water quality prediction based on vmd and igoa optimized for lstm. Front. Environ. Sci. and Eng. 17, 88. doi:10.1007/s11783-023-1688-y
Wu, F., Cattani, C., Song, W., and Zio, E. (2020). Fractional arima with an improved cuckoo search optimization for the efficient short-term power load forecasting. Alexandria Eng. J. 59, 3111–3118. doi:10.1016/j.aej.2020.06.049
Keywords: power load forecasting, MIC, VMD, LSTM, adaboost
Citation: Zhenglei Z, Jun C, Zhou Y, Wenguang W and Hong D (2024) Research on urban power load forecasting based on improved LSTM. Front. Energy Res. 12:1443814. doi: 10.3389/fenrg.2024.1443814
Received: 04 June 2024; Accepted: 17 October 2024;
Published: 31 October 2024.
Edited by:
Yuanxing Xia, Hohai University, ChinaReviewed by:
Renyou Xie, University of New South Wales, AustraliaJilin Cai, Nanjing Tech University, China
Copyright © 2024 Zhenglei, Jun, Zhou, Wenguang and Hong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yang Zhou, MTkxMTI4NzQ4NTJAMTYzLmNvbQ==
 Zhou Zhenglei1
Zhou Zhenglei1 Yang Zhou
Yang Zhou