The static voltage stability analysis of photovoltaic energy storage systems based on NPU algorithm

Although the data-driven static voltage stability problems have been widely studied, most of the classical algorithms focus more on improving the accuracy of the system prediction, ignoring the error classification errors generated during the prediction process. Furthermore, current research ignores the utilization of data-driven voltage stability assessment of energy storage systems. Therefore, this paper proposes a static voltage stability assessment method for photovoltaic energy storage systems based on considering the error classification constraint algorithm using Neyman-Pearson umbrella algorithms. Firstly, the Spearman Correlation Coefficient is employed in the feature selection phase. Secondly, an updated voltage stability assessment (VSA) model is proposed. Compared with the existing data-driven prediction of system static voltage stability in the literature, it can realize voltage stability assessment more quickly. Furthermore, on the basis of rapid voltage stability assessment, the umbrella NP classifier can also effectively limit the first-class error and attenuate the effect of error classification by mirroring the control of the number of cycle splits and the type $\mathbf{I}$ classification error threshold. Finally, the simulation and experimental results show that the effectiveness and robustness of the scheme proposed in this paper in grid-connected photovoltaic energy farms.

1 Introduction

Currently, photovoltaic (PV) power generation is becoming more and more popular due to the integration of modern power systems, thus realizing zero fuel cost, minimum operating cost and zero pollution (Kumar et al., 2019). Meanwhile, there is no doubt that its integration with the distribution grid may lead to greater operational loads on the power system, causing the power system to operate closer to its stabilization thresholds, resulting in severe static voltage instability problems, which can lead to economic losses and adverse social consequences Rui et al., 2020a; Wang et al., 2024). Therefore, plenty of researchers have been investigating the reliability assessment of static voltage stability (VSA), which is essential for the assurance and stability of power systems (Ghahremani et al., 2019; Ni and Paul, 2019). Meanwhile, in recent years, the development of Wide Area Measurement Systems (WAMS) and Phase Measurement Units (PMU) technology has provided strong data support for AI technology in power systems, which provides a new research path for power system researchers to solve the problem of analyzing and evaluating static voltage stability. Although there have been many research have paid attentions on these issues, they are still unable to provide some static voltage stability assessment schemes for grid-connected PV energy storage systems. To fill this gap, this paper proposes a static voltage stability assessment method considering error classification constraints facing photovoltaic energy storage plants.

On one hand, traditional techniques for studying static voltage stability involve singular value decomposition (Zhang et al., 2019b), continuous current flow (CPF) (Liu et al., 2016) and sensitivity analysis (Wang et al., 2016). Based on the idea of continuous current flow (CPF), several different types of methods are included, such as CPFLOW (Chiang et al., 1995) and Ajjarapu-Christy (Ajjarapu and Christy, 1992). The assessment of static voltage stability is an important component of power system security with inherent issues of complexity, nonlinearity, uncertainty, and online monitoring requirements. With the rapid development of Wide Area Measurement Systems (WAMS) obtained in synchronized Phase Measurement Units (PMUs), a large amount of data about the system operation is accumulated in a relatively short period of time and is rapidly updated on this basis. Conventional time-domain simulation methods are limited by data processing speed and computational accuracy; they are usually not suitable for online applications (Zheng et al., 2013) and cannot handle high-resolution synchronous phase data from PMUs. Therefore data-driven static voltage stability assessment based on data has been widely studied for online monitoring and rapid assessment of voltage steady state of complex systems Some data mining tools have been used for on-line voltage stability estimation, such as decision trees (DTs) (Zhu et al., 2016; Zhu et al., 2017a; Zhu et al., 2017b), support vector ma-chines (SVMs) (Yang et al., 2018), random forests (RFs) (Pinzn and Colom, 2019) and stochastic artificial neural networks (ANN), introduced into VSAs in the form of extreme learning machines (ELMs) (Zhang et al., 2019a) or random vector function link (RVFL) units (Ren et al., 2020). Literature (Su and Liu, 2018) designed an enhanced online random forest model, which is effective and fast in assessing static voltage stability. Literature (Fan et al., 2015) proposed a Relational Exploration (RE)-based scheme for power system voltage stability assessment to address the problem of ranking relationships between test-based and modeled variables and relative voltage stability margins. In order to make the classifier more accurate and efficient, literature (Khamis et al., 2018) proposed an integrated classifier consisting of an extreme learning machine with optimal parameters. Literature (He et al., 2013) utilizes an adaptive integrated decision tree learning method to construct a classification with better stability performance. In the literature (Cai and Hill, 2022), a long-term VSA real-time continuous monitoring system using a sliding three dimensional convolutional neural network (3D-CNN) is proposed. In the literature (Ryan et al., 2021), a data-driven grid-supporting control system for battery energy storage systems, which requires no changes to the inverters inner real and reactive power control loops compared with a conventional grid-supporting inverter, is proposed. Literature (Su and Hong, 2021), an online probabilistic Extreme Learning Machine (ELM) algorithm based on the power transformation technique was established to be developed. In this literature (Xia et al., 2021), cumulant-based maximum entropy method (CMEM) combined with Nataf Transform (NT) is proposed to analyze the steady-state voltage stability problem considering correlations and uncertainties of power injections and consumptions. Therefore, data-driven voltage stability assessment has been widely utilized to assess the stability of power systems.

Meanwhile, all of the above data-driven based work assumes that the dataset required for learning can be generated by system simulation as needed. Throughout the training process, the data-driven VSA model adapts to each individual sample without introducing any bias (Zhu et al., 2017a). However, the number of examples showing voltage instability problems is much lower than the number of examples showing voltage stabilization problems, since contemporary power grids usually remain in a stable operating condition most of the time. It tends to establish classification rules that are biased in favor of the stable model due to its superior representativeness. Literature (Wang et al., 2016) categorizes classification errors into two types of problems and proposes a data mining algorithm Core Vector Machine (CVM) based on big data of Phase Measurement Units (PMUs) to solve the problem. It includes the first type of error that judges an unstable state as a stable state and the second type of error that judges a stable state as an unstable state. When the algorithm is utilized to classify new manuals, this bias inevitably leads to more or less classification errors.

Thus, This paper introduces a novel method for static voltage stability assessment tailored to photovoltaic energy storage systems, addressing specific constraints related to error classification. The key advantages of this approach are outlined as follows:

1) Development of a Static Voltage Stability Assessment Model: This model is specifically designed for grid-connected photovoltaic energy storage systems. It enhances the efficiency of detecting voltage instability conditions compared to current methods.

2) Enhanced Adaptability and Error Reduction: The method focuses on minimizing type $\mathbf{I}$ errors in real-time Voltage Stability Assessment (VSA). It establishes a historical operational database comprising Voltage Stability Indices (VSIs) and operational variables. By employing the Spearman Correlation Coefficient, significant operational variables are identified, reducing data dimensionality in high-dimensional datasets. The NPU algorithm leverages this dataset to guide the VSA model, allowing various types of Non-Parametric Units (NPUs) to produce real-time VSA results based on incoming PMU data. This approach forms the basis for an efficient real-time system to monitor potential voltage destabilization in PV energy storage plants.

3) The data-driven data-based static voltage stability assessment scheme for photovoltaic (PV) energy storage systems proposed in this paper has good robustness. It is verified that the scheme is robust even in the face of significant changes in the operating conditions of the power system (data loss, system node failures, etc.).

The theoretical foundation is discussed in Section 2, followed by the proposal of a data-driven VSA strategy specifically tailored for PV energy storage plants in Section 3. Section 4 validates the effectiveness of this strategy through simulations and experiments, while Section 5 provides a comprehensive summary of the paper’s findings.

2 Problem statement and supporting mathematical methods

2.1 Voltage stability index (VSI)

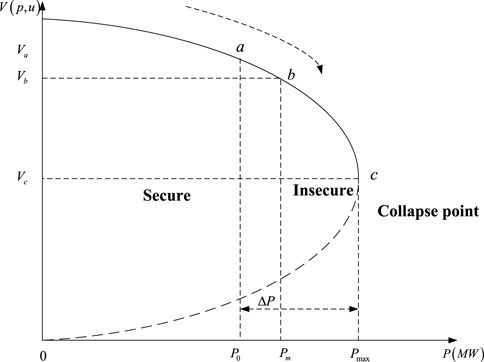
The long-term sustainable active power transmission capacity is a crucial factor for power system operators to consider. This margin can be defined using the P-V curve. In accordance with the Continuation Power Flow (CPF) examination, while the power factor remains constant, and the load active power incrementally rises (Wang et al., 2021). The operational state commences at the starting position and proceeds along the P-V curve in the direction of the voltage instability point. The voltage reaches the stabilizing boundary at point c, and the Jacobi matrix becomes singular at point c. When the load’s active power keeps rising, the voltage will instability, hidden resulting in voltage collapse within the system. So, the SVA margin is, to some degree, reflected in the gap between current active power and maximum active power, and the VSI can be calculated using the following Equation 1.

Where Pi and Pmax depict the existing active power consumption and the peak active power demand, correspondingly. The VSI falls within the range of 0–1, signifying the safety status of voltage stability.

Power system static voltage stability is mainly influenced by the active and reactive power of the nodes in the system, and the core of its stability lies in whether the system is power balanced or not. The explanation of system voltage stabilization and collapse static mechanism is to explain the nature of voltage collapse and the causes of voltage collapse from static analysis theory (Rui et al., 2020b). At present, the static mechanism analysis of voltage collapse mainly includes PV curve analysis, QV curve analysis, reactive power balance analysis, etc. An example of PV curve is shown in Figure 1.

Figure 1

Figure 1. P–V curve.

As depicted in Figure 1, when Pi is smaller than Pm, the system is considered safe. Similarly, the VSI is surpasses than $\eta$. A suitable VSI limit is established by defining a limit value to distinctly differentiate voltage stable conditions. As a result, the calculation formula for $\eta$ is provided in Equation 2, and the categorization designation for voltage safety can be determined based on VSI.

$\frac{P_{\max }-P_i}{P_{\max }}\times 100\%(1)$

$\eta =\frac{P_{\text{max}}-P_m}{P_{\text{max}}}\times 100\%(2)$

2.2 VSA classification problem

As depicted in Table 1, based on the VSA categorization scenarios, a chaos matrix is employed to categorize them under four distinct groups represents the number of samples predicted as class i that really belong to class j. In this context, an unstable condition is denoted by “0,” while a stable condition is denoted as “1.” Hence, the complete classification accuracy (CA) can be determined as follows Equation 3. Within the framework of VSA, it is essential to take into account both the first type mistake and the whole classification accuracy. The risk of the first type error (FE) is defined in formula 4:

$CA=\frac{F_{11}+F_{00}}{F_{11}+F_{10}+F_{00}+F_{01}}(3)$

$FE=\frac{F_{10}}{F_{10}+F_{00}}(4)$

Table 1

Table 1. Confusion matrix.

Furthermore, to fully demonstrate the efficiency of the suggested approach about categorization properties, the FM is employed in the property’s evaluation test. The FM computes the harmonic average between Recall(R) and Accuracy(A), providing a more objective assessment of the ability to identify unstable samples compared to overall accuracy. Accuracy, FM, and Recall are defined byEquations 5–7, separately. A greater FM score indicates superior classification performance.

$\mathrm{A}=\frac{F_{11}}{F_{11}+F_{01}}(5)$

$\mathrm{R}=\frac{F_{11}}{F_{11}+F_{10}}(6)$

$\mathrm{F}\mathrm{M}=\frac{2\times A\times R}{A+R}(7)$

2.3 Spearman correlation coefficient

Traditional statistical correlation coefficients include Pearson product-difference correlation coefficient, Spearman rank correlation coefficient, and Kendall rank correlation coefficient. In this paper, Spearman correlation coefficient is used for feature selection to reduce the dimension of the original dataset. As one of the three statistical correlation coefficients, Spearman correlation coefficient is obtained based on the relative magnitude of the rank and the observations, which is a more general nonparametric method compared to Pearson, which still maintains good performance on nonlinear data and is less sensitive to outliers, and therefore has better tolerance.

Spearman correlation coefficient utilizes the magnitude of the rank order of two variables for linear correlation analysis, and uses the monotonicity of the function to estimate the correlation between the indicators R(X) and R(Y). The Spearman correlation coefficient can be computed by formula 8.

$\rho =\frac{\frac{1}{n}{\sum }_{i=1}^n\left(R\left(x_i\right)-\overline{R\left(x\right)}\right)\cdot \left(R\left(y_i\right)-\overline{R\left(y\right)}\right)}{\sqrt{\left(\frac{1}{n}{\sum }_{i=1}^n{\left(R\left(x_i\right)-\overline{R\left(x\right)}\right)}^2\right)\cdot \left(\frac{1}{n}{\sum }_{i=1}^n{\left(R\left(y_i\right)-\overline{R\left(y\right)}\right)}^2\right)}}(8)$

In this formula, $\rho$ is calculated from the ranked set R(x) and R(y), $R(X_i)$ and $R(y_i)$ are elements of the ranked set R(x) and R(y), $\overline{R(x)}$ and $\overline{R(y)}$ is the average of the ranked set R(x) and R(y) associated characteristics are as follows: 1) $\rho \ge$ 0.80 indicates that there is extremely strong correlation between R(x) and R(y). 2) 0.61 < $\rho$ < 0.80 indicates that there is strong correlation between R(x) and R(y). 3) 0.41<$\rho$ <0.60 indicates that there is moderately relevant between R(x) and R(y). 4) 0.21< $\rho$<0.40 indicates that there is weak correlation between R(x) and R(y). 4) $\rho \le$0.20 indicates that there is extremely weak correlation between R(x) and R(y).

2.4 Umbrella NP algorithm

Suppose a set of samples labeled as 0 is partitioned into two equal-sized groups, each with a size of n. The first group, along with some samples labeled as 1, is utilized to instruct a foundational classifier within a training dataset. Then, a test dataset comprising the other category of samples labeled as 0 is used to assess the performance of classifier, the associated categorization scores can be represented as T1>T2>…>Tn. So, when categorizing a novel sample by $T_k$,the likelihood of a sample labeled as 0 being classified as 1 can be constrained by Equation 9.

$P\left[F\left({\phi }_k\right)\alpha \right]\le {\displaystyle \sum _{j=k}^n}\left(\genfrac{}{}{0.0pt}{}{n}{j}\right){\left(1-\alpha \right)}^j{\alpha }^{n-j}(9)$

where $F({\phi }_k)$ represents the type $\mathbf{I}$ error odd, and the odds is referred to as the “breach rate” of ${\phi }_k$.The $P[F({\phi }_k)>\alpha ]$ can be referred to as the upper limit of the “violation rate” and is denoted as $\nu (k)$.

The value of decreases as k increases, and k is determined by the followingEquation 10:

$k=min\left\{k\in \left\{1,\dots ,n\right\}:v\left\{k\right\}\le \delta \right\}(10)$

where $\delta$ is the upper bound of $\nu (k)$. Equation 11 implies that k ought to be minimized while maintain in $\nu (k)\le \delta$.

Therefore, the effective implementation of the limitation on the type $\mathbf{I}$ error involves setting the error threshold $\alpha$ according to specific needs.

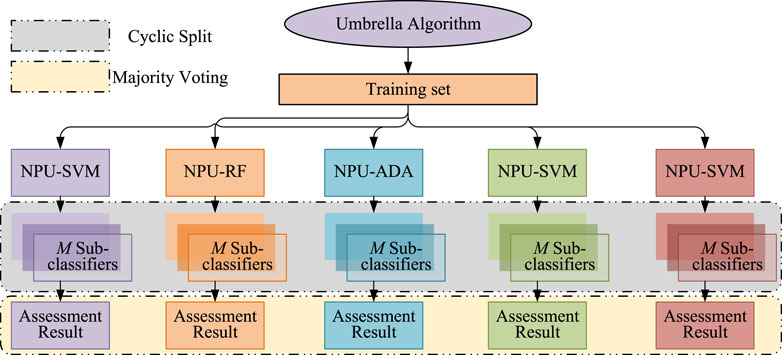
The umbrella algorithm based on the NP criterion can enhance the effectiveness of various traditional data-driven techniques, including RF, non-parametric naive Bayes (NNB), adaptive boosting (ADA), penalized logistic regression (Penlog), and support vector machine (SVM).

The samples labeled as 0 are repeatedly divided M times in a random and uniform manner. Subsequently, M sub-classifiers are created for every category of NPU classifier ${\phi }_k^{\text{i}}$ using these samples. Ultimately, the NPU classifier can be acquired using the selection process of the classifiers, as described in the following Equation 11:

${\varphi }_b=I\left(\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\varphi }_k^i\ge \frac{1}{2}\right)\leftarrow (11)$

In Figure 2, considering the lack of traditional statistical tools in reducing class I errors, this paper uses the umbrella algorithm based on NP theory to construct the classifier. The algorithm can well control the first type of error threshold for each NP classifier.

3 A comprehensive date-driven methods for VSA

This study introduces a comprehensive data-driven approach for VSA, illustrated in Figure 3. This includes a VSA model and a feature value selection process. To begin, a historical PMU data collection is used to create starting database comprising operational parameters and the VSI. Subsequently, the Eigenvalue selection process is employed to select essential variables, forming the offline data. Subsequently, the NPU-based VSA model is trained with this dataset. The model can provide timely results when receiving data from WAMS in real time.

Figure 2

Figure 2. NPU algorithm.

Figure 3

Figure 3. A comprehensive date-driven methods for VSA.

Additionally, a strategy for updating the model is put into action to enhance the VSA model’s ability to adapt to different factors impacting system operation. In conclusion, this approach encompasses feature selection, model training and updating, online assessment.

3.1 Database generation

Creation of the database represents the initial and foundational step in developing the VSA model. This starting database ought to contain a wealth of operational data from power systems. Utilizing simulations derived from historical PMU data, many specimens can be generated through the CPF. These specimens encompass a variety of operational variables along with the Voltage Stability Index (VSI). Subsequently, each sample’s classification label can be determined using the threshold $\eta$ for VSI.

However, relying solely on historical data is often insufficient, as it may not capture all potential operating behaviors of power systems. Therefore, in the process of generating the database, it is crucial to incorporate reasonable fluctuations to encompass a wider range of potential system operational behaviors, thus enhancing the richness of the database. To ensure that the simulation scenarios more closely resemble the real power system environment, the starting load bus power factor is intentionally randomized for all load buses during the system initialization in simulation phase. Ensure that the raw power factor of each load bus is vary. Both active and inactive power of the bus grow proportionally as the load increases. In theory, with the expansion of data generation, the power factor per bus will increase steadily. This allows for the simulation of various power factor scenarios within the sample space received through simulations, ensuring that the VSA data employed for training covers a wide range of power factor scenarios.

3.2 Feature value selection

With the increasing complexity of the power system, the complexity of the initial dataset is increasing, which has a serious impact on the prediction efficiency of the VSA. Therefore, feature selection based on Spearman correlation coefficient is used to identify key variables that are significantly correlated with VSI before model training. Utilizing the database, the Spearman correlation coefficient examines the relationship between the voltage stability index (VSI) and the variables, providing a correlation $\rho$. Identify the basic feature set by adjusting the $\rho$ threshold value to $\ge$0.60. This process effectively reduces the dimensionality of the dataset. In this way, an offline dataset is generated that includes samples with basic attributes and vectors representing categorical labels.

3.3 Model training and updating

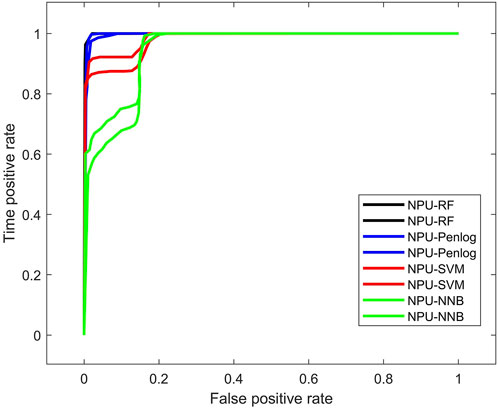
The offline dataset is then used to train the model and establish the mapping relationship. Additionally, the Area Under the Curve (AUC) and the Receiver Operating Characteristic (ROC) curve are employed to assess the classification performance of the NPU classifiers and identify those with superior performance. The horizontal axis of the ROC curve represents the true positive sample rate (TPR) and the vertical axis represents the false positive sample rate (FPR), and the true sample rate and false positive sample rate are calculated as shown in Equations 12, 13. This helps in the selection of the final VSA model. The AUC is a metric that quantifies the area under the ROC curve, with values ranging from 0 to 1. Superior classifier performance is indicated by a grater AUC value. In this study, the ROC curve is utilized to evaluate the performance of the NPU algorithm, enabling the selection of specific NPU classifiers for VSA based on their classification performance (Liu et al., 2023).

$TPR=\frac{F_{00}}{F_{00}+F_{10}}(12)$

$FPR=\frac{F_{01}}{F_{01}+F_{11}}(13)$

In real-world scenarios, the operational conditions of the power system can experience continual fluctuations due to various potential factors. Consequently, a VSA model trained solely on offline data may experience a decline in classification accuracy when faced with the changing operating conditions. The process of updating the model is outlined as follows.

When the modified operating state has already been incorporated. The pertinent NPU classifiers generated during the offline training stage will supplant the existing classifiers within the VSA model.

Should the modified operational states not be present in the offline database, new data samples will be generated for the training of a new NPU-based VSA model. Furthermore, the revised operational states are merged with the previously acquired model within the offline database. Within the database, models and operational conditions continue to accumulate, the likelihood of suffering unfamiliar operating stage will progressively diminish. By implementing the model updating strategy, the pro-posed scheme’s capability to generalize and adapt to changing operating conditions can be enhanced.

3.4 Online assessment

During the real-time data driven VSA phase, data can be collected using PMUs. The data driven VSA model VSA model will swiftly deliver VSA results after receiving real-time data from the PMU.

4 Simulation results

In this section voltage stability prediction on PV-ESS and grid-integrated systems is used to illustrate the effectiveness and good robustness of the proposed voltage stability prediction scheme considering error constraints for voltage stability prediction of PV energy storage systems.

In this research, simulations are carried out to perform automated data collection through Python programs. The power stochastic allocation among loads and genera-tors fluctuates between 70$\%$ and 110$\%$ to enhance the original database. It should be noted that during the screening process of the generated data, check that the voltage at each bus in the system does not violate the specified thresholds, reactive and active power per generator and power transmitted per transfer line. Ultimately, a total of 3,746 specimens were generated through a range of CPF, each of which contained 407 original variables.

4.1 VSA test

The NPU algorithm comprises 5 NPU classifiers. The purpose of this assessment is to pinpoint the best three performing NPU classifiers. Furthermore, the circular splitting times is set to 3 and the type $\mathbf{I}$ error limit is established at 0.006.

Table 2 presents U, representing the region beneath the upper closed curve, and L, representing the region below the lower closed curve. In Figure 4, the horizontal axis depicts the rate of false positives, which is synonymous with the type $\mathbf{I}$ error risk, while the vertical shaft represents accuracy. Therefore, when a classifier’s ROC curve is positioned nearer to the corner, it demonstrates superior performance regarding precision and FD restriction. Figure 4 indicates that all 4 NPU classifiers have ROC bands situated at the upper-left, with NPU-ADA, NPU-Penlog, and NPU-RF being particularly close to the upper-left corner. Similarly, it is obvious from the values of U and L in Table 2 that the performance of NPU-RF, NPU-Penlog, and NPU-ADA outperforms other classifiers. Therefore, we will consider NPU-RF, NPU-Penlog, and NPU-ADA as options and validate the effectiveness of the proposed VSA approach.

Table 2

Table 2. AUC values with Different Tools.

Figure 4

Figure 4. ROC curves for different NPU models.

Table 3 displays the CA, FE, and FM for the chosen NPU classifiers in the context of the system. Notably, the NPU classifier can effectively control FM and CA values above 97.5$\%$ and FE values be less than 0.1$\%$. It should be especially noted here that, to emphasize the excellent performance of the NPU method in limiting the first type of error classification error as objectively as possible, several of the basic classifiers chosen for the simulation experiments are more mature and popular AI algorithms. It may be better if more advanced machine learning algorithms are used to limit the error classification. Therefore, the scheme proposed in this article shows gratifying VSA results in a 23-bus system.

Table 3

Table 3. VSA performance of different classifiers.

4.2 Comparison of performance with conventional classifiers

The proposed integrated scheme based on the NPU models is compared against traditional data-driven methods such as RF, ADA, and Penlog. Furthermore, to high-light the superior performance of NPU classifiers in minimizing the type $\mathbf{I}$ error, this study introduces CS learning and Decision Tree C4.5 algorithm. The comparative results are presented in Table 3. As can be seen from Table 3, Penlog does not perform as well as RF and ADA in the CA, FE, and FM values without the action of the NPU method and the CS method. After optimization with the NPU method and the CS method, Penlog outperforms the performance of unoptimized RF and ADA in terms of FE values in the 23-bus system, which demonstrates that both the NPU and CS methods are effective in limiting the Type $\mathbf{I}$ errors. Nevertheless, the CA and FM of CS-Penlog and NPU-Penlog are smaller than ADA and RF, which may be because the type $\mathbf{I}\mathbf{I}$ error causes a drop in accuracy, leading to the situation in Table. Based on the FE values, it shows that both the NPU method and the CS method can reduce the risk of Type $\mathbf{I}$ errors well, but the NPU method performs better than the CS method in limiting Type $\mathbf{I}$ errors. Comparing the RF algorithm without NPU optimization, its CA, FE and FM performs worse than the Decision Tree C4.5 algorithm. However, after the introduction of the NPU method of optimization, NPU-RF outperforms the decision tree model in both CA, FE and FM. From Table 3, it can be visualized that the FE of CS-ADA and CS-RF is higher than that of NPU-Penlog in the system. Overall, the mechanism consistently outperforms the CS method and C4.5 algorithm in reducing the risk of Type $\mathbf{I}$ errors.

4.3 Impact of data loss on VSA performance

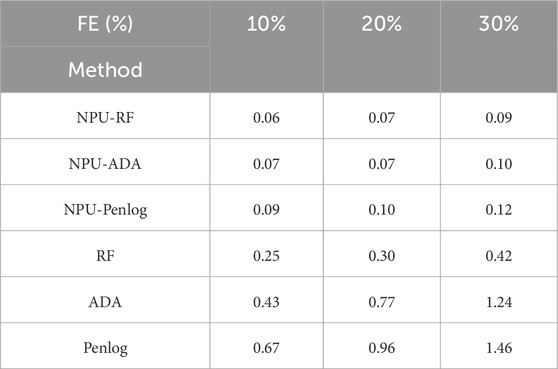
Most current VSA programs assume no loss of PMU data integrity. Nevertheless, in practical operations, factors such as equipment damage, physical faults in communication devices, and equipment maintenance can lead to data gaps. To demonstrate the NPU algorithm’s ability to handle missing data, tests were conducted at data loss levels of 10$\%$, 20$\%$, and 30$\%$. The results for the Type $\mathbf{I}$ error risk are presented in Table 4. From the results in Table 4, it can be observed that the Type $\mathbf{I}$ error risk increases with higher levels of data loss. In fact, the effect of data loss on RF is not significant, while ADA is more affected. Due to limitations in the algorithm’s performance, Penlog’s classification accuracy significantly declines when there is substantial data loss. With the excellence of the NPU algorithm, though the rate of Type $\mathbf{I}$ error inevitably increases to a certain extent with the percentage of data loss, this trend is effectively controlled. This demonstrates the strong adaptability of the NPU classifier in coping with the loss of PMU data.

Table 4

Table 4. First type error risks of various missing data levels.

4.4 Unstable sample test

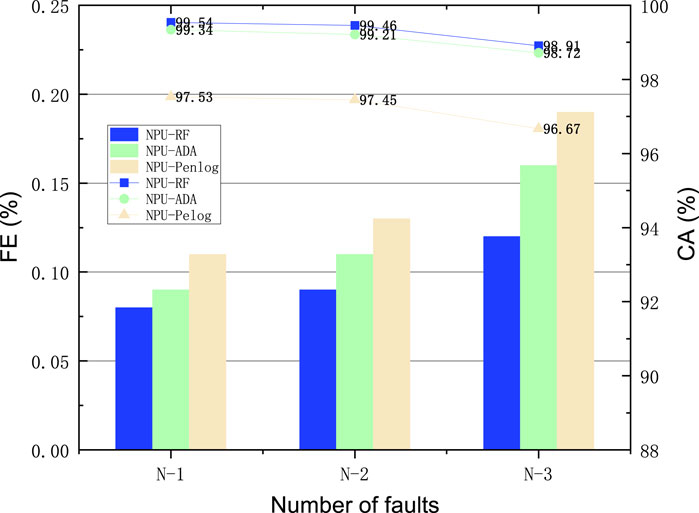
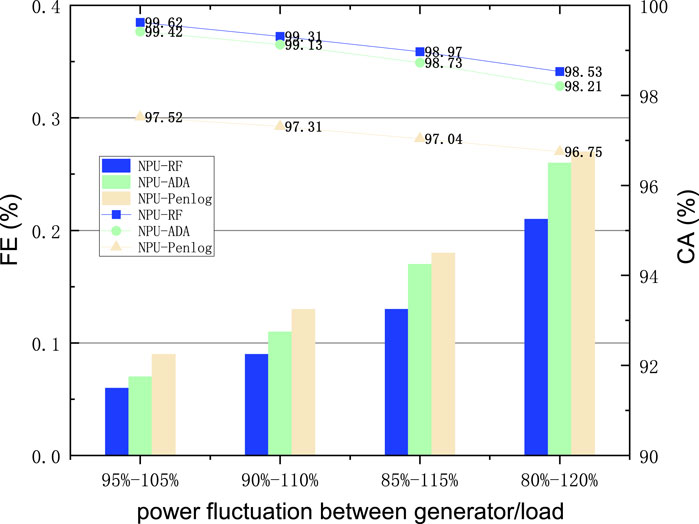
In order to demonstrate the immunity of the VSA scheme to the PV energy storage system, this paper also considers some other influencing factors, for example, the change of the system topology and the fluctuation of the power distribution between the generator and the load, which generate new samples in the system. It is worth noting that the data generated under the original topology should be used to train the model, and then the data under the new topology should be utilized to implement tests to verify the robustness of the VSA model. The CA, FE values of the VSA model for different topologies are shown in Figure 5. Also, the power distribution fluctuation results between generator/load are shown in Figure 6.

Figure 5

Figure 5. Type $\mathbf{I}$ error margin effects on VSA performance.

Figure 6

Figure 6. Distribution fluctuation test results.

As shown in Figure 5, when the number of faults in the system increases from 1 to 3, the CA values of the various types of NPU classifiers in the system decrease to some extent. This is due to the fact that the topology change ultimately leads to a certain degree of change in the operating conditions of the 23-bus system. However, in general the method simultaneously still maintains a high CA value. According to the data, the FE values of these NPU classifiers stay within the same magnitude after the topology change in the 23-bus system, which demonstrates that the NPU classifiers are still more effective in limiting the first type of errors when the topology of the 23-bus system is changed. This shows that this VSA model has good robustness in coping with topology changes.

Based on the data in Figure 6, it is possible to know the changes in the values of CA and FE for the three NPU classifiers when the range of power fluctuation between generator/load is increased from 10$\%$ to 40$\%$. From the values of CA and FE, it is known that the NPU classifier-based VSA model performs tends to decrease as the fluctuation range increases. This is due to the power fluctuation between the generator/load which leads to a significant change in the operating conditions of the system operation. However, as with the effect on the VSA model when changing the topology, the accuracy of the NPU classifier and its performance with respect to the first type of error limitation remains at an order of magnitude set. This demonstrates the good robustness of this VSA model in coping with changes in the system running conditions under conditions of fluctuating power distribution.

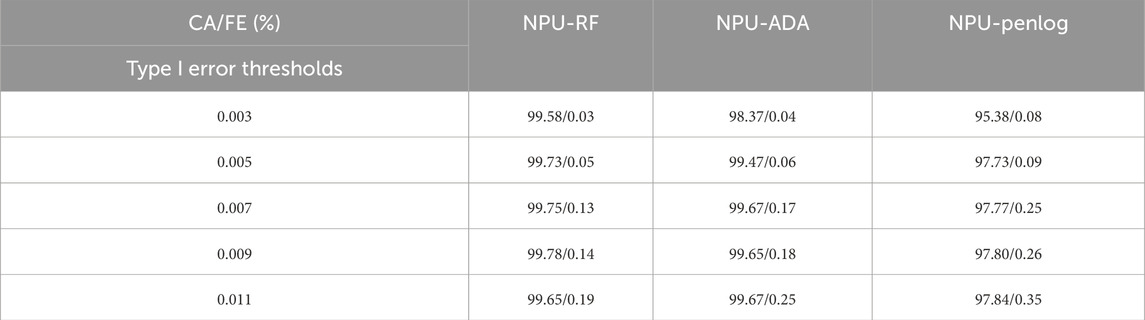
4.5 Effect of type $\mathbf{I}$ error thresholds on VSA model performance

The data-driven integration scheme proposed in this paper can limit the Class I error rate to an acceptable range by changing the Class I error threshold $\alpha$. In order to investigate the effect of the type $\mathbf{I}$ error threshold on the classification performance of VSA. The following operations were also done. For this system, $\alpha$ was set to 0.003, 0.005, 0.007, 0.009, and 0.011 in test, and the circular splitting time M of the system was still set to 3. The experimental results of the values of FE and CA are shown in Table 5. The results show that when $\alpha$ is in a certain range, the first type of error rate of the VSA substantial reduction with the decrease of $\alpha$, while maintaining a high overall accuracy. Therefore, it can be concluded that there is a correlation between type $\mathbf{I}$ error rate and system accuracy. In production practice, the system accuracy can be improved by effectively limiting and adjusting the type $\mathbf{I}$ error according to the requirements.

Table 5

Table 5. Experimental Results for the first type of Error margin.

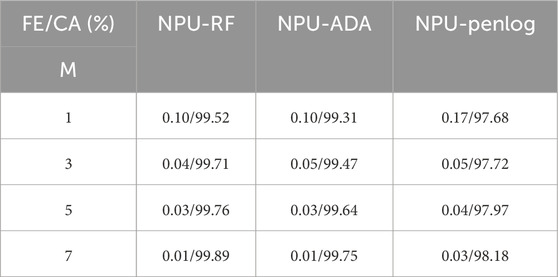
4.6 Impact of circular splitting times

The research in this article uses an integrated data-driven approach to construct subclassifies for each class of classifiers. The cyclic segmentation model was used during training. In order to investigate the effect of the number of cyclic splits on the performance of the VSA model, the number of cyclic splits M of the training set was set to 1, 3, 5, and 7 for each of the next tests. The statistical results of the type $\mathbf{I}$ error rate of the bus system and CA index are shown in Table 6. From the information in the Table, it can be easily known that the first type of error rate gradually decline and stabilizes as the number of cyclic splits M increases, and the accuracy of the program has gradually improved. Therefore, in practical applications, different classification performances can be realized by adjusting the value of M. In addition, the introduction of the cyclic splitting pattern has a better effect on improving the accuracy and generalizability of the VSA model.

Table 6

Table 6. Test results for Circular splits time.

5 Conclusion

The conventional data-driven voltage stability prediction scheme has focused on improving the accuracy of predictions in general systems, and it neglect to consider the fact that misclassification in power system operation can have a different impact as well as in the prediction of voltage stability for energy storage systems. As a result, an integrated algorithm considering error classification constraints has been proposed in this paper to provide voltage stability prediction scheme for PV energy storage systems. The approach includes a feature selection phase and an NPU-based VSA model development phase. First, a Spearman-based feature selection process identifies the key operational variables. Second, the scheme constructs a VSA model based on the NPU algorithm, which effectively controls type $\mathbf{I}$ errors and ensures reliable VSA results.

Finally, the data-driven scheme proposed in this paper is verified on a bus 23 system, the simulation and experiments show that the data-driven tool proposed in this paper has a better accuracy than the traditional data-driven one and can well limit the generation of class I error. The effects of missing data, node failures and other factors on the data-driven scheme proposed in this paper are also verified, which proves that the scheme has good robustness.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

CY: Conceptualization, Writing–original draft. KJ: Supervision, Writing–review and editing. JW: Data curation, Writing–review and editing. MS: Validation, Writing–review and editing. XJ: Data curation, Supervision, Writing–review and editing. DL: Supervision, Visualization, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1443677/full#supplementary-material

References

Ajjarapu, V., and Christy, C. (1992). The continuation power flow: a tool for steady state voltage stability analysis. IEEE Trans. Power Syst. 7, 416–423. doi:10.1109/59.141737

CrossRef Full Text | Google Scholar

Cai, H., and Hill, D. J. (2022). A real-time continuous monitoring system for long-term voltage stability with sliding 3d convolutional neural network. Int. J. Electr. Power and Energy Syst. 134, 107378. doi:10.1016/j.ijepes.2021.107378

CrossRef Full Text | Google Scholar

Chiang, H.-D., Flueck, A., Shah, K., and Balu, N. (1995). Cpflow: a practical tool for tracing power system steady-state stationary behavior due to load and generation variations. IEEE Trans. Power Syst. 10, 623–634. doi:10.1109/59.387897

CrossRef Full Text | Google Scholar

Fan, Y., Liu, S., Qin, L., Li, H., and Qiu, H. (2015). A novel online estimation scheme for static voltage stability margin based on relationships exploration in a large data set. IEEE Trans. Power Syst. 30, 1380–1393. doi:10.1109/TPWRS.2014.2349531

CrossRef Full Text | Google Scholar

Ghahremani, E., Heniche-Oussedik, A., Perron, M., Racine, M., Landry, S., and Akremi, H. (2019). A detailed presentation of an innovative local and wide-area special protection scheme to avoid voltage collapse: from proof of concept to grid implementation. IEEE Trans. Smart Grid 10, 5196–5211. doi:10.1109/TSG.2018.2878980

CrossRef Full Text | Google Scholar

He, M., Zhang, J., and Vittal, V. (2013). Robust online dynamic security assessment using adaptive ensemble decision-tree learning. IEEE Trans. Power Syst. 28, 4089–4098. doi:10.1109/TPWRS.2013.2266617

CrossRef Full Text | Google Scholar

Khamis, A., Xu, Y., Dong, Z. Y., and Zhang, R. (2018). Faster detection of microgrid islanding events using an adaptive ensemble classifier. IEEE Trans. Smart Grid 9, 1–1899. doi:10.1109/TSG.2016.2601656

CrossRef Full Text | Google Scholar

Kumar, N., Singh, B., Panigrahi, B. K., Chakraborty, C., Suryawanshi, H. M., and Verma, V. (2019). Integration of solar pv with low-voltage weak grid system: using normalized laplacian kernel adaptive kalman filter and learning based inc algorithm. IEEE Trans. Power Electron. 34, 10746–10758. doi:10.1109/TPEL.2019.2898319

CrossRef Full Text | Google Scholar

Liu, S., Liu, S., Li, X., Gu, Y., Li, Z., Yang, C., et al. (2023). Neyman-pearson umbrella algorithm-based static voltage stability assessment with misclassification restriction: an integrated data-driven scheme. IEEE Trans. Industrial Inf. 19, 11391–11402. doi:10.1109/TII.2023.3246529

CrossRef Full Text | Google Scholar

Liu, X., Zhang, X., and Venkatasubramanian, V. A. (2016). Distributed voltage security monitoring in large power systems using synchrophasors. IEEE Trans. Smart Grid 7, 982–991. doi:10.1109/TSG.2015.2410219

CrossRef Full Text | Google Scholar

Ni, Z., and Paul, S. (2019). A multistage game in smart grid security: a reinforcement learning solution. IEEE Trans. Neural Netw. Learn. Syst. 30, 2684–2695. doi:10.1109/TNNLS.2018.2885530

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinzn, J. D., and Colom, D. G. (2019). Real-time multi-state classification of short-term voltage stability based on multivariate time series machine learning. Int. J. Electr. Power and Energy Syst. 108, 402–414. doi:10.1016/j.ijepes.2019.01.022

CrossRef Full Text | Google Scholar

Ren, C., Xu, Y., Zhang, Y., and Zhang, R. (2020). A hybrid randomized learning system for temporal-adaptive voltage stability assessment of power systems. IEEE Trans. Industrial Inf. 16, 3672–3684. doi:10.1109/TII.2019.2940098

CrossRef Full Text | Google Scholar

Rui, W., Qiuye, S., Dazhong, M., and Xuguang, H. (2020a). Line impedance cooperative stability region identification method for grid-tied inverters under weak grids. IEEE Trans. Smart Grid 11, 2856–2866. doi:10.1109/TSG.2020.2970174

CrossRef Full Text | Google Scholar

Rui, W., Qiuye, S., Pinjia, Z., Yonghao, G., Dehao, Q., and Peng, W. (2020b). Reduced-order transfer function model of the droop-controlled inverter via Jordan continued-fraction expansion. IEEE Trans. Energy Convers. 35, 1585–1595. doi:10.1109/TEC.2020.2980033

CrossRef Full Text | Google Scholar

Ryan, D. J., Razzaghi, R., Torresan, H. D., Karimi, A., and Bahrani, B. (2021). Grid-supporting battery energy storage systems in islanded microgrids: a data-driven control approach. IEEE Trans. Sustain. Energy 12, 834–846. doi:10.1109/TSTE.2020.3022362

CrossRef Full Text | Google Scholar

Su, H.-Y., and Hong, H.-H. (2021). An intelligent data-driven learning approach to enhance online probabilistic voltage stability margin prediction. IEEE Trans. Power Syst. 36, 3790–3793. doi:10.1109/TPWRS.2021.3067150

CrossRef Full Text | Google Scholar

Su, H.-Y., and Liu, T.-Y. (2018). Enhanced-online-random-forest model for static voltage stability assessment using wide area measurements. IEEE Trans. Power Syst. 33, 6696–6704. doi:10.1109/TPWRS.2018.2849717

CrossRef Full Text | Google Scholar

Wang, B., Fang, B., Wang, Y., Liu, H., and Liu, Y. (2016). Power system transient stability assessment based on big data and the core vector machine. IEEE Trans. Smart Grid 7, 2561–2570. doi:10.1109/TSG.2016.2549063

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Hu, W., Li, Y., Ma, D., and Wang, P. (2021). Soc-based droop coefficients stability region analysis of the battery for stand-alone supply systems with constant power loads. IEEE Trans. Power Electron. 36, 7866–7879. doi:10.1109/TPEL.2021.3049241

CrossRef Full Text | Google Scholar

Wang, R., Yu, X., Sun, Q., Li, D., Gui, Y., and Wang, P. (2024). The integrated reference region analysis for parallel dfigs’ interfacing inductors. IEEE Trans. Power Electron. 39, 7632–7642. doi:10.1109/TPEL.2024.3361091

CrossRef Full Text | Google Scholar

Xia, C., Zheng, X., Guan, L., and Baig, S. (2021). Probability analysis of steady-state voltage stability considering correlated stochastic variables. Int. J. Electr. Power and Energy Syst. 131, 107105. doi:10.1016/j.ijepes.2021.107105

CrossRef Full Text | Google Scholar

Yang, H., Zhang, W., Chen, J., and Wang, L. (2018). Pmu-based voltage stability prediction using least square support vector machine with online learning. Electr. Power Syst. Res. 160, 234–242. doi:10.1016/j.epsr.2018.02.018

CrossRef Full Text | Google Scholar

Zhang, Y., Xu, Y., Dong, Z. Y., and Zhang, R. (2019a). A hierarchical self-adaptive data-analytics method for real-time power system short-term voltage stability assessment. IEEE Trans. Industrial Inf. 15, 74–84. doi:10.1109/TII.2018.2829818

CrossRef Full Text | Google Scholar

Zhang, Y., Xu, Y., Zhang, R., and Dong, Z. Y. (2019b). A missing-data tolerant method for data-driven short-term voltage stability assessment of power systems. IEEE Trans. Smart Grid 10, 5663–5674. doi:10.1109/TSG.2018.2889788

CrossRef Full Text | Google Scholar

Zheng, C., Malbasa, V., and Kezunovic, M. (2013). Regression tree for stability margin prediction using synchrophasor measurements. IEEE Trans. Power Syst. 28, 1978–1987. doi:10.1109/TPWRS.2012.2220988

CrossRef Full Text | Google Scholar

Zhu, L., Lu, C., Dong, Z. Y., and Hong, C. (2017a). Imbalance learning machine-based power system short-term voltage stability assessment. IEEE Trans. Industrial Inf. 13, 2533–2543. doi:10.1109/TII.2017.2696534

CrossRef Full Text | Google Scholar

Zhu, L., Lu, C., Liu, Y., Wu, W., and Hong, C. (2017b). Wordbook-based light-duty time series learning machine for short-term voltage stability assessment. IET Generation, Transm. and Distribution 11, 4492–4499. doi:10.1049/iet-gtd.2016.2074

CrossRef Full Text | Google Scholar

Zhu, L., Lu, C., and Sun, Y. (2016). Time series shapelet classification based online short-term voltage stability assessment. IEEE Trans. Power Syst. 31, 1430–1439. doi:10.1109/TPWRS.2015.2413895

CrossRef Full Text | Google Scholar