Droop control-based fast frequency support of wind power generation integrated grid-forming VSC-HVDC system

Current researches mainly focus on the participation of wind farms in primary frequency regulation, including overspeed load shedding control, propeller control and their coordinated control, etc. The frequency support is realized by reserving reserve capacity of wind turbines, but the influence of the dynamic characteristics of maximum power point tracking (MPPT) on the overall frequency regulation characteristics of wind turbines during frequency support is ignored. To this end, firstly, the frequency response model of the system is constructed, and the main factors that affect the frequency dynamic characteristics are revealed. Secondly, the principle of the grid-forming VSC with the function of self-inertial synchronization is introduced, the influence of the dynamic characteristics of MPPT on the frequency regulation characteristics of the wind turbine generator is clarified. Finally, based on the PSCAD/EMTDC electromagnetic transient simulation software platform, the influence of the dynamic characteristics of MPPT on the frequency regulation characteristics are verified by combining the inertia self-synchronous network control technology. The simulation results indicate that with the increase of setting of droop control, the decrease of output power of MPPT becomes large so as to weaken the frequency support capability.

1 Introduction

The global energy landscape has undergone a significant transformation, with wind energy evolving into an indispensable component of the power industry in Europe, China, and worldwide over the past few decades (Eto et al., 2010). The wind power industry, as a vital force in clean energy, will assume greater responsibilities. China’s commitment to global “carbon peak” and “carbon neutrality” will further propel wind power to become one of the most important pillars in achieving energy transition and addressing global climate change (Rezaei and Kalantar, 2015). Therefore, it is evident that wind power generation will continue to see significant development in the foreseeable future, with further effective harnessing and utilization of wind energy resources (Yang et al., 2024).

The large-scale integration of wind power into the grid will have a significant impact on the transient stability of grid frequency, with the most prominent issue being the deterioration of frequency transient support capability due to the lack of inertia and primary frequency control (Yang et al., 2018; Qin et al., 2021; Xiong et al., 2021; Arévalo Soler et al., 2023). Conventional VSC-HVDC control methods decouple wind farms from grid frequency, rendering them unable to perceive changes in AC grid frequency (Flourentzou et al., 2009; Castro and Acha, 2016). Consequently, wind farm grid-side flexible systems cannot provide transient power support to the grid. It is necessary for wind turbine units to autonomously perceive changes in grid frequency, akin to traditional synchronous generators, and autonomously respond to system frequency changes to provide transient support capabilities (Bianchi and Domnguez-Garca, 2016; Adeuyi et al., 2017).

To address this issue, it is necessary to transmit information about grid frequency changes to the wind farm side. Literature (Bianchi and Domnguez-Garca, 2016) utilizes communication means to transmit information about grid frequency changes, which is subject to limitations in terms of communication costs and stability. This approach in Bianchi and Domnguez-Garca (2016) requires detecting AC grid frequency and controlling DC voltage to track its changes, with the voltage variations reflected on the wind farm side frequency changes by the sending converter station. This method of Arghir et al. (2018) places high demands on the frequency tracking capability of phase-locked loops and the adjustment speed of DC voltage, particularly in weak grid scenarios, where it can lead to system instability issues.

In research on providing inertia support through VSC-HVDC grid integration with wind farms, methods based on communication or actively controlling DC bus voltage are often used to transmit grid frequency changes to the wind farm (Li et al., 2014). However, due to the existence of delays in control, communication, etc., wind farms cannot perceive the actual grid frequency in real-time, making it challenging to ensure inertia support effectiveness (Li et al., 2017). VSC-HVDC still exhibits current-source characteristics to the grid, posing a series of stability issues in parallel with weak grids (Aouini et al., 2016). Although the application of virtual synchronous control at converter stations can avoid stability issues caused by current vector control and weak grids, it is not suitable for occasions with original power fluctuations such as wind farms.

When wind turbines sense changes in the frequency of the AC system, they can adjust their speed, increase or release the rotational energy stored in the blades and rotor, to provide transient power support to the grid. When necessary, they can also provide primary frequency regulation through active power reserves, enhancing grid stability (Markovic et al., 2021; Groß et al., 2022). Literature (Zhong et al., 2022) proposes adding an auxiliary control loop directly coupled with the grid frequency (frequency deviation and rate of change) in the power control loop of wind turbines, to respond to dynamic changes in grid frequency. However, as it still relies on phase-locked loop (PLL) for grid synchronization, it is challenging to ensure stable operation of the control strategy in weak grids. Literature (Subotić and Groß, 2022) suggests using virtual synchronous control (grid-forming technology) in the grid-side converter of wind turbines, simulating the rotor motion equation and excitation equation of traditional synchronous generators to eliminate the dependence on PLL. Externally, it exhibits voltage source characteristics, autonomously responding to grid frequency changes, providing inertia response, and further participating in primary frequency regulation. However, such control methods require the wind turbine’s converter to control the DC bus voltage, leading to significant changes in torque control strategy and requiring evaluation of their impact on the stable operation of wind turbines, with high upgrade costs. Literature (Sang et al., 2022) utilizes the DC bus capacitance of wind turbine converters to simulate the rotor of a synchronous generator, achieving the grid-side converter’s ability to self-synchronize without PLL, automatically tracking the DC bus voltage with grid frequency, so as to achieve grid-forming VSC function.

Current research mainly focuses on wind farms participating in primary frequency regulation, including overspeed load reduction control, pitch control, and coordinated control of both, all utilizing the reserved capacity of wind turbines to provide frequency support. However, they overlook the dynamic characteristics of maximum power point tracking during frequency support, which affects the overall turbine frequency response. In the context of accelerating the construction of new power systems, it is necessary to further explore the control potential of offshore wind power through flexible direct connection systems, making the overall system the dominant power source and taking responsibility for supporting system frequency. In this context, this paper first constructs a system frequency response model to reveal the main factors affecting frequency dynamic characteristics, then the principle of the grid-forming VSC with the function of self-inertial synchronization is introduced, after that this paper clarifies the influence of MPPT dynamic characteristics on the overall turbine frequency response. Finally, based on the PSCAD/EMTDC electromagnetic transient simulation software platform, it establishes an electromagnetic transient simulation model of wind farm clusters connected to the grid via AC/DC, combined with inertia self-synchronization grid construction technology, to verify the influence of MPPT dynamic characteristics on the overall turbine frequency response.

2 Structure of large-scale wind power transmission system through HVDC and principle of grid-forming VSC for self-inertial synchronization

2.1 System structure of large-scale wind power transmission through HVDC and mechanical power modeling

The structure of large-scale wind power transmission system through HVDC is shown in Figure 1, in which WTG uses wind turbines to capture wind energy. Rotor-side converter realizes decoupling control of constant voltage and frequency and power; the grid-side converter is used to maintain the DC voltage constant and adjust the power factor (Xiong et al., 2016).

Figure 1

Figure 1. VSC-HVDC system for wind farm integration.

Figure 2 shows the control strategies for the sending-end converter (SEC) and receiving-end converter (REC). The control strategy of the sending-end converter station has a similar active part to the receiving-end converter station. However, since the wind farm connected to the AC side of the sending-end converter station can quickly lock its frequency and phase angle through a phase-locked loop, changes in the output AC frequency will not directly affect the power output of the wind farm, but only serve to transmit information. The control object of the reactive part is the amplitude of the AC voltage on the wind farm side, which needs to be maintained stable by the sending-end converter station (Yang et al., 2020).

Figure 2

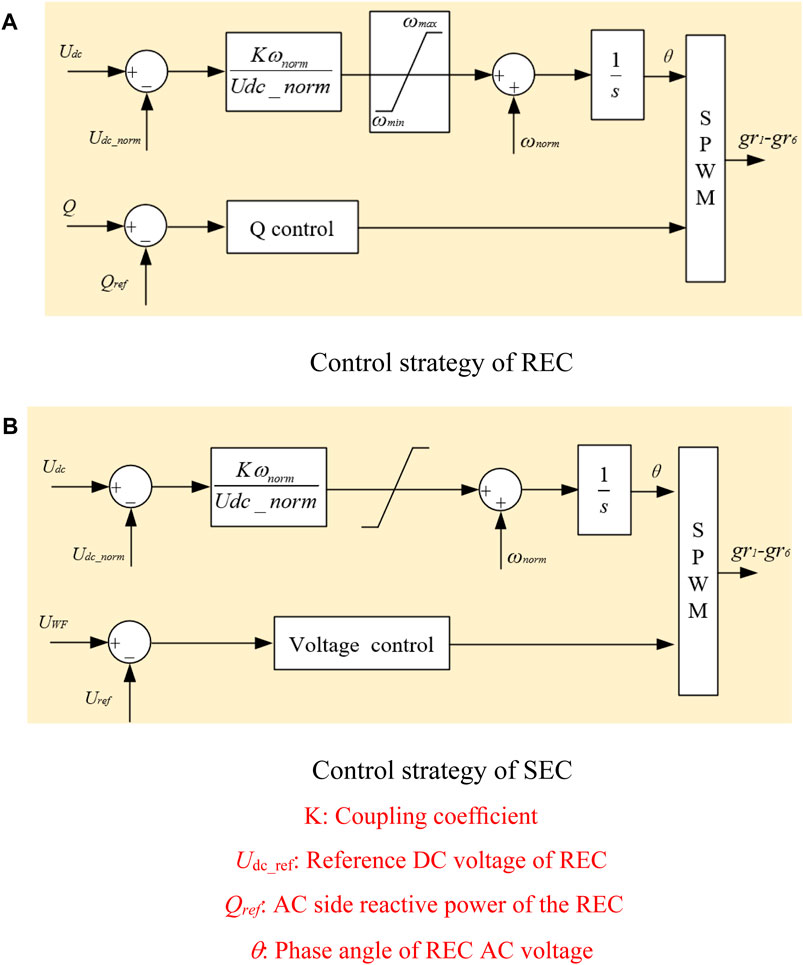
Figure 2. Control strategies of SEC and RES. (A) Control strategy of REC, (B) Control strategy of SEC.

As the penetration rate of offshore wind power continues to increase, the receiving-end AC grid shows increasingly obvious characteristics of low inertia and weak damping. When the traditional backup plan of synchronous generator units cannot meet the requirements for grid frequency regulation capacity and speed, it may lead to problems such as large rate of change of grid frequency and frequency exceeding limits. Therefore, it is urgent to explore the potential of offshore wind power regulation, so that it can actively support system inertia, participate in frequency stability control, and improve the system’s safety and stability.

The mechanical power (P_m) is described as a nonlinear function of various parameters, including air density (ρ), rotor radius (R), pitch angle (β), wind speed (v_w), tip-speed ratio (λ), and power coefficient (c_p), as in Formula 1.

$P_m=\frac{1}{2}\rho \pi R^2{v}_{wind}^3{c}_P\left(\lambda ,\beta \right)(1)$

where c_p could be represented in Formulas 2–4.

$c_P\left(\lambda ,\beta \right)=0.645\left\{0.00912\lambda +\frac{-5-0.4\left(2.5+\beta \right)+116{\lambda }_i}{e^{21{\lambda }_i}}\right\}(2)$

${\lambda }_i=\frac{1}{\lambda +0.08\left(2.5+\beta \right)}-\frac{0.035}{1+{\left(2.5+\beta \right)}^3}(3)$

$\lambda =\frac{{\omega }_{r}R}{v_w}.(4)$

2.2 Principle of grid-forming VSC for self-inertial synchronization

Common grid-forming inverters employ virtual synchronous generation (VSG) technology to simulate the characteristic features of synchronous generators, introducing inertia and damping into the frequency control system to enhance the system’s active support capability and compensate for the lack of inertia in phase-locked loops (PLLs). However, the grid-forming VSG technology exhibits weak responsiveness to grid loads and poor system stability, posing instability risks in weak grid scenarios. Additionally, significant modifications to the inverter structure incur high retrofitting costs. Without altering the structure and control strategy of the machine-side inverter, by modifying the control structure of the grid-side inverter, the voltage phase θ of the output grid-side converter voltage ug is modulated using the integral of the normalized DC capacitor voltage u_dc measured in its control loop with a gain ω_n, achieving real-time correlation between the DC bus voltage u_dc and the output angular frequency ω_g of the grid-side converter. This allows direct observation of grid frequency variations based on changes in the DC bus voltage, presenting the grid with external characteristics of a SG, as “voltage source”. This approach mitigates instability issues caused by PLLs and inaccurate frequency measurements due to voltage fluctuations, facilitating upgrades and improvements in grid-connected wind turbine control structures.

Figure 3 illustrates motion feature similarity between SG and GSC. The relationship between the angular frequency of AC voltage output by grid-side converter and DC voltage is shown in Formula 5

${{\omega }_g}^{*}=u_{dc}^{*}(5)$

where: ω_g is the angular frequency of AC voltage output and u_dc is the DC bus voltage.

Figure 3

Figure 3. Motion feature similarity between SG and GSC.

The dynamic equation of u_dc is given in Formula 6.

$2H_C{u_{dc}}^{*}\frac{d{u_{dc}}^{*}}{dt}={P_m}^{*}-{P_g}^{*}(6)$

where: P_m^* and P_g^* are the nominal values of the output power of the permanent magnet direct driver and the input power of the grid-side converter respectively; HC is the inertia time constant of DC capacitor.

H_C of DC capacitor is given in Formula 7.

$H_C=\frac{C{U}_{dcn}^2}{2S_n}(7)$

where: C is the DC capacitance; U_dcn is the reference value of DC voltage; S_n is the rated power of the wind turbine.

Ignoring the loss of the grid-side converter, the output power of the WTG can be expressed as in Formula 8.

${P_g}^{*}=\frac{{U_t}^{*}{E_g}^{*}}{{x_g}^{*}}\sin \delta (8)$

where: E_g^* is the unit value of the regulation voltage of the grid-side converter; U_t^* is the nominal value of grid voltage; x_g^* is the unit value of reactance between grid-side converter and grid synchronous generator; δ is the phase where the output voltage vector of the grid-side converter leads the grid voltage.

Figure 4 shows the response characteristic curves of the frequency and DC capacitor voltage of HVDC system under over-frequency disturbance. After being disturbed, the change of grid-connected power of wind turbines will cause the natural response of DC bus voltage, and this response is positively related to the grid frequency. Taking the frequency increase as an example, that is, the grid frequency increases, the delta angle decreases, the grid-connected power decreases, and the DC side voltage increases, the natural linkage between DC side voltage and grid frequency is realized by the grid-forming VSC with the function of inertial synchronization and the amplitude change of AC side grid frequency is converted into the amplitude change of DC side voltage, thus realizing the frequency information transmission function and avoiding the need of converter phase-locked loop and communication. Which are highly consistent, and the DC capacitor voltage can be used to characterize the frequency change of the power grid.

Figure 4

Figure 4. DC voltage and frequency under over-frequency disturbance.

2.3 Droop control-based fast frequency support of wind power generation

For large-scale wind power transmission via high-voltage direct current (HVDC) systems, active participation of wind turbines in system frequency support is the future development trend. Currently, the primary frequency regulation resources in the power system are still traditional synchronous generator units, which exhibit significant differences in response speed and control capability compared to wind turbines. After disturbances, the spare capacity of traditional synchronous generator units is sufficient to absorb unbalanced power. However, due to the decreasing proportion of synchronous generator units in the power system, the inertia response capability of the sending-end system weakens. During the initial disturbance, the excessive rate of frequency variation in low-inertia AC systems may trigger wind turbine protection actions, leading to disconnection accidents and causing larger active power deficits, thereby threatening the safety and stability of the system operation.

A comprehensive system frequency response control diagram considering the frequency support characteristics of doubly-fed induction generator (DFIG) and traditional synchronous generator units is shown in Figure 5. Here, H represents the inertia time constant of the sending-end grid; D is the equivalent damping coefficient; T_G is the time constant of the synchronous generator governor; F_HP represents the proportion of steady-state output power of the prime mover high-pressure cylinder; T_RH is the time constant of the prime mover reheating; and s is the Laplace operator (Shi et al., 2018). Referring to the simplified conditions of the traditional system frequency response model, considering the much smaller time constants of fast frequency support strategies (virtual control and droop control) of wind turbine units compared to the time constants of reheating coefficients of synchronous generators, the fast frequency support control loop of wind turbine units is directly introduced into the traditional system frequency response model in Figure 5.

Figure 5

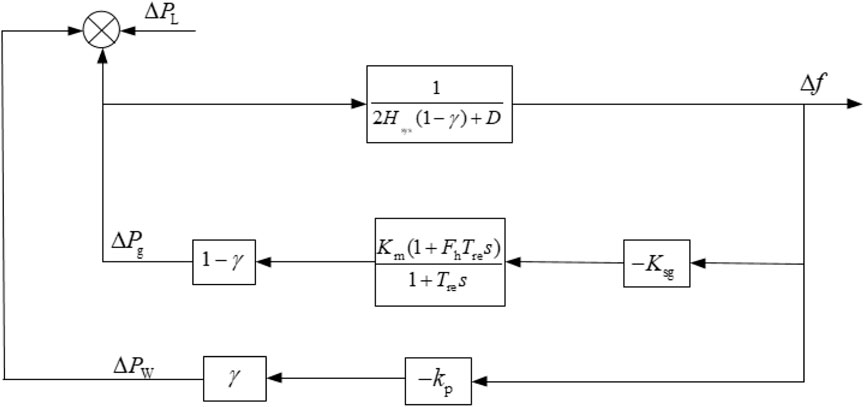
Figure 5. Simplified system frequency response model considering high wind power penetrated power gird.

According to Figure 5, when the system is faced with active power deficiency (∆P_L), the frequency domain expression of system frequency deviation with wind power frequency regulation can be arranged as in Formulas 9, 10.

$\Delta f\left(s\right)=\left(-\gamma k_{\mathrm{d}}s-\left(1-\gamma \right)\Delta f\frac{K_{\mathrm{m}}\left(1+F_{\mathrm{h}}{T}_{\text{re}}s\right)}{1+T_{\text{re}}s}-\Delta P_{\mathrm{L}}-\Delta f{k}_{\mathrm{p}}\right)\times \left(\frac{1}{2H_{\text{sys}}\left(1-\gamma \right)+D}\right)(9)$

$\Delta f\left(s\right)=\left(\frac{K_{\text{sg}}{\omega }_n^2}{\left(D+\gamma k_{\mathrm{P}}\right)K_{\text{sg}}+k_{\mathrm{m}}}\right)\left(\frac{\left(1+T_{\text{re}}s\right)\Delta P_{\mathrm{L}}}{s^2+2\xi {\omega }_{n}s+{\omega }_n^2}\right)(10)$

where K_m is the mechanical power gain coefficient, F_h is a part of the high-pressure turbine power, T_re is the reheat time constant, H_sys is the system inertia time constant, D is the damping coefficient, and ω_n and ζ are the intermediate variables (Shi et al., 2018).

ω_n and ζ are as in Formulas 11, 12.

${\omega }_n=\sqrt{\frac{\left(D+\gamma k_{\mathrm{P}}\right)K_{\text{sg}}+K_{\mathrm{m}}}{\left(2H_{\text{sys}}+\gamma k_{\mathrm{d}}\right)K_{\text{sg}}{T}_{\text{re}}}}(11)$

$\xi =\left(\frac{\left(2H_{\text{sys}}+\gamma k_{\mathrm{d}}\right)K_{\text{sg}}+\left(\left(D+\gamma k_{\mathrm{P}}\right)K_{\text{sg}}+K_{\mathrm{m}}{F}_{\mathrm{h}}\right)T_{\text{re}}}{2\left(\left(D+\gamma k_{\mathrm{P}}\right)K_{\text{sg}}+K_{\mathrm{m}}\right)}\right){\omega }_n(12)$

Performing inverse Laplace transform on the Formula 10, The expression of Δf in time domain can be obtained as in Formula 13.

$\Delta f\left(t\right)=-\frac{K_{\text{sg}}\Delta P_{\mathrm{L}}{\omega }_n^2}{\left[\left(D+\gamma k_{\mathrm{P}}\right)K_{\text{sg}}+K_{\mathrm{m}}\right]}\left[1+\alpha {\mathrm{e}}^{-\zeta {\omega }_{n}t}\sin \left({\omega }_{\mathrm{d}}t+\varphi \right)\right](13)$

where α, ω_d and φ can be expressed by Formulas 14–16.

$\alpha =\sqrt{\frac{1-2T_{\text{re}}\xi {\omega }_n+T_{\text{re}}^2{\omega }_n^2}{1-{\xi }^2}}(14)$

${\omega }_{\mathrm{d}}={\omega }_n\sqrt{1-{\xi }^2}(15)$

$\varphi ={\tan }^{-1}\left(\frac{{\omega }_{\mathrm{d}}{T}_{\text{re}}}{1-\xi {\omega }_n{T}_{\text{re}}}-{\tan }^{-1}\left(\frac{\sqrt{1-{\xi }^2}}{-\xi }\right)\right)(16)$

After a disturbance, the imbalance power in the system causes the grid frequency to exceed the primary frequency regulation deadband of synchronous generator units. Subsequently, the speed control system of the prime mover automatically decreases or increases the mechanical power of synchronous generator units in response to the grid frequency variation, weakening the imbalance in active power and restraining frequency changes. The primary frequency regulation of synchronous generator units is automatically completed under the action of the prime mover’s speed control system. To ensure the safe operation of the units, the imbalance power response of primary frequency regulation is generally limited to within 6% of rated load. Additionally, since the input signal of inertia control is the frequency change rate, which may contain various degrees of noise, it can easily induce system instability. Therefore, based on droop control, this paper conducts research on droop control on the characteristics of the fast frequency support.

After a disturbance, WTG starts the fast frequency support strategy with frequency deviation f as input, and releases the rotational kinetic energy to respond to the frequency change, which is injected into the AC power grid through the DC transmission system. The additional power, ∆P, is:

$\Delta P=-K_P\Delta f(17)$

With the kinetic energy output of DFIG rotor, ω_r decreases. According to Eq. 17, MPPT output is affected, and the change amount of DFIG output ∆P_MPPT is:

$\Delta P_{\text{MPPT}}=k_g{\left({\omega }_0+\Delta {\omega }_{\mathrm{r}}\right)}^3-k_g{\omega }_0^3\approx 3k_g{\omega }_0^2\Delta {\omega }_{\mathrm{r}}(18)$

where ω₀ is the initial rotational speed of DFIG, ∆ω_r is the speed deviation after DFIG frequency regulation.

After integrating Eqs 17, 18, ∆P_e would be represented as

$\Delta P_e=3k_g{\omega }_0^2\Delta {\omega }_{\mathrm{r}}-K_P\Delta f(19)$

As shown in Eqs 18, 19 of the revised manuscript, the decrease of ∆PMPPT depends on two factors: initial rotor speed of wind turbine and variation of rotor speed. This means that in a high wind speed condition or the rotor speed variation is large during the frequency support period, the decrease of ∆P_MPPT is serious, which would give significant negative impact on the frequency support. In the simulation analysis, the coupling relationship between the maximum power tracking power variation, rotor speed of WTG and system frequency will be analyzed.

3 Simulation results

To investigate the influence of the dynamic characteristics of MPPT on the frequency regulation characteristics, the model shown in Figure 4 is employed based on PSCAD/EMTDC. The droop control is implemented in the WTG with the input of deviation of voltage of DC-link. Three scenarios are selected with the setting of Kp for 0, 10, and 30. The parameters of WTG are shown in Table 1 The other parameters are referred to (Yang et al., 2020) As disturbance.

Table 1

Table 1. Parameters of WTG.

3.1 Case 1: 2.5-MW load is connected to the grid

Figure 6 shows comparison results with various control coefficient under low-frequency disturbance. The simulation results show that the DC voltage changes by 0.005 p.u. for no frequency regulation strategy and the frequency changes by 0.005 p.u. This means that the self-synchronization strategy is confirmed, as shown the results of frequency and voltage in Figures 6A, B. When the WTG adopts no additional frequency regulation control, the rotor speed remains constant, and the WTG does not participate in frequency regulation. The maximum frequency deviation is 0.34 Hz due to the large load connection. When kp is set to 10 and 30, respectively, the maximum frequency deviation could be improved to 0.33 Hz and 0.29 Hz, respectively, as shown in Table 2. With the increase of droop coefficient, the maximum frequency deviation gradually decreases, the rotor speed reduction gradually increases, and the active output of the WTG gradually decreases. As in Figure 6C, the rotor speed reduction of kp = 10 is much more than that of kp = 10, the frequency support improvement is not significant clear due to the rapid change of output power in Figure 6D.

Figure 6

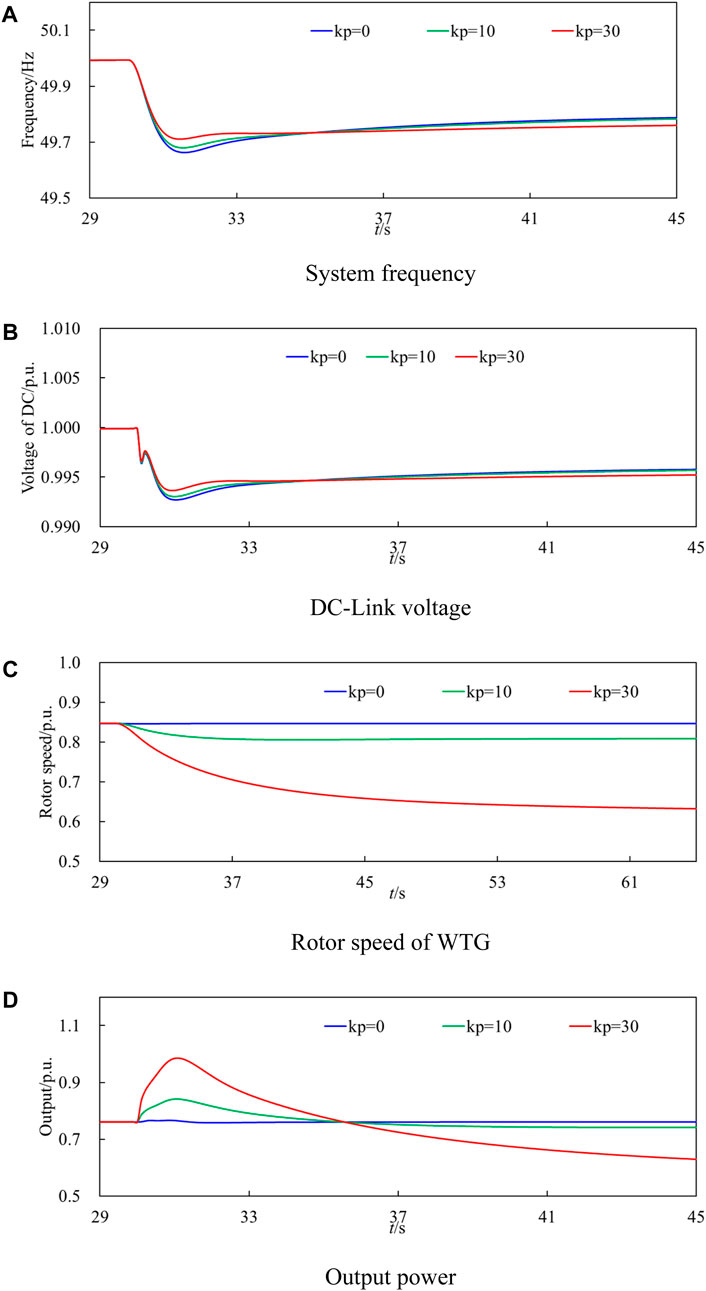
Figure 6. Comparison results with various control coefficient under low-frequency disturbance. (A) System frequency, (B) DC-Link voltage, (C) Rotor speed of WTG, (D) Output power.

Table 2

Table 2. Comparison results low-frequency disturbance.

3.2 Case 2: 1-MW load is disconnected from the grid

Figure 7 shows comparison results with various control coefficient under over-frequency disturbance. The simulation results show that the DC voltage changes by 0.003 p.u. and the frequency changes by 0.003 p.u. The mirror image relationship between frequency and voltage is confirmed, as shown in Figures 7A, B. According to the mirror image relationship between the system frequency and DC voltage, the fluctuation of DC voltage is consistent with the frequency. Among them, the highest frequencies of kp = 0, kp = 10, and kp = 30 are 50.21, 50.20, and 50.17 Hz, respectively, as shown in Table 3. With the increase of droop coefficient, the maximum frequency deviation gradually decreases, the rotor speed reduction gradually increases, and the active output of the WTG gradually decreases. When kp is set to 30, the maximum frequency deviation can be significantly improved and the frequency regulation effect is obvious. kp = 0, kp = 10, and kp = 30 correspond to the highest rotational speeds of 0.847, 0.852, and 0.867 pu, respectively; the corresponding active output is 0.7608, 0.753, and 0.756 pu respectively. As in Figure 7C, the rotor speed increase of kp = 10 is much more than that of kp = 10, the frequency support improvement is not significant clear because of the fast variation of output, as shown in Figure 7D.

Figure 7

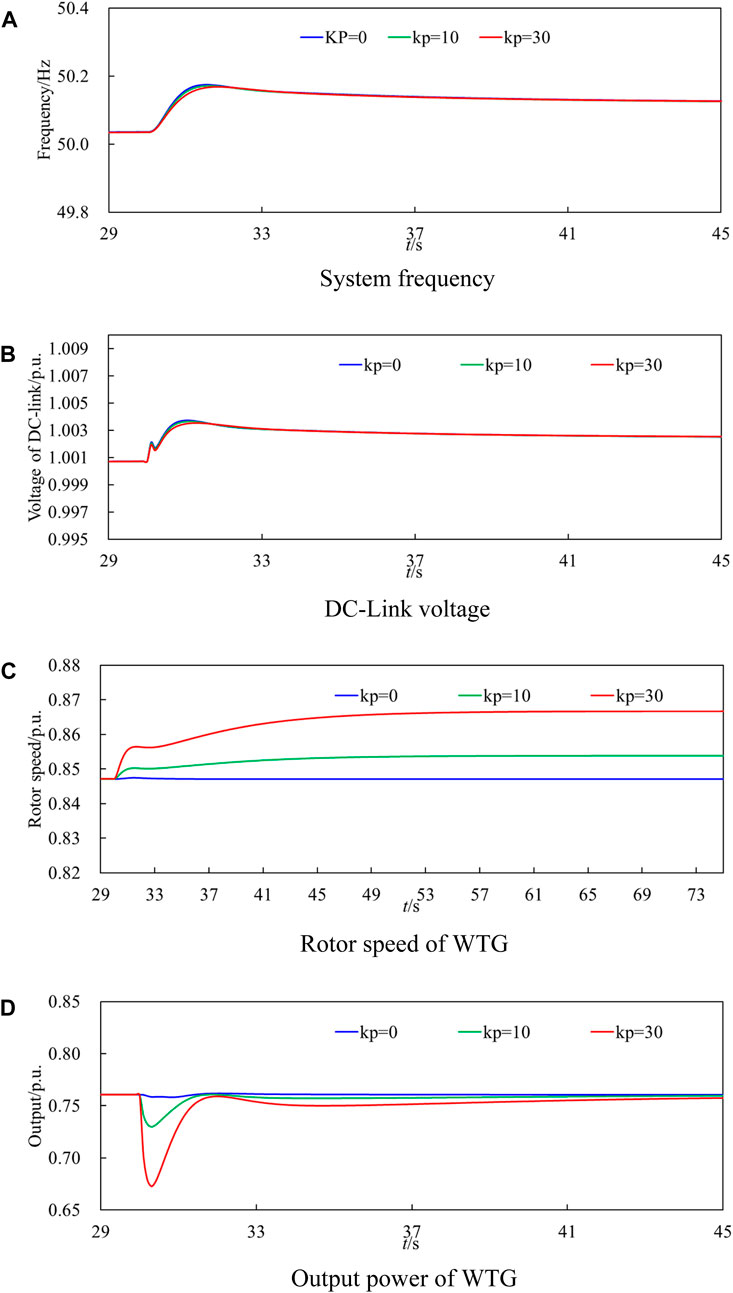
Figure 7. Comparison results with various control coefficient under over-frequency disturbance. (A) System frequency, (B) DC-Link voltage, (C) Rotor speed of WTG, (D) Output power of WTG.

Table 3

Table 3. Comparison results over-frequency disturbance.

4 Conclusion

The frequency support is realized by reserving reserve capacity of wind turbines, but the influence of the dynamic characteristics of MPPT on the overall frequency regulation characteristics of wind turbines during frequency support is ignored. To further tap the regulation potential of offshore wind power through flexible direct interconnection system, firstly, the frequency response model of the system is constructed, and the main factors that affect the frequency dynamic characteristics are revealed. Secondly, the principle of the grid-forming VSC with the function of self-inertial synchronization is introduced and the influence of the dynamic characteristics of MPPT on the frequency regulation characteristics of the WTG is clarified. Finally, based on the PSCAD/EMTDC electromagnetic transient simulation software platform, the electromagnetic transient simulation model of wind farms connected to AC/DC grid is established, and the influence of the dynamic characteristics of MPPT on the frequency regulation characteristics are verified by combining the grid-forming control technology. The simulation results indicate that with the increase of setting of droop control, the decrease of output power of MPPT becomes large so as to weaken the frequency support capability. The contribution of this research is to investigate the influence of the dynamic characteristics of MPPT on the frequency regulation characteristics. In future, the coordinated frequency support strategy between the WTG and energy storage system would be addressed.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the author, without undue reservation.

Author contributions

QC: Conceptualization, Investigation, Methodology, Writing–original draft, Writing–review and editing. GS: Funding acquisition, Investigation, Writing–original draft, Writing–review and editing. YL: Project administration, Resources, Software, Writing–review and editing. PQ: Software, Supervision, Validation, Visualization, Writing–review and editing. JoZ: Conceptualization, Funding acquisition, Methodology, Project administration, Writing–original draft, Writing–review and editing. RY: Investigation, Project administration, Resources, Writing–original draft. JnZ: Methodology, Project administration, Resources, Software, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the Science and Technology Project of State Grid Zhejiang Electric Power Co., Ltd., (5211DS230005), and partly by the National Natural Science Foundation of China (No.52107201).

Conflict of interest

Authors QC, YL, and PQ were employed by Electric Power Research Institute of State Grid Zhejiang Electric Power Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adeuyi, O. D., Cheah-Mane, M., Liang, J., and Jenkins, N. (2017). Fast frequency response from offshore Multiterminal VSC–HVDC schemes. IEEE Trans. Power Del. 32 (6), 2442–2452. doi:10.1109/tpwrd.2016.2632860

CrossRef Full Text | Google Scholar

Aouini, R., Marinescu, B., Kilani, K. B., and Elleuch, M. (2016). Synchronverter-based emulation and control of HVDC transmission. IEEE Trans. Power Syst. 31 (1), 278–286. doi:10.1109/tpwrs.2015.2389822

CrossRef Full Text | Google Scholar

Arévalo Soler, J., Groß, D., Araujo, E. P., and Bellmunt, O. G. (2023). Interconnecting power converter control role assignment in grids with multiple ac and dc subgrids. IEEE Trans. Power Del. 38, 2058–2071. doi:10.1109/tpwrd.2023.3236977

CrossRef Full Text | Google Scholar

Arghir, C., Jouini, T., and Dörffer, F. (2018). Grid-forming control for power converters based on matching of synchronous machines. Automatica 95, 273–282. doi:10.1016/j.automatica.2018.05.037

CrossRef Full Text | Google Scholar

Bianchi, F. D., and Domnguez-Garca, J. L. (2016). Coordinated frequency control using MT-HVDC grids with wind power plants. IEEE Trans. Sustain. Energy 7 (1), 213–220. doi:10.1109/tste.2015.2488098

CrossRef Full Text | Google Scholar

Castro, L. M., and Acha, E. (2016). On the provision of frequency regulation in low inertia AC grids using HVDC systems. IEEE Trans. Smart Grid 7 (6), 2680–2690. doi:10.1109/tsg.2015.2495243

CrossRef Full Text | Google Scholar

Eto, J. H., Undrill, J., Mackin, P., Daschmans, R., Williams, B., Haney, B., et al. (2010). Use of frequency response metrics to assess the planning and operating requirements for reliable integration of variable renewable generation. Berkeley, CA: Lawrence Berkeley National Laboratory.

Google Scholar

Flourentzou, N., Agelidis, V. G., and Demetriades, G. D. (2009). VSC-based HVDC power transmission systems: an overview. IEEE Trans. Power Electron. 24 (3), 592–602. doi:10.1109/tpel.2008.2008441

CrossRef Full Text | Google Scholar

Groß, D., Sa´nchez-Sa´nchez, E., Prieto-Araujo, E., and GomisBellmunt, O. (2022). Dual-port grid-forming control of mmcs and its applications to grids of grids. IEEE Trans. Power Del. 37, 4721–4735. doi:10.1109/tpwrd.2022.3157249

CrossRef Full Text | Google Scholar

Li, Y. J., Zhang, Z. R., Yang, Y., Chen, H., and Xu, Z. (2014). Coordinated control of wind farm and VSC-HVDC system using capacitor energy and kinetic energy to improve inertia level of power systems. Int. J. Electr. Power and Energy Syst. 59 (59), 79–92. doi:10.1016/j.ijepes.2014.02.003

CrossRef Full Text | Google Scholar

Li, Y. J., Xu, Z., Ostergarrd, J., and Hill, D. J. (2017). Coordinated control strategies for offshore wind farm integration via VSC-HVDC for system frequency support. IEEE Trans. Energy Convers. 32 (3), 843–856. doi:10.1109/tec.2017.2663664

CrossRef Full Text | Google Scholar

Markovic, U., Stanojev, O., Aristidou, P., Vrettos, E., Callaway, D., and Hug, G. (2021). Understanding small-signal stability of low-inertia systems. IEEE Trans. Power Syst. 36 (5), 3997–4017. doi:10.1109/tpwrs.2021.3061434

CrossRef Full Text | Google Scholar

Qin, Y., Wang, H., Shao, H., Yang, R., Cai, X., and Cao, Y. (2021) “Self-synchronization and frequency response control of PMSG-based wind turbine generator,” in IEEE energy conversion congress and exposition-Asia, Singapore, 24–27 May 2021, IEEE. doi:10.1109/ECCE-Asia49820.2021.9479272

CrossRef Full Text | Google Scholar

Rezaei, N., and Kalantar, M. (2015). Smart microgrid hierarchical frequency control ancillary service provision based on virtual inertia concept: an integrated demand response and droop controlled distributed generation framework. Energy Convers. Manage 92, 287–301. doi:10.1016/j.enconman.2014.12.049

CrossRef Full Text | Google Scholar

Sang, S., Zhang, C., Zhang, J., Shi, G., and Deng, F. (2022). Analysis and stabilization control of a voltage source controlled wind farm under weak grid conditions. Front. Energy 16 (6), 943–955. doi:10.1007/s11708-021-0793-5

CrossRef Full Text | Google Scholar

Shi, Q., Li, F., and Cui, H. (2018). Analytical method to aggregate multi-machine SFR model with applications in power system dynamic studies. IEEE Trans. Power Syst. 33 (6), 6355–6367. doi:10.1109/tpwrs.2018.2824823

CrossRef Full Text | Google Scholar

Subotić, I., and Groß, D. (2022). Power-balancing dual-port grid-forming power converter control for renewable integration and hybrid ac/dc power systems. IEEE Trans. Control Netw. Syst. 9, 1949–1961. doi:10.1109/tcns.2022.3181551

CrossRef Full Text | Google Scholar

Xiong, L., Zhuo, F., Wang, F., Liu, X., Chen, Y., Zhu, M., et al. (2016). Static synchronous generator model: a new perspective to investigate dynamic characteristics and stability issues of grid-tied PWM inverter. IEEE Trans. Power Electron. 31 (9), 6264–6280. doi:10.1109/tpel.2015.2498933

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Zhang, D., and Liu, Y. (2021). Rapid power compensation-based frequency response strategy for low-inertia power systems. IEEE J. Emerg. Sel. Top. Power Electron. 9 (4), 4500–4513. doi:10.1109/jestpe.2020.3032063

CrossRef Full Text | Google Scholar

Yang, R., Zhang, C., Cai, X., and Shi, G. (2018). Autonomous grid-synchronising control of VSC-HVDC with real-time frequency mirroring capability for wind farm integration. IET Renew. Power Gener. 12 (13), 1572–1580. doi:10.1049/iet-rpg.2017.0824

CrossRef Full Text | Google Scholar

Yang, R., Shi, G., Cai, X., Zhang, C., Li, G., and Liang, J. (2020). Autonomous synchronizing and frequency response control of multi-terminal DC systems with wind farm integration. IEEE Trans. Sustain. Energy 11, 2504–2514. doi:10.1109/TSTE.2020.2964145

CrossRef Full Text | Google Scholar

Yang, D., Jin, Z., Jin, E., Wang, X., Chen, W., Yan, G.-G., et al. (2024). Adaptive frequency droop feedback control-based power tracking operation of a DFIG for temporary frequency regulation. IEEE Trans. Power Syst. 39 (2), 2682–2692. doi:10.1109/tpwrs.2023.3277009

CrossRef Full Text | Google Scholar

Zhong, C., Li, H., Zhou, Y., Lv, Y., and Chen, J. (2022). Virtual synchronous generator of PV generation without energy storage for frequency support in autonomous microgrid. Int. J. Electr. Power and Energy Syst. 134, 107343. doi:10.1016/j.ijepes.2021.107343

CrossRef Full Text | Google Scholar