Economic optimal dispatch of active distribution network with CCHP multi-microgrid based on analytical target cascading

When multiple CCHP microgrids are integrated into an active distribution network (ADN), the microgrids and the distribution network serve as distinct stakeholders, making the economic optimal dispatch of the system more complex. This paper proposes a distributed dispatch model of ADN with CCHP multi-microgrid, and refines the objective functions of each region. The analytical target cascading approach (ATC) is employed to model the power transaction as virtual sources/loads, and solve the optimal dispatch in parallel. Case studies demonstrate the proposed distributed model is capable of achieving economic optimization for both stakeholders.

1 Introduction

Sustainability and low carbon have become the prevailing directions of current global energy development (Kabeyi and Olanrewaju, 2022). Due to the tight supply of traditional energy and environmental pollution problems, distributed energy has developed rapidly in recent years. As a comprehensive integrated technology of distributed energy sources, microgrid is of great significance for promoting the environmental protection and economy of the power system. The combined cooling, heating, and power (CCHP) microgrids which can supply multiple energy to load demand and improve energy efficiency (Yang et al., 2021), has attracted widespread attention both domestically and internationally. However, the traditional distribution network, due to issues such as large energy loss and low automation levels, faces challenges in accommodating the increasing integration of distributed energy sources (Ghadi et al., 2019). Active distribution network (ADN), leveraging its advantage of flexible structure, can proactively manage distributed energy sources (Jamali et al., 2020). The integration of CCHP microgrids into ADN has the potential to enhance the penetration rate of renewable energy sources and improve economic security (Marvasti et al., 2014; Xie et al., 2022). But at the same time, the integration of CCHP microgrids also brings new challenges to the distribution network, the economic optimal dispatch of the system becomes more complicated.

Numerous studies have focused on optimal dispatch models and control methods of CCHP microgrid (Guo et al., 2021). Wang et al. (2020) introduced a coordinated optimization model of CCHP microgrid considering electricity transactions with the electricity market. Luo et al. (2019) established a multi-objective nonlinear capacity optimization model, and solved it using the NSGA-II algorithm. Zhang et al. (2023) presented a multi-objective model aimed at minimizing the operation costs and emissions in a CCHP-based microgrid. This model employed robust optimization method to account for uncertainties. Gu et al. (2017) proposed a dynamic optimization and dispatch strategy for CCHP microgrid based on model predictive control, which provides real-time feedback to correct the deviation of cold and heat load and renewable energy output prediction. Varasteh et al. (2019) introduced a two-layer iterative optimization algorithm designed to optimize the system expansion and planning while simultaneously accounting for the impacts of demand response programs and system reliability.

The above literature mainly focuses on the economic optimal dispatch of a single CCHP microgrid. When multiple microgrids are interconnected, the economic dispatch problem receives extensive research attention. Liu et al. (2019) proposed a new hybrid energy sharing management framework for CCHP microgrids to reduce the operation cost (Du et al., 2018). proposed a cooperative game approach for multi-microgrid to achieve higher energy efficiency and lower operation cost Wang et al. (2018) introduced a two-stage energy management method for renewable energy microgrids Tan et al. (2020) presented a two-stage robust optimization model for CCHP multi-microgrid with uncertainties, aiming at minimizing the operation cost.

Nowadays, the connection of multiple microgrids within the same distribution network has become increasingly prevalent, making the investigation of economic optimal dispatch for ADN with CCHP multi-microgrids of practical significance (Yan et al., 2017; Cheng et al., 2022). Alam et al. (2019) highlighted that the interconnection of microgrids can yield multiple advantages, including the high-efficiency utilization of renewable energy sources and reduction in operation cost. The economic optimal dispatch problem of ADN with multi-microgrids is a nonlinear problem, and there are centralized and distributed modeling methods. (Nikmehr and Ravadanegh, 2015). established a centralized model and took the minimum total operating cost of the system as the objective function. The simulation results show that power sharing between multi-microgrids and the main grid can reduce the total operating cost of future distribution networks (Luna et al., 2017). utilized the mixed integer programming to solve the centralized model. The centralized modeling method can solve the global optimal problem, but this method requires a lot of communication information and a lot of calculations. When a large number of distributed energy sources of various types are connected to the grid, the pressure of information transmission increases sharply, which makes it easy to cause computational dimensionality disaster. At the same time, it also fails to protect the privacy of the distribution network and microgrid as independent individuals.

Distributed optimization has attracted widespread attention due to its advantages such as requiring less interactive information, protecting the privacy of each subject, and fast solution speed (Wu et al., 2017). Xie et al. (2018) introduced the concept of multiple microgrids and the distribution grid as distinct stakeholders, incorporating the analytic target cascading method to achieve parallel solutions for optimizing microgrid scheduling issues (Gao et al., 2018). proposed a novel energy exchange model that uses a distributed approach to coordinate the power exchange between the distribution network and the microgrid. The energy management model of each independent individual adopts a two-stage robust optimization to cope with the randomness of new energy and the predicted load of each independent area. Zhong et al. (2023) established a distributed optimization model between microgrid and distribution network using the alternating direction multiplier method (ADMM) to achieve the optimal energy interaction of all stakeholders, and verifies the algorithm advantages in reducing computational burden and protecting privacy (Ajoulabadi et al., 2020). established a flexible dispatch model for distribution network with microgrids considering network reconstruction and demand response to improve the flexibility of system dispatch Kim et al. (2020) described the energy transaction between multiple microgrids and distribution networks as a Nash bargaining game problem, and proposed a two-stage distributed method to determine the transaction volume and clearing price, which greatly reduced the total cost and improved the overall social welfare. Mohiti et al. (2019) introduced a decentralized robust model aiming to minimize the overall operation cost through coordinated operation of ADN and multi-microgrids.

In order to enhance economic efficiency and energy utilization of microgrids, an economic optimal dispatch of ADN with CCHP multi-microgrid is introduced. Distributed modeling and analytical target cascading approach are utilized to obtain the optimal economic dispatch results. The major contributions of this paper are outlined as follows:

(1) This paper proposes the composition and structure of an ADN with CCHP multi-microgrid, and constructs the mathematical model of equipment within CCHP microgrid.

(2) ADN with CCHP multi-microgrid is divided into local dispatch layer and regional dispatch layer. Based on the differing stakeholders at the regional dispatch layer, centralized and distributed optimal dispatch models are established respectively.

(3) The analytical target cascading approach is used to equivalent the interaction power between microgrid and ADN to virtual sources and virtual loads, to achieve decoupling solution.

(4) Case study compares the results between centralized model and distributed model, and validate the effectiveness of the proposed optimal dispatch model.

The remainder of this paper is organized as follows. Section 2 introduces the structure of ADN with CCHP multi-microgrid and the mathematical model of the equipment within CCHP microgrid. Section 3 proposes the optimal dispatch model of ADN with CCHP multi-microgrid, and analytical target cascading approach is utilized to solve the model. Section 4 presents the case simulation results of local dispatch layer and regional dispatch layer under centralized and distributed model. Finally, conclusions are made in Section 5.

2 Structure of ADN with CCHP multi-microgrid and equipment mathematical model

2.1 Structure of ADN with CCHP multi-microgrid

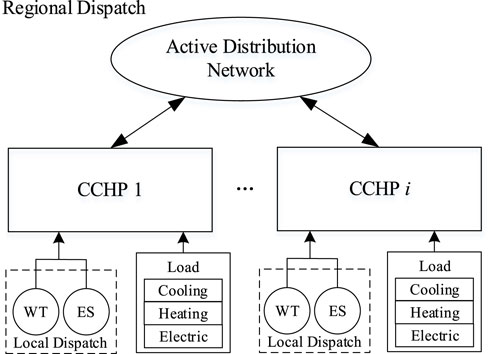
The structure of ADN with CCHP multi-microgrid is divided into local dispatch layer and regional dispatch layer, as illustrated in Figure 1. The local dispatch layer consists of renewable energy generation and energy storage system within CCHP microgrid. At the regional dispatch layer, microgrids are collectively connected to the same ADN. Each CCHP microgrid plans the output schedules of distributed generation and equipment, coordinates the interaction power with ADN, and satisfies multiple loads. ADN allocates the output of each generator to minimize the overall operation cost of ADN while meeting its own electric load.

Figure 1

Figure 1. Structure diagram of ADN with CCHP multi-microgrid.

2.2 Mathematic model of equipment within CCHP microgrid

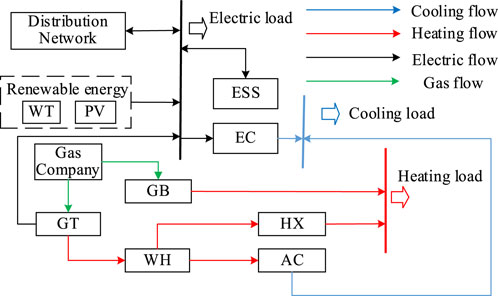
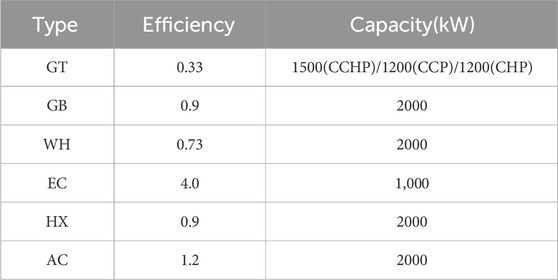
The equipment and energy flow relationships of CCHP microgrid is shown in Figure 2, and the load include cooling load, heating load and electric load. The main equipment in the CCHP microgrid include gas turbine, gas boiler, waste heat boiler, electric chiller, absorption chiller, heat exchanger, wind turbine (WT), photovoltaic unit (PV) and energy storage system. The mathematic model of equipment is given in Equations 1-8.

Figure 2

Figure 2. Structure diagram of CCHP microgrid.

2.2.1 Gas turbine (GT)

$P_{GT}\left(t\right)=P_{gas}^{GT}\left(t\right){\eta }_{GT}(1)$

$H_{GT}\left(t\right)=P_{GT}\left(t\right){\gamma }_{GT}(2)$

Where $P_{GT}\left(t\right)$ is the output of GT; $P_{gas}^{GT}\left(t\right)$ is the amount of gas consumption of GT; ${\eta }_{GT}$ is the generation efficiency of GT; $H_{GT}\left(t\right)$ is the amount of waste heat recovery from GT; ${\gamma }_{GT}$ is the heat-to-electric ratio.

2.2.2 Gas boiler (GB) and waste heat boiler (WH)

$H_{GB}\left(t\right)=P_{gas}^{GB}\left(t\right){\eta }_{GB}(3)$

$H_{WH}\left(t\right)=H_{WH,in}\left(t\right){\eta }_{WH}(4)$

Where $H_{GB}\left(t\right)$ is the heating output of GB; $P_{gas}^{GB}\left(t\right)$ is the amount of gas consumption of GB; ${\eta }_{GB}$ is the efficiency of GB; $H_{WH}\left(t\right)$ is the output of WH; $H_{WH,in}\left(t\right)$ is the input power of WH; ${\eta }_{WH}$ is the efficiency of WH.

2.2.3 Heat exchanger (HX)

$H_{HX}\left(t\right)=H_{WH,heat}\left(t\right){\eta }_{HX}(5)$

Where $H_{HX}\left(t\right)$ is the output of HX; $H_{WH,heat}\left(t\right)$ is the portion of WH output for heating; ${\eta }_{HX}$ is the efficiency of HX.

2.2.4 Absorption chiller (AC) and electric chiller (EC)

$P_{EC}\left(t\right)=P_{EC,in}\left(t\right)CO{P}_{EC}(6)$

$P_{AC}\left(t\right)=P_{WH,cool}\left(t\right)CO{P}_{AC}(7)$

Where $P_{EC}\left(t\right)$ is the output of EC; $P_{EC,in}\left(t\right)$ is the input power of EC; $CO{P}_{EC}$ is the cooling efficiency of EC; $P_{AC}\left(t\right)$ is the output of AC; $P_{WH,cool}\left(t\right)$ is the portion of WH output for cooling; $CO{P}_{AC}$ is the cooling efficiency of AC.

2.2.5 Energy storage system (ESS)

$E_{ess}\left(t\right)=\left(1-u\right)E_{ess}\left(t-1\right)+\left[{\eta }^{ch}{P}_{ch}\left(t\right)-P_{dc}\left(t\right)/{\eta }^{dc}\right]\Delta t(8)$

Where $E_{ess}\left(t\right)$ is the capacity of ESS at time t; u is the energy loss rate of ESS; ${\eta }^{ch}$ and ${\eta }^{dc}$ are the charging and discharging efficiency of ESS; $P_{ch}\left(t\right)$ and $P_{dc}\left(t\right)$ are the charging and discharging power of ESS.

3 Optimal dispatch model of ADN with CCHP multi-microgrid

3.1 Modeling of local dispatch layer

3.1.1 Objective function of local dispatch layer

The local dispatch layer comprises WT and ESS, forming a wind-storage combined system. The local dispatch layer needs to meet two objectives, namely, maximizing the generation revenue of the combined system while minimizing the output fluctuation throughout the entire period to reduce the impact on the microgrid. Therefore, the optimization objective functions of the local dispatch layer are presented in Equations 9-11.

$\max F_{W-S}={\displaystyle \sum _{t=1}^{N_T}}\rho \left(t\right)P\left(t\right),\forall t\in N_T(9)$

$\min L_{W-S}={\displaystyle \sum _{t=1}^{N_T}}{\left(P\left(t\right)-\frac{1}{N_T}{\displaystyle \sum _{t=1}^{N_T}}P\left(t\right)\right)}^2(10)$

$P\left(t\right)=P_{WT}^{\max }\left(t\right)+P_{dc}\left(t\right)-P_{ch}\left(t\right)(11)$

Where $F_{W-S}$ is the generation revenue of the wind-storage combined system; $L_{W-S}$ is the output fluctuation of the combined system; $N_{\mathrm{T}}$ is the period of day-ahead optimal dispatch, which is taken as 24 h in this paper; $\rho \left(t\right)$ is the electricity sales price of the combined system; $P\left(t\right)$ is the output of the combined system; $P_{\text{wind}}^{\max }\left(t\right)$ is the maximum forecast output of WT.

3.1.2 Constraints of local dispatch layer

The constraints of the local dispatch layer include limitations on the charging power, discharging power and state of charge of ESS, as shown in Equation 12.

$\left\{\begin{array}{l}{E}_{ess}\left(t\right)=\left(1-u\right)E_{ess}\left(t-1\right)+\left[{\eta }^{ch}{P}_{ch}\left(t\right)-P_{dc}\left(t\right)/{\eta }^{dc}\right]\Delta t\\ E_{ess}\left(0\right)=20\%E_{ess}^{\max }\\ 10\%E_{ess}^{\max }\le E_{ess}\left(t\right)\le 90\%E_{ess}^{\max }\\ 0\le P_{ch}\left(t\right)\le I_{ch}\left(t\right)P_{ess}^{\max }\\ 0\le P_{dc}\left(t\right)\le I_{dc}\left(t\right)P_{ess}^{\max }\\ I_{ch}\left(t\right)+I_{dc}\left(t\right)\le 1\\ I_{ch}\left(t\right)\in \left\{0,1\right\},I_{dc}\left(t\right)\in \left\{0,1\right\}\end{array}\right.(12)$

Where $E_{ess}\left(0\right)$ is the initial stored energy of ESS; $E_{ess}^{\max }$ is the maximum capacity of ESS; $I_{ch}\left(t\right)$ and $I_{dc}\left(t\right)$ are the charging state and the discharging state of ESS respectively; $P_{ess}^{\max }$ is the maximum charging and discharging power of ESS.

3.2 Modeling of regional dispatch layer

3.2.1 Objective function of centralized optimal dispatch

The optimized outputs of WT at the local dispatch layer are transferred to the CCHP microgrids at the regional dispatch layer, serving as the renewable energy generation inputs. In the centralized optimal dispatch, individual microgrids prioritize the utilization of WT at the local dispatch layer before resorting to other equipment such as GT and ESS. The objective of centralized optimal dispatch at the regional dispatch layer is to minimize the total operation cost of ADN and CCHP multi-microgrid. The objective function is expressed as shown in Equations 13-16.

$\min F_{total}=F_G+F_{gas}+F_{wind}(13)$

$F_G={\displaystyle \sum _{i=1}^M}{\displaystyle \sum _{t=1}^{N_{\mathrm{T}}}}\left(a_i{P}_{Gi}^2\left(t\right)+b_i{P}_{Gi}\left(t\right)+c_i\right)(14)$

$F_{gas}={\displaystyle \sum _{j=1}^N}{\displaystyle \sum _{t=1}^{N_T}}\left(\frac{c_{gas}{P}_{GT,j}\left(t\right)}{{\eta }_c{L}_{NG}}+c_{gas}{F}_{GB,j}\left(t\right)\right)(15)$

$F_{wind}={\displaystyle \sum _{j=1}^N}{\displaystyle \sum _{t=1}^{N_{\mathrm{T}}}}\rho \left(t\right)P_j\left(t\right)(16)$

Where $F_{total}$ is the total operation cost; $F_G$ is the generation cost of ADN; $F_{gas}$ is the gas cost of CCHP multi-microgrid; $F_{wind}$ is the electricity purchase cost from the local dispatch layer; $P_{Gi}\left(t\right)$ is the output of generator i in ADN; $M$ is the number of generators; $N$ is the number of microgrids; a_i, b_i, c_i are cost coefficient; $c_{gas}$ is the gas price; $P_{GT,j}\left(t\right)$ is the output of GT in microgrid j; $F_{GB,j}\left(t\right)$ is the amount of gas consumed by GB in microgrid j; $P_j\left(t\right)$ is the output of WT in microgrid j.

3.2.2 Objective function of distributed optimal dispatch

In practical engineering, the ADN and the CCHP multi-microgrid, as two distinct stakeholders, have their own optimization objectives. In order to investigate the optimal dispatch results of two stakeholders, a distributed optimal dispatch model is introduced, enabling different stakeholders to engage in a game while simultaneously achieving their respective economic optimum. The regional dispatch layer is further divided into ADN layer and CCHP multi-microgrid layer, where separate optimal dispatch models are established for each.

3.2.2.1 ADN layer

The optimization objective of ADN layer is the minimum operation cost, including the generation cost and interaction cost. The objective function of ADN layer is depicted in Equations 17, 18.

$\min F_{ADN}=F_G-F_S(17)$

$F_{\mathrm{S}}={\displaystyle \sum _{j=1}^N}{\displaystyle \sum _{t=1}^{N_T}}{\tau }_j\left(t\right)P_j^L\left(t\right)(18)$

Where $F_{ADN}$ is the operation cost of ADN; $F_S$ is the interaction cost between ADN and CCHP multi-microgrid; $P_j^L\left(t\right)$ is the interaction power between ADN and microgrid j; ${\tau }_j\left(t\right)$ is the time-of-use electricity price between ADN and microgrid j.

3.2.2.2 CCHP multi-microgrid layer

The optimization objective of CCHP multi-microgrid layer is to minimize the total operation cost, including gas cost, interaction cost with ADN, and electricity purchase cost. The objective function is shown in Equations 19-21.

$\min F_{MG}={\displaystyle \sum _{j=1}^N}\left(F_{gas,j}+F_{buy,j}+F_{W-S}\right)(19)$

$F_{gas,j}={\displaystyle \sum _{t=1}^{N_T}}\left[\frac{c_{gas}{P}_{GT,j}\left(t\right)}{{\eta }_c{L}_{NG}}+c_{gas}{F}_{GB,j}\left(t\right)\right](20)$

$F_{buy,j}={\displaystyle \sum _{t=1}^{N_T}}{\tau }_j\left(t\right)P_j^L\left(t\right)(21)$

Where $F_{MG}$ is the total operation cost of CCHP multi-microgrid; $F_{gas,j}$ is the gas cost of microgrid j; $F_{buy,j}$ is the interaction cost between ADN and microgrid j; $F_{W-S}$ is the electricity purchase cost from the local dispatch layer in microgrid j.

3.2.3 Constraints of ADN layer

The constraints of the regional dispatch layer are divided into two categories, ADN layer and CCHP multi-microgrid layer. Both centralized and distributed optimal dispatch model have the same constraints.

3.2.3.1 Electric power balance

The constraints of ADN layer are shown in Equations 22-25.

${\displaystyle \sum _{i=1}^M}{P}_{Gi}\left(t\right)-{\displaystyle \sum _{j=1}^N}{P}_j^L\left(t\right)=P_{load}^{ADN}\left(t\right)(22)$

Where $P_{load}^{ADN}\left(t\right)$ is the electric load of ADN; $P_j^L\left(t\right)$ is interaction power between ADN and microgrid j.

3.2.3.2 The upper and lower limits of power generation

$P_{Gi}^{\min }\le P_{Gi}\left(t\right)\le P_{Gi}^{\max }(23)$

Where $P_{Gi}^{\max }$ and $P_{Gi}^{\min }$ are the maximum and minimum power generation of generator i respectively.

3.2.3.3 Spinning reverse constraints

${\displaystyle \sum _{i=1}^M}{P}_{Gi}^{\max }-{\displaystyle \sum _{j=1}^N}{P}_j^L\left(t\right)\ge P_{load}^{ADN}\left(t\right)+R^{ADN}\left(t\right)(24)$

Where $R^{ADN}\left(t\right)$ is the reverse demand of ADN.

3.2.3.4 Interaction power limits between ADN and microgrids

$P_{\min }^L\le P_j^L\left(t\right)\le P_{\max }^L(25)$

Where $P_{\max }^L$ and $P_{\min }^L$ are the maximum and minimum interaction power respectively.

3.2.4 Constraints of CCHP multi-microgird layer

The constraints of the CCHP multi-microgrid layer comprise both equality and inequality constraints. The equality constraints include the power balance of multiple loads for each CCHP microgrid, as shown in Equations 26-28. The inequality constraints encompass the limits of equipment output and the state of charge of ESS, as shown in Equation 29.

3.2.4.1 Cooling load balance

$Q_{AC,j}\left(t\right)+Q_{EC,j}\left(t\right)=P_{cool,j}\left(t\right)(26)$

Where $Q_{AC,j}\left(t\right)$ is the output of AC in microgrid j; $Q_{EC,j}\left(t\right)$ is the output of EC in microgrid j; $P_{cool,j}\left(t\right)$ is the cooling load in microgrid j.

3.2.4.2 Heating load balance

$P_{GB,j}\left(t\right)+P_{HX,j}\left(t\right)=P_{heat,j}\left(t\right)(27)$

Where $P_{GB,j}\left(t\right)$ is the output of GB in microgrid j; $P_{HX,j}\left(t\right)$ is the output of HX in microgrid j; $P_{heat,j}\left(t\right)$ is the heating load in microgrid j.

3.2.4.3 Electric load balance

$P_{GT,j}\left(t\right)+P_{ESS,j,dc}\left(t\right)+P_{disnet,j}\left(t\right)+P_j\left(t\right)=P_{elec,j}\left(t\right)+P_{EC,j}\left(t\right)+P_{ESS,j,ch}\left(t\right)(28)$

Where $P_{GT,j}\left(t\right)$ is the output of GT in microgrid j; $P_{ESS,j,ch}\left(t\right)$ and $P_{ESS,j,dc}\left(t\right)$ are the charging and discharging power of ESS in microgrid j; $P_{disnet,j}\left(t\right)$ is the interaction power between microgrid j and ADN; $P_j\left(t\right)$ is the output of local dispatch layer in microgrid j; $P_{elec,j}\left(t\right)$ is the electric load in microgrid j; $P_{EC,j}\left(t\right)$ is the power consumption of EC in microgrid j.

3.2.4.4 The upper and lower limits of equipment output

$0\le P_{x,j}\left(t\right)\le P_{x,\max }(29)$

Where $P_{x,j}\left(t\right)$ is the output of equipment in microgrid j; x is the type of equipment, including GT, GB, WH, EC, AC, HX; $P_{x,\max }$ is the maximum capacity of equipment.

3.3 Solving method

The interaction power between ADN and CCHP multi-microgrid influences the optimal dispatch of both systems, rendering the distributed optimal dispatch model difficult to solve.

The analytical target cascading (ATC) is an approach to solving coordination issues in distributed hierarchical structures (Kargarian et al., 2018). It offers advantages such as parallel optimization of multi-level systems and strict convergence. The upper-level system provides design variables for the lower-level system, the lower-level system calculates the response and feeds it back to the upper-level system, then updates the data based on the feedback results. Repeat the above process until it meets the set convergence criteria (Talgorn and Kokkolaras, 2017). The optimization model for each level of ATC is depicted in Equation 30.

$\begin{array}{l}\min f_s\left(x\right)+\mathrm{\pi }\left(t_{ij}-r_{ij}\right)\\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{l}{g}_s\left(x\right)\le 0\\ h_s\left(x\right)=0\end{array}\right.\end{array}(30)$

Where $f_s\left(x\right)$ is the initial system optimization objectives; $t_{ij}$ is the design variables transferred from the upper-level system to the lower-level system after optimization; $r_{ij}$ is the feedback results transferred from the lower-level system to the upper-level system after optimization; $\mathrm{\pi }\left(t_{ij}-r_{ij}\right)$ is the penalty term, the Lagrangian penalty function is chosen in this paper; $g_s\left(x\right)$ is the inequality constraints of this level; $h_s\left(x\right)$ is the equality constraints of this level.

In this paper, the upper-level is ADN, while the lower-level is CCHP multi-microgrid. The design variables and feedback variables are both the power transaction between CCHP multi-microgrid and ADN. The interaction power between CCHP microgrid j and ADN $P_j^L\left(t\right)$ is equivalent to virtual loads $P_{load,j}\left(t\right)$ in ADN, and virtual sources $P_{power,j}\left(t\right)$ in CCHP microgrid j, and participates in the optimal dispatch of the two distinct stakeholders.

The Lagrangian penalty function is added to the objective function in each layer. The objective function of CCHP microgrid j can be modified as shown in Equation 31.

$\min F_{MG,j}+{\displaystyle \sum _{t=1}^{N_T}}{\omega }_j\left(t\right)\left[\overline{P_{load,j}\left(t\right)}-P_{power,j}\left(t\right)\right]+{{\displaystyle \sum _{t=1}^{N_T}}{\gamma }_j\left(t\right)\left[\overline{P_{load,j}\left(t\right)}-P_{power,j}\left(t\right)\right]}^2(31)$

The objective function of ADN can be modified as shown in Equation 32.

$\min F_{ADN}+{\displaystyle \sum _{t=1}^{N_T}}{\displaystyle \sum _{j=1}^N}{\omega }_j\left(t\right)\left[P_{load,j}\left(t\right)-\overline{P_{power,j}\left(t\right)}\right]+{{\displaystyle \sum _{t=1}^{N_T}}{\displaystyle \sum _{j=1}^N}{\gamma }_j\left(t\right)\left[P_{load,j}\left(t\right)-\overline{P_{power,j}\left(t\right)}\right]}^2(32)$

where ω_j and γ_j are the Lagrange multipliers. $\overline{P_{load,j}\left(t\right)}$ and $\overline{P_{power,j}\left(t\right)}$ are the coupling variables from the other system. By introducing the penalty function, the coupling variable is made to approach the boundary power value of the other system’s interactive feedback during the iteration process, and finally the coupling variable is consistent with the boundary value.

The convergence criterion for judging the optimization results can be formulated as Equations 33-35.

$\left|P_{load,j}^k\left(t\right)-P_{power,j}^k\left(t\right)\right|\le {\epsilon }_1(33)$

$\left|\frac{\left(F_{ADN}^k+{\displaystyle \sum _{j=1}^N}{F}_{MG,j}^k\right)-\left(F_{ADN}^{k-1}+{\displaystyle \sum _{j=1}^N}{F}_{MG,j}^{k-1}\right)}{F_{ADN}^k+{\displaystyle \sum _{j=1}^N}{F}_{MG,j}^k}\right|\le {\epsilon }_2(34)$

$\left\{\begin{array}{l}{\omega }_j^k\left(t\right)={\omega }_j^{k-1}\left(t\right)+2{\gamma }_j^{k-1}{\left(t\right)}^2\left[P_{load,j}^{k-1}\left(t\right)-P_{power,j}^{k-1}\left(t\right)\right]\\ {\gamma }_j^k\left(t\right)=\beta {\gamma }_j^{k-1}\left(t\right),2<\beta <3\end{array}\right.(35)$

Where ε₁ and ε₂ are the convergence accuracy; β is a constant, generally taken as (2,3). The initial values of ω_j and γ_j are generally small constants.

In Equation 33, the difference between virtual sources and virtual loads within the same iteration process should meet the specified minimum value requirement. In Equation 34, the total operation cost of ADN with CCHP multi-microgrid should be optimized for the best results.

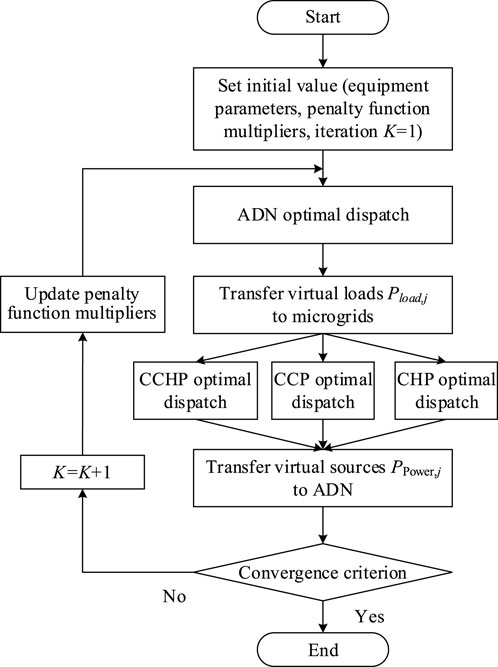
The parallel optimization process is illustrated in Figure 3, the specific steps are described as follows.

Step 1: Set initial value of equipment parameters and the penalty function multipliers. The number of iterations K = 1.

Step 2: Solve the optimal dispatch problem of ADN and transfer the virtual loads $P_{load,j}\left(t\right)$ to microgrids.

Step 3: Each microgrid solves its optimal dispatch problem and transfer the virtual sources $P_{power,j}\left(t\right)$ to ADN.

Step 4: Use Equations 33, 34 to determine whether the convergence criterion is met. If it is met, the optimal dispatch result is output. If it is not met, the penalty function multiplier is updated according to Equation 35 and the process returns to step 2. The number of iterations K = K + 1.

Figure 3

Figure 3. Solving process of analytical target cascading approach.

4 Case study

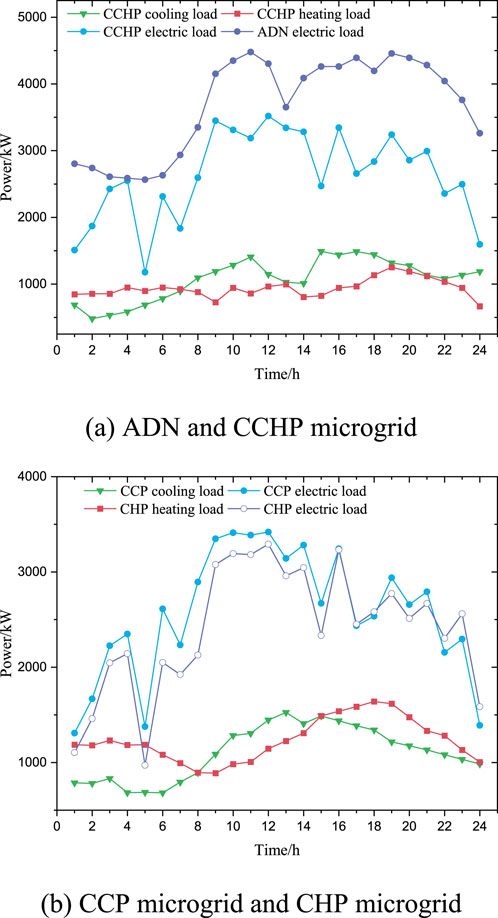
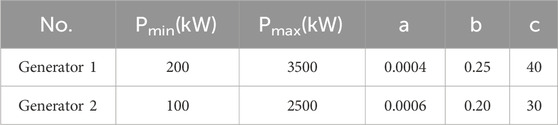
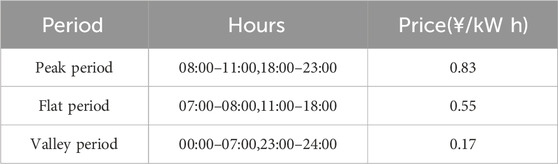
The multi-microgrid consists of CCHP microgrids, CCP microgrids, and CHP microgrids, and each type is only one. Each microgrid holds equal significance, and there is no energy transaction between them. The load forecast data for the three microgrids are provided in Figure 4 below. Parameters of equipment in the microgrids are outlined in Table 1. Parameters of generators in ADN are specified in Table 2. Table 3 shows the time-of-use electricity price, and the natural gas price is set at 2.20 yuan per cubic meter. The proposed optimal dispatch model is written using MATLAB and solved using CPLEX.

Figure 4

Figure 4. Curves of the forecasting load of ADN and CCHP multi-microgrid.

Table 1

Table 1. Parameters of equipment in microgrids.

Table 2

Table 2. Parameters of generators in ADN.

Table 3

Table 3. Time-of-use electricity price.

4.1 Operation results of local dispatch layer

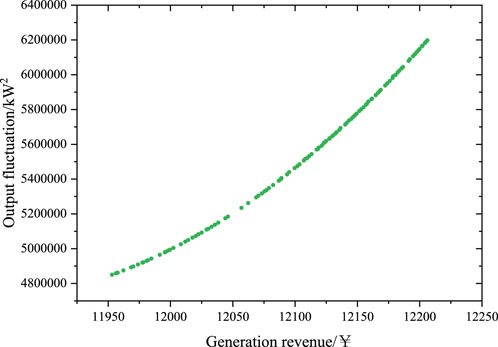
Since the demand for electricity is typically lower at night and higher during the day, the sales price of the combined system is set at 0.2 yuan per kWh from 00:00 to 08:00, while the sales price for the rest of the time is 0.5 yuan per kWh. The multi-objective genetic algorithm (NSGA-II) is applied to solve the dual-objective optimization problem at local dispatch layer (Verma et al., 2021), resulting in the pareto chart shown in Figure 5.

Figure 5

Figure 5. Pareto chart of combined system.

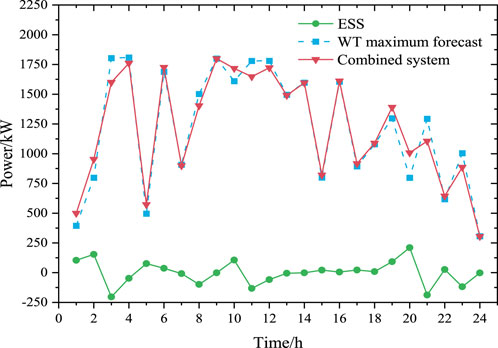
Considering the equal importance of output fluctuation and generation revenue in the combined system, the intermediate value from Figure 5 is selected as the dispatch result of the local dispatch layer. The charging and discharging power of ESS, as well as the output results of the local dispatch layer, are presented in Figure 6. At the local dispatch layer, the generation revenue amounts to 12,107.029 yuan, with an output fluctuation variance of 5506722.607 kW². During the period from 2:00 to 3:00, ESS reaches its maximum charging power of 203.9 kW, whereas ESS reaches its maximum discharging power of 210 kW from 19:00 to 20:00. After the introduction of ESS, the local dispatch layer can significantly reduce the output fluctuation of WT and mitigate the impact on microgrid users.

Figure 6

Figure 6. Output of combined system and ESS.

4.2 Operation results of regional dispatch layer

4.2.1 Centralized optimal dispatch

Under the centralized optimal dispatch model, the regional dispatch layer considers the operation cost of ADN and CCHP multi-microgrid as a common optimization objective. The optimal dispatch results are shown in Figures 7, 8.

Figure 7

Figure 7. Generators output of ADN under centralized optimal dispatch.

Figure 8

Figure 8. Simulation results of CCHP microgrid under centralized optimal dispatch.

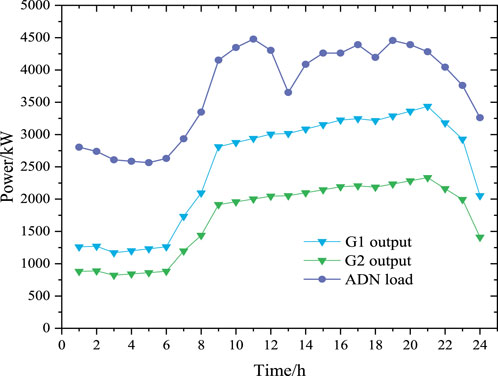
Figure 7 shows the output of two generators maintains the same trend. During the period from 0:00 to 6:00, the output of both generators remains relatively stable. The output of both generators shows a rapid increase from 6:00 to 9:00, while decreasing due to the reduced electric load of ADN from 21:00 to 24:00.

The CCHP microgrid, CCP microgrid, and CHP microgrid can achieve their respective cooling, heating and electric load balance, without wasting energy. The CCHP microgrid is taken as an instance to analyze the results of multi-microgrid. The optimal dispatch results of CCHP microgrid under centralized model will be compared and discussed with the results under distributed model.

4.2.2 Distributed optimal dispatch

The ATC approach is introduced to solve the distributed optimal dispatch model, subsequently yielding the optimal dispatch results of ADN layer and CCHP multi-microgrid layer, as shown in Figures 9–11.

Figure 9

Figure 9. Generators output of ADN under distributed optimal dispatch.

Figure 10

Figure 10. Interaction power between multi-microgrid and ADN.

Figure 11

Figure 11. Simulation results of CCHP microgrid under distributed optimal dispatch.

4.2.2.1 ADN layer

Figure 9 shows the output of two generators varies with the changes in the electric load of ADN. Both generators maintain the identical output levels from 22:00 to 9:00. During the period from 8:00 to 9:00, the output of generator two increases to maximum capacity, and it continues to operate at full capacity from 8:00 to 22:00. During the period from 9:00 to 18:00, the output of generator one alternates between increase and decrease. Whereas generator one generally shows a decreasing trend in power generation from 18:00 to 24:00.

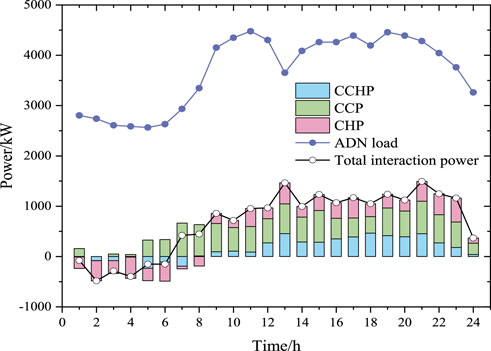
Figure 10 reveals a positive correlation between the total interaction power and the electric load of ADN. Both CCHP and CHP microgrid sell electricity to ADN during the period from 0:00 to 7:00, while purchasing electricity from ADN during other time intervals. In contrast, the CCP microgrid purchases electricity from ADN throughout all time intervals.

4.2.2.2 CCHP multi-microgrid layer

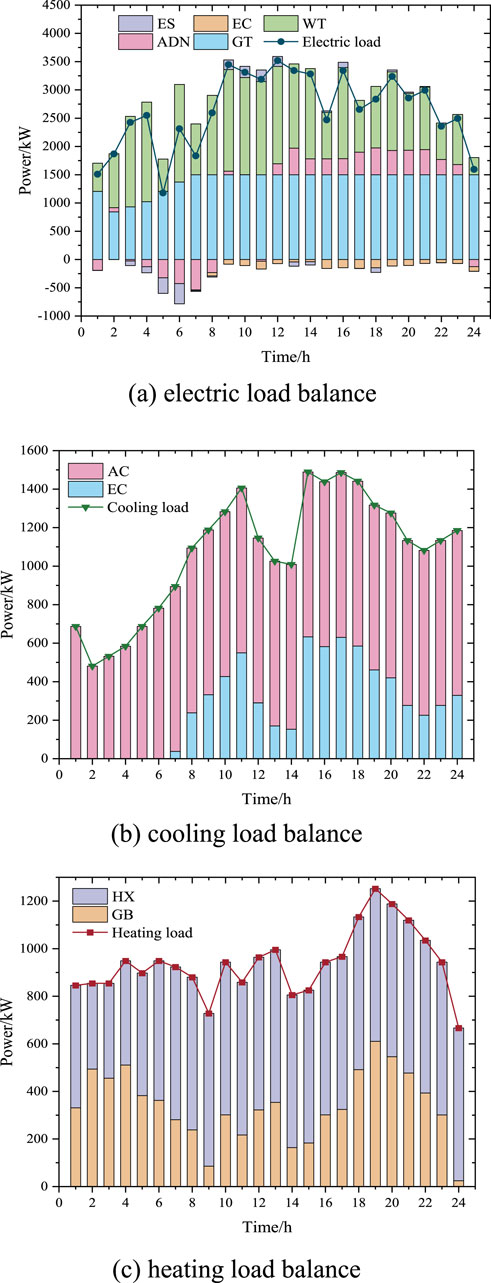
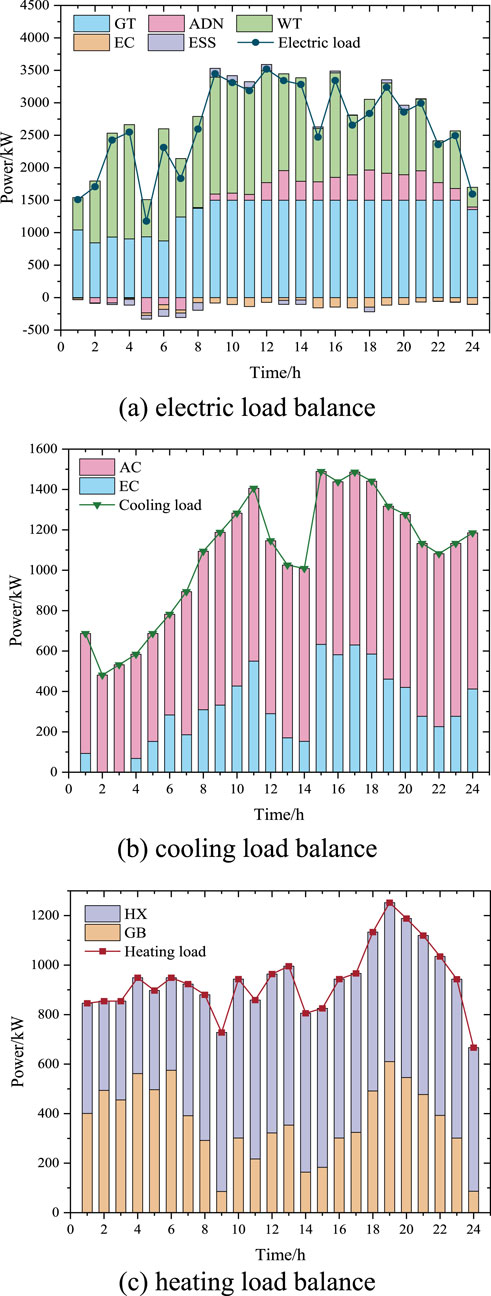
The load balance curve of the CCHP microgrid under distributed optimal dispatch are shown in Figure 11. Figure 11A shows the electric load is balanced by GT, WT, EC, ESS and interaction power with ADN. During the peak electric load period from 8:00 to 23:00, GT operates at its maximum capacity of 1,500 kW. ESS discharges during the peak period from 8:00 to 11:00 and charges during the valley period from 23:00 to 7:00, in accordance with the peak shaving and valley filling functions. The CCHP microgrid sells surplus electricity to ADN from 1:00 to 7:00 and purchases electricity from ADN from 8:00 to 24:00 to meet the electric load.

Figure 11B shows the cooling load is supplied by AC and EC. When the exhaust heat of GT is insufficient to meet the cooling load, supplementary cooling is provided by EC. The output of EC is constrained by the electricity purchase price from ADN, the output capacity of GT, and the cooling load.

Figure 11C shows the heating load is supplied by GB and HX. When the exhaust heat of GT is insufficient to meet the heating load, GB is utilized to fulfill the demand. GB reaches its maximum heating power from 18:00 to 19:00 and its minimum heating power from 8:00 to 9:00.

4.3 Comparative analysis between dispatch models

From the aforementioned optimal dispatch results of the CCHP microgrid under centralized and distributed dispatch models, it is evident that under centralized optimal dispatch, the output of GT is higher at night, resulting in higher interaction power with ADN and charging power of ESS. The cooling load at night is mainly supplied by AC, while EC is not utilized. The dispatch strategy of increasing GT output results in lower total operation cost. The operation cost of CCHP multi-microgrid, ADN, and overall system under two models are presented in Table 4.

Table 4

Table 4. Comparison of centralized and distributed optimal dispatch model.

As shown in Table 4, under centralized optimal model, the total daily operation cost of the system is minimized, yet the cost of multi-microgrid is higher compared to that under distributed optimal model. This suggests that the multi-microgrid may prioritize minimizing the total cost at the expense of its own interests. Under the distributed optimal model, it is possible to refine the benefits between two distinct stakeholders, the distribution network and microgrid only need to transfer the virtual load value of ADN and the virtual source value of CCHP microgrids to obtain the optimal solution, thus protecting the privacy of ADN and CCHP microgrids. While under the centralized optimal model, ADN and CCHP microgrids need to transfer the privacy data of their respective areas, which involves a lot of data.

When the distributed model is solved by ATC, the system operation cost is almost close to that of the centralized model. Meanwhile, the distributed model requires less interactive information, which can enable ADN and CCHP multi-microgrid to achieve their own economic optimality while protecting the privacy of each region. With the promotion of the concept of smart communities, more and more power sellers are entering the market, and the distributed model method proposed in this paper has good applicability.

5 Conclusion

This paper proposes a distributed dispatch model of ADN with CCHP multi-microgrid. In order to overcome the shortcomings of centralized model, ADN and microgrids are regarded as distinct stakeholders to implement energy management of overall system. The analytical target cascading approach is utilized to achieve the solution of distributed optimization. The effectiveness of the proposed strategy is validated through case study, the following conclusions are obtained.

(1) The multiple load in the CCHP multi-microgrid have all reached a balanced state, resulting in full utilization of renewable energy. The output of generators in ADN can satisfy the demand of electric load, power interaction with microgrids, and spinning reverse capacity.

(2) The analytical target cascading approach can reflect the interest game between ADN and multi-microgrid. Under the distributed optimal dispatch, participants are modeled by refined objective functions and constraints. The interaction power is regarded as virtual sources and virtual loads to implement parallel solution.

(3) Simulation results indicate that the distributed dispatch model can achieve simultaneous economic optimum at both ADN and CCHP multi-microgrid in comparison to centralized dispatch model.

This paper does not consider the randomness of wind power and cooling and heating loads, and the equipment model in the actual project is more complex and affected by many factors such as temperature and air pressure. In future research, chance-constrained programming will be used to describe the uncertainty of random variables. The mathematical model of the equipment will be studied in depth to obtain optimal dispatch results closer to the actual project.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YY: Methodology, Software, Writing–original draft. DA: Investigation, Writing–review and editing. LZ: Project administration, Writing–review and editing. YZ: Formal analysis, Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the State Grid Corporation of China Science and Technology Project “Research on multi-objective planning evaluation and demonstration application of collaborative electric heating network in low-carbon industrial parks” (1400-202312333A-1-1-ZN).

Conflict of interest

Authors DA, LZ and YZ were employed by State Grid Tianjin Electric Power Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from State Grid Tianjin Electric Power Company. The funder was involved in the study: design, data collection, and guidance.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ajoulabadi, A., Ravadanegh, S. N., and Mohammadi-Ivatloo, N. B. (2020). Flexible scheduling of reconfigurable microgrid-based distribution networks considering demand response program. Energy 196, 117024. doi:10.1016/j.energy.2020.117024

CrossRef Full Text | Google Scholar

Alam, M. N., Chakrabarti, S., and Ghosh, A. (2019). Networked microgrids: state-of-the-art and future perspectives. IEEE Trans. Ind. Inf. 15 (3), 1238–1250. doi:10.1109/tii.2018.2881540

CrossRef Full Text | Google Scholar

Cheng, Z., Jia, D., Li, Z., Si, J., and Xu, S. (2022). Multi-time scale dynamic robust optimal scheduling of CCHP microgrid based on rolling optimization. Int. J. Electr. Power Energy Syst. 139, 107957. doi:10.1016/j.ijepes.2022.107957

CrossRef Full Text | Google Scholar

Du, Y., Wang, Z., Liu, G., Chen, X., Yuan, H., Wei, Y., et al. (2018). A cooperative game approach for coordinating multi-microgrid operation within distribution systems. Appl. Energy. 222, 383–395. doi:10.1016/j.apenergy.2018.03.086

CrossRef Full Text | Google Scholar

Gao, H., Liu, J., Wang, L., and Wei, Z. (2018). Decentralized energy management for networked microgrids in future distribution systems. IEEE Trans. Power Syst. 33 (4), 3599–3610. doi:10.1109/tpwrs.2017.2773070

CrossRef Full Text | Google Scholar

Ghadi, M. J., Ghavidel, S., Rajabi, A., Azizivahed, A., Li, L., and Zhang, J. (2019). A review on economic and technical operation of Active Distribution Systems. Renew. Sust. Energ. Rev. 104, 38–53. doi:10.1016/j.rser.2019.01.010

CrossRef Full Text | Google Scholar

Gu, W., Wang, Z., Wu, Z., Luo, Z., Tang, Y., and Wang, J. (2017). An online optimal dispatch schedule for CCHP microgrids based on Model Predictive Control. IEEE Trans. Smart Grid. 8 (5), 2332–2342. doi:10.1109/tsg.2016.2523504

CrossRef Full Text | Google Scholar

Guo, J., Tan, J., Li, Y., Gu, H., Liu, X., Cao, Y., et al. (2021). Decentralized incentive-based multi-energy trading mechanism for CCHP-based MG Cluster. Int. J. Electr. Power Energy Syst. 133, 107138. doi:10.1016/j.ijepes.2021.107138

CrossRef Full Text | Google Scholar

Jamali, S., Bahmanyar, A., and Ranjbar, S. (2020). Hybrid classifier for fault location in active distribution networks. Prot. Control Mod. Power Syst. 5 (1), 17. doi:10.1186/s41601-020-00162-y

CrossRef Full Text | Google Scholar

Kabeyi, M. J. B., and Olanrewaju, O. A. (2022). Sustainable energy transition for renewable and low carbon grid electricity generation and supply. Front. Energy Res. 9, 743114. doi:10.3389/fenrg.2021.743114

CrossRef Full Text | Google Scholar

Kargarian, A., Mehrtash, M., and Falahati, B. (2018). Decentralized implementation of unit commitment with analytical target cascading: a parallel approach. IEEE Trans. Power Syst. 33 (4), 3981–3993. doi:10.1109/tpwrs.2017.2787645

CrossRef Full Text | Google Scholar

Kim, H., Lee, J., Bahrami, S., and Wong, V. W. S. (2020). Direct energy trading of microgrids in distribution energy market. IEEE Trans. Power Syst. 35 (1), 639–651. doi:10.1109/tpwrs.2019.2926305

CrossRef Full Text | Google Scholar

Liu, N., Wang, J., and Wang, L. (2019). Hybrid energy sharing for multiple microgrids in an integrated heat–electricity energy system. IEEE Trans. Sustain. Energy. 10 (3), 1139–1151. doi:10.1109/tste.2018.2861986

CrossRef Full Text | Google Scholar

Luna, A. C., Diaz, N. L., Graells, M., Vasquez, J. C., and Guerrero, J. M. (2017). Mixed-integer-linear-programming-based energy management system for hybrid PV-Wind-Battery microgrids: modeling, design, and experimental verification. IEEE Trans. Power Electron. 32 (4), 2769–2783. doi:10.1109/tpel.2016.2581021

CrossRef Full Text | Google Scholar

Luo, Z., Yang, S., Xie, N., Xie, W., Liu, J., Souley Agbodjan, Y., et al. (2019). Multi-objective capacity optimization of a distributed energy system considering economy, environment and energy. Energy Conv. Manag. 200, 112081. doi:10.1016/j.enconman.2019.112081

CrossRef Full Text | Google Scholar

Marvasti, A. K., Fu, Y., DorMohammadi, S., and Rais-Rohani, M. (2014). Optimal operation of active distribution grids: a system of systems framework. IEEE Trans. Smart Grid. 5 (3), 1228–1237. doi:10.1109/tsg.2013.2282867

CrossRef Full Text | Google Scholar

Mohiti, M., Monsef, H., Anvari-moghaddam, A., Guerrero, J., and Lesani, H. (2019). A decentralized robust model for optimal operation of distribution companies with private microgrids. Int. J. Electr. Power Energy Syst. 106, 105–123. doi:10.1016/j.ijepes.2018.09.031

CrossRef Full Text | Google Scholar

Nikmehr, N., and Ravadanegh, S. N. (2015). Optimal power dispatch of multi-microgrids at future smart distribution grids. IEEE Trans. Smart Grid. 6 (4), 1648–1657. doi:10.1109/tsg.2015.2396992

CrossRef Full Text | Google Scholar

Talgorn, B., and Kokkolaras, M. (2017). Compact implementation of non-hierarchical analytical target cascading for coordinating distributed multidisciplinary design optimization problems. Struct. Multidiscip. Optim. 56 (6), 1597–1602. doi:10.1007/s00158-017-1726-0

CrossRef Full Text | Google Scholar

Tan, B., Chen, H., and Zheng, X. (2020). Hierarchical two-stage robust optimisation dispatch based on co-evolutionary theory for multiple CCHP microgrids. IET Renew. Power Gener. 14 (19), 4121–4131. doi:10.1049/iet-rpg.2020.0283

CrossRef Full Text | Google Scholar

Varasteh, F., Nazar, M. S., Heidari, A., Shafie-khah, M., and Catalão, J. P. S. (2019). Distributed Energy Resource and network expansion planning of a CCHP based active microgrid considering demand response programs. Energy 172, 79–105. doi:10.1016/j.energy.2019.01.015

CrossRef Full Text | Google Scholar

Verma, S., Pant, M., and Snasel, V. (2021). A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 9, 57757–57791. doi:10.1109/access.2021.3070634

CrossRef Full Text | Google Scholar

Wang, D., Qiu, J., Reedman, L., Meng, K., and Lai, L. L. (2018). Two-stage energy management for networked microgrids with high renewable penetration. Appl. Energy. 226, 39–48. doi:10.1016/j.apenergy.2018.05.112

CrossRef Full Text | Google Scholar

Wang, Y., Tang, L., Yang, Y., Sun, W., and Zhao, H. (2020). A stochastic-robust coordinated optimization model for CCHP micro-grid considering multi-energy operation and power trading with electricity markets under uncertainties. Energy 198, 117273. doi:10.1016/j.energy.2020.117273

CrossRef Full Text | Google Scholar

Wu, J., Yang, T., Wu, D., Kalsi, K., and Johansson, K. H. (2017). Distributed optimal dispatch of distributed energy resources over lossy communication networks. IEEE Trans. Smart Grid. 8 (6), 3125–3137. doi:10.1109/tsg.2017.2720761

CrossRef Full Text | Google Scholar

Xie, H., Wang, W., Wang, W., and Tian, L. (2022). Optimal dispatching strategy of active distribution network for promoting local consumption of renewable energy. Front. Energy Res. 10, 826141. doi:10.3389/fenrg.2022.826141

CrossRef Full Text | Google Scholar

Xie, M., Ji, X., Hu, X., Cheng, P., Du, Y., and Liu, M. (2018). Autonomous optimized economic dispatch of active distribution system with multi-microgrids. Energy 153, 479–489. doi:10.1016/j.energy.2018.04.021

CrossRef Full Text | Google Scholar

Yan, J., Zhai, Y., Wijayatunga, P., Mohamed, A. M., and Campana, P. E. (2017). Renewable energy integration with mini/micro-grids. Appl. Energy. 201, 241–244. doi:10.1016/j.apenergy.2017.05.160

CrossRef Full Text | Google Scholar

Yang, X., Leng, Z., Xu, S., Yang, C., Yang, L., Liu, K., et al. (2021). Multi-objective optimal scheduling for CCHP microgrids considering peak-load reduction by augmented. Renew. Energy. 172, 408–423. doi:10.1016/j.renene.2021.02.165

CrossRef Full Text | Google Scholar

Zhang, Z., Altalbawy, F. M. A., Al-Bahrani, M., and Riadi, Y. (2023). Regret-based multi-objective optimization of carbon capture facility in CHP-based microgrid with carbon dioxide cycling. J. Clean. Prod. 384, 135632. doi:10.1016/j.jclepro.2022.135632

CrossRef Full Text | Google Scholar

Zhong, J., Li, Y., Cao, Y., Tan, Y., Peng, Y., Zhou, Y., et al. (2023). Robust coordinated optimization with adaptive uncertainty set for a multi-energy microgrid. IEEE Trans. Sustain. Energy. 14 (1), 111–124. doi:10.1109/tste.2022.3203299

CrossRef Full Text | Google Scholar