A multifunctional inverter power quality coordinated optimization strategy based on comprehensive evaluation

The large-scale integration of renewable energy sources and power electronic devices has led to increasingly dispersed and networked characteristics of power quality disturbances in distribution systems. Traditional control devices, limited by their fixed-point control, no longer meet the development needs of modern distribution systems. Considering the distribution and structural characteristics of the current new-type sources and loads, a multifunctional inverter power quality coordinated control strategy based on comprehensive evaluation is proposed. This strategy aims to achieve power quality coordinated control by utilizing optimal compensation capacity while the grid-connected inverter provides active power output. Firstly, the traditional i_pi_q power quality detection method is analyzed and improved to enable detection of harmonics, reactive power, and three-phase imbalance currents in single-phase systems or three-phase four-wire systems. Secondly, in the power quality assessment, a balanced algorithm is employed to obtain the comprehensive evaluation index of power quality, thereby improving the deficiencies of single-weight evaluation. Next, to ensure the grid-connected inverter achieves optimal power quality coordinated control with minimal compensation capacity, an optimization compensation function is established between compensation capacity and comprehensive power quality index. This function is optimized using non-dominated sorting genetic algorithm to enhance equipment utilization and system economy. Finally, the feasibility and effectiveness of the proposed method are validated through simulations, demonstrating the achievement of optimal capacity configuration for power quality coordinated control while ensuring active power output by the grid-connected inverter.

1 Introduction

The substantial integration of renewable energy sources and power electronic devices has led to the emergence of “dual-high” characteristics in power systems. However, with the increasing diversity of source-load types, power quality issues in distribution networks have become more severe, posing significant risks to daily life and production (Zhou et al., 2020; Ratnam et al., 2020; Moghbel et al., 2018). Traditional methods for power quality control primarily involve the installation of additional power quality control equipment. However, the practical placement of such equipment needs to be carefully considered, taking into account factors such as construction, investment, maintenance costs, and inevitable losses during idle operation. Clearly, this approach no longer meets the economic demands of distribution networks (Moghbel et al., 2018; Zhai et al., 2020).

Therefore, in order to ensure the good power quality and governance economy of the distribution network, some scholars put forward the idea of using the coordination ability of photovoltaic, electric vehicles, energy storage and other flexible equipment to carry out collaborative control of power quality (Kumar, 2024; Zanib et al., 2023). Reference (Kumar et al., 2023a) takes into account the difficulty of charging electric vehicles in remote areas, proposes a novel charging adapter topology, which is based on a single current sensor, which further improves the operation economy of distribution network. Reference (Kumar et al., 2023b) introduces a unique adaptive control technique, and an auto-tuned Maximum-power-point tracking (MPPT) control technique for the grid-interfaced photovoltaic (PV) assisted onboard Electric Vehicle (EV) charging infrastructure, which ensures the power management and power quality of photovoltaic and electric vehicles.

At the same time, the power quality of distribution network can be improved by improving the specific control strategy or optimizing the auxiliary service (Saxena et al., 2022). For example, in reference (Kumar et al., 2020), a novel unique FOGI for fundamental component harvesting and HPO for GMPPT have been presented for optimum working behaviour of the integrated grid with a solar PV array, which is partially shaded, undervoltage and waveform distortion of the grid.

In addition, considering that PV power generation systems are highly susceptible to natural environmental factors such as sunlight intensity and temperature, they are typically designed with large capacity margins and operate with significant redundancy. Moreover, grid-connected inverters for renewable energy sources share strong structural and control similarities with control equipment, differing only in output characteristics and control objectives (Sun et al., 2019; Peng et al., 2021; Manrique MacHado et al., 2023). Therefore, multifunctional grid-connected inverters (MFGCI), capable of active power generation, harmonic control, and reactive compensation, have received widespread attention from scholars both domestically and internationally (Wang et al., 2020; Xavier et al., 2019). For instance, utilizing the redundant capacity of grid-connected inverters for harmonic suppression and reactive compensation, or harnessing the coordinated power quality control capability of distributed photovoltaics to manage decentralized power quality disturbances, can not only save space and reduce construction and operating costs but also further improve the equipment utilization of grid-connected inverters (Song et al., 2022; Zhijun et al., 2022; Guo et al., 2024).

Currently, research on MFGCI is relatively scarce, with most focusing on harmonic control and reactive compensation. Moreover, accurately detecting, tracking, and controlling the compensation amount for harmonics, reactive power, and three-phase imbalances in the grid are crucial technical challenges (Jiang et al., 2018). Reference (Jia et al., 2021) proposed a current detection technique for active power filters (APF) without separating positive and negative sequences and reactive currents. Based on the analysis of the topology structure and the construction of an equivalent model, this method utilizes a quasi-proportional resonant control to directly coordinate instruction currents at different frequencies, achieving grid harmonic and reactive power compensation. In addition, Reference (Liang et al., 2018) introduced a novel Discrete Fourier Transform (DFT) algorithm capable of rapidly extracting harmonic components and compensating for harmonic, reactive, and three-phase imbalance components in the grid while considering load types. Furthermore, to ensure the normal operation of MFGCI under voltage imbalance conditions, Reference (Safa et al., 2017) improved the controller for three-phase grid-connected inverters, but still encountered challenges in managing three-phase imbalances.

Meanwhile, due to the limited remaining capacity of inverters, how to optimally manage power quality disturbances using appropriate capacity remains a pressing issue. Reference (Peng et al., 2021) aimed to optimize the power quality level at the Point of Common Coupling (PCC) as the objective function. It optimized the compensation capacity through real-time calculation of optimal compensation currents and secondary weight adjustments and solved it using the Lagrange multiplier method, achieving comprehensive management of power quality at various nodes in microgrids. Reference (Bonaldo et al., 2016), with the objective of minimizing inverter capacity, constrained the post-management comprehensive indicators, enabling flexible adjustment of power quality coordination in microgrids. Reference (Song et al., 2022), considering reactive power and harmonics as the comprehensive indicators for power quality compensation, utilized a multi-objective particle swarm algorithm to obtain the non-dominated set of solutions for optimal comprehensive indicators and minimal management costs, achieving customized power quality indicators at the PCC node. However, the above studies only considered a limited number of power quality indicators such as harmonics and reactive power compensation or optimized compensation using single objectives, without simultaneously considering inverter capacity and multiple power quality indicators, indicating certain shortcomings.

Furthermore, in the process of optimization, it is essential to utilize an appropriate method for comprehensive power quality assessment to establish optimization objectives for power quality and inverter capacity at the PCC node. Currently, both domestic and international scholars have conducted extensive research on comprehensive power quality assessment, primarily integrating multiple evaluation indicators into a single power quality comprehensive indicator by assigning different weights. This approach aims to reflect the overall power quality level of the distribution network (Yingying et al., 2020). Reference (Hongshan et al., 2022) employed the Criteria Importance Through Intercriteria Correlation (CRITC) method to obtain objective weights. Building upon this, they utilized an improved Grey-Technique for Order Preference by Similarity to Ideal Solution (Grey-TOPSIS) method to overcome errors resulting from the single Euclidean distance and fuzzy interval, achieving power quality grading assessment at the PCC node. Reference (Wang et al., 2017) analyzes various power quality indicators, extracts unified parameters for each indicator, calculates subjective and objective weights, and employs projection method to obtain the projection values of boundary data and data to be evaluated, thus determining the power quality level range of the system. However, most current research only considers the influence of a single weight on the evaluation results, potentially leading to significant differences in the excellence levels among indicators and consequently introducing errors in comprehensive evaluation results.

In summary, the stochasticity and volatility of photovoltaic output, along with the uncertainty of loads, lead to frequent fluctuations in power quality and remaining capacity of grid-connected inverters. Addressing the rational establishment of comprehensive power quality indicators and optimal allocation of remaining capacity is imperative. Therefore, this paper proposes a grid-connected inverter power quality cooperative control strategy based on comprehensive weight assessment. Firstly, improvements are made to the traditional i_pi_q method to adapt it to three-phase four-wire systems and accurately measure the harmonic, reactive power, and three-phase imbalance currents at compensation nodes. Secondly, the main and objective weights are determined using the improved Analytic Hierarchy Process (AHP) and the Criteria Importance Through Intercriteria Correlation (CRITIC) method, respectively. The optimal comprehensive weight is then solved using an equilibrium algorithm. Next, based on the idea of matching comprehensive weight indicators with governance capacity, optimization objectives for comprehensive power quality indicators and governance capacity are established. These objectives are solved using the Non-dominated sorting genetic algorithm II (NSGA-II) with an elite strategy. Finally, the feasibility and effectiveness of the proposed method are verified through simulation, providing reference and inspiration for future research on MFGCI.

2 MFGCI control strategy

2.1 Power quality disturbance detection

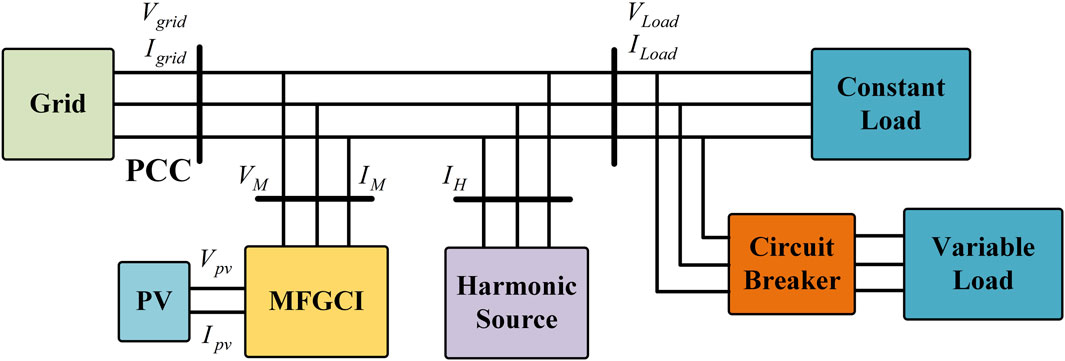
Currently, the detection methods for harmonics and reactive currents primarily fall into two categories: frequency domain methods, represented by Fourier transform and wavelet transform, and time domain methods, represented by analog filters and instantaneous reactive power theory. This paper aims to utilize grid-connected inverters to compensate for harmonics, reactive power, and address the three-phase imbalance issues in cooperative governance systems. However, due to the presence of three-phase imbalance disturbances in the system, traditional detection methods often introduce interference in harmonic detection, leading to inaccurate compensation currents. Therefore, this paper proposes improvements to detection methods based on instantaneous power theory to accurately capture harmonic currents to be compensated, as well as negative or zero-sequence currents in the presence of three-phase imbalance disturbances in the system. The system block diagram is shown in Figure 1.

Figure 1

Figure 1. System block diagram.

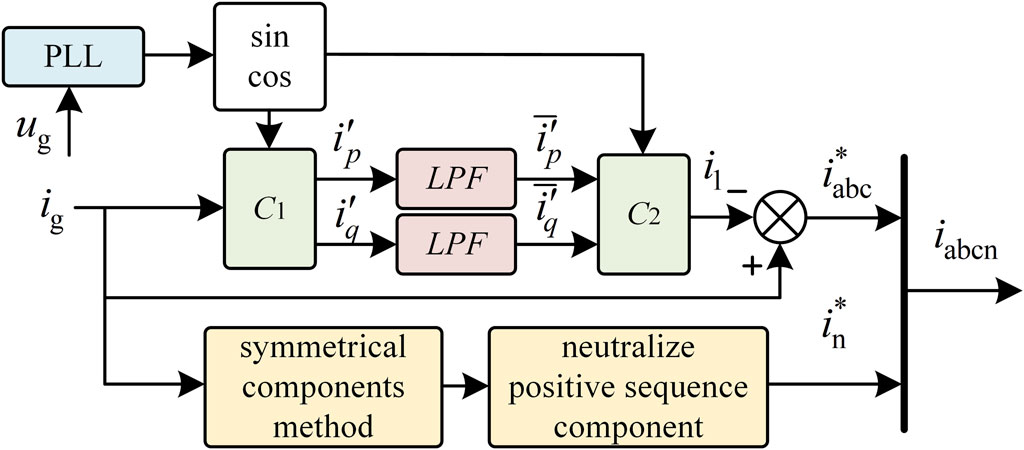
For three-phase four-wire inverters, cooperative governance consists of two parts. First is the compensation of three-phase harmonic and reactive currents, which can be detected using the i_pi_q method (Al-Gahtani et al., 2022). Second is the compensation of neutral current. In this paper, based on the traditional i_pi_q detection method, the symmetrical component method is employed to cancel out the positive-sequence component, resulting in the negative-sequence and zero-sequence currents flowing through the neutral line, thereby obtaining the neutral current compensation. The specific block diagram is shown in Figure 2.

Figure 2

Figure 2. Diagram for harmonic, reactive power, and three-phase imbalance current detection.

In the figure, u_g represents the voltage at the access node, i_g represents the current at the access node, PLL stands for Phase-Locked Loop, LPF denotes Low Pass Filter, i₁ represents the fundamental current, i^*_abc represents the harmonic current, i^*_n represents the neutral line imbalance current, i_abcn represents the compensating current output by the inverter, and C₁, C₂ are as shown in Eqs 1, 2.

$C_1=\left[\begin{array}{c}\cos \left(n{\omega }_{0}t\right)\\ \sin \left(n{\omega }_{0}t\right)\end{array}\right](1)$

$C_2=\left[\begin{array}{cc}2\cos \left(n{\omega }_{0}t\right)& -2\sin \left(n{\omega }_{0}t\right)\end{array}\right](2)$

where ω₀ represents the reference frequency, n represents the harmonic order to be detected, and t represents the corresponding operating time, i’_p and i’_q is instantaneous active current and instantaneous reactive current, respectively. $\overline{i_p^{\prime }}$ and $\overline{i_q^{\prime }}$ are respectively the instantaneous active current and instantaneous reactive current after filtering

The improved i_pi_q method utilized in this paper enables precise detection of any harmonic order in both three-phase four-wire systems and single-phase systems. This method accurately captures all zero-sequence, positive-sequence, and negative-sequence components. By eliminating the positive-sequence component, the neutral current can be obtained, thus determining the harmonic and reactive power components to be compensated, as well as the neutral line imbalance current in the system. This process provides robust support for the subsequent synthesis of command currents for grid-connected inverters.

2.2 Grid-connected command current generation method

Assuming that the active power generated by the grid-connected inverter is P and the reactive power is Q, we can get:

$\left\{\begin{array}{c}P=u_d{i}_d+u_q{i}_q=1.5E_{\mathrm{m}}{I}_{\mathrm{m}}\cos \theta \\ Q=u_q{i}_d-u_d{i}_q=1.5E_{\mathrm{m}}{I}_{\mathrm{m}}\sin \theta \end{array}\right.(3)$

Where u_d, u_q, i_d and i_q represent the d and q-axis components of the terminal voltage and current, respectively. E_m and I_m denote the effective values of the terminal voltage and current, and θ is the angle between them.

Transforming Eq. 3, we obtain Eq. 4:

$\left\{\begin{array}{c}{i}_d=\frac{u_{d}P+u_{q}Q}{u_d^2+u_q^2}\\ i_q=\frac{u_{q}P-u_{d}Q}{u_d^2+{u_q}^2}\end{array}\right.(4)$

The final grid-connected command current is obtained by adding the power command current to the compensation command current, as shown in Eq. 5:

$i_{\text{ref}}^{*}=i_{\text{habcn}}+i_{\text{ref}}(5)$

Where i^*_ref is the output command current of the multifunctional inverter, i_habcn is the compensation command current, and i_ref is the power command current.

In conclusion, the grid-connected command current of the inverter is the sum of the compensation current and the power current. Unlike traditional inverters, multifunctional inverters sacrifice their own output current quality to perform cooperative control over the energy quality in the system. However, further discussion is needed on how to allocate power and perform real-time control.

2.3 Strategy for cooperative control of power quality

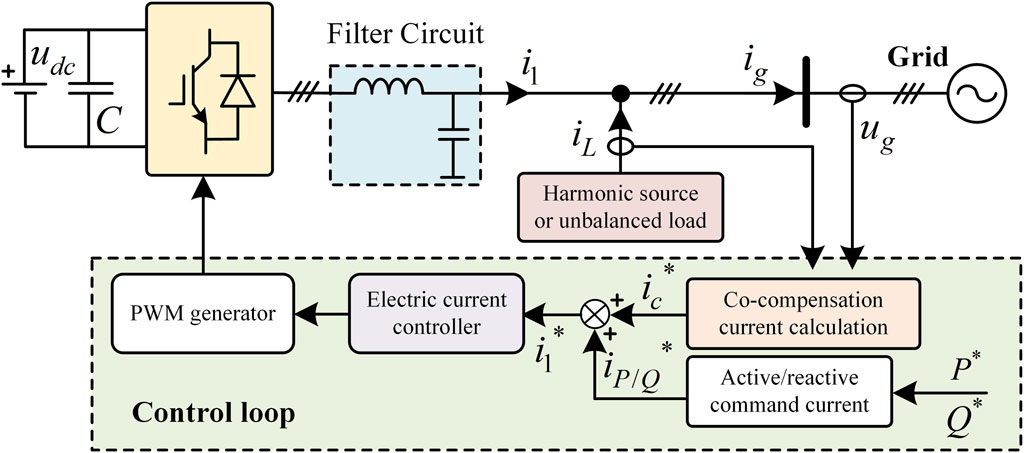
There is no significant difference in the topology between MFGCI and traditional inverters. The difference lies only in the current control section. Moreover, to prevent actual benefits from being compromised, MFGCI should first meet the normal power generation requirements of the system before utilizing the remaining capacity for cooperative power quality control. The control block diagram is shown in Figure 3.

Figure 3

Figure 3. Diagram of multifunctional inverter structure and control strategy.

In the figure, P^* and Q^* represent the specified active power and reactive power, respectively. i_L denotes the load current, i_c represents the inverter output current, u_dc is the source-side voltage, and C denotes the DC-side stabilizing capacitor, i_g indicates the current on the grid side.

3 Determination of composite weight for power quality indices

Based on the aforementioned, the output characteristics of MFGCI, surplus capacity, and power quality disturbances at the PCC node are uncertain. Currently, issues such as the cooperative governance effect and capacity allocation for voltage deviation, harmonics, and three-phase imbalance remain unresolved. Therefore, this paper will establish composite power quality assessment indicators to provide a basis for subsequent optimization objectives for power quality.

3.1 Subjective weight calculation

The AHP is a systematic evaluation method that guides human thinking processes and subjective judgments through standardization and quantification, effectively reducing the influence of numerous uncertainty factors. This method optimizes the process of system analysis and computation, assisting decision-makers in maintaining a consistent mode of thinking during evaluation and decision-making processes. In this paper, the AHP method has been improved, streamlining the process of obtaining hierarchical rankings without the need for consistency checks, significantly reducing computational workload. Furthermore, by only comparing the importance of adjacent criteria, the construction process of the judgment matrix has been optimized, making the importance of each criterion more intuitively clear. The specific steps are as follows:

1) Determine the importance of each power quality indicator and rank them in descending order, as shown in Eq. 6:

$\left\{\begin{array}{cc}{a}_1\mid a_2\mid \dots & \left|a_i\right|\dots \mid a_{n-1}\mid a_n\end{array}\right\}(6)$

Where a_i represents the i-th power quality indicator.

2) Compare adjacent indicators to obtain relative scale values s_i, as shown in Eq. 7:

$\left\{s_1\left|s_2\right|\dots \left|s_i\right|\dots \left|s_{n-2}\right|s_{n-1}\right\}(7)$

Where s_i represents the relative scale value of a_i to a_i+1, with detailed values as per the reference (Liu et al., 2022; Ming et al., 2023).

3) Establish the judgment matrix X for the n indicators, as shown in Eq. 8:

$\mathbf{X}=\left[\begin{array}{cccc}{r}_{11}& r_{21}& \cdots & r_{1m}\\ r_{12}& r_{22}& \cdots & r_{2m}\\ \cdots & \cdots & \cdots & \cdots \\ r_{m1}& r_{m2}& \cdots & r_{mm}\end{array}\right](8)$

4) Determine the subjective weights ω₁ for each indicator, as shown in Eq. 9:

${\omega }_1={}^n\sqrt{{\displaystyle \prod _{i=1}^n}{r}_{ij}}/{\displaystyle \sum _{i=1}^n}{}^n\sqrt{{\displaystyle \prod _{i=1}^n}{r}_{ij}}(9)$

Where r_ij represents the elements of matrix X.

3.2 Objective weight calculation

The CRITIC weighting method is an assessment approach that analyses the information content of evaluation criteria based on two dimensions: comparative intensity and conflict. Comparative intensity measures the differences between evaluation criteria using the concept of mean square deviation, while conflict reflects the correlation between criteria through correlation coefficients. This method integrates the correlation and differences between criteria during the weighting process, effectively overcoming the limitations of entropy weighting by considering the correlation between criteria. As a result, the weighting process becomes more objective and scientific. The specific steps are as follows:

1) Normalize and standardize the collected data to eliminate the influence of different units of measurement for different criteria.

2) Calculate the correlation coefficients for each criterion, as shown in Eq. 10:

${\zeta }_{ij}=\frac{{\displaystyle \sum _{i=1}^{\infty }}\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{{\displaystyle \sum _{i=1}^{\infty }}{\left(x_i-\overline{x}\right)}^2{\displaystyle \sum _{i=1}^{\infty }}{\left(y_i-\overline{y}\right)}^2}}(10)$

In the equation, x_i represents the i-th data point of indicator x, y_i represents the i-th data point of indicator y, which $\overline{x}、\overline{y}$ are the means of the data sets for indicators x and y respectively, and ζ_ij denotes the correlation coefficient between the i-th and j-th indicators.

3) Calculate the information quantity C_j for each indicator, as shown in Eq. 11:

$C_j={\sigma }_j{\displaystyle \sum _{i=1}^n}\left(1-{\zeta }_{ij}\right)(11)$

Where σ_j is the variance of indicator j, and (1-ζ_ij) reflects the conflict between indicators.

4) Calculate the objective weight ω₂ for each indicator, as shown in Eq. 12:

${\omega }_2=C_j/{\displaystyle \sum _{j=1}^n}{C}_j(12)$

3.3 Comprehensive weight of power quality indicators

In the field of power quality assessment, relying solely on subjective weights may overlook the disturbance probability and stochastic characteristics of power quality indicators in different operating conditions. Similarly, relying solely on objective weights may ignore the potential impact and hazards of each indicator, thereby reducing the accuracy of power quality assessment. To address the limitations of single-weight assessment accuracy, this paper utilizes a game equilibrium algorithm to solve comprehensive weights. This algorithm integrates subjective preferences based on expert judgment or user requirements with probability information from objective data, thereby enhancing practicality and accuracy in real-world scenarios. The specific steps are as follows:

1) Constructing the comprehensive weight ω. The comprehensive weight ω can be linearly represented by the subjective weight ω₁ and the objective weight ω₂, as shown in Eq. 13:

$\omega =a{\omega }_1+b{\omega }_2(13)$

Where a and b are the combination coefficients of subjective and objective weights, respectively.

2) To solve the combination coefficients, we formulate an objective function and constraints based on game theory, aiming to minimize the deviations between the subjective, objective, and combined weights. The expression is shown in Eq. 14:

$\left\{\begin{array}{c}\begin{array}{l}\min \left(‖a{\omega }_1^T+b{\omega }_2^T-{\omega }_1^T‖+‖a{\omega }_1^T+b{\omega }_2^T-{\omega }_2^T‖\right)\\ {\displaystyle \sum _{i=1}^m}{\omega }_i=1\\ {\omega }_i\ge 0\end{array}\\ s.t.a+b=1a,b\ge 0\end{array}\right.(14)$

4 MFGCI multi-objective optimization compensation strategy

4.1 Method for corresponding electric power quality indices with capacities

For additional requirements for specific article types and further information please refer to “Article types” on every Frontiers journal page.

In the aspect of coordinated control of electric power quality, due to the differences in disturbance characteristics and dimensions of various electric power quality indices, it is difficult to directly optimize them using multi-objective algorithms. Therefore, this paper proposes a method to calculate the correspondence between electric power quality indices and compensation capacities. Specifically, it is as follows.

The nodal Jacobian matrix J can be determined from the system’s load flow correction equations, as shown in Eq. 15. Inverting it yields the voltage-power sensitivities of each node, represented by the sensitivity matrix as shown in Eq. 16.

$\left[\begin{array}{c}\Delta P\\ \Delta Q\end{array}\right]=J\left[\begin{array}{c}\Delta \theta \\ \frac{\Delta U}{U}\end{array}\right]=\left[\begin{array}{cc}\frac{\partial P}{\partial \delta }& \frac{\partial P}{\partial U}\\ \frac{\partial Q}{\partial \delta }& \frac{\partial Q}{\partial U}\end{array}\right]\left[\begin{array}{c}\Delta \delta \\ \frac{\Delta U}{U}\end{array}\right](15)$

In the equations, ΔP represents the active power change, ΔQ represents the reactive power change, Δδ represents the voltage phase change, ΔU represents the voltage magnitude change, U is the actual voltage at the grid side.

${\left[J_{\text{aco}}\right]}^{-1}=\left[\begin{array}{cc}\partial \delta /\partial P& \partial \delta /\partial Q\\ \partial U/\partial P& \partial U/\partial Q\end{array}\right](16)$

In the equations, $\partial \delta /\partial P$ represents the sensitivity of active power with respect to voltage phase, $\partial \delta /\partial Q$ represents the sensitivity of reactive power with respect to voltage phase, represents the sensitivity of active power with respect to voltage magnitude, and $\partial U/\partial Q$ represents the sensitivity of reactive power with respect to voltage magnitude.

According to the active-reactive voltage sensitivity, the voltage deviation f₁ after coordinated control of grid-connected inverters can be obtained, as shown in Eq. 17:

$f_1=\frac{\Delta U-{\alpha }_1{S}^{*}\frac{\partial U}{\partial Q}}{U_N}(17)$

In the equation, ΔU represents the magnitude of the voltage deviation before control, S^* denotes the compensating capacity used by the grid-connected inverter for coordinated power quality control, and α₁ is the voltage deviation compensation coefficient, U_N indicates the rated voltage of the power grid side.

Assuming the harmonic compensation current is I^*_h, according to circuit principles, its compensation capacity is related to the compensation current as follows:

${I_h}^{*}=\frac{3U{I_h}^{*}}{3U}=\frac{{S_h}^{*}}{3U}(18)$

In the equation, U represents the actual voltage at the PCC, and S^*_h represents the harmonic compensation capacity.

From Eq. 18, the harmonic index f₂ and the three-phase imbalance f₃ after coordinated control of the grid-connected inverter can be obtained as shown in Eq. 19:

$\begin{array}{l}{f}_2=\frac{I_h-{\alpha }_2{S}^{*}/U}{I_1}\\ f_3=\frac{I_n-{\alpha }_3{S}^{*}/U}{I_1}\end{array}(19)$

In the equation, α₂ and α₃ represent the harmonic compensation coefficient and the three-phase imbalance compensation coefficient, respectively. I₁ denotes the actual fundamental current, I_h stands for the harmonic monitoring current, and I_n represents the neutral current monitoring.

4.2 Multi-objective optimization compensation strategy

When harnessing the surplus capacity of inverters for coordinated power quality control, three aspects need to be considered. Firstly, without affecting their active power output characteristics, it is essential to utilize the minimum surplus capacity for optimal control. Secondly, to ensure the equipment operates safely and stably, a certain margin of capacity should be retained. Thirdly, efforts should be made to ensure that all indicators remain within the national standards. Based on these requirements and the analysis above, a multi-objective optimization model for inverters can be established, as shown in Eq. 20:

$\begin{array}{l}\left\{\begin{array}{l}\min F_1={\omega }^{\left(1\right)}{f}_1+{\omega }^{\left(2\right)}{f}_2+{\omega }^{\left(3\right)}{f}_3\\ \min F_2=\sqrt{{\left({\alpha }_1{S}^{*}\right)}^2+{\left({\alpha }_2{S}^{*}\right)}^2+{\left({\alpha }_3{S}^{*}\right)}^2}\end{array}\right.\\ s.t.\left\{\begin{array}{l}0\le \sum {\alpha }_i\le 1\\ 0\le S^{*}\le 0.9S\\ f_1\le {f_1}^{*}\\ f_2\le {f_2}^{*}\\ f_3\le {f_3}^{*}\end{array}\right.\end{array}(20)$

Where, ω⁽ⁱ⁾ represents the comprehensive weights corresponding to each indicator; α_i denotes the compensation coefficients for each indicator; and f^*_i stands for the prescribed limits specified by national standards for each indicator.

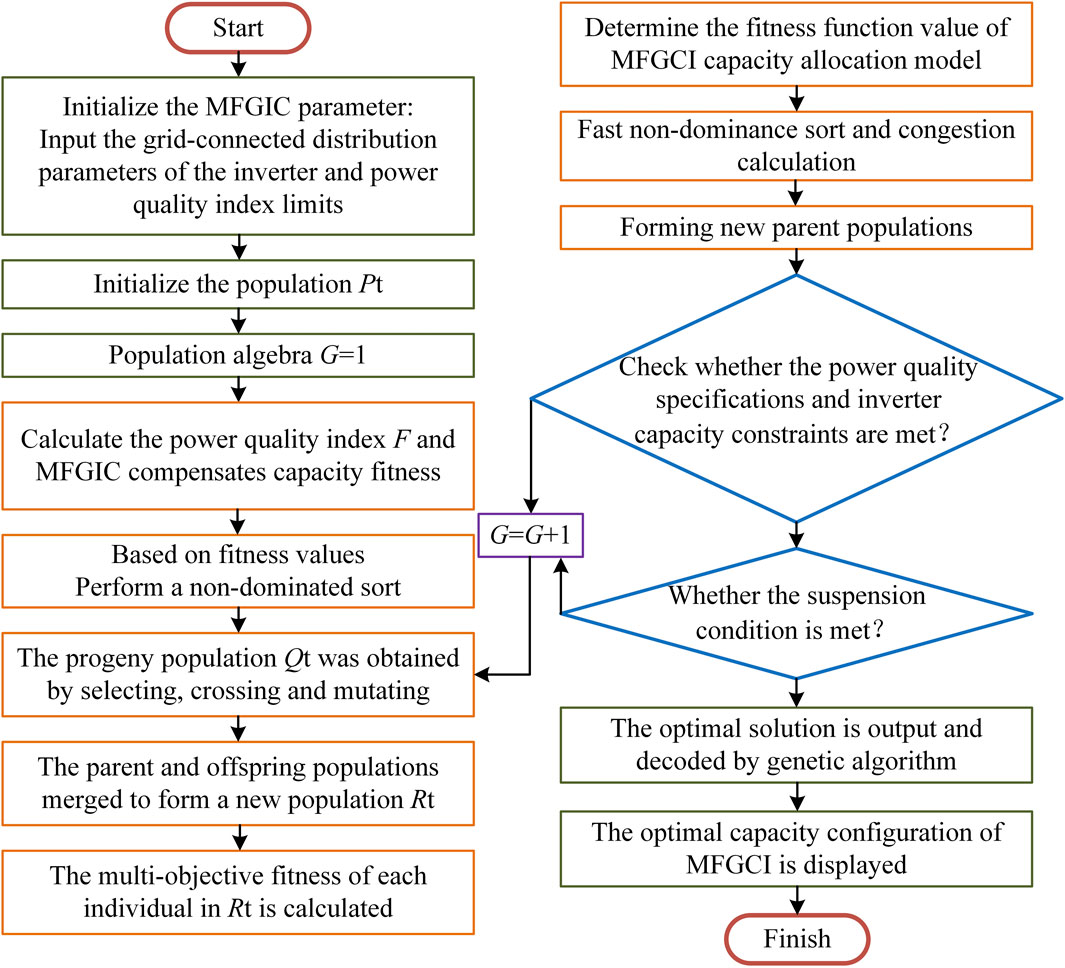
In the comprehensive evaluation and optimization of power quality, there exists a significant trade-off relationship between these two optimization objectives, making it difficult to quantify their relative importance. Therefore, it is not appropriate to simplify this optimization problem into a single-objective optimization problem, but rather it requires the use of effective methods for resolution. NSGA-II, as a novel multi-objective optimization algorithm, has been widely applied in power system generation capacity planning, optimization configuration of new energy sources, and energy storage (Guo et al., 2022; Honghai et al., 2022; Linlin et al., 2022). Given the dynamic operating state of MFGCI, this study employs the NSGA-II algorithm to co-optimize their capacity and power quality, aiming to obtain the Pareto optimal solution set. Based on the practical application scenario requirements, the optimal solution is selected from this set to achieve the optimal configuration of both MFGCI capacity and power quality. The process flowchart is illustrated in Figure 4, with specific steps outlined as follows:

1) Parameter Initialization: Given the parameters of the multifunctional grid-connected inverter, set the objective functions and constraints, including the ranges of voltage deviation, harmonic, and three-phase imbalance compensation coefficients, as well as the limits of each index. Set the population size N, maximum genetic generations G_m, crossover probability P_c, and mutation probability P_m for the NSGA-II algorithm. Initialize the population and generate a population P_t of size N.

2) Fitness Calculation and Nondominated Sorting: Calculate the fitness of individuals in the population for each power quality index and compensation capacity, and perform nondominated sorting on the population to determine the superiority of each individual.

3) Genetic and Mutation Operations: Use selection, single-point crossover, and uniform mutation operations to evolve the population, resulting in a new offspring population Q_t of size N.

4) Population Merging and Selection of New Parent Population: Merge the parent population P_t and offspring population Q_t to form a population R_t of size 2N. Perform fast nondominated sorting and crowding distance calculation on R_t, and select N individuals from R_t based on nondominated relationships and individual crowding distances to form a new parent population.

5) Iteration Process: Repeat steps (3) and (4) until reaching the maximum genetic generations G_m. Output the Pareto optimal solution set and obtain the optimal voltage deviation, harmonic, and three-phase imbalance compensation coefficients.

Figure 4

Figure 4. NSGA-Ⅱ algorithm Flowchart.

5 Simulation verification and analysis

To validate the rationality of the proposed method for obtaining comprehensive weights of power quality and the effectiveness and feasibility of the multi-objective optimization method, simulation experiments were conducted using Matlab/Simulink software. The system was configured with a rated voltage of 220 V, a rated frequency of 50 Hz, line impedance parameters of 0.35 + 0.28j, a capacity of 30 kVA for the grid-connected photovoltaic inverter, which operates in two modes: MPPT flexible power tracking and constant power tracking. The switching frequency was set to 20 kHz, the bus rated voltage was 800 V, the filter inductance was 1.5 mH, the filter capacitance is 32.8 µF, and the damping resistance is 2.6 Ω. The simulation step size was set to 1 ns. The topology structure was as shown in the previous Figure 1. The simulation model included the connection of three-phase unbalanced loads and uncontrollable power electronic devices to simulate the actual operation scenarios of harmonics and three-phase imbalances in the system.

5.1 Full compensation

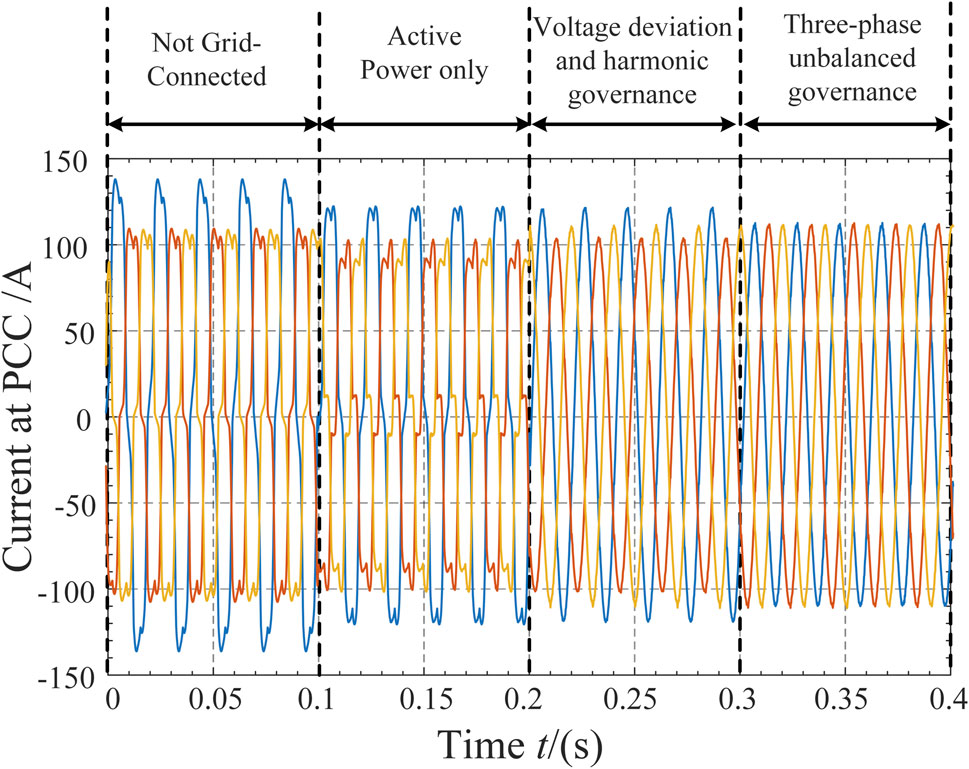
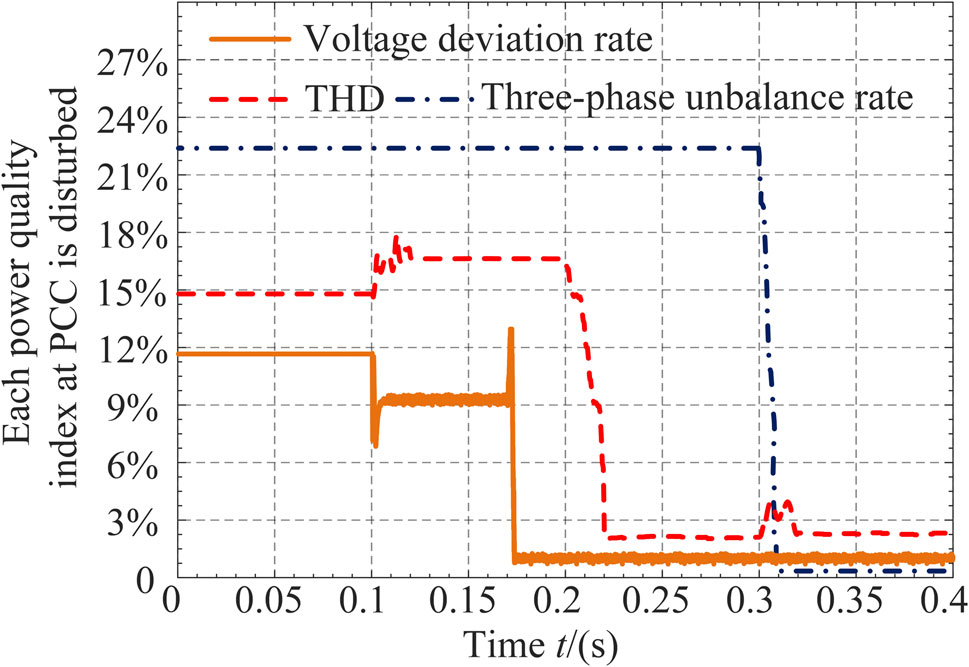
To verify the MFGCI in compensating for harmonic, three-phase imbalance, and voltage deviation issues while outputting active power, assume the following conditions: under sufficient sunlight and suitable temperature, the grid-connected inverter has an active power output of 15 kW. The uncontrollable power electronic rectifier load is 2 mH + 10 Ω. The unbalanced load power for phases ABC is respectively 20 kW, 5 kW, and 5 kW. The simulation experiment proceeds as follows: Before 0.1 s, the photovoltaic system is not grid-connected. At 0.1 s, the PV system starts grid connection. At 0.2 s, full compensation for harmonic and reactive power is applied. At 0.3 s, full compensation for three-phase imbalance is applied. The current waveform at PCC Node 1 is shown in Figure 5, and the various disturbances in electrical power quality are depicted in Figure 6.

Figure 5

Figure 5. The current waveform at the PCC under full compensation.

Figure 6

Figure 6. Power quality disturbances at the PCC node under full compensation.

As shown in Figures 5, 6, during the period from 0 to 0.1 s, the MFGCI did not perform coordinated power quality control. Consequently, there was significant waveform distortion at the PCC node, with the THD around 15%, the three-phase current imbalance reaching 23%, and the voltage deviation rate hitting 10.91%, indicating poor overall power quality.

At 0.1 s, the PV system’s grid connection resulted in the output of a certain amount of active power, causing an uplift effect on the voltage at the PCC node. This reduced the voltage deviation rate from 10.91% to 5.45%. However, due to the harmonic distortion present in the grid-side waveform, the PLL was affected, leading to a roughly 2% increase in harmonics, reaching 17.34%.

At 0.2 s, the MFGCI implemented coordinated control for harmonic and reactive power compensation. This reduced the harmonic distortion rate at the grid connection point from 14.7% to below 2%. Due to the small system size, the reactive power compensation effect was significant, reducing the voltage deviation rate at the grid connection point to less than 1% after compensation.

At 0.3 s, the multifunctional converter performed three-phase unbalanced current compensation at the grid connection node. The neutral current was reduced from 20A to almost 0A, effectively eliminating the three-phase current imbalance disturbances.

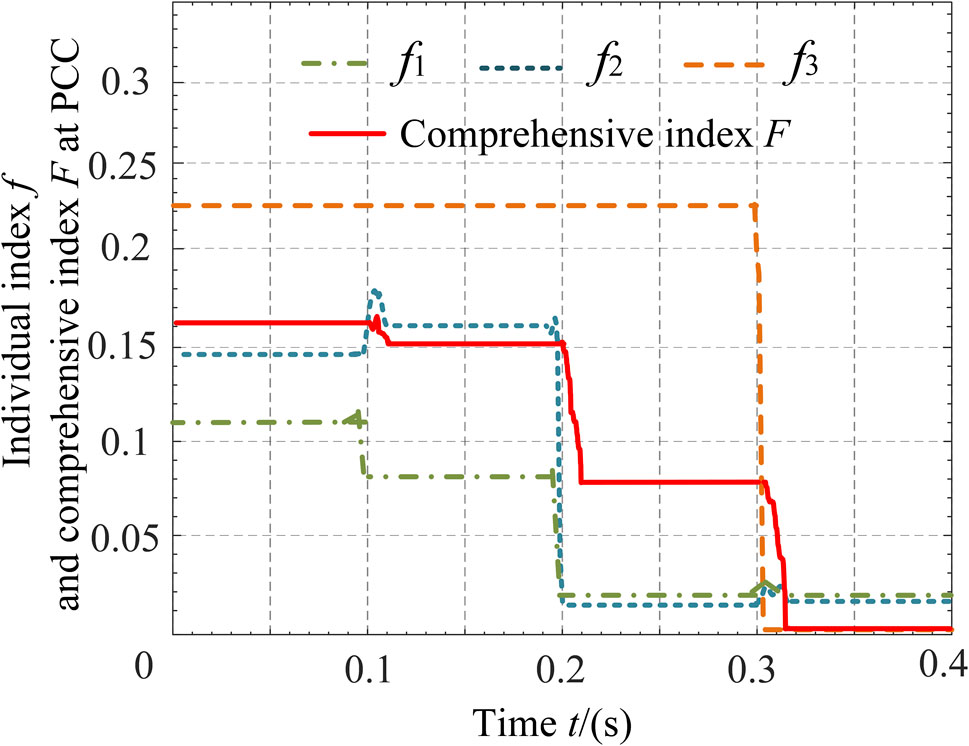
Figure 7 shows the comprehensive and individual power quality disturbance indicators at the PCC node. From Figure 7, it can be observed that when MFGCI is not engaged in coordinated control, the comprehensive power quality indicator F₁ is 0.1611. The effect of voltage rise and harmonic disturbance after the photovoltaic grid connection at 0.1 s reduces F₁ to 0.1502. After compensating for harmonics and voltage deviation at 0.2 s, F₁ decreases to 0.0730. Following the management of three-phase imbalance at 0.3 s, F₁ further reduces to 0.0105. Notably, the voltage deviation is only 0.91%, harmonics are at 1.73%, and the three-phase current imbalance is close to 0%. Overall, under full compensation, the power quality level at the PCC node far exceeds the national standard requirements.

Figure 7

Figure 7. Individual and comprehensive indicators at the PCC node under full compensation.

However, in the case of full compensation, the total capacity of the inverter is 30 kVA, 15 kW is used for active power output, 11.75 kVar is used for power quality collaborative governance, of which 3.3 kVar is used for reactive power compensation, 3.87 kVar is used for harmonic governance, 4.58 kVar is used for three-phase unbalance current compensation, and the residual margin is 3.25 kVA. Meet capacity redundancy requirements. However, it is obvious that if the stronger light intensity leads to greater active power output or more severe power quality disturbance, the required capacity must be greater than the rated capacity of the inverter, and the full compensation strategy will be difficult to deal with such problems, so it is urgent to propose a MFGCI capacity allocation strategy that adapts to different application scenarios.

5.2 Multi-objective optimization compensation

To verify the feasibility and effectiveness of the multi-objective optimization method proposed in this paper, simulation verification is conducted and compared with the case of full compensation. The parameters design of NSGA-II is as shown in Table 1, and the rest of the simulation parameters remain consistent with full compensation.

Table 1

Table 1. NSGA-II and indicator constraint parameters settings.

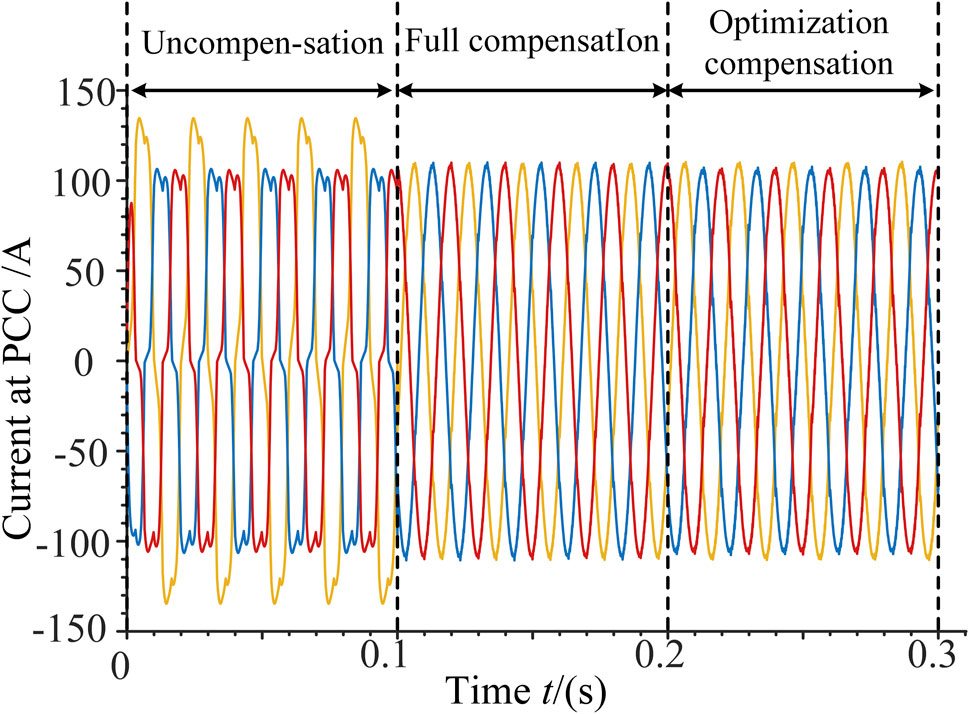
The Pareto Frontier of multi-objective optimization for MFGCI’s coordinated control capacity in terms of electric power quality, using NSGA-II, is shown in Figure 8. As seen in Figure 8A, when F₂ = 0, indicating no coordinated control, the comprehensive electric power quality index F₁ reaches its maximum value of 0.161; as F₂ increases, the corresponding F₁ decreases. When the input capacity is 11.8 kVA, corresponding to full compensation, F₁ decreases to 0, which is consistent with the full compensation mentioned earlier. Considering the limited residual capacity of MFGCI, it is necessary to optimize the compensation coefficients α_i based on the relationship between F₁ and F₂ on the Pareto boundary and actual operating conditions. Figure 8B illustrates the relationship between the electric power quality comprehensive index F₁ and the optimal compensation coefficients α_i determined by NSGA-II. Based on the desired value of F₁ set to 0.02, the optimal compensation coefficients satisfying the Pareto Frontier are obtained as follows: α₁ = 0.17; α₂ = 0.27; α₃ = 0.21. To visually assess the effectiveness of the optimized electric power quality coordinated control, the compensation strategies before and after optimization are segmented for simulation as follows: no compensation from 0 to 0.1 s, full compensation from 0.1 to 0.2 s, and optimized compensation from 0.2 to 0.3 s. The current waveforms of MFGCI under different modes are shown in Figure 9.

Figure 8

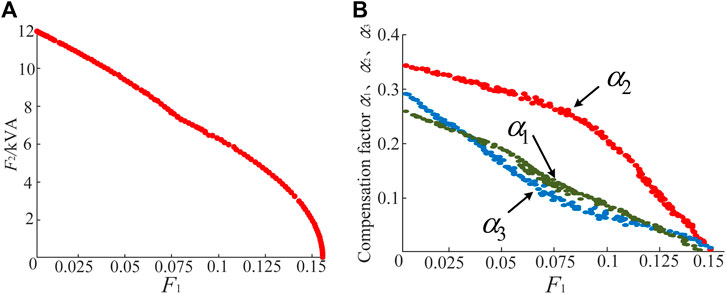
Figure 8. (A) Pareto Frontier of NSGA-Ⅱ solution; (B) The relation of each compensation coefficient of NSGA-II solution.

Figure 9

Figure 9. The current waveform at the PCC node varies under different strategies.

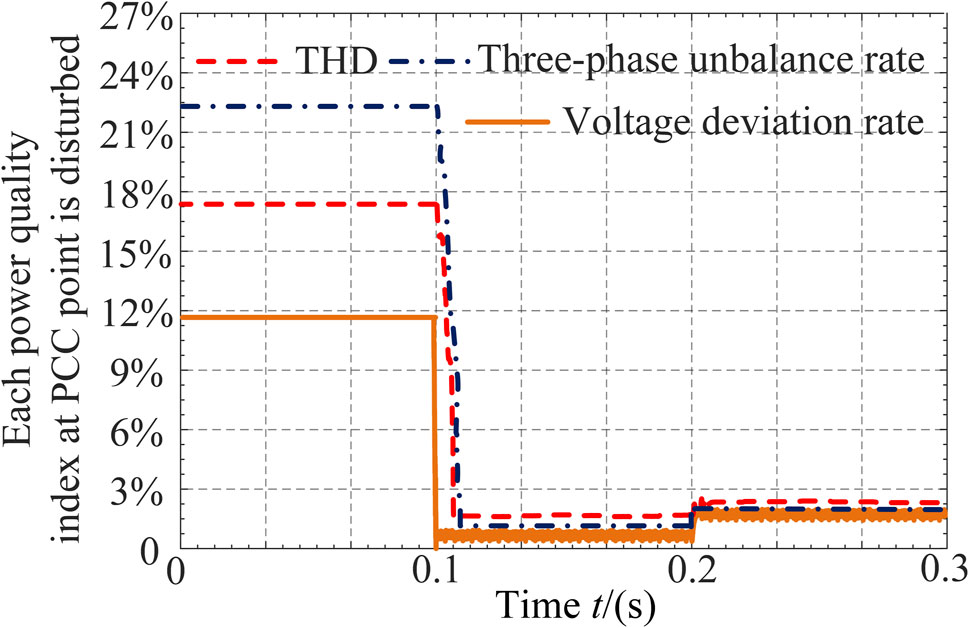
As shown in Figures 9, 10, during the initial stage from 0 to 0.1 s, the grid-connected inverter had not yet implemented power quality coordinated management. Due to the integration of nonlinear devices, the current harmonic distortion at the PCC node reached 17.56%. The three-phase current imbalance reached 22.87% due to asymmetric loads, and the voltage deviation rate at the grid connection node reached 11.65% due to line losses and equipment power demands, indicating poor overall power quality.

Figure 10

Figure 10. Power quality indicators at PCC nodes under different strategies.

At 0.1 s, the grid-connected inverter fully compensated for power quality disturbances at the PCC node. Analysis shows that the current at the PCC node became nearly a standard sine wave. The combined action of active and reactive power increased the node voltage at the PCC, reducing the voltage deviation rate to 0.91%, the harmonic content to 1.73%, and the three-phase current imbalance to 1.04%.

At 0.2 s, the inverter employed an optimized compensation strategy. The analysis indicates that, compared to the full compensation strategy, the optimized compensation strategy resulted in a slight increase in power quality disturbances. The voltage deviation rate rose from 0.91% to 1.61%, the harmonic content from 1.73% to 2.46%, and the three-phase current imbalance from 1.04% to 1.87%. However, considering the optimized compensation coefficients, the compensation capacity required by the inverter decreased by 2.75 kVA, and the compensation efficiency improved by approximately 20%.

The various power quality disturbances under different strategies are shown in Figure 10, while the power quality comprehensive index F₁ is depicted in Figure 11. It can be observed from Figures 10, 11 that under the optimized compensation strategy, although there are still slight power quality disturbances at the PCC node, they are generally consistent with the set target values. Compared to the full compensation strategy, the power quality comprehensive index F under the optimized compensation strategy only increases by around 0.01, while saving 2.75 kVA of compensation capacity, leading to a 20% increase in the utilization rate of remaining capacity. Moreover, compared to directly installing power quality control devices, this strategy saves construction costs by utilizing 9 kVA of capacity and ensures that the power quality index after compensation fully meets national standards.

Figure 11

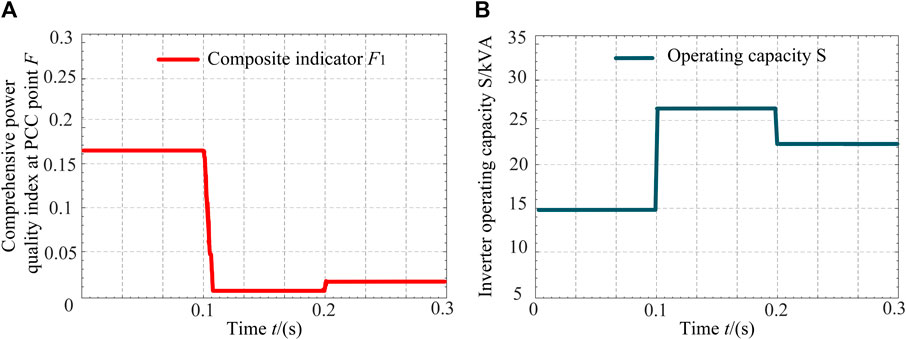
Figure 11. (A) Comprehensive index at PCC under two strategies; (B) MFGCI operating capacity at PCC under two strategies.

The simulation results above validate the feasibility and effectiveness of the proposed multi-functional inverter capacity optimization strategy in this paper. This enables MFGCI to effectively utilize its remaining capacity to coordinate the management of power quality disturbances while delivering active power. Moreover, it can adjust compensation coefficients according to actual operating conditions and the level of power quality supply and demand, thereby providing a high-quality power supply level for the distribution network.

6 Conclusion

This paper proposes a coordinated optimization control strategy for multifunctional inverters based on comprehensive weight evaluation. This strategy aims to address power quality issues such as voltage deviation, harmonics, and three-phase imbalance in the distribution network through the coordinated control of multifunctional converters. The traditional i_pi_q method is improved to make it suitable for detecting power quality disturbances in three-phase four-wire systems and single-phase systems, further achieving the acquisition of grid-connected command current. Then, the improved AHP and CRITIC methods are used to determine subjective and objective weights, respectively. The comprehensive weight is obtained using a game equilibrium algorithm, addressing the limitations of using a single weight evaluation. Furthermore, based on the method of corresponding power quality indices and capacity, the NSGA-II algorithm is employed to obtain the optimal compensation coefficients, ensuring optimal allocation between comprehensive power quality indices and capacity distribution while maintaining active power output. Simulations verify the feasibility and effectiveness of the proposed method, showing that the optimized compensation method proposed in this paper improves equipment utilization by 20% and enhances economic benefits.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YL: Conceptualization, Funding acquisition, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. JL: Conceptualization, Methodology, Resources, Software, Validation, Writing–original draft, Writing–review and editing. LW: Conceptualization, Formal Analysis, Methodology, Supervision, Writing–original draft, Writing–review and editing. YZ: Conceptualization, Data curation, Methodology, Writing–original draft, Writing–review and editing. YX: Validation, Writing–original draft, Writing–review and editing. LQ: Project administration, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by State Grid Fujian Power Co., Ltd. Science and technology project (52130423000R).

Acknowledgments

The authors are very grateful to State Grid Fujian Electric Power Co., Ltd. Science and technology project. (Research on power quality active control technology of power distribution system adapted to large-scale new source load access, 52130423000R) for its support in fund and data.

Conflict of interest

Authors YL, JL, LW, and YZ were employed by State Grid Fujian Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from State Grid Fujian Power Co., Ltd. Science and technology project. The funder had the following involvement in the study: study design, data collection and analysis, and publication decisions.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Gahtani, S. F., Salem, E. Z. M., Irshad, S. M., and Azazi, H. Z. (2022). Improved instantaneous reactive power (PQ) theory based control of DVR for compensating extreme sag and swell. IEEE Access 10, 75186–75204. doi:10.1109/access.2022.3185662

CrossRef Full Text | Google Scholar

Bonaldo, J. P., Paredes, H. K. M., and Pomilio, J. A. (2016). Control of single-phase power converters connected to low-voltage distorted power systems with variable compensation objectives. IEEE Trans. POWER Electron. 31 (3), 2039–2052. doi:10.1109/tpel.2015.2440211

CrossRef Full Text | Google Scholar

Guo, Y., Zhu, X., Deng, J., Li, S., and Li, H. (2022). Multi-objective planning for voltage sag compensation of sparse distribution networks with unified power quality conditioner using improved NSGA-III optimization. Energy Rep. 8, 8–17. doi:10.1016/j.egyr.2022.08.120

CrossRef Full Text | Google Scholar

Guo, W., Xu, W., Long, L., Mengyan., Z, Xuzhe, L., Ke., C, et al. (2024). Optimization method of reactive power and harmonic for photovoltaic multi-function grid-connected inverter under different output states. Electr. Power Autom. Equip. 44 (01), 80–87. doi:10.16081/j.epae.202212022

CrossRef Full Text | Google Scholar

Honghai, K., Fuqing, S., Yurui, C., Kai, W., and Zhiyi, H. (2022). Reactive power optimization for distribution network system with wind power based on improved multi-objective particle swarm optimization algorithm. Electr. POWER Syst. Res. 213, 108731. doi:10.1016/j.epsr.2022.108731

CrossRef Full Text | Google Scholar

Hongshan, Z, Jingxuan, L., Zengqiang, M., Liang, P., and Yangyang, C. (2022). Grading evaluation of power quality based on CRITIC and improved Grey-TOPSIS. Power Syst. Prot. Control 50 (03), 1–8. doi:10.19783/j.cnki.pspc.210386

CrossRef Full Text | Google Scholar

Jia, L, Qunjing, W., Maosong, Z., and Guoli, L. (2021). Research on quasi-proportional resonance control of LCL three-phase four-wire APF. Power Electron. 55 (05), 4–7+77.

Google Scholar

Jiang, Y., Zou, M., Chen, J., and Yilong, C. (2018). Research on control and flexible customization strategy of multi-function grid-connected inverter. Power Electron. 52 (12), 102–106.

Google Scholar

Kumar, N., Saxena, V., Singh, B., and Panigrahi, B. K. (2020). Intuitive control technique for grid connected partially shaded solar PV-based distributed generating system. IET Renew. Power Gener. 14 (4), 600–607. doi:10.1049/iet-rpg.2018.6034

CrossRef Full Text | Google Scholar

Kumar, N., Singh, H. K., and Niwareeba, R. (2023a). Adaptive control technique for portable solar powered EV charging adapter to operate in remote location. IEEE Open J. Circuits Syst. 4, 115–125. doi:10.1109/ojcas.2023.3247573

CrossRef Full Text | Google Scholar

Kumar, N., Saxena, V., Singh, B., and Panigrahi, B. K. (2023b). Power quality improved grid-interfaced PV-assisted onboard EV charging infrastructure for smart households consumers. IEEE Trans. Consumer Electron. 69 (4), 1091–1100. doi:10.1109/tce.2023.3296480

CrossRef Full Text | Google Scholar

Kumar, N. (2024). EV charging adapter to operate with isolated pillar top solar panels in remote locations. IEEE Trans. Energy Convers. 39 (1), 29–36. doi:10.1109/tec.2023.3298817

CrossRef Full Text | Google Scholar

Liang, T., Junzhao, C., Wenxi, W., and Jinwu, G. (2018). Comprehensive compensation device for power quality based on distributed photovoltaic inverter. Electr. Meas. Instrum. 55 (16), 51–56+77.

Google Scholar

Linlin, Y., Lihua, Z., Gaojun, M., Feng, Z., and Wanxun, L. (2022). Research on multi-objective reactive power optimization of power grid with high proportion of new energy. IEEE Access 10, 116443–116452. doi:10.1109/access.2022.3219435

CrossRef Full Text | Google Scholar

Liu, G., Zhang, C., Zhu, Z., and Wang, X. (2022). Power quality assessment based on rough AHP and extension analysis. Energy Eng. 119 (3), 929–946. doi:10.32604/ee.2022.014816

CrossRef Full Text | Google Scholar

Manrique MacHado, S. D. J., Da Silva, S. A. O., Monteiro, J. R. B. D., Sampaio, L. P., and de Oliveira, A. A. (2023). Analysis of a multifunctional inverter active-filtering function influence on the small-signal stability of inverter-based islanded AC microgrids. IEEE Trans. INDUSTRIAL Electron. 70 (8), 8108–8117. doi:10.1109/tie.2022.3222630

CrossRef Full Text | Google Scholar

Ming, Z, Ruoping, X. I. A., Shilu, X. U., and Yisheng, H. (2023). Comprehensive evaluation of power quality based on variation coefficient synthetic weighting of subjective and objective weights. Mod. Electr. Power 40 (04), 441–447. doi:10.19725/j.cnki.1007-2322.2021.0372

CrossRef Full Text | Google Scholar

Moghbel, M., Masoum, M., Fereidouni, A., and Deilami, S. (2018). Optimal sizing, siting and operation of custom power devices with STATCOM and APLC functions for real-time reactive power and network voltage quality control of smart grid. IEEE Trans. Smart Grid 9 (6), 5564–5575. doi:10.1109/tsg.2017.2690681

CrossRef Full Text | Google Scholar

Peng, H, Wei, D., Ying, Z, Minxia, Z., Yueran, W., Jianzhou, F., et al. (2021). Multi-function grid-connected inverter control with APF function. Electr. Power Eng. Technol. 40 (01), 107–114.

Google Scholar

Ratnam, K. S., Palanisamy, K., and Yang, G. (2020). Future low-inertia power systems: requirements, issues, and solutions - a review. Renew. Sustain. Energy Rev. 124, 109773. doi:10.1016/j.rser.2020.109773

CrossRef Full Text | Google Scholar

Safa, A., Berkouk, E. M., Messlem, Y., and Gouichiche, A. (2017). An improved sliding mode controller for a multifunctional photovoltaic grid tied inverter. J. Renew. Sustain. Energy 9 (6), 323–329. doi:10.1063/1.4997694

CrossRef Full Text | Google Scholar

Saxena, N. K., Mekhilef, S., Kumar, A., and Gao, D. W. (2022). Marginal cost-based reactive power reinforcement using dynamic and static compensators. IEEE J. Emerg. Sel. Top. Power Electron. 10 (4), 4001–4013. doi:10.1109/jestpe.2022.3145871

CrossRef Full Text | Google Scholar

Song, Z., Lu, Z., Liu, Z., Heng, W., Mian, F., Guoqing, S., et al. (2022). Power quality optimization control strategy of multi-function grid. China Sci. 17 (03), 339–347. doi:10.13335/j.1000-3673.pst.2018.1765

CrossRef Full Text | Google Scholar

Sun, G., Yongli, L. I., Jin, W., and Yan, G. (2019). A comprehensive power quality control strategy for microgrid based on three-phase multi-function inverters. Power Syst. Technol. 43 (04), 1211–1221.

Google Scholar

Wang, J., Pang, W., Wang, L., Pang, X., and Yokoyama, R. (2017). Synthetic evaluation of steady-state power quality based on combination weighting and principal component projection method. CSEE J. Power Energy Syst. 3 (2), 160–166. doi:10.17775/cseejpes.2017.0020

CrossRef Full Text | Google Scholar

Wang, J., Sun, K., Wu, H., Zhang, L., Zhu, J., and Xing, Y. (2020). Quasi-two stage multifunctional photovoltaic inverter with power quality control and enhanced conversion efficiency. IEEE Trans. Power Electron. 35 (7), 7073–7085. doi:10.1109/tpel.2019.2956940

CrossRef Full Text | Google Scholar

Xavier, L. S., Cupertino, A. F., Pereira, H. A., and Mendes, V. F. (2019). Partial harmonic current compensation for multifunctional photovoltaic inverters. IEEE Trans. Power Electron. 34 (12), 11868–11879. doi:10.1109/tpel.2019.2909394

CrossRef Full Text | Google Scholar

Yingying, L., Dandan, F, Lin, C., and Yi, Z. (2020). Current status and development trend of power quality comprehensive assessment. Power Syst. Prot. Control 48 (04), 167–176. doi:10.19783/j.cnki.pspc.190514

CrossRef Full Text | Google Scholar

Zanib, N., Batool, M., Riaz, S., Afzal, F., Munawar, S., Daqqa, I., et al. (2023). Analysis and power quality improvement in hybrid distributed generation system with utilization of unified power quality conditioner. CMES - Comput. Model. Eng. Sci. 134 (2), 1105–1136. doi:10.32604/cmes.2022.021676

CrossRef Full Text | Google Scholar

Zhai, H., Zhuo, F., Zhu, C., Yi, H., Wang, Z., Tao, R., et al. (2020). An optimal compensation method of shunt active power filters for system-wide voltage quality improvement. IEEE Trans. Industrial Electron. 67 (2), 1270–1281. doi:10.1109/tie.2019.2899561

CrossRef Full Text | Google Scholar

Zhijun, L, Gege, L, and Zhang, J. (2022). Power quality variable weight comprehensive evaluation an multiobjective optimization of multifunctional grid-connected inverter. Acta Energiae Solaris Sin. 43 (11), 515–521. doi:10.19912/j.0254-0096.tynxb.2021-0466

CrossRef Full Text | Google Scholar

Zhou, J., Xu, Y., Sun, H., Li, Y., and Chow, M. Y. (2020). Distributed power management for networked AC–DC microgrids with unbalanced microgrids. IEEE Trans. Ind. Inf. 16 (3), 1655–1667. doi:10.1109/tii.2019.2925133

CrossRef Full Text | Google Scholar