Improved droop control strategy for distributed photovoltaic power generation systems

The control strategy of a distributed photovoltaic (PV) power generation system within a microgrid consists of an inner-loop controller and an outer-loop controller. The inner-loop controller is divided into two types, namely, the maximum power point tracking (MPPT) control strategy and DC bus voltage support strategy. Switching between these two control strategies results in issues such as DC bus overvoltage, system oscillations, or even PV system failure. An improved droop control strategy with a novel inner-loop controller is proposed, incorporating an output power derivative regulator. The control system unifies MPPT and DC bus voltage support strategy without switching the controller structure. A simulation model is built to validate the effectiveness of the proposed control strategy, and the results show that the ripple of DC bus voltage decreases by more than 60%.

1 Introduction

The photovoltaic (PV) power generation system can reduce fossil energy consumption and carbon emissions (Manoj Kumar et al., 2023; Dhinesh and Vijayakumar, 2022). The installed capacity of PV systems has the most spectacular growth all over the world. Because of the features of microgrids and PV systems, it is essential for PV systems to be connected to microgrids through power electronic devices on a large scale (Hu et al., 2022; Shao et al., 2023).

In order to maximize the utilization of solar energy, most available PV systems always adopt the maximum power point tracking (MPPT) control strategy (Xiong et al., 2021; Xuan et al., 2022). Due to the volatility of PV power, which creates an imbalance between generation and local load power, and the lack of DC bus voltage support, additional energy storage devices are required (Shen et al., 2023). As high-density distributed PV systems with increasing capacity are connected to microgrids, there are still problems such as DC bus overvoltage and undervoltage, which result in energy storage devices being overcharged or undercharged (Hadjidj et al., 2019; Xiong et al., 2020). While increasing the capacity of energy storage devices may solve the problem, it also leads to higher maintenance costs.

In order to apply MPPT, the PV controller requires steady and reliable DC bus voltage with small fluctuation and high capacity for proper functioning (Shavolkin et al., 2023; Raj and Kos, 2022; Harag et al., 2022). In island mode, the microgrid is disconnected from the major power grid, so it loses the reliable and stable DC voltage support ability from the bulk power grid. Thus, the power balance between the local load and power generation should be governed within the microgrid itself (Rezaei et al., 2022; Liu et al., 2023). To some extent, a high-capacity energy storage device in the microgrid can support the DC bus voltage (He et al., 2022). Nevertheless, energy storage devices increase construction and maintenance costs, and there are still problems such as overcharging and undercharging (De et al., 2023).

Cai et al. (2018) proposed a control strategy for PV systems in the island mode, which consists of two control loops. The inner control loop is the output voltage loop, and the outer control loop is divided into two categories, namely, MPPT control strategy and DC bus voltage support strategy. When the charging and discharging powers of energy storage devices and the load and output powers of PV systems are unbalanced, the outer loop adopts the DC bus voltage support strategy. Conversely, when these are balanced, the outer loop adopts MPPT. However, switching between MPPT and DC bus voltage support strategies will lead to voltage and power oscillations and may even cause the PV system to crash.

Thus, an advanced and reliable control strategy for PV should meet the following criteria. In island mode, a steady DC bus voltage should be achieved without requiring additional efforts in software and hardware design (Li et al., 2023). In grid-connected mode, PV applies MPPT to maximize the utilization of solar energy (Shubham Kumar and Anshul, 2023). The control strategy can implement MPPT and DC bus voltage support without switching the control configurations (Vijayshree and Sumathi, 2023), and for distributed PV systems in microgrids, the control strategy algorithm is decentralized to reduce the influence of communication systems (Zhu et al., 2022).

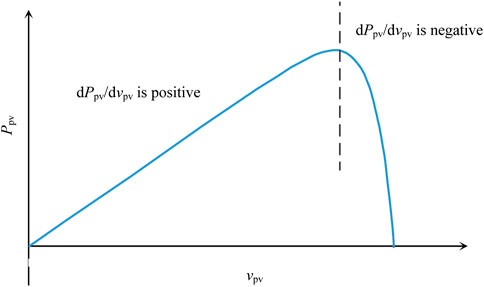
The mathematical formulas for describing photovoltaic arrays tend to be nonlinear. It can be divided into two regions, namely, region I and region II. In region I, dP_pv/dv_pv is positive. P_pv is the output power of the PV array, and v_pv is the output voltage of the PV array. In region II, dP_pv/dv_pv is negative; as P_pv increases beyond the load power, v_pv decreases to maintain a steady DC bus voltage. On the basis of theoretical analysis, an improved droop control strategy is proposed.

The proposed control strategy also consists of two loops. The outer control loop is the droop control loop, and the inner control loop is used to control dP_pv/dv_pv. By controlling dP_pv/dv_pv to be 0, the proposed control strategy becomes equivalent to MPPT. By controlling dP_pv/dv_pv to be negative, the proposed control strategy becomes equivalent to the DC bus voltage support strategy. Thus, with the novel control strategy, the PV system can switch control targets naturally without switching the control strategy.

Since dP_pv/dv_pv and P_pv tend to be nonlinear, the droop coefficients for each distributed PV change to distribute the local power balanced to each PV. A parametric design method for droop coefficients is also proposed.

To verify the feasibility of the proposed control strategy, a simulation model with three distributed PV systems is built, and the results show its effectiveness.

2 PV model

2.1 Mathematics model of photovoltaic arrays

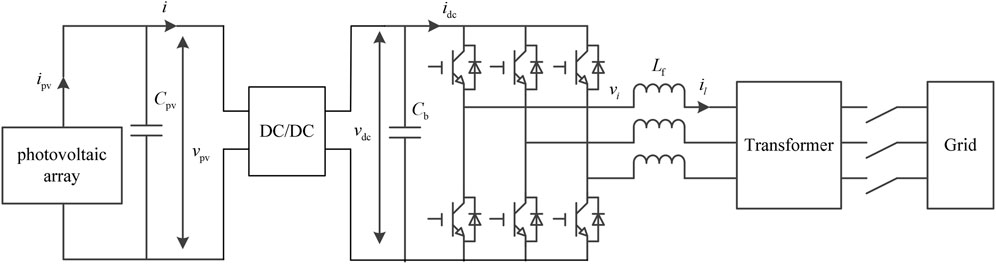
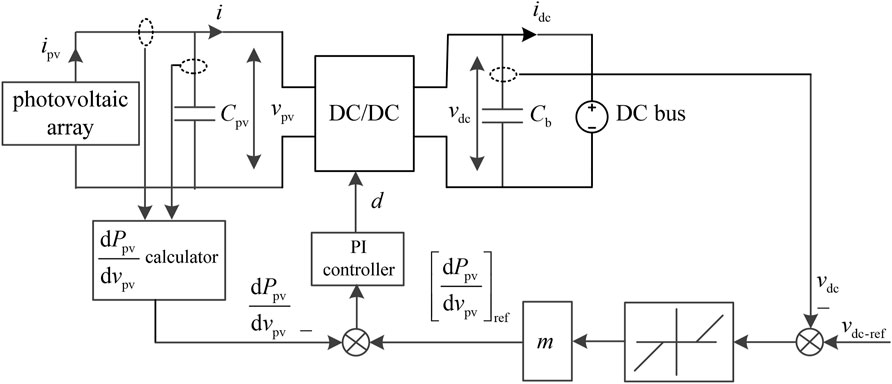
PVs are always connected to the DC bus through a DC/DC converter. The DC/DC converter adopts a control strategy with two control loops, and the outer-loop controller applies MPPT, the inner-loop controller is the output voltage of the photovoltaic array controller. Figure 1 shows the structure diagram of the PV.

Figure 1

Figure 1. Structure diagram of the PV system.

Here, i_pv and v_pv are the output current and output voltage of the photovoltaic array. v_dc and i_dc are the DC bus voltage and the DC bus current, respectively. L_f is the filter inductance. C_pv and C_b are the output capacitance and DC bus capacitance, respectively. v_i and i_i are the output voltage and output current of the DC/AC converter, respectively.

The DC/DC converter can adopt the Boost converter if the serial number of photovoltaic arrays is relatively small, and the DC/DC converter can adopt the Buck converter if the serial number of photovoltaic arrays is relatively large, and the DC/DC converter can adopt the Buck/Boost converter, if the serial number of photovoltaic arrays is reasonable.

The output current of the PV is expressed as

$i_{pv}=N_p{I}_{\text{sc},n}-\frac{N_p{I}_{\text{sc},n}}{e^{\frac{v_{\text{oc},n}}{a{V}_t}}-1}\left(e^{\frac{V_{pv}}{N_{s}a{V}_t}}-1\right),(1)$

where N_p is the number of parallel photovoltaic arrays and N_s is the number of serial photovoltaic arrays. V_oc,n and I_sc,n are, respectively, the open-circuit voltage and short-circuit current of photovoltaic arrays at 298.16 K and 1,000 W/m². a is an equivalent constant of the ideal diode. V_t in Equation 1 is the thermal voltage of the photovoltaic panel, and it is expressed as

$V_t=\frac{NkT}{q},(2)$

where k is the Boltzmann’s constant, T is the environmental temperature, q is the number of elementary charge, and N is the serial number of the photovoltaic power generation unit.

Based on Equations 1, 2, the output power of photovoltaic arrays is expressed as

$P_{\text{pv}}=i_{\text{pv}}{v}_{\text{pv}}=N_p{I}_{\text{sc},n}{v}_{\text{pv}}\left(1-e^{\left(\frac{v_{\text{pv}}}{N_{s}a{V}_t}-\frac{V_{\text{oc},n}}{a{V}_t}\right)}\right).(3)$

The relational expression of the output voltage ripple and the output capacitance is

$C_{\text{pv}}\frac{\mathrm{d}{v}_{\text{pv}}}{\mathrm{d}t}=i_{\text{pv}}-i.(4)$

According to Equation 4, the lager capacitance can reduce the output voltage ripple.

2.2 Control strategy of the PV

The PV system operates in three different modes, namely, “islanding mode,” “grid-connected mode,” and “switching mode.”

In switching mode, once the interconnecting tie of the PV and large power grid breaks, the PV system should switch its operation mode from grid-connected mode to islanding mode. After the fault is cleared, the PV system should switch back to grid-connected mode.

In grid-connected mode, with the support of voltage and frequency from bulk power systems, the PV system always adopts MPPT. In islanding mode, due to the lack of DC bus voltage support, the PV system should be configured with energy storage devices to adopt MPPT. There is still a risk of overcharging energy storage devices if P_pv is larger than the local load and the charging power of the energy storage device, leading to DC bus overvoltage and even system failure. In addition, incorporating the energy storage devices increases the construction and maintenance costs.

Thus, in islanding mode, the control strategy of the PV system can be divided into two categories, namely, MPPT and DC bus voltage support strategy. According to the operating condition, the control system switches the control strategy to meet the performance requirement. Figure 2 shows the control strategy of the PV system.

Figure 2

Figure 2. Control strategy.

As shown in Figure 2, the control system of the PV needs to switch between the two types of control strategies according to the operating condition. The construction of the control system is complicated, and the hardware and software costs increase. The toughest problems caused by switching control strategies are voltage and power fluctuations, which result in poor reliability of the control system. The severe voltage and power fluctuations will result in PV system failure.

Here, d is the duty cycle of the DC/DC converter, i_load is the load current, ${v_{\text{dc}}}^{*}$ is the reference value of DC bus voltage, $v_{\text{dc}}^{\text{ref}}$ is the reference value of the DC bus voltage controller, and $v_{\text{pv}}^{\text{ref}}$ is the reference value of the controller for v_pv.

2.3 Output characteristics of photovoltaic arrays

Figure 3 shows the schematic diagram describing P_pv varying with v_pv of the PV array.

Figure 3

Figure 3. Output characteristics of the photovoltaic array.

As shown in Figure 3, it is divided into two regions, namely, region I and region II. In region I, dP_pv/dv_pv is positive, and in region II, dP_pv/dv_pv is negative. MPPT is equivalent to dP_pv/dv_pv = 0.

As the local load power increases, the DC bus voltage decreases. While in region II, as v_pv decreases, P_pv increases. So, the local load power and P_pv are balanced again. In region I, as v_pv decreases, P_pv decreases, which results in a worse decrease in DC bus voltage. Hence, region II is more stable than region I. By controlling dP_pv/dv_pv to be negative, the DC bus voltage support strategy is achieved.

3 Proposed control strategy

3.1 dP_pv/dv_pv

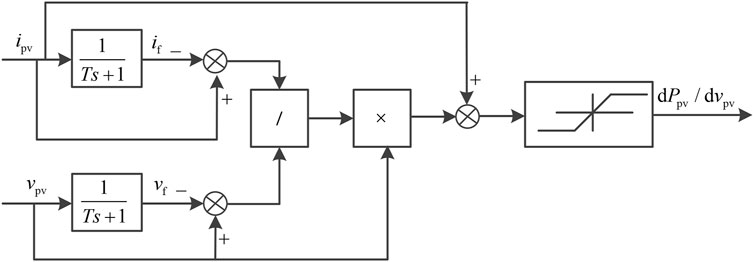
Based on Equation 3, dP_pv/dv_pv can be calculated using the micro-increment of conductance di_pv/dv_pv, and it is expressed as

$\frac{\mathrm{d}{P}_{\text{pv}}}{\mathrm{d}{v}_{\text{pv}}}=\frac{\mathrm{d}\left(v_{\text{pv}}{i}_{\text{pv}}\right)}{\mathrm{d}{v}_{pv}}=i_{\text{pv}}+v_{\text{pv}}\frac{\mathrm{d}{i}_{\text{pv}}}{\mathrm{d}{v}_{\text{pv}}}.(5)$

A low-pass filter is adopted to reduce the influence of noise on i_pv, v_pv, and P_pv. In addition, the micro-increments of i_pv and v_pv are calculated using the low-pass filter. The output voltage and output current of the low-pass filter are expressed as

$i_{\mathrm{f}}\left(s\right)=\frac{1}{Ts+1}{i}_{\text{pv}}\left(s\right),(6)$

$v_{\mathrm{f}}\left(s\right)=\frac{1}{Ts+1}{v}_{\text{pv}}\left(s\right),(7)$

where s is the differential operator and i_pv(s) and v_pv(s) are Laplace transform from i_pv(t) and v_pv(t), respectively. T is the time constant of the low-pass filter. i_f(s) is the output of the low-pass filter for i_pv(s). v_f(s) is the output of the low-pass filter for v_pv(s).

The deviations from Equations 6, 7 are expressed as

$s{i}_{\mathrm{f}}\left(s\right)=\frac{i_{\text{pv}}\left(s\right)-i_{\mathrm{f}}\left(s\right)}{T},(8)$

$s{v}_{\mathrm{f}}\left(s\right)=\frac{v_{\text{pv}}\left(s\right)-v_{\mathrm{f}}\left(s\right)}{T}.(9)$

According to Equations 8, 9 and inverse Laplace transformation theory, di_f/dv_f is expressed as

$\frac{\mathrm{d}{i}_{\text{pv}}}{\mathrm{d}{v}_{\text{pv}}}\approx \frac{d{i}_{\mathrm{f}}}{d{v}_{\mathrm{f}}}=\frac{i_{\text{pv}}-i_{\mathrm{f}}}{v_{\text{pv}}-v_{\mathrm{f}}}.(10)$

Based on Equation 10, the time constant of the low-pass filter has no influence on di_pv/dv_pv. Thus, the time constant of the low-pass filter is designed to reduce the noise. T is set based on the cut-off frequency of the low-pass filter. The cut-off frequency is 1,000 Hz, so T is equal to 1/2000π.

According to Equations 5, 10, dP_pv/dv_pv is expressed as

$\frac{\mathrm{d}{P}_{\text{pv}}}{\mathrm{d}{v}_{\text{pv}}}=i_{\text{pv}}+v_{\text{pv}}\frac{i_{\text{pv}}-i_{\mathrm{f}}}{v_{\text{pv}}-v_{\mathrm{f}}}.(11)$

According to Equation 11, Figure 4 shows the schematic diagram illustrating the computational method of dP_pv/dv_pv.

Figure 4

Figure 4. Schematic diagram illustrating the computational method of dP_pv/dv_pv.

In Figure 4, the limit of dP_pv/dv_pv is equal to y (v_{oc_i}).

3.2 Improved droop control

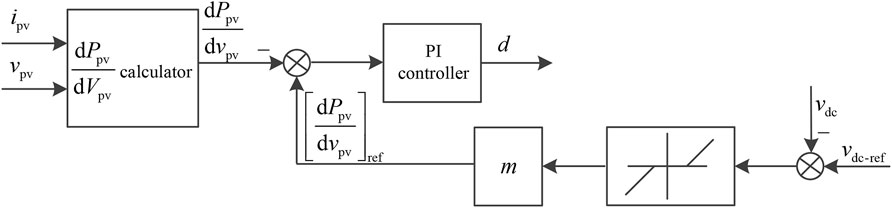
To distribute the local power to multiple PV systems, an improved droop control strategy is proposed. It consists of two control loops, namely, the inner-loop controller, which adopts the dP_pv/dv_pv control strategy, and the outer-loop controller, which adopts droop control with adaptive droop coefficients.

Figure 5 shows the schematic diagram of the improved droop control strategy for the PV system.

Figure 5

Figure 5. Improved control strategy of the PV system.

Here, [dP_pv/dv_pv]_ref is the input reference of the inner-loop controller, and it is expressed as

${\left[\frac{\mathrm{d}{P}_{\text{pv}}}{\mathrm{d}{v}_{\text{pv}}}\right]}_{\text{ref}}={\frac{\mathrm{d}{P}_{\text{pv}}}{\mathrm{d}{v}_{\text{pv}}}}^{\ast }-m\left(v_{\text{dc}}-v_{\text{dc}-\text{ref}}\right),(12)$

where (dP_pv/dv_pv)^* is the reference value of dP_pv/dv_pv. If (dP_pv/dv_pv)^* is equal to 0, the proposed control system of the PV is equivalent to MPPT for the maximum utilization of solar energy, and m is the droop coefficient. v_{dc_ref} is the reference value of DC bus voltage.

As shown in Figure 5, if the difference between the real-time v_dc and v_{dc_ref} is smaller than the dead band, [dP_pv/dv_pv]_ref is 0. If P_Load is smaller than P_pv−P_c, v_dc decreases; thus, v_dc-v_{dc_ref} is negative, which leads to [dP_pv/dv_pv]_ref being negative. Hence, the control system of the PV is equivalent to the DC bus voltage support strategy.

Because of line impedance, power allocation among all PV systems can have errors when using the traditional droop control. To achieve accurate power allocation, a controller with a consensus algorithm in the second layer is necessary. Using the simplified and linear model affects the accuracy of the control system, but power allocation in the first layer is implemented.

3.3 Multiple operating modes of PV

In grid-connected mode, the DC bus voltage is adjusted using the grid-connected converter, and the DC/DC converter adopts MPPT. Thus, (dP_pv/dv_pv)^* is set to 0.

In isolating mode, the comparison expressions between the local load power P_Load, P_pv, the charging power of energy storage devices P_c, and the discharging power of energy storage devices P_D are presented as follows:

Once P_Load < P_pv−P_c, P_pv is excessive. Thus, to obtain a steady DC bus voltage, P_pv should decrease, and dP_pv/dv_pv is controlled to be negative.

Once P_pv−P_c < P_Load < P_pv + P_D, the DC bus voltage is supported by energy storage devices, dP_pv/dv_pv is controlled to be 0 so that MPPT is adopted.

Once P_Load > P_pv + P_D, dP_pv/dv_pv is controlled to be 0 so that MPPT is adopted. If the DC bus voltage continues to decrease, the fractional local load should be cut off to obtain a steady and limited DC bus voltage.

3.4 Calculation method of the droop coefficient

The output power of each PV system to support the local load is dependent on the droop coefficients. To simplify the analysis and calculation, the relationship between P_pv and dP_pv/dv_pv of each PV system is simplified as a linear relation, which is expressed as

${\widehat{P}}_{\text{pv}\_i}=f\left(\frac{d{P}_{\text{pv}-i}}{d{v}_{\text{pv}\_i}}\right)=\frac{P_{\max \_i}}{y\left(v_{\text{oc}\_i}\right)}\times \frac{d{P}_{\text{pv}-i}}{d{v}_{\text{pv}\_i}}+P_{\max \_i},(13)$

where P_{max_i} is the maximum output power of the ith PV, v_{oc_i} is the open-circuit output voltage of the ith PV, y (v_{oc_i}) is dP_pv/dv_pv when the ith PV is an open circuit. ${\widehat{P}}_{\text{pv}\_i}$ is the output power of the ith PV on the linear curve between P_pv and dP_pv/dv_pv.

The control system should distribute local power to each PV system as a rated ratio, which is expressed as

$\frac{{\stackrel{⌢}{P}}_{\text{pv}\_i}}{{\stackrel{⌢}{P}}_{\text{pv}\_j}}=\frac{P_{\max \_i}}{P_{\max \_j}}.(14)$

By applying MPPT and according to Equations 12, 13, with dP_pv/dv_pv = 0, Equation 14 can be expressed as

$\frac{{\stackrel{⌢}{P}}_{\text{pv}\_i}}{{\stackrel{⌢}{P}}_{\text{pv}\_j}}=f\left(\frac{\mathrm{d}{P}_{\text{pv}\_i}}{\mathrm{d}{V}_{\text{pv}\_i}}\right)/f\left(\frac{\mathrm{d}{P}_{\text{pv}\_j}}{\mathrm{d}{V}_{\text{pv}\_j}}\right)=\frac{\frac{P_{\max \_i}}{y\left(v_{\text{oc}\_i}\right)}\cdot m_i\cdot \Delta v+P_{\max \_i}}{\frac{P_{\max \_j}}{y\left(v_{\text{oc}\_j}\right)}\cdot m_j\cdot \Delta v+P_{\max \_j}},(15)$

where Δv is expressed as

$\Delta v=v_{\text{dc}\_\text{ref}}-v_{\text{dc}}.(16)$

According to Equations 15, 16, the droop coefficient of each PV system is expressed as

$m_i=\frac{y\left(v_{\text{oc}\_i}\right)}{v_{\text{dc}\_\max }-v_{\text{dc}\_\text{ref}}},(17)$

where m_i is the droop coefficient of the ith PV and u_{dc_max} is the upper limit value of DC bus voltage.

4 Parameters of the control system

4.1 Proposed control system

Figure 6 shows the whole control system. The inner-loop controller of PV applies a proportional–integral (PI) controller, while the outer-loop controller employs the droop control strategy. And m in Figure 6 is calculated by Equation 17.

Figure 6

Figure 6. Whole control system.

4.2 Parameter design method

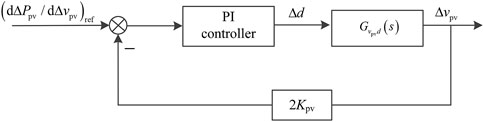
Figure 7 shows the small-signal model of the inner-loop controller.

Figure 7

Figure 7. Small-signal model of the inner-loop controller.

Here, $G_{v_{\text{pv}}d}\left(s\right)$ is the transfer function of Δd to Δv_pv, and K_pv is expressed as Equation 18, and it is obtained by the linear small-signal model of the PV system, which is expressed as

$K_{pv}=\frac{\Delta i_{\text{pv}}}{\Delta v_{\text{pv}}}=\frac{N_p\cdot I_{\text{sc},n}}{e^{\frac{v_{\text{oc},n}}{a\cdot v_t}-1}\cdot a\cdot N_s\cdot v_t}{e}^{\frac{v_{\text{pv}}}{a\cdot N_s\cdot v_{\mathrm{t}}}}.(18)$

The small-signal model of the Buck converter is expressed as

$L\frac{\mathrm{d}\Delta i_l}{\mathrm{d}t}=v_{\text{pv}}\times \Delta d+d\times \Delta v_{\text{pv}}-\Delta v_{\text{dc}},(19)$

$C\frac{\mathrm{d}\Delta v_{\text{dc}}}{\mathrm{d}t}=\Delta i_l-\frac{\Delta v_{\text{dc}}}{R},(20)$

$C_{\text{pv}}\frac{\mathrm{d}\Delta v_{\text{pv}}}{\mathrm{d}t}=K_{\text{pv}}\times \Delta v_{\text{pv}}-d\cdot \Delta i_l-I_l\cdot \Delta d,(21)$

where L is the inductance of the Buck converter, d is the duty cycle of IGBT in the Buck converter, C is the output capacitor in the Buck converter, R is the equivalent load impedance, C_pv is the output capacitor of the photovoltaic array, and Δd is the variation in the duty cycle.

According to Equation 5, the small-signal model of the photovoltaic array is expressed as

$\frac{\mathrm{d}\Delta P_{\text{pv}}}{\mathrm{d}\Delta v_{\text{pv}}}=\Delta i_{\text{pv}}+K_{\text{pv}}\Delta v_{\text{pv}}=2K_{\text{pv}}\Delta v_{\text{pv}}.(22)$

According to Equations 19–21, the transfer function between Δd and Δv_pv is achieved by Laplace transform, which is expressed as

$G_{v_{\text{pv}}d}\left(s\right)=\frac{\Delta v_{\text{pv}}}{\Delta d}=-\frac{I_l\times L\times s+D\times v_{\text{pv}}}{C_{\text{pv}}\times L\times s^2-K_{\text{pv}}\times L\times s+d^2}.(23)$

According to Equations 22, 23, the transfer function between Δv_pv and (dP_pv/dv_pv)_ref is expressed as

$G_1\left(s\right)=\frac{\Delta v_{\text{pv}}}{{\left(\frac{\mathrm{d}{P}_{\text{pv}}}{\mathrm{d}{V}_{\text{pv}}}\right)}_{\text{ref}}}=\frac{G_{v\text{pv}d}\left(s\right)\times T_1\left(s\right)}{G_{v\text{pv}d}\left(s\right)\times T_1\left(s\right)\times 2\times K_{\text{pv}}+1},(24)$

where T₁(s) is the transfer function of the PI controller shown in Figure 6, and it is expressed as

$T_1\left(s\right)=K_{\mathrm{P}1}+\frac{K_{\mathrm{I}1}}{s},(25)$

where K_P1 and K_I1 are the proportional and integral coefficients of the inner-loop controller, respectively.

In this paper, the phase margin of the inner-loop controller is set to 76°, and the bandwidth of the inner-loop controller is set to 580 Hz. And according to the tranfer function expressed by Equations 24, 25 is expressed as

$T_1\left(s\right)=0.001+\frac{0.1}{s}.(26)$

5 Analysis of the results

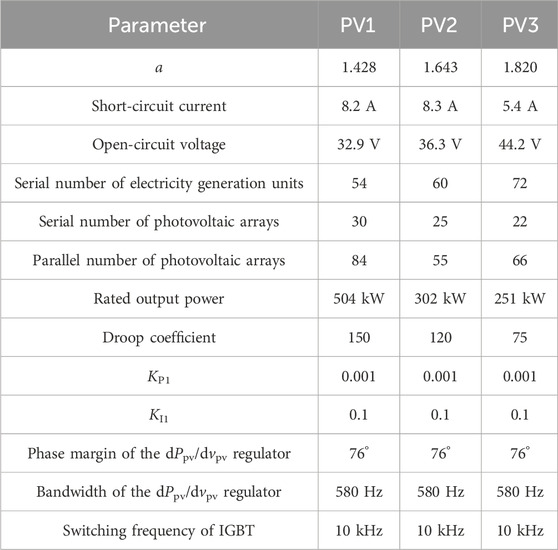
5.1 Parameters of the simulation model

To verify the proposed control strategy, a simulation model is built. The parameters of the distributed PV system are shown in Table 1. The output capacitance of each PV system is 2,000 μF, the equivalent impedance of the transmission line is 0.002 Ω, the equivalent inductance of the transmission line is 0.2 mH, the output capacitance of the DC/DC converter is 10,000 μF, the rated DC bus voltage is 550 V, and the maximum charging and discharging powers are both 280 kW.

Table 1

Table 1. Parameters of distributed PV systems.

5.2 Influence of load in island mode

To verify the DC bus voltage support capability of the proposed control strategy, the DC bus voltage support capability of energy storage devices is neglected. The local load is set to 706 kW in the first stage, and the load impedance is 0.46 Ω. The local load is set to 899 kW in the second stage, and the load impedance is 0.35 Ω. The local load is set to 1,038 kW in the third stage, and the load impedance is 0.24 Ω.

Figure 8 shows the response to a step change in load: a) DC bus voltage waveform, b) output power waveform of each PV system, and c) output voltage waveform of each PV system.

Figure 8

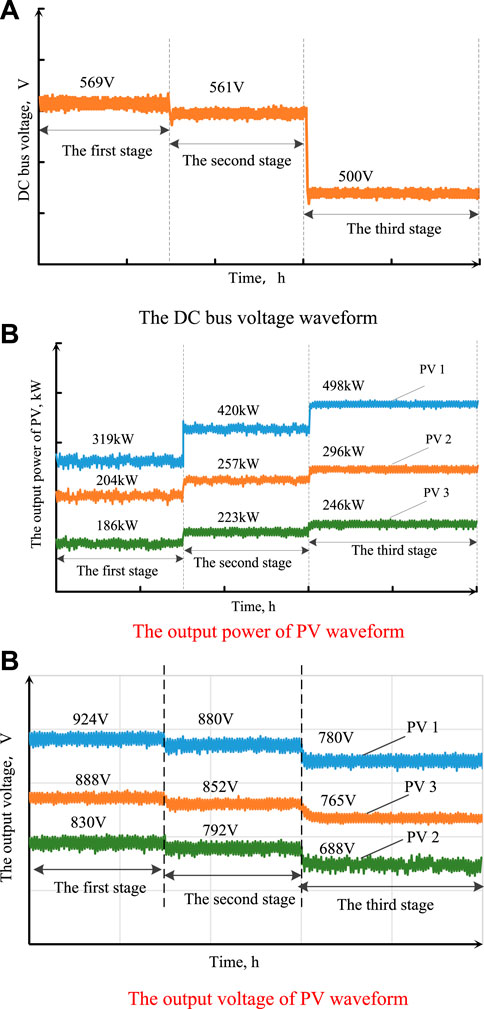
Figure 8. Operation performance of the PV system under different loads. (A) DC bus voltage of the waveform, (B) output power of the PV waveform, and (C) output voltage of the PV waveform.

As shown in Figure 8, in the first and second stages, the local power is less than the maximum output power of PV, so PV applies the DC bus support strategy. Moreover, since dP_pv/dv_pv is controlled to be negative, the output voltage of the photovoltaic array is relatively high. In the third stage, the local load power is more than the maximum output power of PV, so PV applies MPPT, and the DC bus voltage is maintained at 500 V.

In addition, the droop coefficients of each distributed PV system are designed as the rated output power ratio, so the output power of each distributed PV is always 1.67:1:0.83.

5.3 Influence of irradiance in island mode

The local load is set as a constant and equal to 0.6 Ω. In the first stage, irradiance is set to 600 W/m². In the second stage, irradiance is set to 800 W/m². In the third stage, irradiance is set to 1,000 W/m². Figure 9 shows the response to a step change in irradiance: a) DC bus voltage waveform, b) output voltage waveform of each PV, and c) output power waveform of each PV.

Figure 9

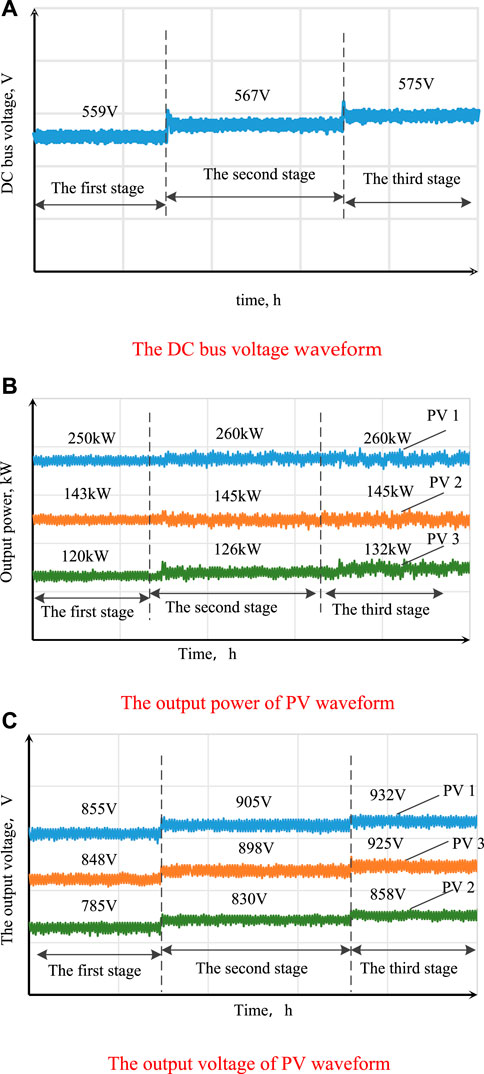
Figure 9. Operation performance of the PV system under different irradiance values. (A) DC bus voltage of the waveform, (B) output power of the PV waveform, and (C) output voltage of the PV waveform.

As shown in Figure 9, the local load power is smaller than the maximum output power of PV, so the control strategy of PV becomes equivalent to the DC bus voltage support strategy to maintain a steady DC bus voltage.

Since PV operates in region II, dP_pv/dv_pv is negative. Thus, the output voltage increases as the output power decreases.

5.4 Performance of the improved control strategy

The initial state-of-charge of energy storage is set to 20% to consider the influence of the energy storage system. Furthermore, the local load power is set to 605 kW in the first stage, it is set to 316 kW in the second stage, and it is reset to 605 kW in the third stage.

By the proposed control strategy, in the first and third stages, the local load power and the charging power of the energy storage device are more than the maximum output power of the PV, so the inner-loop controller adjusts dP_pv/dv_pv to be 0, which is equivalent to MPPT. In the second stage, the local load power and the charging power of the energy storage device are less than the maximum output power of the PV, so the inner-loop controller adjusts dP_pv/dv_pv to be a negative value, which is equivalent to the DC bus voltage support strategy.

By the traditional control strategy, in the first and third stages, the inner-loop controller applies MPPT, and in the second stage, the inner-loop controller applies the DC bus voltage support strategy.

Hence, the proposed control strategy adjusts dP_pv/dv_pv to obtain a different control objective, while the traditional control strategy switches the control system to obtain a different control objective.

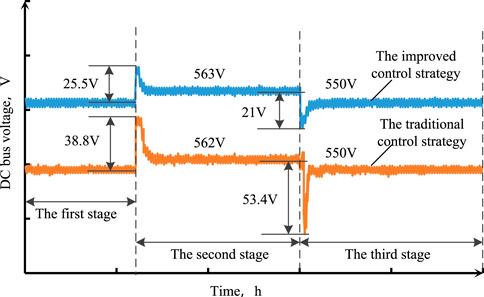
Figure 10 shows the DC bus voltage waveform using the proposed and traditional control strategies.

Figure 10

Figure 10. DC bus voltage waveform.

Figure 10 shows that both the improved and traditional control strategies can maintain the stability of DC bus voltage. In addition, for both control strategies, the ripples of DC bus voltage satisfy PV system requirements. With the proposed control strategy, the ripple of DC bus voltage is relatively small, thereby decreasing the influence of switching the control system on the PV system.

6 Conclusion

An improved droop control strategy for distributed PV systems is proposed; the inner-loop controller adjusts dP_pv/dv_pv, and the outer-loop controller applies droop control with adaptive droop coefficients to allocate local power scientifically to each distributed PV system. Using the proposed inner-loop controller, the PV system can achieve the maximum output power and provide DC bus support without changing the control configurations.

The proposed inner-loop controller can suppress the DC bus voltage oscillation. In the inner-loop controller, if dP_pv/dv_pv is regulated to be 0, the inner-loop controller is equivalent to MPPT. If dP_pv/dv_pv is regulated to be a negative value, the inner-loop controller is equivalent to the DC bus voltage support strategy. Using the proposed droop control strategy, both the maximum available output power of distributed PV systems and the steady DC bus voltage can be obtained.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

DZ: conceptualization, methodology, validation, writing–original draft, and writing–review and editing. GN: data curation, formal analysis, funding acquisition, resources, writing–original draft, and writing–review and editing. ZY: conceptualization, formal analysis, software, supervision, validation, and writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Nantong Natural Science Foundation Project (grant number JCZ2023029) and the Nantong City Social Livelihood Science and Technology Project (grant number MS2023062).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cai, H., Xiang, J., and Wei, W. (2018). Decentralized coordination control of multiple photovoltaic sources for DC bus voltage regulating and power sharing. IEEE Trans. industrial Electron. 65 (7), 5601–5610. doi:10.1109/tie.2017.2779412

CrossRef Full Text | Google Scholar

De, P. J., Ruy, I., Galhardo, B., Costa, T., Pinho, J., Williamson, S., et al. (2023). Influence of photovoltaic microgeneration on the demand profile and its effects on the grid power quality. Electr. Power Syst. Res. 214 (Jan.Pt.B), 1–8. doi:10.1016/j.epsr.2022.108935

CrossRef Full Text | Google Scholar

Dhinesh, V., and Vijayakumar, G. (2022). A switched quasi Z-source three-port (SqZSTP) DC-DC converter for a photovoltaic power generation system. Semicond. Sci. Technol. 37, 045014–45014.22. doi:10.1088/1361-6641/ac419d

CrossRef Full Text | Google Scholar

Hadjidj, S., Bibi-Triki, N., and Faouzi, D. (2019). Analysis of the reliability of photovoltaic-micro-wind based hybrid power system with battery storage for optimized electricity generation at Tlemcen, north west Algeria. Archives Thermodyn. 40 (1), 161–185.

Google Scholar

Harag, N., Imanaka, M., Kurimoto, M., Sugimoto, S., Bevrani, H., and Kato, T. (2022). Autonomous dual active power-frequency control in power system with small-scale photovoltaic power generation. J. Mod. Power Syst. Clean Energy 10 (04), 941–953. doi:10.35833/mpce.2020.000700

CrossRef Full Text | Google Scholar

He, H., Lu, Z., Guo, X., Shi, C., Jia, D., Chen, C., et al. (2022). Optimized control strategy for photovoltaic hydrogen generation system with particle swarm algorithm. Energies 15 (4), 1472–1472.17. doi:10.3390/en15041472

CrossRef Full Text | Google Scholar

Hu, Z., Cao, Wu, Sha, J., and Minhui, Q. (2022). “Improved frequency response model for power system with photovoltaic generation,” in 2022 IEEE 5th international electrical and energy conference (CIEEC), nangjing, China, 2929–2933. doi:10.1109/CIEEC54735.2022.9846523

CrossRef Full Text | Google Scholar

Li, F., Yu, Y., and Yue, S. (2023). Study on characteristics of photovoltaic and photothermal coupling compressed air energy storage system. Trans. Institution Chem. Eng. Process Saf. Environ. Prot. 178, 147–155.

CrossRef Full Text | Google Scholar

Liu, L., Zhai, R., Hu, Y., and Liu, S. (2023). Operation performance analysis of a novel renewable energy-driven multienergy supply system based on wind, photovoltaic, concentrating solar power, proton exchange membrane electrolyzers, and proton exchange membrane fuel cell. Energy Technol. Gener. Convers. Storage, Distrib. 11, 2–17. doi:10.1002/ente.202300291

CrossRef Full Text | Google Scholar

Manoj Kumar, S., Chittaranjan, P., and Kaur, C. R. (2023). A computational intelligence based maximum power point tracking for photovoltaic power generation system with small-signal analysis. Optim. Control Appl. Methods 44 (2), 617–636. doi:10.1002/oca.2798

CrossRef Full Text | Google Scholar

Raj, R., and Kos, A. (2022). A novel method of islanding detection in a distributed power generation system integrated with photovoltaic-array. Przeglad Elektrotechniczny 98 (7), 88–94.

CrossRef Full Text | Google Scholar

Rezaei, J., Golshan, M. E. H., and Alhelou, H. H. (2022). Impacts of integration of very large-scale photovoltaic power plants on rotor angle and frequency stability of power system. IET Renew. power Gener. 16 (11), 2384–2401. doi:10.1049/rpg2.12529

CrossRef Full Text | Google Scholar

Shao, B., Qi, X., Xiong, L., Wang, L., Yang, Y., Chen, Z., et al. (2023). Power coupling analysis and improved decoupling control for the VSC connected to a weak AC grid. Int. J. Electr. Power and Energy Syst. 145, 108645, Feb. doi:10.1016/j.ijepes.2022.108645

CrossRef Full Text | Google Scholar

Shavolkin, O., Shvedchykova, I., Kolcun, M., Dusan, M., and Svitlana, D. (2023). Implementation of planned power generation for a grid-tied photovoltaic system with a storage battery for self-consumption of local object. Przeglad Elektrotechniczny 99 (1), 18–27. doi:10.15199/48.2023.01.04

CrossRef Full Text | Google Scholar

Shen, Fu, Zhang, Y., Qiu, G., Yang, Z., Li, S., and Yang, G. (2023). Generalized discrete-time equivalent model for interfacing the grid-connected photovoltaic system. IET generation, Transm. and distribution 17 (5), 1070–1080. doi:10.1049/gtd2.12656

CrossRef Full Text | Google Scholar

Shubham Kumar, S., and Anshul, A. (2023). A comparative analysis of artificial neural network algorithms to enhance the power quality of photovoltaic distributed generation system based on metrological parameters. Mapan J. Metrology Soc. India 38 (3), 607–618. doi:10.1007/s12647-023-00649-7

CrossRef Full Text | Google Scholar

Vijayshree, G., and Sumathi, S. (2023). Power quality improvement in distributed generation system under varying load conditions using PWM and hysteresis controller. Przeglad Elektrotechniczny 99 (3), 142–147.

Google Scholar

Xiong, L., Liu, X., Zhang, D., and Liu, Y. (2021). Rapid power compensation-based frequency response strategy for low-inertia power systems. IEEE J. Emerg. Sel. Top. Power Electron. 9 (4), 4500–4513. doi:10.1109/jestpe.2020.3032063

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Zhao, C., and Zhuo, F. (2020). A fast and robust real-time detection algorithm of decaying DC transient and harmonic components in three-phase systems. IEEE Trans. Power Electron. 35 (4), 3332–3336. doi:10.1109/tpel.2019.2940891

CrossRef Full Text | Google Scholar

Xuan, Y., Sun, Ke, Wang, J., Yin, J., Fang, X., and Wang, G. (2022). Optimal allocation of energy storage capacity of high-permeability photovoltaic power generation system based on elastic neural network. J. Nanoelectron. Optoelectron. 17 (12), 1641–1647. doi:10.1166/jno.2022.3351

CrossRef Full Text | Google Scholar

Zhu, Y., Wen, H., Chu, G., Wang, X., Peng, Q., Hu, Y., et al. (2022). Power-rating balance control and reliability enhancement in mismatched photovoltaic differential power processing systems. IEEE Trans. Power Electron. 37, 879–895. doi:10.1109/tpel.2021.3094220

CrossRef Full Text | Google Scholar