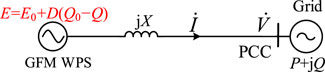Voltage response characterization of grid-forming wind power systems

The widespread integration of wind turbines poses voltage stability challenges to power systems. To enhance the ability of wind power systems to actively support grid voltage, grid-forming control techniques are increasingly being employed. However, current research primarily focuses on voltage stability challenges at the point of common coupling in wind power systems, lacking thorough investigation into system voltage response characterization. This paper establishes the voltage response model of a grid-forming wind power system. Based on this model, mathematical derivation and theoretical analysis are conducted, and the effect factors of the voltage at the point of common coupling are investigated. Furthermore, a voltage stabilization method is explored by adjusting the above effect factors. Finally, based on the MATLAB/Simulink platform, the simulation verification of each effect factor is carried out. The results indicate that voltage response characterization obtained by the theoretical analysis and simulation is similar and that the proposed method is valid.

1 Introduction

Constructing a novel power system characterized by a significant share of renewable energy sources and a high proportion of converters (Kang and Yao, 2017) represents a pivotal approach toward achieving the objectives of carbon peaking and carbon neutrality (Yang et al., 2023). With wind power (Ouyang et al., 2019), photovoltaic power (Kim et al., 2023), and other new energy power sources connected to the grid on a large scale, the traditional power system dominated by synchronous machines is undergoing a transformation. The extensive access of new energy power sources induces the characteristics of low inertia and weak damping for the new power system (Leon et al., 2024), which is difficult for actively supporting the safe and stable operation of the power system (Shang et al., 2022).

To provide the converter with the ability to actively support the grid frequency and voltage and increase the immunity of the grid during load disturbances, grid-forming (GFM) control techniques are widely used (Rosso et al., 2021; Wu and Wang, 2021). Xiong et al. (2021) proposed a rapid power compensation-based frequency response strategy, which can maximize the suppression of frequency deviation and the rate of change of frequency (ROCOF) simultaneously, yet avoiding the limitations due to unknown grid parameters. Xi et al. (2021) presented a decoupling control scheme to optimize the frequency response characteristics of virtual synchronous generator (VSG) (Fang et al., 2018) control using wind power plants as a research object. Shao et al. (2019) proposed a double-fed induction generator model based on equivalent electromotive force and equivalent power angle and evaluated the inertial response characteristics of the system. Verma et al. (2023) proposed a self-regulating configuration strategy and analyzed the frequency characteristics of the system. However, the existing papers related to the GFM system are more focused on the problem of frequency support (Xiong et al., 2016; Xiong et al., 2020; Li et al., 2022), and there is less research on the voltage support problem of the GFM wind power system, but with the change in the load side of the wind power system, the voltage support problem is also subject to severe challenges. Therefore, it is necessary to study the voltage response characteristics of GFM wind power systems.

In order to analyze the problem of voltage support in grid-forming wind power systems (GFM WPSs), Pal et al. (2023) proposed a new current saturation strategy for grid-forming inverters, which provides a solution to the low-voltage ride-through problem of grid-forming inverter systems. Liu and Wang (2021) proposed a voltage–magnitude control scheme and analyzed the system transient stability. Luo et al. (2023) proposed an adaptive-output–voltage-regulation-based solution to mitigate the dc-link undervoltage problem and confirmed it by experimental tests. Shang et al. (2021) presented a novel fast-frequency and voltage regulation method for a battery energy storage system (BESS) based on the amplitude-phase-locked-loop. Most of the above analyses of the voltage response characteristics of the GFM WPS focus on the improvement of the control structure and lack a generalized voltage response model of the GFM WPS to describe it. At the same time, the above studies are not accurate on the influencing factors of the voltage response of GFM WPSs, and a detailed study on the influencing factors of the voltage response is needed.

In summary, this study centers on investigating the voltage response characteristics of GFM WPSs. It establishes a voltage response circuit model and mathematical model of the system, analyzing the influencing factors on voltage at the point of common coupling (PCC). Furthermore, the study explores voltage stabilization strategies at the PCC. Finally, simulation verification is conducted using the MATLAB/Simulink platform, providing a theoretical foundation for addressing the voltage support issue in GFM WPSs.

2 Modeling of grid-forming wind power systems

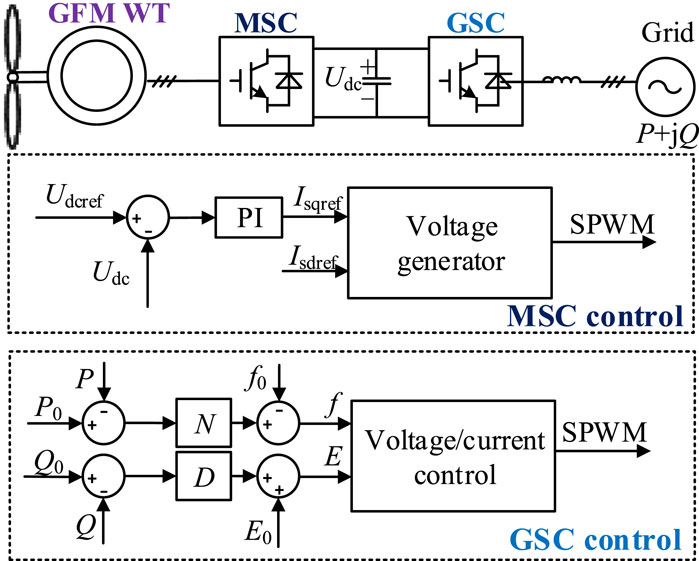
Taking wind permanent-magnet synchronous generators as an example, the structure of a typical GFM WPS is shown in Figure 1, which mainly consists of a wind turbine (WT), machine-side converter (MSC), dc-capacitor, and grid-side converter (GSC). The GFM WT machine-side control is usually in the form of constant voltage control, where the reference values of the rotor d-axis and q-axis currents are controlled by means of dc-capacitor voltage. The control structure used by the GSC is more complex, and the common control structures are droop control, VSG control, and adaptive control. Although the control structures adopted by the GSCs of GFM WT are quite different, their reactive power–voltage control parts and active power–frequency control parts can all be equated with the classical P-f droop control and Q-U droop control (Liu et al., 2022). In the next section, the voltage response of GFM WPSs will be modeled using the Q-U droop control as an example.

Figure 1

Figure 1. Schematic structure of a typical GFM WPS.

2.1 The Q-U droop control of GFM WPSs

When the sum of the inverter equivalent output impedances in GFM WPSs is inductive, the reactive power output from the inverter becomes a primary function of the bus voltage magnitude, so the Q-U droop characteristic equation for GFM WPSs can be described as follows:

$E=E_0+D\left(Q_0-Q\right),(1)$

where $E_0$ is the reference value of the turbine terminal voltage, $E$ is the value of the turbine terminal voltage, $Q_0$ is the reference value of reactive power on the load side, $Q$ is the value of output reactive power on the load side, and $D$ is the $Q$-$U$ droop coefficient, which indicates the slope of the $Q$-$U$ droop curve.

The value of $D$ needs to be selected such that when the reactive power changes by $\mathrm{\Delta }Q$, the voltage amplitude changes within $\mathrm{\Delta }E$, i.e., and the expression for $\mathrm{\Delta }E$ is shown in Equation 2.

$D=\frac{\mathrm{\Delta }E}{\mathrm{\Delta }Q}.(2)$

2.2 Equivalent circuit

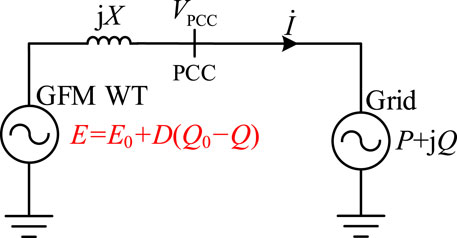
In order to analyze the effect of the GFM wind turbine on the grid voltage, the GFM wind turbine is equated to the form of a three-phase AC voltage source with the phase of the GFM wind turbine as the initial phase while focusing only on the external characteristics of the wind turbine. For the grid side, it can also be equated to the form of a three-phase AC source and disassembled into the form of a superposition of active and reactive power, and the power system can be equated to a single system of GFM wind turbines, as shown in Figure 2, under the premise of considering only the GFM wind turbines and the grid. In Figure 2, ${\dot{V}}_{\text{PCC}}$ is the system voltage phase; $\dot{I}$ is the system current phase; $P$ and $Q$ are the active and reactive power on the load side, respectively; and $X$ is the equivalent output reactance of the inverter, which is shown in Equation 3.

$X=2\pi fL,(3)$

where $f$ is the system frequency and $L$ is the equivalent inductance value of the inverter. According to Equation 1, the wind turbine-side terminal voltage magnitude can be expressed in Equation 4.

$E=E_0+D\left(Q_0-Q\right).(4)$

Figure 2

Figure 2. Equivalent circuit of the GFM WPS.

3 Modeling of voltage response

According to Kirchhoff’s voltage law (KVL), the equivalent circuit voltage equation is

${\displaystyle \dot{E}}-{{\displaystyle \dot{V}}}_{\mathrm{P}\mathrm{C}\mathrm{C}}=\mathrm{j}{\displaystyle \dot{I}}X.(5)$

Taking the phase angle of the voltage at the PCC as a reference and assuming that the phase angle of the terminal voltage at the turbine-side is $\delta$, then, Equation 6 can be obtained through Equation 5.

$E\cos \delta +jE\sin \delta -V_{\mathrm{P}\mathrm{C}\mathrm{C}}=\mathrm{j}X{\displaystyle \dot{I}}.(6)$

The equivalent current can be expressed in Equation 7.

${\displaystyle \dot{I}}=\frac{E\sin \delta }{X}+\mathrm{j}\frac{V_{\mathrm{P}\mathrm{C}\mathrm{C}}-E\cos \delta }{X}.(7)$

For the load-side satisfying Equation 8

$P+jQ=V_{\mathrm{P}\mathrm{C}\mathrm{C}}\left(\frac{E\sin \delta }{X}+\mathrm{j}\frac{E\cos \delta -V_{\mathrm{P}\mathrm{C}\mathrm{C}}}{X}\right).(8)$

Then, the active and reactive power at the load-side can be expressed in Equation 9.

$\left\{\begin{array}{c}P=\frac{E{V}_{\mathrm{P}\mathrm{C}\mathrm{C}}\sin \delta }{X}\hfill \\ Q=\frac{E{V}_{\mathrm{P}\mathrm{C}\mathrm{C}}\cos \delta -V_{\mathrm{P}\mathrm{C}\mathrm{C}}^2}{X}\hfill \end{array}\right..(9)$

Further organizing leads to the following expression which is shown in Equation 10.

$\left\{\begin{array}{c}XP=E{V}_{\mathrm{P}\mathrm{C}\mathrm{C}}\sin \delta \hfill \\ XQ+V_{\mathrm{P}\mathrm{C}\mathrm{C}}^2=E{V}_{\mathrm{P}\mathrm{C}\mathrm{C}}\cos \delta \hfill \end{array}\right..(10)$

Combined with the trigonometric theorem, the above expression can be which is shown in Equation 11.

$X^2{P}^2+{\left(XQ+V_{\mathrm{P}\mathrm{C}\mathrm{C}}^2\right)}^2=E^2{V}_{\mathrm{P}\mathrm{C}\mathrm{C}}^2.(11)$

Furthermore, the square of the voltage magnitude $V_{\text{PCC}}$ at the point of common coupling may be expressed in Equation 12.

$V_{\mathrm{P}\mathrm{C}\mathrm{C}}^2=\frac{E^2-2XQ\pm \sqrt{{\left(2XQ-E^2\right)}^2-4X^2\left(P^2+Q^2\right)}}{2}.(12)$

Mathematically, the following expression needs to be satisfied in order to keep the calculations correct:

${\left(2XQ-E^2\right)}^2-4X^2\left(P^2+Q^2\right)\ge 0.(13)$

Further collation yields the following results which is shown in Equation 14.

$\left\{\begin{array}{cc}2XQ-E^2\ge 2X\sqrt{P^2+Q^2}\hfill & 2XQ\ge E^2\hfill \\ E^2-2XQ\ge 2X\sqrt{P^2+Q^2}\hfill & 2XQ\le E^2\hfill \end{array}\right..(14)$

Combining the above determining conditions, the square of the voltage magnitude $V_{\text{PCC}}$ at the point of common coupling can be expressed in Equation 15.

$2V_{\mathrm{P}\mathrm{C}\mathrm{C}}^2=\left\{\begin{array}{cc}{E}^2-2XQ+\sqrt{{\left(E^2-2XQ\right)}^2-4X^2\left(P^2+Q^2\right)}\hfill & 2XQ\ge E^2\hfill \\ E^2-2XQ-\sqrt{{\left(E^2-2XQ\right)}^2-4X^2\left(P^2+Q^2\right)}\hfill & 2XQ\le E^2\hfill \end{array}\right..(15)$

The above expression is determined by the establishment condition, i.e., $2V_{\mathrm{P}\mathrm{C}\mathrm{C}}^2\ge 0$, and Equation 16 can be obtained:

$\left\{\begin{array}{cc}{E}^2-2XQ+\sqrt{{\left(E^2-2XQ\right)}^2-4X^2\left(P^2+Q^2\right)}\hfill & \ge 0\hfill \\ E^2-2XQ-\sqrt{{\left(E^2-2XQ\right)}^2-4X^2\left(P^2+Q^2\right)}\hfill & \ge 0\hfill \end{array}\right.\Rightarrow \left\{\begin{array}{c}\begin{array}{c}2XQ\le E^2\hfill \end{array}\hfill \\ 2XQ\le E^2.\hfill \end{array}\right.(16)$

Combining the above condition criteria, the calculation result needs to satisfy $2XQ\le E^2$; the above calculation is rounded off, and the square of the dot voltage magnitude $V_{\text{PCC}}$ only has the following expression:

$\left\{\begin{array}{c}\begin{array}{cc}\hfill 2V_{\mathrm{P}\mathrm{C}\mathrm{C}}^2=E^2-2XQ-\sqrt{E^4-4XQ{E}^2-4X^2{P}^2}\hfill & \hfill 2XQ\le E^2\hfill \end{array}\hfill \\ E=E_0+k\left(Q_0-Q\right)\hfill \end{array}\right..(17)$

Substituting Equation 1 into Equation 17 yields the following expression for the voltage magnitude at the point of common coupling which is shown in Equation 18.

$\left\{\begin{array}{c}2V_{\mathrm{P}\mathrm{C}\mathrm{C}}^2={\left[E_0+D\left(Q_0-Q\right)\right]}^2-2XQ\hfill \\ \pm \sqrt{{\left\{{\left[E_0+D\left(Q_0-Q\right)\right]}^2-2XQ\right\}}^2-4X^2\left(P^2+Q^2\right)}\hfill \\ 2XQ\le {\left[E_0+D\left(Q_0-Q\right)\right]}^2\hfill \end{array}\right.(18)$

Combining the above expressions and assuming initial operating conditions where the droop coefficient $D=0$, reactive power $Q=Q_0$, active power $P=P_0$, and initial operating conditions of the voltage amplitude of the grid point can be calculated as shown in Equation 19.

$\left\{\begin{array}{c}2{V_0}^2={E_0}^2-2X{Q}_0\pm \sqrt{{\left({E_0}^2-2X{Q}_0\right)}^2-4X^2\left({P_0}^2+{Q_0}^2\right)}\hfill \\ 2XQ\le {E_0}^2\hfill \end{array}\right..(19)$

Under the condition that the initial working condition is known, in order to facilitate the calculation of voltage magnitude under different working conditions, the expression of voltage magnitude at the point of common coupling is normalized, which can be expressed as follows:

$\left\{\begin{array}{c}{\left(\frac{V_{\mathrm{P}\mathrm{C}\mathrm{C}}}{V_0}\right)}^2=\frac{1}{2}{\left[\frac{E_0+k\left(Q_0-Q\right)}{V_0}\right]}^2-\frac{XQ}{{V_0}^2}\hfill \\ \pm \sqrt{{\left\{\frac{1}{2}{\left[\frac{E_0+k\left(Q_0-Q\right)}{V_0}\right]}^2-\frac{XQ}{{V_0}^2}\right\}}^2-{\left(\frac{X}{V_0}\right)}^2\left(P^2+Q^2\right)}\hfill \\ 2{V_0}^2={E_0}^2-2X{Q}_0\pm \sqrt{{\left({E_0}^2-2X{Q}_0\right)}^2-4X^2\left({P_0}^2+{Q_0}^2\right)}\hfill \end{array}\right.(20)$

4 Voltage response influencing factors and mechanism analysis

According to Equation 20, the voltage amplitude $V_{\text{PCC}}$ is related to four parameters: $P$, $Q$, $X$, and $D$. The effects and mechanisms of these parameters are analyzed subsequently, respectively.

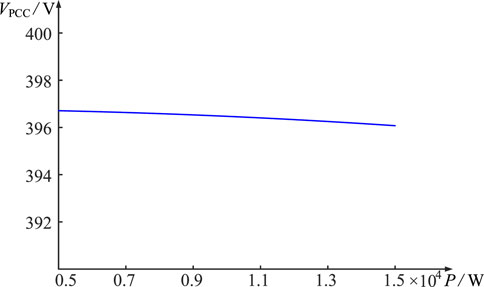
4.1 Effect of active power on voltage magnitude at PCC

According to Figure 3, it can be seen that with the increase in active power $P$, the voltage magnitude $V_{\text{PCC}}$ stays floating at approximately 396.7 V, which is approximated to be unchanged. This is because in the GFM wind turbine inverter control, the active power $P$ is related to the wind turbine frequency but not to the wind turbine terminal voltage, so the increase in the active power $P$ does not affect the common coupling point voltage magnitude, i.e., the active power does not participate in the GFM WPS voltage response process.

Figure 3

Figure 3. Curve of voltage amplitude at PCC with varying active power.

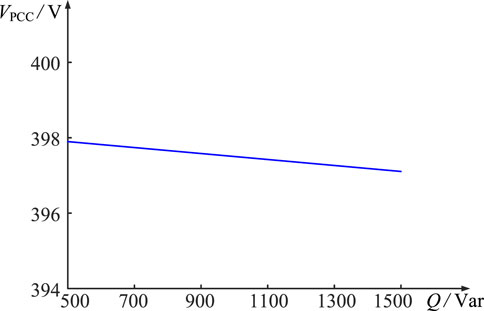
4.2 Effect of reactive power on voltage magnitude at PCC

According to Figure 4, it can be seen that as the reactive power $Q$ increases from 500 Var to 1,500 Var, the voltage magnitude $V_{\text{PCC}}$ shows an overall decreasing trend. This phenomenon arises from the control mechanism of the GFM wind turbine inverter, which is governed by the $Q$-$U$ droop control relationship. As the reactive power $Q$ increases, the wind turbine terminal voltage decreases, consequently reducing the voltage magnitude at the point of common coupling. The slope of the overall curve is directly linked to the droop coefficient $D$.

Figure 4

Figure 4. Curve of voltage amplitude at PCC with varying reactive power.

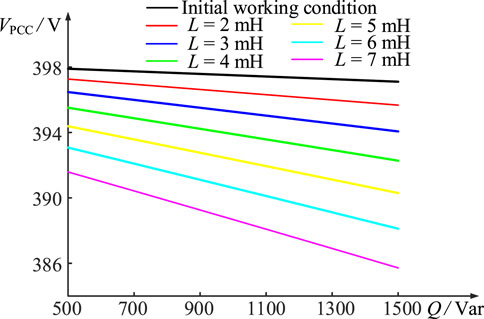
4.3 Effect of equivalent reactance on voltage magnitude at PCC

In order to investigate the effect of the $X$ value on the magnitude of voltage at the point of common coupling, the equivalent inductance value $L$ of the inverter is gradually increased from 1 mH to 7 mH, and the waveform of $V_{\text{PCC}}$ is obtained, as shown in Figure 5.

Figure 5

Figure 5. Curve of voltage amplitude at PCC with varying equivalent reactance.

According to Figure 5, it can be seen that with the increase in the value of $L$, the voltage $V_{\text{PCC}}$ shows an overall decreasing trend. This is because the increase in the $L$ value leads to an increase in the voltage divider on the equivalent reactance of the inverter, while the voltage at the end of the GFM turbine remains unchanged, which results in a gradual decrease in the voltage at the grid point.

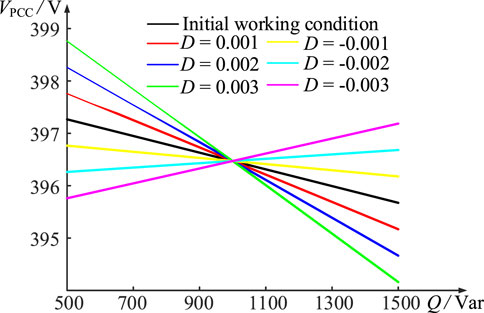
4.4 Effect of droop coefficient on voltage magnitude at PCC

In order to study the effect of the $D$ value on the magnitude of the voltage at the point of common coupling, different values of $D$ were taken and the waveform of $V_{\text{PCC}}$ was obtained, as shown in Figure 6.

Figure 6

Figure 6. Curve of voltage amplitude at PCC with varying droop coefficient.

According to Figure 6, it can be seen that $V_{\text{PCC}}$ shows a complex trend under the influence of $D$: before the image intersection, $V_{\text{PCC}}$ and $D$ are in a positive relationship, i.e., with the increase in $D$, $V_{\text{PCC}}$ is also increased gradually. After the image intersection, $V_{\text{PCC}}$ and $D$ are in an inverse relationship, i.e., with the increase in $D$, $V_{\text{PCC}}$ is decreased gradually. This is because before the intersection point, $Q$ < $Q_0$, and after the intersection point, $Q$ > $Q_0$; the above conclusion can be obtained from the droop relation analysis.

Moreover, in order to achieve better voltage stabilization and explore the reasonableness of the value of $D$, the partial derivative of Equation 5 is taken, i.e.,

$\frac{\mathrm{d}{V}_{\mathrm{P}\mathrm{C}\mathrm{C}}}{\mathrm{d}Q}\to 0.(21)$

Predicting the value of $D$ that satisfies the relation of Equation 13 for different $X$, the waveform of $V_{\text{PCC}}$ under the joint action of $D$ and $X$ is shown in Figure 7.

Figure 7

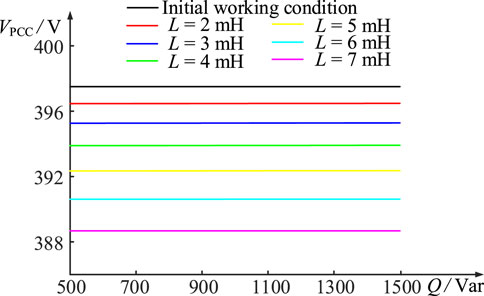
Figure 7. Curve of voltage amplitude at PCC with equivalent reactance and droop coefficient interacting cooperatively.

From Figure 7, it can be seen that under the influence of $D$ and $X$, the waveform of $V_{\text{PCC}}$ is more stable compared to that in Figure 5, and the slope of the waveform is smaller, which plays a role in stabilizing the voltage.

5 Verification

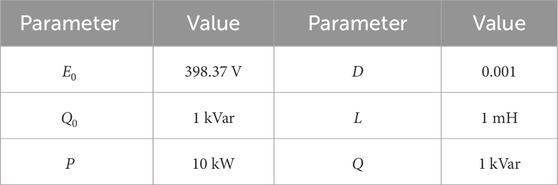
A single WPS was built in the MATLAB/Simulink platform to verify the influence of each influencing factor on the voltage at the point of common coupling in Figure 8. Two simulation conditions were set up to prove the correctness of the above analysis. The specific parameters under the initial working condition are shown in Tables 1, 2.

Figure 8

Figure 8. Circuit structure of the tested WPS.

Table 1

Table 1. Simulation model structural parameters of case 1.

Table 2

Table 2. Simulation model structural parameters of case 2.

Combined with Figures 9, 10, it can be seen that the change in load reactive power $P$ does not have a significant effect on the voltage magnitude $V_{\text{PCC}}$, and it can be assumed that $P$ does not participate in the system voltage response process; however, the change in the three parameters of $Q$, $X$, and $D$ causes the voltage magnitude $V_{\text{PCC}}$ to have a different change, and it can be assumed that $Q$, $X$, and $D$ participate in the voltage response process of the system.

Figure 9

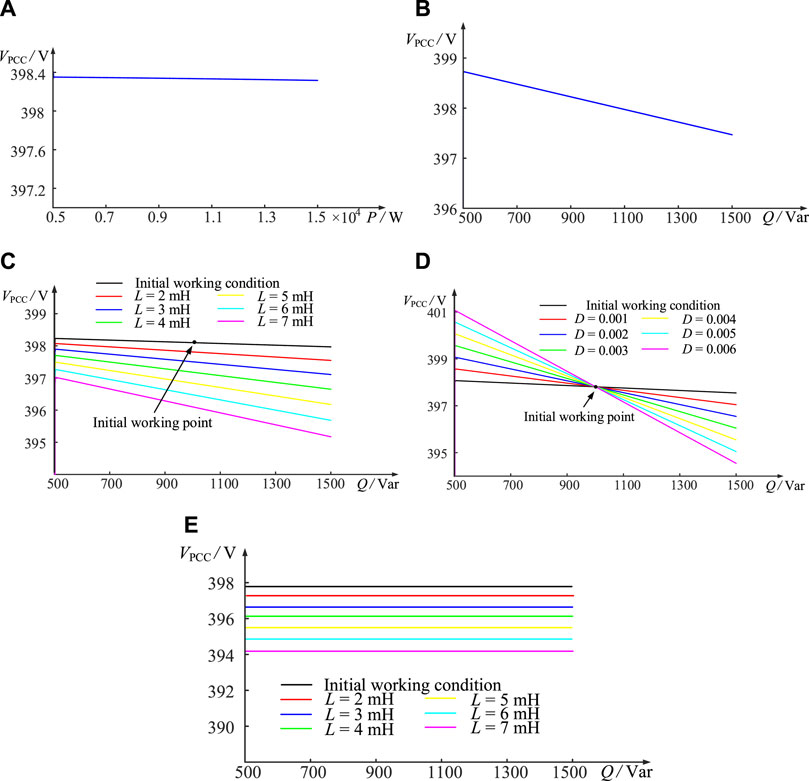
Figure 9. Curve of PCC voltage with different effect factors of case 1. (A) Active power. (B) Reactive power. (C) Equivalent reactance. (D) Droop coefficient. (E) Equivalent reactance and droop coefficient interacting cooperatively.

Figure 10

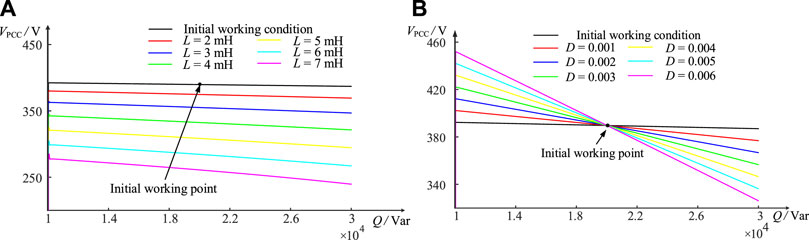
Figure 10. Curve of PCC voltage with different effect factors of case 2. (A) Equivalent reactance. (B) Droop coefficient.

Specifically, in the case of constant inverter equivalent output reactance $X$ and droop coefficient $D$, the voltage magnitude $V_{\text{PCC}}$ gradually decreases with the increase in $Q$. In the case of constant load reactive power $Q$ and droop coefficient $D$, $V_{\text{PCC}}$ gradually decreases with the increase in $X$. In the case of constant load reactive power $Q$ and inverter equivalent output reactance $X$, $V_{\text{PCC}}$ exhibits a complicated trend.

These phenomena are inextricably linked to the $Q$-$U$ droop control relationship of the GFM wind turbine. From Equation 1, it can be seen that with the increase in $Q$, the turbine end voltage $E$ gradually decreases, which indirectly causes the decrease in $V_{\text{PCC}}$. At the same time, with the increase in $Q$, the more partial voltage on $X$ further aggravates the drop of $V_{\text{PCC}}$; in the case of the same reactive power $Q$, the larger the value of $X$, the more the partial voltage on it. The droop coefficient has a more complex impact on $V_{\text{PCC}}$, and unreasonable $D$ will lead to the fluctuation of $V_{\text{PCC}}$ becoming larger. Specifically, before the initial working point (IWP), the amplitude of $V_{\text{PCC}}$ increases as $D$ increases because $Q$ < $Q_0$, and after the IWP, the amplitude of $V_{\text{PCC}}$ decreases instead as $D$ increases because $Q$ > $Q_0$. To ensure that the $V_{\text{PCC}}$ maintains stability, the setting of the droop coefficient should satisfy Equation 21, and its simulation results are shown in Figure 9E. Under the effect of droop control, $V_{\text{PCC}}$ can remain stable when the reactive power $Q$ changes.

In order to better reflect the impact of the effect factors on $V_{\text{PCC}}$, the effect factors were organized into a table, as shown in Table 3.

Table 3

Table 3. Impact of effect factors on $V_{\text{PCC}}$.

6 Conclusion

In this study, the voltage response characteristics of the system at the point of common coupling and the voltage stabilization strategy are investigated by modeling analysis and simulation verification with GFM WPS as the research object. The main conclusions are as follows:

1) The voltage response circuit model and mathematical model of the system are established; the expression for the voltage magnitude $V_{\text{PCC}}$ at the point of common coupling is derived, and the affecting components $P$, $Q$, $X$, and $D$ in the expression are examined. It is discovered that the voltage at the point of common coupling is mainly affected by $Q$, $X$, and $D$, where the voltage magnitude $V_{\text{PCC}}$ is inversely proportional to $Q$ and $X$, while the effect of $D$ is related to the IWP.

2) The voltage stabilization method is further investigated by analyzing the expression for the voltage magnitude $V_{\text{PCC}}$ at the point of common coupling, and its feasibility is theoretically analyzed. Furthermore, the stabilization of $V_{\text{PCC}}$ is achieved by adjusting the droop coefficient $D$.

3) The simulation verification of the influencing elements and voltage stabilization method is performed using the MATLAB/Simulink platform, and the above influencing factors and the proposed voltage stabilization strategy were verified, which proved the reliability of the analysis. At the same time, it provides a theoretical foundation for solving the voltage stabilization support problem in a new energy GFM system.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

QuL: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. QiL: conceptualization, data curation, investigation, software, validation, and writing–review and editing. WT: formal analysis, investigation, project administration, and writing–review and editing. CW: supervision, visualization, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the science and technology project of the State Grid Jiangsu Electric Power Co., Ltd. (J2023021).

Acknowledgments

The authors wish to thank the science and technology project of the State Grid Jiangsu Electric Power Co., Ltd., for the project funding (J2023021).

Conflict of interest

Authors QuL, QiL, WT, and CW were employed by State Grid Jiangsu Electric Power Co., Ltd.

The authors declare that this study received funding from State Grid Jiangsu Electric Power Co., Ltd. The funder had the following involvement in the study: the study design, collection, analysis, interpretation of data, and the writing of this article.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Fang, J., Li, H., Tang, Y., and Blaabjerg, F. (2018). Distributed power system virtual inertia implemented by grid-connected power converters. IEEE Trans. Power Electron. 33, 8488–8499. doi:10.1109/tpel.2017.2785218

CrossRef Full Text | Google Scholar

Kang, C., and Yao, L. (2017). Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy. Dianli Xit. Zidonghua/Automation Electr. Power Syst. 41, 2–11.

Google Scholar

Kim, G. G., Hyun, J. H., Choi, J. H., ahn, S.-H., Bhang, B. G., and Ahn, H.-K. (2023). Quality analysis of photovoltaic system using descriptive statistics of power performance index. IEEE Access 11, 28427–28438. doi:10.1109/access.2023.3257373

CrossRef Full Text | Google Scholar

Leon, A. E., Nozal, Ã. R. d., and Mauricio, J. M. (2024). Frequency support strategy for fast response energy storage systems. IEEE Trans. Power Syst. 39, 5439–5442. doi:10.1109/tpwrs.2024.3358631

CrossRef Full Text | Google Scholar

Li, Y., Hu, J., Wen, W., Wang, Q., Ma, S., and Guo, J. (2022). Concept and definition of dynamic symmetrical components with time-varying amplitude and frequency. IEEE Trans. Energy Convers. 37, 2737–2748. doi:10.1109/tec.2022.3188864

CrossRef Full Text | Google Scholar

Liu, T., Chen, A., Gao, F., Liu, X., Li, X., and Hu, S. (2022). Double-loop control strategy with cascaded model predictive control to improve frequency regulation for islanded microgrids. IEEE Trans. Smart Grid 13, 3954–3967. doi:10.1109/tsg.2021.3129220

CrossRef Full Text | Google Scholar

Liu, T., and Wang, X. (2021). Transient stability of single-loop voltage-magnitude controlled grid-forming converters. IEEE Trans. Power Electron. 36, 6158–6162. doi:10.1109/tpel.2020.3034288

CrossRef Full Text | Google Scholar

Luo, C., Ma, X., Liu, T., and Wang, X. (2023). Adaptive-output-voltage-regulation-based solution for the dc-link undervoltage of grid-forming inverters. IEEE Trans. Power Electron. 38, 12559–12569. doi:10.1109/tpel.2023.3298468

CrossRef Full Text | Google Scholar

Ouyang, J., Li, M., Zhang, Z., and Tang, T. (2019). Multi-timescale active and reactive power-coordinated control of large-scale wind integrated power system for severe wind speed fluctuation. IEEE Access 7, 51201–51210. doi:10.1109/access.2019.2911587

CrossRef Full Text | Google Scholar

Pal, A., Pal, D., and Panigrahi, B. K. (2023). A current saturation strategy for enhancing the low voltage ride-through capability of grid-forming inverters. IEEE Trans. Circuits Syst. II Express Briefs 70, 1009–1013. doi:10.1109/tcsii.2022.3221134

CrossRef Full Text | Google Scholar

Rosso, R., Wang, X., Liserre, M., Lu, X., and Engelken, S. (2021). Grid-forming converters: control approaches, grid-synchronization, and future trends—a review. IEEE Open J. Industry Appl. 2, 93–109. doi:10.1109/ojia.2021.3074028

CrossRef Full Text | Google Scholar

Shang, L., Dong, X., Liu, C., and Gong, Z. (2021). Fast grid frequency and voltage control of battery energy storage system based on the amplitude-phase-locked-loop. IEEE Trans. Smart Grid 13, 941–953. doi:10.1109/tsg.2021.3133580

CrossRef Full Text | Google Scholar

Shang, L., Hua, Z., Liu, C., and Dong, X. (2022). Amplitude-phase-locked-loop-based power injection strategy for wind power generation under three-phase grid fault. IEEE Trans. Energy Convers. 37, 2952–2961. doi:10.1109/tec.2022.3207285

CrossRef Full Text | Google Scholar

Shao, H., Cai, X., Zhou, D., Li, Z., Zheng, D., Cao, Y., et al. (2019). Equivalent modeling and comprehensive evaluation of inertia emulation control strategy for dfig wind turbine generator. IEEE Access 7, 64798–64811. doi:10.1109/access.2019.2917334

CrossRef Full Text | Google Scholar

Verma, P., K, S., and Dwivedi, B. (2023). A self-regulating virtual synchronous generator control of doubly fed induction generator-wind farms. IEEE Can. J. Electr. Comput. Eng. 46, 35–43. doi:10.1109/icjece.2022.3223510

CrossRef Full Text | Google Scholar

Wu, H., and Wang, X. (2021). Passivity-based dual-loop vector voltage and current control for grid-forming vscs. IEEE Trans. Power Electron. 36, 8647–8652. doi:10.1109/tpel.2020.3048239

CrossRef Full Text | Google Scholar

Xi, J., Geng, H., and Zou, X. (2021). Decoupling scheme for virtual synchronous generator controlled wind farms participating in inertial response. J. Mod. Power Syst. Clean Energy 9, 347–355. doi:10.35833/mpce.2019.000341

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Zhang, D., and Liu, Y. (2021). Rapid power compensation-based frequency response strategy for low-inertia power systems. IEEE J. Emerg. Sel. Top. Power Electron. 9, 4500–4513. doi:10.1109/jestpe.2020.3032063

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Zhao, C., and Zhuo, F. (2020). A fast and robust real-time detection algorithm of decaying dc transient and harmonic components in three-phase systems. IEEE Trans. Power Electron. 35, 3332–3336. doi:10.1109/tpel.2019.2940891

CrossRef Full Text | Google Scholar

Xiong, L., Zhuo, F., Wang, F., Liu, X., Chen, Y., Zhu, M., et al. (2016). Static synchronous generator model: a new perspective to investigate dynamic characteristics and stability issues of grid-tied pwm inverter. IEEE Trans. Power Electron. 31, 6264–6280. doi:10.1109/tpel.2015.2498933

CrossRef Full Text | Google Scholar

Yang, B., Li, Y., Yao, W., Jiang, L., Zhang, C., Duan, C., et al. (2023). Optimization and control of new power systems under the dual carbon goals: key issues, advanced techniques, and perspectives. Energies 16, 3904. doi:10.3390/en16093904

CrossRef Full Text | Google Scholar