A new transient phenomenon caused by active current dynamics of grid-following converters during severe grid faults

Existing transient stability analysis of grid-following (GFL) converters mainly focuses on the dynamics of the phase-locked loop (PLL), while current loop dynamics are usually neglected due to their faster response than PLL. However, this article reveals that active current may not be able to track its reference quickly during severe grid faults even with high current loop bandwidth, which leads to a non-negligible impact on the transient stability of GFL converters. Furthermore, this article discusses the intrinsic mechanism of why active current cannot track its reference quickly during severe grid faults and establishes a refined third-order transient synchronization model that offers a more accurate assessment of transient stability during severe grid faults than the conventional second-order model.

1 Introduction

With the continuous integration of renewable energy into modern power systems through grid-following (GFL) converters, the transient stability of GFL converters during grid faults is receiving increasing attention. It has been found that a GFL converter may experience loss of synchronization (LOS) during grid faults (Göksu et al., 2014; Xiong et al., 2020). Various analysis techniques have been applied to understand the synchronization instability mechanism, such as the equal-area criteria (He et al., 2021), phase portraits (Wu and Wang, 2020), and the energy function method (Tian et al., 2022).

The aforementioned studies mainly focus on the dynamics of the phase-locked loop (PLL), neglecting the current loop dynamics due to their faster response. However, it has been pointed out that ignoring current loop dynamics when the current loop bandwidth is not high enough may lead to incorrect transient stability assessment (Chen et al., 2020). Then, a high-order transient synchronization model considering the coupling effect between the PLL and current loop is established to analyze the impact mechanism of current loop dynamics (Hu et al., 2021). Furthermore, the work by Wu et al. (2024) gives a conservative bandwidth boundary that can ignore the current loop dynamics. The above studies suggest that the current loop dynamics may harm the transient stability of GFL converters. Nevertheless, the changes in the current reference are not considered, which could potentially invalidate the conclusion during severe grid faults.

In fact, according to the grid code requirements, GFL converters must inject reactive current to support the grid voltage during the low-voltage ride-through process. Particularly, GFL converters should inject pure reactive current during severe grid faults (Yuan et al., 2019). Under this situation, this article observes that although reactive current tracks its reference quickly, active current may undergo obvious dynamic attenuation even with high current loop bandwidth. This phenomenon challenges the assumption of treating the current loop as a unity gain in transient stability modeling, as the active current dynamics have a non-negligible impact on the transient stability. The zero-pole characteristics of the current loop are analyzed to reveal the intrinsic mechanism of why active current cannot track its reference quickly during severe grid faults. Then, a refined third-order transient synchronization model considering active current dynamics is established, which offers a more accurate assessment of the transient stability during severe grid faults than the conventional second-order model. Finally, the impact of active current dynamics is validated through experimental results.

2 Misjudgment of the second-order model

Figure 1A illustrates the topology and control diagram of the GFL converter. U_pcc = U_pcc∠θ_pcc represents the voltage of the point of common coupling (PCC). U_g = U_g∠θ_g represents the grid voltage. U_c represents the voltage at the converter port. I_pcc is the output current of the converter. L_f and R_f are the filter inductance and parasitic resistance. L_g and R_g are the grid inductance and resistance.

Figure 1

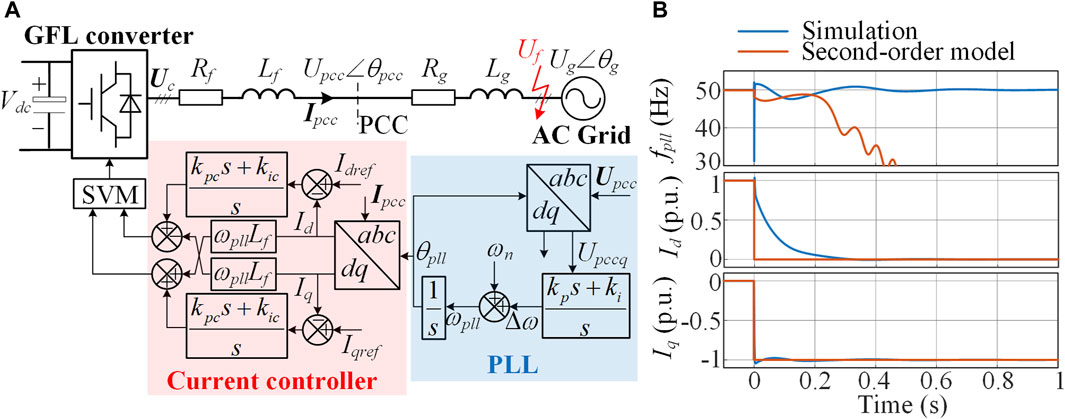
Figure 1. (A) Topology and control diagram of the GFL converter, and (B) simulation results and solutions of the second-order model with a grid fault voltage of U_f = 0.05 p.u.

A synchronous reference frame PLL is used to extract the phase angle information of the point of common coupling (PCC) voltage, in which θ_pll and ω_pll are the output phase angle and angular frequency, respectively. ω_n is the norm angular frequency, which is a constant of 100π. k_p and k_i are the PI parameters of the PLL. The current control in Figure 1A is oriented by the PLL. The outer loop control is disconnected during grid faults, and the current references I_dref and I_qref are directly designated according to the grid code (Yuan et al., 2019; He et al., 2021). The PI parameters of the current control are denoted as k_pc and k_ic.

According to Tian et al. (2022), if the current loop is approximated as a unity gain, that is, I_d ≈ I_dref and I_q ≈ I_qref, the transient synchronization process of the GFL converter during grid faults can be described by a second-order nonlinear model as (1), in which the phase error of the PLL is defined as δ = θ_pll−θ_g.

$\left\{\begin{array}{l}\dot{\delta }=\Delta \omega \\ \Delta \dot{\omega }=\frac{-U_f{k}_p\dot{\delta }\cos \delta +k_i\left(-U_f\sin \delta +{\omega }_{pll}{L}_g{I}_{dref}+R_g{I}_{qref}\right).}{1-k_p{L}_g{I}_{dref}}\end{array}\right.(1)$

When a severe grid fault occurs with a fault voltage of U_f = 0.05 p.u., simulation results and solutions of the second-order model are as shown in Figure 1B. The solutions of the second-order model show that the PLL frequency f_pll is unable to converge, and LOS occurs. However, the simulation results demonstrate that only the reactive current I_q tracks its reference quickly, while active current I_d undergoes obvious dynamic attenuation even with a high current loop bandwidth of 500 Hz. The simulation system ultimately maintains synchronicity with the grid, which contradicts the results of the second-order model. The above results indicate that the second-order model cannot capture the dynamic process of active current during severe grid faults, leading to a misjudgment of transient stability.

3 Intrinsic mechanism of active current dynamics during severe grid faults

According to the main circuit structure in Figure 1A, the dq-axis voltage at the converter port can be obtained as (2), where R = R_f + R_g represents the sum of the parasitic filter resistance and the grid resistance and L = L_f + L_g represents the sum of the filter inductance and the grid inductance. s is the Laplace operator.

$\left\{\begin{array}{c}{U}_{cd}=U_g\cos \delta +R{I}_d-{\omega }_{pll}L{I}_q+sL{I}_d\\ U_{cq}=-U_g\sin \delta +R{I}_q+{\omega }_{pll}L{I}_d+sL{I}_q\end{array}\right..(2)$

The output of the current controller is approximately equal to U_cd and U_cq. So, according to the control structure, the control equations for U_cd and U_cq are obtained as follows:

$\left\{\begin{array}{c}{U}_{cd}=\frac{k_{pc}s+k_{ic}}{s}\left(I_{dref}-I_d\right)-{\omega }_{pll}{L}_f{I}_{q.}\\ U_{cq}=\frac{k_{pc}s+k_{ic}}{s}\left(I_{qref}-I_q\right)+{\omega }_{pll}{L}_f{I}_d\end{array}\right.(3)$

Combining (2) and (3), the dq-axis current can be derived as follows:

$\left\{\begin{array}{c}{I}_d=G_1\left(s\right)I_{dref}+G_2\left(s\right)\left({\omega }_{pll}{L}_g{I}_q-U_g\cos \delta \right)\\ I_q=G_1\left(s\right)I_{qref}+G_2\left(s\right)\left(U_g\sin \delta -{\omega }_{pll}{L}_g{I}_d\right).\end{array}\right.(4)$

$\left\{\begin{array}{c}{G}_1\left(s\right)=\frac{s{k}_{pc}+k_{ic}}{L{s}^2+\left(k_{pc}+R\right)s+k_{ic}}\\ G_2\left(s\right)=\frac{s}{L{s}^2+\left(k_{pc}+R\right)s+k_{ic}}\end{array}\right..(5)$

According to Eqs 4, 5, the impact of grid voltage changes on the current dynamics is characterized by G₂(s). Because G₂(s) is a bandpass filter, the bandwidth of the current loop cannot reflect the speed of dynamic response caused by grid voltage changes. Therefore, even if the current loop bandwidth is large enough, it cannot guarantee that the current dynamics caused by grid voltage changes will be fast.

The zero-pole characteristics of the current loop are analyzed to reveal the intrinsic mechanism of why active current cannot track its reference quickly during severe grid faults. According to the zero-pole elimination approach, the parameters of the current loop are set as k_pc = ω_cL_f and k_ic = ω_cR_f, where ω_c represents the open-loop crossover angular frequency. This configuration results in a non-dominant pole p₁ and a dominant pole p₂ on the negative real axis. The approximate expressions for the poles are given as Eqs 6, 7

$p_1=-\frac{k_{pc}+R+\sqrt{{\left(k_{pc}+R\right)}^2-4k_{ic}L}}{2L}\approx -\frac{k_{pc}+R}{L}.(6)$

$p_2=\frac{k_{ic}}{L{p}_1}\approx -\frac{k_{ic}}{k_{pc}+R.}(7)$

The zero of G₁(s) is z₁ = −k_ic/k_pc, which is approximately equal to the dominant pole p₂ because the P gain of the current controller k_pc is typically much larger than the resistance R. Hence, z₁ and p₂ are canceled out, leading to a fast response to changes in the current reference. However, the zero of G₂(s) is located at the origin, which cannot be canceled by the dominant pole. Therefore, the response speed of G₂(s) is much lower than that of G₁(s).

Based on the above analysis, the current dynamics are dominated by p₂ and the zero of G₂(s), while G₁(s) and the non-dominant pole of G₂(s) can be neglected. Consequently, the expressions for the current dynamics ΔI_dq can be formulated as (8), where δ₀ and I_q0 represent the stable phase error and the reactive current prior to the grid fault, respectively.

$\left\{\begin{array}{l}\Delta I_d=\frac{s}{k_{ic}\left(1-\frac{s}{p_2}\right)}\left({\omega }_{pll}{L}_g{I}_q-{\omega }_g{L}_g{I}_{q0}+U_g\cos {\delta }_0-U_f\cos \delta \right).\\ \Delta I_q=\frac{s}{k_{ic}\left(1-\frac{s}{p_2}\right)}\left(U_f\sin \delta -{\omega }_{pll}{L}_g{I}_d-R_g{I}_{q0}\right)\end{array}\right.(8)$

From the expression of ΔI_q, the input includes three terms: U_f sinδ, −ω_pllL_gI_d, and −R_gI_q0. During severe faults, the fault voltage U_f is small. The converter must output reactive current to support the grid voltage, so the active current I_d cannot be very large. In addition, the pre-fault reactive current I_q0 is generally 0. Therefore, the reactive current dynamics are small, that is, ΔI_q≈0, which means that the reactive current can track its reference quickly. However, the input of the active current dynamics has two large terms ω_pllL_gI_q and U_gcosδ₀, leading to obvious active current dynamics.

4 Third-order transient synchronization model

According to the above analysis, the active current dynamics are much larger than the reactive current dynamics during severe grid faults. Additionally, the input voltage of the PLL includes the grid impedance voltage drop R_gI_q + X_gI_d. Typically, X_g is greater than R_g, so the active current dynamics have a dominant impact on the transient synchronization process, while the impact of the reactive current dynamics can be ignored.

Considering the active current dynamics, the q-axis component of the PCC voltage is corrected as

$\begin{array}{c}{U}_{pccq}=-U_f\sin \delta +R_g{I}_{qref}+{\omega }_{pll}{L}_g{I}_{dref}+\left({\omega }_g+\Delta \omega \right)L_g\Delta I_d\\ \approx -U_f\sin \delta +R_g{I}_{qref}+{\omega }_{pll}{L}_g{I}_{dref}+{\omega }_g{L}_g\Delta I_d\end{array}.(9)$

According to Equation 8, voltage disturbances generate the active current dynamics through a high-pass filter. The grid voltage sag and switching of the reactive current reference have the main impact on the current dynamics, while the slow changes in the phase error δ and the PLL frequency ω_pll have a relatively small impact. Hence, the active current dynamics can be approximated as

$\Delta I_d\approx \frac{s}{k_{ic}\left(1-\frac{s}{p_2}\right)}\left[\left(U_g-U_f\right)\cos {\delta }_0+{\omega }_g{L}_g\left(I_{qref}-I_{q0}\right)\right].(10)$

According to the PLL structure in Figure 1A, the dynamics of the PLL are expressed as

$\ddot{\delta }=k_p{\dot{U}}_{pccq}+k_i{U}_{pccq}.(11)$

Combining Equations 9–11 and taking the phase error δ, the angular frequency error Δω, and the active current dynamics ΔI_d as state variables, a third-order state space equation is derived as

$\left\{\begin{array}{l}\dot{\delta }=\Delta \omega \hfill \\ \Delta \dot{\omega }=\frac{k_p\left(-U_f\dot{\delta }\cos \delta +{\omega }_g{L}_g\Delta {\dot{I}}_d\right)}{1-k_p{L}_g{I}_{dref}}+\frac{k_i\left(-U_f\sin \delta +{\omega }_{pll}{L}_g{I}_{dref}+R_g{I}_{qref}+{\omega }_g{L}_g\Delta I_d\right).}{1-k_p{L}_g{I}_{dref}}\hfill \\ \Delta {\dot{I}}_d=p_2\Delta I_d\end{array}\right.(12)$

According to the Eq 12, a refined third-order transient synchronization model of the GFL converter is established, as illustrated in Figure 2A. The black part is a PLL-based second-order transient synchronization model, while the red part represents the impact of active current dynamics on PLL dynamics. The transient active current ΔI_d generates a transient voltage drop ΔU_L on the grid impedance, which affects the PCC voltage and subsequently affects the transient synchronization process.

Figure 2

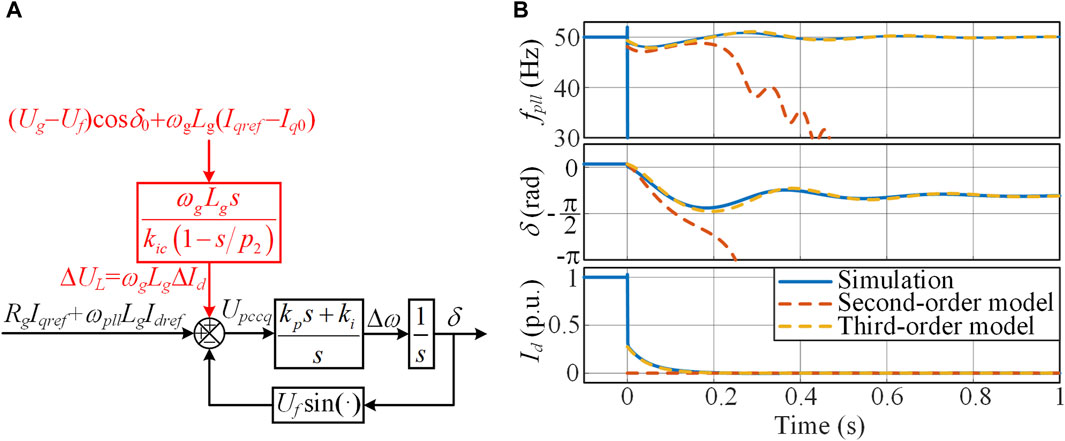
Figure 2. (A) Third-order transient synchronization model, and (B) transient response with a fault voltage of U_f = 0.05 p.u.

5 Simulation and experimental verification

A full-order simulation model based on Figure 1A is constructed using MATLAB/Simulink to validate the correctness of the third-order transient synchronization model, and the simulation results are compared with the solutions of the reduced-order models. The rated voltage and rated power of the system are 690 V and 1.5 MW, respectively. The parameters related to the filter and grid impedance are L_f = 0.1 mH, R_f = 2.1 mΩ, L_g = 0.11 mH, and R_g = 13 mΩ. The damping ratio of the PLL is 1.2, and the bandwidth is approximately 50 Hz. The parameters of the current loop are k_pc = 0.95 and k_ic = 20.

With a fault voltage of U_f = 0.05 p.u., the transient response is shown in Figure 2B. The third-order model closely aligns with the simulation results, while the second-order model does not match the simulation results, validating the correctness of the third-order transient synchronization model.

Experiments are conducted in a control hardware-in-loop (CHIL) platform to verify the impact of active current dynamics. The detailed experimental platform is shown in Figure 3. The main circuit is developed in Typhoon 602+, and the system is controlled by a TMS320F28335/Spartan 6 XC6SLX16 DSP + FPGA control board. The sampling frequency is set as 5 kHz. Other parameters are consistent with the simulation parameters above.

Figure 3

Figure 3. Hardware platform of the CHIL experiment.

The experimental results using the above parameters are shown in Figure 4A. The figure sequentially shows the waveforms of the grid line voltage U_gab, d-axis current I_d, q-axis current I_q, phase error δ, and PLL frequency f_pll. When the grid voltage drops from 1.0 p.u. to 0.05 p.u., the current reference switches quickly. The active current reference I_dref switches from 1.0 p.u. to 0, while the reactive current reference I_qref switches from 0 to −1 p.u. As the steady-state operating point changes, the system enters the transient synchronization process. During this process, the reactive current quickly tracks its reference and stabilizes at −1 p.u., while the active current undergoes a dynamic decay process of over 100 ms. As a result, the system maintains synchronicity with the grid, which is consistent with the theoretical analysis and simulation results.

Figure 4

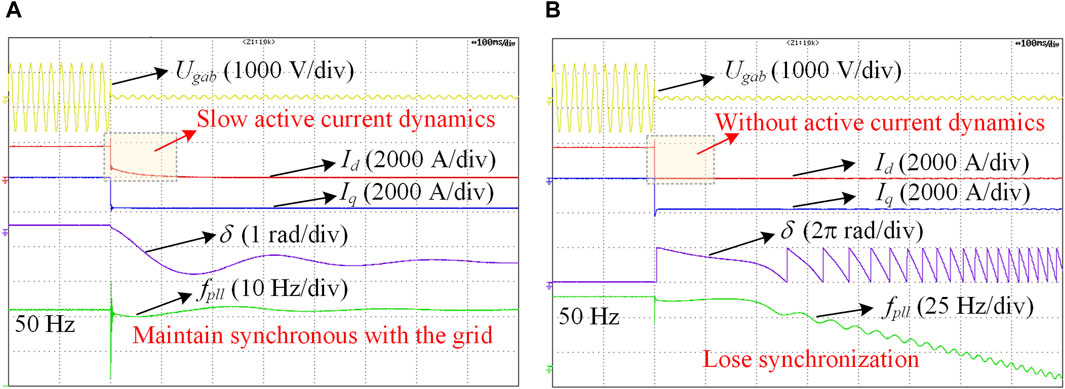
Figure 4. Experimental results. (A) With slow active current dynamics and (B) without active current dynamics.

Increasing k_ic can increase the absolute value of the dominant pole p₂, thereby accelerating the active current dynamics. In this case, the experimental results are shown in Figure 4B. Both active and reactive current can quickly track their references. However, without slow active current dynamics, the PLL frequency decreases continuously, and a loss of synchronization occurs. The experimental results demonstrate that the active current dynamics have a non-negligible impact on the transient stability of GFL converters.

6 Conclusion

This article discusses the intrinsic mechanism of why active current cannot track its reference quickly during severe grid faults. The transfer function from grid voltage disturbance to current output has a zero located at the origin and a dominant pole, resulting in a slow dynamic response. In addition, severe grid faults have a much greater impact on active current dynamics than reactive current dynamics. Therefore, active current will undergo obvious dynamic attenuation during severe grid faults. The coupling of active current dynamics and the grid impedance generates a transient voltage that affects the transient synchronization process. Accordingly, a refined third-order transient synchronization model is established, which offers a more accurate assessment of the transient stability of GFL converters during severe grid faults than the conventional second-order model.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

CW: validation, methodology, supervision, conceptualization, and writing–review and editing. ZH: software, investigation, and writing–original draft. YW: validation, supervision, and writing–review and editing. FB: supervision and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation of China under Grant 52207063.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, J., Liu, M., O’Donnell, T., and Milano, F. (2020). Impact of current transients on the synchronization stability assessment of grid-feeding converters. IEEE Trans. Power Syst. 35, 4131–4134. doi:10.1109/tpwrs.2020.3009858

CrossRef Full Text | Google Scholar

Göksu, Ö., Teodorescu, R., Bak, C. L., Iov, F., and Kjær, P. C. (2014). Instability of wind turbine converters during current injection to low voltage grid faults and PLL frequency based stability solution. IEEE Trans. Power Syst. 29, 1683–1691. doi:10.1109/tpwrs.2013.2295261

CrossRef Full Text | Google Scholar

He, X., Geng, H., Xi, J., and Guerrero, J. M. (2021). Resynchronization analysis and improvement of grid-connected VSCs during grid faults. IEEE J. Emerg. Sel. Top. Power Electron. 9, 438–450. doi:10.1109/jestpe.2019.2954555

CrossRef Full Text | Google Scholar

Hu, Q., Fu, L., Ma, F., Ji, F., and Zhang, Y. (2021). Analogized synchronous-generator model of PLL-based VSC and transient synchronizing stability of converter dominated power system. IEEE Trans. Sustain. Energy. 12, 1174–1185. doi:10.1109/tste.2020.3037155

CrossRef Full Text | Google Scholar

Tian, Z., Tang, Y., Zha, X., Sun, J., Huang, M., Fu, X., et al. (2022). Hamilton-based stability criterion and attraction region estimation for grid-tied inverters under large-signal disturbances. IEEE J. Emerg. Sel. Top. Power Electron. 10, 413–423. doi:10.1109/jestpe.2021.3076189

CrossRef Full Text | Google Scholar

Wu, C., Lyu, Y., Wang, Y., and Blaabjerg, F. (2024). Transient synchronization stability analysis of grid-following converter considering the coupling effect of current loop and phase locked loop. IEEE Trans. Energy Convers. 39, 544–554. doi:10.1109/tec.2023.3314095

CrossRef Full Text | Google Scholar

Wu, H., and Wang, X. (2020). Design-oriented transient stability analysis of PLL-synchronized voltage-source converters. IEEE Trans. Power Electron. 35, 3573–3589. doi:10.1109/tpel.2019.2937942

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Zhao, C., and Zhuo, F. (2020). A fast and robust real-time detection algorithm of decaying DC transient and harmonic components in three-phase systems. IEEE Trans. Power Electron. 35, 3332–3336. doi:10.1109/tpel.2019.2940891

CrossRef Full Text | Google Scholar

Yuan, H., Xin, H., Huang, L., Wang, Z., and Wu, D. (2019). Stability analysis and enhancement of type-4 wind turbines connected to very weak grids under severe voltage sags. IEEE Trans. Energy Convers. 34, 838–848. doi:10.1109/tec.2018.2882992

CrossRef Full Text | Google Scholar