Day-ahead and hour-ahead optimal scheduling for battery storage of renewable energy power stations participating in primary frequency regulation

Due to the fast response characteristics of battery storage, many renewable energy power stations equip battery storage to participate in auxiliary frequency regulation services of the grid, especially primary frequency regulation (PFR). In order to make full use of the battery capacity and improve the overall revenue of the renewable energy station, a two-level optimal scheduling strategy for battery storage is proposed to provide primary frequency regulation and simultaneously arbitrage, according to the peak-valley electricity price. The energy storage output is composed of the droop-based primary frequency regulation output and the economic output, according to the electricity price. First, day-ahead optimization defines the economic output profile and an appropriate droop coefficient, considering regulation needs, with the goal of maximizing the overall return. The scheduling result is then adjusted for hour-ahead optimization based on the updated regulation information to ensure more durable and reliable performance. Simulation results show that the proposed scheduling strategy can fully utilize the battery capacity, realize peak-valley arbitrage while assuming the obligation of primary frequency regulation of the renewable energy power station, and then improve the overall income of the power station.

1 Introduction

Nowadays, many countries in the world are vigorously developing renewable energy power generation, such as wind power and photovoltaic (PV) power. Compared with traditional thermal power generation, renewable energy power generation is more environmentally friendly due to the use of clean and renewable energy. However, most renewable energy power units are connected to the grid through inverters, which decrease the inertia and damping of the grid (Xiong et al., 2022). Moreover, renewable energy units often operate in the maximum power tracking mode, which makes it difficult for them to cope with active power instantaneous fluctuations in the grid; in other words, they lack primary frequency regulation (PFR) capability. Related research equips renewable energy units with the primary frequency regulation ability by improving their control algorithms, but they still have certain shortcomings (Mahish and Pradhan, 2020; Li et al., 2021). For instance, wind turbines need to operate at the right speed to participate in PFR (Ma et al., 2024). PV units are mostly involved in PFR through load shedding, which greatly reduces their operating economy (Cristaldi et al., 2022).

Under the above context, the use of the battery energy storage system (BESS) to undertake the primary frequency regulation task of renewable energy power stations has emerged. It is shown that BESS participating in PFR can effectively improve the system frequency (Turk et al., 2019). With the coordination of energy storage and renewable energy power stations, renewable energy units do not need to participate in PFR, and all generated electricity is connected to the grid. BESS utilizes its speed and flexibility to actively respond to primary frequency regulation signals. As more countries start to implement time-of-use electricity pricing policies, BESS can also perform peak shaving and valley filling based on the output of renewable energy generation when its capacity is sufficient. The combination of the renewable energy power station and BESS mentioned above can not only improve the grid-connected characteristics but also further increase the revenue of the integrated station (IS).

A lot of studies have been conducted on BESSs providing PFR services. Zhu and Zhang (2019) divided the PFR control into frequency regulation and state-of-charge (SOC) recovery phases. For frequency regulation, it optimizes the charge and discharge power of the BESS online based on the determined frequency regulation requirements of the grid. Most of the PFR power of BESSs is obtained by a droop-based control mechanism, according to the system frequency difference (Arrigo et al., 2020; Fang et al., 2020; Xiong et al., 2021; Zhao et al., 2022). Most BESSs under droop control set a fixed droop coefficient in their factory settings, but a fixed droop coefficient cannot satisfy various frequency regulation conditions (Xiong et al., 2021). Schiapparelli et al. (2018); Feng et al. (2024) dynamically adjusted the droop coefficient based on the prediction of future system frequency differences or the SOC of BESSs to maintain a long-term reliable operation. The above research mainly focuses on BESSs participating solely in PFR, while the relevant literature has studied BESSs providing multiple auxiliary services, including PFR. Ma et al. (2022) considered a shared BESS performing PFR and automatic generation control (AGC) for multiple renewable energy power stations. This paper only describes the formulation of the hour-ahead optimization strategy and does not involve the content of the day-ahead optimization strategy. According to Schiapparelli et al. (2018), the BESS capacity in Conte et al. (2020) is divided into PFR sub-battery and PV sub-battery: the former compensates for PV prediction errors, and the latter is for frequency regulation. The proposed method realizes the economic optimal of the IS under the premise of keeping SOC safe in both day-ahead and intra-day markets. However, the sub-battery compresses the available capacity of BESSs, which does not take into account that the effect of sub-batteries on SOC may counteract each other. Wang et al. (2022) proposed a bi-level joint optimization model of BESSs to arbitrage in the energy market and provide PFR services to make profits. The optimization of BESSs in energy and PFR markets helps improve the frequency security and stabilize the clearing price. In this model, the dynamic frequency nonlinear constraints are constructed to ensure the safety of the rate of change of frequency (RoCoF) and the frequency nadir. These constraints are related to the given power imbalance of the system and do not take into account the randomness of actual frequency regulation occurrences.

In this work, an IS containing several renewable energy units and a small-capacity BESS with PFR are considered. Usually, small-capacity BESSs in renewable energy stations are mostly just involved in PFR services (Meng et al., 2021; Li et al., 2022). Here, BESSs participate in PFR without affecting renewable energy generation and utilize the remaining capacity to arbitrage through time-of-use electricity prices. In summary, existing research on BESS optimization scheduling has not paid enough attention to the energy consumption of primary frequency regulation, and most of it has not considered the uncertainty of primary frequency regulation signals. We proposed a two-level optimization strategy for BESSs providing PFR services based on the acquired forecast PFR information. First, day-ahead scheduling (DAS) tunes a suitable droop coefficient and optimizes a preliminary BESS charge and discharge plan for the day to achieve the economic goal of the IS. Because there may be great differences in PFR action between the before-day forecast and actual operation, hour-ahead scheduling (HAS) corrects the results of DAS using updated SOC and PFR forecast to keep the BESS operation safer and more reliable. Due to the strong randomness of the PFR action by units in the real grid, both DAS and HAS use the prediction of system frequency difference integral to construct probability constraints for BESS energy offset in order to describe PFR behavior more accurately.

The remainder of this article is organized as follows: Section 2 presents the modeling of ISs and BESSs. Section 3 and Section 4 introduce the DAS and HAS optimization algorithms, respectively. Section 5 shows the simulation result analysis, and Section 6 provides a summary of our whole work.

2 IS modeling

2.1 System architecture

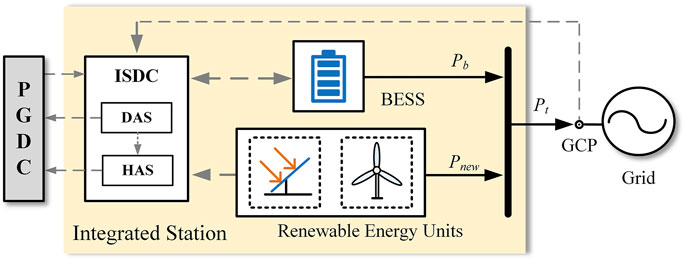
Figure 1 shows the system architecture of the IS. The IS mainly consists of three parts: renewable energy units, BESSs, and an integrated station dispatch center (ISDC). The power grid dispatch center (PGDC) is responsible for communication with the IS, and the total power output $P_t$ from the IS is delivered to the grid at the grid coupling point (GCP). $P_{new}$ and $P_b$ represent the output of all renewable energy units and BESSs, respectively. Here, renewable energy units are composed of several wind turbines or PV plants. We assume these renewable energy units operate in the maximum power tracking mode, with their output decoupled from the system frequency. Therefore, $P_{new}$ is fully connected to the grid.

Figure 1

Figure 1. System architecture of the IS.

The output $P_t$ from the IS is the sum of the output from BESSs and renewable energy units, which is given by Eq. 1.

$P_t=P_b+P_{new}.(1)$

In the IS above, the PFR service is only provided by BESSs, and the power from the PFR service of BESSs is $P_f$, which will be elaborated in Section 2.2. Furthermore, BESS arbitrages through the time-of-use electricity price, and this power is indicated by $P_e$. $P_e$ can be obtained through DAS or HAS. At this point, the BESS output $P_b$ is given by

$P_b=P_f+P_e.(2)$

The ISDC gathers a variety of information from the power station and the grid and then performs scheduling algorithms (DAS and HAS) to plan the operation for the BESS. For running DAS, the ISDC collects the time-of-use electricity price of the day, the forecast PFR needs from PGDC, the initial capacity of BESSs, and the output forecast from renewable energy units. Through DAS, we can obtain the droop coefficient for PFR and the charge and discharge plan for BESSs before the day operation, with the goal of maximum profit. For running HAS during the day, the ISDC adds the newest PFR needs and the real-time SOC of BESSs to correct the DAS results in order to maintain a lasting and reliable operation.

The DAS and HAS optimization results will be sent back to PGDC in order to schedule the operation of other units at the grid level. During the real-time operation of BESSs, the ISDC also needs to obtain information, such as system frequency, from the GCP to provide PFR services.

2.2 Modeling of BESSs

According to droop-based control (Ma et al., 2022), the PFR output $P_f$ from BESSs can be calculated as Eq. 3.

$P_f=-K_f\times \frac{∆f}{f_N}\times P_n,(3)$

where $K_f$ is the droop coefficient; $∆f$ is the system frequency difference from $f_N$; $f_N$ is the rated system frequency value; and $P_n$ is the operating power of the renewable energy power station, which we consider to be the rated power of the renewable energy station.

Suppose we have a BESS with output $P_{b,k}$ at time step $k$ and capacity $E_{\mathrm{n}}$, then the SOC variation in the BESS satisfies the following equation in a discrete process:

${\text{SOC}}_{k+1}={\text{SOC}}_k-\frac{\tau }{3600\cdot E_n}\times P_{b,k},(4)$

where $\tau$ refers to the scheduling interval during optimization. According to the above text, we can conclude that $P_{b,k}$ is composed of $P_{f,k}$ and $P_{e,k}$. $P_{e,k}$ is obtained by DAS and HAS, which we will discuss in detail in Sections 3.1 and 3.2. Because $P_f$ is real-time dependent on $∆f$, in order to get the energy exchange $E_{f,k}$ caused by $P_{f,k}$, we have

$E_{f,k}=-K_f\cdot {{\displaystyle \int }}_{k\tau }^{\left(k+1\right)\tau }∆f\left(t\right)\mathrm{d}t=-K_f\cdot W_{f,k},(5)$

where $W_{f,k}$ is the integral of the frequency difference over time period [$k\tau$, $\left(k+1\right)\tau$]. Schiapparelli et al. (2018) showed that time series {$W_{f,k}$} collected through a large amount of real measurement data can be expressed using an autoregressive (AR) process model and that the predicted value ${\widehat{W}}_{f,k}$ can be used to improve SOC management of BESSs under droop control. Based on this research, in our work, the before-day and intra-day forecast ${\widehat{W}}_{f,k}$ represents the estimation of system frequency regulation needs for DAS and HAS. According to the AR model, $W_{f,k+1}$ is given by Eq. 6.

$W_{f,k+1}={\widehat{W}}_{f,k+1}+{\zeta }_{k+1}=\left(a_1{W}_{f,k}+\dots +a_n{W}_{f,k-n-1}\right)+{\zeta }_{k+1},(6)$

where $W_{f,k}$, … $W_{f,k-n-1}$ are the real measurements of the integral during the last $n$ time steps; ${\widehat{W}}_{f,k+1}$ refers to the prediction at time step $k+1$; $a_1$, …, $a_n$ are the AR coefficients obtained from the database; ${\zeta }_{k+1}$ represents a zero-mean Gaussian random variable with standard deviation $\sigma$, which is closely related to integral intervals. Here, we consider the integral interval to be equal to the scheduling interval $\tau$ as this ensures that more accurate PFR demand information is provided for DAS and HAS under a certain amount of data. An excessively long integral interval may cause the optimization to blur or ignore the PFR demand during this time interval, leading to overly aggressive or conservative BESS operations.

3 Day-ahead scheduling

3.1 DAS objective function

The DAS optimization has the objective of maximizing the overall revenue of the IS by obtaining an appropriate droop coefficient $K_f$ and the daily power delivery plan $\left\{P_{e,k}\right\}$. The objective function of DAS is as follows:

$J_{\text{DAS}}=\underset{\left\{P_{e,k}\right\},K_f}{\max }{c}_{pfr}{K}_f+{\displaystyle {\sum }_{k=0}^{N-1}}{c}_{t,k}{P}_{e,k}-{\displaystyle {\sum }_{k=0}^{N-1}}{P}_{e,k}^2,(7)$

where $c_{pfr}$ is the PFR profit coefficient; $c_{t,k}$ is the time-of-use electricity price; and $N$ is the total length of the scheduling interval with $N=24\cdot 3600/\tau$. Since the renewable energy output is not our decision variable, we consider the overall revenue of the IS to be composed of the PFR revenue and the electricity price revenue from the BESS. Zhang et al. (2018) showed the profit BESS receives by providing PFR is proportional to its standby reserve capacity rather than the actual PFR output. Referring to Conte et al. (2020), we use the droop coefficient $K_f$ to represent the PFR capability of BESSs and let $c_{pfr}{K}_f$ represent the PFR revenue. In Eq. 7, $c_{t,k}{P}_{e,k}$ refers to the electricity price revenue of the BESS output. So, the sum of the first two items in Eq. 7 is equal to the total revenue. The square of $P_{e,k}$ is added as a penalty to make the BESS power smoother and avoid sudden changes in the output. For running DAS before-day, the following data should be available in advance:

(a) the initial SOC of the BESS ${\text{SOC}}_0$;

(b) the PFR profit coefficient $c_{pfr}$;

(c) the time-of-use electricity price $\left\{c_{t,k}\right\}$;

(d) the forecast frequency integral $\left\{{\widehat{W}}_{f,k}\right\}$ and the standard deviation $\sigma$;

(e) the forecast renewable energy power $\left\{{\widehat{P}}_{new,k}\right\}$.

The solution to the DAS problem should also satisfy a certain number of constraints, which are elaborated in detail in the following.

3.2 DAS constraints

• SOC constraints

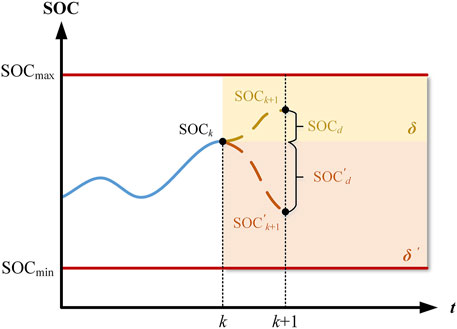
Combining Eqs 2, 4 and Eq. 5, we can obtain SOC variation as Eq. 8.

${\text{SOC}}_{k+1}-{\text{SOC}}_k=-\frac{\tau P_{e,k}-K_f{W}_{f,k}}{3600\cdot E_n}.(8)$

Define ${\text{SOC}}_d={\text{SOC}}_{k+1}-{\text{SOC}}_k$ as the SOC offset between time steps $k$ and $k+1$. During the daily operation of the BESS, we consider the SOC deviation between every two steps to be within an allowable range to avoid SOC being too close to the operating boundary. Here, we introduce $\delta$ to describe the allowable SOC deviation, similar to Eq. 9. Because the SOC offset between two periods could be either positive or negative, there are two possible situations for SOC deviation like Eq. 10.

${\text{SOC}}_d\le \delta ,(9)$

$\delta =\left\{\begin{array}{c}{\text{SOC}}_{\max }-{\text{SOC}}_k,{\text{SOC}}_{k+1}\ge {\text{SOC}}_k\\ {{\text{SOC}}_k-\text{SOC}}_{\min },{\text{SOC}}_{k+1}<{\text{SOC}}_k\end{array}\right..(10)$

Figure 2 shows two situations that satisfy our SOC constraint: variations from ${\text{SOC}}_k$ to ${\text{SOC}}_{k+1}$ and ${\text{SOC}}_k^{\prime }$ to ${\text{SOC}}_{k+1}^{\prime }$ correspond to two possible increasing or decreasing cases. For example, assume that the SOC at time step $k$ is ${\text{SOC}}_k$; as long as the SOC at $k+1$ is within the yellow or red range, the operation of SOC is safe.

Figure 2

Figure 2. SOC offset constraint.

From Eq. 6 we can derive that $W_{f,k}$ is a Gaussian random variable, and it is the only random variable in the definition of ${\text{SOC}}_d$. Therefore, ${\text{SOC}}_d$ is a Gaussian random variable, and its randomness comes from the uncertainty of $W_{f,k}$. In order to maintain the SOC of the BESS safe, we have the following probability constraint:

$\mathbf{P}\left({\text{SOC}}_d\le \delta \right)\ge \rho ,(11)$

where $\rho$ is the confidence level. Eq. 11 means the probability that the SOC offset during every two steps of the BESS is within $\delta$ should be greater than $\rho$. By applying such a probability constraint, the uncertainty of PFR action is taken into account, making the optimization more adaptable and in line with the energy requirements of PFR action in real scenarios. Now, we will convert this chance constraint into a deterministic constraint through derivation.

Eq. 11 can be rewritten as follows:

$\mathbf{P}\left(\frac{K_f{W}_{f,k}-\tau P_{e,k}}{3600\cdot E_n}\le \delta \right)\ge \rho .(12)$

Obviously, if $K_f$ and $E_n$ are greater than zero, then we can normalize the coefficients of $W_{f,k}$ as Eq. 13.

$\mathbf{P}\left(W_{f,k}-\tau P_{e,k}/K_f\le 3600\cdot \delta E_n/K_f\right)\ge \rho .(13)$

In addition, the random events included in the above probability inequality are

$\left\{\begin{array}{c}{W}_{f,k}-\tau P_{e,k}/K_f\le 3600\cdot \left({\text{SOC}}_{\max }-{\text{SOC}}_k\right)E_n/K_f,{\text{SOC}}_{k+1}\ge {\text{SOC}}_k\hfill \\ W_{f,k}-\tau P_{e,k}/K_f\ge -3600\cdot \left({\text{SOC}}_{\mathrm{k}}-{\text{SOC}}_{\min }\right)E_n/K_f,{\text{SOC}}_{k+1}<{\text{SOC}}_k\hfill \end{array}\right..(14)$

Clearly, $W_{f,k}-\tau P_{e,k}/K_f$ is a Gaussian random variable and it follows Eqs 15, 16.

$\left(W_{f,k}-\tau P_{e,k}/K_f\right)\sim \mathcal{N}\left(m_k,{\sigma }_k\right),(15)$

where

$m_k={\widehat{W}}_{f,k}-\tau P_{e,k}/K_f,{\sigma }_k=\sigma .(16)$

Since we have known the mean and standard variance of $W_{f,k}-\tau P_{e,k}/K_f$, Eq. 12 can be solved based on probability theory. The idea is to convert the random variable on the left in Eq. 14 into a standard Gaussian random variable and solve it according to the percentile table. Therefore, we obtain the following inequality:

$\left\{\begin{array}{c}\left(\frac{3600\cdot E_n\left({\text{SOC}}_{\max }-{\text{SOC}}_k\right)}{K_f}-W_{f,k}+\frac{\tau P_{e,k}}{K_f}\right)/\sigma \ge \mu \hfill \\ \left(\frac{3600\cdot E_n\left({{\text{SOC}}_k-\text{SOC}}_{\min }\right)}{K_f}-W_{f,k}+\frac{\tau P_{e,k}}{K_f}\right)/\sigma \le -\mu \hfill \end{array}\right.,(17)$

where $\mu$ is $\rho$th percentile of the zero-mean standard Gaussian random variable. Eq. 17 can be further simplified:

$\left\{\begin{array}{c}\left(3600\cdot E_n\left({\text{SOC}}_{\max }-{\text{SOC}}_k\right)+\tau P_{e,k}\right)\ge K_f\left(\mu \sigma +W_{f,k}\right)\hfill \\ \left(-3600\cdot E_n\left({{\text{SOC}}_k-\text{SOC}}_{\min }\right)+\tau P_{e,k}\right)\le K_f\left(-\mu \sigma +W_{f,k}\right)\hfill \end{array}\right..(18)$

We can see that Eq. 18 expresses the inequality relationship among the BESS capacity margin, energy exchanged by $P_{e,k}$, and PFR energy. The uncertainty of PFR action is ultimately reflected in the parentheses at the right end of the inequality. At each step of DAS, ${\text{SOC}}_k$ can be obtained based on known optimization results, so this constraint is built for the optimization of $P_{e,k}$ and $K_f$. Such two inequalities can constrain the SOC changes in both directions of the BESS at the same time. Eq. 18 can be further extended to the constraints of the BESS operation for a day, similar to Eq. 19:

$\left\{\begin{array}{c}\left(3600\cdot E_n\left({\text{SOC}}_{\max }-{\text{SOC}}_0\right)+\tau {\displaystyle {\sum }_{k=0}^{N-1}}{P}_{e,k}\right)\ge K_f\left(N\mu \sigma +{\displaystyle {\sum }_{k=0}^{N-1}}{W}_{f,k}\right)\hfill \\ \left(-3600\cdot E_n\left({{\text{SOC}}_k-\text{SOC}}_{\min }\right)+\tau {\displaystyle {\sum }_{k=0}^{N-1}}{P}_{e,k}\right)\le K_f\left(-N\mu \sigma +{\displaystyle {\sum }_{k=0}^{N-1}}{W}_{f,k}\right)\hfill \end{array}\right..(19)$

The above equation indicates that after a day of PFR and charging or discharging behavior, the deviation between the final SOC of the BESS and the initial ${\text{SOC}}_0$ should be within the constraint conditions. This constraint contributes to the safety of the next day’s initiation SOC of the BESS.

• Power constraints

The operation of the BESS and IS also needs to meet certain power constraints. First, for the BESS, its droop coefficient $K_f$ should meet the requirements of the scheduling agency, i.e.,

$0\le K_f\le K_{f,\max }.(20)$

The output of the BESS must be within the allowable range of its rated power output $P_{b\mathrm{N}}$, so we have

$-P_{b\mathrm{N}}\le P_{e,k}\le P_{b\mathrm{N}},(21)$

$-P_{b\mathrm{N}}\le \frac{K_f{W}_{f,k}}{\tau }\le P_{b\mathrm{N}},(22)$

$\left.0\le \right|K_f∆f_{\max }\left|\le \right.P_{b\mathrm{N}},(23)$

where $∆f_{\max }$ is the maximum frequency deviation of this region obtained from the historical data and $K_f∆f_{\max }$ refers to the possible maximum power demand by PFR. Eq. 21 is a constraint for the optimization of $P_{e,k}$. Eqs 22, 23 are constraints for PFR output. First, we consider that the average output for PFR cannot exceed the rated power of the BESS. Then, considering extreme situations, the maximum PFR output should also need to be constrained.

$P_{e,k}$ also needs to meet the following ramp constraint:

$\left|P_{e,k+1}-P_{e,k}\left|\le ∆\right.P_{b\max }\right.,(24)$

where $∆P_{b\max }$ is the maximum power variation in the BESS.

Finally, it is necessary to impose constraint on the total output of the IS:

$0\le P_{new,k}+P_{e,k}\le P_{t\mathrm{N}},(25)$

where $P_{t\mathrm{N}}$ is the maximum rated power for the IS. Except for the output in response to the PFR signal, the sum of all other outputs of the power station should be greater than zero, indicating that it should supply electricity to the grid at any time.

4 Hour-ahead scheduling

4.1 Objective function

HAS is an optimization process that corrects the results of DAS based on the latest SOC variation and PFR requirements to maintain the long-term operation capacity of the BESS. The goal of HAS is to improve the safety of SOC without changing the optimization results from DAS as much as possible. For running HAS before-hour, the following data should be available in advance.

(a) the DAS result $\left\{P_{e\mathrm{D},k}\right\}$ and droop coefficient $K_f$;

(b) the penalty coefficient $c_{de}$;

(c) the updated SOC of the BESS ${\text{SOC}}_i$;

(d) the updated frequency integral $\left\{{\widehat{W}}_{fh,k}\right\}$ and the standard deviation $\sigma$;

(e) the updated renewable energy power $\left\{P_{new,k}\right\}$.

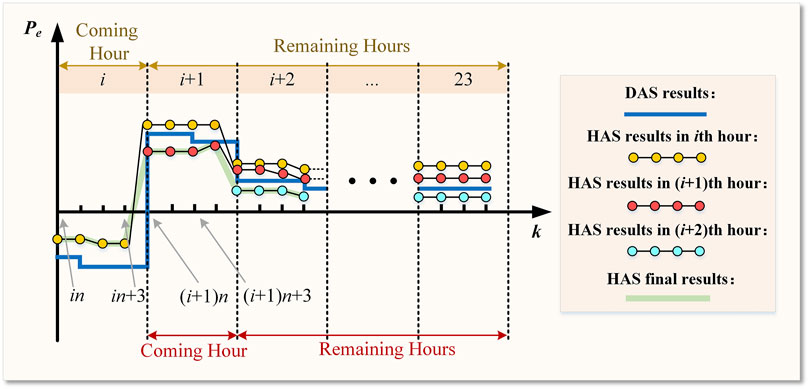
Figure 3 shows the schematic diagram of HAS. Suppose that $i$ represents the number of hours in a day (0, 1, 2, … , 23), $n=3600/\tau$ is the number of scheduling periods within an hour, and $k$ represents the number of scheduling periods in a day ($in$; $in+1$,…,96). Suppose we run HAS in the first hour of the day ($i=0$), and we already have the results from DAS $\left\{P_{e\mathrm{D},k}\right\}$. Then, we obtain the latest optimization results $\left\{P_{e,k}\right\}$ from HAS. Next, the BESS will work based on $\left\{P_{e,k}\right\}$ for $n$ steps, and the SOC of the BESS will update according to real PFR actions and $K_f$. When it comes to $i=1$, HAS gets scheduling for the rest of the day with ${\text{SOC}}_i$, and the process will repeat in the same way as the first hour. Only the results of one coming hour (CH) at $i\text{th}$ hour will be put into the real operation of the BESS, and the results of the remaining hours (RH) of the day are just a subsidiary result for HAS.

Figure 3

Figure 3. HAS example.

The objective function of HAS in the $i\text{th}$ hour is as follows:

$J_{\text{HAS},i}=\underset{\left\{P_{e,k}\right\},{\mu }_c,{\mu }_r}{\max }-c_{de}{\displaystyle {\sum }_{k=in}^{N-1}}\left|P_{e,k}-P_{e\mathrm{D},k}\right|+\left({\alpha }_c{\mu }_c+{\alpha }_r{\mu }_r\right).(26)$

In Eq. 26, $c_{de}$ is the penalty coefficient for the deviation of HAS and DAS results; ${\alpha }_c$ and ${\alpha }_r$ are the weight coefficients for CH and RH, respectively; and ${\mu }_c$ and ${\mu }_r$ are quantiles in probability constraints for CH and RH, respectively. The objective function of HAS optimization consists of two parts: one is the penalty for deviation from the $in$ step to $N-1$ step between DAS and HAS optimization results, and the other is the SOC safety optimization index. The larger the value of $J_{\text{HAS},i}$, the smaller the deviation of the optimization results between DAS and HAS, and ${\alpha }_c{\mu }_c+{\alpha }_r{\mu }_r$ should be larger. The larger the ${\alpha }_c{\mu }_c+{\alpha }_r{\mu }_r$ value, the safer the SOC of the BESS, which is discussed in Section 4.2.

4.2 Constraints

The SOC constraint set for HAS is as follows (CH and RH, respectively):

$\left\{\begin{array}{c}\left(3600\cdot E_n\left({\text{SOC}}_{\max }-{\text{SOC}}_k\right)+\tau P_{e,k}\right)\ge K_f\left({\mu }_c\sigma +W_{fh,k}\right)\hfill \\ \left(-3600\cdot E_n\left({{\text{SOC}}_k-\text{SOC}}_{\min }\right)+\tau P_{e,k}\right)\le K_f\left(-{\mu }_c\sigma +W_{fh,k}\right)\hfill \end{array}\right.,(27)$

${\mu }_{\min }\le {\mu }_c\le {\mu }_{\max },(28)$

$\left\{\begin{array}{c}\left(3600\cdot E_n\left({\text{SOC}}_{\max }-{\text{SOC}}_k\right)+\tau P_{e,k}\right)\ge K_f\left({\mu }_r\sigma +W_{fh,k}\right)\hfill \\ \left(-3600\cdot E_n\left({{\text{SOC}}_k-\text{SOC}}_{\min }\right)+\tau P_{e,k}\right)\le K_f\left(-{\mu }_r\sigma +W_{fh,k}\right)\hfill \end{array}\right.,(29)$

${\mu }_{\min }\le {\mu }_r\le {\mu }_{\max }.(30)$

Eqs 27–30 are actually reformulations of Eq. 18, where $\mu$ and $W_{f,k}$ in the original formula are replaced with ${\mu }_c$ (${\mu }_r$) and $W_{fh,k}$. In DAS, such SOC constraints are implemented for a whole day, while in HAS, they are used separately in CH and RH. These constraints are all derived based on the probability constraints of the SOC offset (Eq. 11) to ensure that the SOC deviation of the BESS at each step is within a safe range. The objective of $J_{\text{HAS},i}$ is to increase the values of ${\mu }_c$ and ${\mu }_r$ as they increase the probability of constraint Eqs 27–29 being satisfied. This can be seen from the calculation formula of $\mu$. The value of $\mu$ that satisfies probability $\rho$ is

$\left\{\begin{array}{c}\mathrm{\Phi }\left(\mu \right)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\mu }{e}^{-\frac{t^2}{2}}\mathrm{d}t\hfill \\ \mathrm{\Phi }\left(\mu \right)=\frac{1}{2}\left(\rho +1\right)\hfill \end{array}\right.,(31)$

where $\mathrm{\Phi }\left(\cdot \right)$ represents the distribution function of the standard Gaussian distribution. We can then obtain the derivative of $\rho$ as Eq. 32.

$\frac{\mathrm{d}\rho }{\mathrm{d}\mu }=\frac{\sqrt{2}}{\pi }{e}^{-\frac{{\mu }^2}{2}}.(32)$

Clearly, $\frac{\mathrm{d}\rho }{\mathrm{d}t}$ is greater than zero. So, as the value of $\mu$ increases, the corresponding probability $\rho$, which refers to the possibility of Eqs 27–29 being valid, also increases. We add constraints for ${\mu }_c$ and ${\mu }_r$ in Eqs 28–30 to limit the range of possibilities that the constraint can satisfy. Therefore, we can ensure the durable operation of the BESS using the above constraints.

There is a contradiction between the two optimization objectives in Eq. 25. The results of DAS have already achieved economic optimality while maximizing the utilization of energy storage capacity. If we want to make the operation of energy storage more conservative, it will inevitably lead to an increase in the deviation of the optimization results between DAS and HAS. Therefore, the size of the three weight coefficients in Eq. 25 will significantly affect the difference in the final optimization results.

The power constraints for HAS are almost the same as those for DAS (i.e., Eqs 21–25) and will not be further elaborated here.

5 Simulation analysis

For the simulation part, first, we focus on a renewable energy power station that consists of 10 wind turbines with a rated capacity of 1.5 MW and a total rated output of 15 MW. Consider equipping these wind turbines with a BESS of 2MW/2 MW·h to provide PFR and peak-valley arbitrage services. We collected historical frequency fluctuation data measured from several stations in the power grid of Henan province, China. We selected several days of system frequency difference data as our simulation scenario and obtained the corresponding frequency regulation demand prediction using the AR model. The time-of-use electricity price released by Henan province is used as the value of $c_{t,k}$. Renewable energy outputs are chosen from Elia Transmission Belgium. For the values of other parameters in our algorithm, please refer to Table 1. Additionally, the programming of DAS and HAS is written using the YALMIP toolbox and solved using CPLEX in MATLAB.

Table 1

Table 1. Simulation parameters.

We first select the operation optimization of the BESS on a certain day as the first part of our simulation. The results of DAS and DAS and HAS will be shown separately. Figure 4 shows the simulation results using DAS optimization only. Figure 4A shows the scheduling result for DAS $\left\{P_{e,k}\right\}$ together with the time-of-use electricity price $\left\{c_{t,k}\right\}$, corresponding to the left and right coordinate axes, respectively. Figure 4B shows the renewable energy forecast $\left\{{\widehat{P}}_{new,k}\right\}$ and the sum of $\left\{{\widehat{P}}_{new,k}\right\}$ and $\left\{P_{e,k}\right\}$. The SOC variation curve calculated by DAS and the realized ones are displayed in Figure 4C. Figure 4D shows the real renewable energy output $\left\{P_{new,k}\right\}$ and the sum of $\left\{P_{new,k}\right\}$ and $\left\{P_{e,k}\right\}$, together with the real total power output $\left\{P_{t,k}\right\}$. First, Figure 4A shows that the trends of $\left\{P_{e,k}\right\}$ and $\left\{c_{t,k}\right\}$ are very similar. The BESS was charged and replenished during low-electricity prices (such as 0–7) and discharged during high-electricity prices (like 10–14) to generate revenue. Figure 4B shows that the economic output of BESS does not change the overall trend of renewable energy output but transfers energy from different periods according to electricity prices. From Figure 4C, we can infer that during DAS, the SOC of the BESS is fully utilized, while in the realized situation, the SOC has crossed the safety boundary at certain hours. This is due to significant errors between the predicted and actual frequency differences, so the results of DAS may be aggressive in practical scenarios. This issue can be addressed through the updated SOC trajectory and frequency regulation requirements in HAS. When SOC exceeds the boundary, the BESS output is zero to ensure safety, as shown in Figure 4D (approximately 13): at a certain time, only renewable energy output constitutes the total output. The long-term operation of energy storage near the SOC boundary not only affects its own safety but also hinders its provision of PFR services. Such a situation should be avoided as much as possible.

Figure 4

Figure 4. DAS results.

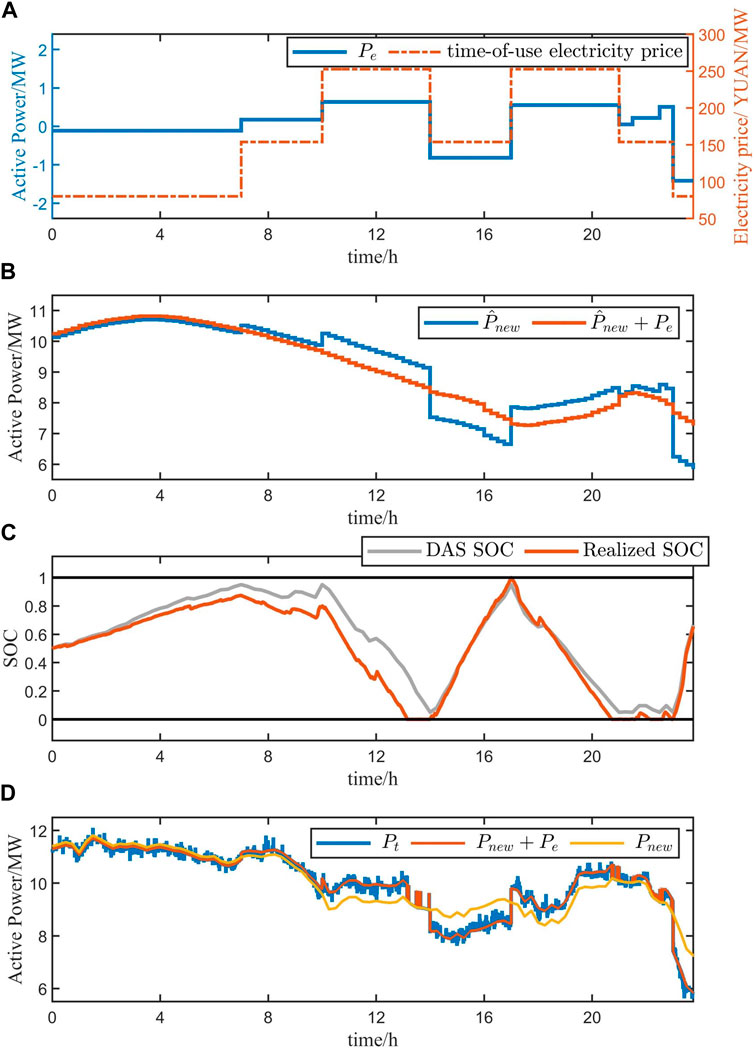
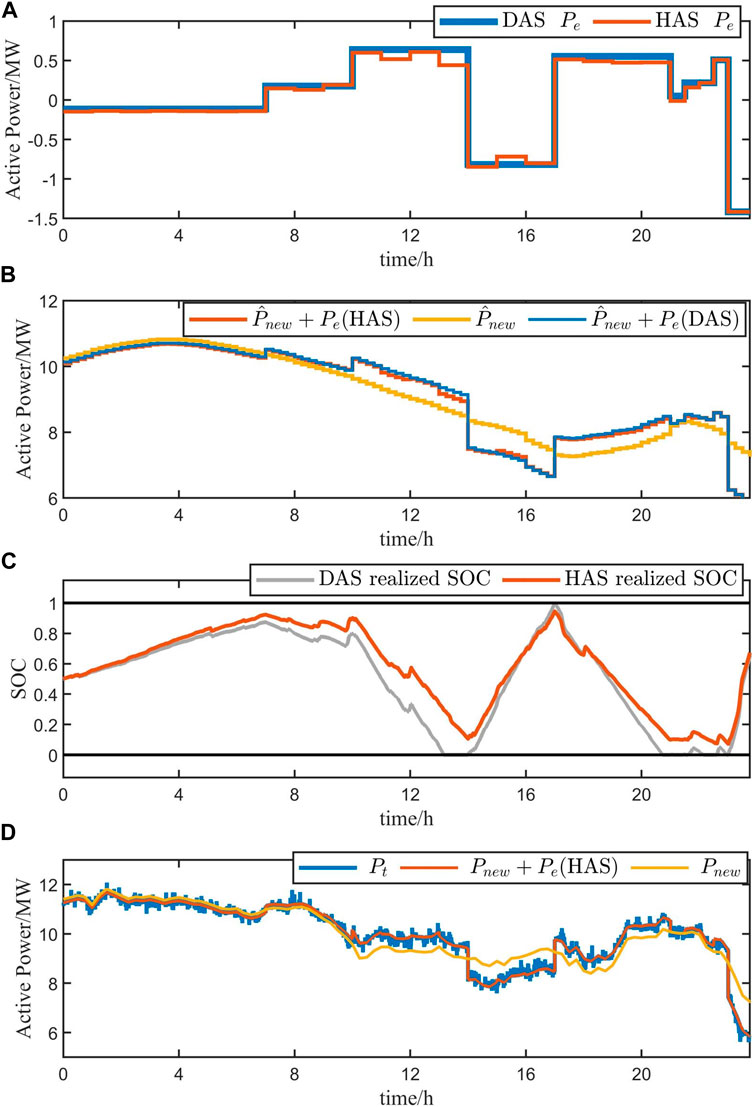
Figure 5 shows the simulation results using DAS and HAS optimization. Figure 5A shows the scheduling results for DAS and HAS. Figure 5B contains the sum of two scheduling results and the prediction of renewable energy output separately. The realized SOC by DAS and HAS is displayed in Figure 5C. Figure 5D shows the real renewable energy output $\left\{P_{new,k}\right\}$, the sum of $\left\{P_{new,k}\right\}$ and $\left\{P_{e,k}\right\},$ together with the real total power output $\left\{P_{t,k}\right\}$ from HAS. We can find from the results of HAS that it comes from a little correction of DAS, which makes the output of BESS more conservative and does not change its overall trend with variation in electricity prices. Through the HAS, the SOC changes calculated based on actual frequency modulation actions did not exceed the upper and lower limits within a day. BESS can provide sufficient PFR services throughout the day. Therefore, HAS can ensure the reliability of the BESS operation.

Figure 5

Figure 5. HAS results.

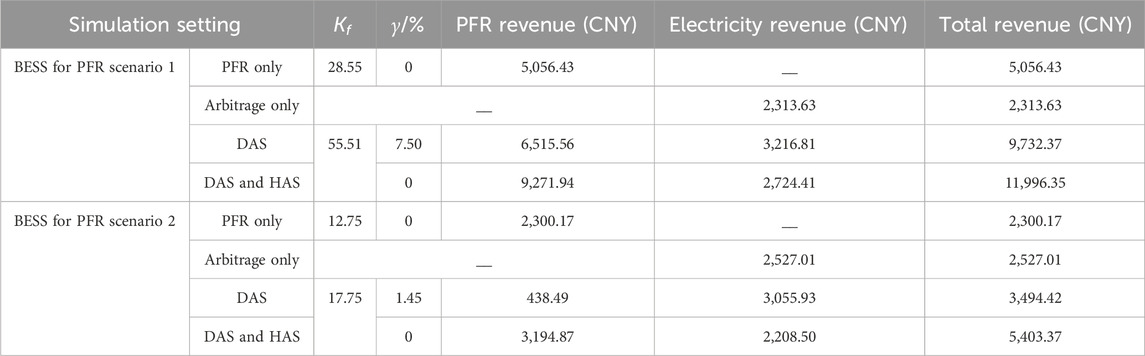
Table 2 summarizes the data results from the above simulations as PFR scenario 1, and we add additional simulation results for another day’s operation as PFR scenario 2. It mainly displays the optimization results of the BESS droop coefficient, PFR revenue, and electricity revenue under different simulation settings. We introduce $\gamma$% to describe the failure rate of the BESS providing primary frequency regulation, which is the proportion of the time when SOC exceeds the limit to the total time of a day. The PFR revenue is obtained by multiplying the original revenue by the actual duration of the PFR provided, and the electricity revenue is the product of the economic output of the BESS and the time-of-use electricity price. We have also imposed penalties for the inability of the BESS to participate in PFR in accordance with the Implementation Rules for Auxiliary Service Management of Central China Electric Power. For PFR scenario 1, it is obvious that the droop coefficient and PFR revenue of the BESS only participating in PFR are lower than those of DAS and HAS. This indicates that the economic output and PFR output within a day can partially offset each other, increasing more space for BESS PFR actions. When BESS output only includes economic output, the electricity price revenue is lower than the optimization results of DAS, which also indicates that our optimization algorithm can increase the freedom of the BESS to participate in PFR and peak-valley arbitrage simultaneously. The low profit of the PFR revenue from DAS is mainly due to the significant punishment it received, which was avoided during the intra-day optimization. The reduction in electricity price revenue through HAS compared to DAS alone is mainly due to the correction of DAS’s overly aggressive charging and discharging behavior. HAS reduces the PFR failure time by 7.5%, and its total revenue is much greater than that of DAS. Therefore, the scheduling results optimized by DAS and HAS can ensure the reliability of PFR by the BESS and achieve maximum total revenue.

Table 2

Table 2. Simulation result data.

The optimization results for PFR scenario 2 show that the PFR task on the day is much heavier, so the optimized droop coefficient is small. We can see that there is still 1.45% of the time that the BESS cannot provide PFR, resulting in a decrease in PFR revenue in DAS. Due to the fact that the PFR penalty stipulated in the implementation rules for auxiliary service management in Central China is related to its rated capacity and the optimized droop coefficient is small, the PFR revenue of DAS is relatively low. We can see that in the current scenario, the total revenue after DAS and HAS is still optimal. The simulation results above show that the proposed optimization scheduling method can ensure that the BESS can provide PFR services stably, as well as increase the overall revenue of the power station.

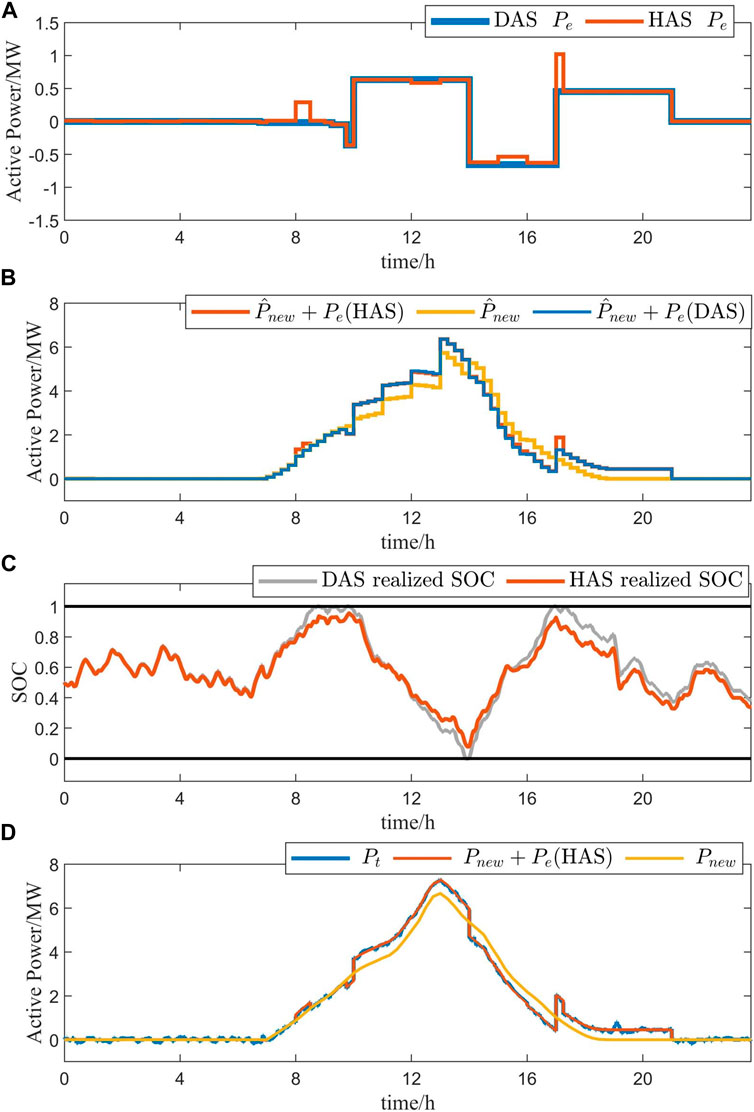
To verify the adaptability of the proposed algorithm in various scenarios, we consider conducting the second simulation for a PV station with a rated capacity of 10 MW. Other simulation configurations remain unchanged. Figure 6 shows the simulation results after using DAS and HAS. Figure 6A shows the scheduling results for DAS and HAS. Figure 6B contains the sum of two scheduling results and the prediction of PV output separately. The realized SOC by DAS and HAS is displayed in Figure 6C. Figure 6D shows the real PV output $\left\{P_{new,k}\right\}$, the sum of $\left\{P_{new,k}\right\}$ and $\left\{P_{e,k}\right\}$, together with the real total power output $\left\{P_{t,k}\right\}$ from HAS. Because the output of the PV station at night is very low, our optimization results are mainly reflected between 7 and 21 o’clock. From Figure 6A, we can see that the BESS roughly goes through two rounds of charging and discharging based on the electricity price. Again, our HAS results are very similar to those of DAS. The DAS SOC curve also showed an out-of-bounds situation, which is improved during HAS. Finally, Figure 6D clearly shows that our optimization has caused a deviation in the trend of the real PV output: when the electricity price is high, the output of the power station is increased (from 10 to 13), while when the electricity price is low, the output of the power station is appropriately reduced (from 13 to 17). Furthermore, the BESS has extended the time for power transmission by the PV (from 18 to 21), achieving the migration of energy from the PV at different periods. These simulation results indicate that the method we proposed has shown good performance in different renewable energy generation scenarios.

Figure 6

Figure 6. HAS results of the PV.

6 Conclusion

In order to fully harness the potential of battery energy storage, it is essential to enhance its capability of supporting primary frequency regulation while simultaneously carrying out peak-valley arbitrage through the time-of-use electricity price. Thus, a day-ahead and hour-ahead optimal scheduling algorithm is proposed in this paper. The main conclusion of the context is as follows.

(1) The proposed algorithm can ensure the long-term operation ability of the energy storage and provide the primary frequency regulation service stably, indicating that the proposed probability constraints can ensure the safety of the energy storage state of charge.

(2) The proposed algorithm can adjust the charge and discharge plan of the energy storage in a day according to the time-of-use electricity price, thereby maximizing the utilization of the energy storage capacity and achieving the maximum energy storage profit.

Data availability statement

The data analyzed in this study are subject to the following licenses/restrictions: The operation data of the power network dispatching organization must not be disclosed. Requests to access these datasets should be directed to Yanzhao Ma, aGVidXRteXpAMTYzLmNvbQ==.

Author contributions

HH: writing–review and editing. YM: writing–original draft. XZ: writing–review and editing and data curation. CH: writing–original draft and investigation. YH: writing–original draft and software.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Author XZ was employed by State Grid Henan Electric Power Company, State Grid Corporation of China (SGCC).

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arrigo, F., Bompard, E., Merlo, M., and Milano, F. (2020). Assessment of primary frequency control through battery energy storage systems. Int. J. Electr. Power Energy Syst. 115, 105428. doi:10.1016/j.ijepes.2019.105428

CrossRef Full Text | Google Scholar

Conte, F., Massucco, S., Schiapparelli, G. –P., and Silvestro, F. (2020). Day-ahead and intra-day planning of integrated BESS-PV systems providing frequency regulation. IEEE Trans. Sustain. Energy 11 (3), 1797–1806. doi:10.1109/TSTE.2019.2941369

CrossRef Full Text | Google Scholar

Cristaldi, L., Faifer, M., Laurano, C., Ottoboni, R., Petkovski, E., and Toscani, S. (2022). “Reduced power model-based tracker for photovoltaic panels,” in 2022 IEEE 16th international conference on compatibility, power electronics, and power engineering (CPE-POWERENG), birmingham, United Kingdom, 2022 (IEEE), 1–6. doi:10.1109/CPE-POWERENG54966.2022.9880905

CrossRef Full Text | Google Scholar

Fang, C., Tang, Y., Ye, R., Lin, Z., Zhu, Z., Wen, B., et al. (2020). Adaptive control strategy of energy storage system participating in primary frequency regulation. Processes 8 (6), 687. doi:10.3390/pr8060687

CrossRef Full Text | Google Scholar

Feng, C., Mai, Z., Wu, C., Zheng, Y., and Zhang, N. (2024). Advantage of battery energy storage systems for assisting hydropower units to suppress the frequency fluctuations caused by wind power variations. J. Energy Storage 78, 109989. doi:10.1016/j.est.2023.109989

CrossRef Full Text | Google Scholar

Li, Z., Cheng, Z., Si, J., Zhang, S., Dong, L., Li, S., et al. (2021). Adaptive power Point tracking control of PV system for primary frequency regulation of AC microgrid with high PV integration. IEEE Trans. Power Syst. 36 (4), 3129–3141. doi:10.1109/TPWRS.2021.3049616

CrossRef Full Text | Google Scholar

Li, Z., Duan, J., Qin, B., Xia, Y., and Chen, B. (2022) “Self-adaptive control strategy of battery energy storage for power grid primary frequency regulation,” in 2022 IEEE/IAS industrial and commercial power system Asia I&CPS Asia. IEEE: Shanghai, China.

CrossRef Full Text | Google Scholar

Ma, R., Yuan, S., Li, X., Guan, S., Yan, X., and Jia, J. (2024). Primary frequency regulation strategy based on rotor kinetic energy of double-fed induction generator and supercapacitor. Energies 17 (2), 331. doi:10.3390/en17020331

CrossRef Full Text | Google Scholar

Ma, Y., Hu, Z., and Song, Y. (2022). Hour-ahead optimization strategy for shared energy storage of renewable energy power stations to provide frequency regulation service. IEEE Trans. Sustain. Energy 13 (4), 2331–2342. doi:10.1109/TSTE.2022.3194718

CrossRef Full Text | Google Scholar

Mahish, P., and Pradhan, A. K. (2020). Distributed synchronized control in grid integrated wind farms to improve primary frequency regulation. IEEE Trans. Power Syst. 35 (1), 362–373. doi:10.1109/TPWRS.2019.2928394

CrossRef Full Text | Google Scholar

Meng, G., Lu, Y., Liu, H., Ye, Y., Sun, Y., and Tan, W. (2021). Adaptive droop coefficient and SOC equalization-based primary frequency modulation control strategy of energy storage. Electronics 10 (21), 2645. doi:10.3390/electronics10212645

CrossRef Full Text | Google Scholar

Schiapparelli, G. P., Massucco, S., Namor, E., Sossan, F., Cherkaoui, R., and Paolone, M. (2018). “Quantification of primary frequency control provision from battery energy storage systems connected to active distribution networks,” in 2018 power systems computation conference (PSCC), IEEE: Dubin, Ireland.

Google Scholar

Turk, A., Sandelic, M., Noto, G., Pillai, J. R., and Chaudhary, S. K. (2019). Primary frequency regulation supported by battery storage systems in power system dominated by renewable energy sources. J. Eng. 2019, 4986–4990. doi:10.1049/joe.2018.9349

CrossRef Full Text | Google Scholar

Wang, X., Ying, L., Wen, K., and Lu, S. (2022). Bi-level non-convex joint optimization model of energy storage in energy and primary frequency regulation markets. Int. J. Electr. Power Energy Syst. 134, 107408. doi:10.1016/j.ijepes.2021.107408

CrossRef Full Text | Google Scholar

Xiong, L., Liu, L., Liu, X., and Liu, Y. (2021). Frequency trajectory planning based strategy for improving frequency stability of droop-controlled inverter based standalone power systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 11 (1), 176–187. doi:10.1109/JETCAS.2021.3052006

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Liu, H., and Liu, Y. (2022). Performance comparison of typical frequency response strategies for power systems with high penetration of renewable energy sources. IEEE J. Emerg. Sel. Top. Circuits Syst. 12 (1), 41–47. doi:10.1109/JETCAS.2022.3141691

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Zhang, D., and Liu, Y. (2021). Rapid power compensation-based frequency response strategy for low-inertia power systems. IEEE J. Emerg. Sel. Top. Power Electron. 9 (4)), 4500–4513. doi:10.1109/JESTPE.2020.3032063

CrossRef Full Text | Google Scholar

Zhang, Y. J. A., Zhao, C., Tang, W., and Low, S. H. (2018). Profit-maximizing planning and control of battery energy storage systems for primary frequency control. IEEE Trans. Smart Grid 9 (2), 712–723. doi:10.1109/TSG.2016.2562672

CrossRef Full Text | Google Scholar

Zhao, P., Gu, C., Li, F., and Yang, X. (2022). Battery storage configuration for multi-energy microgrid considering primary frequency regulation and demand response. Energy Rep. 8 (10), 1175–1183. doi:10.1016/j.egyr.2022.06.086

CrossRef Full Text | Google Scholar

Zhu, D., and Zhang, Y. A. (2019). Optimal coordinated control of multiple battery energy storage systems for primary frequency regulation. IEEE Trans. Power Syst. 34 (1), 555–565. doi:10.1109/TPWRS.2018.2868504

CrossRef Full Text | Google Scholar