A hybrid neural network based on KF-SA-Transformer for SOC prediction of lithium-ion battery energy storage systems

With the widespread application of energy storage stations, BMS has become an important subsystem in modern power systems, leading to an increasing demand for improving the accuracy of SOC prediction in lithium-ion battery energy storage systems. Currently, common methods for predicting battery SOC include the Ampere-hour integration method, open circuit voltage method, and model-based prediction techniques. However, these methods often have limitations such as single-variable research, complex model construction, and inability to capture real-time changes in SOC. In this paper, a novel prediction method based on the KF-SA-Transformer model is proposed by combining model-based prediction techniques with data-driven methods. By using temperature, voltage, and current as inputs, the limitations of single-variable studies in the Ampere-hour integration method and open circuit voltage method are overcome. The Transformer model can overcome the complex modeling process in model-based prediction techniques by implementing a non-linear mapping between inputs and SOC. The presence of the Kalman filter can eliminate noise and improve data accuracy. Additionally, a sparse autoencoder mechanism is integrated to optimize the position encoding embedding of input vectors, further improving the prediction process. To verify the effectiveness of the algorithm in predicting battery SOC, an open-source lithium-ion battery dataset was used as a case study in this paper. The results show that the proposed KF-SA-Transformer model has superiority in improving the accuracy and reliability of battery SOC prediction, playing an important role in the stability of the grid and efficient energy allocation.

1 Introduction

With the transformation of the global energy structure and the increasing popularity of renewable energy, the integration of new energy generation into the power system has become an important aspect. However, due to the inherent randomness and instability of the output power of new energy sources, integrating them into the grid may impact power quality and reliability (Wang et al., 2019; Shi et al., 2022). Electrochemical batteries, as representatives of energy storage systems, provide a promising solution to mitigate the instability and intermittency of new energy integration. They can assist in peak shaving and frequency regulation, thereby enhancing the security and flexibility of energy supply systems. The core of electrochemical energy storage is the Battery Management System (BMS), where the State of Charge (SOC) of the battery is a key parameter. However, due to the non-linear and time-varying electrochemical system inside batteries, SOC estimation can only be based on measurable parameters such as voltage and current, making accurate estimation of battery SOC a challenging task (Rivera-Barrera et al., 2017). Large errors in estimating battery SOC may damage battery capacity and service life, affect the economic operation of the grid, and even lead to catastrophic events such as combustion or explosion, posing a serious threat to grid safety (Zhou et al., 2021).

Currently, the common methods for predicting battery SOC mainly include the Ampere-hour integration method, open circuit voltage method, model-based prediction techniques, and data-driven methods. The Ampere-hour integration method, although simple, is prone to accumulating errors over time (Chang, 2013; Zhang et al., 2020). The accuracy of the open circuit voltage method is influenced by the battery’s rest period. Model-based prediction techniques are based on specific operating conditions and may not be applicable to all conditions; accurate estimation of physical parameters in the model is very difficult, as these parameters change with battery aging and usage conditions, increasing model uncertainty and reducing prediction accuracy (How et al., 2019). Another method is the data-driven approach, which uses data training to identify the complex relationship between feature parameters and SOC, thereby avoiding the need for complex battery models. Typical data-driven methods usually utilize machine learning techniques such as Random Forest (Li et al., 2014) and Support Vector Machine (Song et al., 2020) to predict battery SOC. However, compared to traditional machine learning methods, deep learning methods based on neural networks demonstrate superior performance in extracting latent features and are widely used in SOC prediction, such as Long Short-Term Memory (LSTM) (Chen et al., 2023), Gated Recurrent Unit (GRU) (Dey and Salem, 2017), and Transformer series models (Han et al., 2021). The Transformer model, due to its inherent self-attention mechanism, can perform parallel computation and sequential data processing, making it more effective in handling time series data and providing a solution with higher accuracy and generalization capabilities for SOC prediction (Shen et al., 2022). (Hussein et al., 2024) conducted research on the SOC estimation of lithium-ion batteries using a self-supervised learning Transformer model, which demonstrated lower root mean square error (RMSE) and mean absolute error (MAE) under different ambient temperatures, indicating the potential of self-supervised learning in battery state estimation. However, this method has poor resistance to noise, which affects the robustness of the model in practical applications. (Chen et al., 2022) predicted the remaining useful life (RUL) of lithium-ion batteries based on the Transformer model, using a denoising autoencoder (DAE) to preprocess noisy battery capacity data, and then utilizing the Transformer network to capture temporal information and learn useful features. Eventually, by integrating the denoising and prediction tasks within a unified framework, the performance of RUL prediction was significantly improved. Despite this, the model by Chen et al. has some limitations. Although the DAE preprocessing step can remove noise, it may not fully preserve all the subtle features useful for prediction. To overcome these challenges, a Kalman filter can be added to the Transformer model. (Bao et al., 2024), in response to the limitations of existing methods in extracting time series features, proposed a time Transformer-based sequential network (TTSNet) for SOC estimation of lithium-ion batteries in electric vehicles. TTSNet effectively encodes features of the temporal dimension information through the time Transformer and introduces sliding time window technology and Kalman filtering as pre- and post-processing steps, which not only enhances the processing capability for long sequence data but also improves the accuracy and robustness of the estimation. In summary, these studies have made significant progress in the state monitoring and management of lithium-ion batteries, especially in improving prediction accuracy and handling long sequence data. However, the complexity of these models also brings significant computational costs. The Transformer model usually requires a large number of parameters and computational resources, which not only limits its application in resource-constrained environments but also increases the time cost for training and inference.

To overcome the limitations of the aforementioned methods, this paper introduces Sparse Autoencoder (SA) technology to improve the SA-Transformer model. The core idea of SA is to reduce the number of model parameters and computational complexity by learning the low-dimensional representation of data. It can significantly reduce the number of model parameters, thereby reducing memory usage and computational requirements, making the dimensionality-reduced model more lightweight, which can be trained and inferred more quickly. This is particularly important for application scenarios that require real-time responses. Since the sparse encoder encourages the model to learn more robust and discriminative feature representations, it can also improve the model’s generalization capabilities.

To this end, this paper proposes a new model KF-SA-Transformer, which combines the advantages of the KF, SA, and Transformer. To enhance the model’s resistance to noise and the smoothness of prediction, this paper introduces the KF module; to address the issue of model computational complexity, this paper uses the SA module to improve feature extraction capabilities by learning sparse representations of data, dimensionality reduction of large-scale sequence data, and reducing the input dimensions of the Transformer. The Transformer model is adept at capturing and learning long-term dependencies in the data, which enables the KF-SA-Transformer model to demonstrate higher prediction accuracy and stability in battery SOC prediction tasks. This three-in-one architecture aims to achieve more accurate SOC prediction, which can reduce the risk of overcharging and over-discharging the battery, thereby reducing the frequency of battery replacement and maintenance costs; it can also be used to develop intelligent charging strategies, improve charging efficiency, and reduce the impact on the power grid. In the field of new energy, such as wind and solar power generation, accurate SOC prediction of energy storage systems is of great importance for the stability of the power grid and the effective distribution of energy (Schmietendorf et al.,2017; Yu G. et al., 2022a; Yu G. Z. et al., 2022b).

2 KF-SA-Transformer model for SOC prediction

2.1 Model architecture

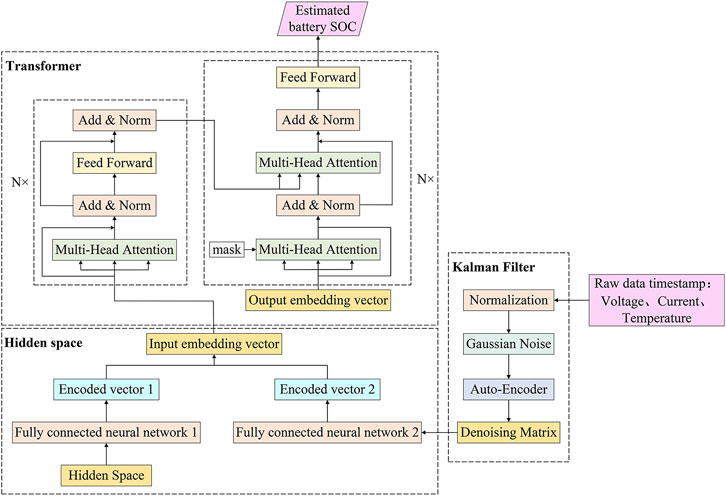
The KF-SA-Transformer model is an innovative battery SOC prediction model that integrates three technologies: the Kalman filter, the sparse autoencoder, and the Transformer module. The input data of battery voltage, current, and temperature are filtered through the Kalman filter to eliminate noise interference and ensure data stability. The filtered data are then fed into the sparse autoencoder module, which extracts key features related to the battery SOC from the data through unsupervised learning, forming an embedding matrix that includes positional information. Finally, the embedding matrix is input into the Transformer module, which uses its unique self-attention mechanism to capture long-distance dependencies in the data, thereby accurately predicting the battery’s SOC. The entire model achieves precise prediction from raw data to the battery SOC through this process, enhancing the accuracy and robustness of the prediction results. The overall architecture of the model is shown in Figure 1. This paper defines a feature input matrix X, with dimensions m × 3, as shown in Eq. 1. Each row represents a sample, and each column represents a feature (current, voltage, or temperature).

$X=\left[\begin{array}{l}{X}_{11}{X}_{12}{X}_{13}\\ X_{21}{X}_{22}{X}_{23}\\ ⋮⋮⋮\\ X_{m1}{X}_{m2}{X}_{m3}\end{array}\right](1)$

Figure 1

Figure 1. Overall model architecture.

Where: X_ij denotes the measurement value of the ith sample on the jth feature, and m is the total number of samples.

2.2 Kalman filter module

Using data-driven methods alone to predict battery SOC has significant limitations, as it requires high-precision battery data and may suffer from limited generalization capabilities. However, the integration of the Kalman filtering method can achieve optimal prediction of system states by minimizing the mean square error (MSE), effectively overcoming the inaccuracy of initial predictions. The Kalman filtering method treats estimated variables as system state variables and measured variables as observation variables. Through a recursive process, the Kalman filtering method can filter out noise and allocate different confidences to estimated and measured variables using Kalman gain until the estimated variables converge to more accurately reflect the actual variables (Peng, 2009). The state transition equation and observation equation are respectively, as shown in Eqs 2, 3:

$X_k=A{X}_{k-1}+w\left(k\right)(2)$

$Z_k=H{X}_k+v\left(k\right)(3)$

Where: X_k, Z_k are the system’s state vector and observation vector at time k; u_k-1 is the control input at time k-1; A, H, are the state transition matrix and observation matrix; w(k), v(k) are the system noise and observation noise.

The core of the Kalman filter lies in two main update steps: Prediction and Update. In the prediction step, the current state is predicted based on the previous moment’s state estimate and process noise, as shown in Eqs 4, 5:

${\widehat{X}}_k^{-}=A{\widehat{X}}_k^{-}(4)$

$P_k^{-}=A{P}_{k-1}{A}^T+Q(5)$

Where: ${\widehat{X}}_k^{-}$ represents the predicted state vector, $P_k^{-}$ is the predicted error covariance matrix, and Q is the process noise covariance matrix. To integrate predicted information with observational data, the concept of the Kalman gain is introduced. By utilizing the Kalman gain, it is possible to update the state estimate and the error covariance, as shown in Eqs 6–8:

$K_K=P_k^{-}{H}^T{\left(H{P}_k^{-}{H}^T+R\right)}^{-1}(6)$

${\widehat{X}}_k={\widehat{X}}_k^{-}+K_k\left(Z_k-H{\widehat{X}}_k^{-}\right)(7)$

$P_k=\left(I-K_{k}H\right)P_k^{-}(8)$

Where: K_k is the Kalman gain, $\widehat{X}$ _k is the corrected state vector, Pk is the corrected error covariance matrix, and R is the observation noise covariance matrix. After processing by the Kalman filter, updated state estimates are obtained, which reflect the optimal estimated state of the battery system at each time step. These state estimates are integrated into a new matrix X_KF, which captures the evolution of the system state over time and filters out the effects of noise.

2.3 Sparse auto-encoder module

The Kalman filter, while effective in processing linear data, has limited capabilities when dealing with nonlinear data and complex relationships. To address this limitation, the integration of a sparse autoencoder into the data processing pipeline is proposed. This autoencoder effectively extracts features from the filtered data, reducing its dimensionality while preserving valuable feature information. This approach helps reduce data dimensionality and identify useful feature information, thereby enhancing the accuracy and performance of the prediction model.

SA introduces modifications to the embedding layer of the Transformer architecture, aiming to lighten the temporal positional encoding and enhance the modeling capabilities for temporal dependencies. As an unsupervised algorithm, SA adjusts its parameters adaptively by calculating the difference between the input and output of the autoencoding process, resulting in a trained final model. This algorithm finds widespread applications in information compression and feature extraction. Its goal is to reconstruct the input data using learned sparse representations.

The sparse autoencoder can sparsely represent battery input features, reduce the dimensionality of the original data, and improve computational efficiency. Its encoder input is the feature vector X_KF obtained after Kalman filtering, with the encoder output and decoder input in the hidden space, where the data is compressed into fewer dimensions while attempting to retain the most important information. The decoder output transforms the representation in the hidden space back to the original data space, attempting to reconstruct data as similar as possible to the input data, as shown in Eqs 9–11:

$A_1=sigmoid\left(W_1{X}_{\text{KF}}+b_1\right)(9)$

$X_{\text{SA}}=sigmoid\left(W_2{A}_1+b_2\right)(10)$

$sigmoid\left(z\right)={\left(1+e^{-z}\right)}^{-1}(11)$

Where: z is any real number; W₁, W₂ are the weights of encoder and decoder; b₁, b₂ are the biases of encoder and decoder. The optimization objective is to minimize the reconstruction loss and approximate the probability density distribution, therefore, the network loss function is derived as shown in Eqs 12–14:

$\begin{array}{c}J\left(W_1,W_2,b_1,b_2\right)=\frac{1}{M}{\displaystyle \sum _{i=1}^M}\left|x^{\left(i\right)}-{\widehat{x}}^{\left(i\right)}{\Vert }^2\right.+\frac{\lambda }{2}‖W_1‖\\ +\frac{\lambda }{2}‖W_2‖+\beta {\displaystyle \sum _{j=1}^d}\left[p\cdot {\log }_2\frac{p}{{\widehat{p}}_j}+\left(1-p\right)\cdot {\log }_2\frac{\left(1-p\right)}{\left(1-{\widehat{p}}_j\right)}\right]\end{array}(12)$

${\widehat{p}}_j=\frac{1}{M}{\displaystyle \sum _{i=1}^M}{a}_j^{\left(i\right)}(13)$

$p=\frac{1}{M}{\displaystyle \sum _{i=1}^M}{s}_j^{\left(i\right)}(14)$

Where: a_j⁽ⁱ⁾ is the jth neuron output value of the ith sample of the hidden space A₁; s_j⁽ⁱ⁾ denotes the jth neuron input value of the ith sample of the encoder A₀; M is the total number of samples; β is the given sparsity constraint coefficient; λ is the given regularization coefficient. The encoder output of the sparse autoencoder results in a processed feature matrix, referred to as X_SA. This matrix encapsulates the salient characteristics of the input data, enabling the subsequent neural network to discern intricate relationships among the sequence elements.

2.4 Transformer module

Due to the inherent complexity and time-varying nature of chemical reaction processes within batteries, model-based prediction methods inherently carry the risk of errors. Enhancing model accuracy further complicates the task of parameter identification. To mitigate this challenge, the Transformer model is introduced, as it excels at capturing long-term dependencies and contextual information within sequence data, thereby enhancing the prediction accuracy of lithium battery SOC.

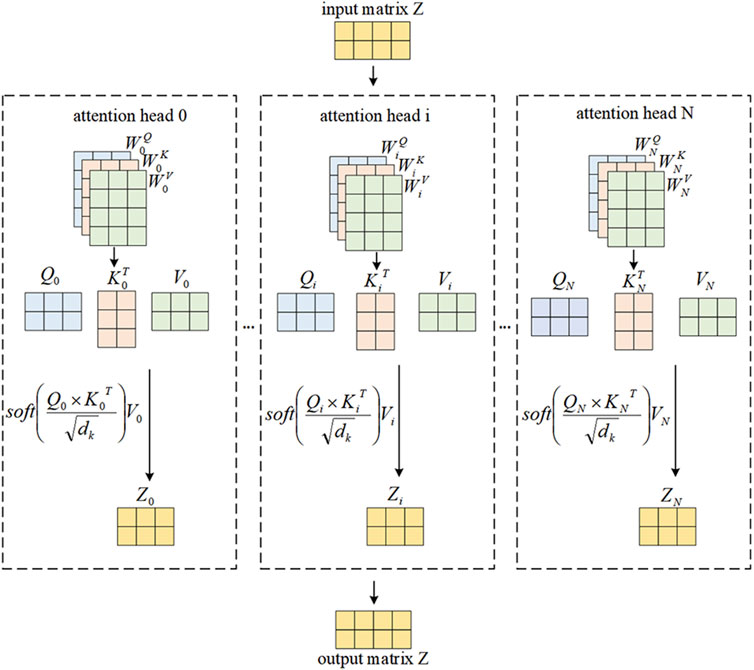
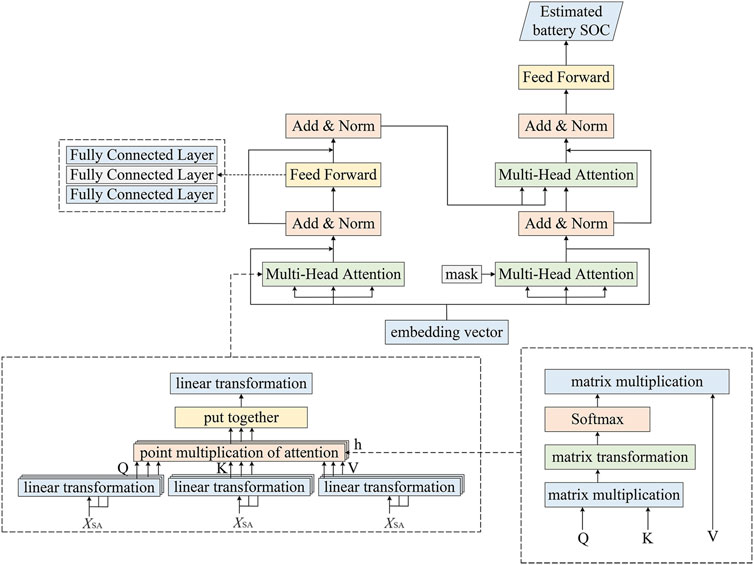
Transformer is a sequence-to-sequence (seq2seq) model based on the attention mechanism, which consists of two parts, Encoder and Decoder. The Transformer model consists of four parts, which are the self-attention mechanism, the multi-head attention mechanism, the positional encoding and the forward propagation network. As shown in Figure 2, the multi-head attention mechanism in the Transformer model allows the model to focus on different parts of the input sequence simultaneously, possessing the ability to globally perceive the input features, which improves the expressiveness of the model and better handles both local and global information. The forward propagation network is a fully-connected feedforward network consisting of two fully-connected layers.

Figure 2

Figure 2. Multi-head attention structure.

The Transformer encoder comprises numerous identical sub-blocks, known as Transformer Blocks, stacked consecutively. The initial sub-layer within each block incorporates the multi-head attention mechanism, followed by a second sub-layer, a fully connected network. These two sub-layers are interconnected through residuals, which effectively prevent gradients from vanishing and enhance the seamless flow of information between them. Additionally, a layer normalization operation is performed after the residuals are connected, further facilitating the algorithm’s convergence. On the other hand, the decoder differs from the encoder in a crucial aspect: the resulting three vectors, along with an ordinal mask, are concurrently fed into the multi-head self-attention layer, as illustrated in Figure 3.

Figure 3

Figure 3. Transformer model.

The Transformer leverages its unique structure to process the feature matrix X_SA refined by the sparse autoencoder, thereby achieving the prediction of the SOC for lithium batteries. The model first captures the interdependencies between sequence data in the input feature matrix through the self-attention mechanism, thereby understanding the long-term dependencies and contextual information within the sequence. And the multi-head attention mechanism allows the Transformer to focus on different parts of the input matrix simultaneously, globally perceiving the input features, which helps the model to better understand and process the input data. Positional encoding is used to provide positional information for each element in the sequence, which is crucial for understanding the sequential relationships. Finally, through the feed-forward neural network, the Transformer integrates this information and translates it into a prediction for the lithium battery SOC. This processing method makes the Transformer highly flexible and accurate when dealing with sequence data, enabling precise prediction of the lithium battery SOC.

3 Case analysis

3.1 Simulation platform and data

3.1.1 Simulation platform

The simulation platform is equipped with an Intel Core i7-7800X processor and an NVIDIA GeForce RTX 2080 Ti graphics card. It utilizes Python 3.8 as a programming language for algorithm development. The algorithmic model is built using TensorFlow, an open-source machine learning framework.

3.1.2 Data preparation

This paper utilized a publicly accessible lithium-ion battery dataset obtained by Dr. Phillip Kollmeyer at McMaster University in Hamilton, Ontario, Canada, to confirm the robustness of the studied model (Philip et al., 2020). This dataset was generated through various charge-discharge cycles on brand-new 3Ah LG 18650HG2 lithium-ion batteries following standard protocols. The collected data includes experiments conducted at six different temperatures ranging from −20°C to 40°C. This paper utilizes the driving condition data at 25°C as the dataset for validating the model’s effectiveness. The dataset includes four standard drives (UDDS, HWFET, LA92, and US06) and eight driving cycles that are randomly combined from the four standard driving cycles.

The KF-SA-Transformer model used the terminal voltage, current, and temperature of the lithium battery as input variables to estimate the battery’s SOC. However, the original data often exhibited significant fluctuations, which could introduce bias during the model parameter optimization process. Consequently, this might affect the effectiveness of the training process and the generalization capability of the model. Additionally, the variables were not uniformly scaled, which could lead to a contraction effect on the data size and range within the neurons of the deep learning model during parameter updates in the backpropagation phase. To address this issue, normalization of the data before prediction becomes imperative. This normalization process adjusts the data to be contained within the [0,1] interval, with the transformation function as show in Eq. 15:

$X=\frac{X_0-X_{\min }}{X_{\max }-X_{\min }}(15)$

Where: X represents the normalized sample data; X₀ represents the original sample data; X_min is the minimum value of the original sample data; X_max is the maximum value of the original sample data.

3.1.3 Assessment indicators

To appraise the precision of the model’s predictive capabilities, this paper employs a suite of metrics: the MSE, MAE. These metrics collectively assess the model’s performance in estimating the SOC of the battery. The specific calculation formula as shown in Eqs 16, 17:

$MSE=\frac{1}{m}{\displaystyle \sum _{i=1}^m}{\left(y_i-{\widehat{y}}_i\right)}^2(16)$

$MAE=\frac{1}{m}{\displaystyle \sum _{i=1}^m}\left|\left(y_i-{\widehat{y}}_i\right)\right|(17)$

Where: m is the number of samples, i is the sample sequence number, y_i is the actual value of the ith sample, $\widehat{y}$ _i is the predicted value of the ith sample, and d_i denotes the average of the real values. The above indicators are used to evaluate the error between the predicted value and the actual value, and the smaller the value is, the more accurate the prediction result is.

3.2 Model performance optimization strategies

3.2.1 Hyper-parameter settings

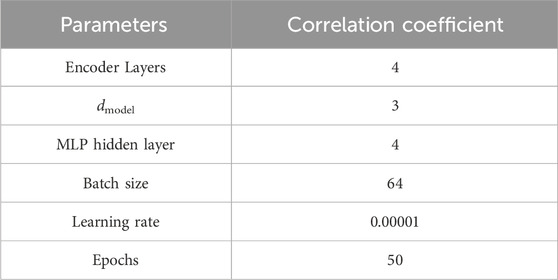
The accuracy of the neural network is influenced by hyper-parameters, which include, but are not limited to, the number of convolutional layers and the dimensions of the convolutional kernel. These hyper-parameters are pivotal in determining the SOC prediction outcomes. Commonly adopted methods for hyper-parameter optimization encompass grid search, random search, and Bayesian optimization. While grid search is a straightforward approach, it can be computationally expensive and time-consuming. To achieve efficient hyper-parameter optimization within a reasonable timeframe, this paper opts for the Bayesian optimization algorithm. The underlying principle of Bayesian optimization involves the construction of a probabilistic model of the objective function. This model is iteratively refined by incorporating new sample points, thereby updating the posterior distribution of the objective function. The optimal hyperparameters selected in this paper are shown in Table 1.

Table 1

Table 1. Model parameter setting.

3.2.2 Comparison of optimization algorithms

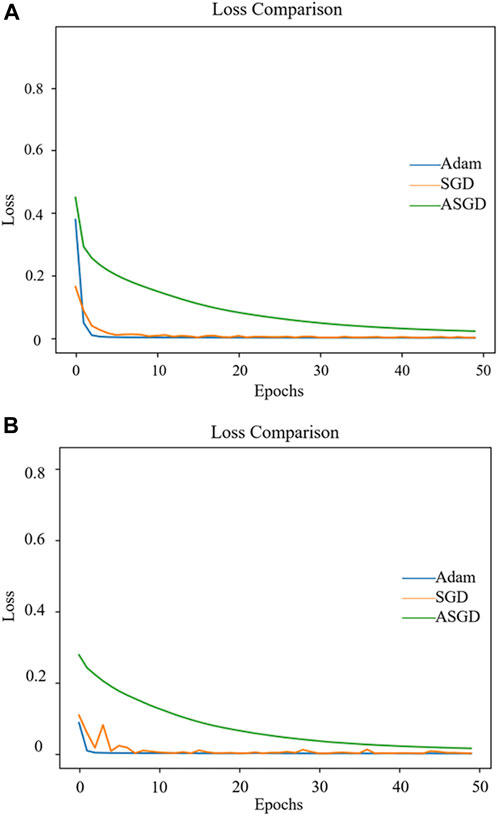
To further enhance the precision of the model’s convergence value, reduce prediction errors, and improve generalization capabilities, it is necessary to introduce a parameter optimization algorithm into the KF-SA-Transformer model. This paper employs Stochastic Gradient Descent (SGD), Average Stochastic Gradient Descent (ASGD), and Adaptive Moment Estimation (Adam) to optimize the KF-SA-Transformer model. As shown in Figure 4, loss curves during iterative training on the training set and validation set for each algorithm are plotted. The analysis indicates that the Adam, SGD, and ASGD algorithms are all capable of achieving model convergence. However, the convergence rate of the ASGD optimization algorithm is relatively slow, failing to reach the convergence value of the other two algorithms even after 50 training epochs. In contrast, the SGD algorithm converges relatively quickly but exhibits significant fluctuations, especially in the loss curve on the validation set. Comparatively, the Adam optimization algorithm has the fastest convergence rate, with the loss value approaching zero and the smallest fluctuations after just 1-3 training epochs. Compared to SGD and ASGD, the Adam algorithm has significantly improved the predictive accuracy of the final model to a greater extent.

Figure 4

Figure 4. Loss profile based on KF-SA-Transformer model (A) training set (B) validation set.

3.3 Results and discussion

3.3.1 Performance comparison of different models

To investigate the performance of the KF-SA-Transformer model, this paper compares it with the SA-Transformer and the Transformer models. Using the UDDS driving data as the test set, the SOC prediction results of these models were compared. Figure 5 illustrates the comparative analysis of the prediction data and the original data for the three models under the UDDS conditions, along with a comparison of their prediction errors.

Figure 5

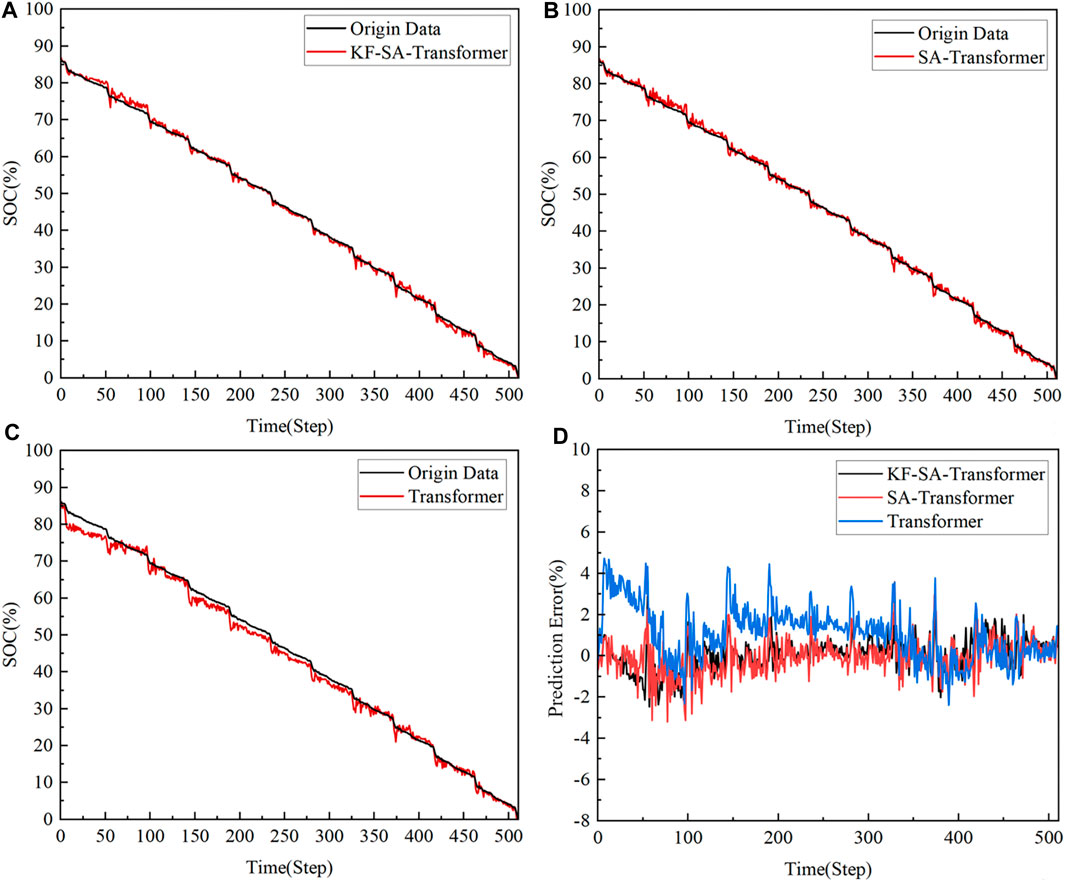
Figure 5. SOC prediction results (A) KF-SA-Transformer (B) SA-Transformer (C) Transformer (D) error comparison of each model.

Based on the thorough data analysis presented in Figure 5, the conclusions drawn are as follows: The KF-SA-Transformer model has exhibited remarkable predictive capabilities. It achieves a low MAE of 0.63% and an RMSE of 0.81% in SOC prediction, while its maximum error is contained within 3.08%. In contrast, the SA-Transformer model’s SOC prediction performance is slightly inferior, with an MAE of 0.65%, an RMSE of 0.88%, and a maximum error of 3.59%. The traditional Transformer model, on the other hand, displays comparatively weaker performance, attaining an MAE of 1.3%, an RMSE of 1.72%, and a maximum error of 4.73%. These findings underscore the KF-SA-Transformer model’s high degree of accuracy and stability in SOC prediction, highlighting its significant advantage over the other models.

3.3.2 Prediction performance under different conditions

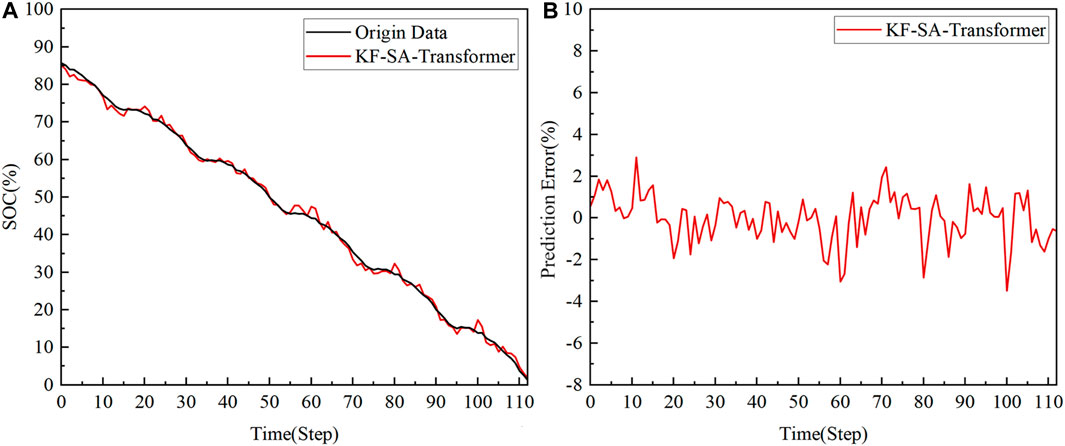
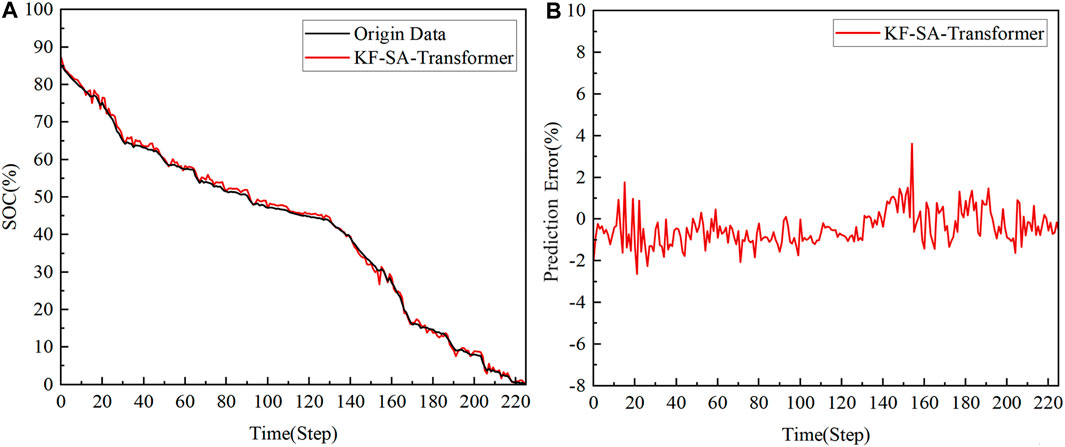
To further explore the performance of the KF-SA-Transformer model in practical applications, this study selected the US06 driving data and a set of mixed driving cycles as the test set, thereby comprehensively evaluating the predictive capability of the KF-SA-Transformer model under variable operating conditions. The predicted results and errors are presented in Figures 6, 7.

Figure 6

Figure 6. SOC prediction results of the US06 driving (A) prediction results (B) error curve.

Figure 7

Figure 7. SOC prediction results of the mixed driving cycle (A) prediction results (B) error curve.

Under the US06, a representative high-speed driving scenario, the KF-SA-Transformer model exhibited outstanding accuracy in predicting the battery’s SOC. Notably, its predicted results achieved an MAE of merely 0.87%, along with an RMSE of 1.13%. Even at the peak of error, the deviation remained within a range of 3.48%. This data unequivocally demonstrates that the KF-SA-Transformer model maintains exceptional predictive accuracy under high-speed and high-load conditions.

In the more complex mixed driving cycles, which encompass a variety of driving speeds and load conditions, the KF-SA-Transformer model’s predictive performance remains equally remarkable. These conditions pose higher demands on the model’s generalization capabilities. However, the KF-SA-Transformer model still demonstrated excellent performance, achieving an MAE of 0.79% and an RMSE of 0.94% for its SOC prediction results. The maximum error was only 3.63%. These data not only validate the model’s adaptability under different operating conditions but also further reinforce the effectiveness of the KF-SA-Transformer model in the field of SOC prediction.

4 Conclusion

This paper introduces a method for predicting the SOC of lithium-ion battery energy storage systems using a hybrid neural network comprising the KF-SA-Transformer architecture. The approach takes current, voltage, and temperature data as inputs, first utilizes a Kalman filter for noise reduction, and then forwards the filtered data to a sparse autoencoder for feature extraction, effectively reducing the data dimensionality. Finally, the Transformer model leverages these low-dimensional features to establish a mapping relationship with the SOC, thereby significantly enhancing the accuracy and overall performance of SOC predictions.

Under identical driving cycle conditions, the KF-SA-Transformer model exhibits significant advantages compared to other models. Moreover, the application of the KF-SA-Transformer model has also yielded favorable results in various other driving cycle conditions. While the model performs exceptionally well on the selected lithium-ion battery dataset, its generalization capabilities to other battery types or varying operating conditions remain to be further validated. Therefore, future research could explore avenues such as enhancing dataset diversity, incorporating datasets from multiple battery models for model training, employing data augmentation techniques, or adopting an ensemble of multiple models to further improve the model’s generalization abilities and foster wider applications and advancements in the field of SOC prediction.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://data.mendeley.com/datasets/cp3473x7xv/3.

Author contributions

YX: Data curation, Formal Analysis, Methodology, Writing–original draft. QS: Validation, Visualization, Writing–original draft. LS: Software, Writing–review and editing. CC: Writing–review and editing, Resources. WL: Writing–review and editing, Conceptualization. CX: Writing–review and editing, Supervision.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study received funding from the Chenguang Program of the Shanghai Education Development Foundation and Shanghai Municipal Education Commission (Grant No. 21CGA63). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication. All authors declare no other competing interests.

Conflict of interest

Author CC was employed by State Grid Xiongan New Area Electric Power Supply Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bao, Z., Nie, J., Lin, H., Gao, K., He, Z., and Gao, M. (2024). TTSNet: state-of-charge estimation of Li-ion battery in electrical vehicles with temporal transformer-based sequence network. IEEE Trans. Veh. Technol., 1–14. doi:10.1109/tvt.2024.3350663

CrossRef Full Text | Google Scholar

Chang, W. Y. (2013). The state of charge estimating methods for battery: a review. Int. Sch. Res. Notices 2013, 1–7. doi:10.1155/2013/953792

CrossRef Full Text | Google Scholar

Chen, D., Hong, W., and Zhou, X. (2022). Transformer network for remaining useful life prediction of lithium-ion batteries. Ieee Access 10, 19621–19628. doi:10.1109/access.2022.3151975

CrossRef Full Text | Google Scholar

Chen, J., Zhang, Y., Wu, J., Cheng, W., and Zhu, Q. (2023). SOC estimation for lithium-ion battery using the LSTM-RNN with extended input and constrained output. Energy 262, 125375. doi:10.1016/j.energy.2022.125375

CrossRef Full Text | Google Scholar

Dey, R., and Salem, F. M. (2017). “Gate-variants of gated recurrent unit (GRU) neural networks,” in 2017 IEEE 60th international midwest symposium on circuits and systems (MWSCAS), Boston, Massachusetts, USA, 6-9 August 2017, 1597–1600. doi:10.1109/mwscas.2017.8053243

CrossRef Full Text | Google Scholar

Han, K., Xiao, A., Wu, E., Guo, J., Xu, C., and Wang, Y. (2021). Transformer in transformer. Adv. neural Inf. Process. Syst. 34, 15908–15919. doi:10.48550/arXiv.2103.00112

CrossRef Full Text | Google Scholar

How, D. N., Hannan, M. A., Lipu, M. H., and Ker, P. J. (2019). State of charge estimation for lithium-ion batteries using model-based and data-driven methods: a review. IEEE Access 7, 136116–136136. doi:10.1109/access.2019.2942213

CrossRef Full Text | Google Scholar

Hussein, H. M., Esoofally, M., Donekal, A., Rafin, S. S. H., and Mohammed, O. (2024). Comparative study-based data-driven models for lithium-ion battery state-of-charge estimation. Batteries 10 (3), 89. doi:10.3390/batteries10030089

CrossRef Full Text | Google Scholar

Li, C., Chen, Z., Cui, J., Wang, Y., and Zou, F. (2014). “The lithium-ion battery state-of-charge estimation using random forest regression,” in 2014 Prognostics and System Health Management Conference (PHM-2014 Hunan), Zhangiiajie City, Hunan, China, 24-27 August 2014, 336–339. doi:10.1109/phm.2014.6988190

CrossRef Full Text | Google Scholar

Peng, D. (2009). Pseudo-linear Kalman Filter in passive target tracking. Softw. Guide 11, 32–34.

Google Scholar

Philip, K., Carlos, V., Mina, N., and Michael, S. (2020). Data from: LG 18650HG2 Li-ion battery data and example deep neural network xEV SOC estimator script. Mendeley Data V3. doi:10.17632/cp3473x7xv.3

CrossRef Full Text | Google Scholar

Rivera-Barrera, J. P., Muñoz-Galeano, N., and Sarmiento-Maldonado, H. O. (2017). SoC estimation for lithium-ion batteries: review and future challenges. Electronics 6 (4), 102. doi:10.3390/electronics6040102

CrossRef Full Text | Google Scholar

Schmietendorf, K., Peinke, J., and Kamps, O. (2017). The impact of turbulent renewable energy production on power grid stability and quality. Eur. Phys. J. B 90, 222–226. doi:10.1140/epjb/e2017-80352-8

CrossRef Full Text | Google Scholar

Shen, H., Zhou, X., Wang, Z., and Wang, J. (2022). State of charge estimation for lithium-ion battery using Transformer with immersion and invariance adaptive observer. J. Energy Storage 45, 103768. doi:10.1016/j.est.2021.103768

CrossRef Full Text | Google Scholar

Shi, K., Zhang, D., Han, X., and Xie, Z. (2022). Digital twin model of photovoltaic power generation prediction based on LSTM and transfer learning. Power Syst. Technol. 46 (4), 1363–1371. (in Chinese). doi:10.13335/j.1000-3673.pst.2021.0738

CrossRef Full Text | Google Scholar

Song, Y., Liu, D., Liao, H., and Peng, Y. (2020). A hybrid statistical data-driven method for on-line joint state estimation of lithium-ion batteries. Appl. Energy 261, 114408. doi:10.1016/j.apenergy.2019.114408

CrossRef Full Text | Google Scholar

Wang, K., Qi, X., and Liu, H. (2019). A comparison of day-ahead photovoltaic power forecasting models based on deep learning neural network. Appl. Energy 251, 113315. doi:10.1016/j.apenergy.2019.113315

CrossRef Full Text | Google Scholar

Yu, G., Liu, C., Tang, B., Chen, R., Lu, L., Cui, C., et al. (2022a). Short term wind power prediction for regional wind farms based on spatial-temporal characteristic distribution. Renew. Energy 199, 599–612. doi:10.1016/j.renene.2022.08.142

CrossRef Full Text | Google Scholar

Yu, G. Z., Lu, L., Tang, B., Wang, S. Y., and Chung, C. Y. (2022b). Ultra-short-term wind power subsection forecasting method based on extreme weather. IEEE Trans. Power Syst. 38 (6), 5045–5056. doi:10.1109/tpwrs.2022.3224557

CrossRef Full Text | Google Scholar

Zhang, L., Xu, G., Zhao, X., Du, X., and Zhou, X. (2020). Study on SOC estimation method of aging lithium battery based on neural network. J. power supply 18 (01), 54–60. doi:10.13234/j.issn.2095-2805.2020.1.54

CrossRef Full Text | Google Scholar

Zhou, W., Zheng, Y., Pan, Z., and Lu, Q. (2021). Review on the battery model and SOC estimation method. Processes 9 (9), 1685. doi:10.3390/pr9091685

CrossRef Full Text | Google Scholar