Abstract
As smart grid advance, Power Load Forecasting (PLF) has become a research hotspot. As the foundation of the forecasting model, the Power Load Monitoring (PLM) data takes on great importance due to its completeness, reliability and accuracy. However, monitoring equipment failures, transmission channel congestion and anomalies result in missing PLM data, which directly affects the performance of the PLF model. To address this issue, this paper proposes an L1-and-L2-Regularized Nonnegative Tensor Factorization (LNTF) model to impute PLM missing data. Its main idea is threefold: (1) combining L1 and L2 norms to achieve effective feature extraction and improve the model’s robustness; (2) incorporating two temporal-dependent linear biases to describe the fluctuations of PLM data; (3) adding nonnegative constraints to precisely define the nonnegativity of PLM data. Extensive empirical studies on two publicly real-world PLM datasets with 1,569,491 and 413,357 known entries and missing rates of 93.35% and 96.75% demonstrate that the proposed LNTF improves 14.04%, 59.31%, and 71.43% on average over the state-of-the-art imputation models in terms of imputation error, convergence rounds, and time cos, respectively. Its high computational efficiency and low imputation error make practical sense for PLM data imputation.
1 Introduction
As one of the most commonly utilized technologies in the electric power industry, the Power Load Forecasting (PLF) (Chakhchoukh et al., 2010; Borges et al., 2012; Zhang et al., 2022; Yang Y. et al., 2023; Wang et al., 2024) is critical to the operation and planning for the power systems, which helps power companies make reasonable decisions to improve the stability and efficiency of the electric grid (Hafeez et al., 2020; Hammad et al., 2020; Li et al., 2021; Duan et al., 2023; Shirkhani et al., 2023). On the other hand, the Power Load Monitoring (PLM) (Tabatabaei et al., 2016; Abubakar et al., 2017; Wang et al., 2023) observes and records various parameters in the power systems, thereby effectively monitoring the power load situation (Zhang et al., 2023; Shao et al., 2023; D’Incecco et al., 2019; Song et al., 2022), and it provides an extensive data foundation for PLF models. However, there are missing PLM data due to sensor failures, network failures, and transmission delays (Wang et al., 2021). In addition, since PLM data needs to be collected frequently, its data scale is large. Therefore, the PLM data is High Dimensional and Incomplete (HDI) (Hu et al., 2020; Luo et al., 2021a; Wu and Luo, 2021; Wu et al., 2023a; Wu et al., 2023b).
Although the existing imputation models are able to complete the imputation of missing PLM data, but their computational and time overheads are expensive and they do not consider the simultaneous missing of multiple monitoring parameters. In contrast, the PLM data collects various monitoring parameters such as electric current, electric voltage, and electric power. On the other hand, temporal variations significantly affect model performance. Since PLM data have temporal characteristics, such as the difference between daytime and nighttime loads, different weekday and weekend usage patterns, and seasonal variations in summer and winter, the static model cannot accurately predict the load variations. Therefore, it is essential to implement a temporal variation-incorporated imputation model that can be applied to multiple monitoring parameters with efficient computation and fast response on HDI PLM data (Wu et al., 2019; Chen J. et al., 2021; Hu et al., 2021; Li Z. et al., 2022; Wu et al., 2022a; Wu et al., 2022b).
By previous studies (Nie et al., 2016; Luo et al., 2019a; Wu et al., 2020; Wu et al., 2021a; Chen K. et al., 2021; Luo et al., 2021b; Zhao et al., 2021; Qin et al., 2023), Tensor Factorization (TF)-based imputation methods are able to efficiently impute missing data by constructing the data as a higher-order tensor. Specifically, based on the Canonical Polyadic Decomposition (CPD) (Wu et al., 2021b), the TF-based model decomposes the higher-order tensor into an outer product of multiple Factor Matrices (FM) to provide a concise and unique representation (Bulat et al., 2020). For instance, Wu et al. (2021a) proposed a Proportional-Integral-Derivative (PID) TF-based model to impute missing data, which adopts the PID control principle to construct the tuning instance error, and optimizes the model parameters by the Stochastic Gradient Descent (SGD) algorithm to achieve a lower imputation error. Wang et al. (2019) incorporated a momentum term into the solving process of SGD based on CPD to accelerate the convergence process. Moreover, the TF-based models can naturally incorporate nonnegative constraints to deal with the data with nonnegativity, called Nonnegative Tensor Factorization (NTF) models (Qin et al., 2022; Xu et al., 2023; Chen et al., 2024). Luo et al. (2022) proposed an NTF model incorporating the neural dynamics principle, which constructs the CPD process as a neural network layer and introduces nonlinearity through the activation functions, thereby achieving efficient imputation of missing data. Che et al. (2023) proposed a sparse and graph regularization TF-based model for fake news detection, which employs a monotonically non-increasing algorithm to solve the model efficiently and obtain excellent model performance.
Therefore, this paper proposes an L
1-and-L
2-regularized-based Nonnegative Tensor-factorization (LNTF) model to impute missing PLM data. It employs a tensor to model PLM data with temporal features. Specifically, during 1 day, we arrange the sampling frequency by time and it preserves the temporal pattern of the monitored parameters. In addition, the cyclical structure of the data is further preserved by arranging the monitoring parameters of each day by time. As a result, the temporal dynamics of the data is fully reflected in the constructed three-order tensor. It further incorporates temporal-dependent linear biases to address the fluctuations of PLM data. Finally, it combines L
1and L
2regularizations to improve the generalization ability and robustness of the model, thereby achieve an efficient model with low imputation error and fast convergence. The main contributions of this paper are presented as follows:
1) A three-order tensor construction. It fully preserves the temporal pattern of PML data.
2) An LNTF model. It provides highly accurate imputation for missing PLM data.
3) An effective LNTF learning scheme. ItschI guarantees the non-negativity of PML data.
Experimental results on two publicly available datasets indicate that the LNTF model is superior to the existing imputation models for PLM data in terms of imputation error, convergence rounds, and time cost.
Section 2 presents the related works, Section 3 gives the Preliminaries, and Section 4 introduces the proposed LNTF model in detail. Section 5 shows the comparative experiments. The conclusions and future work are provided in Section 6.
2 Related works
For data imputation, common methods such as Lagrange interpolation (Allik and Annuk, 2017) and the K-nearest neighbors method (Miao et al., 2016) are often employed. However, these methods perform poorly in scenarios with high missing rates. Liu et al. (2012) defined tensor nuclear norm as the combination of matrix nuclear norms obtained by unfolding the tensor along its modes. Yang and Nagarajaiah (2016) utilized prior knowledge of data structure to minimize the nuclear norm and complete low-rank matrices. Gao et al. (2017) designed a subspace merging method to represent real-world datasets by merging multiple subspaces into a larger one for missing data imputation. However, converting a third-order tensor into matrices loses the original multi-dimensional structural information. Kilmer and Martin (2011) proposed the tensor singular value decomposition method, which demonstrates the multi-dimensional structure by constructing a group ring along the tensor fibers, effectively capturing the inherent low-rank structure of the tensor. He et al. (2019) proposed a Kalman filter model that derives a recursive analytical solution and uses the least squares method to estimate the missing data. To date, researchers have proposed various data imputation models for missing PLM data. Alamoodi et al. (2021) proposed a deep learning-based imputation model for incomplete data, which captures the spatial-temporal relationships of the data through deep learning models and completes the imputation of missing data. Amritkar and Kumar (1995) constructed an encoder-decoder model to impute missing data employing long-short-term memory networks and graph convolution principles. Yang T. et al. (2023) proposed a missing data imputation model based on an improved generative adversarial network, which adopts a deep network model to extract the spatial-temporal correlation of data to achieve better imputation performance. Zhang et al. (2020) proposed a relational graph neural network with a hierarchical attention mechanism, which effectively exploits neighborhood information to highlight the importance of different entities, thereby completing accurately the missing data imputation. Luo et al. (2023) proposed a graph neural network based on attention relation paths, and introduced a neural process based on normalized flow to improve the performance of imputation. Nevertheless, these models generating the entire tensor and calculating the singular values of matrices or tensors, leading to low computational efficiency and excessively high memory requirements.
3 Preliminaries
3.1 Symbol appointment
The symbol system adopted in this paper is presented in Table 1.
TABLE 1
| Symbol | Descriptions |
|---|---|
| Y | An HDI tensor from PLM data |
| I, J, K | Three entity sets |
| H | Rank-one tensor |
| X | Low-rank reconstruction of Y |
| yijk, hijk, xijk | One element indexed by ijk in Y, H, and X |
| R | The rank of the low-rank reconstruction |
| D, T, L | Feature matrices |
| dir, tjr, lkr | Single entries in D, T, and L |
| p, q | Linear bias vectors |
| pi, qk | Single entries in p and q |
| |∙| | Cardinality of an enclosed set |
| ‖∙‖F | Frobenius norm of the enclosed matrix or tensor |
| ◦ | Outer product of two vectors |
| Λ, Γ | Known and unknown data in an HDI tensor |
| Λ(*) | The subsets of Λ linked with entities I, J, and K |
Adopted symbols and their descriptions.
3.2 Problem formulation
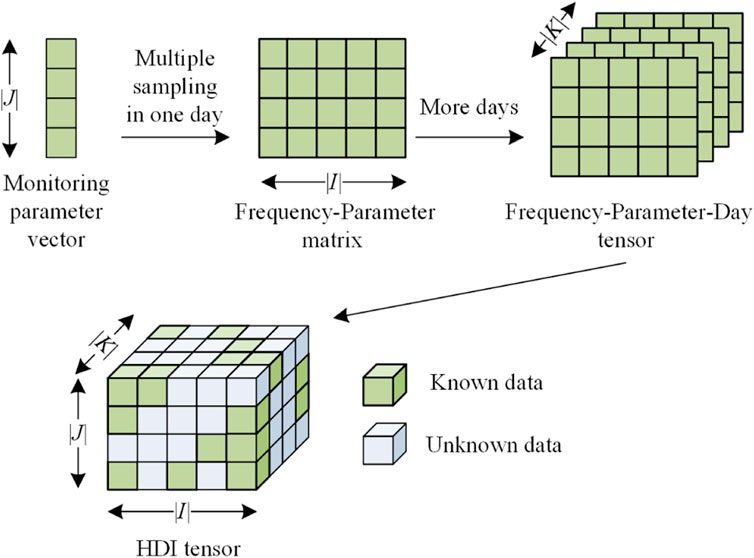
Figure 1 presents the process of modeling PLM data to an HDI tensor. Specifically, a set of monitoring parameter data first forms a parameter vector. Then a frequency-parameter matrix is constituted by multiple samples per day. Finally, multiple frequency-parameter matrices are stacked along the temporal dimension to construct a third-order tensor.
FIGURE 1
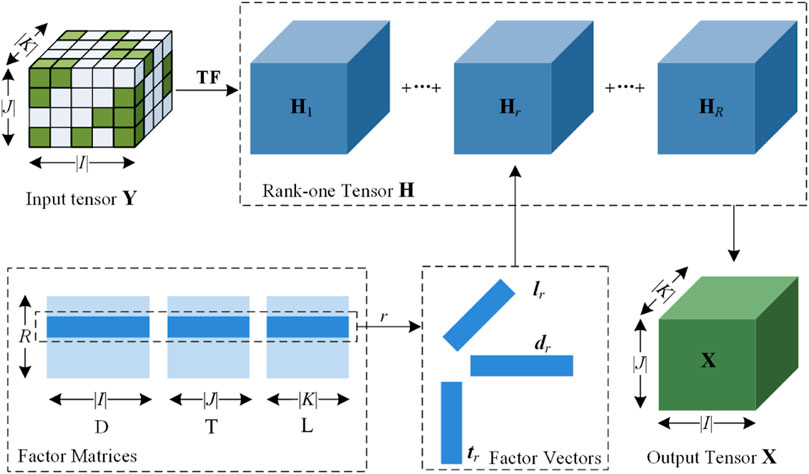
Definition 1(Three-order HDI frequency-parameter-day tensor): Given a parameter-frequency-day tensor Y|I|×|J|×|K|, where each element yijk denotes the ith (i∈I) parameter information in the jth (j∈J) sampling point of kth (k∈K) day. Λ and Γ denote the known and unknown data, respectively. Y is an HDI tensor if |Λ|≪|Γ|.Based on previous research (Luo et al., 2017; Luo et al., 2021c), this paper follows the principle of CPD to implement TF process as shown in Figure 2.With (1), an HDI tensor can be decomposed to R rank-one tensors.
FIGURE 2
Definition 2(Rank-one tensor): Given a rank-one tensor H|I|×|J|×|K|r, it can be written as the outer product of three factor vectors Hr = dr°tr°lr, where dr, tr, and lr are the r-th rows of the factor matrices D|I|×|R|, T|J|×|R|, and L|K|×|R|, respectively.Thus, by unfolding the rank-one tensor, each element xijk in X is expressed by (Eq. 2):To obtain the desired three FMs, we depend on the Euclidean distance (Wang et al., 2005; Shang et al., 2021) to construct an objective function ε, it’s given as (Eq. 3):Note that numerous entries in Y are unknown, and we define ε on known entries Λ to accurately characterize the difference between the original element yijk and the reformulated element xijk as (Eq. 4) (Luo et al., 2015; Luo et al., 2019b):Normally, the PLM data is nonnegative and it is necessary to add nonnegative constraints for FMs to correctly describe the data’s nonnegativity. Therefore, the objective function of the NTF is formulated as (Eq. 5):
4 LNTF model
4.1 Objective function
For the HDI PLM tensor, the monitoring parameter data fluctuate with sampling frequency and time. According to previous research (Li et al., 2016; Yuan et al., 2018), it is essential to incorporate the linear bias (LB) into the model to improve the performance when analyzing fluctuating data. Note that the constructed HDI PLM tensor has time-varying characteristics in I-dimension and K-dimension, we incorporate the corresponding two temporal-dependent LBs into the reformulated element xijk as (Eq. 6):
To deal with the unbalanced distribution of known entries and to avoid overfitting the model, it is necessary to incorporate regularization terms in the objective function (Luo et al., 2019c; Liu et al., 2023). Typically, L1-regularized makes the FMs sparse during the optimization process, which is effective for selecting features since it automatically removes insignificant features. However, incorporating L1-regularized results in a non-smooth objective function (Grasmair et al., 2011; Wu D. et al., 2021). On the other hand, L2-regularized tends to optimize the FMs uniformly by narrowing the feature values and improving the robustness of the model, but it is sensitive towards outliers (Zeng et al., 2017; Jin et al., 2019; Benjamin and Yang, 2021). Hence, we assemble the L1-regularized and L2-regularized to combine their advantages, while adopting an approximation to deal with the absolute value in L1-regularized to make the objective function smooth. Further, the objective function is formulated as (Eq. 7):where λ and λb are the regularized constants for FMs and LBs, respectively, and τ is a tiny positive number.
4.2 Learning scheme
Considering the nonnegativity of PLM data, we implement the NMU for FMs and LBs based on previous studies (Badeau et al., 2010; Liu et al., 2020). Specifically, additive gradient descent (AGD) is applied to (7) to implement the following learning rule:where ηij and ηi denote the learning rates for dir and pi, respectively. Note that we only present the update rules for one FM and one LB, since similar inferences are applied to {tjr, lkr} and qk. Further, we separate the positive and negative components in learning rule as:
In order to cancel the negative component in (8), the learning rates are adjusted as follows:
With (9), (10), we obtain the multiplicative update rules for FMs and LBs as:
With (11), if D, T, L, p, and q are initially nonnegative, they maintain their nonnegativity during the update process.
4.3 Algorithm design and analysis
Based on the above inferences, we design the LNTF model as shown in Algorithm 1. Note that the pseudocodes of procedures {Procedure_D, Procedure_T, Procedure_L} and {Procedure_p, Procedure_q} in LNTF are similar, and we provide the update procedure for U and p as presented in Procedure_D and Procedure_p.
With Algorithm 1, the computational complexity of the LNTF model depends on the complexity of initializing and updating the FMs and LBs. Specifically, the computational complexity of procedure Update_D is presented as (Eq. 12):
Similarly, the computational complexity of procedure Update_ p is given as (Eq. 13):
Therefore, the computational complexity of LNTF model is:
Note that in (14), we omit the constant coefficients and lower order terms since |Λ| ≫ max{|I|, |J|, |K|} for an HDI tensor. With (14), n and R are positive constants in practical application, thus the computational complexity of the LNTF model is linear with the number of known entities in the HDI tensor.
For the storage complexity of the LNTF model, which depends on the number of known entities, the caches of FMs and LBs, the auxiliary matrices and arrays in the update procedures. Therefore, the storage complexity of the LNTF model is:
With (15), constant constants and lower order terms are omitted, and the storage complexity of the LNTF model is linearly related to the number of known entities in the HDI tensor.
5 Empirical studies
5.1 General settings
In this section, all the comparison experiments are run on a desktop computer equipped with a 2.10 GHz Intel Core i7-13700 and a NVIDIA GeForce RTX 3050 GPU card. The versions of Java and Python used are SE-8U212 and Python 3.6.5, respectively.
5.1.1 Datasets
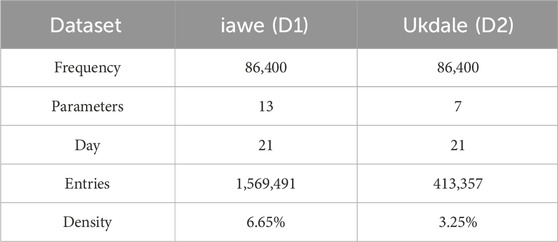
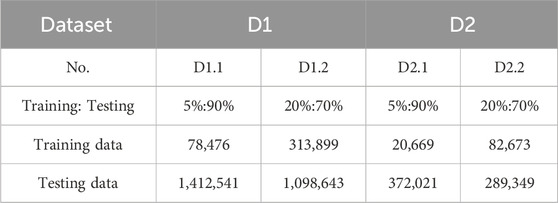
In this paper, two public PLM datasets iawe (Batra et al., 2013) and ukdale (Kelly and Knottenbelt, 2015) are used to compare model performance. They record load monitoring data of multiple appliances in the users’ homes, and the details are shown in Table 2. In D1, the monitoring parameters 13 parameters such as electric current, electric voltage, and electric power, etc., which are sampled 86,400 times per day for 21 days, and the number of known entries is 1,569,491. Note that we further split the datasets proportionally into disjoint training (Φ), validation (Ψ), and test sets (Ω) to evaluate the model performance, as shown in Table 3. In addition, we generate 20 random splits on each dataset to achieve unbiased model results.
TABLE 2
| Dataset | iawe (D1) | Ukdale (D2) |
|---|---|---|
| Frequency | 86,400 | 86,400 |
| Parameters | 13 | 7 |
| Day | 21 | 21 |
| Entries | 1,569,491 | 413,357 |
| Density | 6.65% | 3.25% |
Dataset details.
TABLE 3
| Dataset | D1 | D2 | ||
|---|---|---|---|---|
| No. | D1.1 | D1.2 | D2.1 | D2.2 |
| Training: Testing | 5%:90% | 20%:70% | 5%:90% | 20%:70% |
| Training data | 78,476 | 313,899 | 20,669 | 82,673 |
| Testing data | 1,412,541 | 1,098,643 | 372,021 | 289,349 |
Details settings of training datasets.
5.1.2 Evaluation metrics
The prediction accuracy in a given HDI PLM tensor directly reflects the prediction performance of the model. Based on previous studies (Li W. et al., 2022; Yuan et al., 2022; Bi et al., 2023; Wu et al., 2023c; Qin and Luo, 2023), Root mean squared error (RMSE) and mean absolute error (MAE) are commonly adopted as evaluation metrics for prediction accuracy, and they are given as (Eq. 16):where Ω denotes the testing set. Note that lower RMSE and MAE denote that the model provides higher prediction accuracy for the target tensor.
5.1.3 Compared models
The five state-of-the-art comparison models are given as follows:
• LNTF (M1): The model presented in this paper.
• TCA (M2): A multi-dimensional tensor complementation model based on CP decomposition (Su et al., 2021), which trains the latent feature matrix by applying the least squares and gradient descent methods.
• HDOP (M3): A multilinear algebraic model (Wang et al., 2016), which adopts tensor decomposition and reconstruction optimization for data complementation.
• CTF (M4): A data completion model employing CP decomposition (Ye et al., 2021), which adopts the Cauchy loss to measure the difference between the predicted and true values and to improve the robustness of the model.
• LightGCN-AdjNorm (M5): A graph embedding based model (Zhao et al., 2022) that realizes accurate data complementation by controlling the normalization strength and aggregation process. It computes the average loss by splitting the PLM tensor into a set of slices along the time dimension
• BCLFT (M6): A latent factor TF-based model (Dong et al., 2024) that incorporates transfer learning and builds auxiliary tensors to transfer knowledge from the auxiliary domain to the target domain to alleviate data sparsity.
5.1.4 Training settings
For the choice of rank, larger rank provides more model parameters to capture more complex patterns and structures. However, it also leads to higher computational and time overhead, and we empirically set rank to five for all models to provide fair experimental results. In addition, the hyper-parameters λ and λb significantly affect the performance of the model. The large regularization constants help to reduce the risk of overfitting, thereby increasing the robustness and generalization ability of the model. Relatively, small regularization constants lead to overfitting. Therefore, we search for the optimal hyper-parameters by grid search. Specifically, hyper-parameters λ and λb perform a grid search in the range [10−3,10−2] with a step size of 10−3. For the comparison models, we refer to the reference (Luo et al., 2021c) to set their hyper-parameters as shown in Table 4. Note that the training process of the model is terminated if the iteration count reaches 103 or if the error between two consecutive training iterations is smaller than 10−5.
TABLE 4
| Dataset | M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|---|
| D1 | λ = 0.002 | η = 0.001 | η = 0.004 | λ = 10−8 | K = 3, η = 0.001 | λ = 0.01 |
| λb = 0.004 | λ = 0.01 | λ = 0.01 | γ = 500 | λ = 0.1, min-batch = 2048 | a = β = 0.004 | |
| D2 | λ = 0.004 | η = 0.001 | η = 0.004 | λ = 10−8 | K = 3, η = 0.001 | λ = 0.01 |
| λb = 0.004 | λ = 0.01 | λ = 0.01 | γ = 800 | λ = 0.1, min-batch = 2048 | a = β = 0.004 |
Hyper-parameter settings of all model on datasets.
5.2 Comparison results
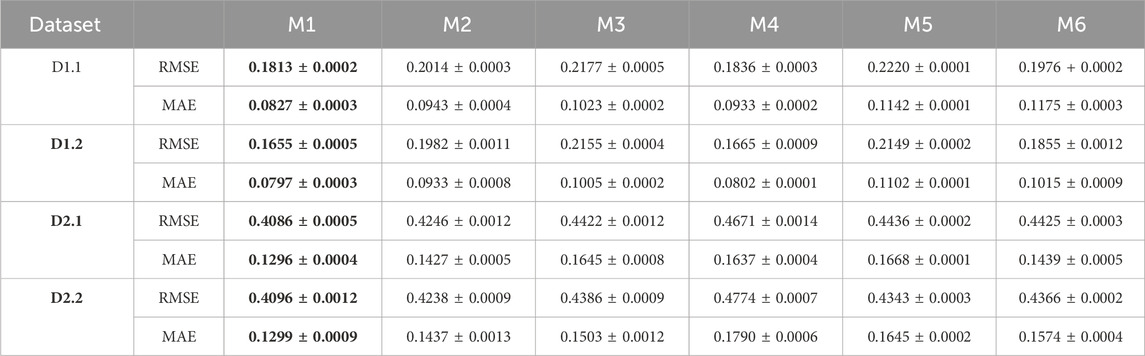
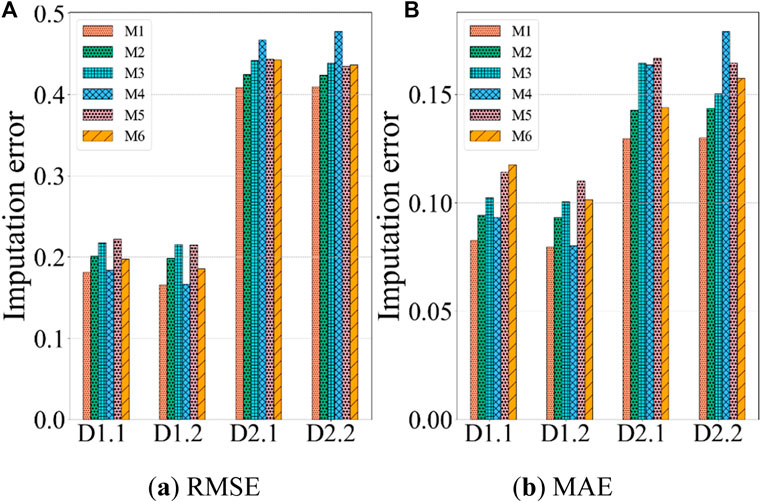
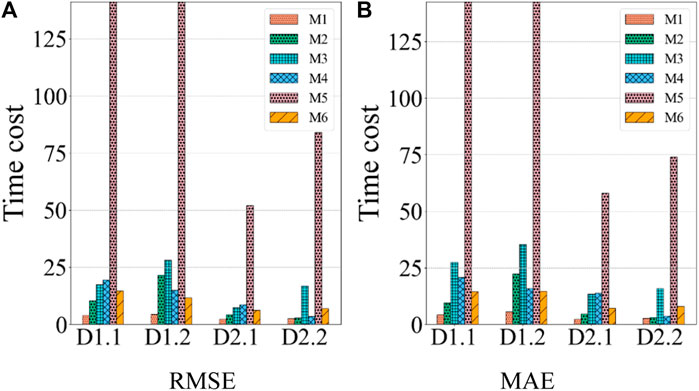
This section presents a comparison of the LNTF model against the five comparison models in terms of prediction error, iteration count, and time cost.
Tables 5–
7present the statistics data of all the models, respectively.
Figures 3–
5chart the comparison of RMSE and MAE for all models on the dataset. From these results, we find that:
• The LNTF model has lower prediction error compared with the comparison models. As shown in Table 5 and Figure 3, the prediction errors of LNTF model in RMSE and MAE are 0.1813 and 0.0827 on the dataset D1.1. Comparatively, the RMSE of the comparison models M2, M3, M4, M5, M6 are 0.2014, 0.2177, 0.1836, 0.2220, 0.1976 and the MAE of them are 0.0943, 0.1023, 0.0933, 0.1142, 0.1175, respectively. The prediction errors of LNTF compared with its peers in RMSE and MAE are reduced by 9.98%, 16.72%, 1.25%, 18.33%, 8.24% and 12.30%, 23.70%, 11.36%, 27.58%, 29.61%, respectively. Note that the training entries in D1.1 are 5% of the known entries, which indicates that the LNTF model outperforms the comparison models in addressing the high missing rate tensor. Further, we increase the number of training entries to 20% of the known entries, as presented in D1.2. Similarly, compared with the comparison models, the prediction error of the LNTF model in RMSE and MAE on D1.2 are reduced by 16.49%, 23.20%, 0.60%, 22.98%, 10.78% and 14.57%, 20.69%, 0.62%, 27.67%, 21.47%. In general, the improvement of LNTF over the comparison models increases with the number of training entries. Similar performance gains can also be obtained in D2.1 and D2.2.
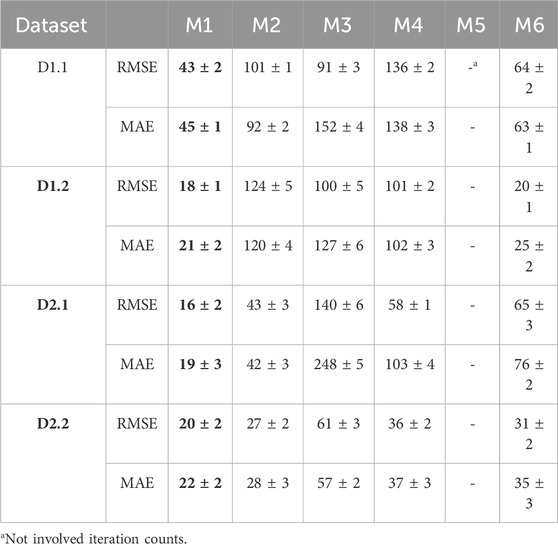
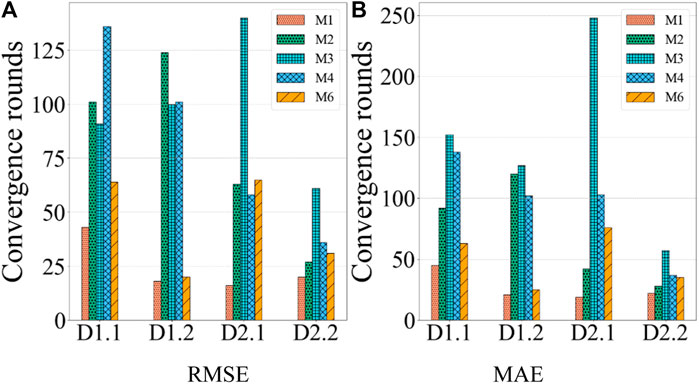
• The LNTF model has fewer iteration count compared with the comparison models. For instance, according to Figure 4 and Table 6, the LNTF model only takes 16 and 19 iterations in RMSE and MAE on D2.1, respectively. It is much fewer than M2’s 43, M3’s 140, M4’s 58, M6’s 65 in RMSE and M2’s 42, M3′248, M4’s 103, M6’s 76 in MAE. By contrast, the iteration counts of the LNTF model in RMSE are 37.20% of M2, 11.42% of M3, 27.58% of M4, 24.61% of M6 and 45.23%, 7.6%, 18.44%, 25% of them in MAE, respectively. Note that M5 is a model based on graph neural networks, which does not involve the iteration count. When the training entries are increased to 20% of the known entries, the iteration count of the LNTF model in RMSE is 20, which is the comparison mode’s 74.07%, 32.78%, 55.55%, and 64.51%, respectively. For MAE, LNTF’s iteration count is 78.57%, 38.59%, 59.45%, and 62.85% of comparison models. Similar results can be encountered on other datasets.
• The LNTF model has fewer time cost compared with the comparison models. As depicted in Figure 5 and Table 7, the LNTF model costs 2.489s to achieve the lowest RMSE on D2.2. Compared to the comparison models of 2.876s, 16.846s, 3.493s, 84s, and 7.024s, the time cost of the LNTF model is 86.54% of M2, 14.77% of M3, 71.25% of M4, 2.69% of M5, and 35.43% of M6. For MAE on D2.2, the LNTF model costs 2.815s to reach the lowest MAE, which is 94.52% of M2’s 2.978s, 17.79% of M3’s 15.821s, 76.41% of M4’s 3.684s, 3.80% of M5’s 74s, and 35.48% of M6’s 7.932s. Note that the lower time cost of the LNTF model can also be observed on D1.1, D1.2, and D2.1.
TABLE 5
| Dataset | M1 | M2 | M3 | M4 | M5 | M6 | |
|---|---|---|---|---|---|---|---|
| D1.1 | RMSE | 0.1813 ± 0.0002 | 0.2014 ± 0.0003 | 0.2177 ± 0.0005 | 0.1836 ± 0.0003 | 0.2220 ± 0.0001 | 0.1976 + 0.0002 |
| MAE | 0.0827 ± 0.0003 | 0.0943 ± 0.0004 | 0.1023 ± 0.0002 | 0.0933 ± 0.0002 | 0.1142 ± 0.0001 | 0.1175 ± 0.0003 | |
| D1.2 | RMSE | 0.1655 ± 0.0005 | 0.1982 ± 0.0011 | 0.2155 ± 0.0004 | 0.1665 ± 0.0009 | 0.2149 ± 0.0002 | 0.1855 ± 0.0012 |
| MAE | 0.0797 ± 0.0003 | 0.0933 ± 0.0008 | 0.1005 ± 0.0002 | 0.0802 ± 0.0001 | 0.1102 ± 0.0001 | 0.1015 ± 0.0009 | |
| D2.1 | RMSE | 0.4086 ± 0.0005 | 0.4246 ± 0.0012 | 0.4422 ± 0.0012 | 0.4671 ± 0.0014 | 0.4436 ± 0.0002 | 0.4425 ± 0.0003 |
| MAE | 0.1296 ± 0.0004 | 0.1427 ± 0.0005 | 0.1645 ± 0.0008 | 0.1637 ± 0.0004 | 0.1668 ± 0.0001 | 0.1439 ± 0.0005 | |
| D2.2 | RMSE | 0.4096 ± 0.0012 | 0.4238 ± 0.0009 | 0.4386 ± 0.0009 | 0.4774 ± 0.0007 | 0.4343 ± 0.0003 | 0.4366 ± 0.0002 |
| MAE | 0.1299 ± 0.0009 | 0.1437 ± 0.0013 | 0.1503 ± 0.0012 | 0.1790 ± 0.0006 | 0.1645 ± 0.0002 | 0.1574 ± 0.0004 |
Prediction error of all models.
TABLE 6
| Dataset | M1 | M2 | M3 | M4 | M5 | M6 | |
|---|---|---|---|---|---|---|---|
| D1.1 | RMSE | 43 ± 2 | 101 ± 1 | 91 ± 3 | 136 ± 2 | -a | 64 ± 2 |
| MAE | 45 ± 1 | 92 ± 2 | 152 ± 4 | 138 ± 3 | - | 63 ± 1 | |
| D1.2 | RMSE | 18 ± 1 | 124 ± 5 | 100 ± 5 | 101 ± 2 | - | 20 ± 1 |
| MAE | 21 ± 2 | 120 ± 4 | 127 ± 6 | 102 ± 3 | - | 25 ± 2 | |
| D2.1 | RMSE | 16 ± 2 | 43 ± 3 | 140 ± 6 | 58 ± 1 | - | 65 ± 3 |
| MAE | 19 ± 3 | 42 ± 3 | 248 ± 5 | 103 ± 4 | - | 76 ± 2 | |
| D2.2 | RMSE | 20 ± 2 | 27 ± 2 | 61 ± 3 | 36 ± 2 | - | 31 ± 2 |
| MAE | 22 ± 2 | 28 ± 3 | 57 ± 2 | 37 ± 3 | - | 35 ± 3 |
Iteration count of all models.
Not involved iteration counts.
TABLE 7
| Dataset | M1 | M2 | M3 | M4 | M5 | M6 | |
|---|---|---|---|---|---|---|---|
| D1.1 | RMSE | 4.013 ± 0.062 | 10.369 ± 0.091 | 17.473 ± 0.098 | 19.492 ± 0.079 | 1,255 ± 13.264 | 14.679 ± 0.034 |
| MAE | 4.287 ± 0.071 | 9.495 ± 0.088 | 27.421 ± 0.113 | 20.752 ± 0.134 | 1,233 ± 12.021 | 14.464 + 0.052 | |
| D1.2 | RMSE | 4.456 ± 0.056 | 21.563 ± 0.156 | 28.136 ± 0.024 | 14.947 ± 0.566 | 804 ± 11.721 | 11.687 ± 0.84 |
| MAE | 5.537 ± 0.059 | 22.365 ± 0.177 | 35.423 ± 0.035 | 15.882 ± 0.622 | 681 ± 9.943 | 14.632 ± 0.16 | |
| D2.1 | RMSE | 2.168 ± 0.029 | 4.238 ± 0.059 | 7.387 ± 0.254 | 8.694 ± 0.097 | 52 ± 6.231 | 6.188 ± 0.042 |
| MAE | 2.294 ± 0.033 | 4.652 ± 0.042 | 13.334 ± 0.235 | 13.798 ± 0.087 | 58 ± 8.349 | 7.236 ± 0.072 | |
| D2.2 | RMSE | 2.489 ± 0.055 | 2.876 ± 0.048 | 16.846 ± 0.078 | 3.493 ± 0.056 | 84 ± 7.493 | 7.024 ± 0.121 |
| MAE | 2.815 ± 0.057 | 2.978 ± 0.057 | 15.821 ± 0.049 | 3.684 ± 0.043 | 74 ± 9.479 | 7.932 ± 0.083 |
Time cost of all models (seconds).
FIGURE 3
FIGURE 4
FIGURE 5
6 Conclusion
In order to achieve the interpolation of PLM missing data, this paper proposes a LNTF model with low imputation error. In the LNTF model, we design two temporal-dependent linear biases to address the fluctuations of monitoring parameters. Further, we combine the advantages of L
1and L
2regularizations to accurately extract features of PLM data and improve the robustness of the LNTF model. In addition, the model parameters are updated by employing the NUM algorithm to accurately describe the nonnegativity of the PLM data. Finally, experiments on two datasets with different missing rates indicate that the LNTF model can effectively impute the PLM missing data, thereby providing a reliable data foundation for following data analysis. However, the following issues still need to be addressed:
• The manual tuning method for two hyper-parameters in LNTF consumes a lot of time. Therefore, it is a desirable work to incorporate the hyper-parameter adaptive learning scheme.
• Can we adopt other learning schemes such as ADMM algorithm (Hu et al., 2018; Luo et al., 2021d), second-order Newton’s method to update the model parameters?
We are aiming to address the above issues in future work.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
XL: Conceptualization, Funding acquisition, Investigation, Resources, Validation, Writing–original draft. ZH: Writing–review and editing, Conceptualization, Data curation, Supervision, Validation, Visualization. ZM: Project administration, Software, Writing–original draft. ZL: Formal Analysis, Validation, Writing–original draft. QW: Data curation, Methodology, Writing–original draft. AZ: Data curation, Validation, Writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by Science and Technology Project of State Grid Jiangsu Electric Power Co., Ltd. (J2023017). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Acknowledgments
Thanks for the funding provided by State Grid Jiangsu Electric Power Co., Ltd.
Conflict of interest
Authors XL, ZH, ZM, and ZL were employed by State Grid Jiangsu Electric Power Co., Ltd., Nanjing Power Supply Company.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
AbubakarI.KhalidS. N.MustafaM. W.ShareefH.MustaphaM. (2017). Application of load monitoring in appliances’ energy management–A review. Renew. Sustain. Energy Rev.67, 235–245. 10.1016/j.rser.2016.09.064
2
AlamoodiA. H.ZaidanB. B.ZaidanA. A.AlbahriO.ChenJ.ChyadM.et al (2021). Machine learning-based imputation soft computing approach for large missing scale and non-reference data imputation. Chaos Solit. Fractals151, 111236. 10.1016/j.chaos.2021.111236
3
AllikA.AnnukA. (2017). “Interpolation of intra-hourly electricity consumption and production data,” in Proceedings of the 6th international conference on renewable energy research and applications (San Diego, CA, USA), 131–136.
4
AmritkarR. E.KumarP. P. (1995). Interpolation of missing data using nonlinear and chaotic system analysis. J. Geophys. Res. Atmos.100, 3149–3154. 10.1029/94jd01531
5
BadeauR.BertinN.VincentE. (2010). Stability analysis of multiplicative update algorithms and application to nonnegative matrix factorization. IEEE Trans. Neural Netw.21, 1869–1881. 10.1109/tnn.2010.2076831
6
BatraN.GulatiM.SinghA. (2013). “It’s Different: insights into home energy consumption in India,” in Proceedings of the 5th ACM workshop on embedded systems for energy-efficient buildings (Roma, Italy), 1–8.
7
BenjaminB. M.YangM. S. (2021). Weighted multiview possibilistic c-means clustering with L2 regularization. IEEE Trans. Fuzzy Syst.30, 1357–1370. 10.1109/tfuzz.2021.3058572
8
BiF.LuoX.ShenB.DongH.WangZ. (2023). Proximal alternating-direction-method-of-multipliers-incorporated nonnegative latent factor analysis. IEEE/CAA J. Autom. Sin.10, 1388–1406. 10.1109/jas.2023.123474
9
BorgesC. E.PenyaY. K.FernandezI. (2012). Evaluating combined load forecasting in large power systems and smart grids. IEEE Trans. Ind. Inf.9, 1570–1577. 10.1109/tii.2012.2219063
10
BulatA.KossaifiJ.TzimiropoulosG. (2020). “Incremental multi-domain learning with network latent tensor factorization,” in Proceedings of the 34th AAAI conference on artificial intelligence (New York, NY, USA), 10470–10477.
11
ChakhchoukhY.PanciaticiP.MiliL. (2010). Electric load forecasting based on statistical robust methods. IEEE Trans. Power Syst.26, 982–991. 10.1109/tpwrs.2010.2080325
12
CheH.PanB.LeungM. F.CaoY.YanZ. (2023). Tensor factorization with sparse and graph regularization for fake news detection on social networks. IEEE Trans. Comput. Soc. Syst.1, 1–11. 10.1109/tcss.2023.3296479
13
ChenJ.LuoX.ZhouM. C. (2021a). Hierarchical particle swarm optimization-incorporated latent factor analysis for large-scale incomplete matrices. IEEE Trans. Big Data8, 1–1536. 10.1109/tbdata.2021.3090905
14
ChenK.LiC.LiA.GaoJ.MaS. (2021b). “Focus on inherent attributes for temporal knowledge graph completion,” in Proceeding of the international joint conference on neural networks (Shenzhen, China), 1–8.
15
ChenM.WangR.QiaoY.LuoX. (2024). A generalized nesterov's accelerated gradient-incorporated non-negative latent-factorization-of-tensors model for efficient representation to dynamic QoS data. IEEE Trans. Emerg. Top. Comput. Intell.1, 2386–2400. 10.1109/tetci.2024.3360338
16
D’InceccoM.SquartiniS.ZhongM. (2019). Transfer learning for non-intrusive load monitoring. IEEE Trans. Smart Grid11, 1419–1429. 10.1109/tsg.2019.2938068
17
DongJ.SongY.LiM.RaoH. (2024). Biased collective latent factorization of tensors with transfer learning for dynamic QoS data predicting. Digit. Signal Process.146, 104360. 10.1016/j.dsp.2023.104360
18
DuanY.ZhaoY.HuJ. (2023). An initialization-free distributed algorithm for dynamic economic dispatch problems in microgrid: modeling, optimization and analysis. Sustain. Energy Grids Netw.34, 101004. 10.1016/j.segan.2023.101004
19
GaoP.WangM.ChowJ. H.BergerM.SeverskyL. M. (2017). Missing data recovery for high-dimensional signals with nonlinear low-dimensional structures. IEEE Trans. Signal Process.65 (20), 5421–5436. 10.1109/tsp.2017.2725227
20
GrasmairM.ScherzerO.HaltmeierM. (2011). Necessary and sufficient conditions for linear convergence of ℓ1‐regularization. Commun. Pure Appl. Math.64, 161–182. 10.1002/cpa.20350
21
HafeezG.AlimgeerK. S.KhanI. (2020). Electric load forecasting based on deep learning and optimized by heuristic algorithm in smart grid. Appl. Energy269, 114915. 10.1016/j.apenergy.2020.114915
22
HammadM. A.JerebB.RosiB.DraganD. (2020). Methods and models for electric load forecasting: a comprehensive review. Logist. Sustain. Transp.11, 51–76. 10.2478/jlst-2020-0004
23
HeJ.ZhangX.XuB. (2019). KF-based multiscale response reconstruction under unknown inputs with data fusion of multitype observations. J. Aerosp. Eng.32 (4), 04019038. 10.1061/(asce)as.1943-5525.0001031
24
HuL.YangS.LuoX. (2020). An algorithm of inductively identifying clusters from attributed graphs. IEEE Trans. Big Data8, 523–534. 10.1109/TBDATA.2020.2964544
25
HuL.YangS.LuoX.YuanH.SedraouiK.ZhouM. (2021). A distributed framework for large-scale protein-protein interaction data analysis and prediction using mapreduce. IEEE/CAA J. Autom. Sin.9, 160–172. 10.1109/jas.2021.1004198
26
HuL.YuanX.LiuX.XiongS.LuoX. (2018). Efficiently detecting protein complexes from protein interaction networks via alternating direction method of multipliers. IEEE/ACM Trans. Comput. Biol. Bioinform.16, 1922–1935. 10.1109/tcbb.2018.2844256
27
JinY. F.YinZ. Y.ZhouW. H.YinJ. H.ShaoJ. F. (2019). A single-objective EPR based model for creep index of soft clays considering L2 regularization. Eng. Geol.248, 242–255. 10.1016/j.enggeo.2018.12.006
28
KellyJ.KnottenbeltW. (2015). The UK-DALE dataset, domestic appliance-level electricity demand and whole-house demand from five UK homes. Sci. Data2, 150007–150014. 10.1038/sdata.2015.7
29
KilmerM. E.MartinC. D. (2011). Factorization strategies for third-order tensors. Linear Algebra Appl.435 (3), 641–658. 10.1016/j.laa.2010.09.020
30
LiH.ZhangQ.DengJ. (2016). Biased multiobjective optimization and decomposition algorithm. IEEE Trans. Cybern.47, 52–66. 10.1109/tcyb.2015.2507366
31
LiP.HuJ.QiuL.ZhaoY.GhoshB. K. (2021). A distributed economic dispatch strategy for power–water networks. IEEE Trans. Control Netw. Syst.9, 356–366. 10.1109/tcns.2021.3104103
32
LiW.LuoX.YuanH.ZhouM. (2022b). A momentum-accelerated Hessian-vector-based latent factor analysis model. IEEE Trans. Serv. Comput.16, 830–844. 10.1109/tsc.2022.3177316
33
LiZ.LiS.BamasagO. O.AlhothaliA.LuoX. (2022a). Diversified regularization enhanced training for effective manipulator calibration. IEEE Trans. Neural Netw. Learn. Syst.34, 8778–8790. 10.1109/tnnls.2022.3153039
34
LiuJ.MusialskiP.WonkaP.YeJ. (2012). Tensor completion for estimating missing values in visual data. IEEE Trans. Pattern Anal. Mach. Intell.35 (1), 208–220. 10.1109/tpami.2012.39
35
LiuZ.LuoX.WangZ. (2020). Convergence analysis of single latent factor-dependent, nonnegative, and multiplicative update-based nonnegative latent factor models. IEEE Trans. Neural Netw. Learn. Syst.32, 1737–1749. 10.1109/tnnls.2020.2990990
36
LiuZ.LuoX.ZhouM. (2023). Symmetry and graph bi-regularized non-negative matrix factorization for precise community detection. IEEE Trans. Autom. Sci. Eng.21, 1406–1420. 10.1109/tase.2023.3240335
37
LuoL.LiY. F.HaffariG. (2023). “Normalizing flow-based neural process for few-shot knowledge graph completion,” in Proceedings of the 46th international ACM SIGIR conference on research and development in information retrieval (Taiwan, China), 900–910.
38
LuoX.ChenM.WuH.LiuZ.YuanH.ZhouM. (2021a). Adjusting learning depth in nonnegative latent factorization of tensors for accurately modeling temporal patterns in dynamic QoS data. IEEE Trans. Autom. Sci. Eng.18, 2142–2155. 10.1109/tase.2020.3040400
39
LuoX.WangZ.ShangM. (2019c). An instance-frequency-weighted regularization scheme for non-negative latent factor analysis on high-dimensional and sparse data. IEEE Trans. Syst. Man. Cybern. Syst.51, 3522–3532. 10.1109/tsmc.2019.2930525
40
LuoX.WuH.LiZ. (2022). NeuLFT: a novel approach to nonlinear canonical polyadic decomposition on high-dimensional incomplete tensors. IEEE Trans. Knowl. Data Eng.35, 1–6166. 10.1109/tkde.2022.3176466
41
LuoX.WuH.WangZ.WangJ.MengD. (2021c). A novel approach to large-scale dynamically weighted directed network representation. IEEE Trans. Pattern Anal. Mach. Intell.44, 9756–9773. 10.1109/tpami.2021.3132503
42
LuoX.WuH.YuanH.ZhouM. (2019a). Temporal pattern-aware QoS prediction via biased non-negative latent factorization of tensors. IEEE Trans. Cybern.50, 1798–1809. 10.1109/tcyb.2019.2903736
43
LuoX.ZhongY.WangZ.LiM. (2021d). An alternating-direction-method of multipliers-incorporated approach to symmetric non-negative latent factor analysis. IEEE Trans. Neural Netw. Learn. Syst.34, 4826–4840. 10.1109/tnnls.2021.3125774
44
LuoX.ZhouM. C.LiS.HuL.ShangM. (2019b). Non-negativity constrained missing data estimation for high-dimensional and sparse matrices from industrial applications. IEEE Trans. Cybern.50, 1844–1855. 10.1109/tcyb.2019.2894283
45
LuoX.ZhouM. C.LiS.XiaY.YouZ. H.ZhuQ.et al (2017). Incorporation of efficient second-order solvers into latent factor models for accurate prediction of missing QoS data. IEEE Trans. Cybern.48, 1216–1228. 10.1109/tcyb.2017.2685521
46
LuoX.ZhouM. C.LiS.YouZ.XiaY.ZhuQ. (2015). A nonnegative latent factor model for large-scale sparse matrices in recommender systems via alternating direction method. IEEE Trans. Neural Netw. Learn. Syst.27, 579–592. 10.1109/tnnls.2015.2415257
47
LuoX.ZhouY.LiuZ.ZhouM. (2021b). Fast and accurate non-negative latent factor analysis of high-dimensional and sparse matrices in recommender systems. IEEE Trans. Knowl. Data Eng.35, 3897–3911. 10.1109/tkde.2021.3125252
48
MiaoX.GaoY.ChenG.ZhengB.CuiH. (2016). Processing incomplete k nearest neighbor search. IEEE Trans. Fuzzy Syst.24 (6), 1349–1363. 10.1109/tfuzz.2016.2516562
49
NieY.JiaY.LiS.ZhuX.ZhouB. (2016). Identifying users across social networks based on dynamic core interests. Neurocomputing210, 107–115. 10.1016/j.neucom.2015.10.147
50
QinW.LuoX. (2023). Asynchronous parallel fuzzy stochastic gradient descent for high-dimensional incomplete data representation. IEEE Trans. Fuzzy Syst.32, 445–459. 10.1109/tfuzz.2023.3300370
51
QinW.LuoX.ZhouM. C. (2023). Adaptively-accelerated parallel stochastic gradient descent for high-dimensional and incomplete data representation learning. IEEE Trans. Big Data10, 92–107. 10.1109/tbdata.2023.3326304
52
QinW.WangH.ZhangF.WangJ.LuoX.HuangT. (2022). Low-rank high-order tensor completion with applications in visual data. IEEE Trans. Image Process.31, 2433–2448. 10.1109/tip.2022.3155949
53
ShangM.YuanY.LuoX.ZhouM. (2021). An α–β-divergence-generalized recommender for highly accurate predictions of missing user preferences. IEEE Trans. Cybern.52, 8006–8018. 10.1109/tcyb.2020.3026425
54
ShaoB.XiaoQ.XiongL.WangL.YangY.ChenZ.et al (2023). Power coupling analysis and improved decoupling control for the VSC connected to a weak AC grid. Int. J. Electr. Power Energy Syst.145, 108645. 10.1016/j.ijepes.2022.108645
55
ShirkhaniM.TavoosiJ.DanyaliS.SarvenoeeA. K.AbdaliA.MohammadzadehA.et al (2023). A review on microgrid decentralized energy/voltage control structures and methods. Energy Rep.10, 368–380. 10.1016/j.egyr.2023.06.022
56
SongJ.MingottiA.ZhangJ.PerettoL.WenH. (2022). Accurate damping factor and frequency estimation for damped real-valued sinusoidal signals. IEEE Trans. Instrum. Meas.71, 1–4. 10.1109/tim.2022.3220300
57
SuX.ZhangM.LiangY.CaiZ.GuoL.DingZ. (2021). A tensor-based approach for the QoS evaluation in service-oriented environments. IEEE Trans. Netw. Serv. Manag.18, 3843–3857. 10.1109/tnsm.2021.3074547
58
TabatabaeiS. M.DickS.XuW. (2016). Toward non-intrusive load monitoring via multi-label classification. IEEE Trans. Smart Grid8, 26–40. 10.1109/tsg.2016.2584581
59
WangH.XuZ.GeX.LiaoY.YangY.ZhangY.et al (2023). A junction temperature monitoring method for IGBT modules based on turn-off voltage with convolutional neural networks. IEEE Trans. Power Electron.38, 10313–10328. 10.1109/tpel.2023.3278675
60
WangL.ZhangY.FengJ. (2005). On the Euclidean distance of images. IEEE Trans. Pattern Anal. Mach. Intell.27, 1334–1339. 10.1109/tpami.2005.165
61
WangM. C.TsaiC. ; F.LinW. C. (2021). Towards missing electric power data imputation for energy management systems. Expert Syst. Appl.174, 114743. 10.1016/j.eswa.2021.114743
62
WangQ.ChenM.ShangM.LuoX. (2019). A momentum-incorporated latent factorization of tensors model for temporal-aware QoS missing data prediction. Neurocomputing367, 299–307. 10.1016/j.neucom.2019.08.026
63
WangS.MaY.ChengB.YangF.ChangR. N. (2016). Multi-dimensional QoS prediction for service recommendations. IEEE Trans. Serv. Comput.12, 47–57. 10.1109/tsc.2016.2584058
64
WangS.ZhengC.MaT.WangT.GaoS.DaiQ.et al (2024). Tooth backlash inspired comb-shaped single-electrode triboelectric nanogenerator for self-powered condition monitoring of gear transmission. Nano Energy123, 109429. 10.1016/j.nanoen.2024.109429
65
WuD.HeY.LuoX. (2023c). A graph-incorporated latent factor analysis model for high-dimensional and sparse data. IEEE Trans. Emerg. Top. Comput.11, 907–917. 10.1109/tetc.2023.3292866
66
WuD.LiZ.YuZ.HeY.LuoX. (2023a). Robust low-rank latent feature analysis for spatiotemporal signal recovery. IEEE Trans. Neural Netw. Learn. Syst.1, 1–14. 10.1109/tnnls.2023.3339786
67
WuD.LuoX.HeY.ZhouM. (2022a). A prediction-sampling-based multilayer-structured latent factor model for accurate representation to high-dimensional and sparse data. IEEE Trans. Neural Netw. Learn. Syst.35, 3845–3858. 10.1109/tnnls.2022.3200009
68
WuD.LuoX.ShangM.HeY.WangG.ZhouM. (2019). A deep latent factor model for high-dimensional and sparse matrices in recommender systems. IEEE Trans. Syst. Man. Cybern. Syst.51, 4285–4296. 10.1109/tsmc.2019.2931393
69
WuD.ShangM.LuoX.WangZ. (2021c). An L 1-and-L 2-norm-oriented latent factor model for recommender systems. IEEE Trans. Neural Netw. Learn. Syst.33, 5775–5788. 10.1109/tnnls.2021.3071392
70
WuD.ZhangP.HeY.LuoX. (2022b). A double-space and double-norm ensembled latent factor model for highly accurate web service QoS prediction. IEEE Trans. Serv. Comput.16, 802–814. 10.1109/tsc.2022.3178543
71
WuD.ZhangP.HeY.LuoX. (2023b). MMLF: multi-metric latent feature analysis for high-dimensional and incomplete data. IEEE Trans. Serv. Comput.17, 575–588. 10.1109/tsc.2023.3331570
72
WuH.LuoX. (2021). “Instance-frequency-weighted regularized, nonnegative and adaptive latent factorization of tensors for dynamic QoS analysis,” in Proceedings of the 28th international conference on web services (Chicago, IL, USA: Virtual Event), 560–568.
73
WuH.LuoX.ZhouM. C. (2020). Advancing non-negative latent factorization of tensors with diversified regularization schemes. IEEE Trans. Serv. Comput.15, 1334–1344. 10.1109/tsc.2020.2988760
74
WuH.LuoX.ZhouM. C. (2021b). “Neural latent factorization of tensors for dynamically weighted directed networks analysis,” in Proceedings of the international conference on systems, man, and cybernetics 2021 (Melbourne, Australia), 3061–3066.
75
WuH.LuoX.ZhouM. C.RawaM. J.SedraouiK.AlbeshriA. (2021a). A PID-incorporated latent factorization of tensors approach to dynamically weighted directed network analysis. IEEE/CAA J. Autom. Sin.9, 533–546. 10.1109/jas.2021.1004308
76
XuX.LinM.LuoX.XuZ. (2023). HRST-LR: a hessian regularization spatio-temporal low rank algorithm for traffic data imputation. IEEE Trans. Intell. Transp. Syst.24, 11001–11017. 10.1109/tits.2023.3279321
77
YangT.XuJ.FeiL. I. (2023b). Electric theft detection based on optimal transform correlation factor and optimized shift-splitting iteration method. Power Syst. Technol.47, 3913–3924. 10.2139/ssrn.4353843
78
YangY.NagarajaiahS. (2016). Harnessing data structure for recovery of randomly missing structural vibration responses time history: sparse representation versus low-rank structure. Mech. Syst. Signal Process.74, 165–182. 10.1016/j.ymssp.2015.11.009
79
YangY.WeiX.YaoW.LanJ. (2023a). Broadband electrical impedance matching of sandwiched piezoelectric ultrasonic transducers for structural health monitoring of the rail in-service. Sens. Actuators A Phys.364, 114819. 10.1016/j.sna.2023.114819
80
YeF.LinZ.ChenC. (2021). “Outlier-resilient web service qos prediction,” in Proceedings of the web conference 2021 (Ljubljana, Slovenia), 3099–3110.
81
YuanY.LuoX.ShangM.WangZ. (2022). A Kalman-filter-incorporated latent factor analysis model for temporally dynamic sparse data. IIEEE Trans. Cybern.53, 5788–5801. 10.1109/tcyb.2022.3185117
82
YuanY.LuoX.ShangM. S. (2018). Effects of preprocessing and training biases in latent factor models for recommender systems. Neurocomputing275, 2019–2030. 10.1016/j.neucom.2017.10.040
83
ZengS.GouJ.DengL. (2017). An antinoise sparse representation method for robust face recognition via joint l1 and l2 regularization. Expert Syst. Appl.82, 1–9. 10.1016/j.eswa.2017.04.001
84
ZhangH.WuH.JinH.LiH. (2022). High-dynamic and low-cost sensorless control method of high-speed brushless DC motor. IEEE Trans. Ind. Inf.19, 5576–5584. 10.1109/tii.2022.3196358
85
ZhangX.GongL.ZhaoX.LiR.YangL.WangB. (2023). Voltage and frequency stabilization control strategy of virtual synchronous generator based on small signal model. Energy Rep.9, 583–590. 10.1016/j.egyr.2023.03.071
86
ZhangZ.ZhuangF.ZhuH. (2020). “Relational graph neural network with hierarchical attention for knowledge graph completion,” in Proceedings of the 34th AAAI conference on artificial intelligence (New York, NY, USA), 9612–9619.
87
ZhaoM.WuL.LiangY. (2022). “Investigating accuracy-novelty performance for graph-based collaborative filtering,” in Proceedings of the 45th international ACM SIGIR conference on research and development in information retrieval (Madrid, Spain), 50–59.
88
ZhaoX.JiaY.LiA.JiangR.ChenK.WangY. (2021). Target relational attention-oriented knowledge graph reasoning. Neurocomputing461, 577–586. 10.1016/j.neucom.2021.03.135
Summary
Keywords
power load forecasting, power load monitoring, missing data, tensor factorization, imputation models, data imputation
Citation
Luo X, Hu Z, Ma Z, Lv Z, Wang Q and Zeng A (2024) An L1-and-L2-regularized nonnegative tensor factorization for power load monitoring data imputation. Front. Energy Res. 12:1420449. doi: 10.3389/fenrg.2024.1420449
Received
08 May 2024
Accepted
27 June 2024
Published
26 July 2024
Volume
12 - 2024
Edited by
Chixin Xiao, University of Wollongong, Australia
Reviewed by
Man Fai Leung, Anglia Ruskin University, United Kingdom
Lei Zhang, Nanjing Normal University, China
Updates
Copyright
© 2024 Luo, Hu, Ma, Lv, Wang and Zeng.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zijian Hu, zijian.hu@foxmail.com
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.