Abstract
This work presents the mathematical/theoretical framework of the “nth-Order Feature Adjoint Sensitivity Analysis Methodology for Response-Coupled Forward/Adjoint Linear Systems” (abbreviated as “nth-FASAM-L”), which enables the most efficient computation of exactly obtained mathematical expressions of arbitrarily-high-order (nth-order) sensitivities of a generic system response with respect to all of the parameters (including boundary and initial conditions) underlying the respective forward/adjoint systems. Responses of linear models can depend simultaneously on both the forward and the adjoint state functions. This is in contradistinction to responses for nonlinear systems, which can depend only on the forward state functions since nonlinear operators do not admit bona-fide adjoint operators. Among the best-known model responses that depend simultaneously on both the forward and adjoint state functions are Lagrangians used for system optimization, the Schwinger and Roussopoulos functionals for analyzing reaction rates and ratios thereof, and the Rayleigh quotient for analyzing eigenvalues and/or separation constants. The sensitivity analysis of such responses makes it necessary to treat linear models/systems in their own right, rather than treating them just as particular cases of nonlinear systems. The unparalleled efficiency and accuracy of the nth-FASAM-L methodology stems from the maximal reduction of the number of adjoint computations (which are “large-scale” computations) for computing high-order sensitivities, since the number of large-scale computations when applying the nth-FASAM-N methodology is proportional to the number of model features as opposed to the number of model parameters (which are considerably more than the number of features). The mathematical framework underlying the nth-FASAM-L is developed in linearly increasing higher-dimensional Hilbert spaces, as opposed to the exponentially increasing “parameter-dimensional” spaces in which response sensitivities are computed by other methods (statistical, finite differences, etc.), thus providing the basis for overcoming the curse of dimensionality in sensitivity analysis and all other fields (uncertainty quantification, predictive modeling, etc.) which need such sensitivities.
1 Introduction
The analysis of computational models fundamentally relies on the use of functional derivatives (called “sensitivities”) of the results (called “model responses”) with respect to the imprecisely known parameters underlying the computational model. Sensitivities are used for many purposes, including: (a) ranking the importance of the various parameters and performing “reduced-order modeling” by eliminating unimportant parameters and/or processes; (b) quantifying the uncertainties induced in a model response due to uncertainties in the model’s parameters; (c) performing “model validation” by comparing computational and experimental results to address the question “does the model represent reality?”; (d) performing data assimilation and model calibration as part of forward and inverse “predictive modeling” to obtain best-estimate predicted results with reduced predicted uncertainties; (e) prioritizing improvements while optimizing the model.
Response sensitivities are computed by using either deterministic or statistical methods. The simplest deterministic method for computing response sensitivities is to use finite-difference schemes in conjunction with re-computations using the model with “judiciously chosen” altered parameter values. Evidently, such methods can at best compute approximate values of a very limited number of sensitivities. Deterministic methods that can compute more exactly the values of first-order sensitivities include the “Green’s function method” (), the “forward sensitivity analysis methodology” (), and the “direct method” (), which rely on analytical or numerical differentiation of the computational model under investigation to compute local response sensitivities exactly. On the other hand, “statistical methods” construct an approximate response distribution (often called “response surface”) in the parameters space, and subsequently use scatter plots, regression, rank transformation, correlations, and so-called “partial correlation analysis,” in order to identify approximate expectation values, variances and covariances for the responses. These statistical quantities are subsequently used to construct quantities that play the role of approximate first-order response sensitivities. Thus, statistical methods commence with “uncertainty analysis” and subsequently attempt an approximate “sensitivity analysis” of the approximately computed model response (called a “response surface”) in the phase-space of the parameters under consideration. The currently popular statistical methods for uncertainty and sensitivity analysis are broadly categorized as sampling-based methods (; ), variance-based methods (; ), and Bayesian methods (). Various variants of the statistical methods for uncertainty and sensitivity analysis are reviewed in the book edited by .
For a computational model comprising many parameters, the conventional deterministic and statistical methods become impractical for computing sensitivities higher than first-order because they are subject to the “curse of dimensionality,” a term coined by to describe phenomena in which the number of computations increases exponentially in the respective phase-space. It is known that the “adjoint method of sensitivity analysis” has been the most efficient method for computing exactly first-order sensitivities, since it requires a single large-scale (adjoint) computation for computing all of the first-order sensitivities, regardless of the number of model parameters. The idea underlying the computation of response sensitivities with respect to model parameters using adjoint operators was first used by to analyze first-order perturbations in nuclear reactor physics and shielding models based on the linear neutron transport (or diffusion) equation, as subsequently described in textbooks on these subjects (; ; ; ; ). is credited (see, e.g., ; ) for having conceived the rigorous “1st-order adjoint sensitivity analysis methodology” for generic large-scale nonlinear (as opposed to linearized) systems involving generic operator responses and having introduced these principles to the earth, atmospheric and other sciences.
, has extended his 1st-order adjoint sensitivity analysis methodology to enable the comprehensive and exact computation of 2nd-order sensitivities of model responses to model parameters (including imprecisely known domain boundaries and interfaces) for large-scale linear and nonlinear systems. The unparalleled efficiency of the 2nd-order adjoint sensitivity analysis methodology for linear systems () was demonstrated (see , and references therein) by applying this methodology to compute exactly the 21,976 first-order sensitivities and 482,944,576 second-order sensitivities (of which 241,483,276 are distinct from each other) for an OECD/NEA reactor physics benchmark (). This benchmark is modeled by the neutron transport equation involving 21,976 uncertain parameters, the solving of which is representative of “large-scale computations.” The neutron transport equation was solved using the software package PARTISN () in conjunction with the MENDF71X cross section library (), which comprises 618-group cross sections based on ENDF/B-VII.1 nuclear data (). The spontaneous fission source was computed using the code SOURCES4C (). Contrary to the widely held belief that second- and higher-order sensitivities are negligeable for reactor physics systems, it was found (see , and references therein) that many 2nd-order sensitivities of this OECD/NEA benchmark’s leakage response to the benchmark’s uncertain parameters were much larger than the largest 1st-order ones, which motivated the investigation of the largest 3rd-order sensitivities, many of which were found to be even larger than the 2nd-order ones. This finding has motivated the development of the mathematical framework for determining and computing the 4th-order sensitivities, many of which were found to be larger than the 3rd-order ones. This sequence of findings has motivated the development by of the “nth-Order Comprehensive Adjoint Sensitivity Analysis Methodology for Response-Coupled Forward/Adjoint Linear Systems” (which is abbreviated as “nth-CASAM-L”). The “nth-CASAM-L” mathematical framework was developed specifically for linear systems because the most important model responses produced by such systems can depend simultaneously on both the forward and adjoint state functions governing the respective linear system. Among the most important responses of linear systems that involve both the forward and adjoint functions are various Lagrangian functionals, the Raleigh quotient for computing eigenvalues and/or separation constants when solving partial differential equations, and the Schwinger functional for first-order “normalization-free” solutions (see, e.g., ; ; ). These functionals play fundamental roles in optimization and control procedures, derivation of numerical methods for solving equations (differential, integral, integro-differential), etc. Nonlinear operators do not admit adjoint operators, so responses in nonlinear systems can only depend on the system’s forward state functions. Therefore, the sensitivity analysis of responses that simultaneously involve both forward and adjoint state functions makes it necessary to treat linear models/systems in their own right, rather than treating them as particular cases of nonlinear systems.
The traditional methods of sensitivity analysis aim at computing sensitivities of responses directly to the primary parameters (i.e., microscopic cross sections, isotopic number densities, etc.) involved in the computational model of the physical system under consideration. Although the sensitivities to the primary model parameters are ultimately of interest for subsequent use in predictive modeling activities (which includes the quantification of the uncertainties induced in responses by uncertainties in the primary model parameters, assimilation of experimental data for calibrating the model’s parameters and improving the model’s predictions), the primary parameters seldom appear explicitly in the equations underlying the model. For example, the primary model parameters (e.g., microscopic cross sections, atomic number densities) do not appear explicitly in the forward and adjoint transport equations modeling () the above-mentioned OECD/NEA reactor physics benchmark. What appear explicitly in these equations are the macroscopic cross sections, which are functions of the primary model parameters, and which can be considered to be features of the transport equation. This fact has motivated the development by , of the “nth-Order Features Adjoint Sensitivity Analysis Methodology for Nonlinear Systems (nth-FASAM-N),” which significantly reduces the computational effort computing efficiently and exactly sensitivities of model responses to model features (i.e., functions of the primary model responses), and subsequently compute the sensitivities to responses to the primary model parameters by using the sensitivities to the model features.
Paralleling the mathematical framework of the nth-FASAM-N, it is the purpose of this work to develop a methodology which will enable the efficient and exact computation of sensitivities of model responses to model features for response-coupled forward and adjoint linear systems; this new methodology will be abbreviated as the “nth-FASAM-L” methodology. The mathematical framework of this methodology is established in Section 2 of this work by using the proof by “mathematical induction” as follows: (i) establish the mathematical framework underlying the nth-CASAM-L for n = 1; (ii) assume that the mathematical framework is valid for an arbitrarily high-order, n; (iii) prove that the mathematical framework proposed for n is also valid for n+1.Section 3 presents a concluding discussion that prepares the ground for an illustrative application of the nth-FASAM-L methodology to a representative energy-dependent neutron slowing down model of fundamental importance to reactor physics, which will be presented in an accompanying manuscript (because of word limitations per article), designated as “Part II ().”
2 The Nth-order function/feature adjoint sensitivity analysis methodology for response-coupled forward and adjoint linear systems (Nth-FASAM-L)
The mathematical framework of the nth-FASAM-L methodology, to be presented in this Section, was established while striving to maximize the computational efficiency of the mathematical framework of the “nth-Order Comprehensive Adjoint Sensitivity Analysis Methodology for Coupled Forward/Adjoint Linear Systems” (abbreviated as: nth-CASAM-L)” conceived by . The starting point for both the nth-CASAM-L and the nth-FASAM-L is the generic mathematical modeling of a response-coupled forward/adjoint linear system, which is presented in Section 2.1, for convenient referencing.
The validity of mathematical framework underlying the nth-FASAM-L methodology will be established in this Section by using the “proof by mathematical induction” comprising the usual steps, as follows:
1. Conjecture the pattern underlying the nth-FASAM-L, for arbitrary n, based on prior experience.
2. Prove that the conjectured pattern for arbitrary n, is valid for the lowest value of , i.e., for .
3. Assuming that that the pattern underlying the nth-FASAM-L is valid for an arbitrarily high-order , prove that this pattern is also valid for , i.e., for the (n + 1)th-FASAM-L.
2.1 Mathematical modeling of response-coupled linear forward and adjoint systems establishing the mathematical framework of the nth-FASAM-L methodology
The mathematical model of a process and/or state of a physical system comprises equations that relate the system’s independent variables and parameters to the system’s state/dependent variables. A linear physical system can generally be modeled by a system of coupled equations written generically in operator form as follows:
The quantities that appear in Eq.
1are defined as follows:
1. The vector is a -dimensional column vector of dependent variables and where the sub/superscript “” denotes the “Total (number of) Dependent variables.” The functions , denote the system’s “dependent variables” (also called “state functions”). The symbol “” denotes “is defined as” or “is by definition equal to.” Transposition is indicated by a dagger superscript.
2. The components of the vector denote the primary model parameters, where the subscript/superscript “TP” indicates “Total number of Primary Parameters” and where denotes the TP-dimensional subset of the set of real scalars. Without loss of generality, the model parameters can be considered to be real scalar quantities, having known nominal (or mean) values and, possibly, known higher-order moments or cumulants (i.e., variance/covariances, skewness, kurtosis), which are usually determined from experimental data and/or processes external to the physical system under consideration. These imprecisely known model parameters are considered to include imprecisely known geometrical parameters that characterize the physical system’s boundaries in the phase-space of the model’s independent variables. The nominal parameter values will be denoted as ; the superscript “0” will be used throughout this work to denote “nominal” or “mean” values.
3. The components of the -dimensional column vector denote the model’s independent variables , where the sub/superscript “” denotes the “Total number of Independent variables.” The vector of independent variables is considered to be defined on a phase-space domain , the boundaries of which may depend on some of the model parameters . The lower boundary-point of an independent variable is denoted as , while the corresponding upper boundary-point is denoted as . The boundary of , which will be denoted as , comprises the set of all of the endpoints of the respective intervals on which the components of are defined, i.e., .
4. The components of the -dimensional matrix , are operators that act linearly on the dependent variables and also depend on the uncertain model parameters .
5. The vector is a -dimensional vector having components , which are real-valued functions of (some of) the primary model parameters . The quantity denotes the total number of such functions which appear exclusively in the definition of the model’s underlying equations. Such functions customarily appear in models in the form of correlations that describe “features” of the system under consideration, such as material properties, flow regimes. etc. Usually, the number of functions is considerably smaller than the total number of model parameters, i.e., . For example, the numerical model () of the OECD/NEA “Polyethylene-Reflected Plutonium” reactor physics benchmark () comprises 21,976 uncertain primary model parameters (including microscopic cross sections and isotopic number densities) but the neutron transport equation, which is solved numerically to determine the neutron flux distribution within the benchmark, does not use these primary parameters directly but instead uses just several hundreds of “group-averaged macroscopic cross sections” which are functions/features of the microscopic cross sections and isotopic number densities (which in turn are uncertain quantities that would be components of the vector of primary model parameters). In particular, a component may simply be one of the primary model parameters , i.e., .
6. The -dimensional column vector , having components , denotes inhomogeneous source terms, which usually depend nonlinearly on the uncertain parameters . Since the right-side of Eq. 1 may contain distributions, the equality in this equation is considered to hold in the weak (i.e., “distributional”) sense. Similarly, all of the equalities that involve differential equations in this work will be considered to hold in the distributional sense.
7. When contains differential operators, corresponding boundary and initial conditions which define the domain of must also be given. Since the complete mathematical model is considered to be linear in , the boundary and/or initial conditions needed to define the domain of must also be linear in . Such linear boundary and initial conditions are represented in the following operator form:
In Eq. 2, the quantity denotes a matrix of dimensions having components denoted as , which are operators that act linearly on and nonlinearly on the components of ; the quantity denotes the total number of boundary and initial conditions. The -dimensional column vector comprises components that are operators which, in general, act nonlinearly on the components of .
Physical problems modeled by linear systems and/or operators are naturally defined in Hilbert spaces. The dependent variables , for the physical system represented by Eqs 1, 2 are considered to be square-integrable functions of the independent variables and are considered to belong to a Hilbert space which will be denoted as , where the subscript “zero” denotes “zeroth-level” or “original.” Higher-level Hilbert spaces, which will be denoted as etc., will also be introduced and used in this work. The Hilbert space is considered to be endowed with the following inner product, denoted as , between two elements and :
The “dot” in Eq. 3 indicates the “scalar product of two vectors,” which is defined in Eq. 4, below, as follows:
The product-notation in Eq. 3 denotes the respective multiple integrals.
The linear operator admits an adjoint operator, which will be denoted as and which is defined through the following relation for a vector :
In Eq. 5, the formal adjoint operator is the matrix comprising elements which are obtained by transposing the formal adjoints of the forward operators . Hence, the system adjoint to the linear system represented by Eqs 1, 2 can generally be represented as follows:
When the forward operator comprises differential operators, the operations (e.g., integration by parts) that implement the transition from the left-side to the right side of Eq. 5 give rise to boundary terms which are collectively called the “bilinear concomitant.” The domain of is determined by selecting adjoint boundary and/or initial conditions so as to ensure that the bilinear concomitant vanishes when the selected adjoint boundary conditions are implemented together with the forward boundary conditions given in Eq. 2. The adjoint boundary conditions thus selected are represented in operator form by Eq. 7.
The results computed using a mathematical model are customarily called “model responses” (or “system responses” or “objective functions” or “indices of performance”). For linear physical systems, the system’s response may depend not only on the model’s state-functions and on the system parameters but may simultaneously also depend on the adjoint state function. As has been discussed by , , , any response of a linear system can be formally represented (using expansions or interpolation, if necessary) and fundamentally analyzed in terms of the following generic integral representation:where is a suitably differentiable nonlinear function of , and . The integral representation of the response provided in Eq. 8 can represent “averaged” and/or “point-valued” quantities in the phase-space of independent variables. For example, if represents the computation or the measurement (which would be a “detector-response”) of a quantity of interest at a point in the phase-space of independent variables, then would contain a Dirac-delta functional of the form . Responses that represent “differentials/derivatives of quantities” would contain derivatives of Dirac-delta functionals in the definition of . The vector , having components , which appears among the arguments of the function , represents functions of primary parameters that often appear solely in the definition of the response but do not appear in the mathematical definition of the model, i.e., in Eqs 1, 2, 6, 7. The quantity denotes the total number of such functions which appear exclusively in the definition of the model’s response. Evidently, the response will depend directly and/or indirectly (through the “feature”-functions) on all of the primary model parameters. This fact has been indicated in Eq. 8 by using the vector-valued function as an argument in the definition of the response to represent the concatenation of all of the “features” of the model and response under consideration. The vector of “model features” is thus defined as follows:
As defined in Eq. 9, the quantity denotes the total number of “feature functions of the model’s parameters” which appear in the definition of the nonlinear model’s underlying equations and response.
Solving Eqs 1, 2, at the nominal (or mean) values, denoted as , of the model parameters, yields the nominal forward solution, which will be denoted as . Solving Eqs 6, 7 at the nominal values, , of the model parameters yields the nominal adjoint solution, which will be denoted as . The nominal value of the response, , is determined by using the nominal parameter values , the nominal value of the forward state function, and the nominal value of the adjoint state function.
The definition provided by Eq. 8 implies that the model response depends on the components of the feature function , and would therefore admit a Taylor-series expansion around the nominal value , having the following form:where . The “sensitivities of the model response with respect to the (feature) functions” are naturally defined as being the functional derivatives of with respect to the components (“features”) of . The notation indicates that the quantity enclosed within the braces is to be evaluated at the nominal values . Since , there will be fewer derivatives of the response with respect to the feature functions than there are response derivatives with respect to the primary model parameters. Hence, the computations of the functional derivatives of with respect to the functions , which appear in Eq. 10, will be considerably less expensive computationally than the computation of the functional derivatives involved in the Taylor-series of the response with respect to the model parameters. The functional derivatives of the response with respect to the primary parameters can be obtained from the functional derivatives of the response with respect to the “feature” functions by simply using the chain rule, i.e.,:
and so on. The evaluation/computation of the functional derivatives , , etc., does not require computations involving the model, and is therefore trivial (computationally) by comparison to the evaluation of the functional derivatives (“sensitivities”) of the response with respect to either the functions (“features”) or the model parameters .
The range of validity of the Taylor-series shown in Eq. 10 is defined by its radius of convergence. The accuracy −as opposed to the “validity”− of the Taylor-series in predicting the value of the response at an arbitrary point in the phase-space of model parameters depends on the order of sensitivities retained in the Taylor-expansion: the higher the respective order, the more accurate the respective response value predicted by the Taylor-series. In the particular cases when the response happens to be a polynomial function of the “feature” functions , the Taylor series is actually exact.
In turn, the functions can also be formally expanded in a multivariate Taylor-series around the nominal (mean) parameter values , namely,:
The domain of validity of the Taylor-series in Eq. 12 is defined by its own radius of convergence.
The choice of feature functions
is not unique but can be tailored by the user to the problem at hand. The two most important guiding principles for constructing the feature functions
based on the primary parameters are as follows:
(i) As shown in Section 2.2 while establishing the mathematical framework underlying the nth-FASAM-L, the number of large-scale computations needed to determine the numerical value of the second- and higher-order sensitivities is proportional to the number of first-order sensitivities of the model’s response with respect to the feature functions . Consequently, it is important to minimize the number of feature functions , while ensuring that all of the primary model parameters are encompassed within the expressions constructed for the feature functions . In the extreme case when some primary parameters, , cannot be grouped into the expressions of the feature functions , then each of the respective primary model parameters becomes a feature function .
(ii) The expressions of the features functions must be independent of the model’s state functions; they must be exact, closed-form, scalar-valued functions of the primary model parameters , so the exact expressions of the derivatives of with respect to the primary model parameters can be obtained analytically (with “pencil and paper”). The motivation for this requirement is to ensure that the numerical determination of the subsequent derivatives of the features functions with respect to the primary model parameters becomes trivial computationally. In the extreme case when no feature function can be constructed, the feature functions are the primary parameters themselves, in which case the nth-FASAM-L methodology becomes identical to the previously established nth-CASAM-L methodology ()
2.2 Establishing the mathematical framework of the nth-FASAM-L methodology
, , has recently developed the “nth-Order Features Adjoint Sensitivity Analysis Methodology for Nonlinear Systems (nth-FASAM-N)” which enables the computation of arbitrarily-high-order sensitivities of responses to features/functions of parameters for nonlinear models/systems. Together, the nth-CASAM-L and the nth-FASAM-N provide the basis for the development of the “nth-Order Features Adjoint Sensitivity Analysis Methodology for Response-Coupled Forward and Adjoint Linear Systems (Nth-FASAM-L)” to be presented in this Section. In particular, comparing the mathematical framework of the 1st-FASAM-L to the framework of the 1st-CASAM-L () suggests that the components , of the “feature function” will play within the 1st-FASAM-L the same role as played by the components , of the “vector of primary model parameters” within the framework of the 1st-CASAM-L. It can therefore be conjectured that the same correspondence would be expected to hold in general, between the general frameworks of the nth-FASAM-L and the nth-CASAM-L methodologies. As will be demonstrated in this Section, this conjecture is indeed correct.
Considering the analogy to the framework of the nth-CASAM-L methodology (), it is conjectured that that the G-differential of the (n-1)th-order sensitivity of the model’s responsewith respect to the componentsof the “feature” function will have the following form:
such that the nth-order sensitivity of the model’s response with respect to the components of the “feature” function is expected to have the following functional form:where denotes the “total number of features,” i.e., functions of the primary model parameters.
It is also conjectured that the nth-level adjoint functions
and
, which are needed to compute the nth-order sensitivities shown in Eq.
14, are obtained as follows:
(i) are the solutions of the following nth-Level Forward/Adjoint System (nth-LFAS) for :
(ii) are the solutions of the following nth-Level Adjoint Sensitivity System (nth-LASS) for :
Through their implicit dependence on lower-level forward and adjoint functions, the block-matrix valued operators and , as well as the source terms and , also depend on lower-level indices , but this dependence is not material to establishing the general framework of the nth-FASAM-L and has therefore been omitted, to keep the notation as simple as possible.
2.3 Proving that the conjectured mathematical framework of the nth-FASAM-L methodology is correct for
The proof that the framework conjectured in Section 2.2 for the nth-FASAM-L methodology is indeed correct/valid when (for the 1st-FASAM-L methodology) parallels the proof used in () to show that the framework of the nth-CASAM-L methodology reduces to the corresponding 1st-CASAM-L methodology when . In preparation for subsequent generalizations towards establishing the generic pattern for computing sensitivities of arbitrarily high-order, the function will be called the “1st-level forward/adjoint function” and the system of equations satisfied by this function (which is obtained by concatenating the original forward and adjoint equations together with their respective boundary/initial conditions) will be called “the 1st-Level Forward/Adjoint System (1st-LFAS)” and will be re-written in the following concatenated matrix-form:where the following definitions were used:
In the list of arguments of the matrix , the argument “” indicates that this square matrix comprises four component sub-matrices, as indicated in Eq. 21. Similarly, the argument “2” that appears in the block-vectors , , and defined in Eq. 22 indicates that each of these column block-vectors comprises two sub-vectors as components. Also, throughout this work, the quantity “” will be used to denote either as a vector with zero-valued components or a matrix zero-valued components, depending on the context. For example, the vector “” in Eq. 20 is considered to have as many components as the vector . On the other hand, the quantity “” which appears in Eq. 21 may represent either a (sub) matrix or a vector of the requisite dimensions.
The primary parameters are subject to uncertainties; their nominal (or mean) values, denoted as , are considered to be known, but these values will differ from the true values , which are unknown, by variations , where . The parameter variations will induce variations in the vector-valued “feature” function , around the nominal value , and will also induce variations and , respectively, around the nominal solutions , through the equations underlying the model. All of these variations will induce variations in the model response .
Formally, the first-order sensitivities of the response with respect to the components of the feature function are provided by the first-order Gateaux (G-)variation of at the phase-space point , which is defined as follows:
The definitions provided in Eq. 24, below, were used in Eq. 23:
The numerical methods (e.g., Newton’s method and variants thereof) for solving large-scale systems require the existence of the first-order G-derivatives of the original model equations and of the model’s response; these will be assumed to exist. When the 1st-order G-derivatives exists, the variation can be written as follows:
In Eq. 25, the “direct-effect” term comprises only dependencies on and is defined as follows:
The following convention/definition was used in Eq. 26:
The notation on the left-side of Eq. 27 represents the inner product between two vectors, but the “dagger” symbol “()” which indicates “transposition” has been omitted in order to keep the notation as simple as possible. “Daggers” indicating transposition will also be omitted in other inner products, whenever possible, while avoiding ambiguities.
In Eq. 25, the “indirect-effect” term depends only on the variations in the state functions, and is defined as follows:
In Eqs 26, 28, the notation has been used to indicate that the quantity within the brackets is to be evaluated at the nominal values of the parameters and state functions. This simplified notation is justified by the fact that when the parameters take on their nominal values, it implicitly means that the corresponding state functions also take on their corresponding nominal values. This simplified notation will be used throughout this work.
The direct-effect term can be computed after having solved the forward system modeled by Eqs 1, 2, as well as the adjoint system modeled by Eqs 6, 7, using the nominal parameter values to obtain the nominal values of the forward and adjoint dependent variables.
On the other hand, the indirect-effect term defined in Eq. 28 can be quantified only after having determined the variations in the state functions of the 1st-Level Forward/Adjoint System (1st-LFAS). The variations are obtained as the solutions of the system of equations obtained by taking the first-order G-differentials of the 1st-LFAS defined by Eqs 19, 20, which are obtained by definition as follows:
Carrying out the differentiations with respect to in Eqs 29, 30 and setting in the resulting expressions yields the following matrix-vector equations:where:
In order to keep the notation as simple as possible in Eqs 31‒38, the differentials with respect to the various components of the feature function have all been written in the form , keeping in mind the convention/notation introduced in Eq. 27. The system of equations comprising Eqs 31, 32 will be called the “1st-Level Variational Sensitivity System (1st-LVSS)” and its solution, , will be called the “1st-level variational sensitivity function,” which is indicated by the superscript “(1)”. The solution, , of the 1st-LVSS will be a function of the components of the vector of variations . In principle, therefore, if the response sensitivities with respect to the components of the feature function are of interest, then the 1st-LVSS would need to be solved as many times as there are components in the variational features-function . On the other hand, if the response sensitivities with respect to the primary parameters are of interest, then the 1st-LVSS would need to be solved as many times as there are primary parameters. Solving the 1st-LVSS involves “large-scale computations.”
Solving the 1st-LVSS can be avoided altogether by using the ideas underlying the “adjoint sensitivity analysis methodology” originally conceived by
, and subsequently generalized by
,
to enable the computation of arbitrarily high-order response sensitivities to primary model parameters for both linear and nonlinear models. Thus, the need for solving repeatedly the 1st-LVSS for every variation in the components of the feature function (or for every variation in the model’s parameters) is eliminated by expressing the indirect-effect term
defined in Eq.
28in terms of the solutions of the “
1st-Level Adjoint Sensitivity System” (1st-LASS), which will be constructed by implementing the following sequence of steps:
1. Introduce a Hilbert space, denoted as , comprising vector-valued elements of the form , where the components , , are square-integrable functions. Consider further that this Hilbert space is endowed with an inner product denoted as between two elements, , , which is defined as follows:
2. In the Hilbert , use Eq. 39 to form the inner product of Eq. 31 with a yet undefined vector-valued function to obtain the following relation:
3. Using the definition of the adjoint operator in the Hilbert space , recast the left-side of Eq. 40 as follows:
where
denotes the bilinear concomitant defined on the phase-space boundary
, and where
is the operator formally adjoint to
, as defined in Eq.
42below:
4. Require the first term on right-side of Eq. 41 to represent the indirect-effect term defined in Eq. 28, to obtain the following relation:
where the source term on the right-side of Eq.
43is defined in Eq.
44, below:
5. Implement the boundary conditions represented by Eq. 32 into Eq. 41 and eliminate the remaining unknown boundary-values of the function from the expression of the bilinear concomitant by selecting appropriate boundary conditions for the function , to ensure that Eq. 43 is well-posed while being independent of unknown values of and of . The boundary conditions thus chosen for the function can be represented in operator form as follows:
The selection of the boundary conditions for
represented by Eq.
45eliminates the appearance of the
unknownvalues of
in
and reduces this bilinear concomitant to a residual quantity containing boundary terms which involve only known values of
,
,
, and
. This residual quantity will be denoted as
. In general, this residual quantity does not automatically vanish, although it may do so occasionally.
6. The system of equations comprising Eq. 43 together with the boundary conditions represented Eq. 45 will be called the 1st-Level Adjoint Sensitivity System (1st-LASS). The solution of the 1st-LASS will be called the 1st-level adjoint sensitivity function. The 1st-LASS is called “first-level” (as opposed to “first-order”) because it does not contain any differential or functional-derivatives, but its solution, , will be used below to compute the first-order sensitivities of the response with respect to the components of the feature function .
7. Using Eq. 40 together with the forward and adjoint boundary conditions represented by Eqs 32, 45 in Eq. 41 reduces the latter to the following relation:
As indicated by the identity shown in Eq. 47, the variations and have been eliminated from the original expression of the indirect-effect term, which now depends on the 1st-level adjoint sensitivity function . Adding the expression obtained in Eq. 47 with the expression for the direct-effect term defined in Eq. 26 yields, according to Eq. 25 the following expression for the total 1st-order sensitivity of the response with respect to the components of the feature function :
The identity which appears in Eq. 48 emphasizes the fact that the variations and , which are expensive to compute, have been eliminated from the final expressions of the 1st-order sensitivities of the response with respect to the components of the “features function” . The dependence on the variations and has been replaced in the expression of by the dependence on the 1st-level adjoint sensitivity function . It is very important to note that the 1st-LASS is independent of variations in the components of the feature function and is consequently also independent of any variations in the primary model parameters. Hence, the 1st-LASS needs to be solved only once to obtain the 1st-level adjoint sensitivity function . Subsequently, the “indirect-effect term” is computed efficiently and exactly by simply performing the integrations required to compute the inner product over the adjoint function , as indicated on the right-side of Eq. 48. Solving the 1st-Level Adjoint Sensitivity System (1st-LASS) requires the same computational effort as solving the original coupled linear system, entailing the following operations: (i) inverting (i.e., solving): the left-side of the original adjoint equation with the source to obtain the 1st-level adjoint sensitivity function ; and (ii) inverting the left-side of the original forward equation with the source to obtain the 1st-level adjoint sensitivity function .
The 1st-order sensitivities , , can be expressed as an integral over the independent variables as follows:
In particular, if the residual bilinear concomitant is non-zero, the functions would contain suitably defined Dirac delta-functionals for expressing the respective non-zero boundary terms as volume-integrals over the phase-space of the independent variables. Dirac-delta functionals would also be used in the expression of to represent terms containing the derivatives of the boundary end-points with respect to the model and/or response parameters.
The response sensitivities with respect to the primary model parameters would be obtained by using the expression obtained in Eq. 49 in conjunction with the “chain rule” of differentiation provided in Eq. 11.
It is important to compare the results produced by the 1st-FASAM-L (for obtaining the sensitivities of the model response with respect to the model’s features) with the results produced by the 1st-CASAM methodology (the 1st-Order Comprehensive Adjoint Sensitivity Analysis Methodology for Response-Coupled Forward/Adjoint Linear Systems), which provides the expressions of the responses sensitivities directly with respect to the model’s primary parameters. Recall that the 1st-CASAM-L () yields the following expression for the 1st-order sensitivities of the response with respect to the primary model parameters:
The same 1st-level adjoint function appears in Eq. 50 as well as in Eq. 49. Therefore, a single “large-scale computation” (needed to solve the 1st-LASS to determine the 1st-level adjoint function) is required for obtaining either the response sensitivities with respect to the components, , , of the feature function using the 1st-FASAM-L, or for obtaining the response sensitivities directly with respect to the primary model parameters , , using the 1st-CASAM-L. On the other hand, the use of the 1st-CASAM-L would require performing a number of integrations to compute all of the response sensitivities with respect to the primary parameters, but the 1st-FASAM-L would require only integrations () to compute all of the response sensitivities with respect to the components of the feature function. Hence, the 1st-FASAM-L is more efficient than the 1st-CASAM-L, so the 1st-FASAM-L is the most efficient method for computing the exact expressions of the first-order sensitivities of a generic model response of the form with respect to the components of the “features” function , and subsequently with respect to the primary model parameters. As will be shown in the sequel, the computational savings provided by the nth-FASAM-L increase massively by comparison to the nth-CASAM-L (or any other method) as the order “n” of the computed sensitivities increases.
The expression obtained in Eq.
48is the same as the particular form taken on by general expression provided in Eq.
13for
, where:
(i) the 1st-level forward/adjoint function is the solution of the 1st-LFAS defined by Eqs 19, 20, which has the same expression as the particular form taken on by the nth-LFAS, cf. Eqs 15, 16, for ;
(ii) the 1st-level adjoint sensitivity function is the solution of the 1st-LASS defined by Eqs 43, 45, which has the same expression as the particular form taken on by the nth-LFAS, cf. Eqs 17, 18, for .
Thus, the first step in the “proof by mathematical induction” of the pattern underlying the nth-FASAM-L has been completed, having shown that this pattern holds for .
2.4 Proving that the conjectured mathematical framework of the nth-FASAM-L methodology also holds for , i.e., for the (n + 1)th-FASAM-L framework
The last step of the “proof by mathematical induction” to establish the validity the nth-FASAM-L framework is to show that the formalism assumed to be correct for the computation of the nth-order sensitivities also holds true for the computation of the (n + 1)th-order sensitivities. This proof entails showing that the formulas obtained by computing the (n + 1)th-order sensitivities using Eqs 14‒18 as the starting point will be the same as would be obtained by replacing “n” with “(n + 1)” in Eqs 14‒18.
The nth-order response sensitivity defined in Eq. 14 can be considered to be a function of the (n + 1)th-level function, which is the solution of the (n + 1)th-Level Forward/Adjoint System, abbreviated as “(n + 1)th-LFAS”, which is obtained by concatenating Eqs 15‒18 and is written in the following form:
The following definitions were used in Eqs 51, 52, where the explicit dependence on the indices , has been omitted, for simplicity:
Next, it will be assumed that, for each index , the 1st-order total G-differential of the nth-order sensitivities exists and is linear in the variational functions and in a neighborhood around the nominal values of the respective state functions and components of the feature function. In this case, the 1st-order total G-differential of is by definition obtained as follows:where the quantity denotes the “indirect-effect term” and is defined as follows:
The vector , which is needed to evaluate the indirect-effect term , is the solution of the (n + 1)th-Level Variational Sensitivity System, abbreviated as (n + 1)th-LVSS, which is obtained by taking the (first-order) G-differential of the (n + 1)th-LFAS defined by Eqs 53, 54. Performing this G-differentiation yields the following relations which define the (n + 1)th-LVSS:
Carrying out the differentiation with respect to in Eqs 57, 58, and setting in the resulting expressions yields the following (n+1)th-LVSS for the (n + 1)th-level variational function:
Solving the
(n + 1)th-LVSSis prohibitive computationally. Therefore, the need for solving the
(n + 1)th-LVSSwill be avoided by expressing the indirect-effect term
in an alternative way, which eliminates the appearance of the variational function
by replacing it with the solution of the “
(n + 1)th-Level Adjoint Sensitivity System,” abbreviated as
(n + 1)th-LASS). This
(n + 1)th-LASSwill be constructed below by implementing the same sequence of logical steps as were followed when constructing the first- (and lower-) level adjoint sensitivity systems, namely,:
(i) The (n + 1)th-LASS is constructed in a Hilbert space, denoted as , comprising block-vectors of the form , , for , each of these comprising elements having the following structure: . The inner product between two elements, and , of the Hilbert space , will be denoted as and is defined as follows:
(ii) Using the definition provided in Eq. 61, form the inner product in of Eq. 59 with a yet undefined vector-valued function , , ; , to obtain the following relation:
where
denotes the bilinear concomitant defined on the phase-space boundary
, evaluated at the nominal values of the model parameter and respective functions, and where
is the formal adjoint of the matrix-valued operator
as defined in Eq.
63, below:
(iii) The first term on right-side of the second equality in Eq. 62 is now required to represent the indirect-effect term . This is achieved by requiring that the (n+1)th-level adjoint sensitivity function , be the solution of the following (n+1)th-LASS defined in Eqs. 64, 65, below, for ; ;… :
where the vector
,
, comprises
components defined in Eq.
66, below, for each
;
;…;
:
(iv) The (n + 1)th-level adjoint boundary conditions represented by Eq. 65 are selected so as to eliminate, in conjunction with the boundary conditions represented by Eq. 60, all of the unknown values of the functions in the expression of the bilinear concomitant . This bilinear concomitant may vanish after implementing the boundary conditions represented by Eqs 60, 65. However, if it does not vanish, this bilinear concomitant will be reduced to a residual quantity which will comprise only known values of , , and , and which will be denoted as .
(v) Using in Eq. 56 the equations underlying the (n + 1)th-LASS together with the relation provided in Eq. 62 yields the following expression for the indirect-effect term in terms of the (n + 1)th-level adjoint sensitivity functions, for each ; ;…; :
Adding the result obtained in Eq. 67 for the indirect effect term to the result provided in Eq. 55 for the direct effect term yields the following expression for the total nth-order G-variation of the response:where denotes the (n + 1)th-order partial sensitivity of the responsewith respect to the components of the feature function, evaluated at the nominal parameter values .
The result obtained in Eq. 68 for the expression of the (n + 1)th-order sensitivity, which was obtained by determining the first-order differential of the nth-order sensitivity, is identical to the expression that would be obtained by advancing the index, from n to (n + 1), in the expression of the nth-order sensitivity that was conjectured in Eq. 13. Thus, the proof by mathematical induction of the general mathematical framework underlying the nth-CASAM-L is thereby completed.
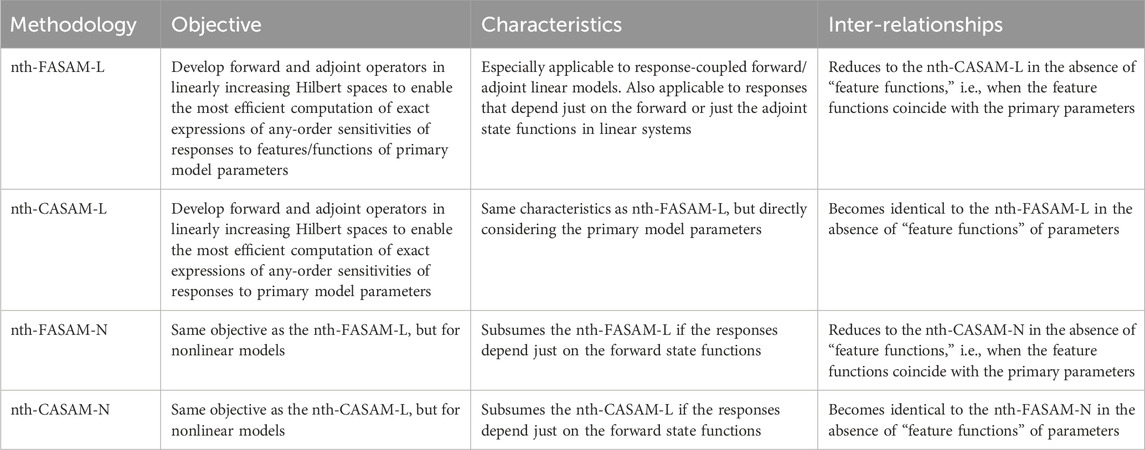
The essential characteristics of the nth-FASAM-L methodology are tabularized in Tables 1‒4, below, to underscore the conceptual parallelism between the nth-FASAM-L and the nth-CASAM-L () methodologies.
TABLE 1
| 1st-LFAS | |
| 1st-LVSS | |
| 1st-Level Hilbert Space | |
| 1st-LASS | ; |
| 1st-Order Resp. Sensitivities to Model Features |
1st-FASAM-L: 1st-order (n = 1) sensitivities of response to model features.
TABLE 2
| 2nd-LFAS = 1st-LFAS +1st-LASS | |
| 2nd-LVSS | |
| 2nd-Level Hilbert space | : |
| 2nd-LASS | |
| 2nd-order Resp. Sensitivities to Model Features | Distinct Sensitivities: |
2nd-FASAM-L: 2nd-order (n = 2) sensitivities of response to model features.
TABLE 3
| nth-LFAS =(n-1)th-LFAS +(n-1)th-LASS | |
| nth-LVSS | |
| nth-Level Hilbert space | : |
| nth-LASS | |
| nth-order Resp. Sensitivities to Model Features | Distinct Sensitivities: |
nth-FASAM-L: nth-order sensitivities of response to model features.
TABLE 4
| (n + 1)th-LASS = nth-LFAS + nth-LASS | |
| (n + 1)th-LVSS | |
| (n + 1)th-Level Hilbert space | : |
| (n + 1)th-LASS | ; |
| (n + 1)th- Resp. Sensitivities to Model Features | Distinct Sensitivities: |
(n + 1)th-FASAM-L: (n + 1)th-order sensitivities of response to model features.
An overview, in tabular form, of the computational frameworks of the nth-CASAM-L, nth-CASAM-N, nth-FASAM-L, and nth-FASAM-N methodologies, highlighting their objectives, characteristics, and interrelationships is presented in Table 5, below.
TABLE 5
| Methodology | Objective | Characteristics | Inter-relationships |
|---|---|---|---|
| nth-FASAM-L | Develop forward and adjoint operators in linearly increasing Hilbert spaces to enable the most efficient computation of exact expressions of any-order sensitivities of responses to features/functions of primary model parameters | Especially applicable to response-coupled forward/adjoint linear models. Also applicable to responses that depend just on the forward or just the adjoint state functions in linear systems | Reduces to the nth-CASAM-L in the absence of “feature functions,” i.e., when the feature functions coincide with the primary parameters |
| nth-CASAM-L | Develop forward and adjoint operators in linearly increasing Hilbert spaces to enable the most efficient computation of exact expressions of any-order sensitivities of responses to primary model parameters | Same characteristics as nth-FASAM-L, but directly considering the primary model parameters | Becomes identical to the nth-FASAM-L in the absence of “feature functions” of parameters |
| nth-FASAM-N | Same objective as the nth-FASAM-L, but for nonlinear models | Subsumes the nth-FASAM-L if the responses depend just on the forward state functions | Reduces to the nth-CASAM-N in the absence of “feature functions,” i.e., when the feature functions coincide with the primary parameters |
| nth-CASAM-N | Same objective as the nth-CASAM-L, but for nonlinear models | Subsumes the nth-CASAM-L if the responses depend just on the forward state functions | Becomes identical to the nth-FASAM-N in the absence of “feature functions” of parameters |
The nth-CASAM-L, nth-CASAM-N, nth-FASAM-L, nth-FASAM-N methodologies: main features.
Formally, the results produced by the nth-FASAM-L can be written in the same mathematical forms as those produced by the nth-CASAM-L, with the fundamental difference that the number of large-scale computations needed within the nth-FASAM-L is dictated by the number of “feature function components” whereas the number of large-scale computations needed within the nth-CASAM-L is dictated by the number of primary model parameters. In particular, a single large-scale adjoint computation is needed to solve the 1st-LASS (which is the same for both the 1st-FASAM-L and the 1st-CASAM-L) to obtain the first-order sensitivities with respect to the model parameters. Obtaining the second-order sensitivities of the response with respect to the primary model parameters requires at most large-scale computations (to solve the 2nd-LASS) within the 2nd-CASAM-L. Obtaining the same second-order sensitivities using the 2nd-FASAM-L requires at most large-scale computations (to solve the 2nd-LASS) followed by analytical derivations to obtain the second-order sensitivities with respect to the model parameters from the second-order sensitivities with respect to the components of the feature function produced by the 2nd-FASAM-L. The same parallel holds for the computation of all of the higher-order sensitivities: the computation of the 3rd-order sensitivities with respect to the primary model parameters requires at most computations if using the 3rd-CASAM-L, as opposed to at most large-scale computations plus analytical derivations if using the 3rd-CASAM-L. The computation of the 4th-order sensitivities with respect to the primary model parameters requires at most computations if using the 4th-CASAM-L, as opposed to at most large-scale computations plus analytical derivations if using the 4th-CASAM-L; and so on. Since , it is evident that the nth-FASAM-L methodology becomes increasingly more efficient than the nth-CASAM-L as the order of computed sensitivities increases.
3 Concluding discussion
This work has presented the “nth-Order Feature Adjoint Sensitivity Analysis Methodology for Response-Coupled Forward/Adjoint Linear Systems” (abbreviated as “nth-FASAM-L”), which is the most efficient methodology for computing exact expressions of sensitivities of model responses to features of model parameters and, subsequently, to the model parameters themselves for such linear systems. This efficiency stems from the maximal reduction of the number of adjoint computations (which are “large-scale” computations), by comparison to the extant high-order adjoint sensitivity analysis methodology nth-CASAM-N (the “nth-Order Comprehensive Adjoint Sensitivity Analysis Methodology for Nonlinear Systems”). Specific details are as follows:
(i) Comparing the mathematical framework of the nth-FASAM-N methodology to the framework of the nth-CASAM-N methodology indicates that the components , of the “feature function” play within the nth-FASAM-N the same role as played by the components , of the “vector of primary model parameters” within the framework of the nth-CASAM-N. It is important to note that the total number of model parameters is always larger (usually by wide margin) than the total number of components of the feature function , i.e., .
(ii) The 1st-FASAM-N and the 1st-CASAM-N methodologies require a single large-scale “adjoint” computations for solving the 1st-LASS (1st-Level Adjoint Sensitivity System), so they are comparably efficient for computing the exact expressions of the first-order sensitivities of a model response to the model’s uncertain parameters, boundaries, and internal interfaces.
(iii) For computing the exact expressions of the second-order response sensitivities with respect to the primary model’s parameters, the 2nd-FASAM-N methodology requires, at most, as many large-scale “adjoint” computations as there are “feature functions of parameters” (where denotes the total number of feature functions) for solving the left-side of the 2nd-LASS with distinct sources on its right-side. By comparison, the 2nd-CASAM-N methodology requires at most (where denotes the total number of model parameters) large-scale computations for solving the same left-side of the 2nd-LASS but with distinct sources. Since , the 2nd-FASAM-N methodology is considerably more efficient than the 2nd-CASAM-N methodology for computing the exact expressions of the second-order sensitivities of a model response to the model’s uncertain parameters, boundaries, and internal interfaces.
(iv) For computing the exact expressions of the third-order response sensitivities with respect to the primary model’s parameters, the 3rd-FASAM-N requires at most large-scale “adjoint” computations for solving the 3rd-LASS with distinct sources, while the 3rd-CASAM-N methodology requires at most large-scale computations for solving the 3rd-LASS with distinct sources. The same computational-count of ”large-scale computations” caries over when computing the higher-order sensitivities, i.e., the formula for calculating the “number of large-scale adjoint computations” is formally the same for both the nth-FASAM-N and the nth-CASAM-N methodologies, but the “variable” in the formula for determining the number of adjoint computations for the nth-FASAM-N methodology is (i.e., total number of feature functions) while the counterpart for the formula for determining the number of adjoint computations for the nth-CASAM-N is methodology is (i.e., total number of model parameters). Since , it follows that the higher the order of computed sensitivities, the mode efficient the nth-FASAM-N methodology becomes by comparison to the nth-CASAM-N methodology.
(v) When a model has no “feature” functions of parameters, but only comprises primary parameters, the nth-FASAM-N methodology becomes identical to the nth-CASAM-N methodology.
(vi) Both the nth-FASAM-N and the nth-CASAM-N methodologies are formulated in linearly increasing higher-dimensional Hilbert spaces −as opposed to exponentially increasing parameter-dimensional spaces− thus overcoming the curse of dimensionality in sensitivity analysis of nonlinear systems. Both the nth-FASAM-N and the nth-CASAM-N methodologies are incomparably more efficient and more accurate than any other methods (statistical, finite differences, etc.) for computing exact expressions of response sensitivities (of any order) with respect to the model’s uncertain parameters, boundaries, and internal interfaces.
The question of “when to stop computing progressively higher-order sensitivities ?” has been addressed by , in conjunction with the question of convergence of the Taylor-series expansion of the response in terms of the uncertain model parameters, cf; Eqs 10, 12. These Taylor-series expansions provide the fundamental premise, even if not explicitly recognized, for obtaining the expressions provided by the “propagation of errors” methodology (as originally proposed by ; and generalized by ) for the cumulants of the model response distribution in the phase-space of model parameters. The convergence of these Taylor-series, which depend on both the response sensitivities with respect to parameters and the uncertainties associated with the parameter distribution, must be ensured. This can be done by ensuring that the combination of parameter uncertainties and response sensitivities are sufficiently small to fall inside the respective radius of convergence of each of these Taylor-series expansions. The application of the nth-FASAM-N to a representative response-coupled forward/adjoint linear model stemming from the field of energy-dependent particle transport in a mixture of materials will be presented in the accompanying work designated as “Part II” ().
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
DC: Conceptualization, Methodology, Project administration, Validation, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
AlcouffeR. E.BakerR. S.DahlJ. A.TurnerS. A.WardR. (2008). PARTISN: a time-dependent, parallel neutral particle transport code system. Los Alamos, NM, USA: Los Alamos National Laboratory. LA-UR-08-07258.
2
BellmanR. E. (1957). Dynamic programming. USA: Rand Corporation, Princeton University Press. Republished: Bellman, RE (2003) Dynamic Programming. Courier Dover Publications, ISBN 978-0-486-42809-3, USA.
3
CacuciD. G. (1981). Sensitivity theory for nonlinear systems: I. Nonlinear functional analysis approach. J. Math. Phys.22, 2794–2802. 10.1063/1.525186
4
CacuciD. G. (2015). Second-order adjoint sensitivity analysis methodology (2nd-ASAM) for computing exactly and efficiently first- and second-order sensitivities in large-scale linear systems: I. Computational methodology. J. Comp. Phys.284, 687–699. 10.1016/j.jcp.2014.12.042
5
CacuciD. G. (2016). The second-order adjoint sensitivity analysis methodology for nonlinear systems—I: theory. Nucl. Sci. Eng.184, 16–30. 10.13182/nse16-16
6
CacuciD. G. (2022). The nth-order comprehensive adjoint sensitivity analysis methodology (nth-CASAM): overcoming the curse of dimensionality in sensitivity and uncertainty analysis, Volume I: linear systems. Cham, Switzerland: Springer Nature, 362. 10.1007/978-3-030-96364-4
7
CacuciD. G. (2023a). The nth-order comprehensive adjoint sensitivity analysis methodology (nth-CASAM): overcoming the curse of dimensionality in sensitivity and uncertainty analysis, volume III: nonlinear systems. Cham, Switzerland: Springer Nature, 369. 10.1007/978-3-031-22757-8
8
CacuciD. G. (2023b). Computation of high-order sensitivities of model responses to model parameters. II: introducing the second-order adjoint sensitivity analysis methodology for computing response sensitivities to functions/features of parameters. Energies16, 6356. 10.3390/en16176356
9
CacuciD. G. (2024a). Introducing the nth-order features adjoint sensitivity analysis methodology for nonlinear systems (nth-FASAM-N): I. Mathematical framework. Am. J. Comput. Math.14, 11–42. 10.4236/ajcm.2024.141002
10
CacuciD. G. (2024b). Introducing the nth-order features adjoint sensitivity analysis methodology for nonlinear systems (nth-FASAM-N): II. Illustrative example. Am. J. Comput. Math.14, 43–95. 10.4236/ajcm.2024.141003
11
CacuciD. G. (2024c). The nth-order features adjoint sensitivity analysis methodology for response-coupled forward/adjoint linear systems (nth-FASAM-L): I. mathematical framework. Front. Energy Res12, 1417594. 10.3389/fenrg.2024.1417594
12
CacuciD. G.FangR. (2023). The nth-order comprehensive adjoint sensitivity analysis methodology (nth-CASAM): overcoming the curse of dimensionality in sensitivity and uncertainty analysis, volume II: application to a large-scale system. Nature Switzerland, Cham: Springer, 463. 10.1007/978-3-031-19635-5
13
ChadwickM. B.HermanM.ObložinskýP.DunnM. E.DanonY.KahlerA. C.et al (2011). ENDF/B-VII.1: nuclear data for science and technology: cross sections, covariances, fission product yields and decay data. Nucl. Data Sheets112, 2887–2996. 10.1016/j.nds.2011.11.002
14
ConlinJ. L.ParsonsD. K.GardinerS. J.GrayM.LeeM. B.WhiteM. C. (2013). MENDF71X: multigroup neutron cross-section data tables based upon ENDF/B-VII.1X; los alamos national laboratory report LA-UR-15-29571. Los Alamos, NM, USA: Los Alamos National Laboratory, 2013.
15
CukierR. I.LevineH. B.ShulerK. E. (1978). Nonlinear sensitivity analysis of multiparameter model systems. J. Comput. Phys.26, 1–42. 10.1016/0021-9991(78)90097-9
16
DunkerA. M. (1984). The decoupled direct method for calculating sensitivity coefficients in chemical kinetics. J. Chem. Phys.81, 2385–2393. 10.1063/1.447938
17
HoraS. C.ImanR. L. (1986). A Comparison of maximum/bounding and Bayesian/Monte Carlo for fault tree uncertainty analysis. Albuquerque, NM, USA: Sandia National Laboratories. Technical Report SAND85-2839.
18
ImanR. L.HeltonJ. C.CampbellJ. E. (1981a). An approach to sensitivity analysis of computer models: Part I—introduction, input variable selection and preliminary variable assessment. J. Qual. Technol.13, 174–183. 10.1080/00224065.1981.11978748
19
ImanR. L.HeltonJ. C.CampbellJ. E. (1981b). An approach to sensitivity analysis of computer models: Part II—ranking of input variables, response surface validation, distribution effect and technique synopsis. J. Qual. Technol.13, 232–240. 10.1080/00224065.1981.11978763
20
KramerM. A.CaloJ. M.RabitzH. (1981). An improved computational method for sensitivity analysis: green’s Function Method with “AIM”. Appl. Math. Model.5, 432–441. 10.1016/s0307-904x(81)80027-3
21
LewinsJ. (1965). IMPORTANCE: the adjoint function. Oxford, UK: Pergamon Press Ltd.
22
LuoZ.WangX.LiuD. (2020). Prediction on the static response of structures with large-scale uncertain-but-bounded parameters based on the adjoint sensitivity analysis. Struct. Multidiscip. Optim.61, 123–139. 10.1007/s00158-019-02349-w
23
PrágerT.KelemenF. D. (2014). “Adjoint methods and their application in earth sciences,” in Advanced numerical methods for complex environmental models: needs and availability. Editors FaragóI.HavasiÁ.ZlatevZ. (Oak Park, IL, USA: Bentham Science Publishers), 203–275. Chapter 4A.
24
Rios InsuaD. (1990). Sensitivity analysis in multiobjective decision making. New York, USA: Springer Verlag.
25
A.Saltarelli,K.Chan,E. M.Scott, (2000). Sensitivity analysis (Chichester, UK: J. Wiley and Sons Ltd).
26
ShultisJ. K.FawR. E. (2000). Radiation shielding. La Grange Park, Illinois, USA: American Nuclear Society.
27
StaceyW. M. (2001). Nuclear reactor physics. New York. USA: John Wiley and Sons.
28
TukeyJ. W. (1957). The propagation of errors, fluctuations and tolerances. Princeton, NJ, USA: Princeton University. Technical Reports No. 10-12.
29
ValentineT. E. (2006). Polyethylene-reflected plutonium metal sphere subcritical noise measurements, SUB-PU-METMIXED-001. International handbook of evaluated criticality safety benchmark experiments, NEA/NSC/DOC(95)03/I-IX, organization for economic Co-operation and development (OECD). Paris, France: Nuclear Energy Agency.
30
WeibergA. M.WignerE. P. (1958). The physical theory of neutron chain reactors. Chicago, Illinois, USA: University of Chicago Press.
31
WeisbinC. R.OblowE. M.MarableJ. H.PeelleR. W.LuciusJ. L. (1978). Application of sensitivity and uncertainty methodology to fast reactor integral experiment analysis. Nucl. Sci. Eng.66, 307–333. 10.13182/nse78-3
32
WignerE. P. (1945). Effect of small perturbations on pile period. Chicago, IL, USA: Scientific Research Publishing. Chicago Report CP-G-3048.
33
WilliamsM. L. (1986). “Perturbation theory for nuclear reactor analysis,” in Handbook of nuclear reactor calculations. Editor RonenY. (Boca Raton, Florida, USA: CRC Press), 63–188. Volume 3.
34
WilliamsM. L.EngleW. W. (1977). The concept of spatial channel theory applied to reactor shielding analysis. Nucl. Sci. Eng.62, 92–104. 10.13182/nse77-a26941
35
WilsonW. B.PerryR. T.ShoresE. F.CharltonW. S.ParishT. A.EstesG. P.et al (2002). “SOURCES4C: a code for calculating (α,n), spontaneous fission, and delayed neutron sources and spectra,” in Proceedings of the American Nuclear Society/Radiation Protection and Shielding Division 12th Biennial Topical Meeting, Santa Fe, NM, USA, 14–18 April 2002.
Summary
Keywords
response-coupled forward/adjoint model, features of model parameters, adjoint operators in Hilbert spaces, exact sensitivities of arbitrarily high order, most efficient computation of high order response sensitivities
Citation
Cacuci DG (2024) The nth-order features adjoint sensitivity analysis methodology for response-coupled forward/adjoint linear systems (nth-FASAM-L): I. mathematical framework. Front. Energy Res. 12:1417594. doi: 10.3389/fenrg.2024.1417594
Received
15 April 2024
Accepted
26 June 2024
Published
13 August 2024
Volume
12 - 2024
Edited by
Yang Zou, Chinese Academy of Sciences (CAS), China
Reviewed by
Jian Guo, Chinese Academy of Sciences (CAS), China
Shichang Liu, North China Electric Power University, China
Updates
Copyright
© 2024 Cacuci.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dan Gabriel Cacuci, cacuci@cec.sc.edu
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.