A semi-analytical fracture high-conductivity location diagnostic method for vertically fractured wells in multilayered reservoirs: field case study

Deep multilayered reservoirs are usually developed using multilayered fracturing techniques; however, the non-uniform placement of proppant causes uneven distribution of fracture conductivity. This study introduces a semi-analytical well test model for hydraulically fractured wells in multilayered reservoirs, accounting for varying fracture conductivity within the hydraulic fracture. The model is built upon the point source function, boundary element method, Duhamel theorem, and pressure superposition principle. Verification tests are conducted to ensure calculation accuracy. Sensitivity analysis is performed on key parameters, encompassing the transmissibility factor, storativity factor, fracture extension, and fracture conductivity. The findings indicate that 1) Increased heterogeneity among layers correlates with a more pronounced pressure drop; 2) Poorly-propped fracture conductivity influences the duration of bilinear flow, becoming negligible after linear flow; 3) The model’s applicability extends to other multilayered reservoirs (e.g., carbonate reservoirs) with minor adjustments. Lastly, a case study from Xinjiang oilfield is presented to demonstrate that the proposed method can derive reservoir and fracture properties for each layer individually. This study contributes to a deeper understanding of the potential of pressure data in characterizing multilayered reservoirs.

1 Introduction

Despite being criticized for CO₂ emissions, fossil fuels remain essential and constitute a significant portion of global energy consumption. In response to growing energy demand, fossil fuel exploration and development have shifted towards deep-layer unconventional oil and gas reservoirs (Shi et al., 2020a; Shi et al., 2020b; Wang et al., 2021; Bai et al., 2024). Recently, China has commercially exploited multiple deep-layer reservoirs, including the Xinjiang oilfield, Tarim oilfield, and Tahe oilfield (Wei et al., 2021a; Shi et al., 2023).

Generally speaking, deep-layer reservoirs have extremely low permeability. Fracturing technique is undoubtedly the most used to improve the well performance. Much work has been reported to study the pressure transient behavior of fractured wells. Muskat (1938) firstly presented the pressure characteristic of vertically fractured wells. Gringarten and Ramey (1973), Gringarten et al. (1974) introduced the instantaneous Green source function, Newman product principle to solve the unsteady-state flow problems of vertical fractures and gave the pressure solutions for uniform-flux and infinite-conductivity fractured wells. Cinco-Ley et al. (1978), Cinco-Ley and Meng (1988) proposed the pressure transient solution for the finite-conductivity fractured wells using the Fredholm integral and boundary element method. Based on their modelling methods, many researchers afterwards presented a large number of models for pressure transient analysis (PTA) of fractured wells (Dejam et al., 2018; Zhang et al., 2019; Luo et al., 2020; Wei et al., 2021b; Al-Kabbawi, 2022; Wei et al., 2022b; Lu et al., 2022). However, the PTA problem in deep-layer tight reservoirs would be different because the deep-layer tight reservoirs usually adopt the separate-layer fracturing for every oil layer and the commingling production for reducing the number and cost of drilling wells. At present, limited attention was given to the fractured wells located in the multilayered reservoir. Bennett et al. (1985) presented the new analytical solutions for fractured wells produced at a constant rate or a constant pressure in layered reservoirs without interlayer communication. Osman M. E. (1993), presented the pressure solutions for uniform-flux, infinite-conductivity and finite-conductivity fractured wells located in a stratified reservoir for the case of infinite-acting and bounded square reservoirs. He has reported that dimensionless pressure and pressure derivative strongly depend on fracture conductivity and fracture extension at early times. Chao et al. (1994) presented the pressure and its derivative responses of the infinite-conductivity fractured wells in commingled systems with mixed boundary conditions. Manrique and Bobby, 2007 designed a unique methodology for determining the single-layer flowrate and evaluating the reservoir and fracture effective properties of multi-fractured wells in stacked pay reservoirs using commingled production. Ali et al. (2010) presented a method for estimating fracture half-lengths and formation permeability for hydraulically fractured vertical gas wells and estimated the drainage area of a single formation.

Another important issue deserved to be considered is about the proppant movement during hydraulically fracturing operation in deep-layer multilayered reservoirs (Wanjing and Changfu, 2015). Proppant movement inside hydraulic fracture is always restricted nearby the wellbore, causing poorly propped at the tip of hydraulic fracture (Mirzaei and Cipolla, 2012). Moreover, proppant crushed by closure stress could reduce the fracture conductivity near the wellbore (Soliman, 1986). Once the oil wells put into production, the width of poorly-propped fracture segments would be rapidly decreased, causing that the conductivity decreases sharply. Soliman (1986) presented two analytical models to describe the performance of hydraulically fractured wells with changing fracture conductivity under either constant pressure and constant rates conditions based on the simplified bilinear flow. Lolon et al. (2003) clearly pointed out that the effect of poorly propped segments should be considerable for making better interpretations. Gonzalez Chavez and Cinco-Ley, 2006 presented a semi-analytical model to investigate the pressure behavior of a vertically fractured well with variable finite-conductivity and fracture skin in infinite reservoir using the boundary element method. More recently, Luo and Tang (2015) presented a semi-analytical model for a vertically fractured well in an infinite reservoir considering variable fracture conductivity and non-Darcy effect. Li et al. (2022) developed a well testing analysis method for multi-layer fractured wells’ fracture changing conductivity using a three-linear flow model. However, their model only considers linear flow in reservoirs and fractures, failing to explain the radial flow that occurs later in the pressure derivative. Moreover, the three-linear flow model exhibits significant ambiguity during the fitting process of actual data.

This study introduces a semi-analytical PTA model for wells with changing fracture conductivity in multilayered reservoirs. Initially, the mathematical model is formulated using the point source function, boundary element theory, Duhamel theorem, and pressure superposition principle. Subsequently, the proposed model undergoes validation against the Cinco-Ley model (1988) to ensure its accuracy and applicability. Additionally, a sensitivity analysis is performed on key parameters, such as fracture extension, fracture conductivity, transmissibility factor, and storativity factor. It is noteworthy that our model not only addresses linear flow within fractures and reservoirs but also encompasses radial flow across the entire reservoir, as evidenced by the pressure derivative curve’s endpoint. This feature enhances the practical applicability of the model. Finally, the pressure buildup data from a commingling-production fractured well in the Xinjiang oilfield are analyzed to demonstrate the feasibility and practicality of the proposed model.

2 Methodology

2.1 Conceptual model

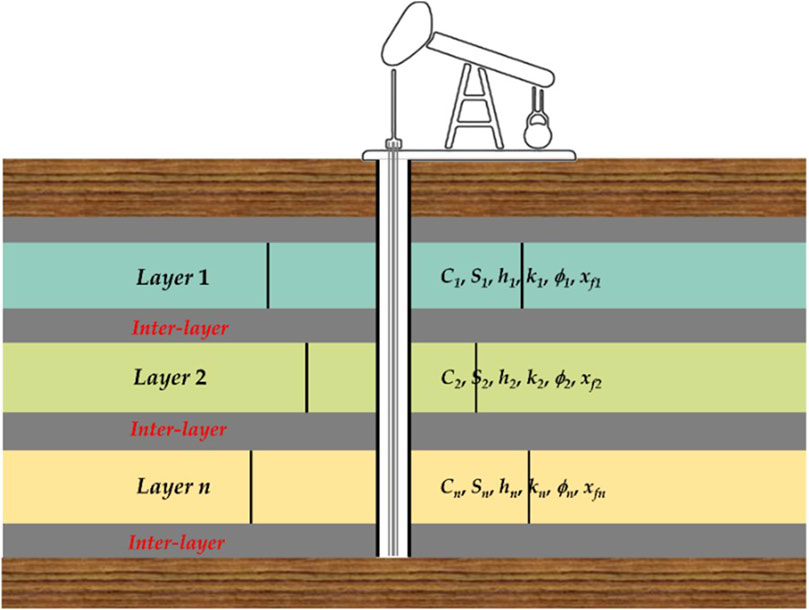
Figure 1 illustrates a multilayered reservoir comprising n oil layers. Each layer is intersected by hydraulic fractures. Each layer is homogeneous and isotropic, containing single-phase, slightly compressible fluid with viscosity μ. The initial formation pressure is represented by p_i. Each layer is separated by non-communicating interlayers. The developed physical model can characterize the impact of uneven proppant distribution on fracture flow conductivity. Other basic assumptions are provided below.

(a) Deep-layer reservoirs exhibit extremely low permeability, n is the numbers of layers. Hydraulic fracturing stimulation is applied to each layer, resulting in a symmetrical hydraulic fracture along the wellbore with permeability k_fn, height h_fn, half-length x_fn, and width w_fn. There is no flow at the fracture extreme.

(b) Each layer possesses distinct physical characteristics, including porosity (ϕ_n), permeability (k_n), thickness (h_n), total compressibility (c_t), wellbore storage (C_n), skin factor (S_n), and production contribution (q_n).

(c) For practical purposes, this study divides the hydraulic fracture into propped and poorly-propped segments. It employs F_cDn1 and F_cDn2 to denote dimensionless fracture conductivity near and far from the wellbore, respectively.

(d) The fluid follows Darcy’s law, neglecting gravity and capillary forces.

(e) The reservoir is homogeneous and of uniform thickness, with permeability and porosity evenly distributed.

Figure 1

Figure 1. Schematic of finite-conductivity fractured well in the stratified reservoirs.

2.2 Mathematical model

To provide comprehensive flow regimes of hydraulically fractured wells in multilayered reservoirs, we use a semi-analytical modeling approach, abandoning the analytical trilinear flow model proposed by Lee and Brockenbrough (1986). Initially, we present the reservoir flow model and fracture flow model for each layer. Subsequently, the reservoir flow model and fracture flow model are coupled using boundary element discretization to derive the pressure solution for each layer. Finally, the Duhamel theorem and pressure superposition principle are employed to account for wellbore storage and skin effects, providing the bottom hole pressure solution based on the pressure solution of each layer. In this study, we account for variations in wellbore storage coefficient and skin factor across each layer.

2.2.1 Reservoir flow model

According to Gringarten’s work (1973), we can easily give the point source function of a well in infinite oil layer n with constant production rate q_n. The detailed derivation of the reservoir flow model is shown in Supplementary Appendix SA.

$p_n=p_{ni}-\frac{1}{4\pi {\varphi }_n{c}_f{\chi }_n{h}_n}{\int }_0^t\frac{q_n\left(\tau \right)}{t-\tau }\mathit{exp}\left[-\frac{{\left(x-x’\right)}^2+{\left(y-y’\right)}^2}{4{\chi }_n\left(t-\tau \right)}\right]d\tau (1)$

where ${\chi }_n=\frac{k_n}{{\varphi }_n\mu c_f}$ is the layer n diffusivity.

Let us regard the fracture as the line source. The pressure solution for a well intercepted by fracture is obtained by integrating Eq. 1 along the hydraulic fracture, given by:

$p_n=p_{ni}-\frac{1}{4\pi {\varphi }_n{c}_f{\chi }_n{h}_n}{\int }_0^t{\int }_{-x_{fn}}^{x_{fn}}\frac{q_{fn}\left(\tau \right)}{t-\tau }\mathit{exp}\left[-\frac{{\left(x-x’\right)}^2+{\left(y-y’\right)}^2}{4{\chi }_n\left(t-\tau \right)}\right]dx’d\tau (2)$

where q_fn is the flow rate per unit of fracture length going from the formation into the fracture of the layer n.

Eq. 2 can be rewritten in Laplace domain with dimensionless form, given by:

${\overline{p}}_{Dn}=\frac{1}{2{\alpha }_n{\lambda }_n}{\int }_{-{\alpha }_n}^{{\alpha }_n}{\overline{q}}_{fDn}\cdot K_0\left[\left(x_D-x’\right)\sqrt{\frac{{\omega }_n}{{\lambda }_n}s}\right]dx’(3)$

The dimensionless variables in Eq. 3 are defined by Eqs 4–8 respectively.

$p_{Dn}=\frac{\overline{kh}\left(p_i-p_n\right)}{1.842Q\mu B}(4)$

${\alpha }_n=\frac{x_{fn}}{{\overline{x}}_f}(5)$

${\lambda }_n=\frac{{\left(kh\right)}_n}{\overline{kh}}(6)$

${\omega }_n=\frac{{\left(\varphi h\right)}_n}{\overline{\varphi h}}(7)$

$x_D=\frac{x}{{\overline{x}}_f}(8)$

Note that the definitions $\overline{kh}={\displaystyle \sum _{n=1}^m}{\left(kh\right)}_n,\overline{\varphi h}={\displaystyle \sum _{n=1}^m}{\left(\varphi h\right)}_n,\overline{x_f}={\displaystyle \sum _{n=1}^m}{\left(x_f\right)}_n$.

Where q_fDn is defined by Eq. 9:

$q_{fDn}=\frac{2q_{fn}{x}_{fn}}{q_n}(9)$

2.2.2 Fracture flow model

The flow within the hydraulic fracture is regarded as the linear flow. The diffusivity equation is now formulated in terms of dimensionless variable in layer n. Note that we neglect the fluid compressibility inside the fracture because the hydraulic fracture volume is very small (Cinco-Ley and Meng, 1988; Wei et al., 2021b). The detailed derivation of the fracture flow model is shown in Supplementary Appendix SB.

$\frac{\partial }{\partial x_D}\left[{F_{cDn}}_{\left(x_D\right)}\frac{\partial p_{fDn}}{\partial x_D}\right]-\frac{\pi q_{fDn}}{{\lambda }_n{\alpha }_n^2}=0(10)$

The initial condition is defined by Eq. 11

$p_{fDn}\left(t_D=0\right)=0(11)$

Eqs 12, 13 are the inner and outer boundary conditions, respectively, expressed as follows

${\left.\frac{\partial p_{fDn}}{\partial x_D}\right|}_{x_D=0}=-\frac{\pi }{{F_{cDn}}_{\left(x_D=0\right)}{\alpha }_n{\lambda }_n}(12)$

${\left.\frac{\partial p_{fDn}}{\partial x_D}\right|}_{x_D={\alpha }_n}=0(13)$

Dimensionless time and dimensionless fracture conductivity are respectively defined by Eqs 14, 15.

$t_D=\frac{3.6\times {10}^{-3}\overline{kh}\cdot t}{\overline{\varphi h}\mu c_t{\overline{x}}_f^2}(14)$

$F_{cDn}=\frac{k_{fn}{w}_{fn}}{k_n{x}_{fn}}(15)$

Integrating Eq. 10 from 0 to x_D, the resulting equation is obtained with the boundary condition, given by:

$F_{cDn\left(x_D\right)}\frac{\partial p_{fDn}}{\partial x_D}+\frac{\pi }{{\alpha }_n{\lambda }_n}-{\int }_0^{x_D}\frac{\pi q_{fDn}}{{\lambda }_n{\alpha }_n^2}d{x}_D=0(16)$

Integrating Eq. 16 from 0 to x_D again, the resulting equation is obtained with the boundary condition, given by:

${\int }_0^{x_D}{F}_{cDn\left(x_D\right)}\partial p_{fDn}+\frac{\pi }{{\alpha }_n{\lambda }_n}{x}_D-{\int }_0^{x_D}{\int }_0^{x_D}\frac{\pi q_{fDn}}{{\lambda }_n{\alpha }_n^2}d{x}_{D}d{x}_D=0(17)$

Equation 17 in Laplace domain can be written as:

${\int }_0^{x_D}{F}_{cDn\left(x_D\right)}\partial {\overline{p}}_{fDn}+\frac{\pi }{s{\alpha }_n{\lambda }_n}{x}_D={\int }_0^{x_D}{\int }_0^{x_D}\frac{\pi {\overline{q}}_{fDn}}{{\lambda }_n{\alpha }_n^2}d{x}_{D}d{x}_D(18)$

2.2.3 Solution of the model

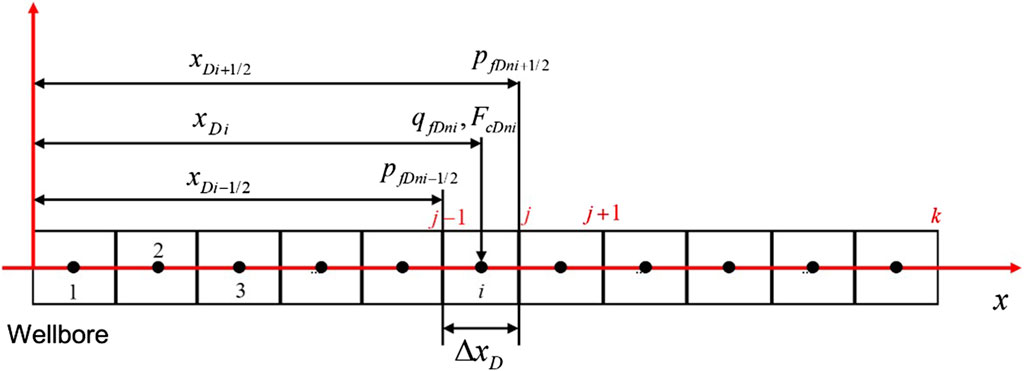
Discretizing the fracture (half length) into k equal-length cells with uniform flux, as shown in Figure 2, Eq. 18 can be written as:

${\displaystyle \sum _{i=1}^j}{F}_{cDni}{\int }_{x_{Di-1/2}}^{x_{Di+1/2}}\partial {\overline{p}}_{fDn}+\frac{\pi }{s{\alpha }_n{\lambda }_n}{x}_{Dj}=\frac{\pi }{{\lambda }_n{\alpha }_n^2}\left(x_{Dj}{\displaystyle \sum _{i=1}^j}{\overline{q}}_{fDni}{\int }_{x_{Di-1/2}}^{x_{Di+1/2}}\partial x_D-{\displaystyle \sum _{i=1}^j}{\overline{q}}_{fDni}{\int }_{x_{Di-1/2}}^{x_{Di+1/2}}{x}_D\partial x_D\right)(19)$

Figure 2

Figure 2. Discretization scheme.

Equation 12 can be further written as:

${\displaystyle \sum _{i=1}^j}{F}_{cDni}\left({\overline{p}}_{fDni+1/2}-{\overline{p}}_{fDni-1/2}\right)+\frac{\pi }{s{\alpha }_n{\lambda }_n}{x}_{Dj}=\frac{\pi }{{\lambda }_n{\alpha }_n^2}\left(\Delta x_D{x}_{Dj}{\displaystyle \sum _{i=1}^j}{\overline{q}}_{fDni}-\Delta x_D{\displaystyle \sum _{i=1}^j}{\overline{q}}_{fDni}{x}_{Di}\right)(20)$

where $\Delta x_D={\alpha }_n/k,x_{Di}=\left(i-0.5\right)\Delta x_D,x_{Dj}=j\cdot \Delta x_D$.

The reservoir and fracture flow model are coupled by the pressure and flowrate continuity condition of every cell. We obtain the ${\overline{p}}_{fDni+1/2}$ by Eq. 3 for the j cell.

$\begin{array}{l}{\overline{p}}_{fDni+1/2}=\frac{1}{2{\alpha }_n{\lambda }_n}{\int }_{-{\alpha }_n}^{{\alpha }_n}{\overline{q}}_{fDni}\cdot K_0\left[\left(x_{Di+1/2}-x’\right)\sqrt{\frac{{\omega }_n}{{\lambda }_n}s}\right]dx’\\ =\frac{1}{2{\alpha }_n{\lambda }_n}{\displaystyle \sum _{i=1}^j}{\int }_{x_{Di-1/2}}^{x_{Di+1/2}}{\overline{q}}_{fDni}\cdot \left\{K_0\left[\left(x_{Di+1/2}+x’\right)\sqrt{\frac{{\omega }_n}{{\lambda }_n}s}\right]+K_0\left[\left(x_{Di+1/2}-x’\right)\sqrt{\frac{{\omega }_n}{{\lambda }_n}s}\right]\right\}dx’\end{array}(21)$

Combining Eqs 20, 21, we obtain an equation system with j equations. The j+1 unknowns for every cell is q_fD1, q_fD2, … q_fDj, and p_wDn. There are j equations and j+1 unknowns. To solve the equation system, one another equation is needed. Recalling that the flow entering the fracture is equal to the flow rate of the layer n; that is

${\displaystyle \sum _{i=1}^k}{\overline{q}}_{fDn}=\frac{k}{s}(22)$

The unknowns are found by solving the system of equations.

$\left[\begin{array}{cccc}& ..& & F_{cDn\left(x_D=0\right)}\\ & A_{ij}& & ..\\ & ..& & F_{cDn\left(x_D=0\right)}\\ 1& ..& 1& 0\end{array}\right]\cdot \left[\begin{array}{c}..\\ {\overline{q}}_{fDni}\left(s\right)\\ ..\\ {\overline{p}}_{wDn}\left(s\right)\end{array}\right]=B_n(23)$

If the wellbore storage and skin effect are considered, we obtain the following equation based on Duhamel theorem and pressure superposition principle (Van Everdingen, 1953). Note that we consider each layer has different wellbore storage coefficient and skin factor.

${\overline{q}}_{Dn}=\frac{1+C_{Dn}{s}^2{\overline{p}}_{wDn}+C_{Dn}s\frac{S_n}{{\lambda }_n}}{s{\overline{p}}_{wDn}+\frac{S_n}{{\lambda }_n}}{\overline{p}}_{wfD}(24)$

where ${\overline{p}}_{wDn}$ is given from Eq. 23. C_Dn and S_n are the wellbore storage coefficient and skin factor of layer n, respectively.

Finally, the bottom-hole pressure of commingling system is obtained with the flowrate condition ${\displaystyle \sum _{n=1}^m}{\overline{q}}_{Dn}=1/s$ in Laplace domain, given by:

${\overline{p}}_{wfD}=\frac{1}{s}{\left({\displaystyle \sum _{n=1}^m}\frac{1+C_{Dn}{s}^2{\overline{p}}_{wDn}+C_{Dn}s\frac{S_n}{{\lambda }_n}}{s{\overline{p}}_{wDn}+\frac{S_n}{{\lambda }_n}}\right)}^{-1}(25)$

and Stehfest numerical inversion method is used to obtain p_wfD in the time domain (Stehfest, 1970). It deserves clarification that total wellbore storage should be $C_D={\displaystyle \sum _{n=1}^m}{C}_{Dn}$ in this work.

Dimensionless wellbore storage is defined as:

$C_D=\frac{C}{2\pi \overline{\varphi h}{c}_t{{\overline{x}}_f}^2}(26)$

Dimensionless production contribution is defined as:

$q_{Dn}=\frac{q_n}{Q}(27)$

Dimensionless propped fracture length is defined as:

$R_{Dn}=\frac{x_{pfn}}{{\overline{x}}_f}(28)$

3 Results and discussion

Based on the solutions proposed by Eqs 23, 25, we derive a semi-analytical solution for vertically fractured wells with varying fracture conductivity within multilayered reservoirs. To address practical concerns, we partition the hydraulic fracture into two segments: propped and poorly-propped. Introducing dimensionless parameters F_cDn1 and F_cDn2, we respectively characterize the fracture conductivity near and far from the wellbore. Additionally, R_Dn denotes the dimensionless fracture length of the segment near the wellbore. Pressure behavior under constant flow rate is analyzed in this study. It is noteworthy that the consideration of wellbore storage and skin effect is omitted in this section for simplification purposes.

3.1 Model validation

When m = 1 (i.e., λ = 1, ω = 1, α = 1) and F_cDn1 = F_cDn2, the proposed model can be simplified as the conventional finite-conductivity fracture model presented by Cinco-Ley and Meng (1988). For the calculation of Cinco-Ley and Meng’s model (1988), the readers may be referred to their work, the methods of which are used unchanged here. We will not repeat it because no new information is available. We compare the pressure and derivative results of the simplified model and Cinco-Ley and Meng’s model (1988) under different dimensionless fracture conductivity. By discretizing the fracture half-length into 10 equal-length cells, we ensure a thorough investigation of the fracture dynamics across different parameter regimes. The graphical representation in Figure 3 serves as a visual testament to the accuracy and reliability of our proposed model. The close correspondence between our results and those obtained from Cinco-Ley and Meng’s model underscores the robustness and correctness of our approach. This alignment not only reaffirms the validity of our simplification but also highlights the consistency and predictive power of the underlying mathematical formulations.

Figure 3

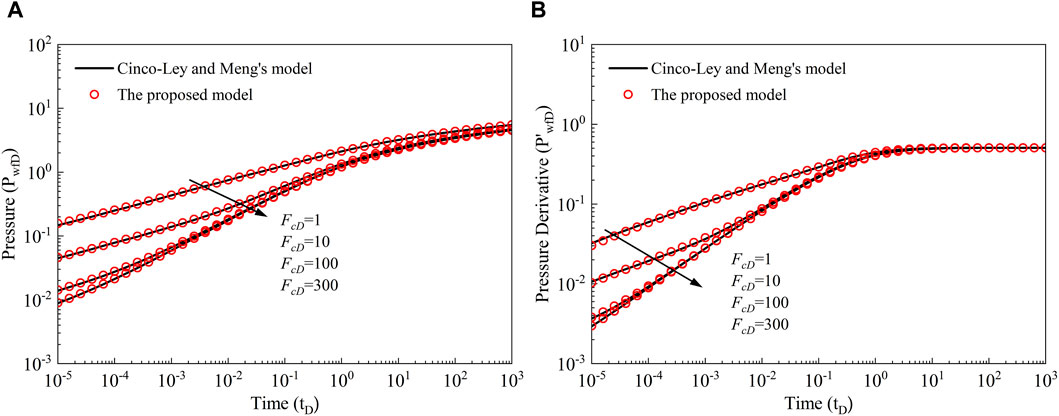
Figure 3. Comparison of the proposed model and Cinco-Ley and Meng’s model under different fracture conductivity. (A) Pressure results, (B) Pressure derivative results.

3.2 Sensitivity analysis

Using a two-layer reservoir as a illustrative example, this subsection performs a sensitivity analysis on key parameters, which encompass the transmissibility factor, storativity factor, fracture extension (r_n = x_fn/x_f1), and fracture conductivity. Through this analysis, we aim to elucidate the influence of these parameters on the overall behavior and performance of the reservoir system.

By systematically varying these crucial parameters, we can gain valuable insights into their respective impacts on reservoir dynamics, productivity, and overall efficiency. Specifically, we examine how changes in the transmissibility factor and storativity factor affect fluid flow and pressure distribution within the reservoir. Additionally, we investigate the sensitivity of fracture extension and conductivity on fracture propagation and fluid mobility. This comprehensive sensitivity analysis serves to identify key factors that significantly influence reservoir performance and productivity. By elucidating the interplay between these parameters, we can optimize reservoir design, production strategies, and hydraulic fracturing operations to maximize recovery and minimize operational costs.

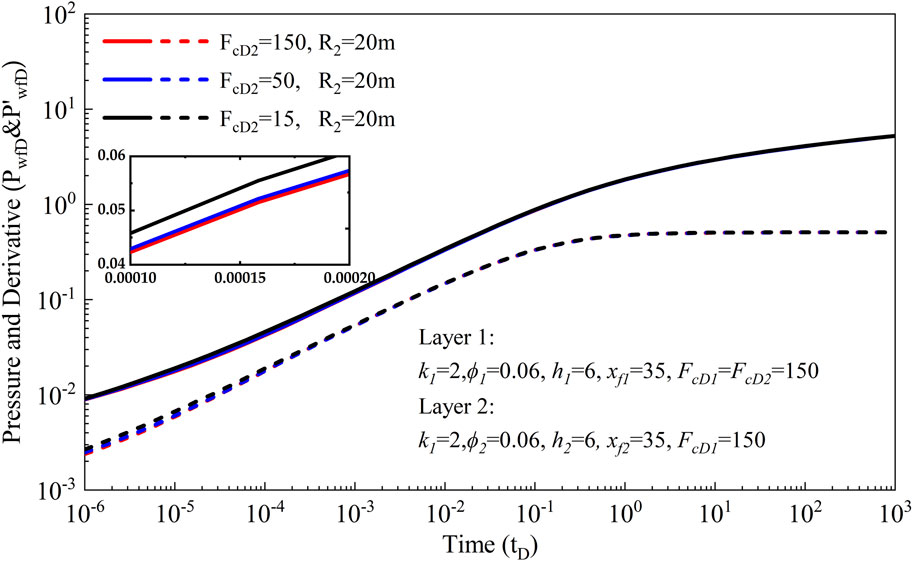
3.2.1 Poorly-propped fracture conductivity

Three scenarios with varying poorly-propped fracture conductivities (F_cD2 = 150, 50, 15) are formulated to examine their impact on pressure behavior and pressure derivative. The calculation results are depicted in Figure 4, providing valuable insights into the influence of poorly-propped fracture conductivity on reservoir performance. It is observed that the duration of bilinear flow is notably affected by the poorly-propped fracture conductivity. Specifically, a decrease in poorly-propped fracture conductivity prolongs the duration of bilinear flow. Conversely, higher values of poorly-propped fracture conductivity lead to shorter durations of bilinear flow. Once the bilinear flow phase concludes, the effect of poorly-propped fracture conductivity diminishes, resulting in a negligible impact on subsequent flow behavior. Furthermore, the heightened heterogeneity arising from variations in fracture conductivity results in a more pronounced increase in both pressure and pressure derivative. This underscores the intricate interplay between reservoir heterogeneity and fracture conductivity, highlighting the need for a comprehensive understanding of these factors in reservoir management and hydraulic fracturing design.

Figure 4

Figure 4. Effect of the poorly-propped fracture conductivity on pressure and derivative.

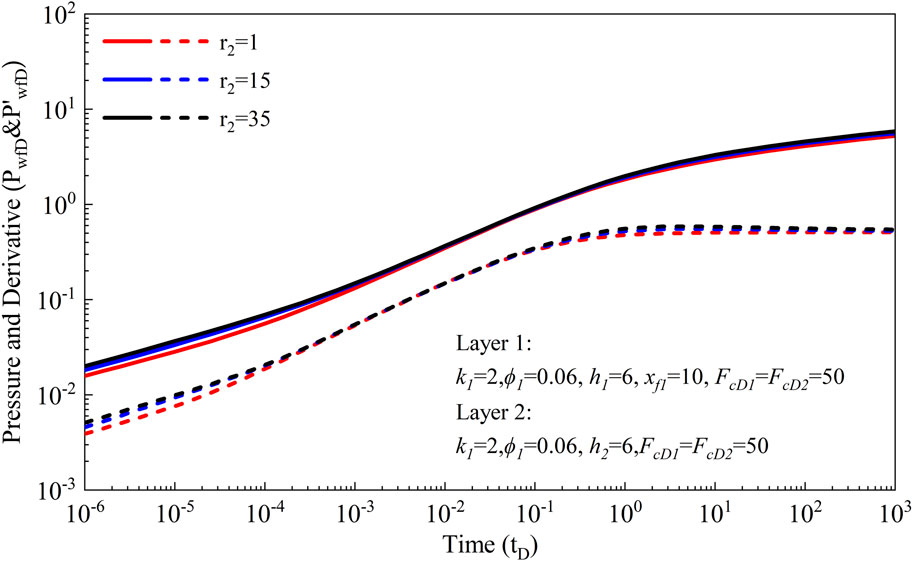
3.2.2 Fracture extension

In addition to examining the impact of poorly-propped fracture conductivity, this subsection delves into the effect of fracture extension on pressure behavior and pressure derivative. To this end, three scenarios with varying fracture extensions (x_f2 = 10 m, 150 m, 350 m) are meticulously designed. The calculation results are presented in Figure 5, providing valuable insights into the influence of fracture extension on reservoir performance. Our analysis reveals that fracture extension significantly influences the duration of bilinear flow and the onset of radial flow. Specifically, as the fracture extension increases, the duration of bilinear flow extends, and the appearance of radial flow is delayed accordingly. Conversely, smaller fracture extensions result in shorter durations of bilinear flow and earlier occurrences of radial flow. Furthermore, the heightened heterogeneity stemming from variations in fracture length exacerbates the increase in both pressure and pressure derivative. This underscores the intricate relationship between fracture extension and reservoir dynamics, emphasizing the need for careful consideration of fracture geometry in reservoir management and hydraulic fracturing design.

Figure 5

Figure 5. Effect of the fracture extension on pressure and derivative.

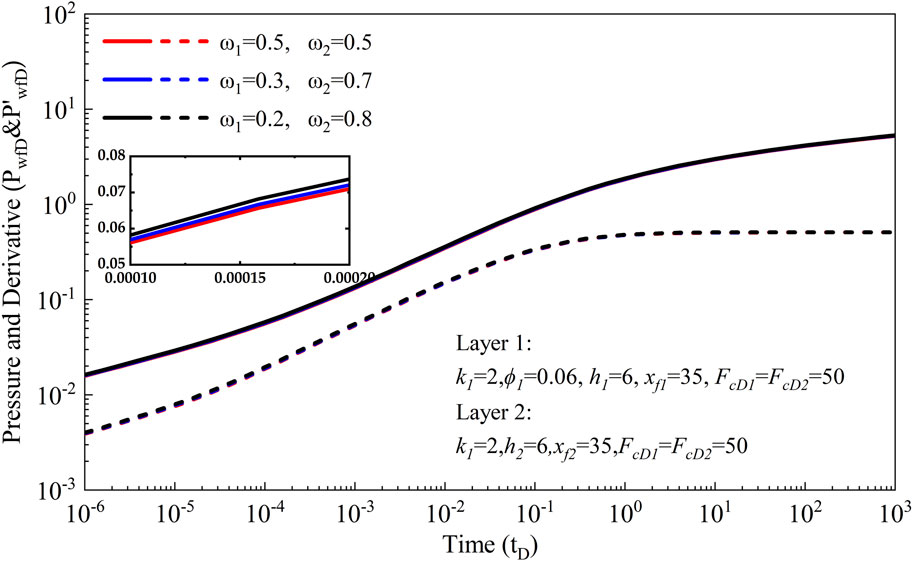
3.2.3 Storativity factor

Furthermore, we investigate the impact of the storativity factor on pressure behavior and pressure derivative. To explore this, three scenarios with varying storativity factors (ω₁ = 0.5, 0.3, 0.2) are meticulously designed in this subsection. The calculation results are depicted in Figure 6, providing valuable insights into the influence of the storativity factor on reservoir performance. Our analysis indicates that the storativity factor significantly affects pressure behavior and pressure derivative. Specifically, variations in the storativity factor lead to changes in reservoir heterogeneity, resulting in increased pressure and pressure derivative. Moreover, the degree of heterogeneity directly correlates with the magnitude of pressure increase, with stronger heterogeneity yielding more pronounced effects on pressure behavior. These findings underscore the importance of considering the storativity factor in reservoir characterization and management. By understanding its impact on reservoir dynamics, engineers can tailor production strategies and optimize reservoir performance to maximize hydrocarbon recovery.

Figure 6

Figure 6. Effect of the storativity factor on pressure and derivative.

3.2.4 Transmissibility factor

In this subsection, we explore the influence of the transmissibility factor on pressure behavior and pressure derivative through the investigation of three scenarios with varying transmissibility factors (λ₁ = 0.5, 0.35, 0.15). The calculation results are illustrated in Figure 7, providing insights into the impact of the transmissibility factor on reservoir performance. Our analysis reveals a clear trend: as the transmissibility factor decreases, both pressure and pressure derivative exhibit an increase. This trend underscores the significant role of transmissibility in governing reservoir dynamics, with lower transmissibility leading to heightened pressure responses. Furthermore, the observed increase in pressure and pressure derivative with decreasing transmissibility reflects the enhanced reservoir heterogeneity resulting from variations in the transmissibility factor. This highlights the intricate relationship between reservoir connectivity and pressure behavior, emphasizing the need for careful consideration of transmissibility in reservoir characterization and management.

Figure 7

Figure 7. Effect of the transmissibility factor on pressure and derivative.

4 Case study

Recently, Xinjiang oilfield companies have made significant strides in exploring deep-layer unconventional oil and gas reservoirs. Within the Junggar Basin, several oil and gas reservoirs characterized by complex geological structures and diverse fluid compositions have been unearthed. These discoveries serve as a foundational reservoir base for enhancing current production rates. The newly identified reservoirs boast burial depths exceeding 5 km and comprise multiple oil layers. Notably, the initial permeability of each oil layer is exceptionally low. To optimize production efficiency, a combination of commingling production and separate-layer fracturing techniques is employed in oil well operations. In light of these developments, there arises a need to apply advanced modeling approaches to interpret recorded buildup data. By doing so, we aim to accurately characterize reservoir parameters while validating the feasibility and practicality of the proposed model. This endeavor not only enhances our understanding of reservoir behavior but also paves the way for informed decision-making in reservoir management and production optimization.

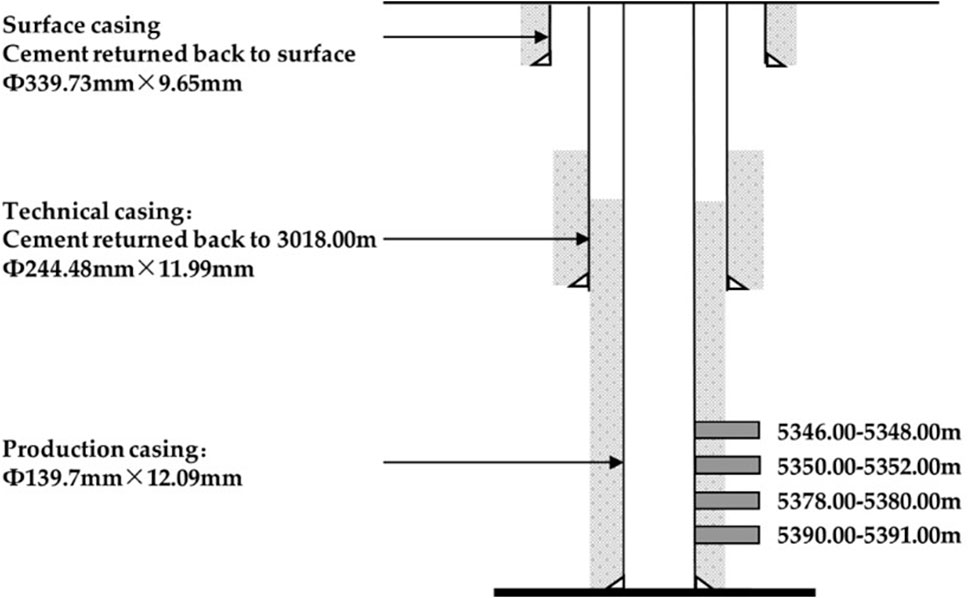
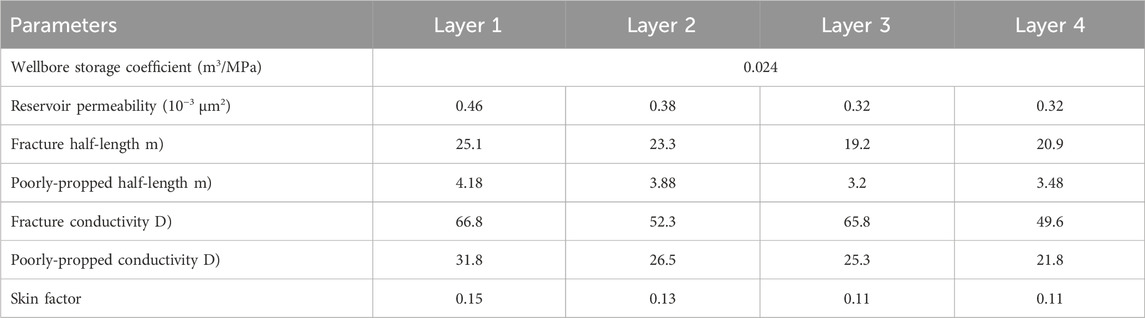
As depicted in Figure 8, well P1 has intersected four distinct oil layers. Each of these oil layers undergoes hydraulic fracturing operations following two rounds of fracturing. The first fracturing operation targets two oil layers spanning depths of 5378–5380 m and 5390–5391 m, while the second operation focuses on the remaining two layers ranging from 5346–5348 m and 5350–5352 m. Well P1 maintains a production rate of 15 m³/d. The essential reservoir and well parameters are detailed in Table 1. Utilizing the proposed model, we analyze the recorded buildup pressure data. As illustrated in Figure 9, the theoretical curves closely align with the field data, validating the accuracy of our interpretation. The results are summarized in Table 2, revealing an average fracture half-length of approximately 22.13 m and an average poorly-propped fracture half-length of approximately 3.69 m. Moreover, the average reservoir permeability is estimated to be around 0.37 mD. These interpretation findings provide valuable insights into reservoir behavior and well performance, facilitating informed decision-making in reservoir management and production optimization strategies.

Figure 8

Figure 8. Wellbore structure description of Well P1.

Table 1

Table 1. The reservoir and Well P1 parameters.

Figure 9

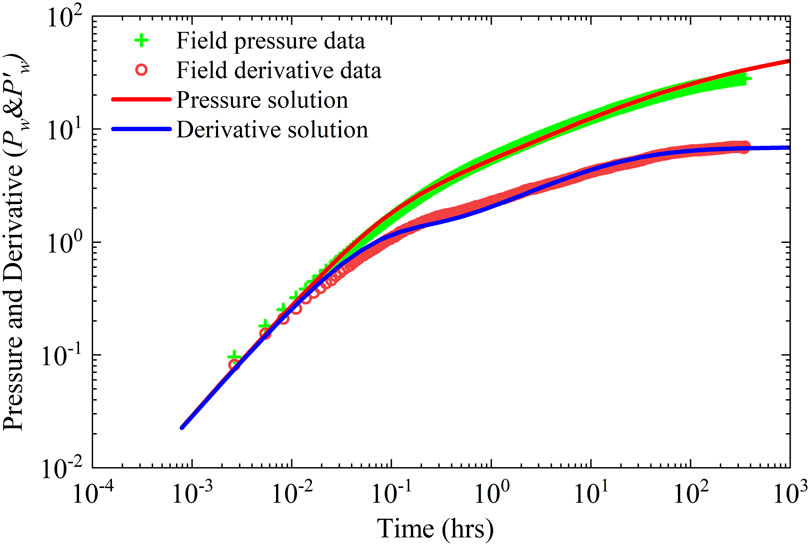
Figure 9. The application of the proposed solution on well test interpretation of Xinjiang oilfield.

Table 2

Table 2. The interpretations results of Well P1.

5 Summary and conclusion

We presented the semi-analytical solution for vertically fractured well with changing fracture conductivity in infinite multilayered reservoir. We presented details of model development, validation, sensitivity analysis and a case study. The developed model could also be extended to other multilayered reservoirs (e.g., carbonate reservoirs) with slightly changed. The proposed model can make a reasonable explanation for the actual well test data of fracture variable conductivity in multi-layer fractured wells, and obtain more reservoir and fracture parameters, which has guiding value for the development of multi-layer reservoirs. The following conclusions can be drawn from this work.

• Boundary element method is used to discretize the hydraulic fracture for obtaining the semi-analytical solution of fractured well with changing conductivity in multilayered reservoirs. The shortcoming is more calculation time demanding due to the fracture discretization.

• The poorly-propped fracture conductivity affects the lasting time of bilinear flow. The bilinear flow lasts longer with a smaller poorly-propped fracture conductivity. The effect of poorly-propped fracture conductivity becomes nil after the linear flow.

• The heterogeneity due to the change in transmissibility, storativity factor, fracture extension, or fracture conductivity among the layers leads to an increase in pressure drop and derivative. The stronger the heterogeneity is, the more the pressure drop and derivative increase. Moreover, the fracture extension and conductivity have more obvious effects than the remains.

• The recorded pressure buildup data from a four-layer vertically fractured well in Xinjiang oilfield is interpreted, indicating that the proposed semi-analytical model is feasibility and practicability to interpret the real field cases for obtaining the reservoir parameters.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YZ: Writing–original draft. WW: Conceptualization, Methodology, Writing–review and editing. DM: Methodology, Validation, Investigation, Writing–review and editing. YX: Methodology, Project administration, Validation, Resources, Writing–review and editing. NW: Investigation, Software, Writing–review and editing. SC: Funding acquisition, Methodology, Writing–review and editing. CW: Funding acquisition, Resources, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors would like to acknowledge the financial support from the Postdoctoral Fellowship Program of CPSF under Grant Number GZC20232200 and The National Natural Science Fund of China (No.11872073).

Conflict of interest

Authors YZ, WW, DM, YX, and NW were employed by Xinjiang Oilfield Company, PetroChina.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1417487/full#supplementary-material

References

Ali, T., Cheng, Y., McVay, D. A., and Lee, W. J. (2010). A practical approach for production data analysis of multilayer commingled tight gas wells. Morgantown, West Virginia, USA: Presented at the SPE Eastern Regional Meeting. doi:10.2118/138882-MS

CrossRef Full Text | Google Scholar

Al-Kabbawi, F. A. (2022). The optimal semi-analytical modeling for the infinite-conductivity horizontal well performance under rectangular bounded reservoir based on a new instantaneous source function. Petroleum 10, 68–84. doi:10.1016/j.petlm.2022.04.005

CrossRef Full Text | Google Scholar

Bai, W., Cheng, S., Wang, Y., Cai, D., Guo, X., and Guo, Q. (2024). A transient production prediction method for tight condensate gas wells with multiphase. Flow. Pet. Explor. Dev 51 (05), 172–179. doi:10.1016/S1876-3804(24)60014-5

CrossRef Full Text | Google Scholar

Bennett, C. O., Reynolds, A. C., and Raghavan, R. (1985). Approximate solutions for fractured wells producing layered reservoirs. Soc. Petroleum Eng. J. 25 (05), 729–742. doi:10.2118/11599-pa

CrossRef Full Text | Google Scholar

Chao, G., Jones, J. R., Raghavan, R., and Lee, W. J. (1994). Responses of commingled systems with mixed inner and outer boundary conditions using derivatives. SPE Form. Eval. 9 (04), 264–271. doi:10.2118/22681-pa

CrossRef Full Text | Google Scholar

Cinco-Ley, H., and Meng, H. Z. (1988). Pressure transient analysis of wells with finite conductivity vertical fractures in double porosity reservoirs. Present. at SPE Annu. Tech. Conf. Exhib. Houst. doi:10.2118/18172-MS

CrossRef Full Text | Google Scholar

Cinco-Ley, H., Samaniego, V. F., and Dominguez, N. (1978). Transient pressure analysis for a well with finite conductivity fracture. Soc. Pet. Eng. AIME J., 253–264. doi:10.2118/6014-PA

CrossRef Full Text | Google Scholar

Dejam, M., Hassanzadeh, H., and Chen, Z. (2018). Semi-analytical solution for pressure transient analysis of a hydraulically fractured vertical well in a bounded dual-porosity reservoir. J. hydrology 565, 289–301. doi:10.1016/j.jhydrol.2018.08.020

CrossRef Full Text | Google Scholar

Gonzalez Chavez, M. A., and Cinco-Ley, H. (2006). Effect of pressure in a well with a vertical fracture with variable conductivity and skin fracture. Present. at Int. Oil Conf. Exhib. Mexico. doi:10.2118/104004-MS

CrossRef Full Text | Google Scholar

Gringarten, A. C., and Ramey, H. J. (1973). The use of source and Green’s functions in solving unsteady-flow problems in reservoirs. Soc. Pet. Eng. J. 13 (5), 285–296. doi:10.2118/3818-pa

CrossRef Full Text | Google Scholar

Gringarten, A. C., Ramey, H. J., and Raghavan, R. (1974). Unsteady-state pressure distributions created by a well with a single infinite-conductivity vertical fracture. Soc. Pet. Eng. J. 14 (4), 347–360. doi:10.2118/4051-pa

CrossRef Full Text | Google Scholar

Lee, S. T., and Brockenbrough, J. R. (1986). A new approximate analytic solution for finite-conductivity vertical fractures. SPE Form. Eval. 1 (01), 75–88. doi:10.2118/12013-pa

CrossRef Full Text | Google Scholar

Li, J., Zhang, C., Xia, Y., Wang, F., Shi, D., and Cheng, S. (2022). Pressure transient analysis for hydraulically fractured wells with changing conductivity in stratified reservoirs: case study in Xinjiang oilfield. ACS Omega 7 (34), 30313–30320. doi:10.1021/acsomega.2c03573

PubMed Abstract | CrossRef Full Text | Google Scholar

Lolon, E. P., McVay, D. A., and Schubarth, S. K. (2003). “Effect of fracture conductivity on effective fracture length,” in SPE annual technical conference and exhibition.

CrossRef Full Text | Google Scholar

Lu, Y. H., Chen, K. P., Jin, Y., Li, H. D., and Xie, Q. (2022). An approximate analytical solution for transient gas flows in a vertically fractured well of finite fracture conductivity. Petroleum Sci. 19, 3059–3067. doi:10.1016/j.petsci.2022.05.001

CrossRef Full Text | Google Scholar

Luo, L., Cheng, S., and Lee, J. (2020). Characterization of refracture orientation in poorly propped fractured wells by pressure transient analysis: model, pitfall, and application. J. Nat. Gas Sci. Eng. 79, 103332. doi:10.1016/j.jngse.2020.103332

CrossRef Full Text | Google Scholar

Luo, W., and Tang, C. (2015). A semianalytical solution of a vertical fractured well with varying conductivity under non-Darcy-flow condition. SPE J. 20 (05), 1028–1040. SPE-178423-PA. doi:10.2118/178423-pa

CrossRef Full Text | Google Scholar

Manrique, J. F., and Bobby, D. P. (2007). “A unique methodology for evaluation of multifractured wells in stacked-pay reservoirs using commingled production and rate transient analysis,” in Presented at the SPE annual technical conference and exhibition (California, U.S.A: Anaheim). doi:10.2118/110576-MS

CrossRef Full Text | Google Scholar

Mirzaei, M., and Cipolla, C. L. (2012). A workflow for modeling and simulation of hydraulic fractures inunconventional gas reservoirs. Present. at SPE Middle East Unconv. Gas Conf. Exhib. doi:10.2118/153022-MS

CrossRef Full Text | Google Scholar

Muskat, M. (1938). The flow of homogeneous fluids through porous media. Soil Sci. 46 (2), 169. doi:10.1097/00010694-193808000-00008

CrossRef Full Text | Google Scholar

Osman, M. E. (1993a). Transient pressure analysis for wells in multilayered reservoir with finite conductivity fractures. Bahrain: Presented at the Middle East Oil Show. doi:10.2118/25665-MS

CrossRef Full Text | Google Scholar

Osman, M. E. (1993b). Pressure analysis of a fractured well in multilayered reservoirs. J. Petroleum Sci. Eng. 9 (1), 49–66. doi:10.1016/0920-4105(93)90028-d

CrossRef Full Text | Google Scholar

Shi, W., Cheng, J., Liu, Y., Gao, M., Tao, L., Bai, J., et al. (2023). Pressure transient analysis of horizontal wells in multibranched fault-karst carbonate reservoirs: model and application in SHB oilfield. J. Petroleum Sci. Eng. 220, 111167. doi:10.1016/j.petrol.2022.111167

CrossRef Full Text | Google Scholar

Shi, W., Yao, Y., Cheng, S., and Shi, Z. (2020a). Pressure transient analysis of acid fracturing stimulated well in multilayered fractured carbonate reservoirs: a field case in western sichuan basin, China. J. Petroleum Sci. Eng. 184, 106462. doi:10.1016/j.petrol.2019.106462

CrossRef Full Text | Google Scholar

Shi, W., Yao, Y., Cheng, S., Shi, Z., Wang, Y., Zhang, J., et al. (2020b). Pressure transient behavior and flow regimes characteristics of vertical commingled well with vertical combined boundary: a field case in xc gas field of northwest sichuan basin, China. J. Petroleum Sci. Eng. 194, 107481. doi:10.1016/j.petrol.2020.107481

CrossRef Full Text | Google Scholar

Soliman, M. Y. (1986). Design and analysis of a fracture with changing conductivity. J. Can. Petroleum Technol. 25 (05). doi:10.2118/86-05-08

CrossRef Full Text | Google Scholar

Stehfest, H. (1970). Algorithm 368: numerical inversion of Laplace transforms [D5]. Commun. ACM 13 (1), 47–49. doi:10.1145/361953.361969

CrossRef Full Text | Google Scholar

Van Everdingen, A. F. (1953). The skin effect and its influence on the productive capacity of a well. J. petroleum Technol. 5 (06), 171–176. doi:10.2118/203-g

CrossRef Full Text | Google Scholar

Wang, Y., Cheng, S., Zhang, F., Feng, N., Li, L., Shen, X., et al. (2021). Big data technique in the reservoir parameters’ prediction and productivity evaluation: a field case in western south China sea. Gondwana Res. 96, 22–36. doi:10.1016/j.gr.2021.03.015

CrossRef Full Text | Google Scholar

Wanjing, L., and Changfu, T. (2015). A semianalytical solution of a vertical fractured well with varying conductivity under non-Darcy-flow condition. SPE J. 20 (05), 1028–1040. doi:10.2118/178423-pa

CrossRef Full Text | Google Scholar

Wei, C., Cheng, S., Song, J., Shi, D., Shang, R., Zhu, L., et al. (2021a). Pressure transient analysis for wells drilled into vertical beads-on-string caves in fracture-caved carbonate reservoirs: field cases in Shunbei Oilfield. J. Petroleum Sci. Eng. 208, 109280. doi:10.1016/j.petrol.2021.109280

CrossRef Full Text | Google Scholar

Wei, C., Cheng, S., Wang, Y., Shi, W., Li, J., Zhang, J., et al. (2021b). Practical pressure-transient analysis solutions for a well intercepted by finite conductivity vertical fracture in naturally fractured reservoirs. J. Petroleum Sci. Eng. 204, 108768. doi:10.1016/j.petrol.2021.108768

CrossRef Full Text | Google Scholar

Wei, C., Liu, Y., Deng, Y., Cheng, S., and Hassanzadeh, H. (2022b). Analytical well-test model for hydraulicly fractured wells with multiwell interference in double porosity gas reservoirs. J. Nat. Gas Sci. Eng. 103, 104624. doi:10.1016/j.jngse.2022.104624

CrossRef Full Text | Google Scholar

Zhang, J., Cheng, S., Zhu, C., and Luo, L. (2019). A numerical model to evaluate formation properties through pressure-transient analysis with alternate polymer flooding. Adv. Geo-Energy Res. 3 (1), 94–103. doi:10.26804/ager.2019.01.08

CrossRef Full Text | Google Scholar

Nomenclature