Fuzzy sliding mode control with adaptive exponential reaching law for inverters in the photovoltaic microgrid

Photovoltaic inverters are widely utilized in microgrid systems working as the key equipment for converting solar energy into usable electricity. This paper presents a fuzzy sliding mode control (FSMC) method for the photovoltaic inverter in a microgrid. The inverter module uses voltage control to achieve stable AC output voltage. Moreover, to deal with system uncertainty and non-linearity in the photovoltaic inverter, a fuzzy controller was designed to realize real-time adaptation of the gains of the constant term and the reaching term in the sliding mode control law, which serves as a compensating controller for traditional sliding mode control. The gains of the exponential reaching law can be adjusted according to the system state instead of fixed gains, which can effectively reduce the chattering phenomenon and improve the robustness of the photovoltaic microgrid. Finally, the Lyapunov stability theory was used to ensure the stability of the entire control system, achieving a high-performance independent power supply for loads in a microgrid. Simulation results show that the designed control system is more robust to load disturbances and has superior dynamic performance.

1 Introduction

Distributed generation has the advantages of low investment, environmental friendliness, and high flexibility (Kakran and Chanana, 2018; Wang C. et al., 2020; Wu et al., 2023). These characteristics have led to the rapid expansion of the development of distributed power generation systems, especially the gradual increase in the proportion of renewable energy sources such as solar energy (Kumar and Kumar, 2017; Li et al., 2021; Mahdavi et al., 2024). Microgrid systems composed of photovoltaic power generation systems can achieve a reliable energy supply for local loads (de la Cruz et al., 2024; Habibi et al., 2024). As a key component connecting photovoltaic power generation systems and power supply loads, photovoltaic inverters can convert the direct current output from photovoltaic panels into alternating current that meets relevant standards. Additionally, photovoltaic inverters can control and adjust parameters such as voltage and frequency to ensure stable output of high-quality electrical energy (Venkatramanan and John, 2020; Yazdani et al., 2020; Singh et al., 2023).

Photovoltaic inverters working in the islanded mode can be controlled to ensure stable and reliable output AC voltage, which meets load requirements, and protect the inverter and connected devices from effects of over-voltage or under-voltage by designing appropriate voltage control strategies. Typically, inverters use closed-loop feedback control to monitor the output voltage and adjust it to rapidly track the given voltage commands (Chander and Kumar, 2017; Nithara and Eldho, 2021). Inverter control strategies include proportional integral (PI) control (Errouissi et al., 2017; Hernández-Jacobo et al., 2021), proportional resonant control (PRC) (Errouissi et al., 2017), and repetitive control (Thang et al., 2015; Yang et al., 2018). Although PIC and PRC control structures are simple, their control accuracy and disturbance rejection performance need improvement, making it difficult to achieve ideal voltage tracking control in the presence of system uncertainties. Repetitive control can suppress periodic disturbances; however, embedding external models complicates control system design and leads to decreased dynamic performance.

Sliding mode control defines a sliding surface to guide the system’s state onto it and applies a control law to achieve stable control of the system, exhibiting strong robustness and disturbance rejection against uncertainties and disturbances. It has extensive applications, particularly in dealing with uncertain complex nonlinear systems and photovoltaic inverter systems (Rezkallah et al., 2015; Chen et al., 2019; Ortega et al., 2019). The sliding mode control method based on the exponential reaching law further improves this technology (Fallaha et al., 2011; Wang and Wei, 2019). By applying a fixed control law, this method can more rapidly guide the system state onto the sliding surface, thereby achieving faster system response and stronger robustness. However, the trade-off between chattering reduction and fast reaching time must be considered, and the inherent chattering phenomenon in sliding mode control limits its practical engineering applications. To address this issue, Wang and Wei (2019) proposed a various exponential reaching law to solve the chattering problem and improve the control performance for the permanent magnet synchronous motor drive system. Han et al. (2020) developed an adaptive reaching law to adjust the sliding mode control law and avoid the undesired chattering phenomenon for a class of second-order nonlinear systems. Jeeranantasin and Nungam (2022) proposed an exponential rate-reaching law with an adaptation gain to reduce chattering in a three-phase AC/DC power converter. However, those methods adjust the controller by analyzing different operating states of the system and selecting different reaching law gains, but this approach suffers from poor generality.

Fuzzy control serves as a versatile approximation, leveraging IF–THEN rules designed through expert experience to approximate unknown variables (Huynh et al., 2020; Nguyen et al., 2021). Fuzzy logic inherently abstracts specific models, thereby enabling fuzzy control to mitigate the improper selection of disturbance ranges and its impact on system responsiveness. A fuzzy controller was designed in this paper to adapt the gains of the constant term and the reaching term of the exponential reaching law in real-time. The gains can be adjusted according to the system state, which can avoid a fixed larger-parameter design. Thereby, it can effectively reduce the chattering phenomenon and improve the robustness of the photovoltaic microgrid.

The main objective of this paper is to design a fuzzy sliding mode control (FSMC) strategy based on the adaptive exponential reaching law to reduce the chattering phenomenon in photovoltaic inverter systems and improve the robustness of the inverter against system uncertainties. The innovativeness of this study is summarized as follows.

1) A mathematical model of three-phase inverters considering the uncertainties of photovoltaic systems is established in the αβ coordinate system, avoiding system coupling in the dq coordinate system and simplifying the design and debugging process of the control system.

2) An FSMC system framework based on the exponential reaching law is designed. To reduce the chattering phenomenon in the system, this article designs a fuzzy controller to achieve adaptive updating of the constant-term gain and reaching-term gain in the exponential reaching law, enabling online updating of the controller gain according to the real-time operating status of the system. Compared with the exponential reaching law with fixed control gain, the proposed FSMC strategy in this paper exhibits better robustness to system uncertainties.

3) The stability of the designed control system is guaranteed by using the Lyapunov stability theory, ensuring the safe and stable operation of the photovoltaic inverter under the proposed control strategy in this study.

The rest of this paper is organized as follows. The dynamic model of the photovoltaic inverter is established in Section 2. Section 3 describes the design process of the proposed FSMC with the adaptive exponential reaching law. Simulation studies of the proposed FSMC strategy are described in Section 4. Finally, some conclusions are summarized.

2 Dynamic model of the photovoltaic inverter

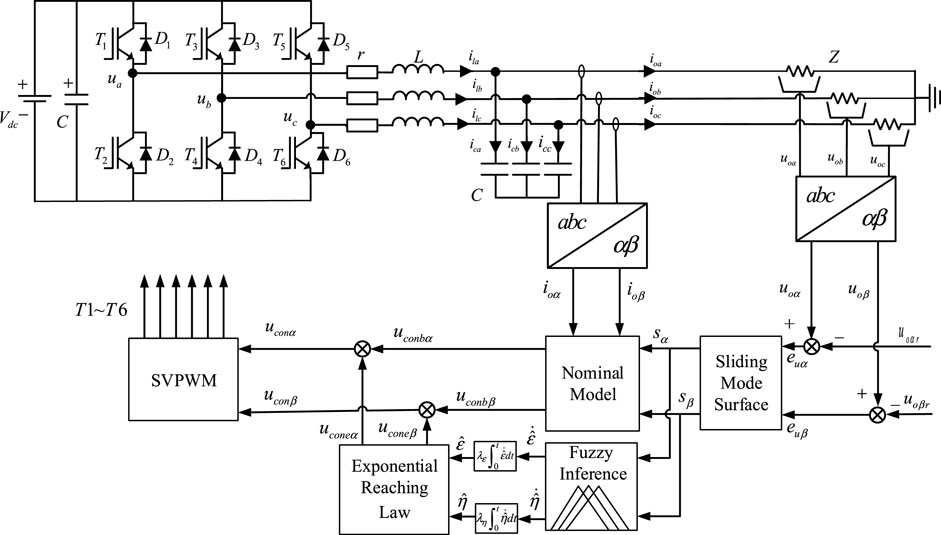
The structure diagram of the three-phase voltage–source inverter used in this article is shown in Figure 1, where V_dc represents the DC bus voltage from the front-stage photovoltaic power generation system; the inverter unit adopts a three-phase bridge structure, with IGBT (T₁∼T₆) as the switching device equipped with freewheeling diodes (D₁–D₆); the filter unit uses an LC filter, r is the equivalent resistance of the inductor L; and Z represents the equivalent load impedance; i_la, i_lb, and i_lc are the currents of the filter-inductor; i_ca, i_cb, and i_cc are the currents of the filter-capacitor; i_ca, i_cb, and i_cc are the currents of the filter-capacitor; and i_oa, i_ob, and i_oc are the currents of the loads.

Figure 1

Figure 1. Diagram of the main circuit structure of the photovoltaic inverter.

The mathematical model of the three-phase inverter in the αβ coordinate system is expressed as follows:

$\begin{array}{l}\left[\begin{array}{l}{\ddot{u}}_{o\alpha }\\ {\ddot{u}}_{o\beta }\end{array}\right]=\left[\begin{array}{l}\frac{K_{\text{PWM}}}{LC}0\\ 0\frac{K_{\text{PWM}}}{LC}\end{array}\right]\left[\begin{array}{l}{u}_{con\alpha }\\ u_{con\beta }\end{array}\right]+\left[\begin{array}{l}-\frac{r}{L}0\\ 0-\frac{r}{L}\end{array}\right]\left[\begin{array}{l}{\dot{u}}_{o\alpha }\\ {\dot{u}}_{o\beta }\end{array}\right]+\left[\begin{array}{l}-\frac{1}{LC}0\\ 0-\frac{1}{LC}\end{array}\right]\left[\begin{array}{l}{u}_{o\alpha }\\ u_{o\beta }\end{array}\right]\\ +\left[\begin{array}{l}-\frac{1}{C}0\\ 0-\frac{1}{C}\end{array}\right]\left[\begin{array}{l}{\dot{i}}_{o\alpha }\\ {\dot{i}}_{o\beta }\end{array}\right]+\left[\begin{array}{l}-\frac{r}{LC}0\\ 0-\frac{r}{LC}\end{array}\right]\left[\begin{array}{l}{i}_{o\alpha }\\ i_{o\beta }\end{array}\right]\end{array},(1)$

where $u_{o\alpha }$, $u_{o\beta }$, $i_{o\alpha }$, and $i_{o\beta }$ are the output voltage and current of the inverter in the $\alpha \beta$ stationary coordinate system; $K_{PWM}=V_{dc}/V_{tri}$ is the equivalent gain of the inverter, in which $V_{tri}$ is the amplitude of the high-frequency triangular carrier signal; $u_{con\alpha }$ and $u_{con\beta }$ are the output voltages, working as the modulation signal.

Choosing the output voltage ($u_{o\alpha }$, $u_{o\beta }$) as the system state and the inverter output voltage ($u_{con\alpha },u_{con\beta }$) as the control input, considering the impact of uncertainties such as circuit parameter variations, DC bus voltage fluctuations, and load disturbances, Eq. 1 can be rewritten as

$\begin{array}{l}{\ddot{u}}_o={\mathit{A}}_{p1}{\dot{\mathit{u}}}_o+{\mathit{A}}_{p2}{\mathit{u}}_o+{\mathit{B}}_p{\mathit{u}}_{con}+{\mathit{C}}_{p1}{\dot{\mathit{i}}}_o+{\mathit{C}}_{p2}{\mathit{i}}_o\\ ={\mathit{A}}_{p1n}{\dot{\mathit{u}}}_o+{\mathit{A}}_{p2n}{\mathit{u}}_o+{\mathit{B}}_{pn}{\mathit{u}}_{con}+{\mathit{C}}_{p1n}{\dot{\mathit{i}}}_o+{\mathit{C}}_{p2n}{\mathit{i}}_o+{\mathit{d}}_p\end{array},(2)$

where ${\mathit{d}}_p\left(t\right)$ in Eq. 2 is defined as the lumped uncertainty vector, which can be expressed as

${\mathit{d}}_p\left(t\right)=\Delta {\mathit{A}}_{p1}{\dot{\mathit{u}}}_o+\Delta {\mathit{A}}_{p2n}{\mathit{u}}_o+\Delta {\mathit{B}}_p{\mathit{u}}_{con}+\Delta {\mathit{C}}_{p1}{\dot{\mathit{i}}}_o+\Delta {\mathit{C}}_{p2}{\mathit{i}}_o,(3)$

where ${\mathit{u}}_o={\left[u_{o\alpha }{u}_{o\beta }\right]}^T$, ${\mathit{u}}_{con}={\left[u_{con\alpha }{u}_{con\beta }\right]}^T$, $\mathit{i}={\left[i_{o\alpha }{i}_{o\beta }\right]}^T$, ${\mathit{A}}_{p1}=diag\left(-r/L,-r/L\right)$, ${\mathit{A}}_{p2}=diag\left(-1/\left(LC\right),-1/\left(LC\right)\right)$, ${\mathit{B}}_p=diag\left(K_{PWM}/\left(LC\right),K_{PWM}/\left(LC\right)\right)$, ${\mathit{C}}_{p1}=diag\left(-1/C,-1/C\right)$, and ${\mathit{C}}_{p2}=diag\left(-r/\left(LC\right),-r/\left(LC\right)\right)$; A_p1n, ,A_p2n, B_pn, C_p1n, and C_p2n are the nominal values of A_p1, A_p2, B_p, C_p1, and C_p2, respectively; △A_p1, △A_p2, △B_p, △C_p1, and △C_p2 denote the parameter variations in the inverter.

Assuming the disturbance term ${\mathit{d}}_p\left(t\right)$ is a bounded vector, with an upper bound of

${‖{\mathit{d}}_p\left(t\right)‖}_1\le \rho ,(4)$

where ${‖\cdot ‖}_1$ represents the one norm operator and $\rho$ is a given positive constant.

3 Fuzzy sliding mode control design

3.1 Sliding mode control design with the exponential reaching law

Define the voltage tracking–error vector as

${\mathit{e}}_u={\mathit{u}}_o-{\mathit{u}}_{or},(5)$

where ${\mathit{u}}_{or}={\left[u_{or\alpha }{u}_{or\beta }\right]}^T$ is the given voltage command vector.

Then, a sliding surface vector is designed as

$\mathit{s}={\dot{\mathit{e}}}_u+k_s{\mathit{e}}_u,(6)$

where k_s is the designed positive constants.

By substituting (1) and (5) into the differential of (8) with respect to time, one can get

$\begin{array}{c}\dot{\mathit{s}}={\ddot{\mathit{e}}}_u+k_s{\dot{\mathit{e}}}_u\\ =({\mathit{A}}_{p1n}{\dot{\mathit{u}}}_o+{\mathit{A}}_{p2n}{\mathit{u}}_o+{\mathit{B}}_{pn}{\mathit{u}}_{con}\\ +{\mathit{C}}_{p1n}{\dot{\mathit{i}}}_o+{\mathit{C}}_{p2n}{\mathit{i}}_o+{\mathit{d}}_p-{\ddot{\mathit{u}}}_{or})+k_s{\dot{\mathit{e}}}_u\end{array}.(7)$

Moreover, design the exponential convergence law as

$\dot{\mathit{s}}=-\epsilon \text{sgn}\left(\mathit{s}\right)-\eta \mathit{s},(8)$

where $\epsilon$ and $\eta$ are designed positive constants.

Design the control law as

$\begin{array}{l}{\mathit{u}}_{con}={\mathit{u}}_{conb}+{\mathit{u}}_{cone}\\ {\mathit{u}}_{conb}={{\mathit{B}}_{pn}}^{-1}\left[{\ddot{\mathit{u}}}_{or}-\left({\mathit{A}}_{p1n}{\dot{\mathit{u}}}_o+{\mathit{A}}_{p2n}{\mathit{u}}_o+{\mathit{C}}_{p1n}{\dot{\mathit{i}}}_o+{\mathit{C}}_{p2n}{\mathit{i}}_o\right)\right],\\ {\mathit{u}}_{cone}=-k_s{\dot{\mathit{e}}}_u-\epsilon \text{sgn}\left(\mathit{s}\right)-\eta \mathit{s}\end{array}(9)$

where u_conb is the control law related to the nominal model and u_cone is the exponential reaching law.

Theorem: If the photovoltaic inverter shown in (2) is controlled by the designed SMC control with the exponential reaching law shown as (9), then the stability of the control system for the voltage control of the photovoltaic inverter will be guaranteed.

Proof: Choosing a Lyapunov function candidate as $V_1=\frac{1}{2}{\mathit{s}}^T\mathit{s}$, then its derivative can be obtained as

$\begin{array}{c}{\dot{V}}_1={\mathit{s}}^T\dot{\mathit{s}}\\ ={\mathit{s}}^T{{\mathit{B}}_{pn}}^{-1}\left[-\epsilon \text{sgn}\left(\mathit{s}\right)-\eta \mathit{s}+{\mathit{d}}_p\right]\\ \le -{{\mathit{B}}_{pn}}^{-1}\eta {\mathit{s}}^T\mathit{s}-{‖{\mathit{s}}^T{{\mathit{B}}_{pn}}^{-1}‖}_1\left(\epsilon -{‖{\mathit{d}}_p‖}_1\right)\\ \le 0\end{array}.(10)$

As long as the condition of $\epsilon >{‖{\mathit{d}}_p‖}_1$ holds, ${\dot{V}}_1\le 0$ in (10) can be guaranteed, which means that $\mathit{s}\left(t\right)$ is a bounded function. It can be concluded that the sliding surface vector s(t) will converge to 0 as $t\to \infty$, according to the Lyapunov stability theory and the Barbalat’s lemma (Astrom and Wittenmark, 1995). The conditions for the existence of the sliding mode hold that once the system reaches the sliding surface, it will remain on the sliding surface.

Exponential reaching law-based sliding mode control requires knowledge of the range of unknown disturbances when facing them. Often, to ensure a rapid entry of the system state into the sliding mode, larger reaching gains are determined based on the disturbance range. However, when the error converges sufficiently, a large reaching gain can easily cause the chattering phenomenon.

3.2 Fuzzy sliding mode control design

By taking the existence conditions ($\dot{V}={\mathit{s}}^T\dot{\mathit{s}}$) of the sliding mode as input and choosing $\dot{\widehat{\eta }}$ and $\dot{\widehat{\epsilon }}$ as outputs of the fuzzy controller, designing fuzzy logic allows for appropriate adjustments of the constant term ($\widehat{\eta }\mathit{s}$) and reaching gain ($\widehat{\epsilon }\text{sgn}\left(\mathit{s}\right)$) in the sliding mode control law shown in Eq. 9 to follow changes in motion states. A fuzzy sliding mode control (AFSMC) with the adaptive exponential reaching law is designed in this section to improve the robustness ability against system uncertainties and alleviate chattering caused by switching and improves the robustness of the control system.

First, fuzzify the input variables, with the assumption of $\dot{V}\in \left[x_l,x_h\right]$, and select discrete quantities as follows:

${\alpha }_{\dot{V}}=k\cdot \left(\dot{V}-\frac{x_h-x_l}{2}\right),(11)$

where $k=2n/\left(x_u-x_l\right),$ in which x_l and x_h represent the lower bound and upper bound of the physical domain, respectively, and n represents the scale of the fuzzy domain. To mitigate the issue of slow controller response caused by excessive computational burden, the value of n = 3 is selected in this paper.

The fuzzy domain of the input variable can be defined as

$F_{\dot{V}}=\left\{-3,-2,-1,0,1,2,3\right\}.(12)$

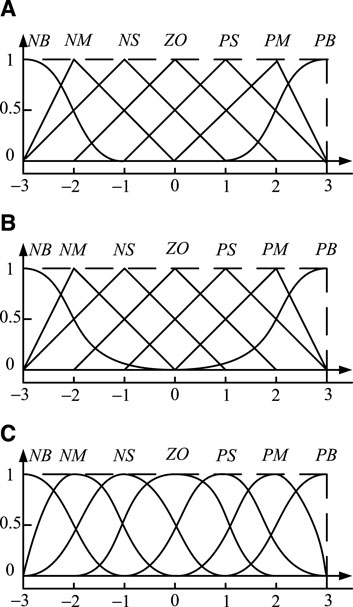
Fuzzy sets $F_{\dot{V}}$ can be assigned values based on experience as

$N_{\dot{V}}=\left\{\begin{array}{c}NB\left(\begin{array}{ccccccc}1& 0.5& 0& 0& 0& 0& 0\end{array}\right)\\ NM\left(\begin{array}{ccccccc}0& 1& 0.5& 0& 0& 0& 0\end{array}\right)\\ NS\left(\begin{array}{ccccccc}0& 0.5& 1& 0.5& 0& 0& 0\end{array}\right)\\ ZO\left(\begin{array}{ccccccc}0& 0& 0.5& 1& 0.5& 0& 0\end{array}\right)\\ PS\left(\begin{array}{ccccccc}0& 0& 0& 0.5& 1& 0.5& 0\end{array}\right)\\ PM\left(\begin{array}{ccccccc}0& 0& 0& 0& 0.5& 1& 0\end{array}\right)\\ PB=\left(\begin{array}{ccccccc}0& 0& 0& 0& 0& 0.5& 1\end{array}\right)\end{array}\right.,(13)$

where NB is negative large, NM is negative middle, NS is negative small, ZO is zero, PS is positive small, PM is positive middle, and PB is positive large.

The outputs ($\dot{\widehat{\epsilon }}$ and $\dot{\widehat{\eta }}$ ) in the fuzzy domain of the fuzzy controller are expressed as follows:

$N_{\epsilon }=\left\{\begin{array}{c}NB\left(\begin{array}{ccccccc}1& 0.5& 0.2& 0& 0& 0& 0\end{array}\right)\\ NM\left(\begin{array}{ccccccc}0& 1& 0.5& 0& 0& 0& 0\end{array}\right)\\ NS\left(\begin{array}{ccccccc}0& 0.5& 1& 0.5& 0& 0& 0\end{array}\right)\\ ZO\left(\begin{array}{ccccccc}0& 0& 0.5& 1& 0.5& 0& 0\end{array}\right)\\ PS\left(\begin{array}{ccccccc}0& 0& 0& 0.5& 1& 0.5& 0\end{array}\right)\\ PM\left(\begin{array}{ccccccc}0& 0& 0& 0& 0.5& 1& 0\end{array}\right)\\ PB\left(\begin{array}{ccccccc}0& 0& 0& 0& 0.2& 0.5& 1\end{array}\right)\end{array}\right.,(14)$

$N_{\eta }=\left\{\begin{array}{c}NB\left(\begin{array}{ccccccc}1& 0.45& 0.2& 0& 0& 0& 0\end{array}\right)\\ NM\left(\begin{array}{ccccccc}0& 1& 0.5& 0& 0& 0& 0\end{array}\right)\\ NS\left(\begin{array}{ccccccc}0& 0.45& 1& 0.5& 0& 0& 0\end{array}\right)\\ ZO\left(\begin{array}{ccccccc}0& 0& 0.5& 1& 0.5& 0& 0\end{array}\right)\\ PS\left(\begin{array}{ccccccc}0& 0& 0& 0.5& 1& 0.45& 0\end{array}\right)\\ PM\left(\begin{array}{ccccccc}0& 0& 0& 0& 0.5& 1& 0\end{array}\right)\\ PB=\left(\begin{array}{ccccccc}0& 0& 0& 0& 0.2& 0.45& 1\end{array}\right)\end{array}\right..(15)$

The membership function of the input are shown in Figure 2A, and the corresponding membership functions of outputs are shown in Figure 2B,C.

Figure 2

Figure 2. Membership function: (A) $\dot{V}$; (B) $\dot{\widehat{\eta }}$ and (C) $\dot{\widehat{\epsilon }}$.

The fuzzy rule is designed as follows:

$Rule=\left\{\begin{array}{c}R1:if{N}_{\dot{V}}isPBthen{N}_{\epsilon }isPBand{N}_{\eta }isPB\\ R2:if{N}_{\dot{V}}isPMthen{N}_{\epsilon }isPMand{N}_{\eta }isPM\\ R3:if{N}_{\dot{V}}isPSthen{N}_{\epsilon }isPSand{N}_{\eta }isPS\\ R4:if{N}_{\dot{V}}isZOthen{N}_{\epsilon }isZOand{N}_{\eta }isZO\\ R5:if{N}_{\dot{V}}isNSthen{N}_{\epsilon }isNSand{N}_{\eta }isNS\\ R6:if{N}_{\dot{V}}isNMthen{N}_{\epsilon }isNMand{N}_{\eta }isNM\\ R7:if{N}_{\dot{V}}isNBthen{N}_{\epsilon }isNBand{N}_{\eta }isNB\end{array}\right..(16)$

By using the Mamdani fuzzy inference and center-average defuzzification, the outputs of the fuzzy system can be presented as

$\dot{\widehat{\epsilon }}=\frac{{\displaystyle \sum _{i=1}^p}{\varpi }_{\epsilon }\left(i\right)\cdot {\mu }_{\epsilon }\left(i\right)}{{\displaystyle \sum _{i=1}^p}{\mu }_{\epsilon }\left(i\right)},(17)$

$\dot{\widehat{\eta }}=\frac{{\displaystyle \sum _{j=1}^p}{\varpi }_{\eta }\left(j\right)\cdot {\mu }_{\eta }\left(j\right)}{{\displaystyle \sum _{j=1}^p}{\mu }_{\eta }\left(j\right)},(19)$

where p is the number of membership functions, ${\varpi }_{\epsilon }$ and ${\varpi }_{\eta }$ are firing weight, and ${\mu }_{\epsilon }$ and ${\mu }_{\eta }$ are fuzzy basis function vectors.

The gain of constant term and the reaching gain in the sliding mode control law can be designed as

$\widehat{\epsilon }={\lambda }_{\epsilon }{\int }_0^t\dot{\widehat{\epsilon }}dt,(20)$

$\widehat{\eta }={\lambda }_{\eta }{\int }_0^t\dot{\widehat{\eta }}dt.(21)$

Then, the designed fuzzy sliding mode control law can be expressed as

${\mathit{u}}_{con}={{\mathit{B}}_{pn}}^{-1}\left[{\ddot{\mathit{u}}}_{or}-\left({\mathit{A}}_{p1n}{\dot{\mathit{u}}}_o+{\mathit{A}}_{p2n}{\mathit{u}}_o+{\mathit{C}}_{p1n}{\dot{\mathit{i}}}_o+{\mathit{C}}_{p2n}{\mathit{i}}_o\right)-k_s{\dot{\mathit{e}}}_u-\widehat{\epsilon }\text{sgn}\left(\mathit{s}\right)-\widehat{\eta }\mathit{s}\right].(22)$

The control block of the proposed FSMC system for the photovoltaic inverter is shown in Figure 3. In which, the sliding mode surface is designed as Eq. 6. Ignoring the influence of disturbances and considering the nominal parameters, the nominal mode of the inverter is described as. First the control law related to the nominal model (u_conb) can be obtained according to Eq. 9. Moreover, fuzzy inference is designed to adjust the constant term and reaching gain of the exponential reaching law (u_cone). Finally, the proposed fuzzy sliding mode control strategy based on the adaptive exponential reaching law (u_cone) is utilized as the input to generate the switching signals for T1–T6 by the space vector pulse width modulation (SVPWM) method.

Figure 3

Figure 3. Control block of the proposed FSMC system for the photovoltaic inverter.

4 Simulation study

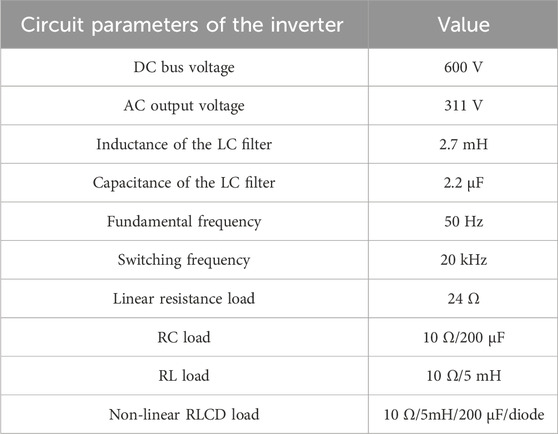
In order to verify the effectiveness and the superiority of the proposed FSMC system for the photovoltaic inverter, steady-state and transient simulation experiments are carried out in MATLAB/Simulink. The detailed parameters of the inverter circuit and the testing loads are described in Table 1.

Table 1

Table 1. Parameters of the inverter circuit and testing loads.

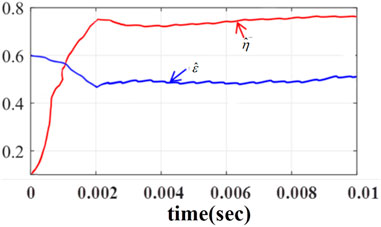
Figure 4 shows the adaptive adjustment of control gain. From Figure 4, it can be observed that, before 0.002 s, the controller rapidly adjusts the gains from the initial state of the system. Under the designed fuzzy controller, the overshoot of the adjustment is small, and it gradually stabilizes after 0.002 s.

Figure 4

Figure 4. Adaptive adjustment of control gain.

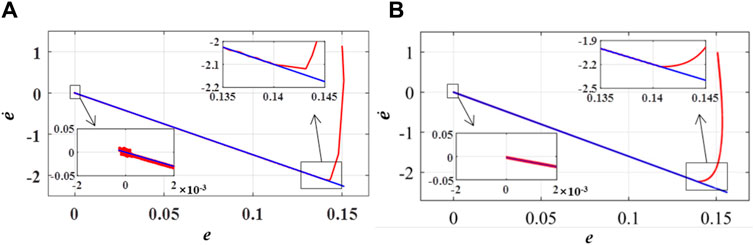
Figure 5 shows the system state trajectory under the SMC and FSMC. By comparing Figure 5A,B from their zoomed-in details, it is evident that the convergence process of the fuzzy sliding mode control is generally smoother compared with the sliding mode control based on the exponential reaching law with fixed gain. Additionally, the chattering phenomenon at the origin is significantly reduced, further demonstrating the effectiveness of the designed fuzzy sliding mode controller.

Figure 5

Figure 5. System state trajectory under the SMC and FSMC: (A) SMC and (B) FSMC.

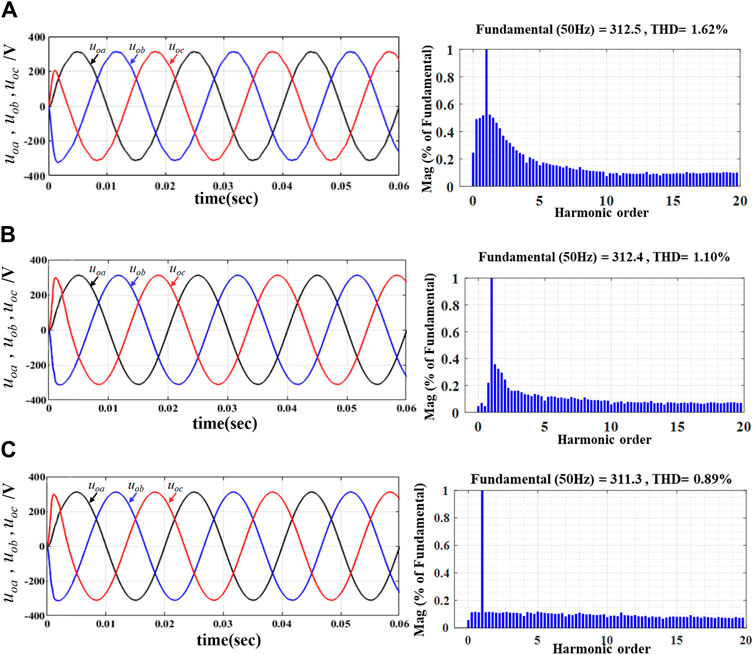
To verify the superiority of the designed FSMC system, comparative simulation experiments were conducted. The simulated results of the three-phase output voltage by PIC, SMC, and the proposed FSMC are depicted in Figure 6, and the corresponding total harmonic analysis is described in Figure 7. Figure 6A shows that under the PIC, the specified voltage command (311 V) is tracked within 0.1 s, and however, there is significant distortion at the peak. According to the THD analysis of the output voltage in Figure 7A, the THD value (1.62%) meets the requirement of less than 5% for resistive loads specified in GB/T 19064-2003. In Figure 6B and Figure 7B, the system has already tracked the reference voltage within 0.01 s with a THD value of 1.10%, demonstrating good speed and stability, which indicates that the output voltage contains fewer harmonic components under the SMC and the quality of the output voltage is superior to that under PIC. Unfortunately, there is slight chattering during the transient process. Furthermore, from Figure 6C and Figure 7C, it can be observed that the response speed of the FSMC is significantly faster than that of the PIC and SMC, with no chattering during transient processes. The THD value (0.89%) of the output voltage is lowest compared with the aforementioned two algorithms, indicating better quality of inverter output power under the proposed FSMC.

Figure 6

Figure 6. Three-phase output voltage and THD analysis with R load: (A) PIC; (B) SMC; (C) FSMC.

Figure 7

Figure 7. Output voltage and current under load variation: (A) PIC; (B) SMC; (C) FSMC.

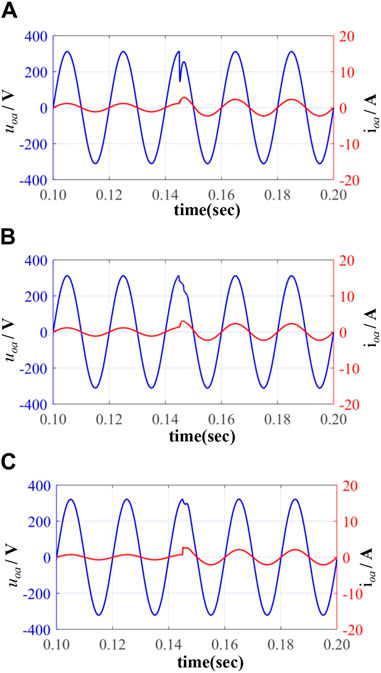
The load disturbance experiments are further conducted to validate the good dynamic performance of the FSMC. The transient simulation results of phase A voltage and current with resistive-load variation from 24Ω to 14Ω are shown in Figure 7. As seen in Figure 7A, under the PIC control, there was an instantaneous voltage drop of approximately 100 V during the upload transition. Compared to the PIC, Figure 7B demonstrates that the phenomenon of voltage drop in the inverter is effectively alleviated under the exponential reaching law sliding mode control. Meanwhile, Figure 7C illustrates the waveform of the inverter’s superior dynamic response with the minimum voltage distortion at the upload transition point under the proposed FSMC. This indicates that the FSMC proposed in this paper can effectively improve the dynamic performance of the inverter and possess superior robustness against load variations.

To validate the capability of the photovoltaic inverter controlled by proposed FSMC powering for different loads, simulation tests were conducted for inductive (RL) loads with a lagging power factor of 0.85, capacitive (RC) loads with a leading power factor of 0.85, and non-linear RLCD loads (specific parameters shown in Table 1). The simulation results are depicted in Figure 8. As shown in Figure 8A, under resistive–inductive load conditions, the tracking absolute error (AE) of the output voltage is 1.12%, and the voltage waveform led the current waveform, with a THD value of 1.91%. In Figure 8B, under capacitive load conditions, the voltage waveform lagged behind the current waveform, with a voltage tracking AE value of 0.84% and a THD value of 1.56%. Figure 8C presents the simulation results for RLCD nonlinear loads. Compared to linear loads, nonlinear loads caused distortion in the output voltage waveform, with a THD value of 2.0%, but still met the requirements of the national standard GB/T 19064-2003.

Figure 8

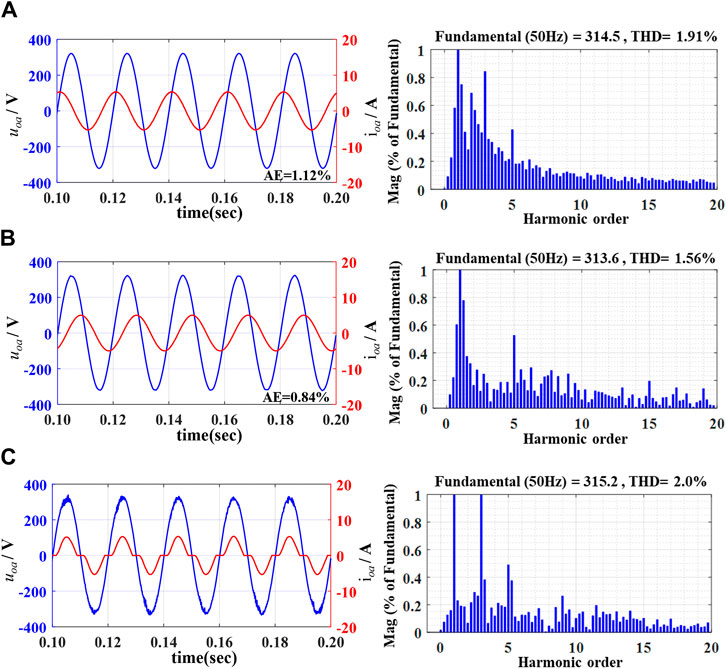
Figure 8. Output voltage and current with different loads and THD analysis by the proposed FSMC: (A) RL load, (B) RC load, and (C) non-linear load.

5 Conclusion

In order to reduce the chattering phenomenon and improve the robustness of the photovoltaic inverter, a fuzzy sliding mode control (FSMC) strategy with adaptive exponential reaching law is proposed in this paper. Based on the dynamic model of the photovoltaic inverter considering system uncertainties, the sliding surface and exponential reaching law are designed first. In addition, by taking the sliding surface vector as the input variable and the estimation value of the gains of the constant term and reaching term as the output variable, a fuzzy controller was designed to realize real-time adaptation of the exponential reaching law. Thereby, the gains of the exponential reaching law can be adjusted according to the system state instead of fixed gains in the proposed FSMC framework. Moreover, the stability of the designed control system is guaranteed by the Lyapunov stability theory. Finally, comparative simulation experiments were conducted among PIC, SMC, and the proposed FSMC. The steady-state and dynamic simulation results demonstrated that the proposed FSMC strategy can supply high-quality output voltage with different loads (resistive, inductive, capacitive, and non-linear loads) and have superior robustness against load variation. The proposed FSMC strategy for the inverter in the photovoltaic microgrid in this study, which exhibits excellent control performance, is of great significance in ensuring the stable operation of photovoltaic inverter systems. Additionally, the proposed FSMC, as an adaptive control method, plays a significant role in handling nonlinearities and load disturbances. Therefore, besides the application in photovoltaic inverter control discussed in this paper, the proposed FSMC strategy also has extensive potential for application in other areas such as power electronic converters and motor drive system control.

The proposed fuzzy sliding mode control strategy based on the adaptive exponential reaching law in this paper effectively reduces the chattering phenomenon in photovoltaic inverter systems and improves the quality of the output electric energy. However, this paper focuses on the controller design for individual photovoltaic inverters. In future research, we will further explore control methods for multiple photovoltaic inverters operating in parallel in microgrids based on virtual synchronous generators (VSGs), aiming to achieve power control for the entire microgrid system and stable control of output voltage and frequency.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

XP: writing–review and editing, funding acquisition, investigation, and supervision. XZ: conceptualization, funding acquisition, methodology, project administration, and writing–original draft. HJ: conceptualization, funding acquisition, supervision, and writing–review and editing. HW: formal analysis, investigation, methodology, and writing–original draft. JL: conceptualization, funding acquisition, supervision, and writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Technology Project from State Grid Shandong Electric Power Corporation “Research and Application of Efficient and Reliable Power Supply Technology for Distributed Photovoltaic Development in County and Urban Areas” (520612220002).

Conflict of interest

Authors XP, XZ, HJ, HW, and JL were employed by Laiwu Power Supply Company of State Grid Shandong Electric Power Corporation.

The authors declare that this study received funding from State Grid Shandong Electric Power Corporation. The funder had the following involvement in the study: study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Astrom, K. J., and Wittenmark, B. (1995) Adaptive control. New York, NY, USA: Addison-Wesley.

Google Scholar

Chander, A. H., and Kumar, L. (2017). “Design of a synchronous reference frame controller for single phase standalone photovoltaic inverter,” in 2017 14th IEEE India Council International Conference (INDICON), Roorkee, India, 15-17 December 2017, 1–6.

CrossRef Full Text | Google Scholar

Chen, Y., Tan, R., Zheng, Y., and Zhou, Z. (2019). Sliding-mode control with multipower approaching law for DC-link voltage of Z-source photovoltaic inverters. IEEE Access 7, 133812–133821. doi:10.1109/access.2019.2941536

CrossRef Full Text | Google Scholar

de la Cruz, J., Wu, Y., Candelo-Becerra, J. E., Vásquez, J. C., and Guerrero, J. M. (2024). Review of networked microgrid protection: architectures, challenges, solutions, and future trends. CSEE J. Power Energy Syst. 10 (2), 448–467. doi:10.17775/CSEEJPES.2022.07980

CrossRef Full Text | Google Scholar

Errouissi, R., Al-Durra, A., and Muyeen, S. M. (2017). Design and implementation of a nonlinear PI predictive controller for a grid-tied photovoltaic inverter. IEEE Trans. Industrial Electron. 64 (2), 1241–1250. doi:10.1109/tie.2016.2618339

CrossRef Full Text | Google Scholar

Fallaha, C. J., Saad, M., Kanaan, H. Y., and Al-Haddad, K. (2011). Sliding-mode robot control with exponential reaching law. IEEE Trans. Industrial Electron. 58 (2), 600–610. doi:10.1109/tie.2010.2045995

CrossRef Full Text | Google Scholar

Habibi, S. I., Sheikhi, M. A., Khalili, T., Abadi, S. A. G. K., Bidram, A., and Guerrero, J. M. (2024). Multiagent-based nonlinear generalized minimum variance control for islanded AC microgrids. IEEE Trans. Power Syst. 39 (1), 316–328. doi:10.1109/tpwrs.2023.3239793

CrossRef Full Text | Google Scholar

Han, H., Wu, X., and Qiao, J. (2020). Design of robust sliding mode control with adaptive reaching law. IEEE Trans. Syst. Man, Cybern. Syst. 50 (11), 4415–4424. doi:10.1109/tsmc.2018.2852626

CrossRef Full Text | Google Scholar

Hernández-Jacobo, C. A., Loera-Palomo, R., Sellschopp-Sánchez, F. S., and Álvarez-Macías, C. (2021). “Stability analysis of a PI controller for a three-phase two-level inverter,” in 2021 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 10-12 November 2021, 1–6.

Google Scholar

Huynh, T.-T., Lin, C. M., Le, T. L., Cho, H. Y., Pham, T. T. T., Le, N. Q. K., et al. (2020). A new self-organizing fuzzy cerebellar model articulation controller for uncertain nonlinear systems using overlapped Gaussian membership functions. IEEE Trans. Industrial Electron. 67 (11), 9671–9682. doi:10.1109/tie.2019.2952790

CrossRef Full Text | Google Scholar

Jeeranantasin, N., and Nungam, S. (2022). Sliding mode control of three-phase AC/DC converters using exponential rate reaching law. J. Syst. Eng. Electron. 33 (1), 210–221. doi:10.23919/jsee.2022.000021

CrossRef Full Text | Google Scholar

Kakran, S., and Chanana, S. (2018). Smart operations of smart grids integrated with distributed generation: a review. Renew. Sust. Energ. Rev. 81, 524–535. doi:10.1016/j.rser.2017.07.045

CrossRef Full Text | Google Scholar

Kumar, L. V. S., and Kumar, G. V. N. (2017). Power conversion in renewable energy systems: a review advances in wind and PV system. Int. J. Energy Res. 41 (2), 182–197. doi:10.1002/er.3601

CrossRef Full Text | Google Scholar

Li, X., Wang, L., Yan, N., and Ma, R. (2021). Cooperative dispatch of distributed energy storage in distribution network with PV generation systems. IEEE Trans. Appl. Supercond. 31 (8), 1–4. doi:10.1109/tasc.2021.3117750

CrossRef Full Text | Google Scholar

Mahdavi, M., Jurado, F., Schmitt, K., and Chamana, M. (2024). Electricity generation from cow manure compared to wind and photovoltaic electric power considering load uncertainty and renewable generation variability. IEEE Trans. Industry Appl. 60 (2), 3543–3553. doi:10.1109/tia.2023.3330457

CrossRef Full Text | Google Scholar

Nguyen, A. T., Ryu, S.-W., Rehman, A. U., Choi, H. H., and Jung, J.-W. (2021). Improved continuous control set model predictive control for three-phase CVCF inverters: fuzzy logic approach. IEEE Access 9, 75158–75168. doi:10.1109/access.2021.3081718

CrossRef Full Text | Google Scholar

Nithara, P., and Eldho, R. P. (2021). “Comparative analysis of different control strategies in single phase standalone inverter,” in 2021 7th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 19-20 March 2021, 1105–1109.

CrossRef Full Text | Google Scholar

Ortega, R., Carranza, O., Rodríguez, J. J., García, V. H., Sosa, J. C., and Alvarado, J. M. (2019). Development and application of a reconfigurable photovoltaic inverter for operation within a microgrid. IEEE Access 7, 98755–98770. doi:10.1109/access.2019.2929946

CrossRef Full Text | Google Scholar

Rezkallah, M., Hamadi, A., Chandra, A., and Singh, B. (2015). Real-time HIL implementation of sliding mode control for standalone system based on PV array without using dumpload. IEEE Trans. Sustain. Energy 6 (4), 1389–1398. doi:10.1109/tste.2015.2436333

CrossRef Full Text | Google Scholar

Singh, Y., Singh, B., and Mishra, S. (2023). Control strategy for multiple residential solar PV system in distribution network with improved power quality. IEEE Trans. Industry Appl. 59 (3), 3686–3699. doi:10.1109/tia.2023.3244533

CrossRef Full Text | Google Scholar

Thang, T. V., Ahmed, A., Kim, C.-i., and Park, J.-H. (2015). Flexible system architecture of stand-alone PV power generation with energy storage device. IEEE Trans. Energy Convers. 30 (4), 1386–1396. doi:10.1109/tec.2015.2429145

CrossRef Full Text | Google Scholar

Venkatramanan, D., and John, V. A. (2020). A reconfigurable solar photovoltaic grid-tied inverter architecture for enhanced energy access in backup power applications. IEEE Trans. Ind. Electron. 67, 10531–10541. doi:10.1109/tie.2019.2960742

CrossRef Full Text | Google Scholar

Wang, A., and Wei, S. (2019). Sliding mode control for permanent magnet synchronous motor drive based on an improved exponential reaching law. IEEE Access 7, 146866–146875. doi:10.1109/access.2019.2946349

CrossRef Full Text | Google Scholar

Wang, C., Lei, S., Ju, P., Chen, C., Peng, C., and Hou, Y. (2020a). MDP-based distribution network reconfiguration with renewable distributed generation: approximate dynamic programming approach. IEEE Trans. Smart Grid 11 (4), 3620–3631. doi:10.1109/tsg.2019.2963696

CrossRef Full Text | Google Scholar

Wang, R., Wang, S., Gong, Z., Li, M., Zhang, Y., and Huang, M. (2020b). “Design of single-phase photovoltaic inverter based on double closed-loop PI and quasi-PR control,” in 2020 IEEE 2nd International Conference on Architecture, Construction, Environment and Hydraulics (ICACEH), Hsinchu, Taiwan, 25-27 December 2020, 80–82.

CrossRef Full Text | Google Scholar

Wu, Q.-H., Bose, A., Singh, C., Chow, J. H., Mu, G., Sun, Y., et al. (2023). Control and stability of large-scale power system with highly distributed renewable energy generation: viewpoints from six aspects. CSEE J. Power Energy Syst. 9 (1), 8–14.

Google Scholar

Yang, Y., Zhou, K., Wang, H., and Blaabjerg, F. (2018). Analysis and mitigation of dead-time harmonics in the single-phase full-bridge PWM converter with repetitive controllers. IEEE Trans. Industry Appl. 54 (5), 5343–5354. doi:10.1109/tia.2018.2825941

CrossRef Full Text | Google Scholar

Yazdani, S., Ferdowsi, M., Davari, M., and Shamsi, P. (2020). Advanced current-limiting and power-sharing control in a PV-based grid-forming inverter under unbalanced grid conditions. IEEE Trans. Emerg. Sel. Top. Power Electron 8 (2), 1084–1096. doi:10.1109/jestpe.2019.2959006

CrossRef Full Text | Google Scholar