Opinions on fast distributed optimization for large-scale scheduling of heterogeneous flexibility resources

1 Introduction

With the high-proportion integration of distributed energy sources such as renewable energy and energy storage systems, the traditional distribution network has evolved from a passive power supply network to an active network with the bidirectional power flow (Sheng et al., 2021). The operation and scheduling of active distribution networks (ADNs) have undergone great challenges due to intrinsic intermittence and volatility from renewable energy resources (Xiang et al., 2017; Li et al., 2023). This has led to the necessity to fully utilize support and adjust the capability of flexibility resources such as distributed energy storage and electric vehicles for reliable power supply (Xu et al., 2022; Lu et al., 2023). Considering the properties of large quantities, decentralized locations, and diverse stakeholders for heterogeneous flexibility resources, the traditional centralized control strategy faces various challenges in the form of system reliability, mass communication, and information privacy (Hu et al., 2018). Hence, distributed optimization is proposed to purge the globally unified control of distribution networks that would enable the efficient management of flexibility resources through distributed clustering (Zhou B. et al., 2021; Fu et al., 2022; Zhong et al., 2023). However, conventional distributed algorithms have slow convergence properties, owing to the gradient-based update process and communication delays (Zhang et al., 2022), which cannot satisfy the fast real-time scheduling of ADNs. Therefore, this paper focuses on providing insightful perspectives and discussions on the fast distributed optimization for large-scale scheduling of heterogeneous flexibility resources.

The main contributions of this paper are two-fold: (1) a bi-level distributed scheduling model of large-scale heterogeneous flexibility resources is proposed to minimize the overall operational cost of ADNs and promote the accommodation of renewable energy resources and (2) a fast distributed asynchronous optimization method is presented to accelerate the convergence speed for the real-time scheduling of ADNs, and the correctness and superiority of the proposed method are demonstrated by case studies.

2 Distributed scheduling model of large-scale heterogeneous flexibility resources

Optimized scheduling of ADNs needs to take into account potential benefits of different dispatching entities such as distribution networks and diversified flexibility resources for minimizing the overall operational costs while stimulating the incorporation of renewable energy. The objective function aims to minimize the costs associated with purchasing electricity, renewable energy curtailment, and dispatching flexibility resources for the purpose of economy enhancement as follows:

$\min F={\displaystyle \sum _{t=1}^T}\left[{\lambda }_t^{\text{buy}}{P}_t^{\text{buy}}+{\displaystyle \sum _{i\in {\mathrm{\Omega }}_{\text{RES}}}}{\lambda }_{i,t}^{\text{RES}.\text{curt}}{P}_{i,t}^{\text{RES}.\text{curt}}+{\displaystyle \sum _{i\in {\mathrm{\Omega }}_{\text{DR}}}}{\lambda }^{\text{DR}}\left|P_{i,t}^{\mathrm{L}.\mathrm{O}}-P_{i,t}^{\mathrm{L}}\right|+{\displaystyle \sum _{i\in {\mathrm{\Omega }}_{\text{ESS}}}}{\lambda }^{\text{ESS}}\left({\eta }_i^{\mathrm{c}}{P}_{i,t}^{\mathrm{c}}+\frac{P_{i,t}^{\text{dc}}}{{\eta }_i^{\text{dc}}}\right)\right]\Delta t,(1)$

where $T$ denotes the total number of scheduling periods; $\Delta t$ denotes the duration of each scheduling period; ${\lambda }_t^{\text{buy}}$, ${\lambda }^{\text{RES}.\text{curt}}$, ${\lambda }^{\text{DR}}$, and ${\lambda }^{\text{ESS}}$ represent the purchase price of electricity in time period $t$, the cost coefficient for the penalty of renewable energy curtailment, the unit dispatch cost of controllable loads, and the cost coefficient for the charging and discharging of the energy storage system, respectively; ${\mathrm{\Omega }}_{\text{RES}}$, ${\mathrm{\Omega }}_{\text{DR}}$, and ${\mathrm{\Omega }}_{\text{ESS}}$ represent the set of renewable energy, demand response, and energy storage system in ADNs, respectively; $P_t^{\text{buy}}$ denotes the purchased active power from the main grid in time period $t$; $P_{i,t}^{\text{RES}.\text{curt}}$ denotes the renewable energy curtailment at node $i$ in time period $t$; $P_{i,t}^{\mathrm{L}}$ and $P_{i,t}^{\mathrm{L}.\mathrm{O}}$ denote the actual dispatch power and original power of controllable load $i$ in time period $t$, respectively; ${\eta }_i^{\mathrm{c}}$ and ${\eta }_i^{\text{dc}}$ denote the charging and discharging efficiencies of energy storage unit $i$, respectively; and $P_{i,t}^{\mathrm{c}}$ and $P_{i,t}^{\text{dc}}$ denote the charging and discharging power of energy storage unit $i$ in time period $t$, respectively.

A bi-level distributed scheduling strategy is proposed to minimize the overall operational cost of ADNs, which is poised to meet the needs of individual economies and privacy preservation for agents with diverse flexible resources (Cao et al., 2024). At the upper level, the scheduling and control center of ADNs serves as a decision-maker to achieve synergies among multiple flexibility resources via information and energy exchange, thereby maximizing the overall economics of scheduling for distribution networks with high renewables. At the lower level, nodes integrated with controllable flexibility resources achieve autonomous operation through the full utilization of the inherent adjustment capacity. The proposed hierarchical optimization scheduling model can be solved by the alternating direction method of multipliers (ADMM) algorithm, which is a popular and efficient method to deal with distributed optimization problems with stable robustness and convergence (Gao et al., 2020; Qi et al., 2023). The distributed scheduling model of large-scale heterogeneous flexibility resources can be decomposed into the master problem of distribution networks at the upper level and subproblems of controllable flexibility resources at the lower level based on the ADMM, as shown in Figure 1A.

Figure 1

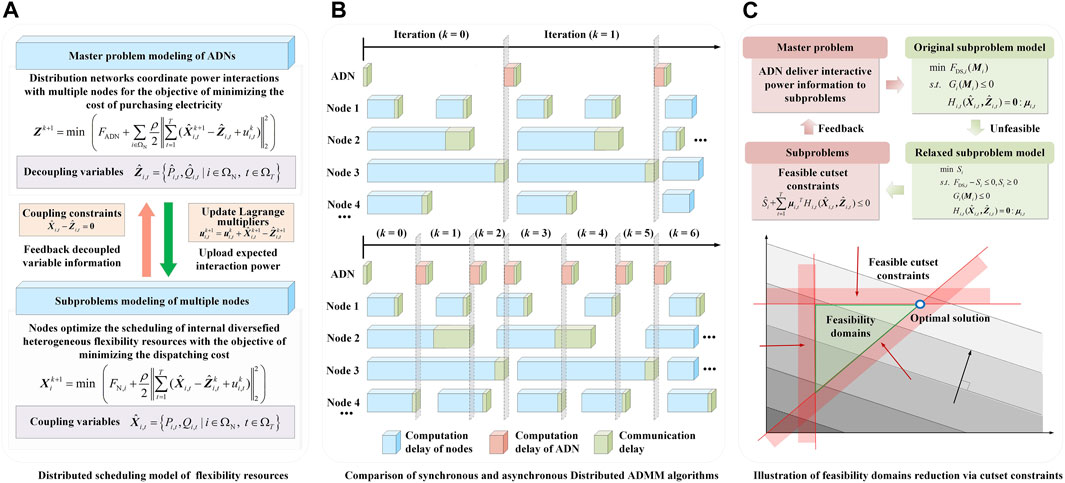
Figure 1. Distributed scheduling model and fast optimization method for active distribution networks (ADNs). (A) Distributed scheduling model of flexibility resources (B) Comparison of synchronous and asynchronous distributed ADMM algorithms (C) Illustration of feasibility domains reduction via cutset constraints.

The objective function can be separated according to the bi-level distributed optimization scheduling strategy as follows:

$F=F_{\text{ADN}}+{\displaystyle \sum _{i\in {\mathrm{\Omega }}_{\mathrm{N}}}}{F}_{\mathrm{N},i},(2)$

$F_{\text{ADN}}={\displaystyle \sum _{t=1}^T}\left({\lambda }_t^{\text{buy}}{P}_t^{\text{buy}}\right)\Delta t,(3)$

$F_{\mathrm{N},i}={\displaystyle \sum _{t=1}^T}\left({\lambda }^{\text{RES}.\text{curt}}{P}_{i,t}^{\text{RES}.\text{curt}}+{\lambda }^{\text{DR}}\left|P_{i,t}^{\text{load}.\mathrm{O}}-P_{i,t}^{\text{load}}\right|+{\lambda }^{\text{ESS}}\left|{\eta }_i^{\mathrm{c}}{P}_{i,t}^{\mathrm{c}}+\frac{P_{i,t}^{\text{dc}}}{{\eta }_i^{\text{dc}}}\right|\right)\Delta t,(4)$

where ${\mathrm{\Omega }}_{\mathrm{N}}$ denotes the set of nodes integrated with flexibility resources; $F_{\text{ADN}}$ is the objective function of the master problem for the ADN; and $F_{\mathrm{N},i}$ is the objective function of subproblem for node $i$. The optimization variables for the master problem mainly comprise the power purchased from or sold to the main grid. The optimization variables for the subproblems include multiple heterogeneous flexibility resources dispatching power, which consist of the energy storage system, photovoltaic generation, wind turbine generation, micro-gas turbine, and demand response resources. Furthermore, there are coupling relationships between the nodes integrated with controllable flexibility resources and ADNs due to their energy interaction. Hence, the power injected to nodes integrated with controllable flexibility resources ${\widehat{\mathit{X}}}_{i,t}=\left\{P_{i,t},Q_{i,t}|i\in {\mathrm{\Omega }}_{\mathrm{N}}\right\}$ is used as coupling variables, and the expected power from the distribution network to nodes ${\widehat{\mathit{Z}}}_{i,t}=\left\{{\widehat{P}}_{i,t},{\widehat{Q}}_{i,t}|i\in {\mathrm{\Omega }}_{\mathrm{N}}\right\}$ is proposed as virtual decoupling variables to establish the consistency coupling constraints as follows (Zhou X. et al., 2021):

${\widehat{\mathit{X}}}_{i,t}-{\widehat{\mathit{Z}}}_{i,t}=\mathbf{0}.(5)$

The variables ${\widehat{\mathit{X}}}_{i,t}$ and ${\widehat{\mathit{Z}}}_{i,t}$ are solved separately at the upper and lower levels, respectively, and the optimization results are delivered iteratively between the two levels to solve the model. A Lagrange penalty function is added to the objective functions of the master problem and subproblems as follows:

${\widehat{\mathit{X}}}_i^{k+1}=\min \left(F_{\mathrm{N},i}+\frac{\rho }{2}{‖{\displaystyle \sum _{t=1}^T}\left({\widehat{\mathit{X}}}_{i,t}-{\widehat{\mathit{Z}}}_{i,t}^k+u_{i,t}^k\right)‖}_2^2\right),(6)$

${\widehat{\mathit{Z}}}^{k+1}=\min \left(F_{\text{ADN}}+{\displaystyle \sum _{i\in {\mathrm{\Omega }}_{\mathrm{N}}}}\frac{\rho }{2}{‖{\displaystyle \sum _{t=1}^T}\left({\widehat{\mathit{X}}}_{i,t}^{k+1}-{\widehat{\mathit{Z}}}_{i,t}+u_{i,t}^k\right)‖}_2^2\right),(7)$

where k denotes the iteration number; $\rho$ is the penalty coefficient; and $u_{i,t}^j$ is the Lagrange multiplier. The proposed distributed scheduling model is solved by optimizing the coupling variables through continuous iterations between the master problem and subproblems. Relevant information about the expected interaction energy for ADNs and nodes integrated with controllable flexibility resources is delivered mutually at the two levels. The Lagrange multipliers will be updated after each iteration step as follows:

${\mathit{u}}_{i,t}^{k+1}={\mathit{u}}_{i,t}^k+{\widehat{\mathit{X}}}_{i,t}^{k+1}-{\widehat{\mathit{Z}}}_{i,t}^{k+1}.(8)$

The primal residual $r^k$ and dual residual $s^k$ are introduced as convergence criteria (Xu et al., 2018), which are calculated after each iteration step as follows:

$r^k={\displaystyle \sum _{i\in {\mathrm{\Omega }}_{\mathrm{N}}}}{‖{\displaystyle \sum _{t=1}^T}\left({\widehat{\mathit{X}}}_{i,t}^k-{\widehat{\mathit{Z}}}_{i,t}^k\right)‖}_2\le {\epsilon }_r,(9)$

$s^k={\displaystyle \sum _{i\in {\mathrm{\Omega }}_{\mathrm{N}}}}\rho {‖{\displaystyle \sum _{t=1}^T}\left({\widehat{\mathit{X}}}_{i,t}^k-{\widehat{\mathit{X}}}_{i,t}^{k-1}\right)‖}_2\le {\epsilon }_{\mathrm{s}},(10)$

where ${\epsilon }_r$ and ${\epsilon }_{\mathrm{s}}$ refer to the convergence threshold for the primal residual and dual residual, respectively. If the convergence criterion is not satisfied, the next iteration will continue with updated Lagrange multipliers along with the latest data on coupling and decoupling variables. Otherwise, the iteration process will be terminated to obtain the optimal scheduling determination of heterogeneous flexibility resources with minimal operational costs for ADNs.

3 Fast distributed asynchronous optimization for real-time scheduling of ADNs

Considering the time-varying nature of communication networks and the varied responsiveness of heterogeneous flexibility resources (Cao et al., 2024), traditional synchronized computation is insufficient to satisfy the fast real-time scheduling of ADNs, owing to the increased communication overhead and limited convergence speed. Specifically, under the synchronous protocol, the optimization model for the master problem is triggered at each iteration only if the scheduling center of ADNs receives the information from all nodes (Zheng et al., 2018). The master problem and computationally fast subproblems will remain idle most of the time, thereby impeding the full utilization of parallel computing resources. Hence, the distributed asynchronous optimization is adopted to improve the convergence efficiency, which allows the master problem to execute the next iterative updates without the reception of complete information from all nodes (Chang et al., 2016), as shown in Figure 1B. Initially, $D_k$ is proposed to denote the index set of nodes from which the scheduling center receives coupling information during iteration k. The variable information of node $i$ is uploaded to the scheduling center if $i\in D_k$. If a node fails to deliver information promptly due to communication delays or slow response speed, the data of the last iteration will be used instead to execute the next optimization updates for the master problem as follows:

${\widehat{\mathit{X}}}_{i,t}^k=\left\{\begin{array}{l}{\widehat{\mathit{X}}}_{i,t}^k,i\in D^k\\ {\widehat{\mathit{X}}}_{i,t}^{k-1},i\notin D^k\end{array}\right..(11)$

Two asynchronous constraints are set in the computation process to guarantee the convergence of the asynchronous optimization algorithm (Chang et al., 2016). On one hand, to ensure the efficacy of each iteration, the master problem proceeds to the next iteration only if the number of nodes in $D_k$ is larger than the set threshold $\kappa \ge 1$. On the other hand, taking into account the hazard of unbounded delays on algorithm convergence (Chang et al., 2016; Bastianello et al., 2021), the inactive iteration of every node, as well as $i\notin D^k$, must be less than the set maximum tolerable delay $\tau$. This means that the coupling variable information per node used by the center must be, at most, τ iterations old (Mohammadi and Kargarian, 2022). The variable $d_i^k$ is introduced to count the delays of node $i$. If $i\in D_k$ at the current iteration k, then $d_i^k$ is set to 0; otherwise, $d_i^k$ is increased by 1 as follows:

$d_i^k=\left\{\begin{array}{l}0,i\in D^k\\ d_i^{k-1}+1,i\notin D^k\end{array}\right..(12)$

When both conditions cannot be satisfied simultaneously, the scheduling center must wait until the updated information from the unusual nodes is received. The master problem and subproblems, with smaller idle time, are frequently updated compared with the synchronous optimization. However, the benefit of the improved update frequency can outweigh the cost of the increased number of iterations, enabling the asynchronous algorithm to converge in the shortest possible time (Bastianello et al., 2021).

In order to further accelerate convergence speed, this paper also proposes a method to curtail the feasibility domains of the master problem (Wu et al., 2018; Hua et al., 2023), as shown in Figure 1C. The feasibility of interactive power information delivered by the master problem is examined during the subproblem of nodes at the lower level. The optimization model of the subproblem for node $i$ can be expressed as follows:

$\begin{array}{l}\min F_{\text{DS},i}\left({\mathit{M}}_i\right)\\ s.t.G_i\left({\mathit{M}}_i\right)\le 0\\ H_{i,t}\left({\widehat{\mathit{X}}}_{i,t},{\widehat{\mathit{Z}}}_{i,t}\right)=\mathbf{0}:{\mathit{\mu }}_{i,t}\end{array},(13)$

where ${\mathit{M}}_i$ denotes the optimization variables for the subproblem of node $i$; $G_i\left({\mathit{M}}_i\right)$ denotes inequality constraints set for the subproblem of node $i$; $H_{i,t}\left({\widehat{\mathit{X}}}_{i,t},{\widehat{\mathit{Z}}}_{i,t}\right)$ denotes the coupling equational constraints of the two levels; and ${\mathit{\mu }}_{i,t}$ denotes the dual multipliers of coupling equational constraints. If the expected interaction power delivered by the scheduling center of the master problem is not feasible for the subproblem of node $i$, the relaxation factor $S_i$ is introduced to transform the subproblem as follows:

$\begin{array}{l}\min S_i\\ s.t.F_{\text{DS},i}-S_i\le 0,S_i\ge 0\\ G_i\left({\mathit{M}}_i\right)\le 0\\ H_{i,t}\left({\widehat{\mathit{X}}}_{i,t},{\widehat{\mathit{Z}}}_{i,t}\right)=\mathbf{0}:{\mathit{\mu }}_{i,t}\end{array}.(14)$

With the optimization solution of the relaxed subproblem, the node $i$ can provide feedback on feasible cutset constraints to the master problem as follows (Wu et al., 2022):

${\widehat{S}}_i+{\displaystyle \sum _{t=1}^T}{{\mathit{\mu }}_{i,t}}^T{H}_{i,t}\left({\widehat{\mathit{X}}}_{i,t},{\widehat{\mathit{Z}}}_{i,t}\right)\le 0,(15)$

where ${\widehat{S}}_i$ denotes the optimal value of the objective function of the relaxed subproblem. Otherwise, no constraints are returned to the master problem if the subproblem is found to be feasible. Therefore, the objective function and constraint conditions are both restricted through the feedback of feasible cutset constraints after feasibility examination. Consequently, an improvement in the convergence speed was observed, owing to a reduction in the feasibility domains of the master problem.

4 Case studies

To validate the effectiveness of the proposed fast distributed optimization method for large-scale scheduling of heterogeneous flexibility resources in this paper, the IEEE33 bus distribution system is used as a specimen for case studies. The quantity of energy storage systems, photovoltaic generation, wind turbine generation, micro-gas turbine, and demand response resources in the distribution system is defined to be 2, 2, 1, 1, and 2, respectively. The proposed model is solved by the centralized algorithm, general synchronous distributed algorithm, and fast distributed asynchronous algorithm, respectively, to verify the preeminence of the presented method through comparative analysis. The comparison between the results of the operational costs for ADNs and convergence properties under different algorithms is shown in Table 1.

Table 1

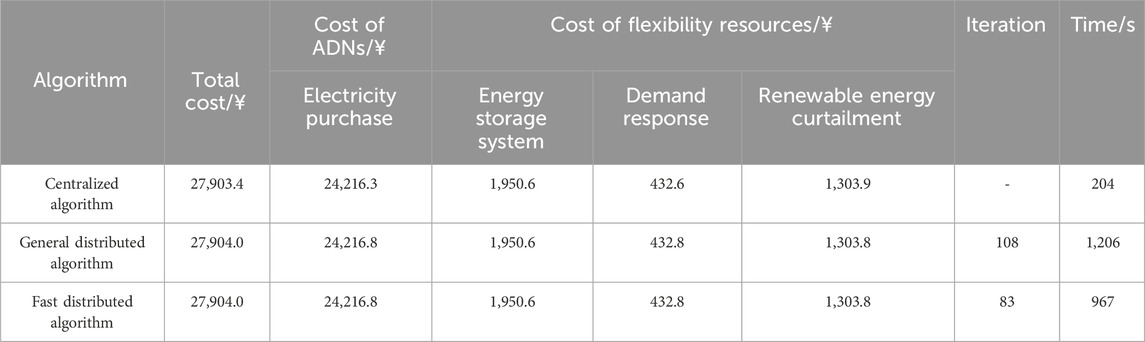
Table 1. Comparison of the operational costs for active distribution networks (ADNs) and convergence properties.

It can be seen that the operational cost results of ADNs obtained by centralized and distributed algorithms are almost the same, proving the correctness of the proposed method in this paper. Since the serial simulation is performed on a single computer, the distributed optimization time shall be the average optimization time of a single node integrated with controllable flexibility resources. Therefore, the average time used for one node by the general synchronous distributed algorithm and fast distributed asynchronous algorithm is 150.75 and 120.875 s, respectively. It shows that the fast asynchronous distributed methods have computational efficiency superior to the centralized and general synchronous distributed algorithms. The model convergence speed can be enhanced by 40.7% and 19.8% through asynchronous iteration and feasibility domain reduction via cutset constraints, respectively.

5 Discussion and conclusion

A fast distributed optimization method for the large-scale scheduling of heterogeneous flexibility resources is presented in the paper. The key conclusions can be summarized as follows: 1) the proposed bi-level distributed scheduling model coordinates multiple heterogeneous flexibility resources to enhance the operational economy of ADNs and facilitate the accommodation of renewable energy resources; 2) compared to the centralized and general synchronous distributed algorithm, the model convergence speed can be enhanced by 40.7% and 19.8%, respectively, through the proposed fast asynchronous distributed optimization method to satisfy the fast real-time scheduling of ADNs; and 3) further research will focus on the distributed economic optimization of ADNs integrated with heterogeneous flexibility resources, considering the uncertainties of renewable energy resources and load demand.

Author contributions

MT: writing–original draft and writing–review and editing. XG: conceptualization, data curation, and writing–review and editing. YL: formal analysis, visualization, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is sponsored by the Guangdong Basic and Applied Basic Research Foundation (2023A1515110105) and the Scientific Research Startup Fund for Shenzhen High-Caliber Personnel of SZPT (No. 6022310042k).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bastianello, N., Carli, R., Schenato, L., and Todescato, M. (2021). Asynchronous distributed optimization over lossy networks via relaxed ADMM: stability and linear convergence. IEEE Trans. Automatic Control 66, 2620–2635. doi:10.1109/TAC.2020.3011358

CrossRef Full Text | Google Scholar

Cao, Y., Zhou, B., Chung, C. Y., Wu, T., Zheng, L., and Shuai, Z. (2024). A coordinated emergency response scheme for electricity and watershed networks considering spatio-temporal heterogeneity and volatility of rainstorm disasters. IEEE Trans. Smart Grid, 1. doi:10.1109/TSG.2024.3362344

CrossRef Full Text | Google Scholar

Chang, T., Hong, M., Liao, W., and Wang, X. (2016). Asynchronous distributed ADMM for large-scale optimization—Part I: algorithm and convergence analysis. IEEE Trans. Signal Process. 64, 3118–3130. doi:10.1109/TSP.2016.2537271

CrossRef Full Text | Google Scholar

Fu, X., Wu, X., Zhang, C., Fan, S., and Liu, N. (2022). Planning of distributed renewable energy systems under uncertainty based on statistical machine learning. Prot. Control Mod. Power Syst. 7, 41. doi:10.1186/s41601-022-00262-x

CrossRef Full Text | Google Scholar

Gao, H., Wang, J., Liu, Y., Wang, L., and Liu, J. (2020). An improved ADMM-based distributed optimal operation model of AC/DC hybrid distribution network considering wind power uncertainties. IEEE Syst. J. 15, 2201–2211. doi:10.1109/JSYST.2020.2994336

CrossRef Full Text | Google Scholar

Hu, J., Cong, H., and Wang, C. (2018). Coordinated scheduling model of power system with active distribution networks based on multi-agent system. J. Mod. Power Syst. Clean Energy 6, 521–531. doi:10.1007/s40565-017-0327-7

CrossRef Full Text | Google Scholar

Hua, Z., Zhou, B., Or, S., Zhang, J., Li, C., and Wei, J. (2023). Robust emergency preparedness planning for resilience enhancement of energy-transportation nexus against extreme rainfalls. IEEE Trans. Industry Appl. 60, 1196–1207. doi:10.1109/TIA.2023.3274615

CrossRef Full Text | Google Scholar

Li, P., Wu, Z., Zhang, C., Xu, Y., Dong, Z., and Hu, M. (2023). Multi-timescale affinely adjustable robust reactive power dispatch of distribution networks integrated with high penetration of PV. J. Mod. Power Syst. Clean Energy 11, 324–334. doi:10.35833/MPCE.2020.000624

CrossRef Full Text | Google Scholar

Lu, Y., Xiang, Y., Huang, Y., Yu, B., Weng, L., and Liu, J. (2023). Deep reinforcement learning based optimal scheduling of active distribution system considering distributed generation, energy storage and flexible load. Energy 271, 127087. doi:10.1016/j.energy.2023.127087

CrossRef Full Text | Google Scholar

Mohammadi, A., and Kargarian, A. (2022). Learning-aided asynchronous ADMM for optimal power flow. IEEE Trans. Power Syst. 37, 1671–1681. doi:10.1109/TPWRS.2021.3120260

CrossRef Full Text | Google Scholar

Qi, J., Ma, D., Li, C., Pan, Y., Zhu, X., and Li, J. (2023). Multilevel optimization of economic dispatching in active distribution network based on ADMM. Front. Energy Res. 10. doi:10.3389/fenrg.2022.1088255

CrossRef Full Text | Google Scholar

Sheng, H., Wang, C., Li, B., Liang, L., Yang, M., and Dong, Y. (2021). Multi-timescale active distribution network scheduling considering demand response and user comprehensive satisfaction. IEEE Trans. Industry Appl. 57, 1995–2005. doi:10.1109/TIA.2021.3057302

CrossRef Full Text | Google Scholar

Wu, C., Gu, W., Zhou, S., and Chen, X. (2022). Coordinated optimal power flow for integrated active distribution network and virtual power plants using decentralized algorithm. IEEE Trans. Power Syst. 36, 3541–3551. doi:10.1109/TPWRS.2021.3049418

CrossRef Full Text | Google Scholar

Wu, Z., Liu, Y., Gu, W., Zhou, J., Li, J., and Liu, P. (2018). Decomposition method for coordinated planning of distributed generation and distribution network. IET Generation, Transm. Distribution 12, 4482–4491. doi:10.1049/iet-gtd.2017.2050

CrossRef Full Text | Google Scholar

Xiang, Y., Han, W., Zhang, J., Liu, J., and Liu, Y. (2017). Optimal sizing of energy storage system in active distribution networks using fourier–legendre series based state of energy function. IEEE Trans. Power Syst. 33, 2313–2315. doi:10.1109/TPWRS.2017.2779042

CrossRef Full Text | Google Scholar

Xu, B., Zhang, G., Li, K., Li, B., Chi, H., Yao, Y., et al. (2022). Publisher Correction: reactive power optimization of a distribution network with high-penetration of wind and solar renewable energy and electric vehicles. Prot. Control Mod. Power Syst. 8, 21. doi:10.1186/s41601-023-00290-1

CrossRef Full Text | Google Scholar

Xu, T., Wu, W., Zheng, W., Sun, H., and Wang, L. (2018). Fully distributed quasi-Newton multi-area dynamic economic dispatch method for active distribution networks. IEEE Trans. Power Syst. 33, 4253–4263. doi:10.1109/TPWRS.2017.2771950

CrossRef Full Text | Google Scholar

Zhang, H., Liang, S., Liang, J., and Han, Y. (2022). Convergence analysis of a distributed gradient algorithm for economic dispatch in smart grids. Int. J. Electr. Power Energy Syst. 134, 107373. doi:10.1016/j.ijepes.2021.107373

CrossRef Full Text | Google Scholar

Zheng, Y., Song, Y., Hill, D., and Zhang, Y. (2018). Multiagent system based microgrid energy management via asynchronous consensus ADMM. IEEE Trans. Energy Convers. 33, 886–888. doi:10.1109/TEC.2018.2799482

CrossRef Full Text | Google Scholar

Zhong, J., Li, Y., Wu, Y., Cao, Y., Li, Z., Peng, Y., et al. (2023). Optimal operation of energy hub: an integrated model combined distributionally robust optimization method with stackelberg game. IEEE Trans. Sustain. Energy 14, 1835–1848. doi:10.1109/TSTE.2023.3252519

CrossRef Full Text | Google Scholar

Zhou, B., Zou, J., Chi, Y., Wang, H., Liu, N., Voropai, N., et al. (2021a). Multi-microgrid energy management systems: architecture, communication, and scheduling strategies. J. Mod. Power Syst. Clean Energy 9, 463–476. doi:10.35833/MPCE.2019.000237

CrossRef Full Text | Google Scholar

Zhou, X., Zou, S., Wang, P., and Ma, Z. (2021b). ADMM-based coordination of electric vehicles in constrained distribution networks considering fast charging and degradation. IEEE Trans. Intelligent Transp. Syst. 22, 565–578. doi:10.1109/TITS.2020.3015122

CrossRef Full Text | Google Scholar