- 1State Grid Shanghai Energy Internet Research Institute Co. Ltd., Shanghai, China
- 2State Grid Shandong Electric Power Company Electric Power Science Research Institute, Jinan, China
As a deep connection between agriculture and energy, the rural integrated energy system (RIES) is a micro-scale supply–distribution–storage–demand network, which provides an important means to realize the utilization of rural clean energy. This paper proposes a day-ahead scheduling model of the RIES to improve its economical effectiveness, where three energy carriers, namely, biogas, electric power, and heat, are integrated. To address the source and load uncertainties composed of photovoltaic power, power load, and heat load, this paper develops a constrained distributionally robust optimization (CDRO), which optimizes the cost expectation related to the extreme distribution to enhance the robustness, while limiting the loss of cost expectation in the historical distribution to ensure economical effectiveness. In addition, an ambiguous set of the source and load uncertainties incorporating 1-norm and infinity-norm constraints is established, which realizes a flexible adjustment for the conservativeness of CDRO. The distributionally robust dispatch is formulated as a deterministic programming in a two-stage solving framework, where the subproblem uploads its extreme probability distribution to the master problem, and these two problems are iteratively optimized until the convergence. Finally, the numerical simulations in a modern farm park prove the performance of the constructed dispatch model and the flexibility of CDRO in balancing the economical effectiveness and robustness of the dispatch.
1 Introduction
To meet the national strategical demand of rural revitalization, clean, low-carbon, and rich-reserve biomass energy is being rapidly developed and utilized in China. It is estimated that in China, by 2030, the installed capacity of biomass plants will reach 52 GW, which can provide more than 330 billion KWh of clean electric power every year (Liang et al., 2024). In addition, the distributed rooftop photovoltaic power generation has also developed into a new trend of rural green development. As a deep connection between agriculture and energy, the rural integrated energy system (RIES) is a micro-scale supply–distribution–storage–demand system, which provides an important means to realize the utilization of rural clean energy. Day-ahead optimal dispatch (Seyednouri et al., 2023) which plays a crucial part in decreasing the operating cost of the RIES and enhancing use of biomass and renewable energies needs more attention.
Recently, many scholars have studied the optimal operation of the RIES. Ma and Fu (2021) studied the coupling principle of agriculture, meteorology, and energy and introduced the advanced applications corresponding to the coupling. Fu et al. (2020) explores the security problems caused by the connection of energy and agriculture and summarizes the security technology to ensure the double security of energy and food. The above research studies conclude the current construction status and development trend of the RIES; however, these research studies have not discussed the technical details for the optimal operation of the RIES. Zhou et al. (2018) established a multi-energy coupling model to clarify the effect of fermentation under external energy injection. Wu et al. (2021) established a novel model for a biogas–solar–wind-based integrated energy system and developed an improved realization of the multitasking paradigm using multiobjective optimization. Yu and Yin (2023) promoted carbon capture technologies for waste power generation in the RIES. Yu et al. (2022) developed a three-participator game mechanism for the RIES considering the interests of the government, farmers, and new energy enterprises to realize optimal and clean operation of the system. However, the aforementioned studies are deterministic optimization that ignores the randomness of photovoltaic power, power, and heat load. The above source and load uncertainties directly influence the intraday power balance, and the dispatch plan obtained from the deterministic dispatch model cannot guarantee the economy of the RIES in intraday operation.
With the deployment of renewable energies, the optimization of integrated energy systems combined with multiple uncertainties has gradually attracted the attention of scholars. Currently, the strategies to cope with uncertainties mainly include stochastic optimization (SO)-based methods and robust optimization (RO)-based methods. SO randomly extracts scenarios with respect to the empirical probability distribution of uncertainty conditions and then establishes the security constraints for each sample scenario and optimizes the operating cost expectation of these sample scenarios (Xu et al., 2017). Jani et al. (2022) adopted the probability distribution function to describe the uncertainty, and the scenario-oriented SO is applied. The scenario-oriented stochastic method is also adopted by Eghbali et al. (2022) to deal with the uncertainty of electric vehicles. However, discrete sample scenarios cannot cover the continuous uncertainty distributions, and it is hard for SO to guarantee secure operation in all scenarios. In addition, the true distribution of the source and load uncertainties does not precisely obey the empirical probability distribution, and, as a result, the robustness of SO under other distributions is affected.
RO models uncertainty conditions using continuously distributed maximum domains and deals with extreme uncertainty conditions using dual theory to ensure the robustness of the dispatch plan. Traditional RO establishes the uncertainty set to formulate the maximum domain of uncertain scenarios and optimizes the operating cost of microgrids under extreme scenarios (Liu et al., 2018; Bolurian et al., 2022; Tan et al., 2022). The widely adopted modeling methods for the uncertainty set include box-based and polyhedron-based sets (Bertsimas et al., 2013). In addition, Zhao et al. (2021) developed an ellipsoid-based uncertainty set to reduce the conservativeness of TRO. Nevertheless, since the probability of extreme scenarios is extremely low, RO is generally very conservative. Compared to RO, the recent widely used distributionally robust optimization (DRO) is less conservative (Zuo et al., 2023). DRO uses the ambiguous set to describe the maximum domain of uncertain probability distributions and minimizes the operating cost expectation under extreme distributions. Siqin (2022) established an ambiguous set for wind and photovoltaic power based on Wasserstein distance and developed a DRO operation of the microgrid considering both power-to-gas and CHP units. Zhang (2022) utilized the multiorder moment information to formulate the ambiguous set of uncertain variables and established a distributionally robust economic operation model for a multi-energy coupled microgrid. Zhai et al. (2022) proposed a DRO-based chance-constrained model for the multi-energy microgrid, and an optimal additional approximation is developed to convert the model to a tractable form. However, the above studies approximate the second-stage decision of microgrids as the affine policy (Qu et al., 2022) to make the DRO tractable; the affine policy restricts the optimization space of recourse actions and significantly affects the economical effectiveness of the dispatch decision. To achieve the optimum, Wei et al. (2016) proposed a dual vertex generation-based two-stage method for adaptive optimization-based distributionally robust optimization, and Zheng et al. (2021) developed an extreme distribution generation-based solution for the complex DRO. However, the solution process of the dual vertex generation-based method or the extreme distribution generation-based method is too complicated, and nonlinear constraints will be generated by the product of uncertain parameters and dual variables.
Recently, a new data-driven DRO method is being developed rapidly, which extracts a certain number of reference samples from the large-scale available historical data and establishes the 1-norm and infinity-norm-based probability density sets to describe the distribution of the uncertainties (Ding et al., 2017). The method has the below advantages: 1) it directly makes full use of the historical observation, rather than the moment information representing the overall performance. 2) The dualization is not required, and thus, the solution procedure is relatively effortless. However, the existing probability density set-based method only focuses on the expected objective under the extreme distribution. The historical distribution generated from the historical observation probably approaches the real distribution of uncertainties, and hence, the cost expectation under the historical distribution deserves more attention. This paper combines the principle of SO and DRO, and the contributions are listed as follows:
1) A novel day-ahead dispatch model of the RIES is established. Three energy carriers, namely, biogas, electric power, and heat, are integrated in the RIES. In addition, the economic operation of the RIES is realized through cooperative regulation of photovoltaic power, biogas generator, heat pump, electric boiler, transferable power load, power, and heat storage, where the diversified regulation resources are modeled accurately.
2) A novel constrained distributionally robust optimization (CDRO) is developed to address source and load uncertainties in the RIES. The principle is to minimize the operating cost expectation in the extreme distribution to enhance the robustness, while further limiting loss of cost expectation in the historical distribution to ensure economical effectiveness. The balance between the robustness and economical effectiveness can be realized through reasonably setting an equilibrium coefficient.
3) A tailored two-stage solution procedure is developed for the proposed distributionally robust dispatch. First, the absolute value constraint in the ambiguous set is convexified. Then, a column and constraint generation (C&CG) method is introduced to solve the convexified problem. The master problem determines the day-ahead decision variables against all known extreme distributions of the probability density. The subproblem receives the obtained decision variables and determines an extreme distribution of the probability density and adds it to the master problem.
The rest of this paper is organized as follows: Section 2 models the distributionally robust day-ahead dispatch of the RIES. Section 3 presents the tailored two-stage solution procedure to solve the dispatch problem. Section 4 describes the numerical simulations and analysis on a modern farm park. Section 5 provides the conclusion of this paper.
2 Distributionally robust day-ahead dispatch of the RIES
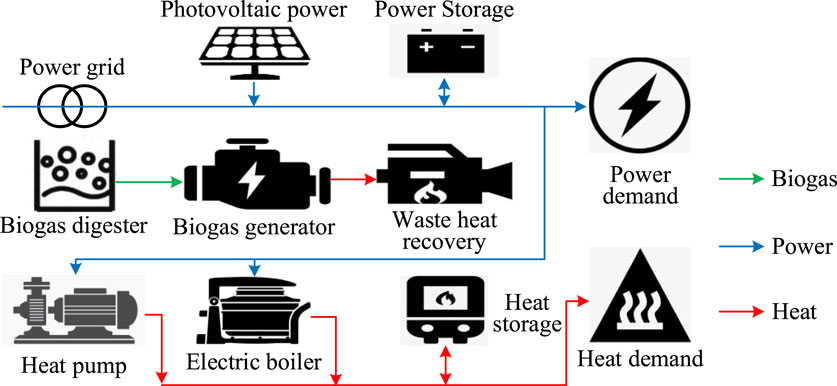
The frame of the constructed RIES is displayed in Figure 1. The energy carrier in the system contains electric power, heat, and biogas. The biogas is generated by the biogas digester and can be stored in the biogas storage. The biogas is fed into the biogas generator to produce electric power and heat. The electric power is produced from the power grid, photovoltaic power, and biogas generator and fed into the heat pump and electric boiler to generate heat, and it can be stored in power storage. The heat is produced by waste heat recovery of the biogas generator and electric boiler and can be stored in heat storage. Finally, the demand of the system includes power load and heat load.
2.1 Day-ahead and intraday operation problem
The distributionally robust day-ahead dispatch is a typical two-stage problem. The day-ahead problem in the first stage is a pre-decision problem, which determines the trading power from the power grid. The intraday operation in the second stage is a regulation problem, which adjusts the intraday trading power and the scheduling plan of the regulating resources to minimize the intraday operating cost.
First stage (day-ahead): in this stage, the RIES trades power from the operator, and the power transaction cost is minimized, i.e.,
where Pttr is the day-ahead trading power, pt is the power price, and
The first-stage problem can be refined as follows:
where x∈χ are decision variables in the first stage, i.e., the day-ahead trading power Pttr, and c are day-ahead cost coefficients.
Second stage (intraday operation): in this stage, the RIES adjusts the intraday trading power and the dispatch plan of power storage, transferable power load, biogas generator, biogas storage, heat pump, electric boiler, and heat storage. The intraday operating cost includes the intraday power trading cost, material cost of the biogas generator, and the cost of the transferable power load:
where
The following security constraints need to be met for the second-stage intraday operation of the RIES.
2.1.1 Photovoltaics and demands
where the real photovoltaic power output Ptv, power load Ptd, and heat load Htd equal the sum of the forecast value and power/heat fluctuation.
2.1.2 Biogas generator
where H is the calorific value of biogas; Ptg and Htg are the power and afterheat produced by the biogas generator, respectively; and ηp and ηh are the power generating efficiency and afterheat efficiency of the biogas generator, respectively.
2.1.3 Waste heat recovery
The heat export of the device does not exceed the afterheat of the biogas generator.
where Htw is the heat export of the waste heat recovery.
2.1.4 Electric boiler
where ηb is the conversion efficiency and Htb and Ptb are the heat output and power input of the electric boiler, respectively.
2.1.5 Transferable power load
where
2.1.6 Power storage
where
2.1.7 Heat storage
where
2.1.8 Power and heat balance
The second-stage problem is refined as follows:
where y is the intraday decision variables; f is intraday cost coefficients; and G, A, B, C, g, and d are the constant matrices and vectors, respectively. The intraday decision y includes the power and afterheat produced by the biogas generator (Ptg; Htg), heat export of the waste heat recovery Htw, heat output and power input of the electric boiler (Htb; Ptb), upregulated and downregulated power of transferable power load (
2.2 Robust form of the dispatch model
In the proposed dispatch model of the RIES, the photovoltaic power output fluctuation utv, the power load utp, and the thermal load fluctuation uth are uncertain variables, and they constitute the source and load uncertainties. The day-ahead scheduling model is essentially a two-stage problem, which optimizes the day-ahead operating cost in the first stage and the expectation of the intraday cost in the second stage. In addition, since the possibility for the occurrence of the extreme distribution is relatively low, we further limit the loss of the cost expectation in the historical distribution to reduce the conservativeness of the distributionally robust dispatch. The constrained distributionally robust day-ahead dispatch can be refined as shown below:
where P and
The maximum limit
where
We formulate the ambiguous set for the source and load uncertainties according to the confidence set theory. K discrete reference samples can be selected from the M historical observations to characterize the possible value of the source and load uncertainties, and the corresponding baseline probability density is obtained. However, the actual probability distribution values of each reference sample are still uncertain, and we can use the probability density uncertainty to describe the uncertainty of the source–demand distribution. We can construct a set with the baseline density of reference samples as the center and the two sets of 1-norm and infinity-norm as the constraints to restrict the actual probability density of source–demand scenarios. Therefore, the ambiguous set of the source and load uncertainties is formulated as follows:
where pk is the actual probability of the reference sample k and θ∞ and θ1 are the maximum gap of the probability density under the infinity-norm and 1-norm restrictions, respectively.
The maximum gap of the probability density θ∞ and θ1 can be determined according to the confidence level (Ding et al., 2017).
Let α∞ and α1 denote the confidence level associated with the right hand of the above equations, and then:
Since the scenarios of the source and load uncertainties are denoted with the reference samples, while the probability density of these reference samples is uncertain, the distributionally robust dispatch Equation 28 is reformulated as follows:
3 Solution method
3.1 Linearization for the absolute value constraint
First, we introduce auxiliary variables to linearize the absolute value constraint in the ambiguous set:
where Δpk is the introduced auxiliary variable.
Therefore, the ambiguous set is reformulated into
3.2 Two-stage optimization procedure
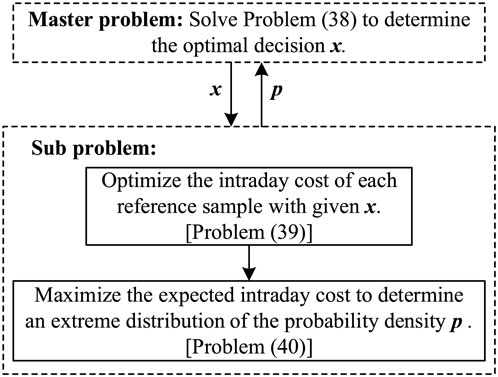
The constrained distributionally robust dispatch in Equation 28 is a typical two-stage optimization problem, and we develop a C&CG-based decomposition solution for the problem. The principle of the method is to split the two-stage optimization to independently solve the master problem and subproblem. The master problem determines the day-ahead decision variables against all known extreme distributions of the probability density. The subproblem receives the obtained decision variables and determines an extreme distribution of the probability density and adds it to the master problem. These two problems are computed alternately, and hence, the extreme distribution set in the master problem will cover enough extreme distributions to ensure the robustness of the dispatch. The computing framework of the two-stage solution is presented in Figure 2.
1) Master problem: the problem obtains the optimal solution against all known extreme distributions of the probability density.
where Λv-1 is the extreme distribution set revised from the previous step. Then, the optimal x is sent to the subproblem. The obtained objective is denoted as the lower bound (LB).
2) Subproblem: The problem determines an extreme distribution of the probability density with given x*. The solution of the subproblem contains two steps. First, the optimal intraday cost of each reference sample is calculated:
Second, the expected intraday cost is maximized to determine an extreme distribution of the probability density:
Then, the extreme distribution p of the probability density is added to the extreme distribution set, and the updated extreme distribution set is uploaded to the master problem.
3) Convergence criterion check: end the iteration until the following convergence criterion; otherwise, go back to step 1 and modify v = v+1.
where ε is a very small constant.
4 Numerical simulations
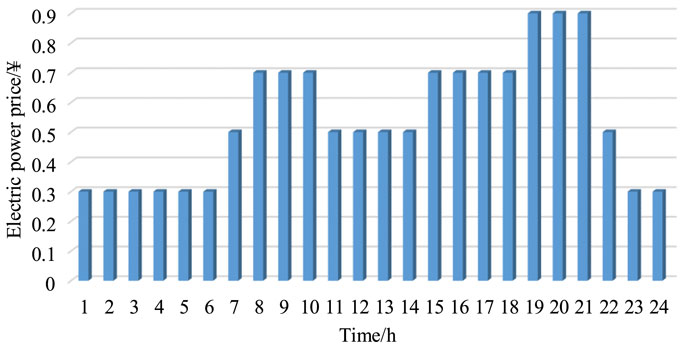
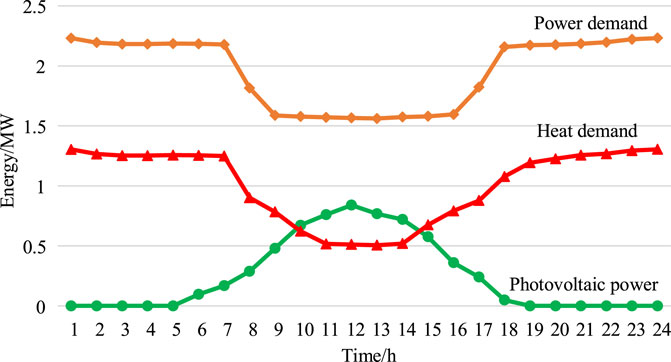
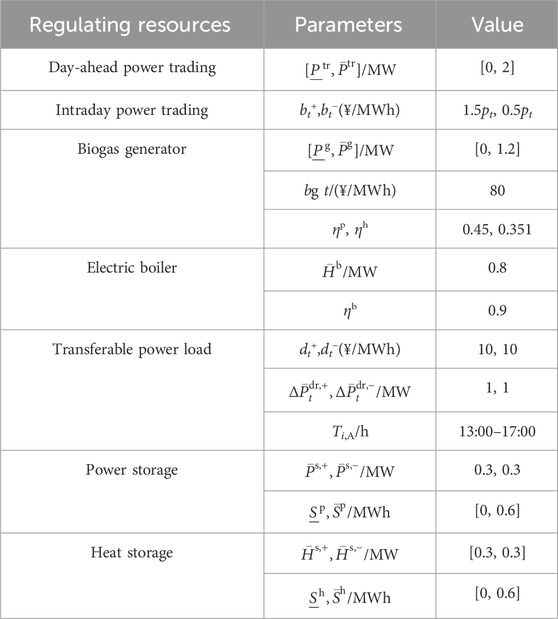
We take a modern farm park in Tsingtao city to validate the superiority of the constrained distributionally robust dispatch of the RIES. The day-ahead dispatch is performed for the next 0–24 h. All the programs are calculated with the CPLEX solver on a computer with an i7-1360P CPU. The power price in the day-ahead stage is displayed in Figure 3. The forecast information of photovoltaic energy, electric power, and heat load is presented in Figure 4, where the maximum prediction error is ±30% of the forecast value. The remaining parameters of the modern farm park are given in Table 1. Finally, the operational effectiveness of the dispatch plan is tested using the expected value of reference samples.
4.1 Analysis for the dispatch plan
In the proposed dispatch model of the RIES, the decision variable x in the day-ahead stage is the trading power, while the intraday decision variables y is constituted by the dispatch plan of power storage, transferable power load, biogas generator, biogas storage, heat pump, electric boiler, and heat storage. Note that the following analysis for the intraday operation is presented with the expected value of the reference samples.
Figure 5 shows the day-ahead trading power and power export of the biogas generator. Due to the low power generation cost of the biogas unit, the power output of the biogas generator is always maintained at a high level. At the dispatch periods t = 10:00–12:00, the power load is at the valley, while the available photovoltaic power output is at a relatively high level, which means that the net power load is at the lowest level during these periods, and hence, the power export of the biogas generator does not reach the maximum. Similarly, the RIES purchases very little electric power at the dispatch periods t = 8:00–16:00, with relatively lower net power load and heat load. During the dispatch periods t = 00:00–7:00 and 17:00–24:00, the power load and heat load are both at the peak while the photovoltaic power output is at the valley, and hence, the RIES purchases much electric power from the power market.
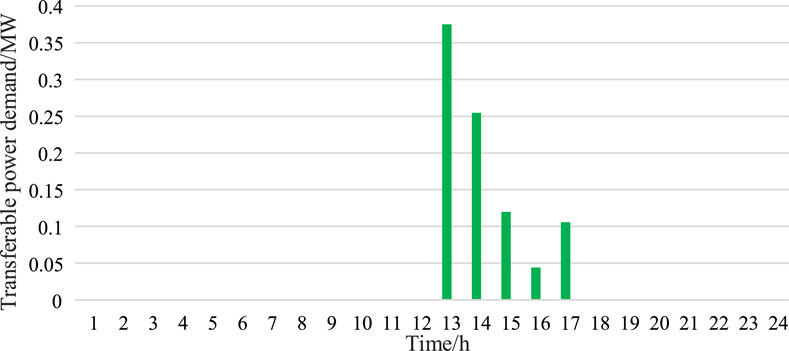
Figure 6 illustrates the distribution of transferable power load whose transferable periods are t = 13:00–17:00. The transferable power load is mostly transferred to t = 13:00–14:00 with lower power price, and thus, the operating cost of the RES is decreased.
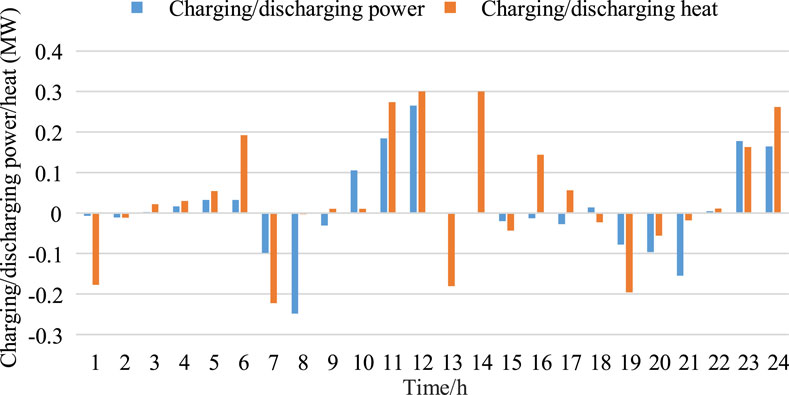
Figure 7 shows the charge–discharge state of the power and heat storage, respectively. The power price is relatively low during the dispatch periods t = 1:00–6:00 and 23:00–24:00, and so, the power storage charges power. While the power price is relatively high during the dispatch periods t = 7:00–9:00 and 19:00–21:00, the power storage discharges power to supply the demand. Finally, during the dispatch periods t = 10:00–12:00, the power load is at the valley while the photovoltaic power output is at a relatively high level, and hence, the power storage charges power to accommodate photovoltaic power. As indicated from the above analysis, the energy storage flexibly charges and discharges power according to the power price, and hence can decrease the operating cost of the RIES. While for the heat storage, its charging and discharging status is similar to that of the power storage since the heat load is supported by the waste heat of the biogas generator and the electric boiler.
4.2 Comparison between different uncertainty methods
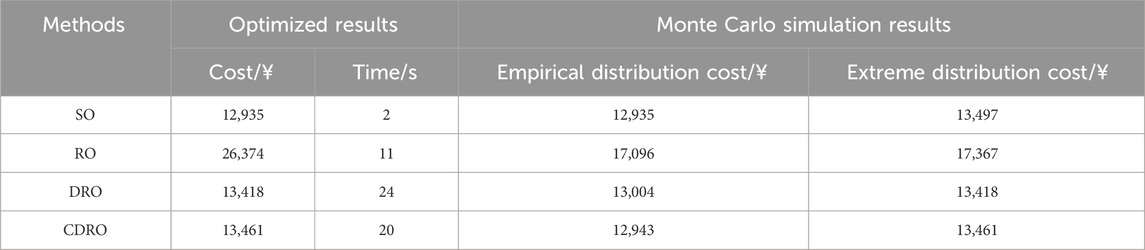
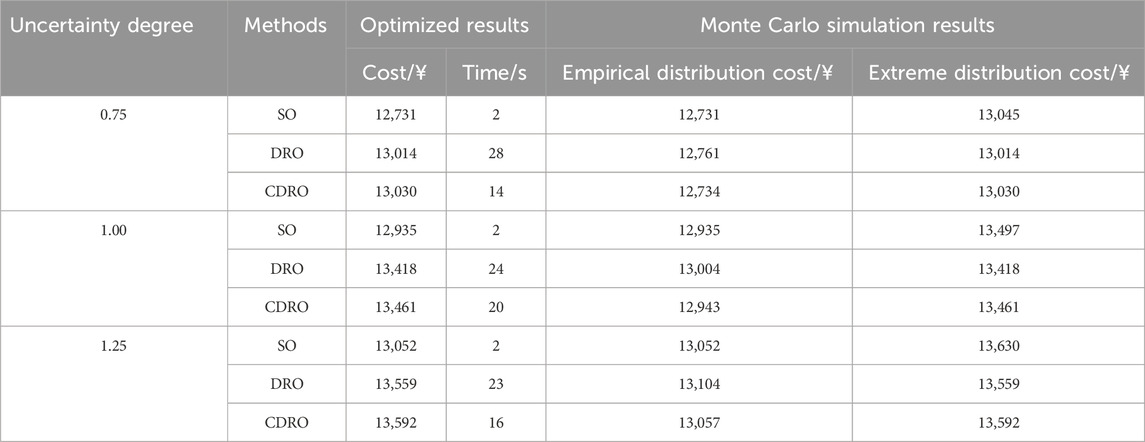
To verify the economy and robustness of the CDRO, this subsection compares the proposed method and the commonly used uncertainty methods, including SO, RO, and DRO. SO minimizes the operating cost expectation corresponding to the historical distribution of the source and load uncertainties, RO minimizes the operating cost corresponding to extreme scenarios, and DRO minimizes the operating cost corresponding to extreme distributions. The proposed CDRO minimizes the operating cost expectation corresponding to extreme distributions while restricting the sacrifice of the operating cost expectation in the historical distribution. The comparison results related to these methods are shown in Table 2. As displayed in the table, SO has the lowest operating cost expectation in the historical distribution, while it is significantly less robust than DRO and CDRO under some extreme distributions. RO minimizes the operating cost corresponding to extreme scenarios, which is very conservative and relatively uneconomical since the probability of extreme scenarios is extremely low. Although the historical distribution cost of the CDRO is slightly higher than that of SO, its economical effectiveness under extreme distributions is significantly better than that of SO. Compared to SO, the historical distribution cost of CDRO is slightly sacrificed by 6.18E-04, while the cost efficiency under extreme distributions is significantly improved by 2.7E-03. In view of that the practical distribution of the source and load uncertainties does not strictly obey the empirical value, it is essential to address the distributional deviation and enhance the robustness of the dispatch plan.
To further verify the performance of the CDRO, we change the fluctuation degrees of source and load uncertainties, i.e., change to 0.75–1.25 times of the original. Since RO is very conservative, we compare the optimization results of SO, DRO, and CDRO. As shown in Table 3, no matter how the uncertainty degree changes, CDRO always achieves a tradeoff between the economical effectiveness and robustness, i.e., it sacrifices the historical distribution cost slightly to significantly improve the robustness. In addition, as the uncertainty degree increases, the advantage of CDRO in balancing the economical effectiveness and robustness becomes more obvious.
4.3 Sensitivity analysis related to the ambiguous set
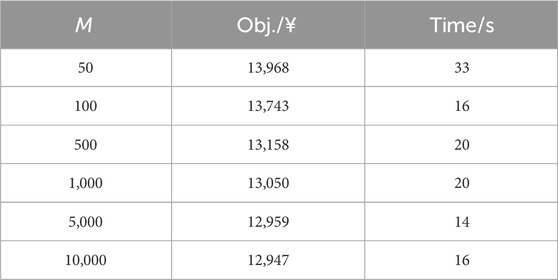
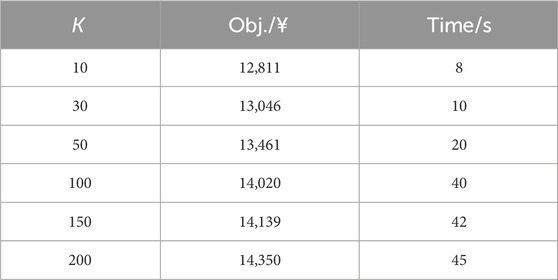
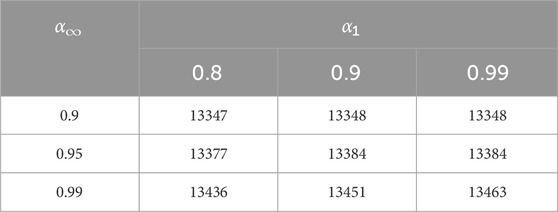
The ambiguous set of the source and load uncertainties is related to the amount of historical scenarios (M), the amount of the reference sample (K), and the confidence degree (α∞ and α1). The default setting of M, K, θ∞, and θ1 in this paper is 200, 50, 0.99, and 0.95, respectively. This subsection will study the impact of these parameters on the optimization performance.
First, we study the influence of the amount of historical scenarios M on the optimization results. The optimization results with different M from 50 to 10,000 are displayed in Table 4. The results in the table reveal that the objective decreases with the increase of the scale of historical observation. The reason is that the increase of historical observation limits the allowable gap of the probability distribution, and hence decreases the conservativeness of the proposed CDRO. It should be noted that the optimization results of CDRO actually approach that of SO with the increase of the scale of the historical observation, which further validates the flexibility of the proposed CDRO.
Second, we study the impact of the amount of reference samples K on the optimization results. The optimization results with different K from 10 to 200 are shown in Table 5. As K increases, the possible scenarios in the probability distribution of the source and load uncertainties are more dispersed, and hence, the maximum possible range of the probability distribution widens. Therefore, the optimized objective increases with the increase in the number of reference samples.
Finally, we study the impact of the confidence degree on the optimization performance, and the simulation results are displayed in Table 6. With the increase in the confidence degree α∞ and α1, the allowable gap of the probability density θ∞ and θ1 widens, and hence, the maximum possible range of the probability distribution widens. Therefore, the optimized objective increases with the increase in the confidence degree. It is worth noting that when α∞ = 0.9, the optimized objectives are the same for α1 = 0.9 and α1 = 0.99. As shown in Equations 30–33, only the infinity-norm works if the infinity-norm and 1-norm share the same confidence degree. At this time, even though the confidence degree for the 1-norm increases, the ambiguous set of the source and load uncertainties remains the same, and so, the optimized objective will not change.
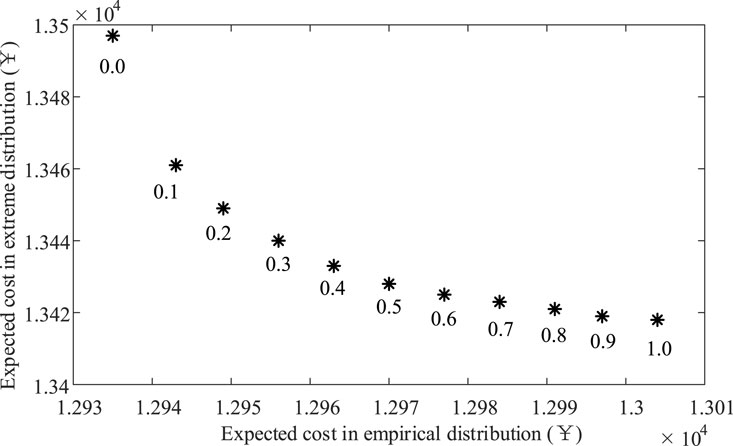
4.4 Influence of the equilibrium coefficient
In the proposed CDRO, the equilibrium coefficient λ plays a crucial part in coordinating the economical effectiveness and the robustness of the dispatch plan. Figure 8 presents the operating cost expectation in the historical distribution and extreme distribution associated with the equilibrium coefficient within [0, 1]. As shown in the figure, if the equilibrium coefficient approaches 1, the operating cost expectation in the historical distribution increases, while the expected cost in extreme distribution decreases, which means that the CDRO pays more attention to the robustness than to economical effectiveness. When the equilibrium coefficient λ approaches 0, the operating cost expectation in the historical distribution increases and the expected cost in extreme distribution decreases, which means that the CDRO pays more attention to economical effectiveness than to robustness. In addition, when the equilibrium coefficient locates between 0 and 0.2, the expected cost in the extreme distribution significantly decreases with a very small loss of the operating cost expectation in the historical distribution, which means that the robustness can be ensured with a very slight sacrifice of economical effectiveness in common distributions. The above numerical results reveal that the CDRO can acquire a tradeoff between the robustness and economical effectiveness through a reasonable setting of the equilibrium coefficient. In practical applications, considering that historical distributions are more likely to occur while extreme distributions are less likely to occur, the proposed CDRO shall give priority to economical effectiveness in the historical distribution. Therefore, the equilibrium coefficient can be set within [0.1, 0.3] in practical applications.
4.5 Computational efficiency of the solution
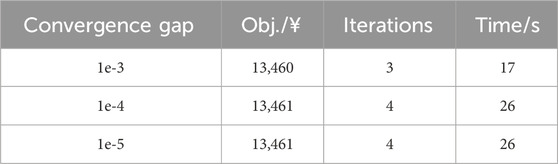
The tailored two-stage solution procedure splits the dispatch problem to independently solvable master and subproblems. The master problem determines the day-ahead decision variables, and the subproblem determines an extreme distribution of the probability density. The iteration steps and computing time with different number of historical scenarios (M) and amount of reference samples (K) are displayed in Table 7. As indicated in the table, the iteration times of the proposed solution are few, and the calculation time is only tens of seconds, which validates the computational efficiency of the solution. In addition, the convergence of the two-stage solution is related to the convergence gap ε. We change the convergence gap and compare the optimization results. As shown in Table 8, the optimized objective descends when the convergence condition becomes strict. Although the iteration times and calculation time increase correspondingly, the computational efficiency of the proposed algorithm is still very high.
5 Conclusion
In this work, a constrained distributionally robust day-ahead dispatch model of a rural integrated energy system is developed, and a tailored two-stage solution is developed for the model. The rural system effectively coordinates the regulation resources such as trading power, biogas generator, electric boiler, transferable power load, power storage, and heat storage to reduce its operating cost. As indicated in the comparison with other uncertainty methods, the proposed constrained distributionally robust optimization (CDRO) sacrifices historical distributional cost slightly to improve its robustness. The ambiguous set of the source and load uncertainties influences the optimization performance of the proposed CDRO. When the scale of historical observation is large, the probability distribution range decreases, and the CDRO approaches SO. In addition, by reasonably setting the confidence level in the 1-norm and infinity-norm constraint, the conservativeness of CDRO can be reduced. The proposed CDRO fully combines the economical effectiveness of SO with the robustness of DRO and can achieve a tradeoff between economical effectiveness and robustness through a reasonable setting of the equilibrium coefficient.
Our future work will consider more regulating devices such as electricity-to-hydrogen devices and interruptible power load to improve the integrality of RIES modeling. In addition, the coordinated operation of the distribution network and multiple RIESs will be studied in the future.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
ZZ: methodology, writing–original draft, and writing–review and editing. SY: data curation and writing–review and editing. YM: formal analysis and writing–review and editing. SS: software, validation, and writing–review and editing. PY: data curation, investigation, and writing–review and editing. FY: formal analysis, validation, and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was sponsored by the Headquarters Science and Technology Project of State Grid Corporation of China, Research and application of distributed flexible low-carbon energy supply technology for rural distribution network (5108-202218280A-2-375-XG).
Conflict of interest
Authors ZZ, YM, and FY were employed by State Grid Shanghai Energy Internet Research Institute Co. Ltd. Authors SoY, SS, and PY were employed by State Grid Shandong Electric Power Company Electric Power Science Research Institute.
The authors declare that this study received funding from State Grid Corporation of China. The funder had the following involvement in the study: data collection and analysis.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bertsimas, D., Litvinov, E., Sun, X., Zhao, J., and Zheng, T. (2013). Adaptive robust optimization for the security constrained unit commitment problem. IEEE Trans. Power Syst. 28 (1), 52–63. doi:10.1109/TPWRS.2012.2205021
Bolurian, A., Akbari, H., and Mousavi, S. (2022). Day-ahead optimal scheduling of microgrid with considering demand side management under uncertainty. Electr. Power Syst. Res. 209, 107965. doi:10.1016/j.epsr.2022.107965
Ding, T., Yang, Q., Yang, Y., Li, C., Bie, Z., and Blaabjerg, F. (2017). A data-driven stochastic reactive power optimization considering uncertainties in active distribution networks and decomposition method. IEEE Trans. Sustain. Energy 9 (5), 4994–5004. doi:10.1109/TSG.2017.2677481
Eghbali, N., Hakimi, S. M., Hasankhani, A., Derakhshan, G., and Abdi, B. (2022). A scenario-based stochastic model for day-ahead energy management of a multi-carrier microgrid considering uncertainty of electric vehicles. J. Energy Storage 52, 104843. doi:10.1016/j.est.2022.104843
Fu, X., Zhou, Y., Sun, H., and Guo, Q. (2020). Online security analysis of a park-level agricultural energy Internet: review and prospect. Proc. CSEE 40 (17), 5404–5412. (in Chinese). doi:10.13334/j.0258-8013.pcsee.200108
Jani, A., Karimi, H., and Jadid, S. (2022). Two-layer stochastic day-ahead and real-time energy management of networked microgrids considering integration of renewable energy resources. Appl. Energy 323, 119630. doi:10.1016/j.apenergy.2022.119630
Liang, R., Yuan, L., Huang, H., Gu, C., Li, J., Lu, W., et al. (2024). Multi-hydraulic retention time rolling optimal operation method for rural biomass power generation system under uncertain temperature. Proc. CSEE. (in Chinese). doi:10.13334/j.0258-8013.pcsee.232154
Liu, Y., Guo, L., and Wang, C. (2018). Economic dispatch of microgrid based on two stage robust optimization. Proc. CSEE 38 (14), 4013–2022. (in Chinese). doi:10.13334/j.0258-8013.pcsee.170500
Ma, L., and Fu, X. (2021). Theory and application of agricultural energy Internet considering coupling of agriculture, meteorology and energy. Electr. Power 54 (11), 115–124. (in Chinese). doi:10.11930/j.issn.1004-9649.202006239
Qu, K., Zheng, X., Li, X., Lv, C., and Yu, T. (2022). Stochastic robust real-time power dispatch with wind uncertainty using difference-of-convexity optimization. IEEE Trans. Power Syst. 37 (6), 4497–4511. doi:10.1109/TPWRS.2022.3145907
Seyednouri, S. R., Safari, A., Farrokhifar, M., Ravadanegh, S. N., Quteishat, A., and Younis, M. (2023). Day-ahead scheduling of multi-energy microgrids based on a stochastic multi-objective optimization model. Energies 16 (4), 1802. doi:10.3390/en16041802
Siqin, Z., Niu, D., Wang, X., Zhen, H., Li, M., and Wang, J. (2022). A two-stage distributionally robust optimization model for P2G-CCHP microgrid considering uncertainty and carbon emission. Energy 260, 124796. doi:10.1016/j.energy.2022.124796
Tan, B., Chen, H., Zheng, X., and Huang, J. (2022). Two-stage robust optimization dispatch for multiple microgrids with electric vehicle loads based on a novel data-driven uncertainty set. Int. J. Elec. Power 134, 107359. doi:10.1016/j.ijepes.2021.107359
Wei, W., Liu, F., and Mei, S. (2016). Distributionally robust co-optimization of energy and reserve dispatch. IEEE Trans. Sustain. Energy 7 (1), 289–300. doi:10.1109/TSTE.2015.2494010
Wu, T., Bu, S., Wei, X., and Zhou, B. (2021). Multitasking multi-objective operation optimization of integrated energy system considering biogas-solar-wind renewables. Energy Convers. Manag. 229, 113736. doi:10.1016/j.enconman.2020.113736
Xu, J., Yi, X., Sun, Y., Lan, T., and Sun, H. (2017). Stochastic optimal scheduling based on scenario analysis for wind farms. IEEE Trans. Sustain. Energy 8 (4), 1548–1559. doi:10.1109/TSTE.2017.2694882
Yu, Y., and Yin, S. (2023). Incentive mechanism for the development of rural new energy industry: new energy enterprise–village collective linkages considering the quantum entanglement and benefit relationship. Int. J. Energy Res. 2023, 1–19. doi:10.1155/2023/1675858
Yu, Y., Yin, S., and Zhang, A. (2022). Clean energy-based rural low carbon transformation considering the supply and demand of new energy under government participation: a three-participators game model. Energy Rep. 8, 12011–12025. doi:10.1016/j.egyr.2022.09.037
Zhai, J., Wang, S., Guo, L., Jiang, Y., Kang, Z., and Jones, C. (2022). Data-driven distributionally robust joint chance-constrained energy management for multi-energy microgrid. Appl. Energy 326, 119939. doi:10.1016/j.apenergy.2022.119939
Zhang, K., Troitzsch, S., and Han, X. (2022). Distributionally robust co-optimized offering for transactive multi-energy microgrids. Int. J. Elec. Power 143, 108451. doi:10.1016/j.ijepes.2022.108451
Zhao, Z., Liu, Y., Guo, L., Bai, L., and Wang, C. (2021). Locational marginal pricing mechanism for uncertainty management based on improved multi-ellipsoidal uncertainty set. J. Mod. Power Syst. Clean. Energy 9 (4), 734–750. doi:10.35833/MPCE.2020.000824
Zheng, X., Qu, K., Lv, J., Li, Z., and Zeng, B. (2021). Addressing the conditional and correlated wind power forecast errors in unit commitment by distributionally robust optimization. IEEE Trans. Sustain. Energy 12 (2), 944–954. doi:10.1109/TSTE.2020.3026370
Zhou, B., Xu, D., Li, C., Chuang, C. Y., Cao, Y., Chan, K. W., et al. (2018). Optimal scheduling of biogas-solar-wind renewable portfolio for multicarrier energy supplies. IEEE Trans. Power Syst. 33 (6), 6229–6239. doi:10.1109/TPWRS.2018.2833496
Zuo, J., Xu, C., Wang, W., and Ji, Y. (2023). Distributionally robust optimization for virtual power plant clusters considering carbon emission-based dynamic dispatch priority. Front. Energy Res. 11. doi:10.3389/fenrg.2023.1214263
Nomenclature
Keywords: rural integrated energy system, day-ahead dispatch, source and load uncertainties, distributionally robust optimization, two-stage optimization
Citation: Zhang Z, Yang S, Ma Y, Sun S, Yu P and Yang F (2024) Constrained distributionally robust optimization for day-ahead dispatch of rural integrated energy systems with source and load uncertainties. Front. Energy Res. 12:1411152. doi: 10.3389/fenrg.2024.1411152
Received: 02 April 2024; Accepted: 15 May 2024;
Published: 11 July 2024.
Edited by:
Zening Li, Taiyuan University of Technology, ChinaReviewed by:
Zhenning Pan, South China University of Technology, ChinaZhiwei Li, North China Electric Power University, China
Copyright © 2024 Zhang, Yang, Ma, Sun, Yu and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhihui Zhang, emhhbmd6aGlodWlAZXByaS5zZ2NjLmNvbS5jbg==
 Zhihui Zhang
Zhihui Zhang Song Yang2
Song Yang2