Robust optimal power flow considering uncertainty in wind power probability distribution

This paper proposes an optimal power flow model that takes into account the uncertainty in the probability distribution of wind power. The model can schedule controllable generators under any possible distribution of wind power to ensure the safe and economic operation of the system. Firstly, considering the incompleteness of historical wind power data, the paper models the uncertainty of wind power using second-order moments of probability distribution and their fluctuation intervals. Subsequently, a robust optimal power flow model based on probability distribution model and joint chance constraints is established. The Lagrangian duality theorem is then employed to eliminate random variables from the optimization model, transforming the uncertainty model into a deterministic linear matrix inequality problem. Finally, a convex optimization algorithm is used to solve the deterministic problem, and the results are compared with traditional chance-constrained optimal power flow model. The feasibility and effectiveness of the proposed method are validated through case study simulations.

1 Introduction

As the penetration rate of intermittent renewable energy sources, such as wind and solar power, continues to rise, the shortcomings of existing operating modes in the power system may limit the integration of new energy sources. The intermittency and incomplete controllability of renewable energy generation pose significant challenges to the safe and economic operation of the power system.

Traditional power systems mainly rely on thermal power generation to meet electricity demand, with no renewable energy generation units in the system. Therefore, traditional optimal power flow models proposed in (Bacher and Van Meeteren, 1988; Hua et al., 1998; Zhang et al., 2020; Kardoš et al., 2022) are not suitable for scenarios considering the uncertainty of new energy output. With the gradual development of low-carbon power construction, the significant injection of new energy has huge impacts on the safe and economic operation of the power system, demanding a reform in the power system’s operational control mode. The volatility of wind power output (Ela and O'Malley, 2012) can be addressed at the planning level by configuring energy storage to smooth out output fluctuations (Wang et al., 2013; Angizeh et al., 2023; Fan et al., 2023). On the operational level, controllable generators can be scheduled to absorb fluctuations. In recent years, research on optimal power flow problems considering the stochastic nature of wind power has attracted considerable attention (Morales and Perez-Ruiz, 2007; Bienstock et al., 2012; Shi et al., 2012; Li et al., 2015; Gao et al., 2017; Sun et al., 2019; Angizeh et al., 2023; Xiao et al., 2024a; Xiao et al., 2024b).

Reference (Li et al., 2015) establishes an optimal power flow model considering wind power uncertainty using stochastic programming. The paper obtains an estimated distribution of wind power output based on observed samples and generates a discrete scenario set based on this estimated distribution. However, the accuracy of the results depends on the number of observed samples and discrete scenarios, which can lead to the “curse of dimensionality.” Reference (Morales and Perez-Ruiz, 2007) proposes a probability optimal power flow algorithm based on three-point estimation, but the computational complexity of point estimation algorithms is high. Additionally, probabilistic power flow analysis should consider the correlation between realistically existing injection amounts, or it may result in significant errors (Sun et al., 2019). Reference (Bienstock et al., 2012) introduces the chance-constrained OPF (CC-OPF) model and proposes a cut-plane algorithm for solving it, assuming that wind power forecast errors follow a Gaussian distribution. To address the issue of modeling wind power stochastic errors with a single deterministic distribution, Reference (Gao et al., 2017) innovatively proposes the robust chance-constrained OPF (RCC-OPF) model, describing wind power forecast errors as random variables with uncertainty in both variance and expectation. However, Reference (Gao et al., 2017) does not provide a model-solving algorithm.

Against this background, this paper proposes a power system optimal power flow calculation method considering the uncertainty of wind power probability distribution. The paper first models the uncertainty of wind power output using partial statistical information (Bofinger et al.). It then describes the optimal power flow problem of a wind farm system with distributionally robust joint chance constraints (DRJCC-OPF) (Zymler et al., 2013; Bian et al., 2014) and employs the Lagrangian duality to eliminate random variables in the model (Ding, 2014), transforming the uncertainty model into a deterministic linear matrix inequality (LMI). Furthermore, convex optimization methods are used to solve the deterministic LMI. This approach, based on partial statistical information of wind power in the power system, innovatively considers the uncertainty of the probability distribution of wind power forecast errors, obtaining generation scheduling plans that can meet the requirements of safe and economic operation of the power system under arbitrary wind power distributions. The feasibility and effectiveness of the method are verified through an IEEE 5-node case study.

2 Traditional chance-constrained optimal flow model

Deterministic optimal power generation scheduling results are based on renewable energy output forecasts and do not take into account fluctuations in new energy output, which often results in frequent line overloads and power system security risks (Zhang et al., 2018). Traditional chance-constrained optimal flow model (traditional-chance-constrained TCC-OPF) can correct this problem and buffer critical renewable energy fluctuations to ensure secure and economic operation of the power system (Ma et al., 2019)

$\min {\displaystyle \sum _{i\in GB}}\mathrm{c}\left(\overline{P_i}\right)(1)$

$s.t.\mathrm{B}\overline{\theta }=P_g+\mu -d(2)$

${\mathrm{P}}_i^{\min }\le \overline{{\mathrm{P}}_i}\le {\mathrm{P}}_i^{\max }\forall i\in GB(3)$

${\mathrm{P}}_L=T\left(\overline{P_g}+\mu -d\right)(4)$

$\left|{\mathrm{P}}_L\right|\le P_L^{\max }(5)$

$\mathrm{Pr}\left(\overline{{\mathrm{P}}_i}-\mathrm{\Omega }{\alpha }_i\le {\mathrm{P}}_i^{\max }\right)\le \gamma \forall i\in GB(6)$

$\mathrm{Pr}\left(\overline{{\mathrm{P}}_i}-\mathrm{\Omega }{\alpha }_i\ge {\mathrm{P}}_i^{\min }\right)\le \gamma \forall i\in GB(7)$

$\mathrm{Pr}\left(\mathrm{\Omega }{\alpha }_i\le {\text{RD}}_i\right)\le \gamma \forall i\in GB(8)$

$\mathrm{Pr}\left(\mathrm{\Omega }{\alpha }_i\ge -{\text{RU}}_i\right)\le \gamma \forall i\in GB(9)$

$\mathrm{Pr}\left(P_{Li}\le P_{Li}^{\max }\right)\le \gamma \forall i\in \mathcal{l}(10)$

$\mathrm{Pr}\left(P_{Li}\ge -P_{Li}^{\max }\right)\le \gamma \forall i\in \mathcal{l}(11)$

${\displaystyle \sum _{i\in GB}}{\alpha }_i=1,{\alpha }_i\ge 0\forall i\in GB(12)$

$\mathrm{\Omega }={\displaystyle \sum _j}{w}_{j}j\in WB(13)$

Where: $\overline{{\mathrm{P}}_i}$ is Generator i power generation at desired wind power output, $\mathrm{c}\left(\overline{P_i}\right)$ is generation cost of generator i, $P_g$, $\mu$ and $d$ are generation power vector, wind power expected output vector and load power vector respectively; $\mathrm{B}$ is node susceptance matrix, $\overline{\theta }$ is node phase angle vector, ${\mathrm{P}}_L$ and $P_{Li}$ are line power flow vector, line power flow random variable vector under expected wind power output considering wind power random fluctuation, $T$ is power distribution coefficient matrix, $w_j$ is wind power prediction error of wind farm i; $\alpha$ is generator dispatch factor, $GB$、 $\mathcal{l}$、 $WB$ are sets of generator nodes, power lines, and wind farm nodes respectively. ${\mathrm{P}}_i^{\max }$ and ${\mathrm{P}}_i^{\min }$ are upper and lower limits of generator i, ${\text{RD}}_i$ and ${\text{RU}}_i$ are upper and lower ramping limits of generator i. $P_L^{\max }$ are thermal limits of power lines, $\gamma$ is confidence level of safe operation of the system. Pr () in Eqs 6–11 stands for the probability of the probabilistic event in the parenthesis.

Equation 2 and 4 are nodal power balance equation and line flow equation; Eqs 3 and (6) and 7 are generation output limits of generators. Eqs 5, 10, 11 are the thermal limits of power lines. Eqs 8–9 are ramping limits of generators. The objective function is minimization of generation costs. TCC-OPF model ensures safe operation of the system at a given confidence level while minimizing power generation costs。

The TCC-OPF model is based on a single accurate probability distribution of wind power prediction errors, and is therefore only suitable for situations where a definite and comprehensive description of wind power or wind speed stochasticity exists.

3 Probabilistic distribution robust joint chance-constrained optimal power flow model and solution

Due to significant wind power fluctuations, we often can only obtain partial information about the probability distribution of wind power or wind power prediction errors (Bienstock et al., 2012). Without loss of generality, this paper assumes knowledge of the second-order moment information of the probability distribution of the wind power prediction error vector $\stackrel{\sim }{\omega }$. Let the empirical estimate of the expectation of the wind power prediction error be denoted as μ_w0 and the empirical estimate of the covariance matrix as Γ₀. In real-world applications, due to limitations in prediction technology, obtaining precise second-order moment information is challenging. Therefore, this paper considers using empirical estimates of the second-order moments and their fluctuation intervals to describe the randomness of wind power prediction errors, as shown in Eqs 14, 15:

${\mu }_0-\eta \le \mathrm{{\rm E}}\left[\omega \right]\le {\mu }_0+\eta (14)$

${\mathrm{\Gamma }}_0+\left({\mu }_0-\eta \right){\left({\mu }_0-\eta \right)}^T\le \mathrm{{\rm E}}\left(w{w}^T\right)\le {\mathrm{\Gamma }}_0+\left({\mu }_0+\eta \right){\left({\mu }_0+\eta \right)}^T(15)$

Where, μ₀ and Γ₀ represents the empirical estimate of the second moment of wind power prediction errors; η denotes the extent of deviation between the actual second moment and its estimated value, reflecting the accuracy of wind power predictions.

Based on the above assumptions, this paper proposes a method of using a series of probability distribution functions that satisfy the given second moment information to describe the uncertainty of wind power prediction errors. Let the probability distribution set formed by the series of probability distribution functions be denoted as Ф(μ_w,Γ).

This section first establishes a robust joint chance-constrained optimal power flow model. Subsequently, the robust joint chance-constrained model is transformed into a deterministic Linear Matrix Inequality (LMI) problem, which does not involve random variables. Finally, a convex optimization algorithm is employed to solve this problem.

3.1 Probabilistic distribution robust joint chance-constrained optimal power flow model

In response to the uncertainty associated with the probability distribution of wind power prediction errors, and in order to obtain a generation scheduling scheme that satisfies system safety constraints under any probability distribution in Ф(μ_w,Γ). Based upon the TCC-OPF models, the DRJCC-OPF is employed to describe the optimal power flow problem considering wind power uncertainty. The specific model is as follows:

$\min {\displaystyle \sum _{i\in GB}}\left\{c_{i2}\left({\overline{P_i}}^2+\text{var}\left(\mathrm{\Omega }\right){\alpha }_i^2\right)+c_{i1}\overline{P_i}+c_{i0}\right\}(16)$

$s.t.\mathrm{B}\overline{\theta }=P_g+\mu -d(17)$

${\mathrm{P}}_i^{\min }\le \overline{{\mathrm{P}}_i}\le {\mathrm{P}}_i^{\max }\forall i\in GB(18)$

${\mathrm{P}}_L=T\left(\overline{P_g}+\mu -d\right)(19)$

$\left|{\mathrm{P}}_L\right|\le P_L^{\max }(20)$

$\underset{\mathrm{\Phi }\left({\mu }_{\omega },\mathrm{\Gamma }\right)}{\mathit{inf}}\mathit{Pr}\left\{\begin{array}{l}{\mathrm{P}}_i^{\min }\le \overline{{\mathrm{P}}_i}+\mathrm{\Omega }{\alpha }_i\le {\mathrm{P}}_i^{\max }\forall i\in GB\\ -{\text{RU}}_i\le \mathrm{\Omega }{\alpha }_i\le {\text{RD}}_i\forall i\in GB\\ \left|P_{Li}\right|\le P_{Li}^{\max }\forall i\in \mathcal{l}\end{array}\right\}\ge 1-\epsilon (21)$

${\displaystyle \sum _{i\in GB}}{\alpha }_i=1,{\alpha }_i\ge 0\forall i\in GB(22)$

$\mathrm{\Omega }={\displaystyle \sum _j}{w}_{j}j\in WB(23)$

Where Eq. 16 represents the objective function, indicating the generation cost considering the regulating output of thermal power units (the specific transformation process of the objective function is detailed in the appendix); var(Ω) represents the variance of Ω. ε denotes the confidence level of violating the robust joint chance constraints; $\underset{\mathrm{\Phi }\left({\mu }_{\omega },\mathrm{\Gamma }\right)}{\mathit{inf}}\left(A\right)$ represents the minimum probability of event A occurrence under all possible distributions; other variable definitions are the same as in Eqs 1–13.

In the above model, the probability distribution of wind power prediction errors is uncertain and can take any form of probability distribution in $\mathrm{\Phi }\left({\mu }_{\omega },\mathrm{\Gamma }\right)$. Therefore, the robust joint chance constraint Eq. 21 indicates that, under all possible probability distributions, the probability of satisfying system safety constraints is not less than $1-\epsilon$. Consequently, the DRJCC-OPF model can obtain scheduling strategies for generation power units that ensure the economic operation of the power system under the worst-case wind power distribution.

The decision variables of the DRJCC-OPF model are represented by $\overline{P_i}$, $\alpha$, $\overline{\theta }$ and ${\mathrm{P}}_L$, denoted as:

$x=\left(\overline{P_i},\alpha ,\overline{\theta },{\mathrm{P}}_L\right)(24)$

Eqs 17–20, 22, 23 are deterministic constraints, while Eq. 21 represents the uncertainty constraint. The challenge in solving the DRJCC-OPF model lies in handling the probability distribution robust joint chance constraint equation.

3.2 Deterministic transformation of probability distribution robust joint chance constraints

Express the constraints in Eq. 21 in the form of unilateral constraints and separate the decision variables from the random variables, as shown below:

$P_i-P_i^{\max }+\left(-{\alpha }_i{\mathrm{e}}^T\right)\stackrel{\sim }{w}\le 0(25)$

$P_i^{\min }-P_i¯\left({\alpha }_i{\mathrm{e}}^T\right)\stackrel{\sim }{w}\le 0(26)$

$-R{D}_i+\left({\alpha }_i{\mathrm{e}}^T\right)\stackrel{\sim }{w}\le 0(27)$

$-R{U}_i-\left({\alpha }_i{\mathrm{e}}^T\right)\stackrel{\sim }{w}\le 0(28)$

For line power flow $P_{Li}$, it can be written in the following form (proof process is provided in the appendix):

$\overline{P_{Li}}-P_{Li}^{\max }+\left(T_i^{\prime }-T_i\alpha {\mathrm{e}}^T\right)\stackrel{\sim }{w}\le 0(29)$

$-\overline{P_{Li}}-P_{Li}^{\max }-\left(T_i^{\prime }-T_i\alpha {\mathrm{e}}^T\right)\stackrel{\sim }{w}\le 0(30)$

Where e^T is the unit vector with all elements equals to 1. After replacing the expression in Eq. 21 with Eqs 25–30, the result is:

$\underset{{\varphi }_{\omega }\in \mathrm{\Phi }\left({\mu }_{\omega },\mathrm{\Gamma }\right)}{\mathit{inf}}\mathit{Pr}\left\{\begin{array}{l}\overline{P_i}-P_i^{\max }+\left(-{\alpha }_i{\mathrm{e}}^T\right)w\le 0\forall i\in \wp \\ P_i^{\min }-\overline{P_i}+\left({\alpha }_i{\mathrm{e}}^T\right)w\le 0\forall i\in \wp \\ -R{D}_i+\left({\alpha }_i{\mathrm{e}}^T\right)w\le 0\forall i\in \wp \\ -R{U}_i-\left({\alpha }_i{\mathrm{e}}^T\right)w\le 0\forall i\in \wp \\ \overline{P_{Li}}-P_{Li}^{\max }+\left(T_i^{\prime }-T_i\alpha {\mathrm{e}}^T\right)w\le 0\forall i\in \mathcal{l}\\ -\overline{P_{Li}}-P_{Li}^{\max }-\left(T_i^{\prime }-T_i\alpha {\mathrm{e}}^T\right)w\le 0\forall i\in \mathcal{l}\end{array}\right\}\ge 1-\epsilon (31)$

Furthermore, by eliminating the random variables in Eq. 31 and transforming it into a deterministic problem (the detailed proof process is provided in the appendix), the resulting deterministic problem corresponding to the DRJCC-OPF model is expressed as follows:

$\begin{array}{l}\min {\displaystyle \sum _{i\in \wp }}\left\{c_{i2}\left({\overline{P_i}}^2+\text{var}\left(\mathrm{\Omega }\right){\alpha }_i^2\right)+c_{i1}\overline{P_i}+c_{i0}\right\}\\ s.t.{\mathrm{y}}_0\mathbb{\in }\mathbb{R},y_1,y_2\in {\mathbb{R}}^{n_w},Y_1,Y_2\in S^{n_w},\\ \beta +\frac{1}{\epsilon }\left(〈{\mathrm{\Omega }}_{+},\left(\begin{array}{cc}{Y}_1& \frac{1}{2}{y}_1\\ \frac{1}{2}{y}_1^T& {\mathrm{y}}_0\end{array}\right)〉-〈{\mathrm{\Omega }}_{-},\left(\begin{array}{cc}{Y}_2& \frac{1}{2}{y}_2\\ \frac{1}{2}{y}_2^T& {\mathrm{y}}_0\end{array}\right)〉\right)\le 0,\\ \left(\begin{array}{cc}{Y}_1& \frac{1}{2}{y}_1\\ \frac{1}{2}{y}_1^T& {\mathrm{y}}_0\end{array}\right)-\left(\begin{array}{cc}{Y}_2& \frac{1}{2}{y}_2\\ \frac{1}{2}{y}_2^T& {\mathrm{y}}_0\end{array}\right)\ge 0,\\ \left(\begin{array}{cc}{Y}_1& \frac{1}{2}{y}_1\\ \frac{1}{2}{y}_1^T& {\mathrm{y}}_0\end{array}\right)-\left(\begin{array}{cc}{Y}_2& \frac{1}{2}{y}_2\\ \frac{1}{2}{y}_2^T& {\mathrm{y}}_0\end{array}\right)-\left(\begin{array}{cc}0& \frac{1}{2}{\mathrm{L}}_i{\left(x\right)}^T\\ \frac{1}{2}{\mathrm{L}}_i\left(x\right)& L_i^0\left(x\right)-\beta \end{array}\right)\ge 0,\forall i=1,...,m,\end{array}(32)$

Where $L_i\left(x\right)$ and $L_i^0\left(x\right)$ correspond to the left side of Eqs 25–30 (details are explained in the appendix); $m$ represents the total number of individual chance constraints in the robust joint chance constraint Eq. 31; $x$ is the decision variable as in Eq. 24; ${\mathrm{\Omega }}_{+}$ and ${\mathrm{\Omega }}_{-}$ is given by Eqs 33, 34:

${\mathrm{\Omega }}_{+}=\left(\begin{array}{cc}{\mathrm{\Gamma }}_0+\left({\mu }_0+\eta \right){\left({\mu }_0+\eta \right)}^T& {\mu }_0+\eta \\ {\mu }_0^T+{\eta }_0^T& 1\end{array}\right)(33)$

${\mathrm{\Omega }}_{-}=\left(\begin{array}{cc}{\mathrm{\Gamma }}_0+\left({\mu }_0-\eta \right){\left({\mu }_0-\eta \right)}^T& {\mu }_0-\eta \\ {\mu }_0^T-{\eta }_0^T& 1\end{array}\right)(34)$

3.3 Solution algorithm

Eq. 32 represents a convex optimization problem with LMI constraints, and a convex optimization algorithm can be employed to obtain the global optimal solution.

4 Case study

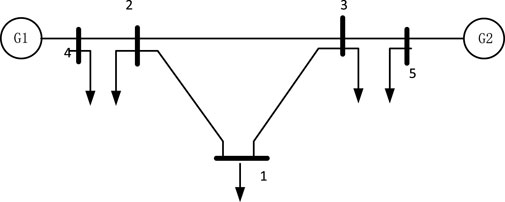
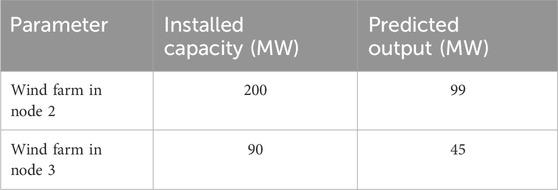
This paper conducts simulation tests using a modified 5-node system as shown in the diagram. The power system topology is illustrated in Figure 1, and specific data can be found in reference (Wang, 2003). Nodes 2 and 3 are connected to a wind farm, and the wind farm data is provided in Table 1. Optimization modeling is performed on the MATLAB platform, and the YALMIP solver is invoked to solve the LMIs in the model.

Figure 1

Figure 1. System topology of 5-nodes power system.

Table 1

Table 1. Wind farm parameters.

For simplicity in analysis, this paper assumes that the output of each wind farm is independent of each other. The expected value of wind power prediction error is denoted as ${\mu }_{\omega }$ μ, and the variance is denoted as $\mathrm{\Gamma }$. For ${\mu }_0$ the empirical estimate of wind power prediction error, it is generally assumed that the predicted output of wind power is equal to the expected output of wind power (Baharvandi et al., 2018). Therefore, it can be assumed that ${\mu }_0=0$. In cases ${\mu }_0\ne 0$ or where wind power outputs are not mutually independent, the problem can still be solved after appropriate transformations (Calafiore et al., 2009).

4.1 Comparison of simulation results between TCC-OPF and DRJCC-OPF

Let ${\mu }_0=0$, ${\mathrm{\Gamma }}_0=0.003$ and $\epsilon =0.0105$ (Bian 2015). The simulation results comparison between TCC-OPF and DRJCC-OPF is illustrated in Figure 2 and Table 2.

Figure 2

Figure 2. The absolute deviation of line power flow from the thermal stability limit.

Table 2

Table 2. Simulation results of TCC-OPF and DRJCC-OPF.

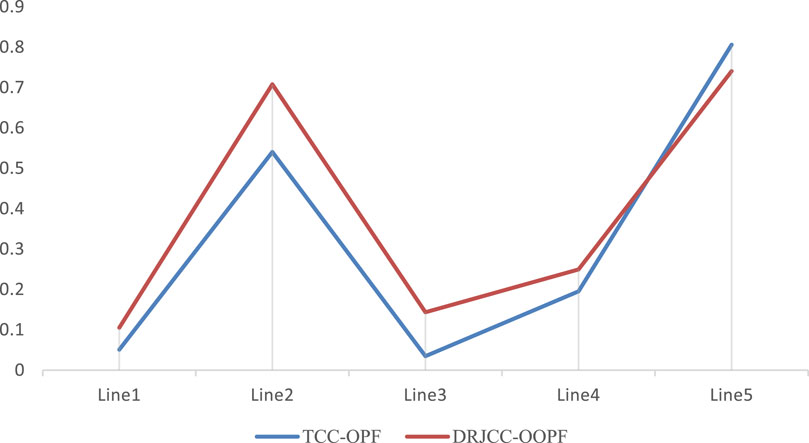
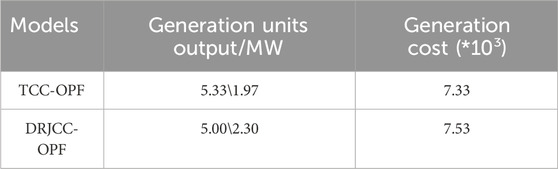
According to Table 2, it is evident that the generation cost in DRJCC-OPF is higher than that in TCC-OPF. This is because DRJCC-OPF represents a more conservative estimate, ensuring system compliance with safety requirements under the worst-case distribution. Additionally, from Figure 2, it can be observed that under DRJCC-OPF, the absolute deviation of line power flow is higher than that under TCC-OPF. This indicates a more uniform distribution of line power flow, making it less prone to overloads.

4.2 Simulation results for robust joint chance-constrained OPF

This section analyzes the impact of system operating parameters and wind power uncertainty parameters on the system generation cost. The system operating parameters include the confidence level of safe operation, which is the probability $1-\epsilon$ of satisfying the robust joint chance constraints. The wind power uncertainty parameters consist of the prediction reliability $\eta$ and the empirical estimate ${\mathrm{\Gamma }}_0$ reflecting the volatility of wind power forecasting errors.

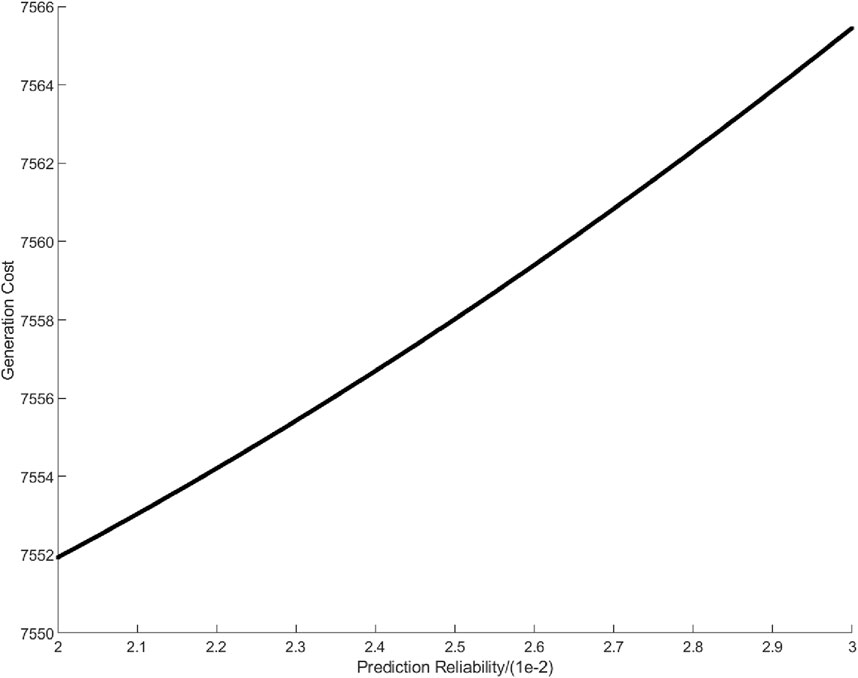
4.2.1 Impact of wind power prediction reliability on cost

Let $\epsilon =0.01$ and ${\mathrm{\Gamma }}_0=0.003$. Since it is assumed that the predicted output of wind power is equal to the expected output of wind power, this paper only considers the case of a smaller value of $\eta$, with values ranging from 0.02 to 0.03. The results of DRJCC-OPF are as follows:

Figure 3 shows that as the prediction reliability decreases (or increases), the generation cost increases. This is because when the prediction accuracy decreases, the system needs to dispatch generators, especially Generator 2 with greater regulating capacity, to cope with the fluctuations in uncertain parameters, leading to an increase in generation cost.

Figure 3

Figure 3. Graph of Generation Cost vs. Prediction Reliability.

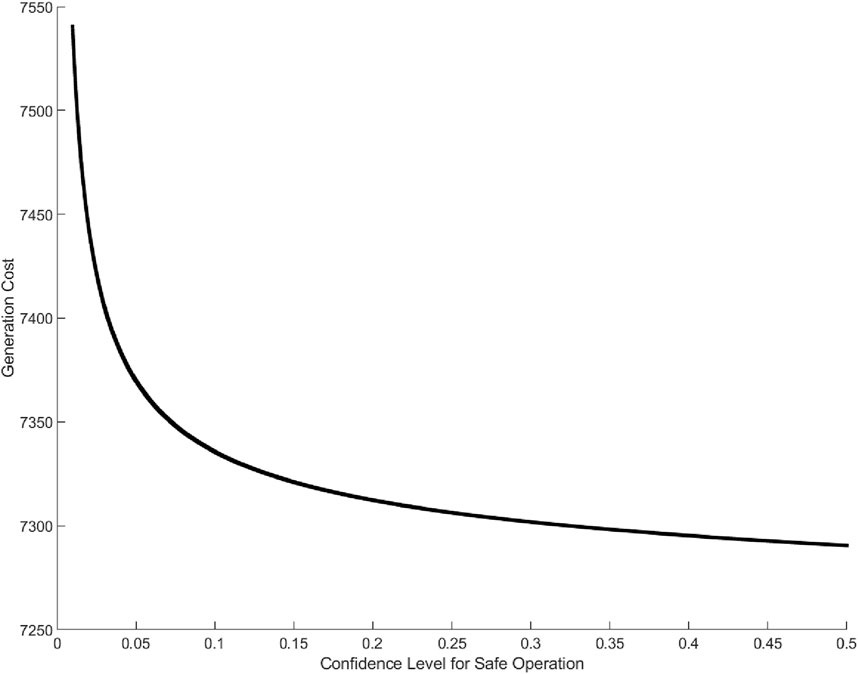
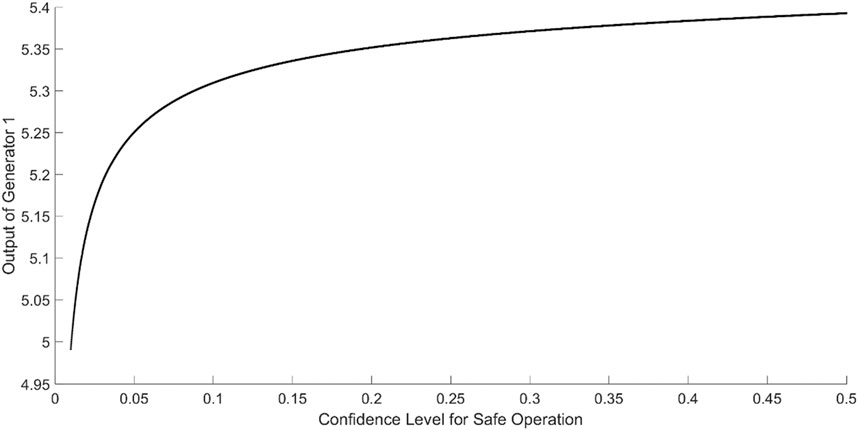
4.2.2 Impact of system safety operation confidence level on generation cost

Let $\eta =0$ and ${\mathrm{\Gamma }}_0=0.003$, $\epsilon$ ranging between 0.01 and 0.5, the results of DRJCC-OPF model are as follows:

Figure 4 indicates that with the relaxation of the system’s safety operation constraints, the generation cost decreases. In Figure 5, as the safety constraints increase, the controllable output of the generating units decreases to reserve more regulating capacity to cope with the fluctuations in wind power output. When the confidence level of violating chance constraints is greater than 0.1, the impact of safety constraints on the output of generating units is relatively small. This is because, in this case, the less strict system’s safety constraints demands less regulating capacity for the generating units. The generating units can operate under optimal conditions with lower impact. When the confidence level of violating chance constraints is less than 0.1, the safety constraints become more stringent, and further increasing the safety constraints significantly affects the output of generating units.

Figure 4

Figure 4. Graph of Generation Cost vs. Confidence Level for Safe Operation.

Figure 5

Figure 5. Graph of Output of Generator 1 vs. Confidence Level for Safe Operation.

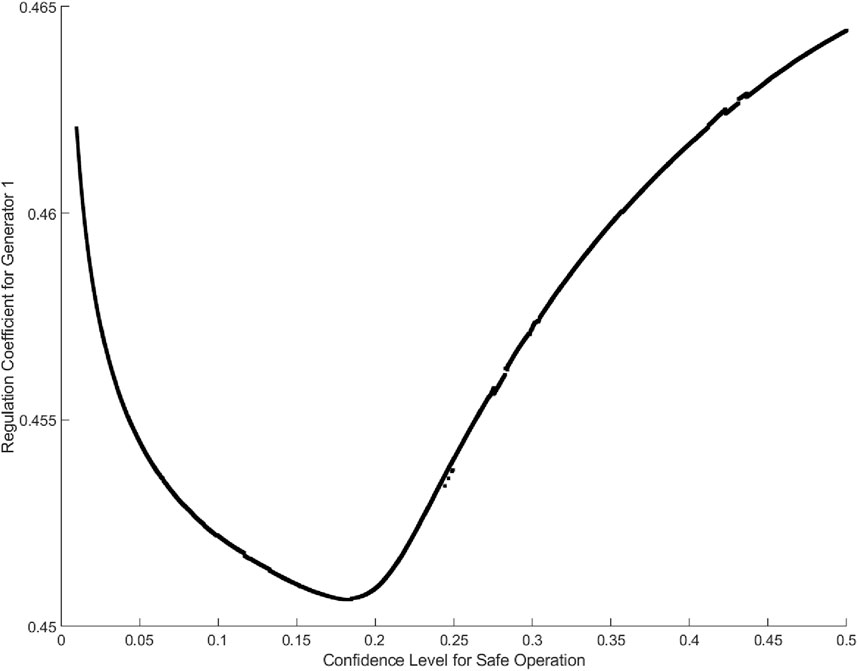
Moreover, combining Figures 5, 6, it can be observed that when $\epsilon \le 0.2$, the regulation coefficient of Generator 1 is constrained by its regulating capacity, leading to a decrease in the regulation coefficient. In contrast, when $\epsilon \ge 0.2$, the regulation coefficient of Generator 1 increases to reduce the generation cost. This demonstrates that the DRJCC-OPF model can flexibly adapt to different operational requirements of the system.

Figure 6

Figure 6. Graph of Regulation Coefficient for Generator 1 vs. Confidence Level for Safe Operation.

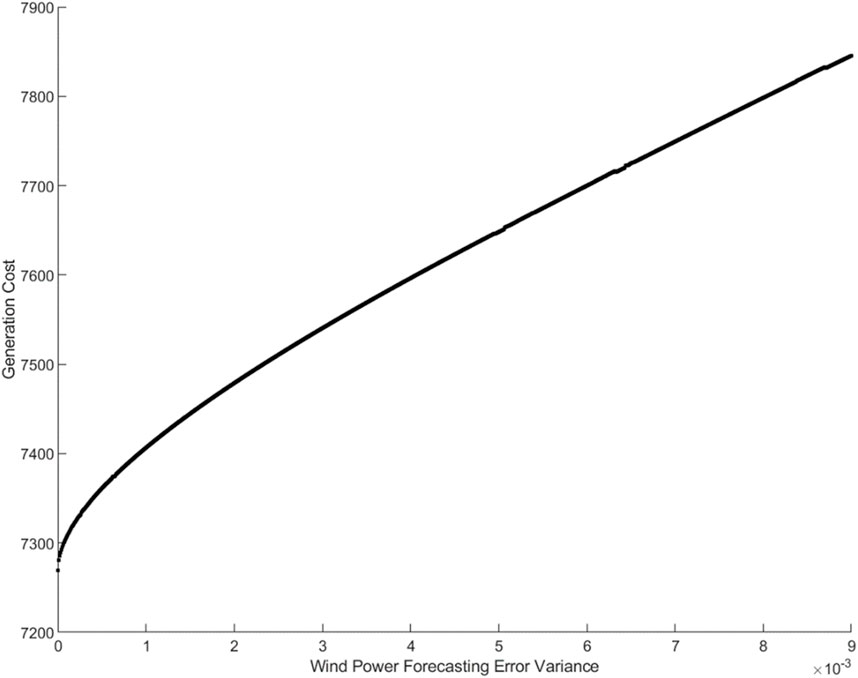
4.2.3 Impact of wind power output fluctuations on generation cost

Let $\eta =0$ and $\epsilon =0.01$, When the variance of wind power prediction errors ${\mathrm{\Gamma }}_0$ varies between 0.0 and 0.009, the results of DRJCC-OPF are as follows:

Figure 7 indicates that after an increase in wind power fluctuations, the system needs to increase the planned output of Generator 2 to maintain safe operation, leading to an increase in generation cost. Additionally, from Figure 8, it can be observed that considering wind power fluctuations, the system decreases the planned output of Generator 1 and increases the output of Generator 2 to enhance the system’s ability to cope with wind power fluctuations. At the same time, the regulation coefficient for Generator 1 rapidly decreases and then gradually increases. This is because when wind power fluctuations start to increase from zero, Generator 1 is constrained by the output limit, leading to a rapid decrease in its regulation coefficient. As Generator 1 deviates from the output limit due to a decrease in output, if wind power fluctuations continue to increase, the system gradually decreases the regulation coefficient for Generator 2 and increases the regulation coefficient for Generator 1 to reduce generation cost. This indicates that DRJCC-OPF can ensure safe and economic operation even when wind power fluctuations are significant.

Figure 7

Figure 7. Graph of Generation Cost vs. Wind Power Forecasting Error Variance.

Figure 8

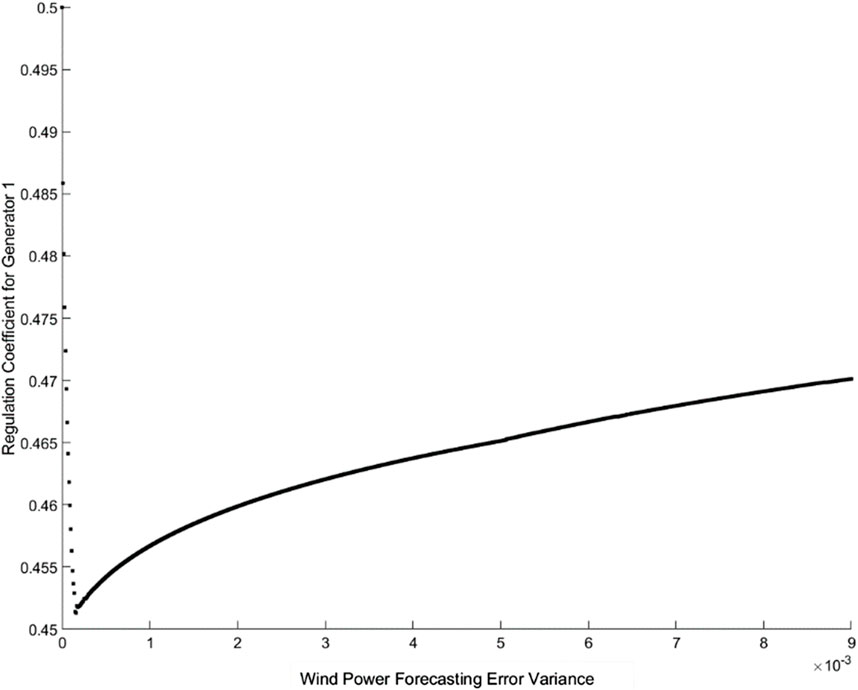
Figure 8. Graph of Regulation Coefficient for Generator 1 vs. Wind Power Forecasting Error Variance.

5 Conclusion

The large-scale integration of new energy sources, especially wind power, poses significant challenges to the secure operation of power systems. This paper focuses on the uncertainty in wind power prediction errors and proposes a probabilistic distribution robust joint chance-constrained optimal power flow model for wind power systems. This model can obtain scheduling schemes for thermal power units that ensure safe and economic operation under the worst-case wind power distribution. The analysis also explores the impact of factors such as prediction reliability, confidence level for safe system operation, and wind power fluctuations on system generation cost and unit dispatch strategies. This approach provides a new perspective for the economic dispatch of power systems incorporating renewable energy sources. The findings can serve as a reference for system operators and control personnel in managing power systems with renewable energy integration.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

LD: Investigation, Methodology, Writing–original draft. HX: Software, Validation, Writing–review and editing. PY: Data curation, Resources, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by Guangdong Basic and Applied Basic Research Foundation under Grant 2024A1515011537.

Conflict of interest

Author LD was employed by Guangzhou Power Supply Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Angizeh, F., Bae, J., Chen, J., Klebnikov, A., and Jafari, M. A. (2023). Impact assessment framework for grid integration of energy storage systems and renewable energy sources toward clean energy transition. IEEE Access 11, 134995–135005. doi:10.1109/ACCESS.2023.3337133

CrossRef Full Text | Google Scholar

Bacher, R., and Van Meeteren, H. P. (1988). Real-time optimal power flow in automatic generation control. IEEE Trans. Power Syst. 3, 1518–1529. doi:10.1109/59.192961

CrossRef Full Text | Google Scholar

Baharvandi, A., Aghaei, J., Niknam, T., Shafie-Khah, M., Godina, R., and Catalão, J. P. S. (2018). Bundled generation and transmission planning under demand and wind generation uncertainty based on a combination of robust and stochastic optimization. IEEE Trans. Sustain. Energy 9, 1477–1486. doi:10.1109/TSTE.2018.2789398

CrossRef Full Text | Google Scholar

Bian, Q. (2015). Transmission system planning considering uncertainty of wind power probability distribution. Power Syst. Autom. 20. doi:10.7500/AEPS20141029009

CrossRef Full Text | Google Scholar

Bian, Q., Xin, H., Wang, Z., Gan, D., and Wong, K. P. (2014). Distributionally robust solution to the reserve scheduling problem with partial information of wind power. IEEE Trans. Power Syst. 30, 2822–2823. doi:10.1109/TPWRS.2014.2364534

CrossRef Full Text | Google Scholar

Bienstock, D., Chertkov, M., and Harnett, S. (2012). Chance constrained optimal power flow: risk-aware network control under uncertainty. Siam Rev. 56 (3), 461–495. doi:10.1137/130910312

CrossRef Full Text | Google Scholar

Bofinger, S., Luig, A., and Beyer, H. G. “Qualification of wind power forecasts,” in Global Wind power Conference, Paris, France, 2002

Google Scholar

Calafiore, G., Topcu, U., and El Ghaoui, L. (2009). Parameter estimation with expected and residual-at-risk criteria. Syst. Control Lett. 58, 39–46. doi:10.1016/j.sysconle.2008.07.007

CrossRef Full Text | Google Scholar

Ding, K. (2014). Distributionally robust joint chance constrained problem under moment uncertainty. J. Appl. Math. 2014, 1–8. doi:10.1155/2014/487178

CrossRef Full Text | Google Scholar

Ela, E., and O'Malley, M. (2012). Studying the variability and uncertainty impacts of variable generation at multiple timescales. IEEE Trans. Power Syst. 27, 1324–1333. doi:10.1109/TPWRS.2012.2185816

CrossRef Full Text | Google Scholar

Fan, W., Tan, Q., Zhang, A., Ju, L., Wang, Y., Yin, Z., et al. (2023). A Bi-level optimization model of integrated energy system considering wind power uncertainty. Renew. Energy 202, 973–991. doi:10.1016/j.renene.2022.12.007

CrossRef Full Text | Google Scholar

Gao, H., Liu, J., and Wang, L. (2017). Robust coordinated optimization of active and reactive power in active distribution systems. IEEE Trans. Smart Grid 9, 4436–4447. doi:10.1109/TSG.2017.2657782

CrossRef Full Text | Google Scholar

Hua, W., Sasaki, H., Kubokawa, J., and Yokoyama, R. (1998). An interior point nonlinear programming for optimal power flow problems with a novel data structure. IEEE Trans. Power Syst. 13, 870–877. doi:10.1109/59.708745

CrossRef Full Text | Google Scholar

Kardoš, J., Kourounis, D., Schenk, O., and Zimmerman, R. (2022). BELTISTOS: a robust interior point method for large-scale optimal power flow problems. Electr. Power Syst. Res. 212, 108613. doi:10.1016/j.epsr.2022.108613

CrossRef Full Text | Google Scholar

Li, J., Lan, F., and Wei, H. (2015). A scenario optimal reduction method for wind power time series. IEEE Trans. Power Syst. 31, 1657–1658. doi:10.1109/TPWRS.2015.2412687

CrossRef Full Text | Google Scholar

Ma, R., Li, X., Luo, Y., Wu, X., and Jiang, F. (2019). Multi-objective dynamic optimal power flow of wind integrated power systems considering demand response. CSEE J. Power Energy Syst. 5, 466–473. doi:10.17775/CSEEJPES.2017.00280

CrossRef Full Text | Google Scholar

Morales, J. M., and Perez-Ruiz, J. (2007). Point estimate schemes to solve the probabilistic power flow. IEEE Trans. Power Syst. 22, 1594–1601. doi:10.1109/TPWRS.2007.907515

CrossRef Full Text | Google Scholar

Shi, L., Wang, C., Yao, L., Ni, Y., and Bazargan, M. (2012). Optimal power flow solution incorporating wind power. IEEE Syst. J. 6, 233–241. doi:10.1109/JSYST.2011.2162896

CrossRef Full Text | Google Scholar

Sun, W., Zamani, M., Zhang, H.-T., and Li, Y. (2019). Probabilistic optimal power flow with correlated wind power uncertainty via Markov chain quasi-monte-carlo sampling. IEEE Trans. Industrial Inf. 15, 6058–6069. doi:10.1109/TII.2019.2928054

CrossRef Full Text | Google Scholar

Wang, C., Sun, W., Yi, T., Yan, Z., and Zhang, Y. (2013). Review on energy storage application planning and benefit evaluation methods in smart grid. Zhongguo Dianji Gongcheng Xuebao/Proceedings Chin. Soc. Electr. Eng. 33, 33–41.

Google Scholar

Wang, X. (2003). Modern power system analysis. Science Press.

Google Scholar

Xiao, H., Gan, H., Yang, P., Li, L., and Hao, Q. (2024b). Robust submodule fault management in modular multilevel converters with nearest level modulation for uninterrupted power transmission. IEEE Trans. Power Deliv. 39, 931–946. doi:10.1109/TPWRD.2023.3343693

CrossRef Full Text | Google Scholar

Xiao, H., He, H., Zhang, L., and Liu, T. (2024a). Adaptive grid-synchronization based grid-forming control for voltage source converters. IEEE Trans. Power Syst. 39, 4763–4766. doi:10.1109/TPWRS.2023.3338967

CrossRef Full Text | Google Scholar

Zhang, C., Jian, J., and Yang, L. (2020). Regularised primal–dual interior-point method for dynamic optimal power flow with block-angular structures. IET Gener. Transm. Distrib. 14, 1694–1704. doi:10.1049/iet-gtd.2019.1528

CrossRef Full Text | Google Scholar

Zhang, Y., Han, X., Xu, B., Wang, M., Ye, P., and Pei, Y. (2018). Risk–based admissibility analysis of wind power integration into power system with energy storage system. IEEE Access 6, 57400–57413. doi:10.1109/ACCESS.2018.2870736

CrossRef Full Text | Google Scholar

Zymler, S., Kuhn, D., and Rustem, B. (2013). Distributionally robust joint chance constraints with second-order moment information. Math. Program. 137 (1-2), 167–198. doi:10.1007/s10107-011-0494-7

CrossRef Full Text | Google Scholar