- 1Industrial Training Centre, Shenzhen Polytechnic University, Shenzhen, China
- 2Department of Computer Science, Hong Kong Baptist University, Kowloon, Hong Kong, China
- 3College of Electrical and Information Engineering, Hunan University, Changsha, China
The intermittence and unpredictability of large-scale renewable integration poses significant challenges to the operation of the electricity market. New paradigms of the joint electricity spot market (EM) and ancillary service market (ASM) incorporating frequency regulation (FR) and flexible ramping product (FRP) are considered as potential solutions, addressing the challenge of limited compatibility in the electricity market with the widespread integration of renewable sources. This work focuses on three critical technical obstacles: optimizing the joint market mechanisms, constructing bidding models, and exploring algorithmic solutions. This paper presents a brief review of recent research on bidding mechanisms, models, and strategies for the electricity joint market with high-penetration renewable integration. Furthermore, challenges and future research prospects of these issues are also discussed.
1 Introduction
Global climate change problem has become increasingly serious in recent years, and reducing greenhouse gas emissions is one of the main challenges facing the industry. Burning fossil fuels at thermal power plants play a significant role in greenhouse emissions, accounting for over 60% of the European Union’s total emissions (Andersson and Börjesson, 2021). Therefore, decarbonizing power sector, i.e., promoting wide-scale penetration of renewable generation to replace thermal generators, has drawn considerable attention from academia and industry (Bistline and Blanford, 2021). Nevertheless, the uncertainty and intermittence of renewable generations also threaten the security of power grid operation.
Facing these new challenges, the electricity market is considered the macro-level approach to achieving power system operation security, economic efficiency, and environmental friendliness. In order to accommodate the vast amount of renewable generation resources, the emerging features of the worldwide electricity market can be summarized as follows: (1) High penetration distributed resources such as photovoltaics and wind power are more inclined to generate and participate in the electricity market as stakeholders. (2) The demand for balancing products in the ancillary service market (ASM) has increased due to the necessity of hedging uncertainties caused by high penetrations of renewable generations (Nelson and Johnson, 2020; Wang and Hobbs, 2015). For instance, the flexible ramping product (FRP) proposed by California ISO (CAISO) facilitates real-time (RT) balancing in a time slot of 5–15 min (Wang et al., 2020). Therefore, the joint energy spot market (EM) and ASM will become a dominant force in the global power industry, making it necessary to extensively study the joint market mechanism. This paper reviews the market mechanism optimization, the construction of the bidding models, and the algorithmic solutions.
2 Literature review
2.1 Current research on market mechanism optimization theory for large-scale penetration of renewable energy
Optimizing market mechanisms, typically grounded in microeconomic theory, involves the proposal of bidding or pricing mechanisms, which are then validated through equilibrium analysis. This process often models the market as an Equilibrium Problem with Equilibrium Constraints (EPEC). Worldwide research has explored the strategic bidding behaviors of large-scale renewable energy suppliers in electricity markets, such as wind farms, electric vehicle integrators, and energy storage facilities (Morales et al., 2010; Pousinho et al., 2013; Zugno et al., 2013; Alabdulwahab et al., 2016; Zou et al., 2016; Xiao et al., 2023). Some research has considered the collaborative operational bidding strategies of various renewable energy sources (Mohammadi et al., 2011; Vagropoulos et al., 2013; Agustin et al., 2016; Cao et al., 2024), while others have proposed short-term bidding strategies for virtual power plants that incorporate various flexibility resources (Rahimiyan and Baringo, 2016). Countries like Denmarkanticipate a complete transition to renewable energy for power supply by 2050, particularly in Northern Europe. However, China faces the challenge of being unable to replace fully traditional power plants with renewable energy sources in the short term (Jacobson et al., 2017). Consequently, when investigating the strategic bidding of large-scale renewable energy suppliers in the market, the presence of traditional power plants should not be overlooked alongside flexible resources like wind, solar, and energy storage. Furthermore, integrating carbon markets into the power market has prompted studies on the effects of European Union carbon emission trading rights and carbon emission costs on power market dynamics and generator bidding strategies (Weigt et al., 2013; Anke et al., 2020). With the spot market overlooking the carbon market’s impact on power market transactions, electricity-carbon market mechanisms operate relatively independently in regions such as Guangdong Province.
Research on market mechanisms varies depending on the type of market. Some focus on the bidding and settlement mechanisms of the energy quantity market from the generation side (Ela et al., 2016; Mozdawar et al., 2022; Silva-Rodriguez et al., 2022), while others concentrate on the pricing and deployment strategies of ancillary services, primarily frequency regulation (Arteaga and Zareipour, 2019; Maria Luisa et al., 2019; Godoy et al., 2020; Stavros et al., 2020; Luis et al., 2022). These studies explore various market clearing methods (deterministic or stochastic) and compensation mechanisms (pay-as-bid or opportunity cost payment). In the United States, markets such as CAISO and MISO independently trade, optimize, and price ramp capabilities, introducing a new ancillary service product, FRP (Casio, 2015; Navid and Rosenwald, 2024). This addition mitigates the uncertainty of system load and renewable energy variations, ensuring sufficient ramping capability to match net load changes and maintain system real-time balance. Although the introduction of FRP for joint market clearing can enhance the regulatory capacity of the system, research in this area is still in its nascent stages. Various studies have examined the market mechanisms of Energy Markets (EM) and Ancillary Service Markets (ASM) from different perspectives, including market time frames, equilibrium models based on non-strategic bidding (actual cost functions), incentive-compatible clearing mechanisms, and the formulation of Locational Marginal Pricing (LMP) (Sorourifar et al., 2018; Zhou et al., 2018; Wu et al., 2020; Zhang et al., 2020; Hu et al., 2021). In the joint optimization of the Energy Market (EM) and Ancillary Services Market (ASM), FPR does not possess the autonomy to bid independently.
The ultimate objective of optimizing market mechanisms is to maximize the overall social welfare of the integrated market. The mechanisms across different markets must be harmonized to gradually steer the bidding strategies of market participants towards Pareto optimality while preventing cross-market collusion arbitrage and market power abuse. For example, the compensation that market participants receive is tied to the difference between Day Ahead (DA) and real-time EM prices. If there are flaws in the market mechanisms, speculators can manipulate DA and real-time prices to reap substantial profits. However, the current evaluation of market mechanisms lacks quantitative indicators, making it challenging to verify their effectiveness. Indeed, existing market mechanisms, primarily established based on domestic and international experience and theoretical knowledge, are constrained by computational limitations. The efficiency and security of the market largely hinge on the bidding strategies of participants, but assessing the impact of market mechanisms on participants’ bidding strategy preferences remains a formidable challenge. Thus, optimizing market efficiency and stability through empirical market mechanisms is not feasible.
2.2 Current research on the multi-agent bidding model of the electricity market
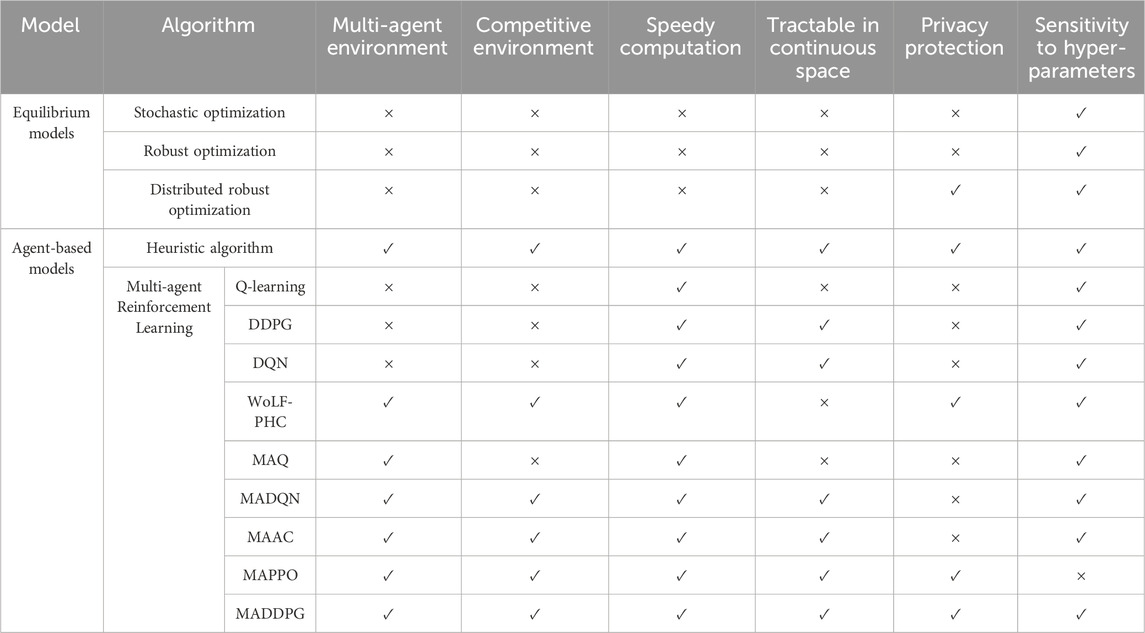
In the Multi-agent bidding model, human candidates with varying degrees of expertise in electricity markets will participate in the trading with a virtual market environment, representing different generation companies to submit their bids to maximize potential profits. After repeated bids submission, the game may gradually converge to the equilibrium, allowing for the detection of potential abuses of market power through the convergence procedure. The aforementioned process can be simulated as a two-layer bidding game model of GENCOs, and the solutions for this model are typically obtained through mathematical methods based on equilibrium models (Dou et al., 2016) and Agent-based Models (ABM) (Guevara C et al., 2012). A significant number of research on equilibrium models using mathematical programming focused on optimizing bidding strategies, including chance-constrained stochastic optimization (Zhao et al., 2018; Hosseini et al., 2020), robust optimization (Pousinho et al., 2015; Baringo and Sánchez Amaro, 2017), and distributional robust optimization (Han and Hug, 2020; Hajebrahimi et al., 2020). However, the diverse operational characteristics (such as on-and-off or up-and-down constraints for switches and generators) and the immense scale of expanded power networks render these problems highly dimensional, non-convex, and subject to non-observable uncertainty. Consequently, using traditional optimization tools in these contexts becomes exceedingly complex and imposes a substantial computational load. The existing research regarding scale and market rules is overly simplified compared to real-world electricity markets. ABM is typically more flexible, as it allows us to model all market participants individually and treat them as distinct agents. Each agent continuously updates its data through repeated interactions with the simulated market environment. After repeated bidding, the game may gradually converge to an equilibrium state. It should be noted that potential market power abuse phenomena can be discovered through the convergence process, resembling a real electricity market (Azadeh et al., 2012). In the ABM model, heuristic algorithm models are commonly used (Boonchuay and Ongsakul, 2011a; Elsakaan et al., 2018; Kong et al., 2019a; Hematabadi and Foroud, 2019; Du et al., 2021; Qiu et al., 2023), including genetic algorithms (GA) (Boonchuay and Ongsakul, 2011a), particle swarm optimization (PSO) (Kong et al., 2019a), artificial immune system algorithms (AIS) (Qiu et al., 2023), bacterial foraging optimization (BFO) (Elsakaan et al., 2018), krill herd algorithms (KHA) (Hematabadi and Foroud, 2019), and water wave optimization (WWO) (Du et al., 2021). These algorithms are inspired by the cooperative behaviors of gregarious animals, evolution, and heredity and have exhibited superior computational performance compared to conventional mathematical programming techniques. Model-based intuitive learning and applying genetic algorithms are utilized separately to determine the optimal bidding curves, as demonstrated in (Zhang et al., 2014; Weidlich and Veit, 2008). However, these algorithms are designed to formulate the bidding strategy of individual agents, where each agent makes decisions independently without considering the actions of the competitors. Although numerous studies (Boonchuay and Ongsakul, 2011b; Javaid et al., 2017; Kong et al., 2019b) have utilized group optimization algorithms to model the dynamic bidding process, these methods yield the optimal Pareto frontier in a cooperative setting, where agents can freely exchange search strategies. Nevertheless, this study aims to find the Nash Equilibrium within a competitive bidding environment. This necessitates fully distributed training that precludes any communication among the participating GENCOs. This strategy ensures privacy and mitigates the risk of collusion, thereby preserving the competitive integrity of the bidding process. Consequently, these methods prove unsuitable for a competitive market where each agent seeks to achieve its objectives by adjusting its behavior in response to other agents. As the model-free characteristic of reinforcement learning techniques, they eliminate the need for intricate mathematical modeling, empowering the agent to pursue the optimal decision more conveniently through direct interaction with the environment. The comparison of various electricity market bidding models is presented in Table 1.
2.3 Current research on bidding strategy algorithms of multi-agent market participant
This section comprehensively reviews the Reinforcement Learning (RL) fundamentals, encompassing all necessary concepts and algorithms that will be further utilized in elaborating the RL applications on marketized power systems presented in the subsequent sections. An RL algorithm comprises a model-based RL such as dynamic programming and model-free RL, further extending to value-based RL (including Q-learning, DQN and WoLF-PHC) and policy-search-based RL (including stochastic and deterministic policy gradient, Actor-critic (AC), Trust Region/Proximal Policy Optimization (TRPO/PPO), Deep Deterministic Policy Gradient (DDPG) methods). As a set of RL algorithms, numerous Q-learning algorithms have found broad application in the multi-agent electricity market for exploring bidding strategies. Najafi et al. (2019) present the development of a decentralized multi-agent model for bidding by Electric Vehicle (EV) owners, which is based on a Q-learning algorithm and crafted without the necessity for environmental modeling. For instance, Liu et al. (2021) introduced a quarter-hourly dynamic pricing strategy, leveraging the DDPG algorithm, to address the discretization issue encountered in traditional time-division pricing models. Lee et al. (2021) present an innovative energy trading system among Microgrids (MGs), incorporating a DDQN algorithm and a double Kelly strategy. Although these techniques have explored the dynamic interaction of numerous agents, the optimality search process relies on cooperation and communication among individual agents, which is inconsistent with competitive market bidding in the absence of knowledge about other rivals.
Qiu et al. (2023) and Elsakaan et al. (2018) employ the Multi-Agent-Based Models (MABM) for simulating market participant bidding models and consider the game issues of updating the multi-agent bidding strategies of energy suppliers in large power systems and regional integrated energy systems, respectively. However, in the process of making bidding decisions, multi-agents require historical bidding information of competitors. Although this model offers certain advantages compared to models with fully disclosed information, the real market is an incomplete information market. Indeed, in a real market, each participant only knows their own cost function and bidding strategy, lacking any information about other competitors (Hematabadi and Foroud, 2019). Moreover, market participants are unwilling to share their historical bidding information with competitors, rendering this algorithm still impractical for real-world market scenarios.
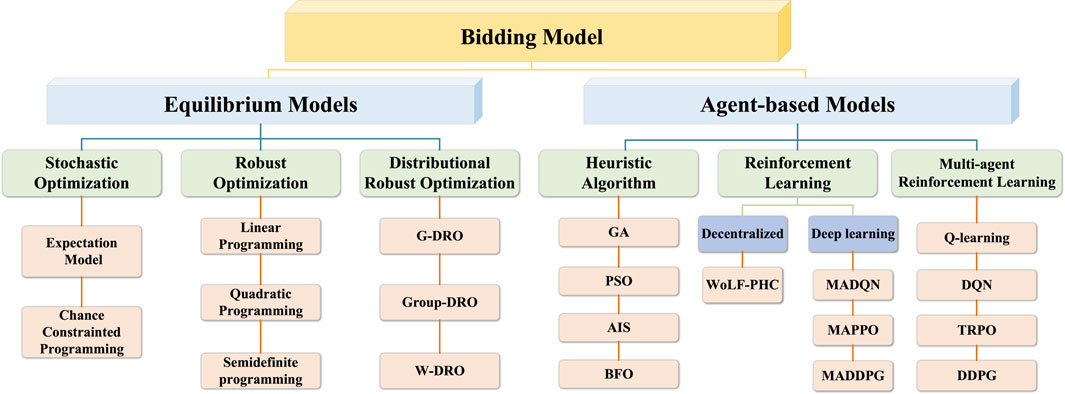
Zhao et al. (2022) list several Multi-agent Reinforcement Learning (MARL) methods and developed a time-varying model with an updating strategy to simulate bidding games with incomplete information. Gao et al. (2021) employ the WoLF-PHC method to ascertain the Nash Equilibrium (NE) in a pool-based energy market comprised of large-scaled wind turbines and EV aggregators. However, the computational performance is unstable with the increase of variables. Fang et al. (2021) introduce a market mechanism for double auctions in regional microgrids (MGs), utilizing a Multi-Agent Deep Q-Network (MADQN) algorithm to identify the optimal bidding strategy for these MGs. Furthermore, an Optimal Equilibrium Selection (OES) is proposed to guarantee benefit fairness, execution efficiency, and privacy protection during the interactive learning process of MADQN. Ye et al. (2023) introduced a generalized strategic bidding model for energy producers and solved it using the Deep Deterministic Policy Gradient (DDPG) method, which uses a neural network to estimate the optimal Q function. However, this algorithm based on policy gradient descent is constrained by the instability of the learning environment and the interaction of multiple agents, rendering it unsuitable for multi-agent environments. In Xu et al. (2018), Qiu et al. (2021), Li et al. (2022), and Mehdipourpicha et al. (2023), the Multi-agent Deep Deterministic Policy Gradient (MADDPG) algorithm and its modified versions were used to simulate the bidding game in competitive electricity markets taking into account privacy protection. Overall, the computational performance of existing RL algorithms is highly sensitive to hyperparameters. Therefore, for the bidding simulation of large-scale electricity markets, adjusting hyperparameters significantly impacts them and affects simulation convergence’s stability. Moreover, pressure on storage space can also make equilibrium point calculations time-consuming and challenging. The applicability of these MARL algorithms in bidding strategy is compared as shown in Table 1. The bidding model with corresponding algorithms is summarized as Figure 1.
3 Challenges and future trends
Although the research mentioned above has played a significant role in integrating renewable energy into the optimal mechanism of the emerging joint energy and ancillary service market, this paper proposes three major technical challenges and future trends:
(1) Integrating large-scale renewable energy entities into the combined electricity spot and ancillary services markets has rendered the research into power market mechanisms increasingly complex. The inherent intermittency of renewable energy sources poses substantial threats to the reliability and safety of the power system, consequently impacting the dispatching, investment, and operation of the electricity market. Inadequate market mechanisms may lead to some renewable energy participants engaging in detrimental price competition or exploiting market power to establish monopolies, thereby affecting overall societal welfare and market efficiency. Furthermore, there has been little research on how to optimize the market mechanisms and improve market operational efficiency. With the penetration of large-scale renewable energy, future research could focus on investigating integrated electricity market mechanisms to address the aforementioned challenges. Integrated market encompasses the Energy Market (EM) and the Ancillary Services Market (ASM), which includes components such as Frequency Regulation (FR) and Flexible Ramping Product (FRP). It would be beneficial to develop pertinent evaluation metrics to optimize these market mechanisms effectively.
(2) The bidding model utilized in the current electricity market trading mechanisms is overly simplified, particularly in the market scale, the simulation of participant bidding strategies, and market rules. Compared to the real electricity market, this excessive simplification leads to a lack of reliability and credibility in the simulated results of the model. In response to the issues outlined above, future research should focus on MABM to simulate the bidding behavior of market participants in a competitive market environment. The model will explore the relationship among factors such as bidding, profitability, and market settlement conditions to validate and iteratively optimize the market mechanisms.
(3) Existing methodologies employed to solve bidding models of multi-agent market participants encounter limitations in computational performance. This is particularly evident in the bidding simulations of large-scale electricity markets, where adjusting hyperparameters in reinforcement learning methods can significantly impact the algorithm’s convergence performance. Further research should explore a multi-agent deep reinforcement learning algorithm for the bidding model of market participants. The method safeguards agents’ privacy, allowing them to fully exert their autonomy in bidding without any information exchange among them. Moreover, this approach successfully mitigates the influence of hyperparameters and exhibits excellent convergence properties.
4 Conclusion
In a carbon-constrained environment, the fundamental purpose of market mechanisms, with the electricity market as the primary tool, is to promote the development of the electricity industry towards cleaner, more efficient, and lower-carbon directions. It also aims to facilitate the large-scale penetration of renewable energy generation replacing fossil-fuel-based power generation. The intermittent and uncertain nature of large-scale renewable energy grid-integrated generation poses significant challenges to the operation of electricity markets. To address the issue of suboptimal compatibility in electricity markets, this paper reviews three aspects: the optimization of mechanisms in the integrated market of electricity spot and ancillary services, the construction of bidding models, and the resolution of associated algorithms. In addition, the challenges and potential future developments in the field are also discussed.
Author contributions
XG: Conceptualization, Writing–original draft, Writing–review and editing. CY: Data curation, Formal Analysis, Writing–review and editing. ZZ: Visualization, Writing–original draft. YW: Visualization, Writing–review and editing. YC: Visualization, Writing–original draft. ZM: Visualization, Writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is sponsored by Scientific Research Startup Fund for Shenzhen High-Caliber Personnel of SZPT (No. 6022310042k).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Agustin, S., Jamshid, A., Miadreza, S., Sanchez de la Nieta, A. A., and Catalao, J. P. S. (2016). Risk-constrained offering strategy for aggregated hybrid power plant including wind power producer and demand response provider. IEEE Trans. Sustain. Energy 7, 513–525. doi:10.1109/TSTE.2015.2500539
Alabdulwahab, A., Abusorrah, A., and Wu, H. (2016). A game theoretic approach to risk-based optimal bidding strategies for electric vehicle aggregators in electricity markets with variable wind energy resources. IEEE Trans. Sustain. Energy 7, 374–385. doi:10.1109/TSTE.2015.2498200
Andersson, Ö., and Börjesson, P. (2021). The greenhouse gas emissions of an electrified vehicle combined with renewable fuels: life cycle assessment and policy implications. Appl. Energy 289, 116621. doi:10.1016/j.apenergy.2021.116621
Anke, C., Hobbies, H., Schreiber, S., and Möst, D. (2020). Coal phase-outs and carbon prices: interactions between EU emission trading and national carbon mitigation policies. Energy Policy 144, 111647. doi:10.1016/j.enpol.2020.111647
Arteaga, J., and Zareipour, H. (2019). A price-maker/price-taker model for the operation of battery storage systems in electricity markets. IEEE Trans. Smart Grid 10, 6912–6920. doi:10.1109/TSG.2019.2913818
Azadeh, A., Pourvalikhan Nokhandan, B., and Sheikhalishahi, M. (2012). A new genetic algorithm approach for optimizing bidding strategy viewpoint of profit maximization of a generation company. Expert Syst. Appl. 39, 1565–1574. doi:10.1016/j.eswa.2011.05.015
Baringo, L., and Sánchez Amaro, R. (2017). A stochastic robust optimization approach for the bidding strategy of an electric vehicle aggregator. Electr. power Syst. Res. 146, 362–370. doi:10.1016/j.epsr.2017.02.004
Bistline, J., and Blanford, G. (2021). Impact of carbon dioxide removal technologies on deep decarbonization of the electric power sector. Nat. Commun. 12, 3732. doi:10.1038/s41467-021-23554-6
Boonchuay, C., and Ongsakul, W. (2011a). Optimal risky bidding strategy for a generating company by self-organising hierarchical particle swarm optimisation. Energy Convers. Manag. 52, 1047–1053. doi:10.1016/j.enconman.2010.08.033
Boonchuay, C., and Ongsakul, W. (2011b). Optimal risky bidding strategy for a generating company by self-organising hierarchical particle swarm optimisation. Energy Convers. Manag. 52, 1047–1053. doi:10.1016/j.enconman.2010.08.033
Cao, Y., Zhou, B., Chung, C. Y., Wu, T., Zheng, L., and Shuai, Z. (2024). A coordinated emergency response scheme for electricity and watershed networks considering spatio-temporal heterogeneity and volatility of rainstorm disasters. IEEE Trans. Smart Grid, 1. doi:10.1109/TSG.2024.3362344
Casio Flexible ramping product revised draft final proposal (2015). Available at: http://www.caiso.com/Documents/DraftFinalTechnicalAppendix-FlexibleRampingProduct.pdf.
Dou, C., Yue, D., Li, X., and Xue, Y. (2016). MAS-based management and control strategies for integrated hybrid energy system. IEEE Trans. Industrial Inf. 12, 1332–1349. doi:10.1109/TII.2016.2569506
Du, Y., Li, F., Zandi, H., and Xue, Y. (2021). Approximating nash equilibrium in day-ahead electricity market bidding with multi agent deep reinforcement learning. J. Mod. power Syst. clean energy 9, 534–544. doi:10.35833/MPCE.2020.000502
Ela, E., Milligan, M., Bloom, A., Botterud, A., Townsend, A., Levin, T., et al. (2016). Wholesale electricity market design with increasing levels of renewable generation: incentivizing flexibility in system operations. Electr. J. 29, 51–60. doi:10.1016/j.tej.2016.05.001
Elsakaan, A. A., El-Sehiemy, R. A., Kaddah, S. S., and Elsaid, M. I. (2018). An enhanced moth-flame optimizer for solving non-smooth economic dispatch problems with emissions. Energy 157, 1063–1078. doi:10.1016/j.energy.2018.06.088
Fang, X., Zhao, Q., Wang, J., Han, Y., and Li, Y. (2021). Multi-agent deep reinforcement learning for distributed energy management and strategy optimization of microgrid market. Sustain. cities Soc. 74, 103163. doi:10.1016/j.scs.2021.103163
Gao, X., Chan, K. W., Xia, S., Zhang, X., Zhang, K., and Zhou, J. (2021). A multiagent competitive bidding strategy in a pool-based electricity market with price-maker participants of WPPs and EV aggregators. IEEE Trans. industrial Inf. 17, 7256–7268. doi:10.1109/TII.2021.3055817
Godoy, G., Lez, D., and Gil, E. (2020). Ramping ancillary service for cost-based electricity markets with high penetration of variable renewable energy. Energy Econ. 85, 104556. doi:10.1016/j.eneco.2019.104556
Guevara C, J. Y., Palma B, R., and Uribe, R. (2012). Experimental economics for teaching the functioning of electricity markets. IEEE Trans. Educ., doi:10.1109/TE.2012.2189886
Hajebrahimi, A., Kamwa, I., Abdelaziz, M. M. A., and Moeini, A. (2020). Scenario-wise distributionally robust optimization for collaborative intermittent resources and electric vehicle aggregator bidding strategy. IEEE Trans. power Syst. 35, 3706–3718. doi:10.1109/TPWRS.2020.2985572
Han, X., and Hug, G. (2020). A distributionally robust bidding strategy for a wind-storage aggregator. Electr. power Syst. Res. 189, 106745. doi:10.1016/j.epsr.2020.106745
Hematabadi, A. A., and Foroud, A. A. (2019). Optimizing the multi-objective bidding strategy using min–max technique and modified water wave optimization method. Neural Comput. Appl. 31, 5207–5225. doi:10.1007/s00521-018-3361-0
Hosseini, S. A., Toubeau, J.-F., De Grève, Z., and Vallée, F. (2020). An advanced day-ahead bidding strategy for wind power producers considering confidence level on the real-time reserve provision. Appl. energy 280, 115973. doi:10.1016/j.apenergy.2020.115973
Hu, Q., Zhu, Z., Bu, S., Wing Chan, K., and Li, F. (2021). A multi-market nanogrid P2P energy and ancillary service trading paradigm: mechanisms and implementations. Appl. energy 293, 116938. doi:10.1016/j.apenergy.2021.116938
Jacobson, M. Z., Delucchi, M. A., Bauer, Z. A. F., Goodman, S. C., Chapman, W. E., and Cameron, M. A. (2017). 100% clean and renewable wind, water, and sunlight all-sector energy roadmaps for 139 countries of the world. Joule 1, 108–121. doi:10.1016/j.joule.2017.07.005
Javaid, N., Javaid, S., Abdul, W., Ahmed, I., Almogren, A., Alamri, A., et al. (2017). A hybrid genetic wind driven heuristic optimization algorithm for demand side management in smart grid. Energies 10, 319. doi:10.3390/en10030319
Kong, X., Liu, D., xiao, J., and Wang, C. (2019a). A multi-agent optimal bidding strategy in microgrids based on artificial immune system. Energy 189, 116154. doi:10.1016/j.energy.2019.116154
Kong, X., Liu, D., Xiao, J., and Wang, C. (2019b). A multi-agent optimal bidding strategy in microgrids based on artificial immune system. Energy 189, 116154. doi:10.1016/j.energy.2019.116154
Lee, S., Seon, J., Kyeong, C., Kim, S., Sun, Y., and Kim, J. (2021). Novel energy trading system based on deep-reinforcement learning in microgrids. Energies 14, 5515. doi:10.3390/en14175515
Li, J., Yu, T., and Zhang, X. (2022). Coordinated load frequency control of multi-area integrated energy system using multi agent deep reinforcement learning. Appl. Energy 306, 117900. doi:10.1016/j.apenergy.2021.117900
Liu, D., Wang, W., Wang, L., Jia, H., and Shi, M. (2021). Dynamic pricing strategy of electric vehicle aggregators based on DDPG reinforcement learning algorithm. IEEE access 9, 21556–21566. doi:10.1109/ACCESS.2021.3055517
Luis, B., Carlos, M., and Zhou, Y. (2022). Assigning shadow prices to synthetic inertia and frequency response reserves from renewable energy sources. IEEE Trans. Sustain. Energy. doi:10.1109/TSTE.2022.3198324
Maria Luisa, D., Pierluigi, G., and Giuseppe, M. (2019). Ancillary services in the energy blockchain for microgrids. IEEE Trans. Industry Appl., doi:10.1109/TIA.2019.2909496
Mehdipourpicha, H., Rui, B., and Siyuan, W. (2023). Optimal offering strategy of GenCo with joint participation in FTR auction and day-ahead market considering virtual bidding. IEEE Trans. Power Syst. 38, 2247–2260. doi:10.1109/TPWRS.2022.3189592
Mohammadi, J., Rahimi-Kian, A., and Ghazizadeh, M. (2011). Aggregated wind power and flexible load offering strategy. IET Renew. Power Gener. 5, 439. doi:10.1049/iet-rpg.2011.0066
Morales, J., Conejo, A., and Pérez-Ruiz, J. (2010). Short-term trading for a wind power producer. IEEE Trans. Power Syst. 25, 554–564. doi:10.1109/TPWRS.2009.2036810
Mozdawar, S., Akbari, A., and Amirahmadi, M. (2022). Interdependent electricity markets design: market power and gaming. Int. J. Electr. Power & Energy Syst. 136, 107641. doi:10.1016/j.ijepes.2021.107641
Najafi, S., Shafie-khah, M., Siano, P., Wei, W., and Catalão, J. P. (2019). Reinforcement learning method for plug-in electric vehicle bidding. IET Smart Grid 2, 529–536. doi:10.1049/iet-stg.2018.0297
Navid, N., and Rosenwald, G. (2024). EnergRamp capability product design for MISO markets. MISO Mark. Dev. Analysis. Available at: https://www.misoenergy.org/Library/Repository/Communication%20Material/Key%20Presentations%20and%20Whitepapers/Ramp%20Product%20Conceptual%20Design%20Whitepaper.pdf.
Nelson, J., and Johnson, N. (2020). Model predictive control of microgrids for real-time ancillary service market participation. Appl. Energy 269, 114963. doi:10.1016/j.apenergy.2020.114963
Pousinho, H., Contreras, J., Bakirtzis, A., and Catalao, J. P. S. (2013). Risk-constrained scheduling and offering strategies of a price-maker hydro producer under uncertainty. IEEE Trans. Power Syst. 28, 1879–1887. doi:10.1109/TPWRS.2012.2229473
Pousinho, H. M. I., Contreras, J., Pinson, P., and Mendes, V. (2015). Robust optimisation for self-scheduling and bidding strategies of hybrid CSP–fossil power plants. Int. J. Electr. power & energy Syst. 67, 639–650. doi:10.1016/j.ijepes.2014.12.052
Qiu, D., Ye, Y., Papadaskalopoulos, D., and Strbac, G. (2021). Scalable coordinated management of peer-to-peer energy trading: a multi-cluster deep reinforcement learning approach. Appl. energy 292, 116940. doi:10.1016/j.apenergy.2021.116940
Qiu, Y., Li, Q., Ai, Y., Chen, W., Benbouzid, M., Liu, S., et al. (2023). Two-stage distributionally robust optimization-based coordinated scheduling of integrated energy system with electricity-hydrogen hybrid energy storage. Prot. Control Mod. Power Syst. 8, 33. doi:10.1186/s41601-023-00308-8
Rahimiyan, M., and Baringo, L. (2016). Strategic bidding for a virtual power plant in the day-ahead and real-time markets: a price-taker robust optimization approach. IEEE Trans. Power Syst. 31, 2676–2687. doi:10.1109/TPWRS.2015.2483781
Silva-Rodriguez, L., Sanjab, A., Fumagalli, E., Virag, A., and Gibescu, M. (2022). Short term wholesale electricity market designs: a review of identified challenges and promising solutions. Renew. Sustain. Energy Rev. 160, 112228. doi:10.1016/j.rser.2022.112228
Sorourifar, F., Zavala, V. M., and Alexander, W. (2018). Integrated multiscale design, market participation, and replacement strategies for battery energy storage systems. IEEE Trans. Sustain. Energy. doi:10.1109/TSTE.2018.2884317
Stavros, K., Jannick, G., Gabriela, H., Aristidou, P., and Hug, G. (2020). Active distribution grids offering ancillary services in islanded and grid connected mode. IEEE Trans. Smart Grid 11, 623–633. doi:10.1109/TSG.2019.2927299
Vagropoulos, S., Simoglou, C., and Bakirtzis, A. (2013). Synergistic supply offer and demand bidding strategies for wind producers and electric vehicle aggregators in day-ahead electricity markets, Bulk Power Syst. Dyn. Control-IX Optim. Secur. Control Emerg. Power Grid. doi:10.1109/IREP.2013.6629390
Wang, B., and Hobbs, B. (2015). Real-time markets for flexiramp: a stochastic unit commitment-based analysis. IEEE Trans. Power Syst. 31, 846–860. doi:10.1109/TPWRS.2015.2411268
Wang, J., Jiang, C., Zhang, H., Ren, Y., Chen, K. C., and Hanzo, L. (2020). Thirty years of machine learning: the road to Pareto-Optimal wireless networks. IEEE Commun. Surv. Tutorials 22, 1472–1514. doi:10.1109/COMST.2020.2965856
Weidlich, A., and Veit, D. (2008). A critical survey of agent-based wholesale electricity market models. Energy Econ. 30, 1728–1759. doi:10.1016/j.eneco.2008.01.003
Weigt, H., Ellerman, D., and Delarue, E. (2013). CO2 abatement from renewables in the German electricity sector: does a CO2 price help? Energy Econ. 40, S149–S158. doi:10.1016/j.eneco.2013.09.013
Wu, Y., Shi, J., Lim, G. J., Fan, L., and Molavi, A. (2020). Optimal management of transactive distribution electricity markets with co-optimized bidirectional energy and ancillary service exchanges. IEEE Trans. Smart Grid 11, 4650–4661. doi:10.1109/TSG.2020.3003244
Xiao, D., Chen, H., Cai, W., Wei, C., and Zhao, Z. (2023). Integrated risk measurement and control for stochastic energy trading of a wind storage system in electricity markets. Prot. Control Mod. Power Syst. 8, 60. doi:10.1186/s41601-023-00329-3
Xu, H., Zhang, K., and Zhang, J. (2018). Optimal joint bidding and pricing of profit-seeking load serving entity. IEEE Trans. Power Syst. 33, 5427–5436. doi:10.1109/TPWRS.2018.2821132
Ye, Y., Papadaskalopoulos, D., Yuan, Q., Tang, Y., and Strbac, G. (2023). Multi-agent deep reinforcement learning for coordinated energy trading and flexibility services provision in local electricity markets. IEEE Trans. Smart Grid 14, 1541–1554. doi:10.1109/TSG.2022.3149266
Zhang, J., Yuan, X., and Yuan, Y. (2014). A novel genetic algorithm based on all spanning trees of undirected graph for distribution network reconfiguration. J. Mod. Power Syst. Clean Energy 2, 143–149. doi:10.1007/s40565-014-0056-0
Zhang, K., Troitzsch, S., Hanif, S., and Hamacher, T. (2020). Coordinated market design for peer-to-peer energy trade and ancillary services in distribution grids. IEEE Trans. smart grid 11, 2929–2941. doi:10.1109/TSG.2020.2966216
Zhao, T., Pan, X., Yao, S., Ju, C., and Li, L. (2018). Strategic bidding of hybrid AC/DC microgrid embedded energy hubs: a two-stage chance constrained stochastic programming approach. IEEE Trans. Sustain. energy 11, 116–125. doi:10.1109/TSTE.2018.2884997
Zhao, Z., Feng, C., and Liu, A. L. (2022). Comparisons of auction designs through multiagent learning in peer-to-peer energy trading. IEEE Trans. Smart Grid 14, 593–605. doi:10.1109/TSG.2022.3190814
Zhou, Y., Wei, Z., Sun, G., Cheung, K. W., Zang, H., and Chen, S. (2018). A robust optimization approach for integrated community energy system in energy and ancillary service markets. Energy 148, 1–15. doi:10.1016/j.energy.2018.01.078
Zou, P., Chen, Q., Xia, Q., He, G., Kang, C., and Conejo, A. J. (2016). Pool equilibria including strategic storage. Appl. Energy 177, 260–270. doi:10.1016/j.apenergy.2016.05.105
Keywords: renewable sources, spot market, ancillary service market, market mechanisms, bidding model
Citation: Gao X, Yang C, Zhu Z, Wu Y, Chen Y and Mu Z (2024) A mini-review on trading mechanisms of emerging joint energy markets with high shares of renewables. Front. Energy Res. 12:1391813. doi: 10.3389/fenrg.2024.1391813
Received: 26 February 2024; Accepted: 05 April 2024;
Published: 17 April 2024.
Edited by:
Kaiping Qu, China University of Mining and Technology, ChinaReviewed by:
Li Lin, North China Electric Power University, ChinaGaoqi Liang, Harbin Institute of Technology, Shenzhen, China
Copyright © 2024 Gao, Yang, Zhu, Wu, Chen and Mu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chongming Yang, eWFuZ2Nob25nbWluZzMxOEBzenB1LmVkdS5jbg==
 Xiang Gao
Xiang Gao Chongming Yang1*
Chongming Yang1*