Optimal scheduling of electricity-hydrogen coupling virtual power plant considering hydrogen load response

With the rapid development of hydrogen production by water electrolysis, the coupling between the electricity-hydrogen system has become closer, providing an effective way to consume surplus new energy generation. As a form of centralized management of distributed energy resources, virtual power plants can aggregate the integrated energy production and consumption segments in a certain region and participate in electricity market transactions as a single entity to enhance overall revenue. Based on this, this paper proposes an optimal scheduling model of an electricity-hydrogen coupling virtual power plant (EHC-VPP) considering hydrogen load response, relying on hydrogen to ammonia as a flexibly adjustable load-side resource in the EHC-VPP to enable the VPP to participate in the day-ahead energy market to maximize benefits. In addition, this paper also considers the impact of the carbon emission penalty to practice the green development concept of energy saving and emission reduction. To validate the economy of the proposed optimization scheduling method in this paper, the optimization scheduling results under three different operation scenarios are compared and analyzed. The results show that considering the hydrogen load response and fully exploiting the flexibility resources of the EHC-VPP can further reduce the system operating cost and improve the overall operating efficiency.

1 Introduction

Optimizing the energy structure based on fossil energy and developing clean energy networks have become one of the important ways to solve energy depletion and environmental problems in the world (Rafique et al., 2018). However, the large-scale integration of new energy power generation has brought a severe test to the power system security and stability (Li, 2022; Wang et al., 2023). On the one hand, the output of renewable energy has great uncertainty, which puts forward higher requirements for the regulation ability of the power grid (Zhao et al., 2023). It is an urgent problem to stabilize the volatility of renewable energy power generation. On the other hand, with the increasing installed capacity of renewable energy, the problem of abandoning wind and light is becoming more and more serious. It is also one of the challenges to fully absorb renewable energy and improve energy efficiency.

As an independent subject of aggregating distributed flexible resources, virtual power plant (VPP) has the characteristics of bidirectional power flow (Gholami et al., 2022; Li et al., 2022). It can not only be used as a controllable power source to intensify the power supply capacity and provide peaking services for the power grid (Li et al., 2023), but also as a controllable load to boost the consumption of power, cooperate with the system to realize valley filling, moderate the output and demand of the system, and ensure the power system stability. In addition to protecting the operation of the power system to earn compensation benefits, VPP can also engage in the power market at all levels such as capacity and electricity as an independent subject, and obtain economic benefits through market transactions (Wu et al., 2022). Tan et al. (2023) added operation constraints considering demand response to VPP operation constraints, and constructed a VPP cost model considering the influence of uncertainty, which effectively reduces the charging cost of users using VPP to participate in reverse power supply. Priyanka et al. (2022) proposed a multi-stage stochastic programming method to simulate the participation of VPPs in the intraday power market transactions.

However, most of the above studies focus on the operation regulation of power system resources, while ignoring the flexible resources of hydrogen energy systems. As a clean energy, hydrogen energy has the characteristics of high energy density, large capacity, easy storage, and transmission (Zhou et al., 2023). With the speedy development of hydrogen production by water electrolysis technology, the coupling between electric-hydrogen systems is closer, which provides an effective way to absorb surplus new energy power generation (Ma et al., 2023). Pei et al. (2022) proposed the modeling method of electrolytic cells under various hydrogen production systems and considered the operation constraints and static and dynamic characteristics of hydrogen energy storage systems in DC microgrids. BAN et al. (2017) proposed an energy center with both electrolytic cell and gas power generation facilities and verified the feasibility of the operation mode and its effectiveness in wind power consumption.

At present, hydrogen, as an important chemical raw material, plays an indispensable role in ammonia synthesis (Miao et al., 2022) and other chemical fields. The hydrogen chemical industry park with hydrogen as the main raw material is widespread in northern China (Lin and Cai, 2023). At the same time, the load characteristics of the chemical industry determine that it has the potential to participate in the demand side response (Wang et al., 2023), which can provide adjustable flexibility resources for the power system. Therefore, it is necessary to study the electricity-hydrogen coupling virtual power plant (EHC-VPP) to aggregate the electricity-hydrogen coupling resources in the region to achieve renewable energy consumption.

In summary, this paper models a detailed model of the whole process of the hydrogen energy system. Regarding hydrogen fuel cell (HFC) and hydrogen to ammonia (H2A) as dispatchable resources, an EHC-VPP economic dispatch model considering hydrogen load response is proposed to fully exploit its flexibility. To minimize the cost of the EHC-VPP, the model considers the operational constraints of the power system and hydrogen system, and simulates the optimal scheduling of the coupling system. A carbon emission penalty is also added to realize the green development of energy saving and emission reduction.

2 Operational framework of EHC-VPP considering hydrogen load response

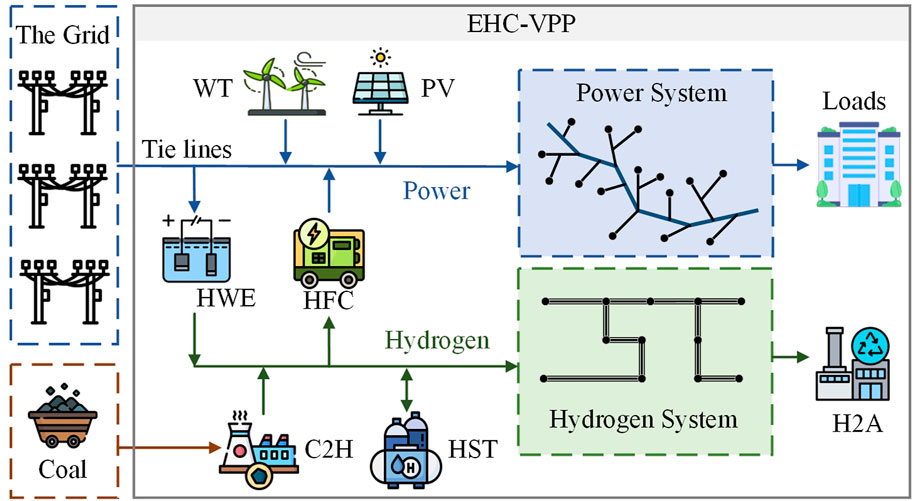
The operation architecture of the EHC-VPP studied in this paper is shown in Figure 1, which is composed of wind turbine (WT), photovoltaic (PV), coal to hydrogen (C2H), hydrogen production by water electrolysis (HWE), hydrogen storage tank (HST), H2A, HFC, and other equipment. Among them, the hydrogen energy system can realize the mutual conversion of electricity and hydrogen through the coupling of electrolytic cells, HFC, and other equipment with the power grid. As a load-side resource that can be flexibly adjusted, H2A can provide demand response to achieve peak shaving and valley filling, which helps to improve system flexibility. At the same time, the EHC-VPP participates in the day-ahead market for electricity trading in the form of price recipients (Zhao et al., 2021).

FIGURE 1

FIGURE 1. The operational framework of EHC-VPP.

3 Hydrogen energy system model of EHC-VPP

3.1 Model of hydrogen source

In this paper, C2H and HWE are used as hydrogen sources at the same time. HWE can not only consume surplus electricity in the EHC-VPP but also replace part of the coal to hydrogen, realizing the organic synergy between coal and renewable energy.

3.1.1 Hydrogen production by water electrolysis

The commonly used water electrolysis technology mainly includes alkaline electrolysis and proton exchange membrane electrolysis. Because the alkaline electrolytic cell has the characteristics of stable operation under high voltage, high current density, and low voltage, the unit hydrogen production cost of the alkaline electrolytic cell is lower than that of the proton exchange membrane electrolytic cell (Gambou et al., 2022). Therefore, the alkaline electrolytic cell is selected as one of the hydrogen sources in this paper.

HWE requires first converting the alternating current of the power grid into direct current by rectification, and then decomposing the water into hydrogen gas using an electrolytic cell. The aforementioned method can be stated as follows Eq. 1:

$\left\{\begin{array}{l}{P}_{j,t}^{DC}={\eta }^{D2A}{P}_{j,t}^{AC}\\ m_{j,t}^{P2H}=\frac{{\eta }^{EC}{P}_{j,t}^{DC}{\rho }^{H_2}}{HC{V}^{H_2}},j\in {\mathrm{\Psi }}_{nd}^P,t\in T\end{array}\right.(1)$

where, $P_{j,t}^{DC}$ and $P_{j,t}^{AC}$ represent the power of DC and AC power used for the jth HWE at time t, ${\eta }^{D2A}$ represents the efficiency of the rectification process, $m_{i,t}^{P2H}$ is the mass flow rate of the jth HWE at time t, ${\eta }^{EC}$ is the production efficiency of the electrolysis cell, ${\rho }^{H_2}$ denotes the density of hydrogen in the standard state, $HC{V}^{H_2}$ is the low calorific value of hydrogen, ${\mathrm{\Psi }}_{nd}^P$ is index set of nodes of power distribution system (PDS). $T$ is the scheduling time period.

3.1.2 Coal to hydrogen

C2H refers to the process in which coal combines with water vapor at high temperature and high pressure to create carbon dioxide and hydrogen, and the amount of hydrogen produced is linearly related to the amount of coal used, so it can be expressed as Eq. 2:

$m_{i,t}^{C2H}={\eta }^{C2H}{m}_{i,t}^{Coal},i\in {\mathrm{\Psi }}_{nd}^H,t\in T(2)$

where, $m_{i,t}^{C2H}$ is the mass flow rate of the hydrogen output at time t, ${\eta }^{C2H}$ is the conversion rate of the feedstock coal to hydrogen, $m_{i,t}^{Coal}$ is the mass flow rate of the feedstock coal inflow for coal-to-hydrogen production at time t, ${\mathrm{\Psi }}_{nd}^H$ is index set of nodes of hydrogen energy system.

In the process of C2H, the CO₂ in the exhaust gas is mainly formed by the oxidation of the carbon components in the coal. Therefore, based on the oxidation rate ${\eta }^O$, average low-level heating value $F^C$ and carbon content per unit calorific value of coal $H^C$, the CO₂ emissions from the hydrogen production process of coal gasification can be analyzed as follows Eq. 3:

$m_{i,t}^{C{O}_2}=F^C{H}^C{\eta }^O{\lambda }^C{m}_{i,t}^{Coal},i\in {\mathrm{\Psi }}_{nd}^H,t\in T(3)$

where, ${\lambda }^C$ is the relative molecular mass ratio of CO₂ to elemental carbon.

3.2 Model of hydrogen pipeline network

For hydrogen pipelines, the relationship between pipeline airflow and node pressure is described by the Weymouth equation as Eq. 4:

${\left(m_{ij}^{H_2}\right)}^2=\text{sgn}\left(p_i-p_j\right)\times C_{ij}^2\times \left|p_i^2-p_j^2\right|(4)$

where, $m_{ij}^{H_2}$ is the hydrogen flow rate flowing through the pipeline at the endpoints of node i and node j during time t, $p_i$ and $p_j$ respectively represent the node pressure at both ends of the pipeline. $C_{ij}$ is the Weymouth coefficient of the pipeline, which is determined by factors such as the length, diameter, roughness, gas density, and temperature of the pipeline. Normally, the gas temperature and density during hydrogen transmission do not change in the short term.

$\text{sgn}\left(p_i-p_j\right)$ is a symbolic function, with its physical meaning defined as Eq. 5: natural gas flows from node i to node j as the reference direction. If $p_i>p_j$, the pressure at node i is greater than that at node i, the actual flow direction of natural gas is the same as the reference direction. If $p_i<p_j$, the pressure at node i is less than that at node j, the actual flow direction of natural gas is opposite to the reference direction:

$\text{sgn}\left(p_i-p_j\right)=\left\{\begin{array}{l}1,p_i>p_j\\ -1,p_i<p_j\end{array}\right.(5)$

In addition, it is necessary to satisfy the node equilibrium equation, which means that the algebraic sum of any node flow rate is zero, and the inflow of hydrogen gas is equal to the outflow of hydrogen gas, which can be expressed as Eq. 6:

$m_{i,t}^{P2H}+m_{i,t}^{C2H}+m_{ki,t}^{H_2}+m_{i,t}^{out}=m_{ij,t}^{H_2}+m_{i,t}^{in}+m_{i,t}^{H2N}+m_{i,t}^{H2P},i,j,k\in {\mathrm{\Psi }}_{nd}^H,t\in T(6)$

3.3 Model of hydrogen load

In real hydrogen chemical parks, hydrogen is often used as a feedstock for ammonia synthesis as well as power generation. Therefore, H2A and HFCs are considered as hydrogen loads for the EHC-VPP in this paper.

3.3.1 Hydrogen to ammonia

H2A utilizes the reaction between hydrogen and nitrogen at high temperature and pressure to generate ammonia, and the process also consumes a large amount of electrical energy. In this paper, a linear model of H2A established by Li based on Braun axial three-beds insulation reactor (BATIR) is used (Li et al., 2020), which are expressed as follows Eq. 7:

$\left\{\begin{array}{l}{m}_{i,t}^{N{H}_3}=c_1{m}_{i,t}^{H2N}+d_1\\ P_{j,t}^{H2N}=c_2{m}_{i,t}^{H2N}+d_2\end{array}\right.,i\in {\mathrm{\Psi }}_{nd}^H,j\in {\mathrm{\Psi }}_{nd}^P,t\in T(7)$

where, $m_{i,t}^{N{H}_3}$ denotes the mass flow rate of ammonia out of the product at time t, $P_{j,t}^{H2N}$ is the amount of electricity needed to produce ammonia by hydrogen at time t, and $m_{i,t}^{H2N}$ is the mass flow rate of hydrogen into the feedstock at time t.

3.3.2 Hydrogen fuel cells

HFCs can utilize hydrogen stored in hydrogen storage tanks for power generation, and their output power is expressed as Eq. 8:

$P_{j,t}^{H2P}={\eta }^{H2P}{m}_{i,t}^{H2P}C{V}^{H_2}/{\rho }^{H_2},i\in {\mathrm{\Psi }}_{nd}^H,j\in {\mathrm{\Psi }}_{nd}^P,t\in T(8)$

where, $P_{j,t}^{H2P}$ denotes the output power of the jth hydrogen fuel cell at time t, ${\eta }^{H2P}$ is the energy conversion efficiency, $m_{i,t}^{H2P}$ is the mass flow rate of hydrogen entering at time t, $C{V}^{H_2}$ is the calorific value of hydrogen, and ${\rho }^{H_2}$ is the density of hydrogen in the standard state.

3.4 Model of hydrogen storage tank

The HST is used to store hydrogen produced by the electrolysis of water in an alkaline electrolytic cell (Liu et al., 2023). It can also provide hydrogen for hydrogen fuel cells. The mathematical model can be expressed as follows Eq. 9:

$M_{i,t}^{HT}=M_{i,t-1}^{HT}+\left(m_{i,t-1}^{in}-m_{i,t-1}^{out}\right)\Delta t,i\in {\mathrm{\Psi }}_{nd}^H,t\in T(9)$

where, $M_{i,t}^{HT}$ is the total mass of hydrogen in the ith hydrogen storage tank at time t, $m_{i,t-1}^{in}$ and $m_{i,t-1}^{out}$ are the mass of input and output hydrogen of the ith hydrogen storage tank at time t, $\Delta t$ is the time step.

4 Optimal scheduling model of EHC-VPP considering hydrogen load response

4.1 Objective function

To minimize the operating costs of the EHC-VPP and decrease carbon emissions, this article establishes the following objective function as Eq. 10:

$\min {\displaystyle \sum _{t=1}^{24}}\left({\lambda }_t^E{p}_t^E+{\lambda }_t^{C2H}{\displaystyle \sum _i}{m}_{i,t}^{C2H}+{\lambda }_t^{C{O}_2}{\displaystyle \sum _i}{m}_{i,t}^{C{O}_2}-{\lambda }_t^{N{H}_{\mathit{3}}}{\displaystyle \sum _i}{m}_{i,t}^{N{H}_3}\right)(10)$

where, $p_t^E$ denotes the amount of electricity traded between the EHC-VPP and the external grid at time t. When $p_t^E>0$, it means that the EHC-VPP buys electricity from the grid, otherwise the EHC-VPP sells electricity to the grid. the coefficient ${\lambda }_t^E$ is the time-of-day price of electricity at time t. ${\lambda }_t^{C2H}$ is the price of purchasing coal and ${\lambda }_t^{C{O}_2}$ is the carbon emission penalty coefficient. ${\lambda }_t^{N{H}_3}$ denotes the yield coefficient of hydrogen-to-ammonia production.

4.2 Constraints

4.2.1 Hydrogen system operation constraints

4.2.1.1 Hydrogen source constraints

${\underset{\_}{m}}^{Coal}\le m_{i,t}^{Coal}\le {\overline{m}}^{Coal},\forall t\in T(11)$

${\underset{\_}{P}}^{AC}\le P_{j,t}^{AC}\le {\overline{P}}^{AC},\forall j\in {\mathrm{\Psi }}_{nd}^P,\forall t\in T(12)$

Eq. 11 specifies the upper limit ${\overline{m}}^{Coal}$ and lower limit ${\underset{\_}{m}}^{Coal}$ of its coal usage. Eq. 12 specifies the maximum value ${\overline{P}}^{AC}$ and minimum value ${\underset{\_}{P}}^{AC}$ of the electrical energy input to the electrolytic cell.

4.2.1.2 Hydrogen pipeline network constraints

$p_{i,t}^{C2H}={\widehat{p}}^{C2H},p_{i,t}^{P2H}={\widehat{p}}^{P2H},\forall i\in {\mathrm{\Psi }}_{nd}^H,\forall t\in T(13)$

$\underset{\_}{p}\le p_{i,t}\le \overline{p},\forall i\in {\mathrm{\Psi }}_{nd}^H,\forall t\in T(14)$

where, ${\widehat{p}}^{C2H}$ and ${\widehat{p}}^{P2H}$ are the pressure setting values of the hydrogen source, $\overline{p}$ and $\underset{\_}{p}$ are the upper and lower limits of node pressure.

Eq. 13 assumes that the pressure of the pipeline at the hydrogen source node is a constant value. Eq. 14 represents the pressure range to which the pipeline is subjected.

4.2.1.3 Hydrogen load constraints

To realize the demand response by treating H2A as a shiftable load, the input hydrogen quantity at each moment is regarded as a variable, which should satisfy the constraints of H2A capacity expressed in Eq. 15. Eq. 16 represents the total daily ammonia production constraint.

${\underset{\_}{m}}^{H2N}\le m_{i,t}^{H2N}\le {\overline{m}}^{H2N},\forall i\in {\mathrm{\Psi }}_{nd}^H,\forall t\in T(15)$

${\underset{\_}{M}}^{N{H}_3}\le {\displaystyle \sum _{t=0}^{24}}{\displaystyle \sum _i}{m}_{i,t}^{N{H}_3}\le {\overline{M}}^{N{H}_3},\forall i\in {\mathrm{\Psi }}_{nd}^H,\forall t\in T(16)$

where, ${\overline{m}}^{H2N}$ and ${\underset{\_}{m}}^{H2N}$ are the upper and lower limits of the mass flow rate of hydrogen into the raw material, ${\overline{M}}^{N{H}_3}$ and ${\underset{\_}{M}}^{N{H}_3}$ represent the maximum and minimum values of the total daily ammonia production.

Eq. 17 specifies the upper bound ${\overline{P}}^{H2P}$ and lower bound ${\underset{\_}{P}}^{H2P}$ for HFC power generation.

${\underset{\_}{P}}^{H2P}\le P_{j,t}^{H2P}\le {\overline{P}}^{H2P},\forall j\in {\mathrm{\Psi }}_{nd}^P,\forall t\in T(17)$

4.2.1.4 Hydrogen storage tank constraints

${\underset{\_}{M}}_{i,t}^{HT}\le M_{i,t}^{HT}\le {\overline{M}}_{i,t}^{HT},\forall i\in {\mathrm{\Psi }}_{nd}^H,\forall t\in T(18)$

$0\le m_{i,t}^{in}\le {\overline{m}}_{i,t}^{in},0\le m_{i,t}^{out}\le {\overline{m}}_{i,t}^{out},\forall i\in {\mathrm{\Psi }}_{nd}^H,\forall t\in T(19)$

Eq. 18 specifies the maximum capacity ${\underset{\_}{M}}_{i,t}^{HT}$ and minimum capacity ${\overline{M}}_{i,t}^{HT}$ of the hydrogen storage tank, and Eq. 19 limits the rate of hydrogen charging ${\overline{m}}_{i,t}^{in}$ and discharging ${\overline{m}}_{i,t}^{out}$.

4.2.2 PDS operation constraints

$P_t^{ab}={\displaystyle \sum _c}{P}_t^{bc}+p_t^E+P_{j,t}^W+P_{j,t}^{H2P}-P_{j,t}^{AC}-P_{j,t}^{Load}-P_{j,t}^{H2N},\forall j\in {\mathrm{\Psi }}_{nd}^P,\forall t\in T(20)$

$-{\underset{\_}{P}}^{ab}\le P_t^{ab}\le {\overline{P}}^{ab},\forall t\in T(21)$

$0\le P_{j,t}^W\le {\overline{P}}^W,{\underset{\_}{P}}^{H2N}\le P_{j,t}^{H2N}\le {\overline{P}}^{H2N},\forall j\in {\mathrm{\Psi }}_{nd}^P,\forall t\in T(22)$

where, $P_t^{ab}$ denotes the active power on line ab. $P_{j,t}^{WT}$ is the power generated by distributed new energy units, $P_{j,t}^{Load}$ is the electrical loads in the EHC-VPP.

Eq. 20 is the power balance constraint for the EHC-VPP (Du et al., 2024), Eq. 21 limits the line capacity, and Eq. 22 gives the upper and lower power limits for the power units.

5 Case studies

5.1 Test system description

The optimal scheduling model presented in this article is an optimization problem with nonlinear constraints. All tests are executed using IPOPT interfaced through MATLAB (Jones and Gerogiorgis, 2023), and the experimental computer environment is 11th Gen Intel(R) Core (TM) i7-1165G7 @2.80 GHz dual-core processor, 16 GB RAM, and Windows 10 system.

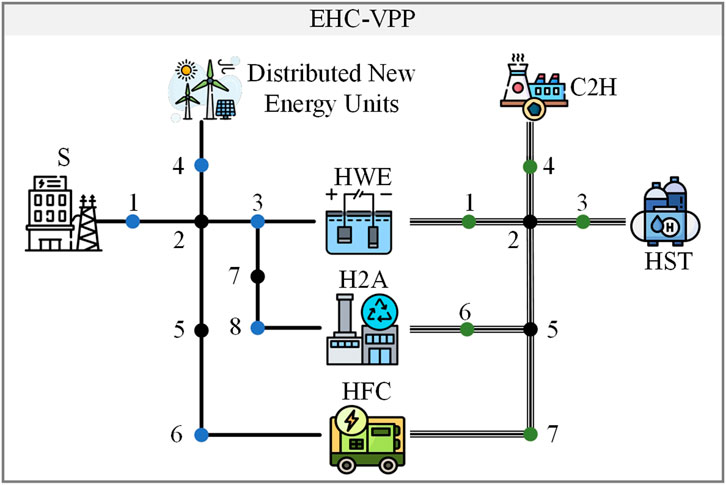
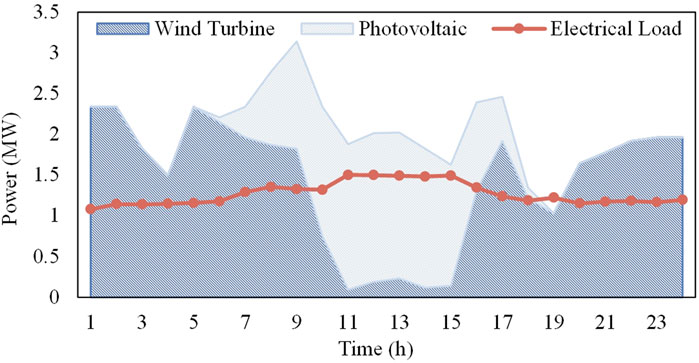
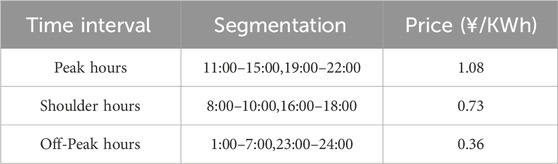
The topology of the EHC-VPP is shown in Figure 2, which contains an 8-node power system and a 7-node hydrogen energy system. The EHC-VPP trades power with the external power grid through a substation at node 1, and the distributed new energy units are located at node 4 of the power system, and nodes 3, 6, and 8 are equipped with a HWE, a HFC, and a H2A, which are coupled with nodes 1, 7, and 6 of the hydrogen energy system, respectively. In addition, node 3 in the hydrogen energy system is provided with one HST, and node 4 is provided with a C2H. Among them, the distributed new energy unit output data, the total power supply of the EHC-VPP, and the user electricity load data are shown in Figure 3. The time-of-use electricity price adopted in this paper is shown in Table 1. The operating parameters of the H2A are shown in Table 2.

FIGURE 2

FIGURE 2. Topology of the P8H7 system.

FIGURE 3

FIGURE 3. Renewable energy output and load data in the EHC-VPP.

TABLE 1

TABLE 1. Time-of-use electricity price.

TABLE 2

TABLE 2. The operating parameters of the H2A.

5.2 Scenarios setting and result analysis

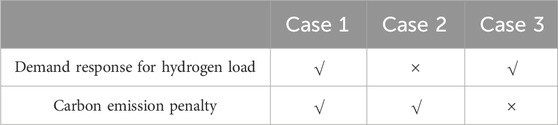
The following three cases are considered as shown in Table 3.

TABLE 3

TABLE 3. Test case.

The operation results of the EHC-VPP under three cases are shown in Figure 4, Figure 5, and Figure 6, respectively, including the amount of electricity used and generated by the units in the power system, and the amount of hydrogen used and produced in the hydrogen system.

1) Case 1: In this case, the demand response of H2A is considered, i.e., its operating power is adjustable. Meanwhile, the effect of the carbon emission penalty is considered in the objective function.

FIGURE 4

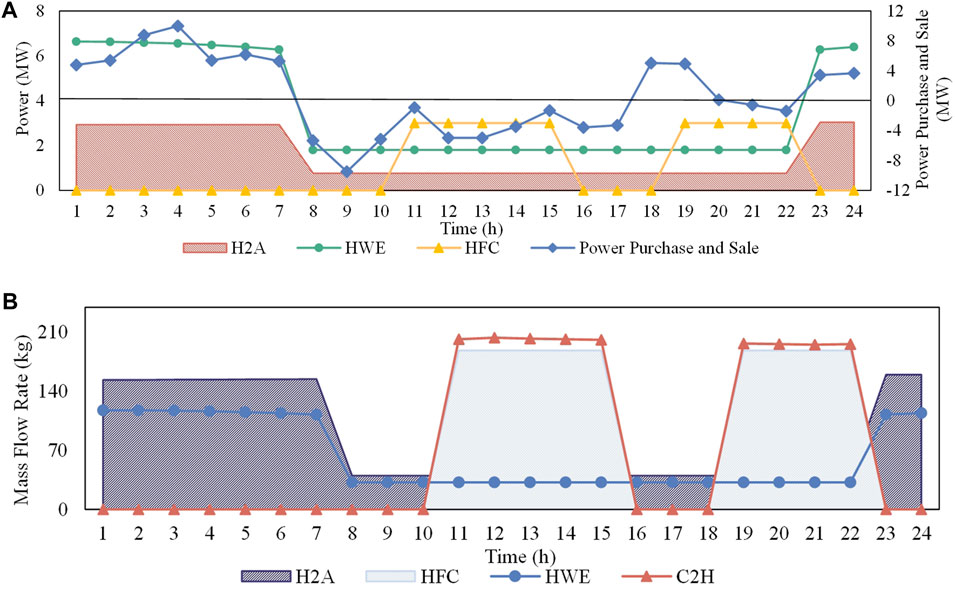
FIGURE 4. Operation results of Case 1: (A) Units in the power system. (B) Units in the hydrogen system.

FIGURE 5

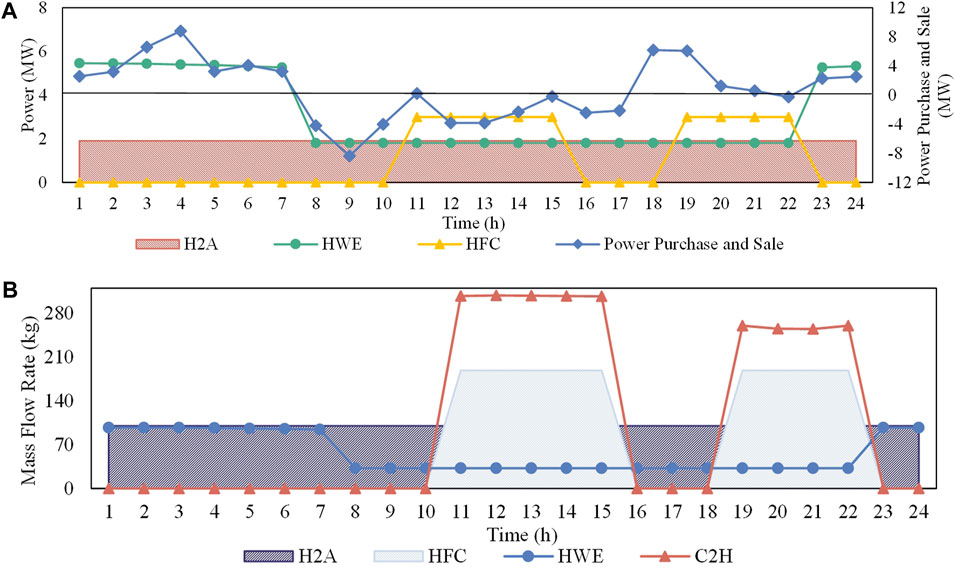
FIGURE 5. Operation results of Case 2: (A) Units in the power system. (B) Units in the hydrogen system.

FIGURE 6

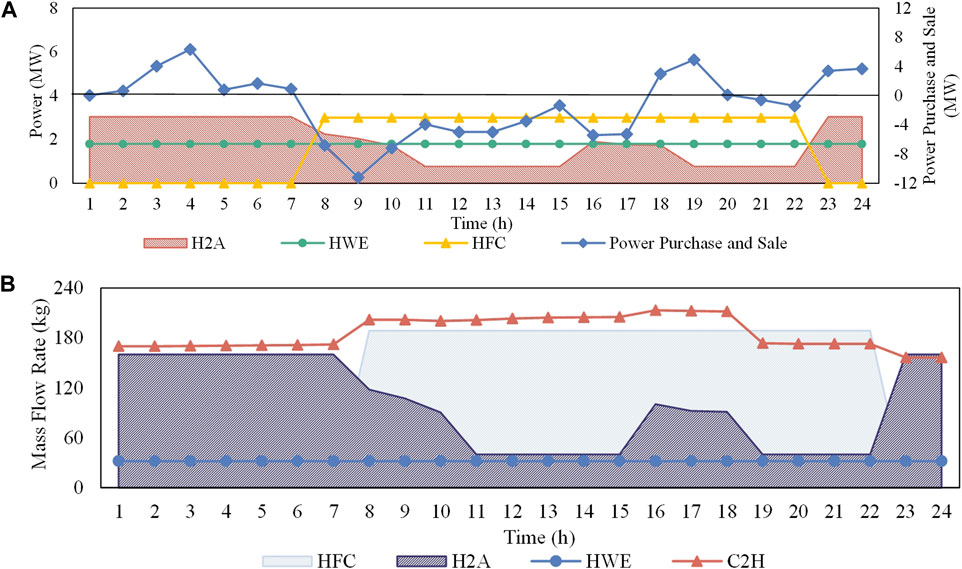
FIGURE 6. Operation results of Case 3: (A) Units in the power system. (B) Units in the hydrogen system.

When the electricity price is in the off-peak hours, purchasing electricity from the external grid to provide more power for the HWE can result in more ammonia sales proceeds through the H2A. Moreover, the C2H is not activated during this period because of the carbon penalty added to the objective function; When the electricity price is in the shoulder hours, the EHC-VPP can sell the surplus power generation to the power grid for profit. At this time, the power generation of new energy is far more than the internal load of the EHC-VPP, and it is not economical to provide power through the HFC. Therefore, the HWE and H2A are operated at the lowest power, and the C2H is still not started; When the price of electricity is in the peak hours, the EHC-VPP should sell as much electricity as possible to the grid and reduce the internal electricity consumption. Therefore, the C2H is run at higher power during this period, while the HWE and H2A are still run at minimum power, and most of the hydrogen produced is used to generate electricity in the HFC.

2) Case 2: In this case, the demand response of H2A is not considered, i.e., it operates at a constant power operation state. At the same time, the impact of carbon emission penalties is also considered in the objective function.

When the electricity price is in the off-peak hours, the power required for the HWE is reduced because the operating power of the H2A is fixed and cannot be operated at a large power. The C2H is also not started; When the electricity price is in the shoulder hours, the HWE and H2A run at the lowest power and the C2H still does not start similar to Case 1; When the electricity price is in the peak hours, compared with the lower power of the H2A in Case 1, the power generation of the HFC in Case 2 decreases due to the fixed power operation of the H2A, resulting in a significant reduction in the electricity sales of the EHC-VPP. As can be seen in Table 4, when the demand response of H2A is not considered, the overall revenue of the EHC-VPP decreases by 9.1%.

3) Case 3: In this case, the demand response of H2A is considered, but the impact of carbon emission penalty is not considered in the objective function.

TABLE 4

TABLE 4. Costs and revenues in Case 1 to Case 3.

Since carbon penalties are not considered, the EHC-VPP chooses to use the more economical C2H during each dispatch period, while the HWE is always operated at the lowest power level. Although the coal consumption increases significantly, the EHC-VPP gains more revenue by purchasing less power and buying more power.

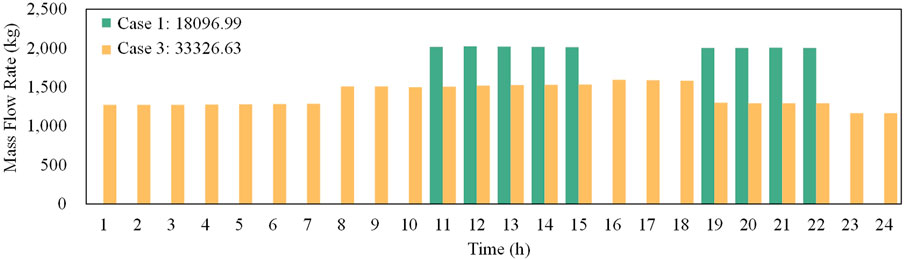
Figure 7 depicts the coal usage of Case 1 and Case 3 respectively. It can be seen that the total coal consumption in Case 3 is 33326.63 Kg, which is an increase of 84.15% compared to 18096.99 Kg in Case 1.

FIGURE 7

FIGURE 7. Quantity of coal consumed in Case 1 and Case 3.

Table 4 shows the various costs and revenues for Case 1 to Case 3. The final total cost is negative, indicating that the EHC-VPP will ultimately gain revenue. When considering the demand response of H2A, its operating power can follow the real-time changes in power supply and electric load to respond to the time-of-use electricity price, to achieve the effect of minimizing the overall operating cost of the EHC-VPP as well as maximizing the revenue. Comparing Case 1 with Case 2, although the ammonia production revenue remains largely unchanged, the addition of adjustable flexibility resources further reduces the cost of purchasing electricity, coal, and carbon penalty costs, which in turn improves the total revenue of the park by about 10.0%.

6 Conclusion

In this paper, the whole chain of the hydrogen energy system is modeled in a refined way, and a virtual power plant economic dispatch model considering hydrogen load response is proposed. The proposed model involves distributed new energy units as well as a hydrogen energy system includes a hydrogen production unit, a hydrogen storage unit, and a hydrogen use unit. In addition, to practice the green development concept of energy saving and emission reduction, this paper also considers the impact of the carbon emission penalty. From the case study, it can be seen that considering the demand-side response on the hydrogen load side and fully exploiting the flexibility resources of the park can further decrease the system operation cost and increase the overall operation efficiency of the park.

In future studies, we plan to model the virtual power plant in a more refined way and consider various types of uncertainties that may be encountered during operation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

WL: Writing–original draft, Conceptualization. TX: Writing–original draft, Conceptualization. PF: Writing–original draft, Investigation. HL: Writing–original draft, Methodology. XY: Writing–review and editing. YZ: Writing–review and editing. RM: Writing–review and editing. YL: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was supported by Guizhou Power Grid Co., Ltd. (No. 0676002023030201XT00001) and the National Natural Science Foundation of China (52307131).

Conflict of interest

Authors WL, RM, and YL were employed by the Power Grid Planning Research Center of Guizhou Power Grid Co., Ltd. Authors TX, XY, and YZ were employed by the Energy Planning and Research Institute of Southwest Electric Power Design Institute Co., Ltd., of China Power Engineering Consulting Group.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared shared affiliation with the authors PF and HL at the time of review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ban, M., Yu, J., Shahidehpour, M., and Yao, Y. (2017). Integration of power-to-hydrogen in day-ahead security-constrained unit commitment with high wind penetration. J. Mod. Power Syst. Clean. Energy 5 (3), 337–349. doi:10.1007/s40565-017-0277-0

CrossRef Full Text | Google Scholar

Du, Y., Xue, Y., Wu, W., Shahidehpour, M., Shen, X., Wang, B., et al. (2024). Coordinated planning of integrated electric and heating system considering the optimal reconfiguration of district heating network. IEEE Trans. Power Syst. 39 (1), 794–808. doi:10.1109/TPWRS.2023.3242652

CrossRef Full Text | Google Scholar

Gambou, F., Guilbert, D., Zasadzinski, M., and Rafaralahy, H. (2022). A comprehensive survey of alkaline electrolyzer modeling: electrical domain and specific electrolyte conductivity. Energies 15, 3452. doi:10.3390/en15093452

CrossRef Full Text | Google Scholar

Gholami, K., Behi, B., Arefi, A., and Jennings, P. (2022). Grid-forming virtual power plants: concepts, technologies and advantages. Energies 15, 9049. doi:10.3390/en15239049

CrossRef Full Text | Google Scholar

Jones, W., and Gerogiorgis, D. I. (2023). Dynamic optimisation of fed-batch bioreactors for mAbs: sensitivity analysis of feed nutrient manipulation profiles. Processes 11 (11), 3065. doi:10.3390/pr11113065

CrossRef Full Text | Google Scholar

Li, J., Lin, J., and Song, Y. (2020). Capacity optimization of hydrogen buffer tanks in renewable power to ammonia (P2A) system. 2020 IEEE Power and Energy Society General Meeting (PESGM), 1–5. doi:10.1109/PESGM41954.2020.9282084

CrossRef Full Text | Google Scholar

Li, P., Chen, Y., Yang, K., Yang, P., Yu, J., Yao, S., et al. (2022). Optimal peak regulation strategy of virtual and thermal power plants. Front. Energy Res. 10, 799557. doi:10.3389/fenrg.2022.799557

CrossRef Full Text | Google Scholar

Li, Y. (2022). New energy utilization in environmental design and realization. Energy Rep. 8, 9211–9220. doi:10.1016/j.egyr.2022.07.029

CrossRef Full Text | Google Scholar

Li, Y., Deng, Y., Wang, Y., Jiang, L., and Shahidehpour, M. (2023). Robust bidding strategy for multi-energy virtual power plant in peak-regulation ancillary service market considering uncertainties. Int. J. Electr. Power and Energy Syst. 151, 109101. doi:10.1016/j.ijepes.2023.109101

CrossRef Full Text | Google Scholar

Lin, J., and Cai, R. (2023). Optimal planning for industrial park-integrated energy system with hydrogen energy industry chain. Int. J. Hydrogen Energy 48 (50), 19046–19059. doi:10.1016/j.ijhydene.2023.01.371

CrossRef Full Text | Google Scholar

Liu, Y., Xue, Y., Zhou, Z., Han, X., Chang, X., Su, J., et al. (2023). Coordinated dispatch of power and transportation systems considering hydrogen storage based on heterogeneous decomposition. IEEE Trans. Transp. Electrification, 1. doi:10.1109/TTE.2023.3332357

CrossRef Full Text | Google Scholar

Ma, S., Mei, S., and Yu, L. (2023). Research on multi-timescale operation optimization of a distributed electro-hydrogen coupling system considering grid interaction. Front. Energy Res. 11, 1251231. doi:10.3389/fenrg.2023.1251231

CrossRef Full Text | Google Scholar

Miao, B., Zhang, L., Wu, S., and Chan, S. H. (2022). The economics of power generation and energy storage via Solid Oxide Cell and ammonia. Int. J. Hydrogen Energy 47 (63), 26827–26841. doi:10.1016/j.ijhydene.2022.06.066

CrossRef Full Text | Google Scholar

Pei, W., Zhang, X., Deng, W., Tang, C., and Yao, L. (2022). Review of operational control strategy for DC microgrids with electric-hydrogen hybrid storage systems. CSEE J. Power Energy Syst. 8 (2), 329–346. doi:10.17775/CSEEJPES.2021.06960

CrossRef Full Text | Google Scholar

Priyanka, S., Iasonas, K. L., and Mikael, A. (2022). Multistage stochastic programming for VPP trading in continuous intraday electricity markets. IEEE Trans. Sustain. Energy 13 (2), 1037–1048. doi:10.1109/TSTE.2022.3144022

CrossRef Full Text | Google Scholar

Rafique, S. F., Shen, P., Wang, Z., Rafique, R., Iqbal, T., Ijaz, S., et al. (2018). Global power grid interconnection for sustainable growth: concept, project and research direction. IET Gener. Transm. Distrib. 12, 3114–3123. doi:10.1049/iet-gtd.2017.1536

CrossRef Full Text | Google Scholar

Tan, Y., Zhi, Y., Luo, Z., Fan, H., Wan, J., and Zhang, T. (2023). Optimal scheduling of virtual power plant with flexibility margin considering demand response and uncertainties. Energies 16, 5833. doi:10.3390/en16155833

CrossRef Full Text | Google Scholar

Wang, K., Xue, Y., Guo, Q., Shahidehpour, M., Zhou, Q., Wang, B., et al. (2023). A coordinated reconfiguration strategy for multi-stage resilience enhancement in integrated power distribution and heating networks. IEEE Trans. Smart Grid 14 (4), 2709–2722. doi:10.1109/TSG.2022.3231590

CrossRef Full Text | Google Scholar

Wang, S., Wang, S., Zhao, Q., Dong, S., and Li, H. (2023). Optimal dispatch of integrated energy station considering carbon capture and hydrogen demand. Energy 269, 126981. doi:10.1016/j.energy.2023.126981

CrossRef Full Text | Google Scholar

Wu, Y., Wu, J., and De, G. (2022). Research on trading optimization model of virtual power plant in medium- and long-term market. Energies 15 (3), 759. doi:10.3390/en15030759

CrossRef Full Text | Google Scholar

Zhao, H., Wang, B., Pan, Z., Sun, H., Guo, Q., and Xue, Y. (2021). Aggregating additional flexibility from quick-start devices for multi-energy virtual power plants. IEEE Trans. Sustain. Energy 12 (1), 646–658. doi:10.1109/TSTE.2020.3014959

CrossRef Full Text | Google Scholar

Zhao, L., Xue, Y., Sun, H., Du, Y., Chang, X., Su, J., et al. (2023). Benefit allocation for combined heat and power dispatch considering mutual trust. Appl. Energy 345, 121279. doi:10.1016/j.apenergy.2023.121279

CrossRef Full Text | Google Scholar

Zhou, J., Ji, W., Cao, X., He, W., Fan, J., and Yuan, Y. (2023). A current perspective on the renewable energy hydrogen production process. J. Therm. Sci. 32, 542–596. doi:10.1007/s11630-023-1749-3

CrossRef Full Text | Google Scholar