Load frequency control of new energy power system based on adaptive global sliding mode control

Owing to the challenges of unstable generation and random load disturbance in new energy power system, this paper integrates the battery energy storage model into the traditional load frequency control (LFC) framework, and proposes a LFC scheme based on adaptive global sliding mode control to stabilize the frequency of power systems amid unpredictable load frequency deviation. First of all, the nonlinear time-varying function is added to the sliding mode surface to make the system globally robust. Then, an adaptive sliding mode control law is crafted to dynamically adjust the frequency variations caused by random load disturbance. Moreover, by utilizing the improved Lyapunov function and Bessel-Legendre inequality, the stabilization criteria of multi-area interconnected power system are built. Finally, the efficacy of the proposed method is demonstrated through single and double area LFC simulation experiments with the common system parameters.

1 Introduction

With the increasingly severe global energy crisis and the sharp decline in non-renewable resources, new energy generation will become a major trend of power system (Tan et al., 2023). The reliability of power systems that integrate wind, solar photovoltaic (SPV) and battery energy storage (BES) is also improved (Kundu et al., 2021; Kundu et al., 2023). However, the output uncertainty of new energy generation is large, bringing challenges to the frequency stability of power system (Wang et al., 2022a; Zhang et al., 2023a; Ojha and Maddela, 2023). When the frequency of the power system fluctuates prominently, the equipment of power system is likely to fail to work properly. In severe cases, the power system may collapse, triggering large-scale power outages. In order to avoid the above circumstances, it is particularly vital to maintain the frequency stability of the power system. And LFC is a vital method to confine the frequency deviations of power system within certain pre-specified limits (Ranjitha et al., 2022; Khokhar and Parmar, 2023; Singh and Ramesh, 2024). Therefore, LFC is critical for ensuring the stable operation of power system, which is of great significance and research value for further study.

In order to control the load frequency, numerous researchers and scholars have conducted in-depth studies on LFC, and a number of LFC method strategies have been proposed, such as proportion integration differentiation (PID) control, predictive control, fuzzy control, and so on. In Veerendar et al. (2023), a dual-loop control method was proposed by using teaching-learning optimization (TLO) for the LFC of a multi-area non-heating thermal power system (NRTPS), which prominently improved the response of the system. In Sharma et al. (2022), a proportion integration (PI) controller was designed to determine the parametric uncertainty margin (PUM) to cope with problems caused by the changes of parameters. From Tang et al. (2023), a model predictive control (MPC) technique was presented, and a state feedback MPC controller was designed to deal with wind interference, communication delay, and denial-of-service (DoS) attacks. In Naderipour et al. (2023), based on the fuzzy logic, through a novel meta-heuristic whale algorithm, a self-tuning controller was designed to enable the proposed controller to operate better. In Hasen et al. (2023), a frequency-domain exact method was presented to increase the LFC system stability delay margin. For active/reactive power (AP/RP) regulation and energy storage management of an independent microgrid (MG), a new type-2 fuzzy logic control (T2FLC) was proposed to reduce voltage oscillation created by variation of output power in Mohammadi Moghadam et al. (2022). From Li and Ye (2022), for nonlinear interconnected power systems under a switching topology, a new event-based distributed fuzzy LFC approach was presented to ensure the asymptotic stability of the system. In Zhang et al. (2023b), for large-scale wind farm control, through introducing a multivariate power model, a communication based reinforcement learning method was presented to achieve satisfactory output power and stable performance. Although the above approaches enhance the performance of LFC, they are more demanding in terms of system and more difficult to implement physically. Besides, they are not robust to system uncertainties. Compared with these methods, sliding mode control (SMC) boasts numerous advantages. Firstly, the stability of it is high. When facing external disturbances in power system, appropriate control laws can be chosen to cope with the external disturbances, thus keeping the system frequency within the expected range. Secondly, the response is swift, enabling quick restoration of power system frequency through state transitions on the sliding mode surface. In addition, its physical implementation is simple and does not need a high standard of structure for the system, which can be applied in practice in a short time. So, the SMC is a promising method for LFC and deservesfurther study.

Therefore, an increasing number of researchers and scholars have studied LFC methods based on SMC. For example, an area-based event-triggered (ET) sliding mode control scheme was presented to suppress rapid fluctuations caused by load and wind power generation in Xu et al. (2022). From Guo (2021), a novel sliding mode control approach was presented to reduce the frequency deviation. In Yang et al. (2021), a generalized extended state observer and fractional-order theory based integral sliding mode control strategy were presented to relieve the chattering of frequency deviation and tie-line power deviation. For multiarea interconnected power systems under deception attack, an observer-based event-triggered transmission scheme was proposed to ensure the attacked power system can reach a stable position in Qiao et al. (2021). In Ansari et al. (2023), for two-area thermal interconnected power system, a novel sliding-mode LFC strategy was designed to achieve better tracking performance. From Ge et al. (2021), for a microgrid with hybrid energy storage system (HESS), based on sliding mode method, a frequency coordinated control strategy was designed to avoid unreasonable power output. In Deng and Xu (2022), for multi-area interconnected power systems integrated with wind farms, a derivative and integral terminal sliding-mode-based controller was proposed to eliminate the frequency deviation in each area. However, there are still some drawbacks to these methods. For instance, the variation of some parameters in power system may lead to the degradation of its performance and the phenomenon of oscillation. For the problem of system parameter variation, more scholars have studied the adaptive controller (Mazinan, 2013; Li et al., 2019; Zou, 2020; Wang et al., 2022b).

In order to solve the above problems better, LFC based on adaptive global sliding mode control (AGSMC) is studied in this article. Through this approach, the advantages of adaptive control, global control, and SMC are combined, significantly improving the control capability of LFC. When the external load disturbances occur or the parameters of rhe system change, through this method, the parameters of controller can be adjusted to adapt to the changes of external disturbance. And the specified characteristics can be maintained under certain conditions. This method demonstrates excellent anti-disturbance ability, strong robustness, rapid response, and high fault tolerance of the model. Therefore, this method can play a crucial role in achieving better control performance, which is worthy of in-depth study.

2 Problem statement

2.1 Describe of LFC model

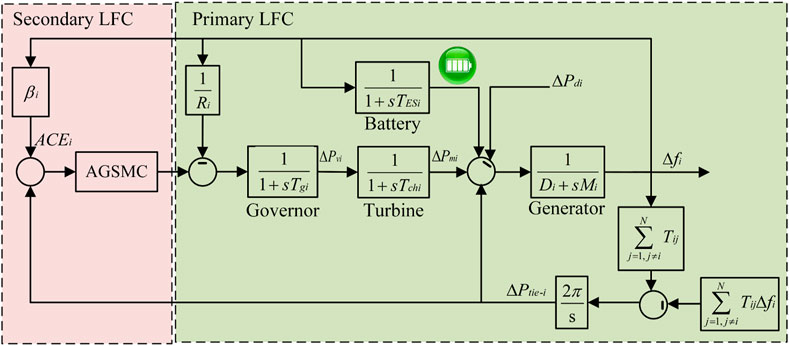
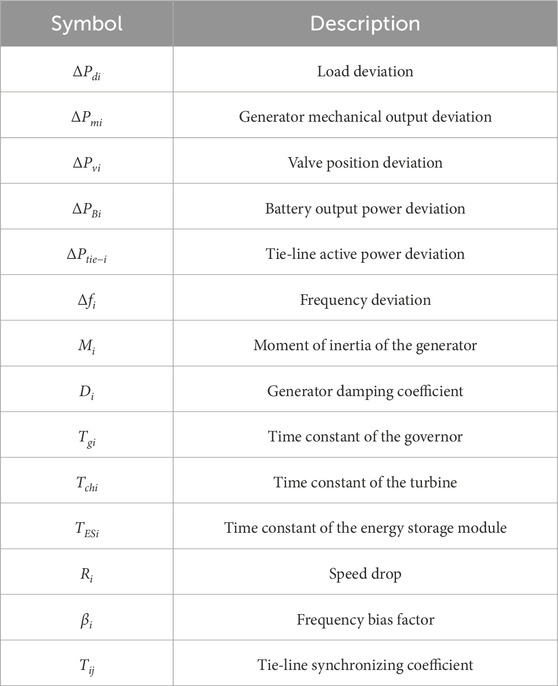
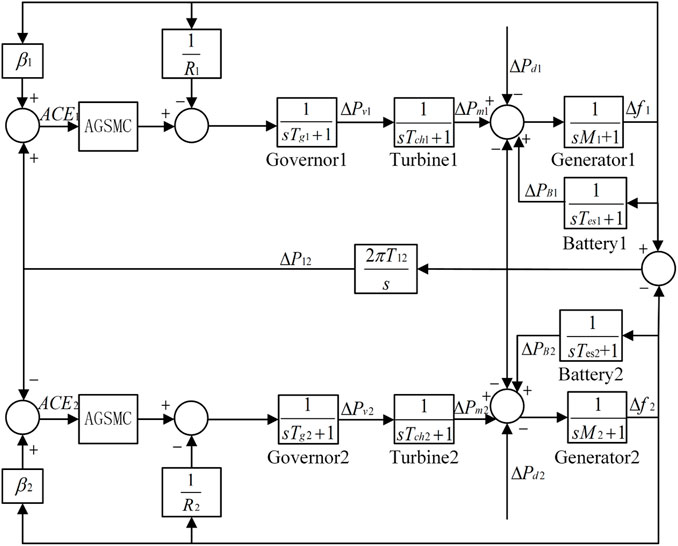
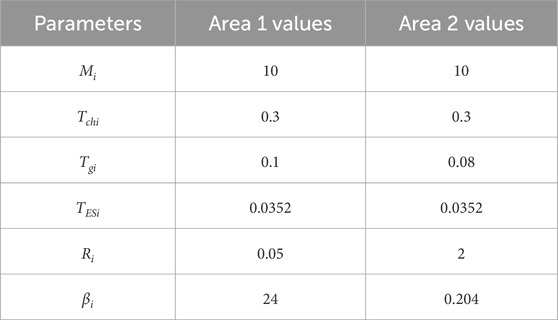
Consider a multi-area power systems, the LFC system model of the i-th area can be depicted in Figure 1. The parameters of i-th control area are presented in Table 1.

Figure 1

Figure 1. The model of i-th area in a multi-area LFC scheme.

Table 1

Table 1. Explanation of symbols for multi-area power system LFC.

The multi-area power system LFC model studied in this paper can be described as Eq. 1:

$\left\{\begin{array}{c}\dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)+J\omega \left(t\right)\hfill \\ y\left(t\right)=Cx\left(t\right)\hfill \end{array}\right.(1)$

where:

$\begin{array}{lll}\hfill & x_i\left(t\right)={\left[\begin{array}{cccccc}\hfill \mathrm{\Delta }{f}_i\hfill & \hfill \mathrm{\Delta }{P}_{mi}\hfill & \hfill \mathrm{\Delta }{P}_{vi}\hfill & \hfill \mathrm{\Delta }{P}_{Bi}\hfill & \hfill \int AC{E}_i\hfill & \hfill \mathrm{\Delta }{P}_{\mathit{tie-i}}\hfill \end{array}\right]}^T\hfill & \hfill \\ \hfill & x\left(t\right)={\left[\begin{array}{ccccc}\hfill x_1^T\left(t\right)\hfill & \hfill x_2^T\left(t\right)\hfill & \hfill x_3^T\left(t\right)\hfill & \hfill \dots \hfill & \hfill x_n^T\left(t\right)\hfill \end{array}\right]}^T\hfill & \hfill \\ \hfill & {\omega }_i\left(t\right)={\left[\begin{array}{c}\hfill \mathrm{\Delta }{P}_{di}\hfill \end{array}\right]}^T,A_{ij}=\left[\left(\mathrm{6,1}\right)=-2\pi T_{ij}\right]\hfill & \hfill \\ \hfill & u\left(t\right)={\left[\begin{array}{ccccc}\hfill u_1^T\left(t\right)\hfill & \hfill u_2^T\left(t\right)\hfill & \hfill u_3^T\left(t\right)\hfill & \hfill \dots \hfill & \hfill u_n^T\left(t\right)\hfill \end{array}\right]}^T\hfill & \hfill \\ \hfill & y_i\left(t\right)={\left[\begin{array}{cc}\hfill AC{E}_i\hfill & \hfill \int AC{E}_i\hfill \end{array}\right]}^T,B=\text{diag}\left\{B_1,\dots ,B_n\right\}\hfill & \hfill \\ \hfill & \omega \left(t\right)={\left[\begin{array}{ccccc}\hfill {\omega }_1^T\left(t\right)\hfill & \hfill {\omega }_2^T\left(t\right)\hfill & \hfill {\omega }_3^T\left(t\right)\hfill & \hfill \dots \hfill & \hfill {\omega }_n^T\left(t\right)\hfill \end{array}\right]}^T\hfill & \hfill \\ \hfill & y\left(t\right)={\left[\begin{array}{ccccc}\hfill y_1^T\left(t\right)\hfill & \hfill y_2^T\left(t\right)\hfill & \hfill y_3^T\left(t\right)\hfill & \hfill \dots \hfill & \hfill y_n^T\left(t\right)\hfill \end{array}\right]}^T\hfill & \hfill \\ \hfill & A_{ii}=\left[\begin{array}{cccccc}\hfill -\frac{D}{M_i}\hfill & \hfill \frac{1}{M_i}\hfill & \hfill 0\hfill & \hfill \frac{1}{M_i}\hfill & \hfill 0\hfill & \hfill -\frac{1}{M_i}\hfill \\ \hfill 0\hfill & \hfill -\frac{1}{T_{\mathit{chi}}}\hfill & \hfill \frac{1}{T_{\mathit{chi}}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\frac{1}{R{T}_{gi}}\hfill & \hfill 0\hfill & \hfill -\frac{1}{T_{gi}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{1}{T_{\mathit{ESi}}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{1}{T_{\mathit{ESi}}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\beta }_i\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 2\pi {\displaystyle {\sum }_{j=1,j\ne i}^n}{T}_{ij}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\hfill & \hfill \\ \hfill & A=\left[\begin{array}{ccc}\hfill A_{11}\hfill & \hfill \dots \hfill & \hfill A_{1n}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill A_{n1}\hfill & \hfill \dots \hfill & \hfill A_{nn}\hfill \end{array}\right]\hfill & \hfill \\ \hfill & B_i=\left[\begin{array}{cccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{T_{gi}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\hfill & \hfill \\ \hfill & C_i=\left[\begin{array}{cccccc}\hfill {\beta }_i\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\hfill & \hfill \\ \hfill & J_i={\left[\begin{array}{cccccc}\hfill -\frac{1}{M_i}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]}^T\hfill & \hfill \\ \hfill & C=\text{diag}\left\{C_1,\dots ,C_n\right\},J=\text{diag}\left\{J_1\right\}\hfill & \hfill \end{array}$

The Area Control Error (ACE) is a crucial parameter for each control area in a power system, comprising frequency deviation and tie-line active power deviation. It is defined by the following Eq. 2:

$AC{E}_i={\beta }_i\mathrm{\Delta }{f}_i+\mathrm{\Delta }{P}_{\mathit{tie-i}}(2)$

2.2 Design of adaptive global sliding mode control

The power system model with parameter uncertainty is set as follows:

$\dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)+\psi \left(t\right)(3)$

where ψ(t) = Jω(t).

To maintain the stability of LFC system and ensure the power quality, an AGSMC is proposed to control the frequency of load disturbance. Based on global sliding mode control (GSMC), this controller combines the adaptive law that designed under unknown disturbance fluctuation range to realize the rapid response of the system frequency. To prove that the system based on AGSMC is stable, the following assumptions hold.

Assumption 1: A and B are completely controllable matrices, and defining $\psi (t)=B\widehat{\psi }(t)$.

Assumption 2: The unknown disturbance $\widehat{\psi }(t)$ is bounded, setting $‖\widehat{\psi }(t)‖\le D$.

First, based on the above equation of state model, the sliding mode surface is selected as:

$s\left(t\right)=Gx\left(t\right)-{\int }_0^{t}G\left(A-BL\right)x\left(\upsilon \right)d\upsilon (4)$

where G and L are constant matrices, and meet the following requirements: 1) GB is a nonsingular matrix; 2)A− BL < 0, when s(t) = 0 and $\dot{s}(t)=0$ are met, the power system described by Eq. 3 reaches sliding mode surface.

Due to the initial state of the system is unknown, in order to make the whole system possesses global robustness, allowing the system to reach a stable state more quickly. A nonlinear time-varying function $f\left(t\right)$ is added to the Eq. 4 designed above. The improved sliding mode surface is redesigned to the following form:

$s\left(t\right)=Gx\left(t\right)-{\int }_0^{t}G\left(A-BL\right)x\left(\upsilon \right)d\upsilon +f\left(t\right)(5)$

where f(t) meet the following requirements: 1) The function f(t) possesses a first-order derivative; 2) When t = 0, s(t) = 0 are satisfied; 3) When t → ∞, f(t) can converge to zero.

Considering the above conditions, f(t) is designed as a monotonically decreasing exponential function in Eq. 6.

$f\left(t\right)=\lambda e^{-kt}(6)$

where λ = −Gx(0). It can be calculated from the following equation: $Gx\left(0\right)+\lambda e^{-k\cdot 0}=0$, when t = 0.

Combining Eq. 3 and Eq. 5 yields the following result:

$\begin{array}{ll}\hfill \dot{s}\left(t\right)& =G\dot{x}\left(t\right)-G\left(A-BL\right)x\left(t\right)+\dot{f}\left(t\right)\hfill \\ \hfill & =G\left(Ax\left(t\right)+Bu\left(t\right)+\psi \left(t\right)-Ax\left(t\right)+BLx\left(t\right)\right)-\lambda k{e}^{-kt}\hfill \\ \hfill & =G\left(Bu\left(t\right)+BLx\left(t\right)+\psi \left(t\right)\right)-\lambda k{e}^{-kt}\hfill \end{array}(7)$

When the system state reaches the sliding mode surface, it slides along this surface, and this sliding motion helps the system to remain in the desired operating state. Thus, the equivalent controller is derived as:

$u_{eq}\left(t\right)=-{\left(GB\right)}^{-1}\left[GBLx\left(t\right)+G\psi \left(t\right)\right](8)$

When Assumption 1 is satisfied, Eq. 8 can be rewritten as follows:

$\begin{array}{c}\hfill u_{eq}\left(t\right)=-{\left(GB\right)}^{-1}\left[GBLx\left(t\right)+GB\widehat{\psi }\left(t\right)\right]-Lx\left(t\right)-\widehat{\psi }\left(t\right)\end{array}(9)$

Substituting Eq. 9 into Eq. 3, we obtain Eq. 10.

$\begin{array}{c}\hfill \dot{x}\left(t\right)=Ax\left(t\right)+B\left\{-Lx\left(t\right)-\widehat{\psi }\left(t\right)\right\}+\psi \left(t\right)=\left(A-BL\right)x\left(t\right)\end{array}(10)$

Due to A− BL < 0, this means that all eigenvalues of the matrix A− BL have negative real parts, thus proving Eq. 3 is exponentially stable under the action of Eq. 9.

Remark 1: Based on the preceding analysis, it has been established that SMC demonstrates insensitivity to disturbances. It is worth noting that system 3 is exponentially stable. To make the system globally robust, a time-varying function f(t) is proposed. The global sliding mode controller drives the system’s initial movement along the sliding mode surface, thereby enhancing the response speed of the LFC system. To ensure the stable operation of each area in an area-interconnected power system and to deal with the influence of unknown load disturbances, the following adaptive laws are designed to estimate the unknown upper bound.

$\dot{\widehat{D}}\left(t\right)=‖GB‖‖s\left(t\right)‖(11)$

where $\widehat{D}(t)$ is the estimate of D(t), $\tilde{D}(t)=\widehat{D}(t)-D(t)$ is the evaluated error.

Theorem 1: Under the action of the following Eq. 12, the sliding mode Eq. 5 is asymptotically stable.

$\begin{array}{ll}\hfill u\left(t\right)& =-Lx\left(t\right)-\widehat{D}\left(t\right){\left(GB\right)}^{-1}‖GB‖\mathrm{s}\mathrm{g}\mathrm{n}s\left(t\right)\hfill \\ \hfill & -m{\left(GB\right)}^{-1}\mathrm{s}\mathrm{g}\mathrm{n}s\left(t\right)-ns\left(t\right)+{\left(CB\right)}^{-1}\lambda k{e}^{-kt}\hfill \end{array}(12)$

where m and n are the controller parameters to be set, m > 0, n > 0. In the exponential reaching law, n determines the reaching rate, and m guarantees that the system reaches stability in a limited time. To reduce buffeting while ensuring fast stability, n should be greater than m.

Proof: Define the Lyapunov function can be expressed as follows in Eq. 13.

$V_0\left(t\right)=\frac{1}{2}s{\left(t\right)}^{T}s\left(t\right)+\frac{1}{2}{\tilde{D}}^2\left(t\right)(13)$

Taking the derivative of V₀(t), the result is given below:

${\dot{V}}_0\left(t\right)=s{\left(t\right)}^T\dot{s}\left(t\right)+\tilde{D}\left(t\right)\dot{\stackrel{̃}{D}}\left(t\right)(14)$

Substituting Eq. 7 and Eq. 11 into Eq. 14 gives the following result:

${\dot{V}}_0\left(t\right)=s\left(t\right)\left[GBu\left(t\right)+GBLx\left(t\right)+GB\widehat{\psi }\left(t\right)-\lambda k{e}^{-kt}\right]+\tilde{D}\left(t\right)‖s\left(t\right)‖(15)$

Inserting the Eq. 12 into the above Eq. 15, the expression is shown in Eq. 16:

$\begin{array}{ll}\hfill {\dot{V}}_0\left(t\right)& =s\left(t\right)\left[-GBLx\left(t\right)-m\mathrm{s}\mathrm{g}\mathrm{n}s\left(t\right)-ns\left(t\right)+\lambda k{e}^{-kt}\right.\hfill \\ \hfill & \left.-\widehat{D}\left(t\right)\Vert GB\Vert \mathrm{s}\mathrm{g}\mathrm{n}s\left(t\right)+GBLx\left(t\right)+GB\widehat{\psi }\left(t\right)-\lambda k{e}^{-kt}\right]\hfill \\ \hfill & +\tilde{D}\left(t\right)\Vert s\left(t\right)\Vert \hfill \end{array}(16)$

According to $-s(t)\mathrm{s}\mathrm{g}\mathrm{n}s(t)\le ‖s(t)‖$, the following inequality can be derived.

$\begin{array}{ll}\hfill {\dot{V}}_0\left(t\right)& \le -m‖s\left(t\right)‖-n{‖s\left(t\right)‖}^2+‖s\left(t\right)‖‖GB‖D\hfill \\ \hfill & -\widehat{D}\left(t\right)‖GB‖‖s\left(t\right)‖+\left(\widehat{D}\left(t\right)-D\right)‖GB‖‖s\left(t\right)‖\hfill \end{array}(17)$

Considering that controller parameters m and n in Eq. 17 are real positive, the result of Eq. 18 can be obtained:

${\dot{V}}_0\left(t\right)\le -m‖s\left(t\right)‖-n{‖s\left(t\right)‖}^2\le 0(18)$

Therefore, the above analysis proves that system expressed in Eq. 3 is stable under the action of the proposed controller.

3 Stability analysis of multi-area LFC

In this section, an improved Lyapunov function and the Bessel-Legendre (B-L) inequality are applied to study the stability criteria for the multi-area LFC.

Lemma 1 (Lu et al., 2021): For an integer N > 0, and there exists [α, β] → Rⁿ, where α, β are given real scalars with α < β. For any symmetric matrices R > 0, the following Eq. 19 holds:

${\int }_{\alpha }^{\beta }{\dot{\upsilon }}^T\left(s\right)R\dot{\upsilon }\left(s\right)ds\ge \frac{1}{\beta -\alpha }{\tilde{\upsilon }}_N^T{\varsigma }_N^T{\mathrm{\Psi }}_N^T{\tilde{R}}_N{\mathrm{\Psi }}_N{\varsigma }_N{\tilde{\upsilon }}_N(19)$

where:

$\begin{array}{lll}\hfill & {\varsigma }_N=\left[\begin{array}{cccccc}\hfill I\hfill & \hfill -I\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -I\hfill & \hfill I\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -I\hfill & \hfill 0\hfill & \hfill 2I\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill -I\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill NI\hfill \end{array}\right]\hfill & \hfill \\ \hfill & {\mathrm{\Psi }}_N=\left[\begin{array}{ccccc}\hfill I\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill {\left(-1\right)}^{1}I\hfill & \hfill {\left(-1\right)}^1{q}_1^{1}I\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill {\left(-1\right)}^{2}I\hfill & \hfill {\left(-1\right)}^2{q}_1^{2}I\hfill & \hfill {\left(-1\right)}^2{q}_2^{2}I\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\left(-1\right)}^{N}I\hfill & \hfill {\left(-1\right)}^N{q}_1^{N}I\hfill & \hfill {\left(-1\right)}^N{q}_2^{N}I\hfill & \hfill \cdots \hfill & \hfill {\left(-1\right)}^N{q}_N^{N}I\hfill \end{array}\right]\hfill & \hfill \\ \hfill & {\tilde{R}}_N=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{R,3R,\cdots ,\left(2N+1\right)R\right\}\hfill & \hfill \\ \hfill & {\tilde{\upsilon }}_N=\mathrm{c}\mathrm{o}\mathrm{l}\left\{\upsilon \left(\beta \right),\upsilon \left(\alpha \right),{\epsilon }_1,\cdots ,{\epsilon }_N\right\},\hfill & \hfill \\ \hfill & {\epsilon }_i=\frac{1}{{\left(\beta -\alpha \right)}^i}{\int }_{\alpha }^{\beta }{\left(\beta -s\right)}^{i-1}\upsilon \left(s\right)ds,i=\mathrm{1,2},\cdots ,N\hfill & \hfill \\ \hfill & q_j^i={\left(-1\right)}^j\left(\genfrac{}{}{0.0pt}{}{i}{j}\right)\left(\genfrac{}{}{0.0pt}{}{i+j}{j}\right),\left(\genfrac{}{}{0.0pt}{}{i}{j}\right)=\frac{i!}{\left(i-j\right)!j!}\hfill & \hfill \end{array}$

Lemma 2: For a given positive matrix R > 0, and differentiable function {φ(u)|u ∈ [a, b]}, the following Eq. 20 and Eq. 21 can be hold as:

$\underset{a}{\overset{b}{\int }}\underset{\beta }{\overset{b}{\int }}{\dot{\phi }}^T\left(\alpha \right)R\dot{\phi }\left(\alpha \right)\mathrm{d}\alpha \mathrm{d}\beta \ge 2{\mathrm{\Omega }}_1^{T}R{\mathrm{\Omega }}_1+4{\mathrm{\Omega }}_2^{T}R{\mathrm{\Omega }}_2(20)$

$\underset{a}{\overset{b}{\int }}\underset{a}{\overset{\beta }{\int }}{\dot{\phi }}^T\left(\alpha \right)R\dot{\phi }\left(\alpha \right)\mathrm{d}\alpha \mathrm{d}\beta \ge 2{\mathrm{\Omega }}_3^{T}R{\mathrm{\Omega }}_3+4{\mathrm{\Omega }}_4^{T}R{\mathrm{\Omega }}_4(21)$

where:

$\begin{array}{lll}\hfill & {\mathrm{\Omega }}_1=\phi \left(b\right)-\frac{1}{b-a}{\int }_a^b\phi \left(\alpha \right)\mathrm{d}\alpha \hfill & \hfill \\ \hfill & {\mathrm{\Omega }}_2=\phi \left(b\right)+\frac{2}{b-a}{\int }_a^b\phi \left(\alpha \right)\mathrm{d}\alpha -\frac{6}{{\left(b-a\right)}^2}{\int }_a^b{\int }_{\beta }^b\phi \left(\alpha \right)\mathrm{d}\alpha \mathrm{d}\beta \hfill & \hfill \\ \hfill & {\mathrm{\Omega }}_3=\phi \left(a\right)-\frac{1}{b-a}{\int }_a^b\phi \left(\alpha \right)\mathrm{d}\alpha \hfill & \hfill \\ \hfill & {\mathrm{\Omega }}_4=\phi \left(a\right)-\frac{4}{b-a}{\int }_a^b\phi \left(\alpha \right)\mathrm{d}\alpha +\frac{6}{{\left(b-a\right)}^2}{\int }_a^b{\int }_{\beta }^b\phi \left(\alpha \right)\mathrm{d}\alpha \mathrm{d}\beta \hfill & \hfill \end{array}$

Lemma 3: For a real scalar α ∈ (0, 1), symmetric matrices γ₁ > 0, γ₂ > 0 and arbitrary matrices ϑ₁ > 0, ϑ₂ > 0, the following matrix inequality holds:

$\begin{array}{c}\hfill \left[\begin{array}{cc}\hfill \frac{1}{\alpha }{\gamma }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{1-\alpha }{\gamma }_2\hfill \end{array}\right]\ge \left[\begin{array}{cc}\hfill {\gamma }_1+\left(1-\alpha \right){\mathrm{\Gamma }}_1\hfill & \hfill \left(1-\alpha \right){\vartheta }_1+\alpha {\vartheta }_2\hfill \\ \hfill \ast \hfill & \hfill {\gamma }_2+\alpha {\mathrm{\Gamma }}_2\hfill \end{array}\right]\end{array}(22)$

where: ${\mathrm{\Gamma }}_1={\gamma }_1-{\vartheta }_2{{\gamma }_2}^{-1}{\vartheta }_2$, ${\mathrm{\Gamma }}_2={\gamma }_2-{\vartheta }_1{{\gamma }_1}^{-1}{\vartheta }_1$

Theorem 2: For given positive integers N ∈ {1, 2, 3, ⋯ }, scalars d₂ > d₁ > 0, disturbance attenuation level γ > 0, the closed-loop system is asymptotically stable under the event-triggering scheme. If there exist positive definite matrices P, Q, R, S and real matrices S_N, U_N, such the following inequalities holds:

$\begin{array}{l}\hfill \begin{array}{cc}\hfill \mathrm{\Theta }\left(d\left(t\right)=d_1|\alpha =0\right)& =\left[\begin{array}{cc}\hfill {\displaystyle \sum _{k=1}^5}{\mathrm{\Phi }}_k+{\mathrm{\Pi }}_3^T{\mathrm{\Pi }}_3\hfill & \hfill {\mathrm{\Psi }}_{1N}^T{U}_N\hfill \\ \hfill \ast \hfill & \hfill -\left(R_{1N}+R_{4N}\right)\hfill \end{array}\right]<0\hfill \\ \hfill \mathrm{\Theta }\left(d\left(t\right)=d_m|\alpha =1\right)& =\left[\begin{array}{cc}\hfill {\displaystyle \sum _{k=1}^5}{\mathrm{\Phi }}_k+{\mathrm{\Pi }}_3^T{\mathrm{\Pi }}_3\hfill & \hfill {\mathrm{\Psi }}_{2N}^T{S}_N^T\hfill \\ \hfill \ast \hfill & \hfill -\left(R_{1N}+R_{3N}\right)\hfill \end{array}\right]<0\hfill \end{array}\end{array}(23)$

where:

$\begin{array}{ll}\hfill {\mathrm{\Pi }}_1& =e_1{\upsilon }_1{e}_1^T-e_2{Q}_2{e}_2^T-e_3{\upsilon }_3{e}_3^T\hfill \\ \hfill {\mathrm{\Pi }}_2& ={\displaystyle \sum _{k=1}^4}{\mathrm{\Phi }}_k+\left(1-\alpha \right){\mathrm{\Psi }}_{1N}^T{U}_N{\left(R_{1N}+R_{4N}\right)}^{-1}{U}_N^T{\mathrm{\Psi }}_{1N}\hfill \\ \hfill & +\alpha {\mathrm{\Psi }}_{2N}^T{S}_N^T{\left(R_{1N}+R_{3N}\right)}^{-1}{S}_N{\mathrm{\Psi }}_{2N}\hfill \\ \hfill {\mathrm{\Pi }}_3& =C{e}_1\hfill \\ \hfill {\upsilon }_1& =Q_2+Q_3+d_m{R}_2\hfill \\ \hfill {\upsilon }_2& =d_m^2{R}_1+\frac{d_m^2}{2}{S}_1+\frac{d_m^2}{2}{S}_2\hfill \\ \hfill {\upsilon }_3& =\left(1-\dot{d}\left(t\right)\right)Q_3-\lambda \left(t_k\right)h\mathrm{\Omega }\hfill \\ \hfill {\mathrm{\Psi }}_{1N}& ={\mathrm{\Psi }}_N{\varsigma }_N\mathrm{c}\mathrm{o}\mathrm{l}\left\{e_1,e_3,H_2{e}_9,\dots ,H_2{e}_{N+8}\right\}\hfill \\ \hfill {\mathrm{\Psi }}_{2N}& ={\mathrm{\Psi }}_N{\varsigma }_N\mathrm{c}\mathrm{o}\mathrm{l}\left\{e_3,e_2,H_3{e}_9,\dots ,H_3{e}_{N+8}\right\}\hfill \\ \hfill R_{1N}& =\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{R_1,3R_1,\dots ,\left(2N+1\right)R_1\right\}\hfill \\ \hfill R_{3N}& =\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{S_1,3S_1,\dots ,\left(2N+1\right)S_1\right\}\hfill \\ \hfill R_{4N}& =\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{S_2,3S_2,\dots ,\left(2N+1\right)S_2\right\}\hfill \\ \hfill h_3& =\left[e_1-e_4,e_1+2e_4-3e_6,e_3-e_5,e_3+2e_5-3e_7\right]\hfill \\ \hfill {\phi }_3& =\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{-2S_1,-4S_1,-2S_1,-4S_1\right\}\hfill \\ \hfill h_4& =\left[e_3-e_4,e_3-4e_4+3e_6,e_2-e_5,e_2-4e_5+3e_7\right]\hfill \\ \hfill {\phi }_4& =\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{-2S_2,-4S_2,-2S_2,-4S_2\right\}\hfill \\ \hfill {\mathrm{\Phi }}_1& =-\left(2-\alpha \right){\mathrm{\Psi }}_{1N}^T\left(R_{1N}+R_{3N}\right){\mathrm{\Psi }}_{1N}-\left(1+\alpha \right){\mathrm{\Psi }}_{2N}^T\hfill \\ \hfill & \times \left(R_{1N}+R_{4N}\right){\mathrm{\Psi }}_{2N}-\mathrm{S}\mathrm{y}\mathrm{m}\left\{{\mathrm{\Psi }}_{1N}^T\left[\left(1-\alpha \right)S_N+\alpha U_N\right]{\mathrm{\Psi }}_{2N}\right\}\hfill \\ \hfill & +{\mathrm{\Psi }}_{1N}^T{R}_{3N}{\mathrm{\Psi }}_{1N}+{\mathrm{\Psi }}_{2N}^T{R}_{4N}{\mathrm{\Psi }}_{2N}\hfill \\ \hfill {\mathrm{\Phi }}_2& =-h_3{\phi }_3{h}_3^T,{\mathrm{\Phi }}_3=-h_4{\phi }_4{h}_4^T\hfill \\ \hfill {\mathrm{\Phi }}_4& ={\mathrm{\Pi }}_1+2P{\chi }_1+{\chi }_1{\upsilon }_2{\chi }_1^T\hfill \\ \hfill {\mathrm{\Phi }}_5& =-{\gamma }^2{e}_9^T{e}_9\hfill \\ \hfill {\chi }_1& =A{e}_1+BKC{e}_3\hfill \end{array}$

Proof: Defining the Lyapunov function as:

$V\left(t\right)=V_1\left(t\right)+V_2\left(t\right)+V_3\left(t\right)+V_4\left(t\right)(24)$

where:

$\begin{array}{ll}\hfill V_1\left(t\right)& =x^T\left(t\right)Px\left(t\right)\hfill \\ \hfill V_2\left(t\right)& ={\int }_{t-{\tau }_M}^t{x}^T\left(s\right)Q_{2}x\left(s\right)ds+{\int }_{t-d\left(t\right)}^t{x}^T\left(s\right)Q_{3}x\left(s\right)ds\hfill \\ \hfill V_3\left(t\right)& =d_M{\int }_{-d_M}^0{\int }_{t+\alpha }^t{\dot{x}}^T\left(s\right)R_1\dot{x}\left(s\right)dsd\alpha \hfill \\ \hfill & +{\int }_{-d_M}^0{\int }_{t+\alpha }^t{x}^T\left(s\right)R_{2}x\left(s\right)dsd\alpha \hfill \\ \hfill V_4\left(t\right)& ={\int }_{-d_M}^0{\int }_{\beta }^0{\int }_{t+\alpha }^t{\dot{x}}^T\left(s\right)S_1\dot{x}\left(s\right)dsd\alpha d\beta \hfill \\ \hfill & +{\int }_{-d_M}^0{\int }_{-d_M}^{\beta }{\int }_{t+\alpha }^t{\dot{x}}^T\left(s\right)S_2\dot{x}\left(s\right)dsd\alpha d\beta \hfill \\ \hfill & P,Q,R,Sarepositivedefinitematrices.\hfill \end{array}$

Calculating the derivation of V(t) obtains the following Eq. 25:

$\mathrm{\Delta }V\left(t\right)=\mathrm{\Delta }{V}_1\left(t\right)+\mathrm{\Delta }{V}_2\left(t\right)+\mathrm{\Delta }{V}_3\left(t\right)+\mathrm{\Delta }{V}_4\left(t\right)(25)$

where:

$\begin{array}{ll}\hfill \mathrm{\Delta }{V}_1\left(t\right)& =2{\dot{x}}^T\left(t\right)Px\left(t\right)\hfill \\ \hfill \mathrm{\Delta }{V}_2\left(t\right)& =x^T\left(t\right)Q_{2}x\left(t\right)-x^T\left(t-d_M\right)Q_{2}x\left(t-d_M\right)+x^T\left(t\right)\hfill \\ \hfill & \times Q_{3}x\left(t\right)-\left(1-\dot{d}\left(t\right)\right)x^T\left(t-d\left(t\right)\right)Q_{3}x\left(t-d\left(t\right)\right)\hfill \\ \hfill \mathrm{\Delta }{V}_3\left(t\right)& =d_M^2{\dot{x}}^T\left(t\right)R_1\dot{x}\left(t\right)-d_M{\int }_{t-d_M}^t{\dot{x}}^T\left(\alpha \right)R_1\dot{x}\left(\alpha \right)d\alpha \hfill \\ \hfill & +d_M{x}^T\left(t\right)R_{2}x\left(t\right)-{\int }_{t-d\left(t\right)}^t{x}^T\left(\alpha \right)R_{2}x\left(\alpha \right)d\alpha \hfill \\ \hfill \mathrm{\Delta }{V}_4\left(t\right)& =\frac{d_M^2}{2}{\dot{x}}^T\left(t\right)S_1\dot{x}\left(t\right)-{\int }_{-d\left(t\right)}^0{\int }_{t+\alpha }^t{\dot{x}}^T\left(s\right)S_1\dot{x}\left(s\right)dsd\alpha \hfill \\ \hfill & -{\int }_{-d_M}^{-d\left(t\right)}{\int }_{t+\alpha }^{t-d\left(t\right)}{\dot{x}}^T\left(s\right)S_1\dot{x}\left(s\right)dsd\alpha \hfill \\ \hfill & -\left(d_M-d\left(t\right)\right){\int }_{t-d\left(t\right)}^t{\dot{x}}^T\left(\alpha \right)S_1\dot{x}\left(\alpha \right)d\alpha +\frac{d_M^2}{2}{\dot{x}}^T\left(t\right)\hfill \\ \hfill & \times S_2\dot{x}\left(t\right)-{\int }_{-d\left(t\right)}^0{\int }_{t-d\left(t\right)}^{t+\alpha }{\dot{x}}^T\left(s\right)S_2\dot{x}\left(s\right)dsd\alpha \hfill \\ \hfill & -{\int }_{-d_M}^{-d\left(t\right)}{\int }_{t-d_M}^{t+\alpha }{\dot{x}}^T\left(s\right)S_2\dot{x}\left(s\right)dsd\alpha \hfill \\ \hfill & -d\left(t\right){\int }_{t-d_M}^{t-d\left(t\right)}{\dot{x}}^T\left(s\right)S_2\dot{x}\left(s\right)ds\hfill \end{array}$

In Eq. 26, we define the following augmenting state variable ξ(t):

$\begin{array}{cc}\hfill \xi \left(t\right)& =col\left\{x\left(t\right),e\left(t\right),x\left(t-d_m\right),x\left(t-d\left(t\right)\right),\right.\hfill \\ \hfill & \frac{1}{d\left(t\right)}{\int }_{t-d\left(t\right)}^{t}x\left(\alpha \right)d\alpha ,\frac{1}{d_m-d\left(t\right)}{\int }_{t-d_m}^{t-d\left(t\right)}x\left(\alpha \right)d\alpha ,\hfill \\ \hfill & \frac{2}{{\left(d\left(t\right)\right)}^2}{\int }_{-d\left(t\right)}^0{\int }_{t+\beta }^{t}x\left(\alpha \right)d\alpha d\beta ,\frac{2}{{\left(d_m-d\left(t\right)\right)}^2}{\int }_{-d_m}^{-d\left(t\right)}\hfill \\ \hfill & \left.\times {\int }_{t+\beta }^{t-d\left(t\right)}x\left(\alpha \right)d\alpha d\beta ,w\left(t\right),{\psi }_1\left(t\right),\dots ,{\psi }_N\left(t\right)\right\}\hfill \\ \hfill {\psi }_i\left(t\right)& =col\left\{{\int }_{t-d_1}^t\frac{{\left(t-s\right)}^{i-1}}{{d_1}^i}x\left(s\right)ds,{\int }_{t-d\left(t\right)}^{t-d_1}\frac{{\left(t-d_1-s\right)}^{i-1}}{{\left(d\left(t\right)-d_1\right)}^i}\right.\hfill \\ \hfill & \times \left.x\left(s\right)ds,{\int }_{t-d_2}^{t-d\left(t\right)}\frac{{\left(t-d\left(t\right)-s\right)}^{i-1}}{{\left(d_2-d\left(t\right)\right)}^i}x\left(s\right)ds\right\},\hfill \\ \hfill & i=\mathrm{1,2},\dots ,N\hfill \\ \hfill {\theta }_i\left(t\right)& ={\int }_{t-d_2}^{t-d_1}\frac{{\left(t-d_1-s\right)}^{i-1}}{{\left(d_{12}\right)}^i}x\left(s\right)ds\hfill \end{array}(26)$

Thus, the following inequality can be yielded:

$\begin{array}{ll}\hfill \mathrm{\Delta }V\left(t\right)& \le {\xi }^T\left(t\right){\mathrm{\Pi }}_1\xi \left(t\right)+2\dot{x}\left(t\right)P{x}^T\left(t\right)+\dot{x}\left(t\right){\upsilon }_2{\dot{x}}^T\left(t\right)\hfill \\ \hfill & +\mathrm{\Delta }{\tilde{V}}_1\left(t\right)+\mathrm{\Delta }{\tilde{V}}_2\left(t\right)+\mathrm{\Delta }{\tilde{V}}_3\left(t\right)\hfill \end{array}(27)$

where:

$\begin{array}{ll}\hfill \mathrm{\Delta }{\tilde{V}}_1\left(t\right)& =-d_m{\int }_{t-d_m}^t\dot{x}\left(s\right)R_1{\dot{x}}^T\left(s\right)ds-\left(d_m-d\left(t\right)\right)\hfill \\ \hfill & \times {\int }_{t-d\left(t\right)}^t\dot{x}\left(s\right)S_1{\dot{x}}^T\left(s\right)ds\hfill \\ \hfill & -\dot{d}\left(t\right){\int }_{t-d_m}^{t-d\left(t\right)}\dot{x}\left(s\right)S_2{\dot{x}}^T\left(s\right)ds\hfill \\ \hfill \mathrm{\Delta }{\tilde{V}}_2\left(t\right)& =-{\int }_{-d\left(t\right)}^0{\int }_{t+\alpha }^t\dot{x}\left(s\right)S_1{\dot{x}}^T\left(s\right)dsd\alpha \hfill \\ \hfill & -{\int }_{-d_m}^{-d\left(t\right)}{\int }_{t+\alpha }^{t-d\left(t\right)}\dot{x}\left(s\right)S_1{\dot{x}}^T\left(s\right)dsd\alpha \hfill \\ \hfill \mathrm{\Delta }{\tilde{V}}_3\left(t\right)& =-{\int }_{-d\left(t\right)}^0{\int }_{t-d\left(t\right)}^{t+\alpha }\dot{x}\left(s\right)S_2{\dot{x}}^T\left(s\right)dsd\alpha \hfill \\ \hfill & -{\int }_{-d_m}^{-d\left(t\right)}{\int }_{t-dm}^{t+\alpha }{\dot{x}}^T\left(s\right)S_2\dot{x}\left(s\right)dsd\alpha \hfill \end{array}$

where: $\mathrm{\Delta }{\tilde{V}}_1(t)$ can be rewritten. The item $-d_m{\int }_{t-d_m}^t\dot{x}(s)R_1{\dot{x}}^T(s)ds$ in the Equation will be decomposed into the following form:

$\begin{array}{ll}\hfill -d_m{\int }_{t-d_m}^t\dot{x}\left(s\right)R_1{\dot{x}}^T\left(s\right)ds& =-d_m{\int }_{t-d\left(t\right)}^t\dot{x}\left(s\right)R_1{\dot{x}}^T\left(s\right)ds\hfill \\ \hfill & -d_m{\int }_{t-d_m}^{t-d\left(t\right)}\dot{x}\left(s\right)R_1{\dot{x}}^T\left(s\right)ds\hfill \end{array}(28)$

Applying Lemma 1 and assuming $\alpha =\frac{d(t)}{d_m},\beta =\frac{d_m-d(t)}{d_m}=1-\alpha$, then Eq. 28 is less than the following Equation:

$\begin{array}{c}\hfill -\frac{1}{\alpha }{\xi }^T\left(t\right){\mathrm{\Psi }}_{1N}^T{R}_{1N}{\mathrm{\Psi }}_{1N}\xi \left(t\right)-\frac{1}{1-\alpha }{\xi }^T\left(t\right){\mathrm{\Psi }}_{2N}^T{R}_{1N}{\mathrm{\Psi }}_{2N}\xi \left(t\right)\end{array}(29)$

Rewrite the relevant items in Eq. 29 into the following form:

$\begin{array}{ll}\hfill -{\left[\begin{array}{c}\hfill {\mathrm{\Psi }}_{1N}\hfill \\ \hfill {\mathrm{\Psi }}_{2N}\hfill \end{array}\right]}^T{M}_1\left[\begin{array}{c}\hfill {\mathrm{\Psi }}_{1N}\hfill \\ \hfill {\mathrm{\Psi }}_{2N}\hfill \end{array}\right]& \le -{\left[\begin{array}{c}\hfill {\mathrm{\Psi }}_{1N}\hfill \\ \hfill {\mathrm{\Psi }}_{2N}\hfill \end{array}\right]}^T{M}_2\left[\begin{array}{c}\hfill {\mathrm{\Psi }}_{1N}\hfill \\ \hfill {\mathrm{\Psi }}_{2N}\hfill \end{array}\right]+\left(1-\alpha \right){\mathrm{\Psi }}_{1N}^T\hfill \\ \hfill & \times U_N{R}_{1N}^{-1}{U}_N^T{\mathrm{\Psi }}_{1N}+\alpha {\mathrm{\Psi }}_{2N}^T{S}_N^T{R}_{1N}^{-1}\hfill \\ \hfill & \times S_N{\mathrm{\Psi }}_{2N}\hfill \end{array}(30)$

where:

$\begin{array}{lll}\hfill & M_1=\left[\begin{array}{cc}\hfill \frac{1}{\alpha }{R}_{1N}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{1-\alpha }{R}_{1N}\hfill \end{array}\right]\hfill & \hfill \\ \hfill & M_2=\left[\begin{array}{cc}\hfill \left(2-\alpha \right)R_{1N}\hfill & \hfill \left(1-\alpha \right)S_N+\alpha U_N\hfill \\ \hfill *\hfill & \hfill \left(1+\alpha \right)R_{1N}\hfill & \hfill \hfill \end{array}\right]\hfill & \hfill \end{array}$

Applying Lemma 1 to the other two terms of $\mathrm{\Delta }{\tilde{V}}_1(t)$ yields the following inequality:

$\begin{array}{cc}\hfill & -\left(d_m-d\left(t\right)\right){\int }_{t-d\left(t\right)}^t\dot{x}\left(s\right)S_1{\dot{x}}^T\left(s\right)ds\hfill \\ \hfill & \le \left(1-\frac{1}{\alpha }\right){\xi }^T\left(t\right){\mathrm{\Psi }}_{1N}^T{R}_{3N}{\mathrm{\Psi }}_{1N}\xi \left(t\right),\hfill \\ \hfill & -d\left(t\right){\int }_{t-d_m}^{t-d\left(t\right)}\dot{x}\left(s\right)S_2{\dot{x}}^T\left(s\right)ds\hfill \\ \hfill & \le \left(1-\frac{1}{\beta }\right){\xi }^T\left(t\right){\mathrm{\Psi }}_{2N}^T{R}_{4N}{\mathrm{\Psi }}_{2N}\xi \left(t\right)\hfill \end{array}(31)$

Combine the items involving $\frac{1}{\alpha }$ and $\frac{1}{\beta }$ from Eq. 31 with Eq. 30 to obtain the Eq. 32:

$\begin{array}{ll}\hfill -{\left[\begin{array}{c}\hfill {\mathrm{\Psi }}_{1N}\hfill \\ \hfill {\mathrm{\Psi }}_{2N}\hfill \end{array}\right]}^T{M}_3\left[\begin{array}{c}\hfill {\mathrm{\Psi }}_{1N}\hfill \\ \hfill {\mathrm{\Psi }}_{2N}\hfill \end{array}\right]& \le -{\left[\begin{array}{c}\hfill {\mathrm{\Psi }}_{1N}\hfill \\ \hfill {\mathrm{\Psi }}_{2N}\hfill \end{array}\right]}^T{M}_4\left[\begin{array}{c}\hfill {\mathrm{\Psi }}_{1N}\hfill \\ \hfill {\mathrm{\Psi }}_{2N}\hfill \end{array}\right]\hfill \\ \hfill & +\left(1-\alpha \right){\mathrm{\Psi }}_{1N}^T{U}_N{\left(R_{1N}+R_{4N}\right)}^{-1}{U}_N^T\hfill \\ \hfill & \times {\mathrm{\Psi }}_{1N}+\alpha {\mathrm{\Psi }}_{2N}^T{S}_N^T{\left(R_{1N}+R_{3N}\right)}^{-1}{S}_N\hfill \\ \hfill & \times {\mathrm{\Psi }}_{2N}\hfill \end{array}(32)$

where:

$\begin{array}{lll}\hfill & M_3=\left[\begin{array}{cc}\hfill \frac{1}{\alpha }\left(R_{1N}+R_{3N}\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{1-\alpha }\left(R_{1N}+R_{4N}\right)\hfill \end{array}\right],\hfill & \hfill \\ \hfill & M_4=\left[\begin{array}{cc}\hfill \left(2-\alpha \right)\left(R_{1N}+R_{3N}\right)\hfill & \hfill \left(1-\alpha \right)S_N+\alpha U_N\hfill \\ \hfill *\hfill & \hfill \left(1+\alpha \right)\left(R_{1N}+R_{4N}\right)\hfill \end{array}\right]\hfill & \hfill \end{array}$

Thus, the result is given by Eq. 33.

$\begin{array}{ll}\hfill \mathrm{\Delta }{\tilde{V}}_1\left(t\right)& \le {\xi }^T\left(t\right)\left\{{\mathrm{\Phi }}_1+\left(1-\alpha \right){\mathrm{\Psi }}_{1N}^T{U}_N{\left(R_{1N}+R_{4N}\right)}^{-1}{U}_N^T{\mathrm{\Psi }}_{1N}\right.\hfill \\ \hfill & \left.+\alpha {\mathrm{\Psi }}_{2N}^T{S}_N^T{\left(R_{1N}+R_{3N}\right)}^{-1}{S}_N{\mathrm{\Psi }}_{2N}\right\}\hfill \end{array}(33)$

Applying Lemma 2 to scale $\mathrm{\Delta }{\tilde{V}}_2(t)$ and $\mathrm{\Delta }{\tilde{V}}_3(t)$, the result is shown in Eqs. 34, 35.

$\begin{array}{c}\mathrm{\Delta }{\tilde{V}}_2\left(t\right)\le -{\xi }^T\left(t\right)h_3{\phi }_3{h}_3^T\xi \left(t\right)={\xi }^T\left(t\right){\mathrm{\Phi }}_2\xi \left(t\right)\hfill \\ \mathrm{\Delta }{\tilde{V}}_3\left(t\right)\le -{\xi }^T\left(t\right)h_4{\phi }_4{h}_4^T\xi \left(t\right)={\xi }^T\left(t\right){\mathrm{\Phi }}_3\xi \left(t\right)\hfill \end{array}(34)$

$\begin{array}{ll}\hfill \mathrm{\Delta }V\left(t\right)& \le {\xi }^T\left(t\right){\mathrm{\Pi }}_1\xi \left(t\right)+2\dot{x}\left(t\right)P{x}^T\left(t\right)+\dot{x}\left(t\right){\upsilon }_2{\dot{x}}^T\left(t\right)+\mathrm{\Delta }{\tilde{V}}_1\left(t\right)\hfill \\ \hfill & +\mathrm{\Delta }{\tilde{V}}_2\left(t\right)+\mathrm{\Delta }{\tilde{V}}_3\left(t\right)\le {\xi }^T\left(t\right){\mathrm{\Pi }}_2\xi \left(t\right)\hfill \end{array}(35)$

Consider the event-triggering condition shown in Eqs. 36, 37:

$\mathrm{\Delta }V\left(t\right)\le {\xi }^T\left(t\right)\mathrm{\Xi }\xi \left(t\right)-y^T\left(t\right)y\left(t\right)+{\gamma }^2{w}^T\left(t\right)w\left(t\right)(36)$

$\begin{array}{ll}\hfill \mathrm{\Xi }& ={\displaystyle \sum _{k=1}^5}{\mathrm{\Phi }}_k+{\mathrm{\Pi }}_3^T{\mathrm{\Pi }}_3+\left(1-\alpha \right){\mathrm{\Psi }}_{1N}^T{U}_N{\left(R_{1N}+R_{4N}\right)}^{-1}{U}_N^T{\mathrm{\Psi }}_{1N}\hfill \\ \hfill & +\alpha {\mathrm{\Psi }}_{2N}^T{S}_N^T{\left(R_{1N}+R_{3N}\right)}^{-1}{S}_N{\mathrm{\Psi }}_{2N}\hfill \end{array}(37)$

Applying the Schur complement theorem, it can be seen that Ξ < 0 is equivalent to:

$\left\{\begin{array}{c}\mathrm{\Theta }=\left[\begin{array}{cc}\hfill {\mathrm{\Theta }}_{11}\hfill & \hfill {\mathrm{\Theta }}_{12}\hfill \\ \hfill \ast \hfill & \hfill {\mathrm{\Theta }}_{22}\hfill \end{array}\right]<0\hfill \\ {\mathrm{\Theta }}_{11}={\displaystyle \sum _{k=1}^5}{\mathrm{\Phi }}_k+{\mathrm{\Pi }}_3^T{\mathrm{\Pi }}_3\hfill \\ {\mathrm{\Theta }}_{12}=\left[\sqrt{1-\alpha }{\mathrm{\Psi }}_{1N}^T{U}_N\sqrt{\alpha }{\mathrm{\Psi }}_{2N}^T{S}_N^T\right]\hfill \\ {\mathrm{\Theta }}_{22}=diag\left\{-\left(R_{1N}+R_{4N}\right),-\left(R_{1N}+R_{3N}\right)\right\}\hfill \end{array}\right.(38)$

Therefore, if the conditions listed in Theorem 2 are satisfied, then under zero initial conditions, when w(t) = 0 and ${‖y(t)‖}_2\le \gamma {‖w(t)‖}_2$, the closed-loop system is asymptotically stable, thereby proving Theorem 2.

4 Simulation and analysis

To verify the performance of the designed LFC with AGSMC, the models of single area LFC with AGSMC and double area LFC with AGSMC, which include battery energy storage, are established using MATLAB/Simulink toolbox. For the above two LFC system models under load disturbances, the frequency deviations are analyzed based on their response curves. To demonstrate the effectiveness of the proposed scheme, the results are compared with the controllers in the existing literature, such as GSMC (Radosevic et al., 2008), SMC (Lv et al., 2020), PID control (Fu et al., 2022).

4.1 Case study 1

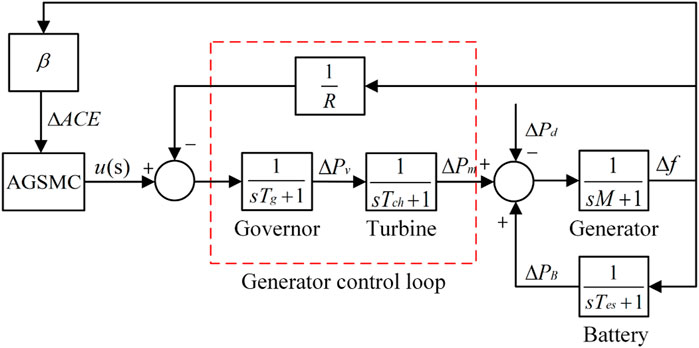
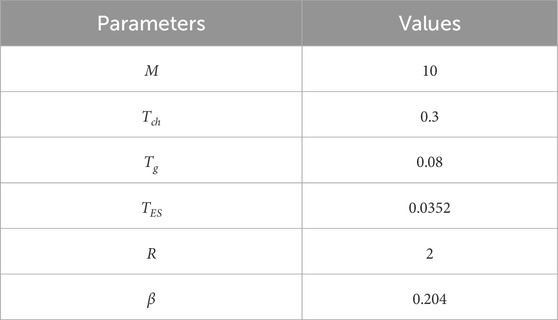
The LFC model of a single area power system is shown in Figure 2, and the system parameters are listed in Table 2.

Figure 2

Figure 2. Single area power system model diagram.

Table 2

Table 2. Parameters of the single area power system model.

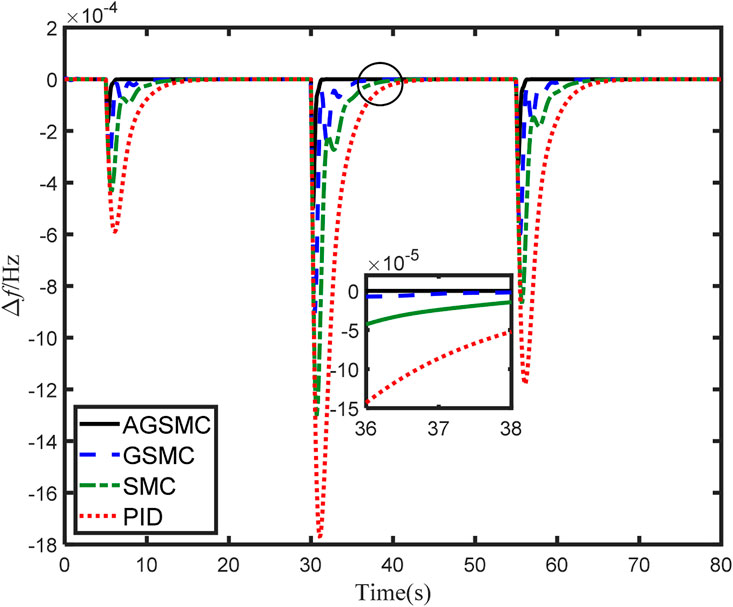
In this subsection, a single area LFC system with battery energy storage is taken as an example to separately examine the impact of normal disturbances and random disturbances on the performance of the LFC system. On the one hand, the first normal disturbance is set to 0.01Hz at t = 5s, the second normal disturbance is set to 0.03Hz at t = 30s, and the final normal disturbance is set to 0.02Hz at t = 55s. Moreover, amplitude-limited random disturbances with their upper limit are set to 0.01Hz, which occurs at t = 0s, 20s, 40s, 60s, 80s. The simulation results are depicted in Figures 3, 4, respectively.

Figure 3

Figure 3. Comparison of controller performance under normal disturbances for a single area system.

Figure 4

Figure 4. Comparison of controller performance under random disturbances for a single area system.

As can be seen from Figure 3, all existing control technologies are capable of stabilizing the single area LFC system. Investigating the normal disturbance ψ = 0.03Hz which happened at t = 30s, the overshoot is 5.89% and the response time is 13.4s for the single area system based on PID control. Meanwhile, considering the single area system under SMC and GSMC, the overshoot is 4.33% and 3.02% respectively, and the response time is 8.75s and 6.49s approximately. Compared with the preceding three control schemes, adopting the AGSMC approach significantly reduces the overshoot to just 1.60%, while the stabilization time dramatically decreases to roughly 1.47s. It is worth noting that upon reaching the system’s frequency stability state, the oscillation amplitude of the system based on AGSMC is notably minimal. In contrast, the proposed control method has the characteristics of fast response and low overshoot. The single area LFC system can quickly move to a stable state under the action of this controller.

From the curve in Figure 4, for these controllers, when facing random disturbance, the single area LFC system will be stabilized within 15s. Under PID control, the single area system exhibits the highest overshoot and the longest response time. By comparing with GSMC, SMC, and PID control schemes, the AGSMC achieves a stable state within 1.63s, and the average overshoot was controlled within 1.72% even in the presence of random load disturbances. It can be seen that adaptive law effectively counters random disturbances, ensuring the stability of system performance.

4.2 Case study 2

The double area LFC system can be seen in Figure 5, and the parameter values are presented in Table 3.

Figure 5

Figure 5. Double area power system model diagram.

Table 3

Table 3. Parameters of the double area power system model.

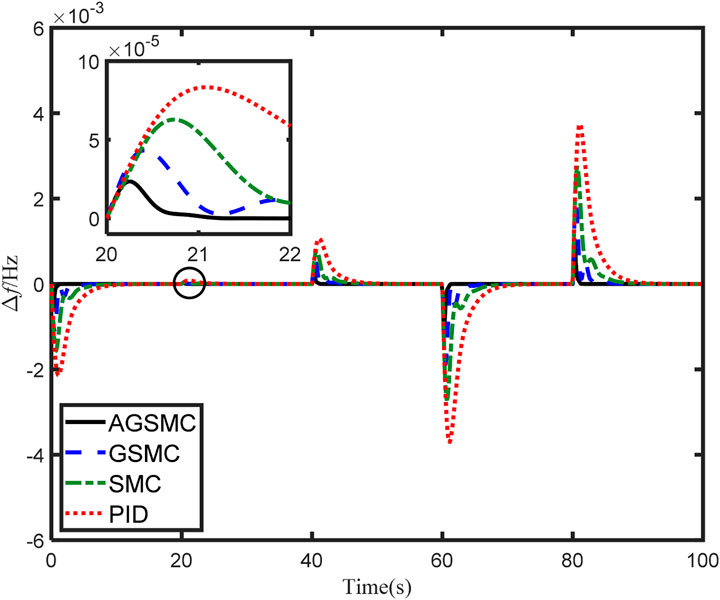
In this subsection, examining the double area interconnected power system equipped with battery energy storage as an example, the simulation time is set to 100s, and normal or random disturbances are applied simultaneously to both areas. Firstly, the normal disturbances of area 1 are set to 0.01Hz at t = 0s and 0.02Hz at t = 50s, the disturbances of area 2 are set to 0.02Hz at t = 0s and 0.04Hz at t = 50s, respectively. Secondly, two random disturbances happened at t = 0s while the upper limits are established as follows: ψ_{1 max} = 0.08Hz, ψ_{2 max} = 0.04Hz. The simulation results are shown in Figures 6, 7, respectively. Δf₁ is the load frequency deviation of area 1, Δf₂ is the load frequency of area 2, and ΔP₁₂ presents the tie-line power between the two areas.

Figure 6

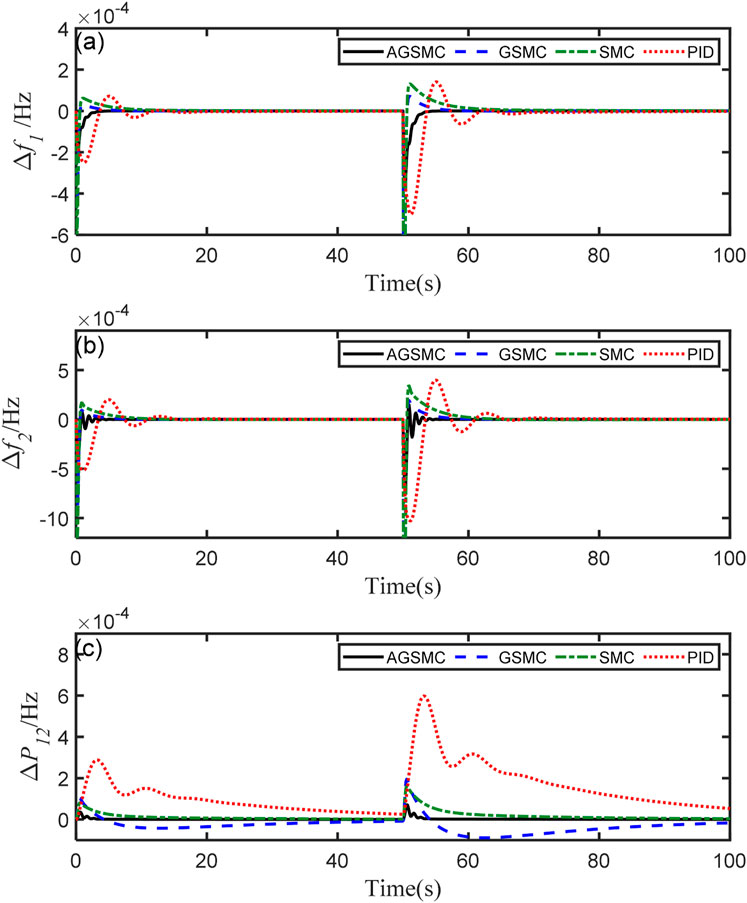
Figure 6. Comparison of controller performance under normal disturbances for a double area system. (A) The load frequency deviation of area 1, (B) the load frequency deviation of area 2, and (C) the tie-line power deviation between the two areas.

Figure 7

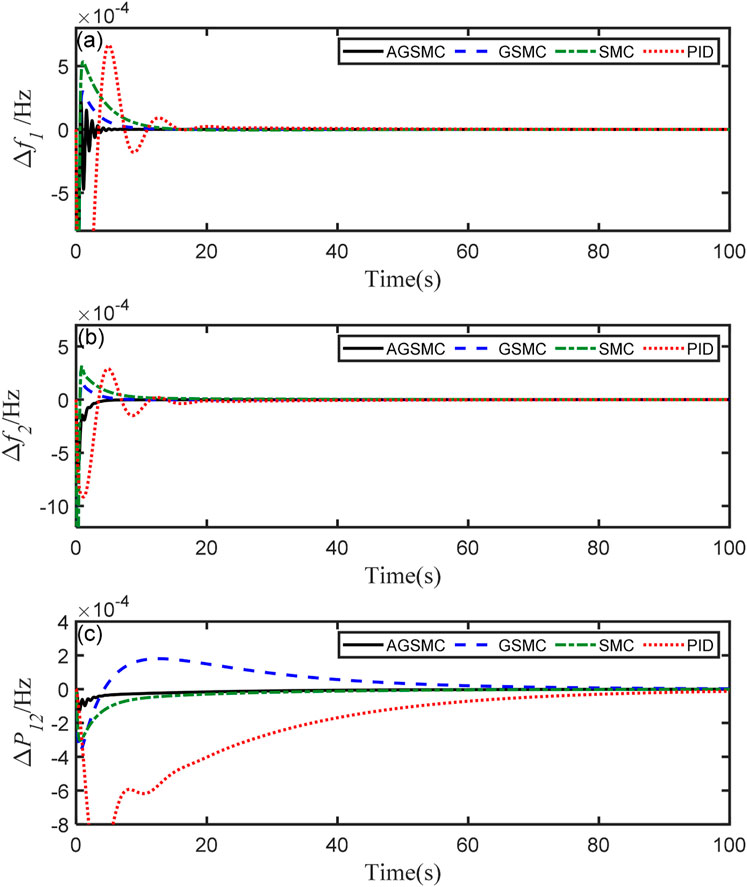
Figure 7. Comparison of controller performance under random disturbances for a double area system. (A) The load frequency deviation of area 1, (B) the load frequency deviation of area 2, and (C) the tie-line power deviation between the two areas.

From the curves in Figure 6A, it can be seen that, with a frequency deviation ψ₁₁ = 0.01Hz happened in area 1, no control scheme can maintain the overshoot in area 1 within 1%, and the power system will stabilize at t = 20s. Compared to PID control, the double area system governed by SMC and GSMC shows faster response speed and larger overshoot from the curves of Δf₁ and Δf₂. But the more significant overshoot amounts are still acceptable. While the proposed controller has a small superiority over the other three controllers by comparing the overshoot and the degree of oscillation. The ΔP₁₂ curve in Figure 6 indicates that these control schemes can effectively eliminate system fluctuations caused by normal load disturbances. Simultaneously, upon the occurrence of disturbances, the AGSMC technology can suppress the disturbance rapidly, resulting in the double area system exhibiting the smallest overshoot and swiftly returning to a stable state, and the tie-line power deviation decrease to zero within 4.23s. Based on the above simulation results and analysis, GSMC, SMC and PID controller have a good performance in dealing with the frequency deviation, but the control effect has not yet reached optimal level.

In Figure 7, when load disturbances occur randomly, one aspect illustrates the double area interconnected power system employing AGSMC maintains stable frequency deviation responses and possesses robust dynamic performance. In the case of unknown disturbance, the overshoot of the system Δf₁, Δf₂, Δf₃ is 75.1%, 74.3%, 12.1% of the overshoot of the PID control system, and the response time is 5.47s, 5.54s and 5.77s respectively. Conversely, from Figure 7C, it is expected that the system operated by other controllers will eventually not continue to remain stable as time increases due to ΔP₁₂ long response time. By comparing Figure 4 with Figure 7, it can be seen that under the control of AGSMC, both single area power system and double area power system show excellent control performance under random load frequency disturbance. Therefore, from the above analysis, it can be concluded that, due to its superior response efficiency and control precision, AGSMC can replace existing control technologies, whether in handling normal disturbances or uncertain system frequency deviations.

5 Conclusion

This paper introduces new energy sources into the conventional power system, establishing a LFC model that includes a battery energy storage module. The AGSMC scheme is crafted to effectively tackle the challenge of normal or random load frequency disturbances. Based on this model, by utilizing an enhanced Lyapunov function and B-L inequalities, the stability criteria for the multi-area LFC have been successfully established. Furthermore, simulations of single and double area LFC power systems were conducted to validate the proposed method, which incorporates a nonlinear time-varying function and an adaptive sliding mode control law designed to estimate the upper bounds of external disturbances. In comparison to existing control strategies, the mentioned controller is superior in terms of overshoot and response speed, presenting excellent disturbance rejection capabilities and improved robustness while ensuring the consistency of system parameters. This research not only addresses the integration challenges of new energy sources into the power grid but also advances a robust framework for maintaining system stability and reliability under randomly variable load conditions.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YL: Conceptualization, Data curation, Formal Analysis, Writing–original draft. QJ: Methodology, Resources, Supervision, Writing–original draft. LX: Funding acquisition, Methodology, Resources, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by Zhejiang Provincial Natural Science Foundation of China under Grant 21022311-Y, in part by General Projects of Zhejiang Provincial Department of Education under Grant Y202250499, in part by Science Foundation of Zhejiang Sci-Tech University under Grant 21022311-Y.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ansari, J., Homayounzade, M., and Abbasi, A. R. (2023). Load frequency control in power systems by a robust backstepping sliding mode controller design. Energy Rep. 10, 1287–1298. doi:10.1016/j.egyr.2023.08.008

CrossRef Full Text | Google Scholar

Deng, Z., and Xu, C. (2022). Frequency regulation of power systems with a wind farm by sliding-mode-based design. IEEE/CAA J. Automatica Sinica 9, 1980–1989. doi:10.1109/jas.2022.105407

CrossRef Full Text | Google Scholar

Fu, Q. J., Zhang, Y., and Zhang, C. (2022). “Load frequency control of the two regions interconnected power system with wind and photovoltaic based on improved differential evolution algorithm,” in 2022 41st Chinese Control Conference (CCC), USA, 25-27 July 2022 (IEEE), 6036–6040.

CrossRef Full Text | Google Scholar

Ge, S., He, X., Liu, H., Mi, Y., and Wang, C. (2021). Frequency coordinated control strategy based on sliding mode method for a microgrid with hybrid energy storage system. IET Generation, Transm. Distribution 15, 1962–1971. doi:10.1049/gtd2.12148

CrossRef Full Text | Google Scholar

Guo, J. (2021). Application of a novel adaptive sliding mode control method to the load frequency control. Eur. J. Control 57, 172–178. doi:10.1016/j.ejcon.2020.03.007

CrossRef Full Text | Google Scholar

Hasen, S. A., Aydın, Ö., Ayasun, S., and Sönmez, Ş. (2023). Impact of virtual inertia and damping control on stability delay margins of load frequency control systems with renewable energy sources. Electr. Eng. 106, 323–341. doi:10.1007/s00202-023-01984-3

CrossRef Full Text | Google Scholar

Khokhar, B., and Parmar, K. S. (2023). Utilizing diverse mix of energy storage for lfc performance enhancement of a microgrid: a novel mpc approach. Appl. Energy 333, 120639. doi:10.1016/j.apenergy.2023.120639

CrossRef Full Text | Google Scholar

Kundu, S., Singh, M., and Giri, A. K. (2021). “Design and control of a standalone wind–solar system with seig feeding linear/nonlinear loads,” in Proceedings of Symposium on Power Electronic and Renewable Energy Systems Control: PERESC 2020, China, January 2021 (IEEE), 317–327.

CrossRef Full Text | Google Scholar

Kundu, S., Singh, M., and Giri, A. K. (2023). Spv-wind-bes-based islanded electrical supply system for remote applications with power quality enhancement. Electr. Eng. 106, 279–294. doi:10.1007/s00202-023-01979-0

CrossRef Full Text | Google Scholar

Li, G., Lu, W., Bian, J., Qin, F., Wu, J., Song, J., et al. (2019). Development and validation of a CIMP-associated prognostic model for hepatocellular carcinoma. Front. Energy Res. 7, 128–141. doi:10.1016/j.ebiom.2019.08.064

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., and Ye, D. (2022). Event-based distributed fuzzy load frequency control for multiarea nonlinear power systems with switching topology. IEEE Trans. Fuzzy Syst. 30, 4262–4272. doi:10.1109/tfuzz.2022.3146981

CrossRef Full Text | Google Scholar

Lu, H., Deng, Y., and Zhou, W. (2021). Hierarchical type stability and stabilization of networked control systems with event-triggered mechanism via canonical bessel–legendre inequalities. J. Frankl. Inst. 358, 6592–6611. doi:10.1016/j.jfranklin.2021.06.024

CrossRef Full Text | Google Scholar

Lv, X., Sun, Y., Cao, S., and Dinavahi, V. (2020). Event-triggered load frequency control for multi-area power systems based on markov model: a global sliding mode control approach. IET Generation, Transm. Distribution 14, 4878–4887. doi:10.1049/iet-gtd.2020.0186

CrossRef Full Text | Google Scholar

Mazinan, A. (2013). Applying an intelligence-based adaptive multi-predictive control strategy to a two-area interconnected power system. Trans. Inst. Meas. Control 35, 464–475. doi:10.1177/0142331212451993

CrossRef Full Text | Google Scholar

Mohammadi Moghadam, H., Mohammadzadeh, A., Hadjiaghaie Vafaie, R., Tavoosi, J., and Khooban, M.-H. (2022). A type-2 fuzzy control for active/reactive power control and energy storage management. Trans. Inst. Meas. Control 44, 1014–1028. doi:10.1177/01423312211048038

CrossRef Full Text | Google Scholar

Naderipour, A., Abdul-Malek, Z., Davoodkhani, I. F., Kamyab, H., and Ali, R. R. (2023). Load-frequency control in an islanded microgrid pv/wt/fc/ess using an optimal self-tuning fractional-order fuzzy controller. Environ. Sci. Pollut. Res. 30, 71677–71688. doi:10.1007/s11356-021-14799-1

CrossRef Full Text | Google Scholar

Ojha, S. K., and Maddela, C. O. (2023). Load frequency control of a two-area power system with renewable energy sources using brown bear optimization technique. Electr. Eng., 1–25. doi:10.1007/s00202-023-02143-4

CrossRef Full Text | Google Scholar

Qiao, S., Liu, X., Xiao, G., and Ge, S. S. (2021). Observer-based sliding mode load frequency control of power systems under deception attack. Complexity 2021, 1–11. doi:10.1155/2021/8092206

CrossRef Full Text | Google Scholar

Radosevic, T., Vrdoljak, K., and Peric, N. (2008). “Optimal sliding mode controller for power system’s load-frequency control,” in 2008 43rd International Universities Power Engineering Conference, USA, 1-4 Sept. 2008 (IEEE), 1–5.

Google Scholar

Ranjitha, K., Sivakumar, P., and Monica, M. (2022). Load frequency control based on an improved chimp optimization algorithm using adaptive weight strategy. COMPEL-The Int. J. Comput. Math. Electr. Electron. Eng. 41, 1618–1648. doi:10.1108/compel-07-2021-0231

CrossRef Full Text | Google Scholar

Sharma, J., Hote, Y. V., and Prasad, R. (2022). Computation of parametric uncertainty margin using stability boundary locus: an application to load frequency control. Trans. Inst. Meas. Control 44, 2308–2322. doi:10.1177/01423312221083762

CrossRef Full Text | Google Scholar

Singh, R., and Ramesh, L. (2024). Comparison between pid and pso-pid controllers in analysing the load frequency control in interconnected microgrids in a deregulated environment. Int. J. Glob. Energy Issues 46, 1–136. doi:10.1504/ijgei.2023.10053492

CrossRef Full Text | Google Scholar

Tan, C., Tan, Z., Yin, Z., Wang, Y., Geng, S., and Pu, L. (2023). Study on grid price mechanism of new energy power stations considering market environment. Renew. Energy 203, 177–193. doi:10.1016/j.renene.2022.12.065

CrossRef Full Text | Google Scholar

Tang, X., Wu, Y., Li, Y., and Wen, Y. (2023). Load frequency predictive control for power systems concerning wind turbine and communication delay. Optim. Control Appl. Methods 44, 205–222. doi:10.1002/oca.2955

CrossRef Full Text | Google Scholar

Veerendar, T., Kumar, D., and Sreeram, V. (2023). Fractional-order pid and internal model control-based dual-loop load frequency control using teaching–learning optimization. Asian J. Control 25, 2482–2497. doi:10.1002/asjc.3022

CrossRef Full Text | Google Scholar

Wang, X., Cui, J., Ren, B., Liu, Y., and Huang, Y. (2022a). Integrated energy system scheduling optimization considering vertical axis wind turbines and thermal inertia in oilfield management areas. Front. Energy Res. 12, 1340580. doi:10.3389/fenrg.2024.1340580

CrossRef Full Text | Google Scholar

Wang, Y., Liu, D., Shen, Y., Tang, Y., Chen, Y., and Zhang, J. (2022b). Adaptive balancing control of cell voltage in the charging/discharging mode for battery energy storage systems. Front. Energy Res. 10, 794191. doi:10.3389/fenrg.2022.794191

CrossRef Full Text | Google Scholar

Xu, K., Niu, Y., and Yang, Y. (2022). Load frequency control for wind-integrated multi-area power systems: an area-based event-triggered sliding mode scheme. J. Frankl. Inst. 359, 9451–9472. doi:10.1016/j.jfranklin.2022.10.010

CrossRef Full Text | Google Scholar

Yang, F., Shao, X., Muyeen, S., Li, D., Lin, S., and Fang, C. (2021). Disturbance observer based fractional-order integral sliding mode frequency control strategy for interconnected power system. IEEE Trans. Power Syst. 36, 5922–5932. doi:10.1109/tpwrs.2021.3081737

CrossRef Full Text | Google Scholar

Zhang, G., Khan, I. A., Daraz, A., Basit, A., and Khan, M. I. (2023a). Load frequency control of marine microgrid system integrated with renewable energy sources. J. Mar. Sci. Eng. 11, 844. doi:10.3390/jmse11040844

CrossRef Full Text | Google Scholar

Zhang, Y., Chen, X., Gong, S., and Chen, J. (2023b). Collective large-scale wind farm multivariate power output control based on hierarchical communication multi-agent proximal policy optimization. Renew. Energy 219, 119479. doi:10.1016/j.renene.2023.119479

CrossRef Full Text | Google Scholar

Zou, Q. (2020). Adaptive sliding mode control for chain driving system with disturbance observer. Proc. Institution Mech. Eng. Part I J. Syst. Control Eng. 234, 1050–1059. doi:10.1177/0959651819895693

CrossRef Full Text | Google Scholar