- 1State Grid Liaoning Electric Power Supply Co., Ltd, Branch Materials, Shenyang, China
- 2School of Electrical Engineering, Shenyang University of Technology, Shenyang, China
Combining green warehousing with wind-solar-storage systems can enhance economic power consumption, energy saving, and emission reduction in green warehousing. To achieve efficient and stable operation of the wind-solar-storage microgrid, this paper proposes an optimal microgrid scheduling strategy based on the Improved Sparrow Algorithm (ISSA). Firstly, a comprehensive benefit model is established based on the economic and environmental benefits of microgrid daily operation. Then, an innovative improved sparrow search algorithm is proposed, which aims to improve the global search and local search capability of the microgrid scheduling problem by introducing improvements such as Logistic-Circle chaotic mapping, Bottle Sea Sheath swarm optimization algorithm, dynamic inertia weights, water wave dynamic factor, and Cauchy-Gaussian variational strategy. Finally, the microgrid optimal scheduling model is solved by the improved sparrow search algorithm and compared with other algorithms. In this paper, Matlab 2016b is used for simulation, and the simulation results show that the ISSA algorithm outperforms other algorithms in terms of solution stability and optimization search capability. Under three modes of operation, ISSA improves the microgrid operation revenue by 6.29%, 5.98%, and 6.31% at least. Therefore, the optimal scheduling scheme obtained based on ISSA improves the daily operating total revenue and the system operation stability of the microgrid.
1 Introduction
With the construction of green warehousing and logistics system to promote the depth of the exploration to create a zero-carbon warehouse and the study of warehouse energy saving and emission reduction, carbon neutrality and the use of renewable energy and other technologies to become an important part of the development of green warehousing (Gao and Hou, 2022). Among all renewable energy sources, solar and wind energy are more common (Gbadamosi and Nwulu, 2021; Kiani et al., 2021). At the same time, wind and solar power generation has the characteristics of no pollution and low power generation cost, which is especially in line with the future development of green warehousing. Therefore, the combination of green warehousing and distributed wind-solar-storage systems can actively promote the development and construction of green warehousing and help the logistics warehousing industry achieve the “double carbon” goal (Liu et al., 2021). However, compared with traditional power, the random characteristics of renewable energy technology make it less reliable. This stochastic nature, especially the intermittency of sunlight and the instability of wind, affects the continuity and reliability of energy supply (Kumar et al., 2019; Vaziri Rad et al., 2020). However, through the rational planning and control of the wind-solar-storage microgrid, the wind-solar power generation and energy storage system can achieve more efficient, reliable, and economical energy utilization, to meet the electricity demand of green warehousing (Thirunavukkarasu et al., 2022). Therefore, using a more efficient microgrid power optimization scheduling method is of far-reaching significance for promoting clean energy applications, improving energy efficiency, and developing green warehousing.
Microgrid scheduling strategies aim to optimize the operation of microgrids to ensure the reliability, economy, and environmental friendliness of energy supply (Xu et al., 2024). The basic structure of the microgrid and the desired objectives of the microgrid need to be considered when developing a microgrid dispatch strategy. The objective of the literature (Li et al., 2021) is to improve economic efficiency and environmental protection while meeting the basic needs of power supply. Therefore, a multi-objective optimal scheduling model in grid-connected mode that integrates the operating costs of the microgrid system and environmental protection costs is proposed. Literature (He et al., 2023) proposed a microgrid active power scheduling model considering demand side response, which takes the microgrid economic and environmental protection optimization as the objective function, and comprehensively considers the system operation constraints, battery operation constraints, and user satisfaction (introducing load response compensation). Literature (Zeng et al., 2023) studies a microgrid cluster containing two AC microgrids operating off-grid and one DC microgrid and constructs a microgrid cluster architecture containing a centralized energy storage system. By taking the operating cost and environmental impact cost as multi-objective functions, they are transformed into single-objective functions by utilizing the binary contrast weighting method. Literature (Song et al., 2023) proposes a novel scheduling approach that achieves a balance between scheduling reliability and flexibility, as well as model accuracy and complexity, by combining the advantages of robust and stochastic optimization and applying multi-granularity modeling techniques. Based on the background of “fishery-photovoltaic complementary”, literature (Yang et al., 2023a) established a light-storage-load microgrid system model and proposed a multidimensional dynamic objective function including economy, environmental protection, and comprehensiveness. All the above literatures are devoted to solving the problem of optimal scheduling in microgrids to ensure the reliability, stability, and economy of microgrids. However, the total objectives established are all operating costs, the consideration of the microgrid’s revenue situation is not comprehensive and cannot visualize the effect of the microgrid’s revenue. Literature (Zhang et al., 2024) proposes a price-matching-based market model for multi-energy trading to promote multi-energy collaboration and improve energy utilization efficiency through individual participation. Therefore, this paper will fully consider the power market factors and build a comprehensive microgrid revenue model (Cheng et al., 2022).
Due to the complex nonlinear, multi-constraint, and multi-dimensional characteristics of microgrid scheduling model solving, optimization algorithms are widely used in model solving. Literature (Zhu et al., 2018) used the improved Tennessee whisker search algorithm for microgrids scheduling research, the results show that the algorithm has a fast search speed, however, there are certain deficiencies in the search accuracy. Literature (Jasim et al., 2022) utilizes the hybrid grey wolf with cuckoo search optimization algorithm to optimize the scale and performance of the hybrid grid-connected wind-solar generation microgrid integrated with biomass and energy storage systems. Literature (Yang et al., 2023b) presents an adaptive energy management method based on hybrid policy reinforcement learning (HPRL) for optimizing the operation of energy systems in island groups with limited energy transmission. Literature (Wang et al., 2023) improved the particle swarm algorithm (PSO) to effectively improve the convergence speed of the algorithm and reduce the comprehensive cost of the system. Literature (Lagouir et al., 2021) utilized the ant-lion algorithm for microgrid scheduling problem solving, which showed advantages in convergence speed compared to the particle swarm algorithm. Literature (Luo and Yu, 2022) proposed an improved cuckoo search algorithm based on reinforcement learning, aiming to solve the economic scheduling problem. Literature (Toopshekan et al., 2023) used a Teaching-Learning-Based Optimization (TLBO) algorithm to determine the optimal sizing of an integrated Combined Heat and Power (CHP) system and developed a new scheduling strategy that takes into account the future power demand, solar radiation, temperature, and wind speed to reduce the cost and reduce the excess power. Literature (Le et al., 2023) compares the Coati Optimization Algorithm (COA) and War Strategy Optimization (WSO) in various aspects and finally concludes that WSO performs better in dealing with the optimal tidal current problem containing wind turbines. Literature (Mishra and Shaik, 2024) presents the Economic-Emission Load Distribution (EELD) problem using the very efficient African Vulture Optimization Algorithm (AVOA) to solve the EELD problem. The results of the study show that AVOA significantly outperforms other optimization techniques in terms of cost and emission reduction, making it the best approach to solving the microgrid optimization problem. Although there have been several papers on solving scheduling problems, there is an urgent need to explore meta-heuristic optimization algorithms with strong exploration and development capabilities to find globally optimal solutions for such complex, large-scale, and nonlinear problems. In addition, few papers have compared the improved algorithms with other algorithms and applied them to complex scheduling problems.
Based on the above considerations, this paper proposes an improved sparrow search algorithm. Firstly, Logistic-Circle chaotic mapping is used to generate more complex and more diversified populations to enhance the global search capability of the sparrow search algorithm. Secondly, the bottleneck sea squirt group optimization algorithm and dynamic inertia weights are introduced to expand the retrieval range in the early iteration period, accelerate the convergence speed in the late iteration period, and improve the algorithm’s local search capability greatly. Then, the water wave dynamic factor is introduced to improve the global search ability of the algorithm. Finally, the Cauchy-Gauss variation strategy is adopted to make the algorithm jump out of the local optimum. At the same time, this paper develops a comprehensive target by combining the economic and environmental benefits of the daily operation of the microgrid system. By then, the optimized scheduling model is solved using the improved sparrow search algorithm. By verifying the effectiveness of the improved algorithm, the scheduling strategy based on the revenue model is obtained. The strategy can facilitate the transformation of traditional warehousing, as well as improve the economy and reliability of electricity consumption in green warehousing and reduce its carbon emissions.
2 Unit modeling of wind-solar-storage systems for green warehousing
2.1 Modeling of photovoltaic power generation
A photovoltaic (PV) power generation system is composed of multiple solar cells connected in series and parallel. Due to the influence of different environmental factors, the operating characteristics of each PV module are different, and hence the actual output power of the whole PV power generation system varies. The two most influential factors are light intensity and temperature so that the mathematical model of the PV cells converted into output power can be expressed as Equation 1 (Guo et al., 2022):
Where:
The operation and maintenance (O&M) costs of photovoltaic power generation mainly include module cleaning, maintenance of module racks and foundations, planned maintenance of equipment, and preventive testing of equipment. By converting the above into PV O&M cost coefficients, the O&M cost can be calculated with the Equation 2:
Where:
2.2 Wind power generation model
As one of the important power generation modes in microgrids, wind power generation is based on the principle that wind energy is generated by rotating the blades of a wind turbine (WT) at different wind speeds, and then the wind energy is converted into mechanical energy through a gear system, which is then converted into alternating current (AC) electricity by the wind turbine. The output power and wind speed of the wind turbine can be expressed by Equation 3 (Lacal-Arántegui, 2015):
Where:
Wind power operation and maintenance costs mainly include five aspects: routine maintenance costs, fault repair costs, spare parts purchase costs, insurance costs, and management costs. By converting the above into WT O&M cost coefficients, the O&M costs can be calculated with the Equation 4:
Where:
2.3 Storage battery model
The storage battery as an energy storage device occupies an important position in the microgrid. The storage battery can supplement the demand when other equipment is underpowered. When the load is low and generates too much power, it can store the excess power for backup. It plays the role of peak shaving and valley filling. The battery satisfies Equation 5 in the process of charging and discharging (Yang, 2010).
Where:
The operation and maintenance costs of storage batteries mainly include labor costs, cleaning costs, overhaul costs, replacement costs, plant electricity costs, and other related costs. These costs vary according to the type, size, use of the battery environment, and other factors, but they are all necessary inputs to ensure the normal operation of the battery. Through reasonable maintenance and management, the operation and maintenance cost of the battery can be reduced, and its service life and economic benefits can be improved. Then the O&M cost of the energy storage system can be expressed as Equation 6:
Where:
3 Optimized scheduling model of wind-solar-storage system
The objective function of the wind-solar-storage microgrid includes the daily operational economic and environmental benefits under the consideration of grid-connected operation conditions.
3.1 Economic benefits
This paper considers the economic returns of the microgrid after it is integrated into the main grid. Its daily operating economic returns include operation and maintenance costs, tariff revenue (Chen et al., 2023), energy storage system revenue, and government subsidy. Its formula can be expressed as Equation 7:
Where:
3.1.1 O&M costs
The formula for O&M costs is shown in Equation 8:
Where:
3.1.2 Tariff revenue
The tariff revenue is essentially the revenue generated from using new energy sources to generate electricity without the need to purchase electricity from the larger grid. Based on real-time electricity prices, the formula is as in Equation 9:
Where:
3.1.3 Energy storage system benefits
The energy storage system revenue is the revenue earned by the energy storage system due to the difference in its price tariff by storing electricity when the price of electricity is low and then using it to supply electricity when the price of electricity is peak. The formula can be expressed as Equation 10:
Where:
3.1.4 Government subsidy
According to the national policy, the government will subsidize a certain amount of money for every kilowatt of clean electricity used. The formula is as in Equation 11:
Where:
3.2 Environmental benefits
Wind-solar-storage systems use clean energy, so only microgrids are considered to produce polluting gases during interaction with the larger grid. At the same time, renewable energy (solar, wind) is used as the main source of electricity in microgrids, thus reducing greenhouse gas emissions. Therefore the environmental benefits include environmental management costs and carbon reduction benefits.
In the wind-solar-storage system, wind-solar systems do not produce pollutant gases, which are mainly generated by the main grid. However, the CO2, generated by the main grid is eliminated when considering the environmental management, so that the whole microgrid and the main grid have no carbon emissions, then the formula for calculating the environmental benefits is shown in Equations 12, 13:
Where:
3.3 Objective function
When oriented towards green warehousing, the overall consideration of daily operational economic gain and environmental gain is used to develop the integrated objective. To reflect the impacts of economic operation and environmental operations on the microgrid system, the impacts are visualized by dynamically weighting the integrated objectives under the maximum economic gain and environmental gain of daily operation, respectively. The function-defining equation is shown in Equation 14:
Where:
3.4 Constraints
To ensure that the microgrid system can operate safely, stably, and efficiently, the above model also needs to satisfy the following constraints. Moreover, these constraints also ensure that the microgrid system achieves the desired performance level in all aspects while meeting the multiple environmental and economic requirements.
3.4.1 Distributed power output constraints
The output power limit of the distributed power supply is shown in Equation 15:
Where:
3.4.2 Energy storage charge/discharge constraints
To prolong the life of the energy storage system and ensure its continuous utilization, the charging and discharging power and the state of charge of the energy storage system must be constrained. The state of charge should be consistent at the beginning and end of the day. The expressions are shown in Equations 16, 17:
Where:
3.4.3 Power balance constraints
The power balance equation is shown in Equation 18:
Where:
4 ISSA for optimal scheduling of green warehousing microgrids
The sparrow search algorithm (SSA) is a heuristic algorithm inspired by the foraging behavior of the sparrow population (Xue and Shen, 2020). SSA divides the population into three subpopulations, namely, discoverers, followers, and watchers, and searches for the optimal solution of the objective function by continuously updating their positions. The microgrid scheduling problem is a complex, large-scale, nonlinear problem, so there is a need to explore meta-heuristic optimization algorithms with strong exploratory and developmental capabilities to find the global optimal solution for such problems. SSA searches for the optimal solution through the positional updating formula, and it also has the advantages of strong local optimization capability, simple structure, and few optimization parameters. SSA has the advantages of high convergence accuracy, fast convergence speed, and robustness in function optimization problems. Therefore SSA can solve the microgrid scheduling problem efficiently. However, the algorithm has some challenges, such as poor diversity and low quality of the population when initializing the population. In the preliminary stage of the algorithm, the sparrow search range is small, the global search ability is relatively poor, and the lack of mutation sparrow perturbation mechanism makes it easy to fall into the local optimal solution. Consequently, this paper improves the traditional SSA by introducing improvements such as Logistic-Circle chaotic mapping, Bottle Sea Sheath Swarm optimization algorithm, dynamic inertia weights, water wave dynamics factor, and Cauchy-Gaussian variable strategy.
4.1 Improved sparrow search algorithm
4.1.1 Logistic-circle chaos mapping
Sparrow search algorithms usually require an initial population as the starting point of the search space. Seeds generated by traditional pseudo-random number generators tend to have fixed characteristics, leading to insufficient diversity in the initial population, which in turn affects the algorithm’s global search capability. On the contrary, chaotic sequences can provide better initial diversity due to their traversal and randomness, thus helping the algorithm to explore the search space more comprehensively. In order to improve the performance and global search capability of the Sparrow algorithm, this paper proposes a Logistic-Circle chaotic mapping method. This method combines the classical Logistic mapping and Circle mapping to generate more complex and diverse chaotic sequences by utilizing the nonlinear properties of both.
Logistic mapping is a classical chaotic system that generates sequences with complex dynamic behavior, but may not be sufficient to provide enough diversity in some cases. Circular mapping is another classical chaotic system that can produce rich chaotic sequences by modulating the initial angle. Combining these two mappings to form the Logistic-Circle chaotic mapping can enhance the complexity and diversity of chaotic sequences. Specifically, Logistic-Circle chaotic mapping generates more complex and diverse chaotic sequences by combining the nonlinear properties of Logistic mapping with the periodic and nonlinear properties of Circle mapping. This approach is more effective in initializing the population of a sparrow search algorithm than a traditional pseudo-random number generator or a single chaotic mapping. In this way, the algorithm can cover the search space more comprehensively and avoid falling into local optima, thus improving the chances of finding a globally optimal solution. The expression of Logistic-Circle chaotic mapping is as in Equation 19:
Where:
When t = 1,000, and r takes 0.51, the distribution and histogram of the Logistic-Circle chaotic sequence are shown in Figure 1. In Figure 1A, as the number of iterations increases the mapping values are randomly averaged over [0,1]. In Figure 1B, the frequency of occurrence of the mapped values is counted up and it is found that the difference in the frequency of occurrence of each value is very small. Therefore, at the beginning of the algorithm iteration, the initial population is randomly distributed, and the Logistic-Circle chaotic mapping randomly and evenly disperses the originally inhomogeneous population, avoiding letting the population concentrated in a certain narrow space, which enables the sparrow algorithm to explore the search space more efficiently and improves its performance and global search capability.
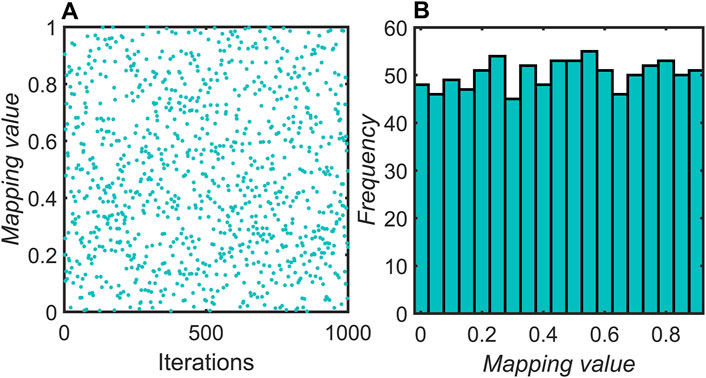
Figure 1. Distribution of initial values of the algorithm: (A) Chaotic sequence distribution map (B) Histogram of chaotic sequences.
4.1.2 Discoverer formula improvements
In the sparrow population, the role of the discoverer is to guide the search direction and scope of the whole population. The search strategy of the discoverer directly affects the optimal solution result of the algorithm. However, the defects of the sparrow search algorithm itself during the search process of the discoverer may cause the population to search only in the local range and thus fall into the local optimal solution. Therefore, this paper introduces the Bottle Sea Sheath swarm optimization algorithm with nonlinear inertia weights
Where:
Where:
4.1.3 Follower formula improvement
Due to the fast convergence property of the Sparrow Search Algorithm (SSA), it results in followers with lower adaptation values being farther away from the food relative to individuals with higher adaptation values, and thus having less access to the food. To solve this problem, a water wave dynamic factor is introduced to improve the follower’s position update formula. By taking advantage of the fact that water waves are periodic and fluctuating, the follower can respond more flexibly to the dynamic changes of water waves during the search process, thus avoiding following the discoverer too blindly. This flexibility helps the follower to explore the search space more broadly and not just limited to the region where the discoverer is located. The introduction of the water wave dynamics factor allows the follower to simulate the fluctuating behavior of water waves when updating their position. The fluctuating nature of the water waves makes the follower’s position update more diverse, no longer simply following the discoverer, but adjusting its position according to the periodic changes of the water waves. This mechanism allows the follower to have more degrees of freedom in the whole search space to explore more potential optimal solution regions and avoid premature convergence to local optimal solutions.
By guiding the follower to move to a wider region, the global search capability of the algorithm is significantly improved. Instead of just focusing on the vicinity of the discoverer, the follower can search over a wider area, thus increasing the probability of finding a globally optimal solution. This improvement not only increases the search efficiency of the algorithm but also enhances its adaptability and robustness in complex optimization problems. Its improved formula is shown in Equation 23:
Where:
Where:
4.1.4 Cauchy-Gauss variation strategy
In the late iteration, the diversity of sparrow populations observed by traditional sparrow algorithms is weakened, and it is easy to fall into local optimal solutions. To cope with this problem, this paper introduces the Cauchy-Gaussian mutation strategy (Yue et al., 2023). The Gaussian distribution performs well in local search because it generates variances that are mostly concentrated around the mean value, which helps in the careful optimization of the current solution. At the same time, the Gaussian distribution has good stability with moderate variances to avoid excessive jumps. On the other hand, the Cauchy distribution has a long tail and can generate large variance values, which can help the algorithm to jump out of the dilemma of local optimal solutions and increase the chance of exploring the global optimal solution. By combining these two distributions, the Cauchy-Gaussian variational strategy can perform both fine search locally and effective exploration globally, thus improving the overall performance of the algorithm. The specific implementation of this strategy is to select the individual with the best current fitness for mutation, compare its position after mutation, and then select the superior position for the next iteration. The Cauchy-Gaussian mutation strategy can be expressed as Equations 25, 26:
Where:
The mutation strategy generates a mutated candidate position after each iteration based on the optimal sparrow position in the current iteration. The algorithm is initialized with a small t-value, which gives the Cauchy mutation a larger weight. This results in a larger step size and helps to prevent the algorithm from falling into a locally optimal solution. As the value of t gradually increases, the weight of the Gaussian variation slowly dominates. Because of the excellent local search ability of the Gaussian variant, the algorithm’s optimization accuracy is greatly improved.
4.2 Optimization process of green warehousing microgrid based on ISSA
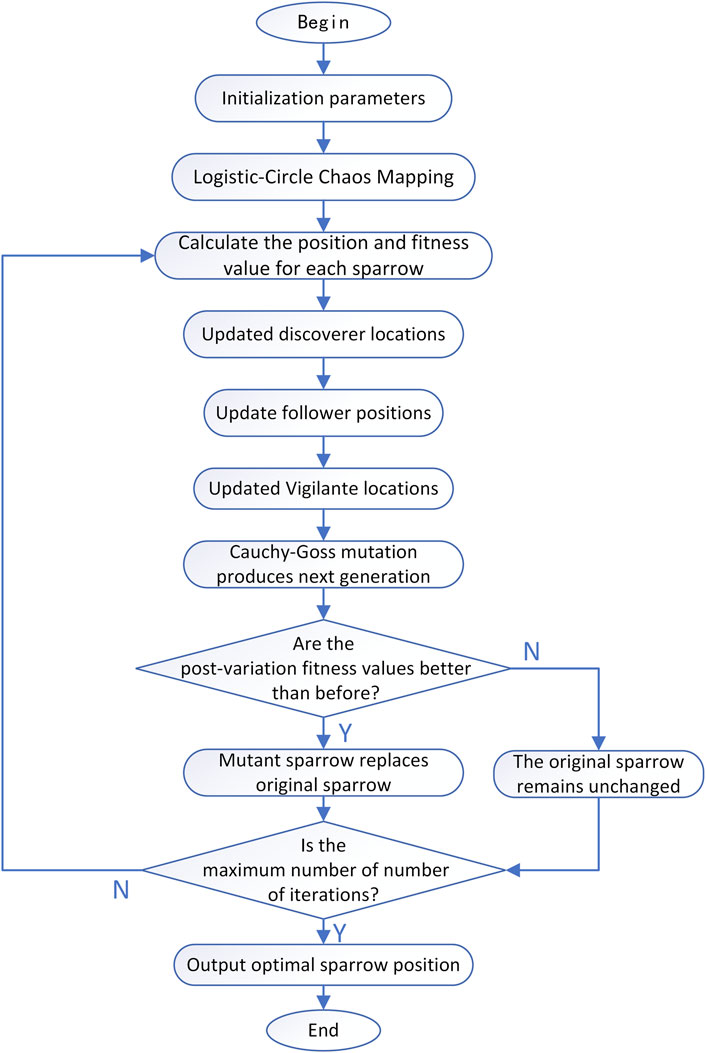
The optimal scheduling process of a wind-solar-storage microgrid based on an improved sparrow search algorithm is shown in Figure 3.
Optimization Steps for Improved Sparrow Search Algorithm:
1) Input algorithm and microgrid parameters.
2) Generate a diverse population using Logistic-Circle chaotic mapping.
3) Calculate the initial fitness value of individual sparrows and sort them.
4) Update the positions of discoverer, follower, and alert according to the improved formula.
5) Calculate the fitness value of the updated individual sparrows and apply the Cauchy-Gaussian mutation to them.
6) Judge whether the mutated After the sparrow is better than the original, if yes, replace the original position, otherwise no change.
7) Judge whether the termination condition is reached, if yes, output the optimal position, otherwise return to 3).
8) End. Output the optimal fitness value and position.
5 Analysis of example results
5.1 Parameters of the algorithm
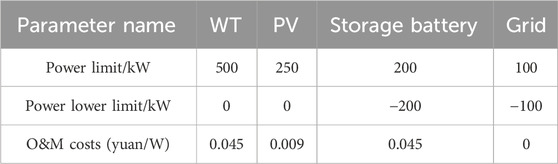
The microgrid system studied in this paper focuses on green warehousing applications. Based on the green warehousing in Liaoning Province, the daily load and wind-solar forecast output of its green warehousing wind-solar-storage system in July are analyzed. The system includes a variety of distributed power sources, including photovoltaic, wind turbine, and energy storage systems. The operating parameters and associated costs of individual distributed generation (DG) devices in the microgrid are detailed in Table 1. In addition, Table 2 provides the pollutant emission factors and corresponding costs for each DG (Shen et al., 2019). The energy storage battery has a turnaround capacity of 400 kW-h, an initial capacity of 200 kW-h, a maximum capacity of 300 kW-h, and a minimum capacity of 100 kW-h. The data for real-time electricity prices is shown in Table 3. The carbon trading price is taken as 150 Yuan/t, then the government subsidized electricity price is taken as 0.08 Yuan/(kW-h), and finally the carbon emission allowance per unit of electricity supplied is taken as 0.03467/(MW-h).
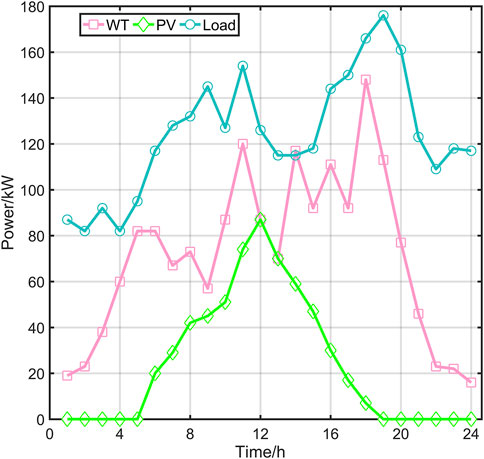
The 24-hour monthly average wind speed, solar irradiance, and electrical load data for the month of July for the area were used in the study. Hourly data on wind speed, ambient temperature, and solar irradiance for the location were obtained from the National Meteorological Administration of China. The cut-in wind speed was taken as 3 m/s, the cut-out wind speed was taken as 25 m/s and the rated wind speed was taken as 12 m/s. Therefore, the daily load and wind and light output data used in this paper are shown in Figure 4.
5.2 Analysis and comparison of results
Firstly, the improved sparrow search algorithm is compared with the PSO, SSA, Whale optimization algorithms (WOA) (Tahmasebi et al., 2021) and improved particle swarm algorithm (IPSO) to analyze the superiority of the improved sparrow algorithm in terms of convergence speed, stability, and optimal value. Then, based on the improved sparrow algorithm, the optimal scheduling strategy for wind-solar-storage is derived. Finally, the scheduling strategy is derived under another wind-solar forecasting model.
5.2.1 Comparative analysis of optimization results
These 5 algorithms have the same parameters, a population size of 100, and a maximum number of iterations of 500. In the improved SSA algorithm, a and b are 0.9 and 0.4, respectively, with a 30% share of the discoverer, a 70% share of the follower, and a 15% share of the initial vigilant. After setting the parameters, four algorithms are used to solve for the maximum daily operational gain of the microgrid in three cases. Finally, the total benefit value in the case of maximum daily operation economic benefit, maximum environmental benefit, and maximum comprehensive objective is obtained. And compare the convergence number of ISSA with the other four algorithms and the optimal values in the three modes. Different comparison metrics represent the algorithm’s other capabilities. Among them, the fact that the algorithm converges with a smaller number of iterations indicates the better convergence performance of the algorithm; the larger objective value derived at the end of the algorithm represents the better optimization ability of the function; and the better the first two metrics of the algorithm indicate the better stability of the algorithm in different modes. The algorithm optimization results are shown below.
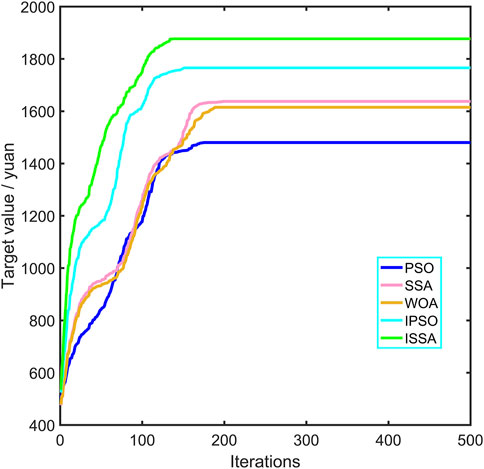
When considering the maximum daily economic operation of the microgrid from Figure 5, it can be seen that the traditional particle swarm algorithm converges at 175 iterations, and its integrated maximum value is 1,480.08 yuan; the sparrow algorithm converges at 189 iterations, and its integrated maximum value is 1,639.73 yuan; the whale optimization algorithm converged in 181 iterations, with a comprehensive maximum of 1,614.62 yuan; the improved particle swarm algorithm converges at 151 iterations, and its integrated maximum value is 1,765.76 yuan; the improved sparrow algorithm converges at iterations The improved sparrow algorithm converges at 137 iterations, and the comprehensive maximum value is 1,876.89 yuan. In terms of optimization results, compared to PSO, SSA, and IPSO, ISSA yields maximum gains of 26.81%, 14.46%, 16.24%, and 6.29% respectively. It can be seen that the improved sparrow algorithm is optimal in terms of convergence speed as well as optimization results when solving for the maximum economic gain.
When considering the microgrid environment with the maximum benefit from Figure 6, it can be seen that the traditional particle swarm algorithm converges at 164 iterations, and its integrated maximum value is 1,200.42 yuan; the sparrow algorithm converges at 181 iterations, and its integrated maximum value is 1,356.62 yuan; the whale optimization algorithm converged in 175 iterations, with a comprehensive maximum of 1,308.56 yuan; the improved particle swarm algorithm converges at 143 iterations, and its integrated maximum value is 1,476.39 yuan; the improved sparrow algorithm converges at iterations The improved sparrow algorithm converges at 126 iterations, and the integrated maximum value is 1,564.63 yuan. It can be seen that in the optimization results, compared to PSO, SSA, and IPSO, ISSA optimization yields a maximum gain of 30.34%, 15.33%, 19.56%, and 5.98% respectively. Therefore, the improved sparrow algorithm is better than the other algorithms in terms of convergence speed as well as optimization results when environmental benefits are the objective.
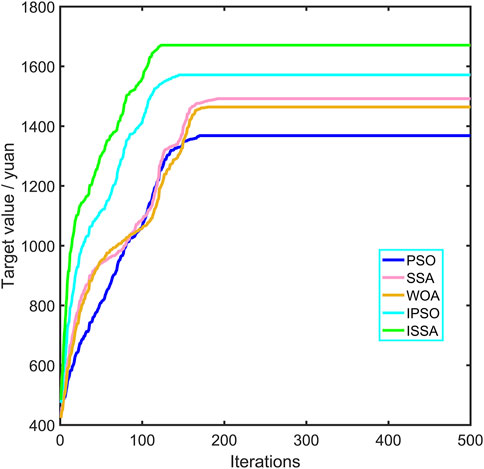
When considering the maximum total microgrid revenue from Figure 7, it can be seen that the traditional particle swarm algorithm converges at 169 iterations with a combined maximum value of 1,368.17 yuan; the sparrow algorithm converges at 179 iterations with a combined maximum value of 1,493.86 yuan; the whale optimization algorithm converges at 170 iterations with a combined maximum value of 1,463.85 yuan; the improved particle swarm algorithm converges at 145 iterations with a combined maximum value of 1,571.49 yuan; and the improved sparrow algorithm at 123 iterations The improved sparrow algorithm converges at 123 iterations with a combined maximum value of 1,670.64 yuan. Based on the above optimization results, it can be seen that ISSA improves the daily combined maximum gain by 20.52%, 11.83%, 14.12%, and 6.31% compared to PSO, SSA, and IPSO respectively. Therefore, the stability, convergence speed, and optimization value of the improved sparrow search algorithm are better than the other algorithms in the three cases, which verifies the superiority of the improved sparrow algorithm and the optimization results are more reliable.
The above three scenarios are considered in more specific scenarios. The first considers only economic gains and ignores environmental impacts. The second focuses on environmental impacts and discards some of the benefits. The third is a combination of economic and environmental impacts. In all three cases, the iteration speed of ISSA is significantly faster than the other algorithms, and the convergence stability is better in all cases. In the three modes, ISSA increased the optimal value by at least 6.29%, 5.98%, and 6.31% compared to the other algorithms. In conclusion, ISSA has strong space exploration and searching ability, and its solution results are stable and reliable.
5.2.2 Scheduling strategy analysis
The feasibility of the improved sparrow algorithm has been verified above, and the following section derives the optimal scheduling strategy for wind-solar-storage microgrids based on the improved sparrow algorithm. The scheduling strategy is divided into a total of three cases, which are the scheduling strategy under the maximum economic benefit, the maximum environmental benefit, and the maximum comprehensive objective, the scheduling results are shown below.
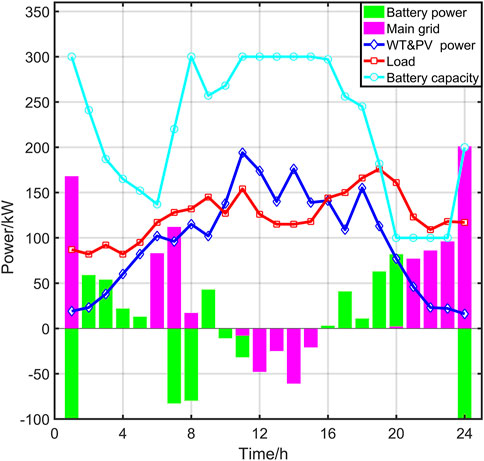
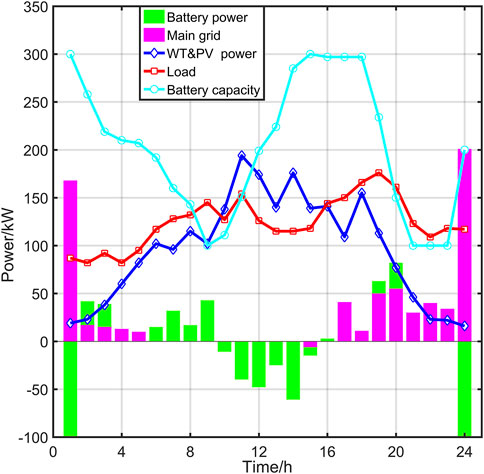
Considering the maximum economic gain scenario in Figure 8, the following conclusions can be drawn. During the phase of cheap electricity price from 23:00 to 8:00 the next day, when the output of the wind power generation system is insufficient, the microgrid system first buys electricity from the main grid for power supply. If the battery power is insufficient, it is charged. Therefore, the power of the big grid is larger and the battery power is negative. During 9:00–20:00, the peak electricity price time, the system will first supply power to the load through the energy storage device. When the wind and photovoltaic power output exceeds the needs of the load, the excess power will be stored preferentially in the battery bank. After the battery bank has been fully recharged, the surplus power can be sold to the grid. As a result, the power of the main grid goes negative. Subsequently, the batteries are continuously supplied with power because they are at peak electricity prices. This operating strategy aims to maximize the use of renewable energy sources while ensuring the reliability and economy of the system under different operating conditions. In addition, the battery is charged at a low price and discharged at a high price to maximize the economic return.
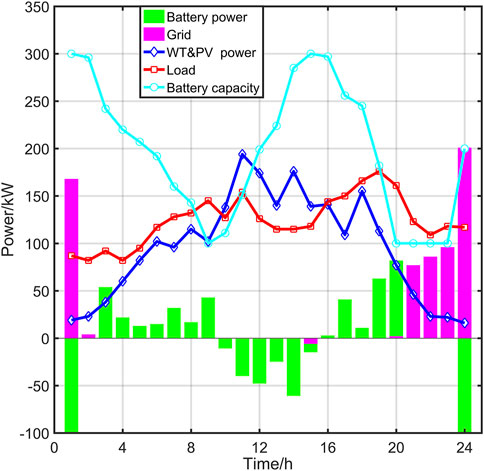
With the consideration of maximizing the environmental benefits, the following conclusions can be drawn from Figure 9. The environmental benefit is mainly considered in terms of the electrical energy interacting with the main grid, and the more interaction there is the higher the environmental impact. Therefore, from 23:00 to 8:00 the next day, the battery is charged first, and in the case of insufficient output from the wind and PV systems, the system first obtains power from the battery to supply the loads to minimize the polluting emissions from the main grid. At 9:00–20:00, when the remaining power in the battery bank is below a certain threshold value, the system neither supplies nor purchases power from the main grid. Instead, when the output of the wind and photovoltaic power generation systems is sufficient to meet the load demand, the excess power is used to recharge the system. Subsequently, the main grid continues to supply power and charge the batteries. The above scheduling strategy minimizes the power interaction with the main grid to reach the environmental protection requirements.
Considering the economic and environmental benefits in Figure 10, the following conclusions can be drawn. In case of insufficient output from the wind and PV systems, the system’s operation strategy is adjusted according to the characteristics of the current period. During the low tariff hours, battery power is supplied and the power deficit is compensated by purchasing power from the main grid. From 8:00 to 16:00 when the wind and PV power output can meet the load demand, the system prioritizes the use of the wind and PV power systems to supply power to the load and stores the excess power in the battery bank. When the batteries are fully charged, the surplus power can be sold on the larger grid. At 17:00–22:00, the batteries and the main grid work together to meet the power demand. This strategy aims to make full use of renewable energy and environmental protection and to use flexible power supply methods at different times of the day to improve the economy and reliability of the system.
To summarize, this paper designs three scheduling strategies for wind-photovoltaic-storage microgrids using an improved sparrow search algorithm: maximum economic efficiency, maximum environmental efficiency, and combined economic and environmental efficiency. The maximum economic efficiency strategy optimizes costs by charging when electricity prices are low and discharging when they are high while prioritizing the use of renewable energy. The maximum environmental benefit strategy, on the other hand, focuses on reducing power interactions with the main grid to reduce pollution emissions. The integrated benefit strategy combines the advantages of the first two, flexibly adapts to the period, maximizes the use of renewable energy, and improves the economy and reliability of the system. To further improve the stability of microgrids, more accurate forecasting of wind turbines and photovoltaic output will be used in the future, and the economics of microgrids will be improved (Cui et al., 2019; Sun et al., 2020). Furthermore, the scheduling strategy based on the improved sparrow search algorithm can effectively optimize the operation of wind-solar-storage microgrids to meet the dual goals of economy and environmental protection.
5.2.3 Integrated target analysis
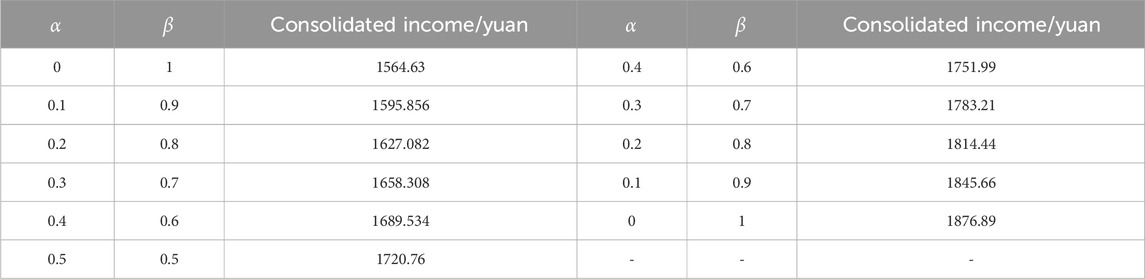
The application of wind-solar-storage microgrids in green warehousing will develop scheduling strategies according to different needs. In this paper, the scheduling strategy is mainly affected by economic and environmental benefits, so the weighting coefficients are set to adjust the impact of the two benefits on the maximum comprehensive benefit. In other words, whether the microgrid focuses more on the economic gain or the impact on the environment when developing the scheduling strategy. The results of the different weighted integrated returns are shown in Table 4.
As can be seen from Table 4, when the coefficients,
6 Conclusion
In this paper, an improved sparrow search algorithm is proposed for solving the green warehousing microgrid scheduling problem. The comparative analysis of ISSA and other algorithms is completed in three different cases. The results show that the improved sparrow algorithm exhibits the advantages of a high-quality initial population, strong global optimization capability, excellent iteration speed, and better optimization results. The combined gains derived using ISSA compared to IPSO, SSA, WOA, and PSO methods are improved by 20.52%, 11.83%, 14.12%, and 6.31% respectively. Then a dynamic weighting strategy is adopted to balance the impacts of economic operation and environmental protection on the microgrid. Finally, based on the ISSA algorithm, the scheduling strategy for different cases is derived, which improves the energy utilization of green warehousing.
This paper solves the practical problems of microgrids and provides a new idea for the development of green warehousing. In addition, this study is also informative for factories transitioning to greening. To solve the load instability problem, techniques such as artificial intelligence (AI) and evolutionary gaming are further applied to optimize load forecasting and dispatching strategies. With the continuous development and application of these technologies, more accurate and efficient microgrid operation management can be expected. Therefore, the next step of this paper will focus on the power market and user side, and use more advanced machine learning algorithms or deep learning models to improve the accuracy of load forecasting.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
LL: Writing–original draft, Writing–review and editing, Conceptualization, Funding acquisition, Supervision. SZ: Conceptualization, Methodology, Writing–original draft, Writing–review and editing. HZ: Investigation, Project administration, Writing–review and editing. ZZ: Data curation, Validation, Visualization, Writing–review and editing. YL: Conceptualization, Data curation, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was financially supported by the State Grid Liaoning Electric Power Co., Ltd. Science and Technology Project (2023YF-160).
Acknowledgments
The authors would like to thank the State Grid Liaoning Electric Power Supply Co., Ltd. and the Shenyang University of Technology for their support. The authors also thank the reviewers for their valuable comments.
Conflict of interest
Authors LL, SZ, HZ, and ZZ were employed by State Grid Liaoning Electric Power Supply Co., Ltd.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors declare that this study received funding from State Grid Liaoning Electric Power Co., Ltd. The funder had the following involvement in the study: Conceptualization, Supervision, Methodology, Investigation, Project administration, Date curation, Validation, Visualization.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Chen, K., Xiao, X., Tian, P., Feng, K., and Sun, P. (2023). A comprehensive optimization method for planning and operation of building integrated photovoltaic energy storage system. Proc. CSEE 43 (13), 5001–5012. doi:10.13334/j.0258-8013.pcsee.220820
Cheng, L., Chen, Y., and Liu, G. (2022). 2PnS-EG: a general two-population n-strategy evolutionary game for strategic long-term bidding in a deregulated market under different market clearing mechanisms. Int. J. Electr. Power and Energy Syst. 142, 108182. doi:10.1016/j.ijepes.2022.108182
Cui, M., Zhang, J., Wang, Q., Krishnan, V., and Hodge, B.-M. (2019). A data-driven methodology for probabilistic wind power ramp forecasting. IEEE Trans. Smart Grid 10 (2), 1326–1338. doi:10.1109/TSG.2017.2763827
Gao, J., and Hou, Y. (2022). The material company taps the potential of the warehousing network to release the vitality of physical resources. North China Power 12, 62. doi:10.1002/adfm.202108044
Gbadamosi, S. L., and Nwulu, N. I. (2021). A comparative analysis of generation and transmission expansion planning models for power loss minimization. Grids Netw. 26, 100456. doi:10.1016/j.segan.2021.100456
Guo, W., Mao, Y., Chen, Y., and Zhang, X. (2022). Multi-objective optimization model of micro-grid access to 5G base station under the background of China’s carbon peak shaving and carbon neutrality targets. Front. Energy Res. 10, 1032993. doi:10.3389/fenrg.2022.1032993
He, Y., Xie, K., Sun, K., Jiao, L., Wang, H., Du, X., et al. (2023). Optimal scheduling of microgrid source-load-storage power based on improved cuckoo algorithm. Electr. Power Sci. Eng. 39 (10), 14–25. doi:10.3969/j.ISSN.1672-0792.2023.10.002
Jasim, A., Jasim, B., and Bureš, V. (2022). A novel grid-connected microgrid energy management system with optimal sizing using hybrid grey wolf and cuckoo search optimization algorithm. Front. Energy Res. 10, 960141. doi:10.3389/fenrg.2022.960141
Kiani, H., Hesami, K., Azarhooshang, A., Pirouzi, S., and Safaee, S. (2021). Adaptive robust operation of the active distribution network including renewable and flexible sources. Sustain. Energy, Grids Netw. 26, 100476. doi:10.1016/j.segan.2021.100476
Kumar, N., Singh, B., and Panigrahi, B. K. (2019). Grid synchronisation framework for partially shaded solar PV-based microgrid using intelligent control strategy. IET Generation, Transm. and Distribution 13 (6), 829–837. doi:10.1049/iet-gtd.2018.6079
Lacal-Arántegui, R. (2015). Materials use in electricity generators in wind turbines–state-of-the-art and future specifications. J. Clean. Prod. 87, 275–283. doi:10.1016/j.jclepro.2014.09.047
Lagouir, M., Badri, A., and Sayouti, Y. (2021). Multi-objective optimization dispatch based energy management of A microgrid running under grid connected and standalone operation mode. Int. J. Renew. Energy Dev. 10 (2), 333–343. doi:10.14710/ijred.2021.34656
Le, T. M. C., Le, X. C., Huynh, N. N. P., Doan, A. T., Dinh, T. V., and Duong, M. Q. (2023). Optimal power flow solutions to power systems with wind energy using a highly effective meta-heuristic algorithm. Int. J. Renew. Energy Dev. 12 (3), 467–477. doi:10.14710/ijred.2023.51375
Li, X., Zhang, J., He, Y., Zhang, Y., Liu, Y., and Yan, K. (2021). Multi-objective optimization dispatching of microgrid based on improved particle swarm algorithm. Electr. Power Sci. Eng. 37 (03), 1–7. doi:10.3969/j.ISSN.1672-0792.2021.03.001
Liu, Q., Zhao, Y., Li, N., Ma, B., Shang, Y., and Li, W. (2021). Multiple objective optimization of a microgrid based on a distributed neural dynamics algorithm. Power Syst. Prot. Control 49 (11), 105–114. doi:10.19783/j.cnki.pspc.200986
Luo, W., and Yu, X. (2022). Reinforcement learning-based modified cuckoo search algorithm for economic dispatch problems. Knowledge-Based Syst. 257, 109844. doi:10.1016/j.knosys.2022.109844
Mishra, S., and Shaik, A. G. (2024). Solving bi-objective economic-emission load dispatch of diesel-wind-solar microgrid using African vulture optimization algorithm. Heliyon 10 (3), e24993. doi:10.1016/j.heliyon.2024.e24993
Shen, C., Wang, M., and Li, X. (2019). Multi-objective optimal dispatch based on wind-solar-pumped storage-thermal combined power system. Power Syst. Clean Energy 35 (11), 74–82.
Song, Y., Xia, M., Yang, L., Chen, Q., and Su, S. (2023). Multi-granularity source-load-storage cooperative dispatch based on combined robust optimization and stochastic optimization for a highway service area micro-energy grid. Renew. Energy 205, 747–762. doi:10.1016/j.renene.2023.02.006
Sun, M., Zhang, T., Wang, Y., Strbac, G., and Kang, C. (2020). Using bayesian deep learning to capture uncertainty for residential net load forecasting. IEEE Trans. Power Syst. 35 (1), 188–201. doi:10.1109/TPWRS.2019.2924294
Tahmasebi, M., Pasupuleti, J., Mohamadian, F., Shakeri, M., Guerrero, J. M., Basir Khan, M. R., et al. (2021). Optimal operation of stand-alone microgrid considering emission issues and demand response program using whale optimization algorithm. Sustainability 13 (14), 7710. doi:10.3390/su13147710
Thirunavukkarasu, G., Seyedmahmoudian, M., Jamei, E., Horan, B., Mekhilef, S., and Stojcevski, A. (2022). Role of optimization techniques in microgrid energy management systems—a review. Energy Strategy Rev. 43, 100899. doi:10.1016/j.esr.2022.100899
Toopshekan, A., Abedian, A., Azizi, A., Ahmadi, E., and Vaziri Rad, M. A. (2023). Optimization of a CHP system using a forecasting dispatch and teaching-learning-based optimization algorithm. Energy 285, 128671. doi:10.1016/j.energy.2023.128671
Vaziri Rad, M. A., Toopshekan, A., Rahdan, P., Kasaeian, A., and Mahian, O. (2020). A comprehensive study of techno-economic and environmental features of different solar tracking systems for residential photovoltaic installations. Renew. Sustain. Energy Rev. 129, 109923. doi:10.1016/j.rser.2020.109923
Wang, Y., Hao, Y., Wang, L., Dang, X., Jiang, L., Zhang, Y., et al. (2023). Multi-objective optimal dispatching for multi-energy microgrid based on improved particle swarm optimization algorithm. Electr. Meas. and Instrum. 60 (11), 29–36. doi:10.19753/j.issn1001-1390.2023.11.004
Xu, B., Zhang, F., Bai, R., Sun, H., and Ding, S. (2024). The energy management strategy of a loop microgrid with wind energy prediction and energy storage system day-ahead optimization. Front. Energy Res. 11, 1334588. doi:10.3389/fenrg.2023.1334588
Xue, J., and Shen, B. (2020). A novel swarm intelligence optimization approach: sparrow search algorithm. Syst. Sci. control Eng. 8 (1), 22–34. doi:10.1080/21642583.2019.1708830
Yang, C., Yang, Y., Guo, F., and Zhang, Z. (2023). Multi-objective energy optimization scheduling strategy of microgrid under “Fisheries and Light Complementarity”. J. Shanghai Ocean Univ. 32 (05), 986–996. doi:10.12024/jsou.20230604217
Yang, L., Li, X., Sun, M., and Sun, C. (2023). Hybrid policy-based reinforcement learning of adaptive energy management for the energy transmission-constrained island group. IEEE Trans. Industrial Inf. 19 (11), 10751–10762. doi:10.1109/TII.2023.3241682
Yang, W. (2010). “Optimization scheduling of distributed power sources,”. master's thesis (Anhui: Hefei University of Technology).
Yue, Y., Liu, J., Zhao, H., and Wang, H. (2023). Short-term PV power prediction considering feature extraction and optimized LSSVM. J. Shaanxi Univ. Sci. and Technol. 41 (03), 200–207. doi:10.19481/j.cnki.issn2096-398x.2023.03.009
Zeng, Z., Li, X., Yin, L., and Yang, M. (2023). Energy optimization method for microgrid cluster based on improved bat algorithm. Electron. Meas. Technol. 46 (10), 53–60. doi:10.19651/j.cnki.emt.2211323
Zhang, N., Yan, J., Hu, C., Sun, Q., Yang, L., Gao, D. W., et al. (2024). Price-matching-based regional energy market with hierarchical reinforcement learning algorithm. IEEE Trans. Industrial Inf., 1–12. doi:10.1109/TII.2024.3390595
Keywords: green warehousing, wind-solar-storage, improved sparrow search algorithm, optimal scheduling, economic optimization
Citation: Liu L, Zhang S, Zhang H, Zhang Z and Liu Y (2024) Optimal scheduling study of green warehousing microgrid based on improved sparrow search algorithm. Front. Energy Res. 12:1383376. doi: 10.3389/fenrg.2024.1383376
Received: 07 February 2024; Accepted: 30 August 2024;
Published: 12 September 2024.
Edited by:
Morteza Nazari-Heris, The Pennsylvania State University (PSU), United StatesReviewed by:
Tahir Khurshaid, Yeungnam University, Republic of KoreaLinfei Yin, Guangxi University, China
Minh Quan Duong, The University of Danang, Vietnam
Yushuai Li, Aalborg University, Denmark
Copyright © 2024 Liu, Zhang, Zhang, Zhang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Liyang Liu, MTM4NDIwOTU2NjVAMTYzLmNvbQ==
 Liyang Liu
Liyang Liu Shiyu Zhang1
Shiyu Zhang1