
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 04 April 2024
Sec. Sustainable Energy Systems
Volume 12 - 2024 | https://doi.org/10.3389/fenrg.2024.1381857
This article is part of the Research Topic Clean Energy and Low-carbon Transportation View all 6 articles
As the proportion of new energy continues to increase, the safety and stability of the new power system are challenged, urgently requiring the allocation of new flexible resources. This paper proposes a two-stage robust capacity optimization model considering flexibility demand constraints. Firstly, the uncertain characteristics of new energy are described, and a model of flexible resource adjustment capacity is established. Then, uncertain parameters are introduced to construct a robust capacity optimization model considering supply-demand balance, solved by column constraint generation algorithm and KKT theorem. Finally, a power system in a certain region of China is selected as the simulation object for empirical analysis to verify the effectiveness of the constructed model. The results show that the two-stage robust configuration optimization model constructed in this paper can address the uncertainty of power system and the flexibility demand brought by new energy, and the planning results can achieve a balance between the safety and economy of the new power system.
With the ongoing development of the new type of power system, the increasing penetration rate of new energy sources, such as wind and photovoltaic, in the power system has brought about significant challenges and uncertainties. Flexibility has emerged as a core attribute for assessing the power system’s resilience in handling uncertainty. Therefore, it is of paramount importance to conduct capacity optimization configuration of multiple types of new flexible resources with flexibility adjustment capability, attending to effectively accommodate new energy sources and address uncertainty.
The planning and configuration resources are the foundation for constructing a new type of power system with safety and stability. New types of flexibility resources such as distributed generation (Pandey and Awasthi, 2020), data center (Sun et al., 2016) and hydrogen energy storage system (Ren et al., 2015) are playing an increasingly important role in the new power system. TORREGLOSA et al. established a dispatching optimization model for multiple types of flexibility resources on the basis of Model Predictive Control (MPC) (Torreglosa et al., 2015). As the proportion of new energy generation continues to increase, scholars have adopted series of methods such as to model the impact of uncertainty of new energy on flexibility resource configuration robust optimization (Chen and Li, 2021) and stochastic programming (Grover-Silva et al., 2018), et al. Based on the uncertainty of wind and PV, Ju L et al. established a multi-objective robust model to maximize the benefits of virtual power plants and minimize operational risks (Ju et al., 2019). Hong developed a two-stage robust optimization model to optimize the configuration of a hybrid hydroelectric and pumped system, which is designed to address uncertainties in wind and photovoltaic power generation and aims to achieve efficient complementarity between different energy sources (Hong et al., 2023). The above literature research still focused on meeting the energy balance and neglected the impact of system flexibility requisite on resource allocation. As a result, it fails to effectively meet the system’s flexibility requisite, leading to compromised operational stability. In considering flexibility requirements within the resource allocation model, ensuring flexibility supply-demand matching will result in allocating more resources. Although this slightly reduces economic efficiency, it guarantees system flexibility and ensures stable and secure system operation.
Accurately characterizing the flexibility requisite is a prerequisite for achieving a balance between the requisite for flexibility in the new power system and its corresponding supply. Currently, there are two main methods for quantifying flexibility requisite: circumstance-based approach and interval-based approach. For circumstance-based approach, referring to the correlation between the output of wind power and solar power, some scholars use probability density functions to describe flexibility requisite (Ji et al., 2018; LI et al., 2020). However, this method cannot accurately describe the flexibility requisite in each time period, and thus has certain limitations. For interval-based approach, some scholars adopted the fluctuation coefficient to manually set the top and bottom limits of prediction deviation attending to describe the range of flexibility requisite (Nicholas and Pierluigi, 2019; Lin et al., 2023). HUO establishes a joint fluctuation domain for renewable energy, thereby transforming it into flexibility requisite, based on the consideration of volatility and correlation (Huo et al., 2020).
Taking flexibility requisite into account during the process of power system planning can be an efficient mechanism for strengthening the integration capacity of renewable energy and mitigating the negative consequences caused by the uncertainties associated with renewable energy and power load. Zhang proposed a hybrid energy storage optimization model that took into account requisite of the upward and downward regulation from the power system. The model aims to ensure the economic and stable operation of the system by optimizing the configuration of energy storage technologies (Zhang et al., 2023). DANESHVAR et al. constructed a two-stage optimal model of types of flexibility resources based on stochastic programming to meet the stable operation of the system considering flexibility of the new power system (Daneshvar et al., 2020). Du constructed a planning model with uncertainty of new energy using Conditional Value-at-Risk (CVaR) considering the flexibility constraints of the system and verified the effectiveness of the model (Mingkun et al., 2021). MIANAEI et al. incorporated flexibility constraints into their study and developed a capacity configuration model for wind, solar, and hydro-pumped storage systems utilizing the chance-constrained planning method, which ensured reliable operation while considering uncertainties (Mianaei et al., 2022).
In summary, although domestic and foreign scholars have proposed the configuration optimization model for flexibility resources, there is a lack of consideration for the planning and configuration of new flexibility resources and constructing a configuration optimization model for the new flexibility resources considering the challenge of addressing requisite of the upward and downward regulation of the power system in relation to the uncertainty of renewable energy generation has persisted. Referring to the above shortcomings, this paper establishes a two-stage robust capacity optimization configuration model considering flexibility requirements. Firstly, attending to quantify the impact of the uncertain output of new energy on the flexibility requisite, this paper characterizes the flexibility requisite to achieve the coordination of economy and flexibility of the new flexible resource allocation. Secondly, considering the uncertainty of new energy output, a two-stage robust capacity optimization configuration model considering flexibility requirements is constructed, and the model is solved by CCG and KKT methods. Finally, the power system of a certain place in China is selected as the simulation object for empirical analysis to assess the effectiveness of the proposed model.
Flexibility requisite arises as a result of upward and downward regulation requisite in different directions by net loads influenced by the uncertainty of output of new energy in conjunction with electric load fluctuations. For quantitatively analyzing the flexibility requisite of the power system, this section proposes a flexibility portrayal methodology considering the uncertainty.
The goal of flexibility resource capacity configuration is to satisfy power system flexibility requisite at minimal economic cost. Therefore, flexibility characterization becomes a key prerequisite for flexibility resource capacity configuration. In this paper, the interval method is used to characterize the flexibility requisite of the power system, and the following are the specific procedures to be followed.
(1) Determine the top and bottom bounds of forecasting error of net load. Flexibility requisite arises from the forecast deviation of net load. Its essence is difference between the net load of adjacent time intervals, due to the prediction deviation makes the actual regulation produce a higher upward requisite than the prediction result or a downward requisite opposite to the prediction. Attending to more comprehensively characterize the flexibility requisite due to net load forecast deviation, this paper sets fluctuation coefficients to define the top and bottom bounds of the deviation for wind, PV and electric loads.
where,
The top and bottom bounds for net load deviation are as follows:
where,
(2) Characterize the flexibility requisite intervals. In general, the flexibility requisite of net load is to subtract the net load forecast value at a certain moment from the net load forecast value at the previous moment, which ignores the forecast deviation caused by the uncertainty of net load. The net load forecast deviation is included in the net load fluctuation range to calculate the flexibility requisite. By analyzing the net load curve and considering the top and bottom limits, the deviations in net load can be determined, which allows for the identification of flexibility requirements in both upward and downward directions for each time period.
As known in Figure 1, if
In addition to the time-series fluctuations that characterize net loads, the uncertainty of net loads is also an important trigger for flexibility requisite. Therefore, determining the uncertainty variation interval of net load is a necessary step in portraying flexibility requisite. From formular Eqs. 1, 2, net load deviation, top and bottom bounds can be obtained.
where,
In addition, flexibility requisite needs to take into account directionality, encompassing both upward and downward directions:
where,
New flexibility resources have tremendous flexibility regulation capabilities, fast response speed, and are increasingly involved in the interaction with the power system, playing an increasing role in meeting the flexibility regulation requisite of the power system.
There are many types of distributed power sources, which can be categorized into controllable distributed power sources and uncontrollable distributed power sources according to whether they can participate in the scheduling of the distribution network. Controllable power supply includes micro-gas generations, fuel power, etc., whose output power can regulate the net load, and can provide flexibility regulation on the scale of 15 ∼ 60 min.
where,
New energy storage mainly includes electrochemical energy storage and hydrogen energy storage system and so on. Among them, the hydrogen energy storage system has a fast response speed and can provide a certain degree of flexibility in smaller or longer time scales, but due to technical constraints, the scale of hydrogen production is relatively limited, resulting in a smaller response depth. Therefore, hydrogen energy storage systems are suitable for providing flexibility regulation on 15–60 min time scales. Electrochemical energy storage has a faster charge/discharge rate, which can be quickly realized to smooth out random fluctuations with high fluctuation frequency and low energy on short time scales, and is suitable to provide flexibility regulation on short time scales of <15 min, and also can provide some regulation capability on medium time scales. The flexibility regulation capability of the new energy storage mainly depends on the maximum storage power, top limit of charging and discharging power, as shown in the following equation.
where,
Two-stage robust optimization aims to attend to the phenomenon of parameter uncertainty in the optimization problem and is committed to optimizing the solution under the worst case, so that the final solution owns the very strong capacity to resist uncertainty or risk. The goal of two-stage robust optimization is to jointly optimize the two-stage decision-making while considering the uncertainty of the second-stage parameters (Zeng and Zhao, 2013). The decision of the first stage needs to be made first, and the decision of the second stage needs to be made after the decision of the first stage is determined, and then the corresponding second stage decision is made after the parameters are revealed.
The abstract constraint model for two-stage robust optimization is as follows:
where,
The new flexibility resource is configured with a total target with minimizing the comprehensive cost
where,
Starting from the planning and operation stages of new flexible resources, this paper considers the capacity constraints of new flexibility resources, the operation constraints of each new flexibility resource, and the constraints of power-load and flexibility supply and requisite balance, as follows:
The model models the planning stage from the constructed cost of distributed generation, electrochemical energy storage and hydrogen energy storage systems, and the corresponding constructed capacity constraints are as follows:
where,
Due to the nature of electricity, it is necessary to balance the power generation resources and the load at each time.
where,
Between the power generation resource and the external power grid, the amount of electricity can be purchased when the external electricity price is low, and the electricity can be sold when the electricity surplus can be used to reduce operating costs, which can be expressed as:
where,
Electrochemical energy storage and hydrogen energy storage system energy storage are both new types of energy storage (Xiaoyan et al., 2023), which need to meet the charge-discharge power constraints and state-of-charge constraints during operation, which can be expressed as:
where,
Distributed generation is subject to power constraints and flexibility adjustment capacity constraints in operation:
where,
As a traditional flexibility resource, thermal power units are constrained by output constraints and climbing performance:
where,
The flexibility of a power system is determined by the flexibility supply capability and flexibility requisite.
where From formular Eqs. 8–10,
The goal of the planning and simulation stage is to minimize the sum of planning and operating costs during the planning period. The deterministic problems for objective functions in the planning and operating parts are shown as follows:
where,
To analyze the impact of uncertainty factors in the planning process of new type flexibility resources, this paper establishes an uncertain set
where,
Considering the flexibility requisites, integrate the formula Eqs 11–38, can reconstruct the new flexibility resources configuration model with the goal of minimizing the total cost of the system into a two-stage robust optimization model, and for the planning model, it is necessary to consider the planning results to meet the needs of different operating situations, so the operation model of the sub-stage is represented by the expectation of each typical daily operating cost.
Where,
For the above two-stage robust model, the CCG algorithm is an effective way to solve the problem refer to Eqs. 39, 40. The CCG algorithm divides the solution of the model into two stages: the main and the sub-stage, and continuously adds the tangent plane of the original problem, so that the two stages are continuously iterative to obtain the optimal solution. In the first stage, a new flexibility resources allocation scheme is considered to meet the needs of the known circumstance and ensure safety, economy and stability, so as to minimize the equipment investment cost, as shown in Eq. 41. The second stage is based on the installed capacity of the equipment in the first phase, aiming to find the worst circumstance so that the operating cost of each resource is minimized in the worst circumstance, as shown in Eqs. 42, 43.
The objective function and constraint conditions of the main problem are expressed as follows:
where,
The objective function of the subproblem is expressed as follows:
The sub-problem in the second stage is a two-layer optimization problem, which can be solved by using the KKT condition to convert the model of the subproblem into a single-layer mixed integer programming. The transformation process is to transform the inner layer minimization problem into a maximization problem through the Lagrange dual theory, and then combine the KKT condition to transform the inner layer subproblem into a KKT conditional equation, so that the nonlinear model can be transformed into a linearized form. The expressions are simplified and integrated to obtain:
where,
The solution process, based on the column and constraint generation approach, can be summarized as follows:
(1) Initialize a set of net load forecasts as the most extreme circumstance of the model.
(2) Set the number of iterations
(3) According to the results obtained by solving the main problem, the calculated values are substituted into the sub-problem model, and the objective function values and the new most extreme values are obtained, which are returned to the main problem. Updates the result of the solution to the top bound.
(4) Determine whether the gap between the top bound
In summary, the flowchart of the two-stage robust configuration optimization algorithm combining KKT conditions and C&CG method is shown in Figures 1–3.
In this paper, the empirical analysis conducted on a specific power system in China, and the data of historical annual load and wind and photovoltaic are reduced to three typical daily curves through clustering, and a new flexibility resource capacity configuration optimization is carried out to verify the effectiveness of the proposed method. Based on historical experience, the uncertain fluctuation range of wind power and photovoltaic output is set to be 15%, and the uncertain fluctuation range of load is 10% (Jabr, 2013). Figure 3–5 show the typical daily curves of wind and solar power and load power. In terms of setting the case parameters, the discharge time of the electrochemical energy storage and hydrogen energy storage system is 4 h, the service life is 20 years, and the charging and discharging efficiency of the electrochemical energy storage system is 90%, and the hydrogen energy storage system is affected by the performance of the electrolyze and fuel cell, with the charging efficiency of 88% and the discharge efficiency of 60%. The discount rate is 8%. Table 1 lists the flexible resource allocation parameters.
The article discusses, using the data of load, wind and photovoltaic from the third typical day as examples, the equipment planning costs and operational costs under different conservativeness levels, and determines the optimal capacity configuration of various new flexibility resources.
According to the algorithm flow in Figure 2, iterative solution of the master-subproblem is performed with a convergence accuracy of 0.01. As shown in Figure 6, the CCG algorithm exhibits good convergence and can achieve satisfactory convergence accuracy with fewer iterations. The result of the third iteration indicates convergence within the top and bottom bounds, as shown in Figure 7. The typical daily net load is depicted in the top part of Figure 7, where thermal power units, external power grid purchases, and output from new flexibility resources collectively contribute to load balancing, as illustrated in the bottom part of Figure 7.
As shown in Figure 7, in the most severe circumstance, the deviation of net load is concentrated during peak load periods. For instance, the net load reaches the top limit of deviation during time periods 6–12 and 16–19, while during time period 24, the net load exhibits the most extreme circumstance of downward deviation due to being at a bottom level. During time periods 6–12 and 16–19, there is a high flexibility requisite in the power system. Due to the slow ramping rate of thermal power units, distributed generation provides the main flexibility capability for the system. Between time periods 12–14, the cost is higher due to the influence of time-of-use electricity prices when purchasing power from the external grid. Choosing discharge from electrochemical energy storage can reduce operating costs caused by purchasing electricity at higher prices. At time period 17, as the electrochemical energy storage is at its minimum state of charge, the hydrogen energy storage system discharges to meet the load requisite. The new energy storage system effectively balances the system’s flexibility and economic efficiency.
Under the circumstance where the deviation of wind and solar power output remains within 15% and the load deviation remains within 10%, with conservatism parameters set as parameters, the planning capacity of distributed generation, electrochemical energy storage, and hydrogen energy storage systems as new flexible resources is determined. The planning costs and equivalent comprehensive costs are then calculated. The results are presented in Table 2.
Based on the data in Table 2, it can be observed that the higher the conservatism of the model, the higher the planning cost and the more conservative the model. As the conservatism parameter increases, the deviation of net load increases, resulting in increased capacity planning for distributed generation and electrochemical energy storage, and overall increased planning cost. Figures 4–6 shows the planning and operation results of the model with a fluctuation deviation of 10% and a conservatism parameter of 12.
As Figure 8 shows that new energy storage systems such as electrochemical energy storage and hydrogen energy storage are important means to solve the large-scale integration of new energy into the power grid. Electrochemical energy storage effectively absorbs excess renewable energy generation during off-peak hours through off-peak charging and peak discharge. However, it is limited by factors such as battery degradation and can only charge and discharge at rated power. Hydrogen energy storage systems are needed to balance the power. From Figure 7, it can be seen that during periods of low net load levels at night, thermal power units still operate at minimum technical output and reverse, causing the net load to be at a trough or even negative. Electrochemical energy storage and hydrogen energy storage systems charge during this period to absorb excess wind and solar power generation and discharge during daylight hours when the net load level is higher, effectively alleviating the pressure of power supply during peak hours. In addition, due to cost factors and energy conversion efficiency limitations, the current capacity of hydrogen energy storage systems is relatively low. However, with the continuous progress of technologies such as hydrogen production through water electrolysis and hydrogen fuel cell power generation, the development prospects of hydrogen energy storage systems will be broader.
To verify the effectiveness of the planning model constructed in this paper, it is necessary to compare the configuration results under different robust parameters. Figures 9, 10 show the sensitivity analysis of the configuration results under different robust parameters, calculating the planning cost and capacity configuration of the power system’s new flexible resources.
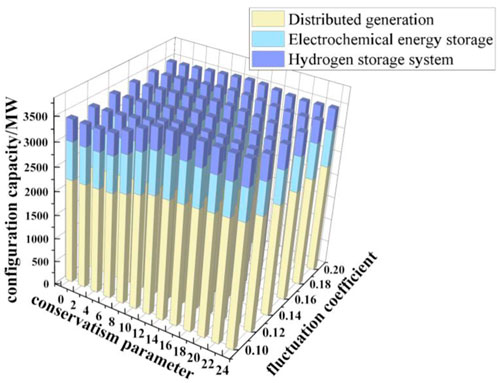
Figure 9. The resource configuration with different conservatism parameters and deviation coefficients.
As shown in Figure 9, during the robust optimization and configuration process, the two uncertainty parameters, conservatism parameter
In Figure 10, assuming a fixed fluctuation coefficient
As shown in Figures 4–8, the selection of the conservatism parameter will greatly affect the objective function of the planning model. The overall cost of the model is positively correlated with the CP. When the CP increases, it represents an increase in the severity of the circumstance, i.e., an increase in the net load deviation. The overall cost also increases accordingly.
From Table 3, it can be seen that in terms of capacity configuration, the hydrogen energy storage system in the two-stage robust model did not show significant changes in its configuration capacity, while the configuration capacity of distributed generation increased by 13.8% and that of electrochemical energy storage increased by 11.2%. In terms of planning and operating costs, the capacity planning cost increased by 7.91%, and the overall cost increased by 17.12% in the two-stage robust model. It can be concluded that the two-stage robust model considers the most extreme circumstance of net load fluctuations, which effectively enhances the robustness of the system’s capacity planning, but also makes the planning more conservative, leading to an increase in the system’s planning and operating costs.
This article addresses the challenge of ensuring safe and stable operation of the new power system with rapidly increasing penetration of new energy. A two-stage robust capacity optimization configuration model is proposed and applied to a power system in a certain region of China for empirical analysis to validate the effectiveness of the model. The empirical analysis leads to the following conclusions:
(1) The flexibility requisite caused by uncertainty of renewable energy sources is considered, and the flexibility supply-requisite balance constraint is incorporated into the model constraints to better address the integration of renewable energy sources.
(2) This paper considers a two-stage robust optimization model in the form of max-min-max within the range of load and new energy uncertainty. Under the worst-case scenario, the optimal capacity allocation is pursued with minimum cost. The allocated capacities are 2,490.80 MW, 865.01 MW, and 444.31 MW, respectively.
(3) The results of the model analysis validate the significant role of emerging energy storage technologies, such as electrochemical storage and hydrogen storage in addressing the uncertainty of renewable energy sources and peak shaving. It confirms that new energy storage is a critical factor in dealing with the uncertainty of renewable energy sources.
(4) An analysis of the optimal configuration and operation of new flexibility resources when robust parameters change is conducted. Compared with the deterministic model, the capacity configuration of distributed generation increases by 13.8%, and the capacity configuration of electrochemical energy storage increases by 11.2%. This validates that the planning result achieves a balance between economy and safety.
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
HY: Writing–original draft, Methodology, Conceptualization, Validation. FL: Methodology, Validation, Writing–original draft, Writing–review and editing. HY: Writing–original draft, Writing–review and editing. XZ: Visualization, Writing–review and editing. LL: Writing–review and editing, Visualization.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
We gratefully acknowledge the support provided by the State Grid Corporation of China, SGQHJY00GHIS2310311.
Authors HY, FL, XZ, and LL were employed by Economic and Technological Research Institute of State Grid Qinghai Electric Power Company.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Chen, X., and Li, N. (2021). Leveraging two-stage adaptive robust optimization for power flexibility aggregation. IEEE Trans. Smart Grid 12 (5), 3954–3965. doi:10.1109/tsg.2021.3068341
Daneshvar, M., Mohammadi-Ivatloo, B., Zare, K., and Asadi, S. (2020). Two-stage stochastic programming model for optimal scheduling of the wind-thermal-hydropower-pumped storage system considering the flexibility assessment. Energy 193, 116657. doi:10.1016/j.energy.2019.116657
Grover-Silva, E., Heleno, M., Mashayekh, S., Cardoso, G., Girard, R., and Kariniotakis, G. (2018). A stochastic optimal power flow for scheduling flexible resources in microgrids operation. Appl. energy 229, 201–208. doi:10.1016/j.apenergy.2018.07.114
Hong, Z., Liang, L., Li, S., Zhang, P., Wen, Y., Jiang, H., et al. (2023). Two-stage robust optimal capacity configuration of a wind, photovoltaic, hydropower, and pumped storage hybrid energy system. Front. Energy Res. 11. doi:10.3389/fenrg.2023.1275232
Huo, Y., Bouffard, F., and Joos, G. (2020). Spatiotemporal flexibility management in low-carbon power systems. IEEE Trans. Sustain. Energy 11 (4), 2593–2605. doi:10.1109/tste.2020.2967428
Jabr, R. A. (2013). Robust transmission network expansion planning with uncertain renewable generation and loads. IEEE Trans. Power Syst. 28 (4), 4558–4567. doi:10.1109/tpwrs.2013.2267058
Ji, H., Wang, C., Li, P., Zhao, J., Song, G., and Wu, J. (2018). Quantified flexibility evaluation of soft open points to improve distributed generator penetration in active distribution networks based on difference-of-convex programming. Appl. Energy 218, 338–348. doi:10.1016/j.apenergy.2018.02.170
Ju, L., Zhao, R., Tan, Q., Lu, Y., and Wang, W. (2019). A multi-objective robust scheduling model and solution algorithm for a novel virtual power plant connected with power-to-gas and gas storage tank considering uncertainty and demand response. Appl. Energy 250, 1336–1355. doi:10.1016/j.apenergy.2019.05.027
Lin, Y., Lin, W., Wu, W., and Zhu, Z. (2023). Optimal scheduling of power systems with high proportions of renewable energy accounting for operational flexibility. Energies 16 (14), 5537. doi:10.3390/en16145537
Li, Y., Liu, H., Fan, X., and Tian, X. (2020). Engineering practices for the integration of large-scale renewable energy VSC-HVDC systems. Glob. Energy Interconnect. 3 (2), 149–157. doi:10.1016/j.gloei.2020.05.007
Mianaei, , Khorshidian, P., Faghri, S., Ensaf, M., Ghasemi, A., and Abdoos, A. A. (2022). Chance-constrained programming for optimal scheduling of combined cooling, heating, and power-based microgrid coupled with flexible technologies. Sustain. Cities Soc. 77, 103502. doi:10.1016/j.scs.2021.103502
Mingkun, D., Yuan, H., Junyong, L., Wu, G., and Jawad, S. (2021). CVaR-based generation expansion planning of cascaded hydro-photovoltaic-pumped storage system with uncertain solar power considering flexibility constraints. IET Gener. Transm. Distrib. 15 (21), 2953–2966. doi:10.1049/gtd2.12232
Nicholas, G., and Pierluigi, M. (2019). Flexibility in multi-energy communities with electrical and thermal storage: a stochastic, robust approach for multi-service requisite response. IEEE Trans. Smart Urid 10 (1), 503–513. doi:10.1109/TSG.2017.2745559
Pandey, R. S., and Awasthi, S. R. (2020). A multi-objective hybrid algorithm for optimal planning of distributed generation. Arabian J. Sci. Eng. 45 (4), 3035–3054. doi:10.1007/s13369-019-04271-1
Ren, J. Z., Gao, S. Z., Tan, S. Y., and Dong, L. (2015). Hydrogen economy in China: strengths-weaknesses-opportunities-threats analysis and strategies prioritization. Renew. Sustain. Energy Rev. 41, 1230–1243. doi:10.1016/j.rser.2014.09.014
Sun, Q., Wu, C., Li, Z., and Ren, S. (2016). Colocation demand response: joint online mechanisms for individual utility and social welfare maximization. IEEE J. Sel. Areas Commun. 34 (12), 3978–3992. doi:10.1109/jsac.2016.2611918
Torreglosa, J. P., Garcla, P., Fernandez, L. M., and Jurado, F. (2015). Energy dispatching based on predictive controller of an off-grid wind turbine/photovoltaic/hydrogen/battery hybrid system. Renew. Energy 74, 326–336. doi:10.1016/j.renene.2014.08.010
Xiaoyan, L., Xingmei, L., and Chuanbo, X. (2023). A robust optimization model for capacity configuration of PV/battery/hydrogen system considering multiple uncertainties. Int. J. Hydrogen Energy 48 (21), 7533–7548. doi:10.1016/j.ijhydene.2022.11.220
Zeng, B., and Zhao, L. (2013). Solving two-stage robust optimization problems using a column-and-constraint generation method. Operations Res. Lett. 41 (5), 457–461. doi:10.1016/j.orl.2013.05.003
Keywords: new flexibility resource, configuration model, uncertainty, two-stage robust optimization, flexibility characterization
Citation: Yang H, Liu F, Yang H, Zhang X and Liu L (2024) A two-stage robust configuration optimization model and solution algorithm for new flexibility resources considering uncertainty response characterization. Front. Energy Res. 12:1381857. doi: 10.3389/fenrg.2024.1381857
Received: 04 February 2024; Accepted: 07 March 2024;
Published: 04 April 2024.
Edited by:
Haonan Zhang, North China Electric Power University, ChinaReviewed by:
Shenbo Yang, Beijing University of Technology, ChinaCopyright © 2024 Yang, Liu, Yang, Zhang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hui Yang, MTM3NTk4MjU0NEBxcS5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.