
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 04 June 2024
Sec. Electrochemical Energy Storage
Volume 12 - 2024 | https://doi.org/10.3389/fenrg.2024.1379576
 Ruijie Ye1*
Ruijie Ye1* Yin-Ying Ting2,3
Yin-Ying Ting2,3 Enkhtsetseg Dashjav1
Enkhtsetseg Dashjav1 Qianli Ma1
Qianli Ma1 Sou Taminato4
Sou Taminato4 Daisuke Mori4
Daisuke Mori4 Nobuyuki Imanishi4
Nobuyuki Imanishi4 Piotr M. Kowalski2,3
Piotr M. Kowalski2,3 Michael H. Eikerling2,3
Michael H. Eikerling2,3 Payam Kaghazchi1
Payam Kaghazchi1 Martin Finsterbusch1,5
Martin Finsterbusch1,5 Olivier Guillon1,5
Olivier Guillon1,5Garnet-type solid electrolytes stand out as promising Li-ion conductors for the next-generation batteries. It has been demonstrated that the inherent properties of garnets can be tailored by introducing various dopants into their crystal structures. Recently, there has been a growing interest in the concept of high entropy stabilization for materials design. In this study, we synthesized high-entropy garnets denoted as Li6La3Zr0.7Ti0.3Ta0.5Sb0.5O12 (LLZTTSO), wherein Ti, Sb, and Ta occupy the Zr site. The formation of the cubic garnet phase in LLZTTSO was confirmed through X-ray diffraction (XRD), and the resulting lattice parameter agreed with predictions made using computational methods. Despite the substantial porosity (relative density 80.6%) attributed to the low sintering temperature, LLZTTSO exhibits a bulk ionic conductivity of 0.099 mS cm−1 at 25°C, and a total ionic conductivity of 0.088 mS cm−1, accompanied by an activation energy of 0.497 eV. Furthermore, LLZTTSO demonstrates a critical current density of 0.275 mA cm−2 at 25°C, showcasing its potential even without any interfacial modification.
The current state of lithium-ion battery (LIB) technology has reached its physicochemical limit concerning energy density (Janek and Zeier, 2016). To address the increasing demand for energy storage, urgent efforts are required to develop next-generation battery technologies, with solid-state lithium batteries (SSLBs) emerging as a promising approach (Sang et al., 2023). Beyond the advantages of increased energy density, SSLBs offer a notable safety enhancement over current LIBs. This is attributed to the replacement of flammable organic liquid electrolytes in LIBs with solid electrolytes, especially crucial as battery cells are scaled up.
Among the solid electrolyte materials, the garnet-type Li+ conductor Li7La3Zr2O12 (LLZ) stands out due to its high ionic conductivity and exceptional (electro-)chemical stability against the lithium metal anode (Wang et al., 2020a). LLZ exhibits two stable crystal structures: a cubic phase and a tetragonal phase. The cubic phase demonstrates an ionic conductivity two orders of magnitude higher than that of the tetragonal phase, although the latter is the thermodynamically favored phase at room temperature (Ramakumar et al., 2017). Despite the known phase transition of the tetragonal phase to the cubic phase around 625°C–645°C, with subsequent return to the tetragonal phase upon cooling (Matsui et al., 2014; Stockham et al., 2022a), stabilizing the high-conductive cubic phase at room temperature has been a significant challenge. Efforts to achieve this stabilization primarily involve a doping strategy, with various dopant elements explored in the garnet structure to modify its properties. Isovalent elements such as Sn, Hf, Ti, Sc, Ce, and Ge, as well as aliovalent elements like Ta, Nb, Sb, Te, W, Mo, Bi, Cr, Gd, and Y, can replace the Zr site. The La site can be occupied by Nd, Ba, Ca, and Sr, while the Li site can be doped with Al, Ga, Fe, Co, or Ge (Samson et al., 2019). Although significant research has focused on single, double, or triple doping, the exploration of multiple doping (involving more than three dopants) has been scarce in the past decade. This highlights a potential approach for future investigations in the pursuit of enhanced stability and performance in garnet-type solid electrolyte materials.
Recently, the concept of high entropy has gained significant attention in materials design. The introduction of multiple elements, randomly distributed on the same lattice site within crystal structures, enhances the configurational entropy of the system, resulting in the stabilization of a single-phase crystal structure (Rost et al., 2015). Following the discovery of high entropy alloys, high entropy materials have diversified into various non-metallic branches, including oxides, sulfides, carbides, borides, nitrides, fluorides, and oxyhalides (Sarkar et al., 2019). Notably, high-entropy oxides are attracting interest for their application in energy materials, particularly as oxide-based cathode and anode materials for Li-ion batteries (LIBs) (Ma et al., 2021; Fracchia et al., 2022). As summarized in Table 1, some high-entropy garnets (HEGs) have been developed, demonstrating the flexibility of lithium garnet materials to multiple doping.
Stockham et al. reported the first HEGs with 9- (Li5.75Ga0.2La2.5Nd0.5ZrNb0.65Ce0.1Ti0.25O12) and 11-element (Li5.75Ga0.2La2.5Nd0.5Zr0.75Ta0.3Nb0.35Ce0.1Hf0.25Ti0.25O12) systems (Stockham et al., 2022a). Despite a low Li content of 5.75 per formula unit (pfu), these HEGs exhibit room-temperature conductivities of 0.1 and 0.2 mS cm−1 for the 9- and 11-element systems, respectively. Subsequently, they developed a HEG with Zr site dopants only: Li6.5La3ZrNb0.5Ce0.25Ti0.25O12, which demonstrated an improved ionic conductivity of 0.5 mS cm−1 at 25°C (Stockham et al., 2022b). Fu et al. synthesized Li6La3Zr0.5Nb0.5Ta0.5Hf0.5O12, where Zr, Nb, Ta, and Hf are equimolarly distributed on the Zr site in the garnet structure (Fu and Jacob, 2022). This cubic HEG exhibits an ionic conductivity of 4.67 × 10−4 S cm−1 with an activation energy of 0.25 eV, and a low electronic conductivity in the order of 10–8 S cm−1. They also observed that the HEG has finer grain size (∼10 µm) compared to its low-entropy counterpart Li6.75La3Zr1.75Ta0.25O12 (>100 µm), resulting in higher flexural strength and hardness (Fu and Jacob, 2023). Chen et al. elucidated the influence of multiple cations on the short-range structure of Li6La3Zr0.5Nb0.5Ta0.5Hf0.5O12, resulting in extended bottleneck size, elongated Li-O bond length, and local clustering of 16a sites (Chen et al., 2023). Other HEGs with equimolar distribution of dopants on the Zr site such as Li7La3Zr0.5Hf0.5Sc0.5Nb0.5O12, Li7La3Zr0.4Hf0.4Sn0.4Sc0.5Ta0.5O12, and Li6.6La3Zr0.4Hf0.4Sn0.4Sc0.2Ta0.6O12 were investigated by Jung et al. (Jung et al., 2022). They found the cubic phase is stabilized with the increasing entropy and the introduction of those aliovalent elements in the garnet structure. While the Li = 6.6 HEG exhibits higher ionic conductivity (0.32 mS cm−1 at 25°C) than the Li = 7 HEG (0.17 mS cm−1 at 25°C), the Li = 7 HEG shows better reduction stability against lithium metal. Feng et al. prepared Li6.6La3Zr0.4Sn0.4Sc0.4Ta0.4Nb0.4O12, demonstrating a high ionic conductivity of 0.357 mS cm−1 (Feng et al., 2023). Interestingly, when they increased the number of elements on the Zr site to 8 and 10, i.e., increased entropy, the ionic conductivity decreases. Hence, the cation combination, which determines the bottlenecks for the ionic conduction pathways, appears to plays a more significant role in the ionic conduction than the configuration entropy. Further research is needed to elucidate the relationship between ion diffusion and the composition and structure of HEGs.
Herein, we analyze the high-entropy garnet Li6La3Zr0.7Ti0.3Ta0.5Sb0.5O12 (LLZTTSO), where Ti, Sb, and Ta occupy the Zr site, as the combination of Sb/Ta/Ti exhibits the lowest formation enthalpy among all the investigated elements (Ting et al., 2024). Our investigation encompasses the characterization of phase formation, microstructure, including sintering behaviors, and electrochemical properties of this HEG compound. Complementary to experimental approaches, we employ computational methods to delve into the configuration entropy and crystal structure of LLZTTSO. Additionally, we explore the effects induced by the high-entropy stabilization strategy, providing a comprehensive discussion on its implications.
The high-entropy garnet LLZTTSO was synthesized by conventional solid-state reaction. The starting materials Li2CO3, La(OH)3, ZrO2, TiO2, Ta2O5, and Sb2O5 were mixed in stoichiometric amounts with 5 wt% Li2CO3 in excess. One batch of the synthesis is to obtain around 5 g target products. The starting powder was ball-milled in a ZrO2 milling jar filled with hexane and ZrO2 beads for 2 h at a rotation speed of 300 rpm in a planetary milling machine (Fritsch Pulverisette). Afterwards, the powder was dried at 80°C to evaporate hexane. After collected through a 300-mesh sieve, the dried powder was placed on a gold sheet inside an alumina crucible for calcination. The calcinations were performed in air at various temperatures (800°C, 850°C, and 950°C) for 12 h. After cooling down to 400°C in the furnace, the crucibles were transferred into a drying chamber for further cooling. After the temperature reached room temperature, the calcined powder was ball-milled again in hexane at a rotation speed of 300 rpm for 2 h. After dried at 80°C, the powder went through a 300-mesh sieve and was stored in desiccator. The calcined powder was pressed to form pellets at 13.7 MPa by using uniaxial hydraulic press, and the pellets were subsequently pressed at 150 MPa in an isostatic press. The obtained pellets were sandwiched between two gold sheets and sintered in an alumina crucible. The sintering was performed in air at 1,050°C for 2, 6, or 12 h. After cooling down to 400°C in the furnace, the crucibles were transferred into a drying chamber for further cooling. After the temperature reached room temperature, the sintered pellets were collected and stored in desiccator.
Serving as the control samples, garnets Li7La3Zr2O12 (LLZO), Li7La3ZrTiO12 (Ti-LLZO), Li6La3ZrTaO12 (Ta-LLZO), and Li6La3ZrSbO12 (Sb-LLZO) were prepared in the same way. The calcination and final sintering were performed at 850°C for 12 h and 1,050°C for 12 h, respectively.
The samples were characterized for their phase purities by XRD on a Bruker D4 Endeavor device (Bruker, Germany) using Cu Kα radiation equipped with a 1D detector LynxEye. The qualitative phase analyses were done using Panalytical’s HighScore software, and LeBail profile fitting for lattice parameters of the investigated samples were carried out using the software Jana2006 (Petříček, Dušek, and Palatinus, 2014) based on the structure model in the cubic space group of Ia-3d (ICSD 158372), which is described by Murugan et al. (Murugan et al., 2007). The quantitative phase analysis was carried out using the software PowderCell (Kraus and Nolze, 1996). The apparent densities of sintered pellets were determined by Archimedes’ Method. For microstructural investigation on cross-section, samples were embedded in EpoFix epoxy resin (Struers, Germany) and mirror-polished. Back-scattered electron (BSE) images and energy-dispersive X-ray spectroscopy (EDS) analysis were taken by a scanning electron microscope (SEM) (TM3000 tabletop microscope, Hitachi).
After polished on 400, 800, 1,500, and 4,000 grid sandpapers, the sintered LLZTTSO pellets were transferred into an Ar-filled glovebox. The pellets were polished again on 4,000 grid sandpaper to remove possible impurities. Two lithium metal foils with a diameter of 6 mm were pressed onto both sides of the pellets. Such Li|LLZTTSO|Li symmetric assembly was then sealed in a pouch bag with two Ni bars as current collectors for electrochemical characterization.
Electrochemical impedance spectroscopy (EIS) was measured in the frequency range from 10 MHz to 1 Hz with an electrical field perturbation of 50 mV using an impedance analyzer by Novocontrol Technologies, or in the frequency range from 1 MHz to 0.1 Hz with an electrical field perturbation of 10 mV using a frequency response analyzer by Solartron Analytical. A fitting of the impedance spectrum was conducted in the software ZView (Scribner). For the determination of the critical current density (CCD) of LLZTTSO, a VMP-300 multi-potentiostat (BioLogic) combined with a climate chamber (Vötsch VT4002EMC) was used. The current density was increased stepwise from 25 μA cm−2–300 μA cm−2 with an interval of 25 μA cm−2. The stripping/plating process was controlled by limiting the areal capacity of 0.1 mAh cm−2, and repeated 5 times for each step.
First-principle density functional theory (DFT) calculations were performed to obtain the theoretical lattice parameters and density of garnet structures, information essential for the analysis of measured data. These calculations utilized the gpu-enabled 7.2 version of plane-wave Quantum Espresso code (Giannozzi et al., 2009; Giannozzi et al., 2020). We employed ultrasoft pseudopotentials (Vanderbilt, 1990) and the PBEsol exchange-correlation functional (Perdew et al., 2008), which have been shown to give good structural parameters for cathode materials in lithium-ion batteries (Kowalski et al., 2021; Ting and Kowalski, 2023). The pure cubic phase-LLZO atomic bulk structure was modeled with a space group of Ia-3d and a unit cell formula of Li56La24Zr16O96.
The spatial distribution of elements within the multi-doped LLZO was modeled with the Special Quasirandom Structure (SQS) method (Zunger et al., 1990), implemented through the Alloy Theoretic Automated Toolkit (ATAT) package (van de Walle et al., 2013). This approach creates a unit cell with an atomic arrangement that mimics the disorder found in a fully random solid solution. A plane-wave cutoff energy of 50 Ry and a Monkhorst-Pack 4 × 4 × 4 k-point mesh were employed to ensure convergence of the results (Monkhorst and Pack, 1976). All structures underwent full optimization, adhering to a convergence threshold of 10–5 Ry and 10–4 Ry/a0 (where a0 is the Bohr radius) for energy and forces, respectively.
In the case of ideal mixing of n species, the configurational entropy per mole, Sconf, was calculated using the Stirling’s approximation:
where R is the universal gas constant, and xi the concentration ratio of element i.
When considering garnet structures, the formula for configurational entropy was adapted to include sublattices:
where ms denotes the multiplicity of a sublattice s, and x{i,s} represents the mole fractions of species i on the sublattice s sites.
We have chosen Ta5+, Sb5+, and Ti4+ as doping cations on the Zr site due to the commonality of Ta5+ as a dopant in most investigated Li-garnets, the similar ionic radius of Sb5+ (0.62 Å) to Ta5+ (0.64 Å), and the known ability of Ti4+ to suppress lithium dendrite formation (Gao et al., 2021; Zhu et al., 2021). Deviating from the equimolar Li6La3Zr0.5Ti0.5Ta0.5Sb0.5O12 composition, we have slightly reduced the Ti content from 0.5 per formula unit (pfu) to 0.3 pfu in LLZTTSO. This adjustment is based on the stability of Ti4+ within the garnet structure against Li metal (Shao et al., 2017). LLZTTSO powders were synthesized at different calcination temperatures (800°C, 850°C, and 950°C). XRD results (Figure 1A) indicate the formation of a cubic garnet phase at 800°C, accompanied by intermediate products such as LaTiO3 and La2Zr2O7 in the powder. The phase formation of LaTiO3 could be attributed to the reduction of La2Ti2O7 induced by Li2CO3 (Zhang et al., 2022). With the increased calcination temperature, the quantity of these intermediate products diminishes, and the powder calcined at 950°C exhibits the cubic garnet phase exclusively. Subsequently, all three calcined powders were pelletized and sintered at 1,050°C. As depicted in Figure 1B, pure cubic garnet phases are observed in all samples after sintering regardless the dwell time (2, 6 or 12 h) and the purity of the calcined powders. The sharpening reflections of sintered pellets, compared to the broader reflections of calcined powder, also indicate the increase in crystallinity. In comparison, undoped LLZO and Ti-LLZO prepared under the same condition exhibit a tetragonal structure, while Ta- and Sb-LLZO are presented in the cubic form (Figure 1C). This suggests that the doping by aliovalent element on Zr site stabilize the cubic phase, consistent with the finding by Logéat et al. (Logéat et al., 2012). Profile fitting of the XRD pattern of LLZTTSO (Figure 1D) reveals a lattice parameter of a = 12.87239 (13) Å, in good agreement with the predicted value by the computational method (12.877 Å), affirming the successful synthesis of LLZTTSO (Table 2). Additionally, the calculated configurational entropy values are 3.71R, 5.84R, and 7.10R for undoped LLZO, mono-doped LLZO (e.g., Ta-LLZO and Sb-LLZO), and LLZTTSO, respectively. It is noteworthy that for undoped LLZO, the cubic phase exhibits a theoretical configurational entropy of 3.71R per mole of formula unit, in contrast to the tetragonal phase, where the configurational entropy is 0, attributable to the complete occupation of lattice sites. With the increase of configuration entropy, the tetragonal phase turn into cubic phase in the samples. We postulate that this high configurational entropy contributes to stabilize the cubic phase at elevated temperatures.
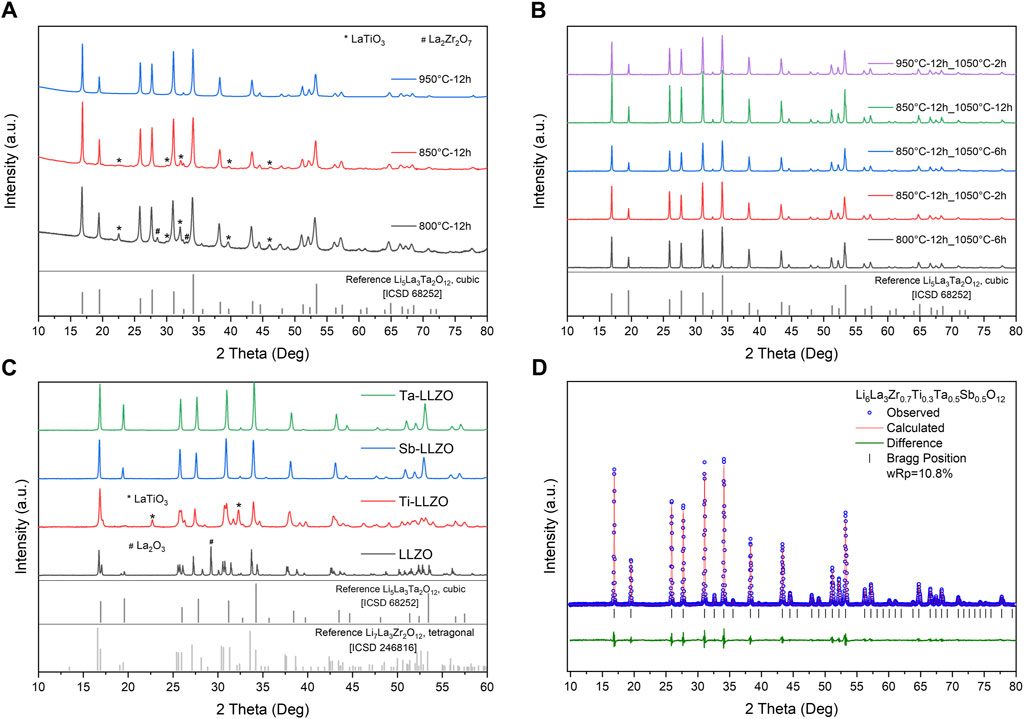
Figure 1. XRD patterns of (A) calcined LLZTTSO powders, (B) sintered LLZTTSO pellets, and (C) sintered garnet pellets of LLZO, Ti-, Ta- and Sb-LLZO; (D) Profile fitting of XRD of LLZTTSO.
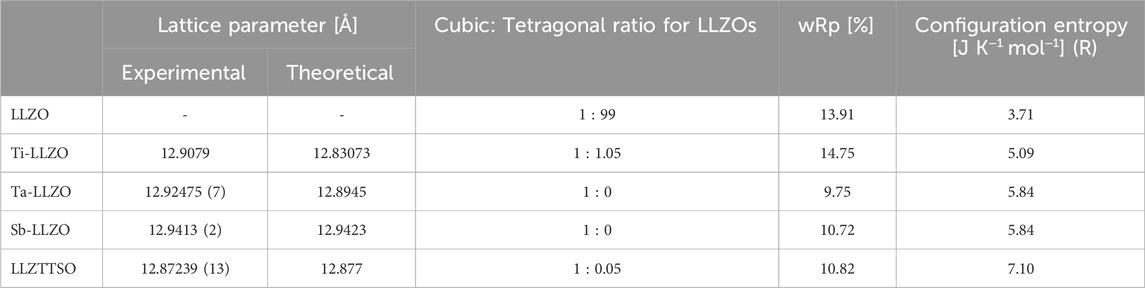
Table 2. Lattice parameter of cubic phase, cubic phase content, R factors for fitting, and configuration entropy of LLZO, LLZTTSO, Ti-, Ta-, and Sb-LLZO.
The LLZTTSO pellets prepared from powder calcined at 800°C and 850°C have similar relative densities above 70%, whereas those made from powder calcined at 950°C have much lower relative densities below 70% (Table 3). A dwell time of 6 h is found optimal for achieving the highest density, and an extension to 12 h results in a decrease in density. The LLZTTSO pellet calcined at 850°C and subsequently sintered at 1,050°C for 6 h attains the highest relative density of 80.6%. In contrast, both Ta-LLZO and Sb-LLZO exhibit relative densities lower than 60%. This discrepancy underscores the superior sintering performance of high-entropy garnet LLZTTSO compared to mono-doped garnets, suggesting that the introduction of Ti in this system may enhance the sintering process. To prevent Al3+-diffusion from the alumina crucible into the pellets, gold sheets are utilized as sintering substrates in our processing. However, the sintering temperature is constrained by the melting point of gold, which is 1,064°C. Consequently, sintering is performed only at 1,050°C, a temperature that may not be sufficiently high to fully densify the samples. The use of platinum as a substrate, with its significantly higher melting point of 1768°C, could be a more effective option for obtaining dense pellets. Alternatively, advanced sintering technologies, such as field-assisted sintering technique (Bram et al., 2020) or ultrafast high-temperature sintering (Wang et al., 2020b) utilizing carbon materials as substrates, are also viable approaches for preparing high-entropy garnets.
Figure 2 depicts BSE-SEM images on the fracture surface of the sintered LLZTTSO pellets, providing insights into the microstructure and highlighting the impact of calcination temperature and sintering time on the material. All LLZTTSO pellets exhibit noticeable porosity, consistent with the relative density results obtained. Garnet grain sizes range from 2 to 4 µm. Pellets produced from the powder calcined at 800°C and 850°C (Figures 2A–D) display distinct intergranular grain boundaries and pores along grain junctions. Some densified regions are already evident, indicating a progression from an intermediate to a final sintering stage. In contrast, pellets from powders calcined at 950°C (Figure 2E) are in an intermediate sintering stage, displaying continuous pore channels through the pellets. This suggests that LLZTTSO powder calcined at lower temperatures exhibits superior sinterability compared to that calcined at higher temperatures. Comparatively, Ta-LLZO (Figure 2F) exhibits a microstructure similar to LLZTTSO, transitioning from the intermediate to the final sintering stage. On the other hand, Sb-LLZO (Figure 2G) shows small necks at particle junctions and continuous pore channels through the pellets, indicating the transition from initial to intermediate sintering stage. The microstructure of Ti-LLZO (Figure 2H) differs significantly from all other samples, with particles undergoing coarsening rather than densification, resulting in larger grain sizes up to 10 µm. The intergranular spaces are filled with side phases (dark regions in the BSE-SEM image), potentially corresponding to the LaTiO3 phase detected by XRD. This Ti-containing phase is also detected in the LLZTTSO powder calcined at 800°C or 850°C, and may contribute to sintering, possibly through a reactive sintering mechanism along with another side phase, La2Zr2O7 (Zheng et al., 2022). This observation might explain the higher relative density of LLZTTSO obtained from the powders calcined at 800°C or 850°C compared to those calcined at 950°C. EDS element mapping of LLZTTSO (Figure 2I) shows homogeneous distribution of La, Zr, Ta, Sb, and Ti within the investigated region, aligning with the characteristic features of high entropy materials.

Figure 2. (A–H) BSE-SEM images on the fracture surface of LLZTTSO, Ta-, Sb-, and Ti-LLZO sintered pellets; (I) EDS mapping of the elements La, Zr, Ti, Ta, and Sb in the LLZTTSO pellet sintered at 1,050°C for 6 h.
The electrochemical properties of the LLZTTSO sintered pellets prepared from powder calcined at 850°C are evaluated. The Nyquist plot of LLZTTSO sintered at 1,050°C for 6 h (Figure 3A) exhibits two semicircles. An equivalent circuit consisting of two parallel elements of resistor (R) and constant phase element (CPE) is used to fit the two semicircles. The first semicircle at high frequency range having a capacitance of 4.89 × 10−11 F represents the bulk contribution of LLZTTSO, whereas the second semicircle at medium to low frequency having a capacitance of 4.22 × 10−8 F represents the grain boundary contribution of LLZTTSO. The impedance contribution of Li/LLZTTSO-interface is missing. A possible explanation can be that this part impedance is buried in the second semicircle, as the fitting result of the second CPE shows large error, especially in the capacitance, and it is also difficult to distinguish them by simply applying another parallel (R) (CPE) element. From these results we obtain the bulk and total conductivity of LLZTTSO at 25°C as 0.099 and 0.088 mS cm−1, respectively. In addition, the sample sintered from the 950°C calcination powder also has a bulk conductivity of 0.098 mS cm−1 (Supplementary Figure S3), but a lower total conductivity of 0.016 mS cm−1 due to the higher porosity. As shown in Figure 3B, the total ionic conductivity of LLZTTSO sintered at 1,050°C for 12 h is 0.046 mS cm−1 at 25°C, surpassing the total ionic conductivity of Ta-LLZO and Sb-LLZO (0.023 and 0.0053 mS cm−1, respectively). This conductivity enhancement can be attributed to the higher density of LLZTTSO achieved through the high-entropy strategy. Figure 3C presents the Arrhenius plots of LLZTTSO pellets sintered at 1,050°C for different dwell time (e.g., 6 h or 12 h). The sample with a dwell time of 6 h exhibits higher conductivity and a lower activation energy of 0.497 eV, while the sample with dwell time of 12 h has a higher activation energy of 0.507 eV. The obtained activation energy values, though higher than those reported for other HEGs (Fu and Jacob, 2022; Stockham et al., 2023), may be influenced by the low density of LLZTTSO resulting from the relatively low sintering temperature and the consequent formation of suboptimal grain boundaries (Naqash et al., 2019). It is noteworthy that the impact of the local structure created by different dopants is not addressed in this study, which could contribute to the observed increased energy barrier for Li+ diffusion.
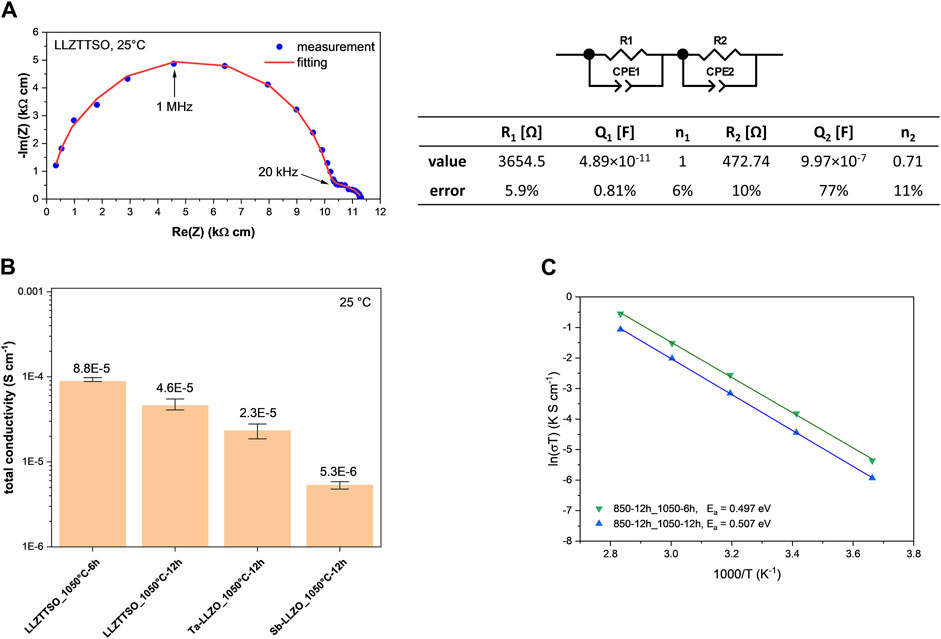
Figure 3. (A) Nyquist plot of LLZTTSO sintered at 1,050°C for 6 h, with the equivalent circuit used for fitting, and fitting results; (B) Total conductivity of LLZTTSO, Ta-, and Sb-LLZO at 25°C; (C) Arrhenius plots of LLZTTSO sintered pellets.
Subsequently, the LLZTTSO pellet with the highest ionic conductivity underwent the critical current density test (Figure 4A). The capacity-controlled CCD measurement at 25°C, with the capacity of Li stripping/plating limited to 0.1 mAh cm−2 for each polarization step, reveals flat plateaus for the current densities smaller than 0.1 mA cm−2, indicating favorable Li plating/stripping behavior. At 0.125 mA cm−2, the polarization curve increases slightly at the end stage of each step, suggesting possible void formation at the Li/LLZTTSO interface. Despite void formation, the measured polarization voltages remain constant within the cycling steps with the same current densities, underscoring the highly reversible void formation and refilling process. A soft short circuit occurs at 0.30 mA cm−2, with the highest reached current density before short-circuit being 0.275 mA cm−2. The impedance spectra in Figure 4B reveal that the first semicircle at high-to-medium frequency range, representing the solid electrolyte, remains unchanged after each cycling step, indicating the robust stability of LLZTTSO against Li metal. In contrast, the second semicircle at medium and low frequency ranges, representing the grain boundary and Li/LLZTTSO-interface, increases, suggesting the possible Li filament formation at the grain boundary and void formation at the Li/LLZTTSO-interface after cycling. Notably, no interfacial modification on LLZTTSO was performed prior to attaching Li metal, and the Li metal was not even molten to improve the interface. Considering the high porosity of the LLZTTSO sample, the achievement of the high CCD of 0.275 mA cm−2 is particularly noteworthy.
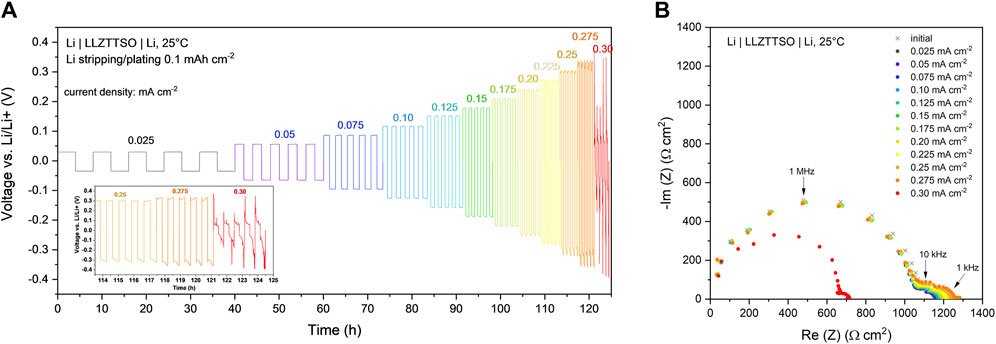
Figure 4. (A) CCD test of LLZTTSO sintered pellet in a Li symmetric cell; (B) Nyquist plots after each CCD test step. The tested LLZTTSO pellet was sintered at 1,050°C for 6 h from the powder calcined at 850°C for 12 h.
In summary, the synthesis of the high-entropy garnet LLZTTSO with Ti, Sb, and Ta occupying Zr site is successfully performed for the first time. After sintering at 1,050°C, a pure cubic garnet phase is obtained, as confirmed by the agreement between the experimentally obtained lattice parameter and the simulated counterpart. Despite the microstructure not reaching full density, the introduction of Ti into the garnet structure is found to promote the sintering, as HEGs with Ti exhibit significantly higher sinterability than any mono-doped LLZO with Sb or Ta. Furthermore, the initial calcination temperature proves crucial for final densification, with the secondary phase LaTiO3 formed at 800 or 850°C potentially contributing to sintering through a conceivable reactive sintering mechanism. Concerning the electrochemical performance, the sintered LLZTTSO pellet exhibits a bulk and total ionic conductivity of 0.099 and 0.088 mS cm−1 at 25°C, respectively, with an activation energy of 0.497 eV. Impressively, the critical current density reaches 0.275 mA cm−2 at 25°C, which is promising for the case without any interfacial modification. Besides, the stable cycling of its symmetric cell with Li metal electrodes proves that the Ti dopant in LLZTTSO is chemically stable against the Li metal anode.
It is noteworthy that the LLZTTSO samples prepared in this study exhibit significant porosities (>20%) due to the relatively low sintering temperature of 1,050°C, constrained by the melting point of the employed gold sintering substrate. Future investigations exploring LLZTTSO properties sintered at higher temperatures, facilitated by the use of platinum as a substrate or other advanced sintering techniques, would be interesting. In addition, increasing the Li content to 6.4–6.6 pfu by further replacing Zr4+ with M3+ cations or reducing M5+ is prospective approach to explore for potentially higher ionic conductivity. Moreover, the unexplored impact of the local structures induced by different dopants remains a topic for future investigation.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
RY: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Validation, Writing–original draft, Writing–review and editing. Y-YT: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. ED: Data curation, Formal Analysis, Investigation, Methodology, Writing–review and editing. QM: Data curation, Investigation, Methodology, Writing–review and editing. ST: Resources, Supervision, Writing–review and editing. DM: Resources, Supervision, Writing–review and editing. NI: Project administration, Resources, Supervision, Writing–review and editing. PiK: Funding acquisition, Methodology, Project administration, Supervision, Writing–review and editing. ME: Funding acquisition, Project administration, Supervision, Writing–review and editing. PaK: Methodology, Supervision, Writing–review and editing. MF: Funding acquisition, Project administration, Supervision, Writing–review and editing. OG: Supervision, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. International Research Fellowship of Japan Society for the Promotion of Science (Postdoctoral Fellowships for Research in Japan) under grant No. SP21320. Jülich Aachen Research Alliance—Center for Simulation and Data Science (JARA-CSD) under Project No. cjiek61. Clusters of competency Festbatt2 (project 13XP0434A and 13XP0432B) by the German Federal Ministry of Education and Research (BMBF).
Japan Society of the Promotion of Science (JSPS) is gratefully acknowledged for the research support. RY would like to thank Mr. Yuzo Kanamori (Mie University), Mr. Kazuki Yonezawa (Mie University), and Dr. Xuefu Shang (Mie University) for their aids in experiments.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1379576/full#supplementary-material
Bram, M., Laptev, A. M., Prasad Mishra, T., Nur, K., Kindelmann, M., Ihrig, M., et al. (2020). Application of electric current-assisted sintering techniques for the processing of advanced materials. Adv. Eng. Mater. 22 (6), 2000051. doi:10.1002/adem.202000051
Chen, Y., Wang, T., Chen, H., Kan, W. H., Wen, Y., Song, Z., et al. (2023). Local structural features of medium-entropy garnet with ultra-long cycle life. Matter 6, 1530–1541. doi:10.1016/j.matt.2023.03.002
Feng, Y., Yang, L., Yan, Z., Zuo, D., Zhu, Z., Zeng, L., et al. (2023). Discovery of high entropy garnet solid-state electrolytes via ultrafast synthesis. Energy Storage Mater. 63, 103053. doi:10.1016/j.ensm.2023.103053
Fracchia, M., Callegari, D., Coduri, M., Anselmi-Tamburini, U., Manzoli, M., Quartarone, E., et al. (2022). Electrochemical performance of high and medium entropy oxides for lithium batteries. Front. Energy Res. 10. doi:10.3389/fenrg.2022.883206
Fu, Z., and Jacob, F. (2022). Processing and characterization of an Li7La3Zr0.5Nb0.5Ta0.5Hf0.5O12 high-entropy Li–garnet electrolyte. J. Am. Ceram. Soc. 105, 6175–6183. doi:10.1111/jace.18576
Fu, Z., and Jacob, F. (2023). Fine and strengthened Li7La3Zr0.5Nb0.5Ta0.5Hf0.5O12 high-entropy Li-garnet: a comparison study with Ta doped Li-garnet. Ceram. Int. 49, 33981–33990. doi:10.1016/j.ceramint.2023.08.094
Gao, J., Zhu, J., Li, X., Li, J., Guo, X., Li, H., et al. (2021). Rational design of mixed electronic-ionic conducting Ti-doping Li7La3Zr2O12 for lithium dendrites suppression. Adv. Funct. Mater. 31 (2), 2001918. doi:10.1002/adfm.202001918
Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21 (39), 395502. doi:10.1088/0953-8984/21/39/395502
Giannozzi, P., Baseggio, O., Bonfà, P., Brunato, D., Car, R., Carnimeo, I., et al. (2020). Quantum ESPRESSO toward the exascale. J. Chem. Phys. 152 (15), 154105. doi:10.1063/5.0005082
Janek, J., and Zeier, W. G. (2016). A solid future for battery development. Nat. Energy 1, 16141. doi:10.1038/NENERGY.2016.141
Jung, S.-K., Gwon, H., Kim, H., Yoon, G., Shin, D., Hong, J., et al. (2022). Unlocking the hidden chemical space in cubic-phase garnet solid electrolyte for efficient quasi-all-solid-state lithium batteries. Nat. Commun. 13 (1), 7638. doi:10.1038/s41467-022-35287-1
Kowalski, P. M., He, Z., and Cheong, O. (2021). Electrode and electrolyte materials from atomistic simulations: properties of LixFEPO4 electrode and zircon-based ionic conductors. Front. Energy Res. 9. doi:10.3389/fenrg.2021.653542
Kraus, W., and Nolze, G. (1996). POWDER CELL - a program for the representation and manipulation of crystal structures and calculation of the resulting X-ray powder patterns. J. Appl. Crystallogr. 29, 301–303. doi:10.1107/S0021889895014920
Logéat, A., Köhler, T., Ulrich, E., Stiaszny, B., Harzer, A., Tovar, M., et al. (2012). From order to disorder: the structure of lithium-conducting garnets Li7−xLa3TaxZr2−xO12 (x=0–2). Solid State Ionics 206, 33–38. doi:10.1016/j.ssi.2011.10.023
Ma, Y., Yuan, Ma, Wang, Q., Schweidler, S., Botros, M., Fu, T., et al. (2021). High-entropy energy materials: challenges and new opportunities. Energy & Environ. Sci. 14 (5), 2883–2905. doi:10.1039/D1EE00505G
Matsui, M., Takahashi, K., Sakamoto, K., Hirano, A., Takeda, Y., Yamamoto, O., et al. (2014). Phase stability of a garnet-type lithium ion conductor Li7La3Zr2O12. Dalton Trans. 43 (3), 1019–1024. doi:10.1039/C3DT52024B
Monkhorst, H. J., and Pack, J. D. (1976). Special points for Brillouin-zone integrations. Phys. Rev. B 13 (12), 5188–5192. doi:10.1103/PhysRevB.13.5188
Murugan, R., Werner, W., Schmid-Beurmann, P., and Thangadurai, V. (2007). Structure and lithium ion conductivity of bismuth containing lithium garnets Li5La3Bi2O12 and Li6SrLa2Bi2O12. Mater. Sci. Eng. B 143 (1), 14–20. doi:10.1016/j.mseb.2007.07.009
Naqash, S., Sebold, D., Tietz, F., and Guillon, O. (2019). Microstructure–conductivity relationship of Na3Zr2(SiO4)2(PO4) ceramics. J. Am. Ceram. Soc. 102 (3), 1057–1070. doi:10.1111/jace.15988
Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., et al. (2008). Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100 (13), 136406. doi:10.1103/PhysRevLett.100.136406
Petříček, V., Dušek, M., and Palatinus, L. (2014). Crystallographic computing system JANA2006: general features. Z. für Kristallogr. - Cryst. Mater. 229 (5), 345–352. doi:10.1515/zkri-2014-1737
Ramakumar, S., Deviannapoorani, C., Dhivya, L., Shankar, L. S., and Murugan, R. (2017). Lithium garnets: synthesis, structure, Li+ conductivity, Li+ dynamics and applications. Prog. Mater. Sci. 88, 325–411. doi:10.1016/j.pmatsci.2017.04.007
Rost, C. M., Sachet, E., Borman, T., Ali, M., Dickey, E. C., Dong, H., et al. (2015). Entropy-stabilized oxides. Nat. Commun. 6 (1), 8485. doi:10.1038/ncomms9485
Samson, A. J., Hofstetter, K., Bag, S., and Thangadurai, V. (2019). A bird's-eye view of Li-stuffed garnet-type Li7La3Zr2O12 ceramic electrolytes for advanced all-solid-state Li batteries. Energy & Environ. Sci. 12 (10), 2957–2975. doi:10.1039/C9EE01548E
Sang, J., Tang, B., Pan, K., He, Y.-B., and Zhou, Z. (2023). Current status and enhancement strategies for all-solid-state lithium batteries. Accounts Mater. Res. 4, 472–483. doi:10.1021/accountsmr.2c00229
Sarkar, A., Wang, Q., Schiele, A., Reda Chellali, M., Bhattacharya, S. S., Wang, Di, et al. (2019). High-entropy oxides: fundamental aspects and electrochemical properties. Adv. Mater. 31 (26), 1806236. doi:10.1002/adma.201806236
Shao, C., Yu, Z., Liu, H., Zheng, Z., Sun, N., and Diao, C. (2017). Enhanced ionic conductivity of titanium doped Li7La3Zr2O12 solid electrolyte. Electrochimica Acta 225, 345–349. doi:10.1016/j.electacta.2016.12.140
Stockham, M. P., Dong, Bo, James, M. S., Zhu, P., Kendrick, E., and Slater, P. R. (2023). Rapid sintering of Li6.5La3Zr1Nb0.5Ce0.25Ti0.25O12 for high density lithium garnet electrolytes with current induced in-situ interfacial resistance reduction. Energy Adv. 2, 1660–1673. doi:10.1039/D3YA00123G
Stockham, M. P., Dong, Bo, and Slater, P. R. (2022a). High entropy lithium garnets – testing the compositional flexibility of the lithium garnet system. J. Solid State Chem. 308, 122944. doi:10.1016/j.jssc.2022.122944
Stockham, M. P., Griffiths, A., Dong, Bo, and Slater, P. R. (2022b). Assessing the importance of cation size in the tetragonal-cubic phase transition in lithium-garnet electrolytes. Chem. – A Eur. J. 28 (6), e202103442. doi:10.1002/chem.202103442
Ting, Y.-Y., and Kowalski, P. M. (2023). Refined DFT+U method for computation of layered oxide cathode materials. Electrochimica Acta 443, 141912. doi:10.1016/j.electacta.2023.141912
Ting, Y.-Y., Ye, R., Dashjav, E., Ma, Q., Taminato, S., Mori, D., et al. (2024). Thermodynamic and structural characterization of high-entropy garnet electrolytes for all-solid-state battery. Front. Energy Res. 12. doi:10.3389/fenrg.2024.1393914
Vanderbilt, D. (1990). Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41 (11), 7892–7895. doi:10.1103/PhysRevB.41.7892
van de Walle, A., Tiwary, P., de Jong, M., Olmsted, D. L., Asta, M., Dick, A., et al. (2013). Efficient stochastic generation of special quasirandom structures. Calphad 42, 13–18. doi:10.1016/j.calphad.2013.06.006
Wang, C., Fu, K., Kammampata, S. P., McOwen, D. W., Samson, A. J., Zhang, L., et al. (2020a). Garnet-type solid-state electrolytes: materials, interfaces, and batteries. Chem. Rev. 120 (10), 4257–4300. doi:10.1021/acs.chemrev.9b00427
Wang, C., Ping, W., Bai, Q., Cui, H., Hensleigh, R., Wang, R., et al. (2020b). A general method to synthesize and sinter bulk ceramics in seconds. Science 368 (6490), 521–526. doi:10.1126/science.aaz7681
Zhang, Yi, Zhou, C., Zhang, Q., Yin, P., Sun, X., Wang, K., et al. (2022). Change from La2Ti2O7 to LaTiO3 induced by Li2CO3 addition: higher local symmetry and particle uniformity achieved an efficient Mn4+ activated far red phosphor for agricultural cultivation. J. Luminescence 248, 119000. doi:10.1016/j.jlumin.2022.119000
Zheng, C., Lu, Y., Su, J., Song, Z., Xiu, T., Jin, J., et al. (2022). Grain boundary engineering enabled high-performance garnet-type electrolyte for lithium dendrite free lithium metal batteries. Small Methods 6 (n/a), 2200667. doi:10.1002/smtd.202200667
Zhu, J., Li, X. L., Wu, C., Gao, J., Xu, H., Li, Y., et al. (2021). A multilayer ceramic electrolyte for all-solid-state Li batteries. Angew. Chem. Int. Ed. 60 (7), 3781–3790. doi:10.1002/anie.202014265
Keywords: garnet, high entropy, solid electrolyte, ionic conductor, first-principle, DFT
Citation: Ye R, Ting Y-Y, Dashjav E, Ma Q, Taminato S, Mori D, Imanishi N, Kowalski PM, Eikerling MH, Kaghazchi P, Finsterbusch M and Guillon O (2024) Preparation and electrochemical properties of Li6La3Zr0.7Ti0.3Ta0.5Sb0.5O12 high-entropy Li-garnet solid electrolyte. Front. Energy Res. 12:1379576. doi: 10.3389/fenrg.2024.1379576
Received: 31 January 2024; Accepted: 15 May 2024;
Published: 04 June 2024.
Edited by:
Lili Han, Chinese Academy of Sciences (CAS), ChinaReviewed by:
Shreyas Pathreeker, University of Pennsylvania, United StatesCopyright © 2024 Ye, Ting, Dashjav, Ma, Taminato, Mori, Imanishi, Kowalski, Eikerling, Kaghazchi, Finsterbusch and Guillon. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ruijie Ye, ci55ZUBmei1qdWVsaWNoLmRl
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.