Charging station service scope division and real-time pricing strategy based on the strongest occupation method

With the rapid construction of charging stations (CSs), charging station operators need to enhance their core competitiveness by precisely planning their service areas and formulating reasonable and effective pricing strategies. However, the regional competition among multiple charging station operators is generally ignored. In the traditional model, the service scope of CSs appears as regular circles, which is inconsistent with the market distribution law. In response to the irregular relationship between the dynamic service scope of CSs and the real-time charging price, a charging station service scope (CSSS) model is proposed by introducing the variable service field strength (SFS). First, the competitiveness of CSs is evaluated quantitatively, and the SFS of CSs is defined to describe the service scope of CSs by the strongest occupation method. Second, the impact of the charging price on the charging demand is analyzed based on the CSSS division model. In addition, the revenue of charging station operators and the stability of the power grid are considered to establish a real-time pricing optimization model. Finally, the numerical simulation is operated in Furong District of Changsha. It is shown that the proposed method effectively achieves more profits for charging stations and decreases the average power deviation of the whole region.

1 Introduction

The electric vehicle (EV) market has experienced rapid growth since the latter half of 2020. The global sales of EVs exceeded 10 million units in 2022, and it is expected to exceed 70 million units by 2030. EVs have a penetration rate of up to 79.3% in Norway, ranking first in the world. Sweden ranks second globally, with EVs accounting for 32.1%. In addition, China ranks third in the world, with EVs accounting for 19.9% (ITF, 2022; Liu, 2022). As the public infrastructure of power supply, charging facilities play a critical role in the promotion of EVs. The China Electric Vehicle Charging Infrastructure Promotion Alliance (EVCIPA) released that the charging infrastructure increased up to 2.593 million units in 2022, increasing by 225.5% year-on-year (China News Network, 2023), which reflects the fierce competition in the charging station (CS) industry. In addition, the service scope could be expanded by various parameters, such as advanced charging piles, large contracts, and low-cost charging prices (CPs) (Liu et al., 2019; Yang et al., 2022; Zhou et al., 2023a). Thus, it is necessary to propose the precise division of service scope and reasonable pricing strategies to enhance the core competence among charging station operators.

The service scope of CSs reflects the market competitiveness of CSs directly, which is important for its operators to analyze the market situation (Chen et al., 2019a; Wang et al., 2019). However, recent works seldom discuss the service scope of CSs. Their service scope research is mainly in target with airports (Anna et al., 2019), logistics parks (Wu et al., 2016), and urban economic zones (Dai, 2018). Notably, an inevitable market competition exists among multiple CSs in the region (Li et al., 2023a), and this competition also leads to an uneven market distribution. At present, most present facility planning methods are based on the Wilson model or breaking point theory by the regularized circle or the weighted Voronoi diagram (Chen et al., 2017; Li et al., 2023b), which can only divide the market area within a fixed range. Unfortunately, the symmetrically distributed shape cannot precisely describe the service scope of CSs in terms of practical reality (Zhou et al., 2023b). Thus, a reasonable service scope of the charging station is inevitably irregular and varies with the relevant parameters. Furthermore, the Isard method, i.e., the strongest occupation method (Wilson, 1972), is used to quantify the attraction strength of CSs and further recognize the service scope in this paper.

The real-time charging price has a great influence on the charging habits of EV users (Chen et al., 2019b; Gong et al., 2020), which further affects the service scope of CSs. An effective charging pricing strategy should aim to achieve four objectives, namely, guiding EV users to charge in an orderly manner, increasing the profits of operators, improving the utilization rate of charging piles, and reducing the load peak–valley difference (Yang et al., 2021; Zhou et al., 2022). Considering the willingness of the users (CA et al., 2022; Khan et al., 2022), the demand-side response (Shinde and Shanti, 2018; Lai et al., 2023), and the complex time-varying relationship between the charging price and charging demand (Wang et al., 2021; Yang et al., 2023), various models have been proposed to formulate a real-time pricing strategy. However, the existing literature often neglects the impact of a dynamic charging price on the market division, resulting in no changes in service scope.

On the basis of the abovementioned work, this paper studies the service scope division and real-time pricing strategy of CSs based on the Isard method. First, an evaluation index system is established to quantitatively evaluate the comprehensive strength of CSs. Then, the charging station service scope (CSSS) model with the service field strength of CSs is built based on the Isard method. Second, the impact of the charging price on the charging demand is analyzed based on the initial CSSS division. Third, a dynamic charging price strategy is proposed considering the profit of the CSs and the auxiliary service of the power grid. Finally, the relationship between the charging price and the service scope is analyzed in a real-world scenario to provide reasonable pricing suggestions for CS operators. It is significant for enhancing the operational efficiency of CSs and promoting the healthy development of charging infrastructure. The contributions of this paper are as follows.

1) The CSSS division model is built to describe the dynamic service scope of CSs.

2) The impact of the charging price on the charging demand is analyzed based on the charging station service scope.

3) The real-time charging price is formulated via multi-objective optimization with the goals of increasing operator revenue and decreasing power deviation to modify the charging station service scope.

The rest of this paper is organized as follows: Section 2 defines the service field strength (SFS) and builds the CSSS division model based on the Isard method; Section 3 shows the impact of the charging price on the charging demand; Section 4 establishes a real-time pricing optimization model with multi-objectives including the power deviation rate and the operator profitability; the case study and conclusion are presented in Section 5 and 6, respectively.

2 SFS and CSSS division model based on the strongest occupation method

2.1 Comprehensive strength of CSs

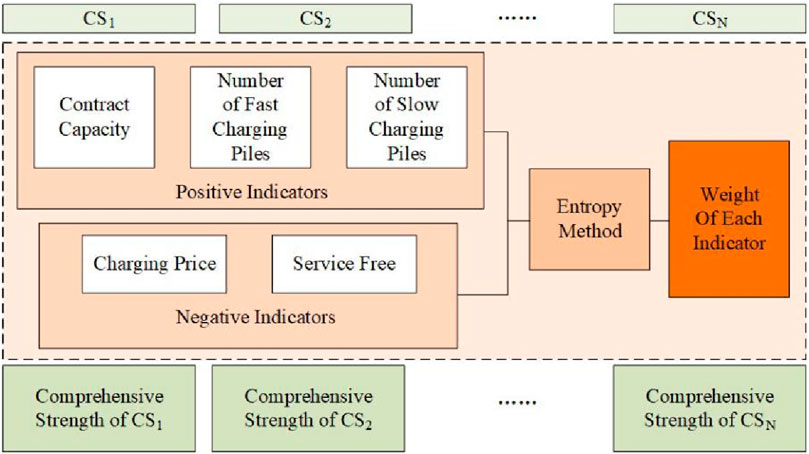
The CSSS is closely related to its comprehensive strength. The evaluation index system for the comprehensive strength of CSs is shown in Figure 1, mainly including the contract capacity of CSs, the number of fast/slow charging piles, service fees, and charging prices.

Figure 1

Figure 1. Charging station evaluation index system.

In Figure 1, the contract capacity and the number of fast/slow charging piles are positive factors. The higher the value of these factors, the stronger the comprehensive strength C_n of CSs. It also indicates a stronger attraction to the surrounding demand area, where more users are willing to go to CS_n for charging, resulting in a larger service scope S_n. Conversely, the charging price and service fees are negative factors. The higher the value, the smaller the CSSS.

The evaluation indicators are standardized by the extreme value method as follows. The positive and negative indicators are standardized, as shown in Eqs 1, 2, respectively:

$T_{n,i}=\frac{T_{n,i}-T_{\min ,i}}{T_{\max ,i}-T_{\min ,i}},(1)$

$T_{n,i}=\frac{T_{\min ,i}-T_{\mathrm{n},i}}{T_{\max ,i}-T_{\min ,i}},(2)$

where T_n.i is the original value of index i of CS_n and T_max.i and T_min.i represent the maximum and minimum values of index i, respectively.

The contribution of CS_n is calculated with index i, as shown in Eq. 3:

$p_{n,i}=\frac{T_{n,i}}{{\displaystyle \sum _{i=1}^N}{T}_{n,i}},(3)$

where p_n.i is the contribution of CS_n with index i and N is the number of CSs.

The entropy of index i is calculated as shown in Eq. 4:

$e_i=-\frac{1}{\ln N}{\displaystyle \sum _{i=1}^N}{p}_{n,i}\ln \left(p_{n,i}\right).(4)$

The evaluation index weight of CSs could be obtained as shown in Eq. 5:

${\gamma }_i=\frac{g_i}{{\displaystyle \sum _{i=1}^N}{g}_i},(5)$

$g_i=1-e_i,(6)$

where γ_i is the weight of index i and g_i and e_i are the coefficients of difference and entropy, respectively.

Then, the comprehensive strength of CS_n could be quantified as shown in Eq. 7:

$C_n={\displaystyle \sum _{i=1}^5}{c}_i{\gamma }_i\frac{T_{n.i}}{T_{\max .i}},(7)$

where C_n represents the comprehensive strength of CS_n and c_i indicates the correlation coefficient. c_i = 1 when γ_i is positive, and c_i = −1 if γ_i is negative.

2.2 Definition of SFS

The formula of the point charge field strength is obtained by Eq. 8:

$E_e=k_e\frac{q_e}{r_e^2},(8)$

where E_e represents the point charging field strength, k_e is the electrostatic force constant with the unit N·m²/C², q_e is the charge electric quantity, and r_e indicates the distance between the center and charge.

Analogous to the electrostatic field generated by a point charge, the attraction of CSs to the surrounding area will not change abruptly, in accordance with the characteristics of the typical non-rotating scattered field. According to the Helmholtz theorem, the function of the non-rotating scattered field is always inversely proportional to the distance vector R². Therefore, the SFS of the CSSS, akin to the electric field strength of a point charge, is defined to quantify the attraction strength of CSs to the surrounding charging demand areas (CDAs).

It is assumed that a certain area is divided into K small grid areas with a certain precision, which is defined as CDAs. Taking CS_n as the center, SFS E_n.k of CS_n for CDA_k is defined considerating the average distance and the comprehensive strength, which is obtained by Eq. 9:

$E_{n.k}=k_c\frac{C_n}{r_{n.k}^2},(9)$

where k_c is the service constant and r_n.k represents the distance between CS_n and CAD_k, which can be calculated by the longitude and latitude.

The Wilson model is appropriate for studying spatial interactions (Zhang et al., 2010). Thus, the charging service capacity ratio of CS_n to CDA_k can be described as shown in Eq. 10:

$T_{n.k}=K{C}_n{D}_k{e}^{-\beta r_{n.k}},(10)$

where K represents the normalization factor, describing the regional difference of the CSs and the demand area. K = 1 when the regional difference is ignored. D_k indicates the total charging demand in CDA_k. β is the attenuation factor, determining the speed of service attenuation.

Combined with the electrostatic force constant k_e, and assuming each CS has the same service constant, k_c is derived as follows:

$k_c=\frac{K{C}_{ave}{D}_{ave}{e}^{-\beta r_{ave}}{r}_{ave}^2}{C_{ave}^2},(11)$

$\beta =\sqrt{\frac{2N}{t_{\max }{S}_{ave\_n}}},(12)$

where C_ave is the average comprehensive strength of all CSs, D_ave represents the average demand of all demand areas, and r_ave is the average distance between the CSs and demand areas. Calculated using Statistical Product and Service Solutions (SPSS) software, t_max represents the number of CSs with a comprehensive score greater than 0. S_{ave_n} represents the average area of each CS served.

2.3 CSSS division model

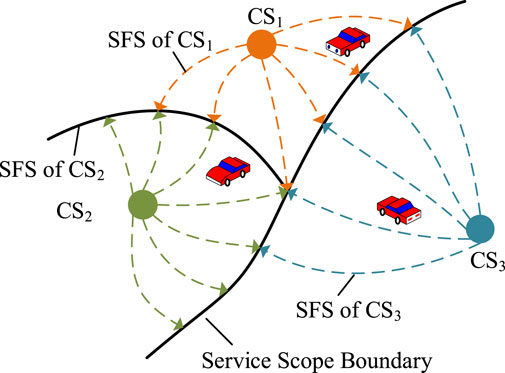
In the two-dimensional space, a facility or an enterprise is attractive to the users within a certain range of its surroundings, catering to their needs and preferences. Similarly, as the charging service provider, the CSs act as the central hub, offering charging service to electric vehicle users in their vicinity. Then, CSSS, defined as the geographical spatial distribution range of electric vehicle users who receive charging services from that CS, is usually of an irregular shape, as shown in Figure 2. Notably, the dotted line represents the SFS emitted by CSs, and the CSs are attractive to EVs at the same time.

Figure 2

Figure 2. Charging station service scope diagram.

Any CS_n will attract the CDAs, resulting in a CSSS that is constrained by the parameters of the surrounding CS and itself. According to the strongest occupation method proposed by Isard, if SFS E_n.k of CS_n to the demand area k is larger than SFS E_m.k of other CS_m, the demand area k is identified as the CSSS of CS_n, as shown in Eq. 13:

$S_n=\left\{S\left|E_{n.k}\ge E_{m.k},m=1,...,N\left(m\ne n\right)\right.\right\},(13)$

where S_n represents the CSSS of CS_n and the demand area k is defined as the market demand area. Eq. 13 indicates that among all CSs, CS_n has the greatest attraction to the demand area k, and the demand area k belongs to the CSSS of CS_n.

3 CSSS-based charging demand

The initial CSSS $S*=\left(S{*}_1,S{*}_2,\dots ,S{*}_{\mathrm{N}}\right)$ is obtained from Eq. 13. Ignoring the difference between areas, the initial charging demand proportion is determined by the CSSS. In addition, the initial charging demand proportion is shown in Eq. 14.

${\lambda }_{n.t}=\frac{S_n^{*}}{{\displaystyle \sum _{n=1}^N}{S}_n^{*}}.(14)$

The charging demand of CS_n is jointly affected by its own charging price and the price of other CSs, as shown in Eq. 15. The charging demand is a negative correlation function of its own price. As the charging price increases, the charging demand for CS_n decreases and shifts to other CSs in the area, which results in the CSSS reduction in CS_n and the CSSS increase in other CSs.

$q_{n.t}={\lambda }_{n.t}{q}_{ev.t}-k_{p.n}\left(\frac{P_{n.t}-P_{r.t}}{P_{r.t}}\right)+k_{av.n}\frac{\left({\displaystyle \sum _{\begin{array}{l}m=1\\ m\ne n\end{array}}^{N-1}}{C}_m^{*}{P}_{m.t}\right)-P_{r.t}}{P_{r.t}},(15)$

where $q_{ev.t}$ represents the predicted value of the day-ahead charging load at time t. k_p.n is the influence parameter of the policy price difference between the CS price and policy price on the charging demand. In addition, k_av.n indicates the influence parameter of the charging price difference between CS_n and other CSs. P_n,t represents the charging price of CS_n at time t, and P_r.t represents the policy electricity price at time t, satisfying the peak–valley–flat electricity price. C_m* is the ratio of the comprehensive strength of CS_m to the sum of all CSs.

The income of CSs in a day is shown in Eq. 16.

$E_n={\displaystyle \sum _{t=1}^{96}}{P}_{n.t}\cdot q_{n,t},(16)$

where E_n is the income of CS_n in a day.

The proof of the existence and uniqueness of the Nash equilibrium of the proposed model is given in Appendix A.

4 CSSS-based real-time pricing optimization model

4.1 Pricing optimization model

In a scenario of a perfectly competitive market, it is assumed there are N CSs with different sizes, which belong to H different operators, H ≤ N. All charging loads are evenly distributed throughout the area; users will only choose one of the N CSs to charge when needed.

A multi-objective real-time pricing model is established considering the profit rate and power deviation rate. The objective is optimized by maximizing the total profit rate of all CSs and minimizing the power deviation rate, as shown in Eq. 17.

$\max E=\max \left({\omega }_n{E}_{p\_lr}+{\omega }_{bc}{E}_{p\_pc}\right),(17)$

$E_{p\_lr}={\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{n=1}^N}\frac{P_{n.t}-\left(P_e+P_{n.w}\right)}{P_{r.t}},(18)$

$E_{p\_pc}={\displaystyle \sum _{t=1}^T}\frac{\Delta P_t-\left({\displaystyle \sum _{n=1}^N}{q}_{n.t}-q_{ev.t}\right)}{\Delta P_t},(\mathrm{19a})$

$\Delta P_t=P_{W.t}+P_{L.t}-P_{w.t}-P_{l.t},(\mathrm{20a})$

where E_{p_lr} and E_{p_pc} represent the profit rates of the CS and the reduced power deviation rate, respectively. ω_n and ω_ab represent the weights of the above two, respectively. P_e and P_n.w are the electricity purchasing cost and the operation and maintenance cost of the CS, respectively. ΔP_t is the power deviation between the real-time output of renewable energy and the day-ahead forecast. P_W.t and P_w.t are the real-time and day-ahead wind power output, respectively. P_L.t and P_l.t are the real-time and day-ahead photovoltaic outputs, respectively. If ΔP_t >0, indicating that the real-time output of wind power and photovoltaic at time t is greater than the predicted output, it is necessary to guide users to charge and increase the charging load to absorb the excess wind and photovoltaic power. Otherwise, if ΔP_t <0, indicating that the real-time output of wind and photovoltaic power at time t is less than the day-ahead predicted output, users need to be encouraged to reduce the charging load.

The constraints of optimization model are as follows:

Market demand constraint

$0<q_{n.t}<q_{ev.t}.(21)$

Eq. 21 implies that the charging demand of the CS does not exceed the predicted charging load.

Charging load constraint

${\xi }_l{q}_{ev.t}\le {\displaystyle \sum _{n=1}^N}{q}_{n.t}\le {\xi }_h{q}_{ev.t},(\mathrm{19b})$

where ξ_l and ξ_h represent the lower and upper limit coefficients, respectively, which means that the sum of the charging demand should not exceed a certain range of the day-ahead charging load.

Charging price constraint

$P_{r.n}\left(1-{\phi }_l\right)\le P_{n.t}\le P_{r.n}\left(1+{\phi }_h\right),(\mathrm{20b})$

where φ_l and φ_h represent lower and upper limits of the charging price, respectively.

4.2 Relationship between CSSS and real-time pricing

The basic idea of a real-time pricing optimization model based on CSSS is shown in Figure 3. First, the initial CSSS was obtained by the strongest occupation method. Then, based on the pricing optimization model, the charging station operator obtains the real-time charging price of charging stations, which affects the initial CSSS, and further develops into the real-time CSSS.

Figure 3

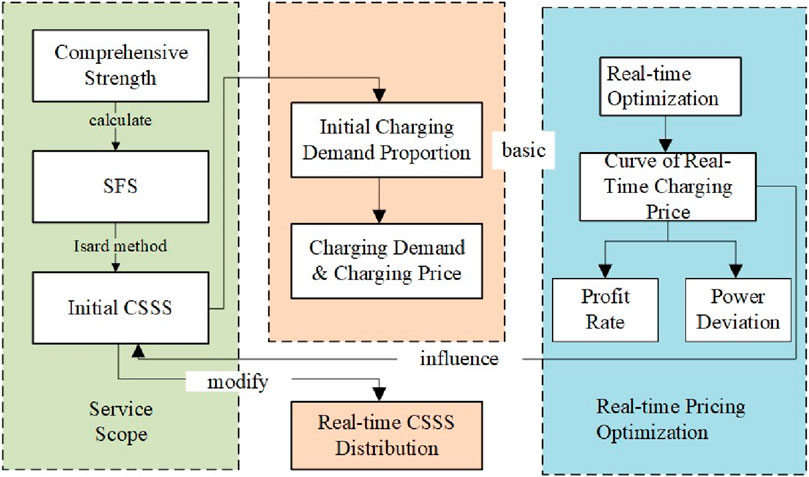
Figure 3. Real-time pricing optimization model based on charging station service scope (CSSS) and solution flowchart.

The detailed steps of real-time pricing optimization based on CSSS are designed as follows:

Step 1: The CSSS is calculated

1) Based on the basic data on CSs and the day-ahead wind power and photovoltaic predicted data, the weight of each index was calculated according to the entropy method, and the real-time output data of wind power and photovoltaic were obtained by adding the power deviation.

2) The comprehensive strength of CSs was quantitatively evaluated according to Eq. 7, and then SFS E_n.k of each CS was calculated according to Eq. 9.

3) According to Eq. 13, the initial CSSS S*_n based on the strongest occupation method proposed by Isard was obtained.

4) The initial charging demand proportion λ was calculated, as shown in Eq. 14.

5) The relationship between the charging price and charging demand was established, and the CS income model was built, as shown in Eqs 15, 16.

Step 2: The real-time price is optimized

1) The multi-objective real-time pricing model with the profit rate and power deviation was built.

2) A day was divided into 96 time points at a resolution of 15 min, taking 1 h as the operation cycle and optimizing the pricing model using CPLEX. Then, the dynamic charging price of CSs at 96 time points, as well as the optimized profit rate and power deviation rate of each CS, was obtained.

3) With the real-time change in the dynamic charging price, the comprehensive strength and the SFS of the CS will also change. Finally, the real-time dynamic CSSS at each time was simulated and obtained

5 Case study

5.1 Basic data

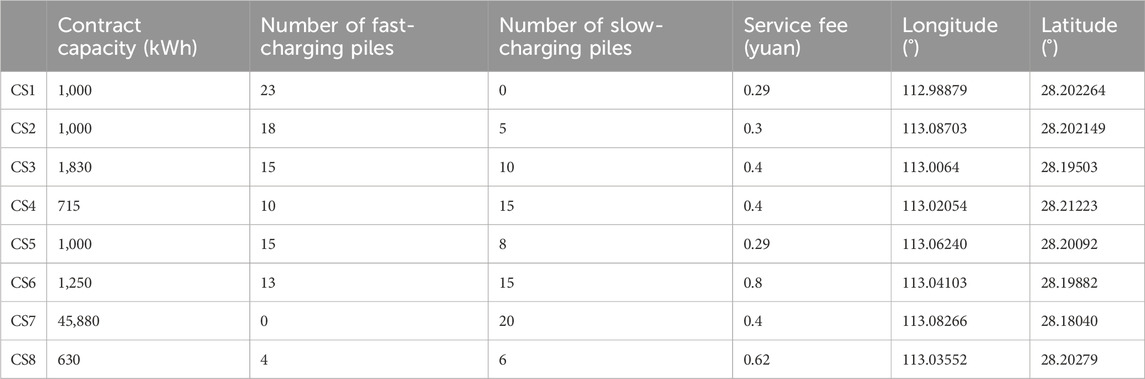
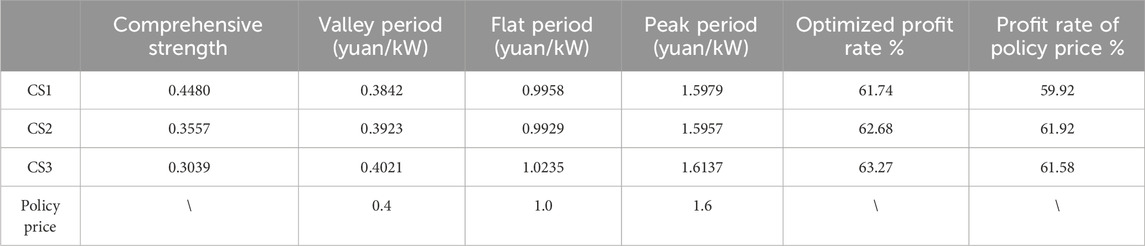
Furong District in Changsha is taken as an example for simulation, and the data on CSs are all obtained from Hunan Economic and Technological Research Institute of the State Grid. Notably, the output data of wind power and photovoltaic are for the total province. First, the map of Furong District is divided into 16,288 market areas with latitude and longitude accuracy of 0.0005 using ArcGIS drawing software. Then, the first three representative CSs are selected from Furong District for calculation as examples. The basic data of these three CSs are shown in Table 1. Based on the evaluation index system, the weight of each index of the CS is obtained by the entropy method. The weight of the contract capacity, the number of fast/slow-charging piles, the service fee, and the charging price are 0.221, 0.486, 0.201, 0.051, and 0.041 yuan/kWh, respectively. Afterward, SPSS is employed for the factor analysis. A total of 143 CSs have a comprehensive score greater than 0.

Table 1

Table 1. Basic data on charging stations (CSs).

For the load of the three charging stations q_1,t, q_2,t, and q_3,t, its boundary is given by setting ξ_l = 0.8 and ξ_h = 1.2 in Eq. 19a and φ_l = φ_h = 0.1 in Eq. 20a. In addition, according to the related policy issued by the Comprehensive Department of the National Energy Administration, the electricity purchasing price in Hunan Province is 0.46244 yuan/kWh. The daily maintenance cost of each CS is P_1.w = 600 yuan, P_2.w = 550 yuan, and P_3.w = 500 yuan. Based on the project data, the day-ahead wind power and photovoltaic output data of a typical day are shown in Supplementary Figure AB1. It is assumed that the wind power and photovoltaic prediction error is 10%, and the real-time output meets the normal distribution.

5.2 Analysis of the charging price

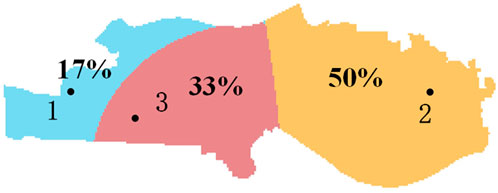
Without considering the interaction of the charging price, the initial CSSS and occupancy of each CS are calculated based on the strongest occupation method, as shown in Figure 4.

Figure 4

Figure 4. Initial service scope of three charging stations.

As shown in Figure 4, the CSSS of CS₂ is the largest without considering the influence of the charging price. It is noted that CS₂ has the largest number of fast charging piles, and also, no other competing CS is present in the surrounding area. Thus, its CSSS occupies half of Furong District. As shown in Table 2, the comprehensive strength of CS₁ is the strongest. However, due to the remote location and the competition from CS₃, the CSSS of CS₁ only occupied 17% of the market share and is smallest among the three CSs. In addition, from the shape of the CSSS of CS₁ and CS₃, the boundary presents an inward curved arc, which indicates that the further away from the two CSs, the more area belongs to CS₁. That is, compared to CS₃, the distance from one point to CS₁ is larger, but it is still attracted by CS₁. Therefore, it can be concluded that the SFS of CS₁ is greater than that of CS₃. The average peak–valley–flat charging price of CSs is then calculated by the real-time pricing optimization model mentioned in Section 4, as shown in Table 2.

Table 2

Table 2. Comprehensive strength and average charging price of three charging stations (CSs).

Table 2 shows that the charging prices of CS₁ and CS₂ are lower than the policy price, while the charging price of CS₃ is higher than the policy price. Due to the higher comprehensive strength of CS₁ and CS₂, the electric vehicle users will pay more attention and be more sensitive to price changes. Accordingly, the influence parameter of the policy price difference k_p.n in Eq. 16 is also larger, indicating that charging prices can increase the charging demand and profit if they are lower than the policy price. In comparison, the comprehensive strength of CS₃ is the smallest, and users pay the least attention to its price change. Thus, CS₃ will maintain its income by setting a higher price than the policy price, increasing by 0.0137 yuan/kWh during the peak period and 0.0235 yuan/kWh during the flat period.

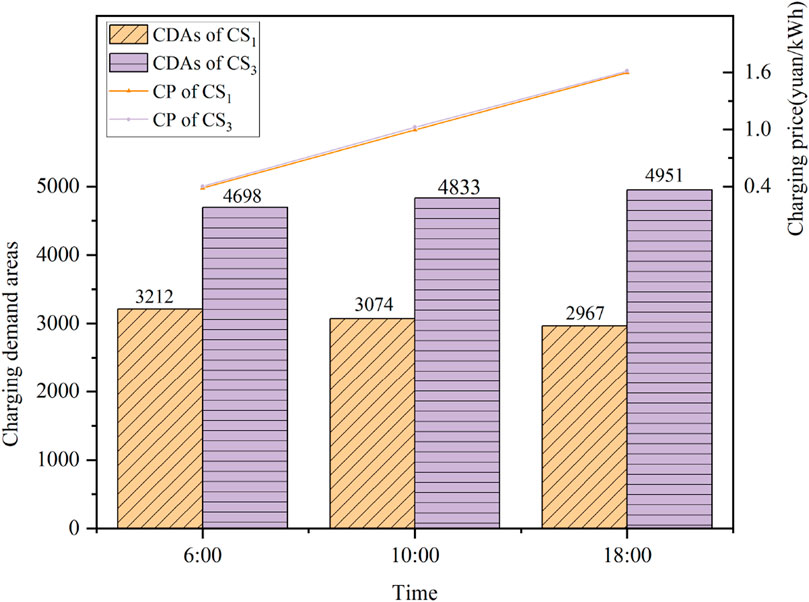
Then, the change in CDAs is analyzed for the peak, valley, and flat periods, and three time points of 6:00, 10:00, and 18:00 are selected. The number of CDAs occupied by each CS at these time points is shown in Supplementary Figure AB2. It is observed that there is no significant change in the CSSS of CS₂ due to the small competitive pressure. On the contrary, the CSSS changed with the charging price mainly for CS₁ and CS₃. Therefore, the CSSS changes for CS₁ and CS₃ are discussed as primary. The number of CDAs occupied by CS₁ and CS₃ and their CP changes are shown in Figure 5.

Figure 5

Figure 5. Number of charging demand areas and charging price of three charging stations.

Afterward, the real-time charging price is taken into consideration. Since charge station 1 has a higher comprehensive strength and a small charging price difference of 0.02 yuan, the market share increases from 17% in Figure 4 to 20% (the number of CDAs is 3,212 at 6:00). Correspondingly, CS₃, which is closer to CS₁, lost part of its CSSS due to its smaller comprehensive strength, and its market share decreased from 33% to 29%.

With the increase in the charging price, the number of CDAs occupied by CS₁ decreased by 245 from 6:00 to 18:00. At the same time, the number of CDAs occupied by CS₃ increased by 253. This can be attributed to the fact that CS₁ has stronger comprehensive strength, and users are more responsive to its charging price changes. Thus, as the charging price of charge station 1 increases, the number of users of CS₁ decreases faster than those of CS₃, resulting in a more significant change in the CSSS of CS₁.

It can be seen that the charging price and CSSS are affected by many factors, such as comprehensive strength, geographical location, and number of competitors around.

5.3 Analysis of the number of charging stations

The impacts of the number of CSs on the CSSS, power deviation rate, and profit margin are analyzed to verify the relevant conclusions given in Section 5.2. Taking five CSs and eight CSs as examples, the data of CSs are shown in Table 1.

5.3.1 Analysis of five CSs

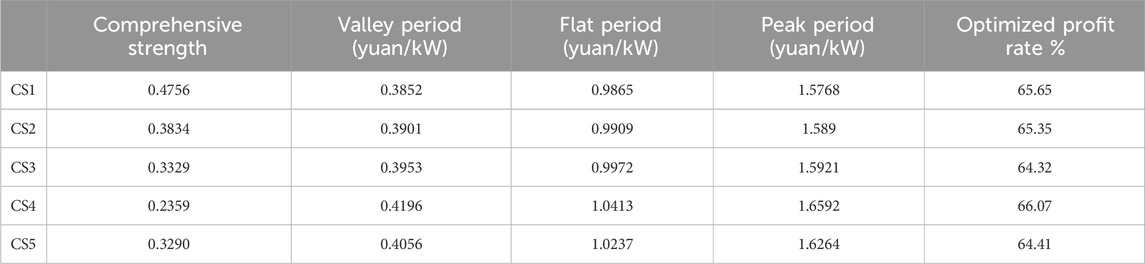
Without considering the interaction of the real-time charging price, the initial CSSS and the market share of five CSs are shown in Figure 6. It was notes that the density of CSs in the western region is relatively high. CS₁, CS₃, and CS₄, due to their close distribution and fierce market competition, have a limited CSSS, and their market share is 13.8%, 14.4%, and 14%, respectively. However, only CS₂ and CS₅ exist in the eastern region, and they are located far from the CSs in the west, resulting in less competition. Therefore, the CSSS of CS₂ and CS₅ is relatively large, and their market share is 22.2% and 35.6%, respectively.

Figure 6

Figure 6. Initial service scope of five charging stations.

The charging price and comprehensive strength of five CSs are calculated and shown in Table 3. It is found that CS₄, with smaller comprehensive strength, has higher charging prices than the other CSs in each period. It can gain more profits by setting a higher charging price than the policy price. However, with higher comprehensive strength, CS₁ and CS₂ can obtain more charging demand and profit with a lower charging price.

Table 3

Table 3. Comprehensive strength and average charging price of five charging stations (CSs).

Similarly, three time points of 6:00, 10:00, and 18:00 are selected for simulation, and the number of CDAs occupied by each CS is shown in Figure 7. It is observed that the CSSS of CS₃ increases 89 CDAs and the CSSS of CS₄ decreases 207 CDAs with the increase in the charging price. The reason for such a great change is that CS₃ and CS₄ have weak comprehensive strength, and they are in the center of a region surrounded by many CSs.

Figure 7

Figure 7. Number of charging demand areas and charging price of five charging stations.

5.3.2 Analysis of eight CSs

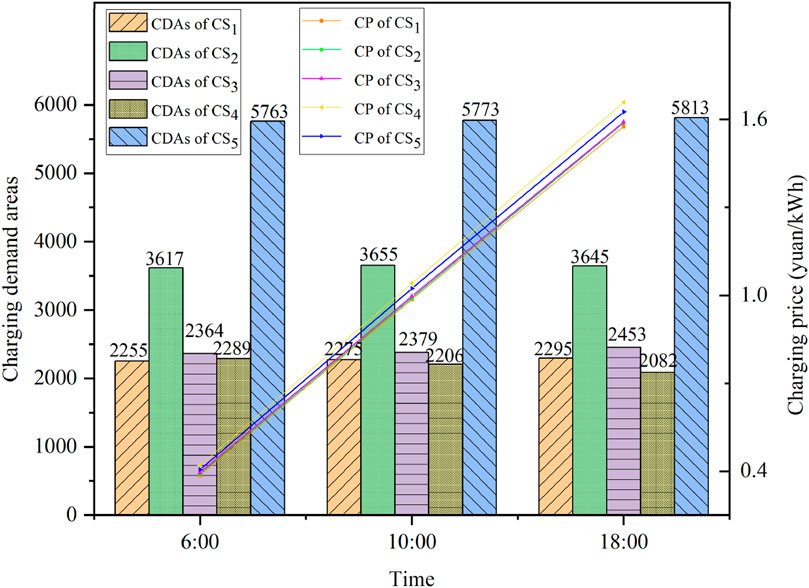
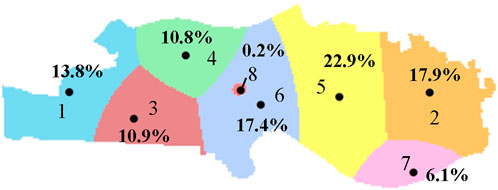
The initial CSSS of eight CSs is calculated, as shown in Figure 8. It can be seen that, interestingly, due to the strong comprehensive strength and the remote location, the market share of the CS₁ is unchanged compared to the condition of the five charging stations. However, CS₈ has the smallest comprehensive strength and is close to the other CSs, making the CDAs less competitive than other CSs, resulting in a very small CSSS, and its market share is only 0.2%.

Figure 8

Figure 8. Initial service scope of eight charging stations.

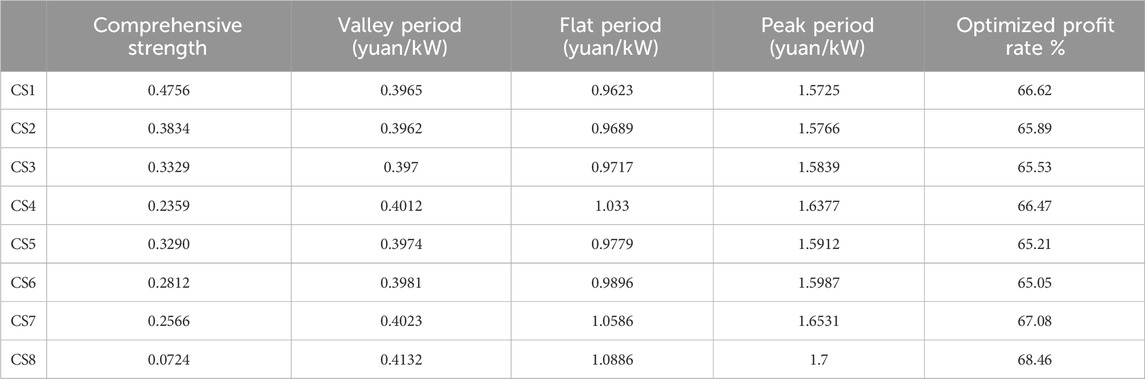
The charging price and comprehensive strength of eight CSs are shown in Table 4. Due to higher user attention, CSs with larger comprehensive strength have lower real-time charging prices than policy electricity prices. However, CSs with smaller comprehensive strength will set higher real-time charging prices to ensure profits.

Table 4

Table 4. Comprehensive strength and average charging price of eight charging stations (CSs).

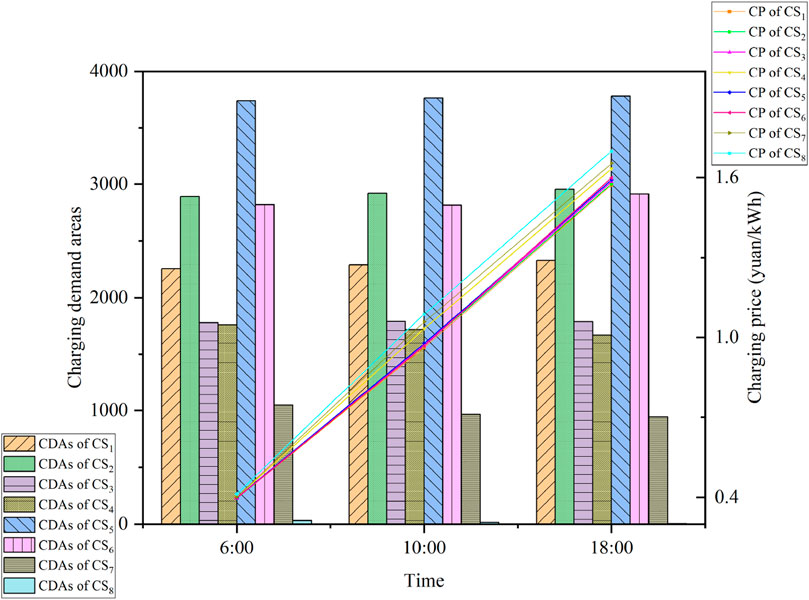
The number of CDAs occupied by eight CSs is shown in Figure 9. With the increase in the number of CSs, market competition becomes increasingly fierce. Furthermore, the reduction in the distance between stations results in little difference in the CSSS, and CS₅, with the largest CSSS, does not account for more than 4,000 CDAs. Meanwhile, due to the weak market competitiveness of CS₇ and CS₈, the CDAs of CS₂, CS₅, and CS₆ account for more than half (58%). Compared to the scenario of five CSs, due to the addition of CS₆, the number of CDAs of CS₃ and CS₄ has decreased, while CS₁, with the strongest market competitiveness, has not been affected, and the CSSS has not changed. With the increase in the charging price, it is observed that the CSSS of CS₄, CS₇, and CS₈ decreased due to the weak market competitiveness, and the CSSS of CS₁, CS₂, and CS₅ increased due to the strong market competitiveness. In addition, the insignificant change in CSSS of CS₃ and CS₄ is mainly because they are in the center of a region surrounded by other CSs.

Figure 9

Figure 9. Number of charging demand areas and charging price of eight charging stations.

Table 5 presents the profit rate and power deviation rate of different CSs. It is noted that the profits obtained by the policy electricity price will decrease gradually with the increase in competitive CSs. Furthermore, when the number of CSs involved in real-time pricing optimization increases from 3 to 5 and 8, the profit margin increases by 2.60% and 4.05%, respectively; meanwhile, the power deviation decreases by 764 kW and 1,309 kW, respectively. That is because the increase in CSs expands the optimize adjustment space. Consequently, the total charging demand participating in optimization increases, and the profit distribution between CSs becomes more reasonable, which improves the CS profit rate significantly and reduces the power deviation of wind and photovoltaic power. However, for this case, the adjustment effect of power deviation is not obvious for all of Hunan Province because of the small number of CSs.

Table 5

Table 5. Profit rate and power deviation rate of different charging stations (CSs).

6 Conclusion

A dynamic CSSS division model is proposed based on the strongest occupation method and pricing strategy in this paper. Notably, the variation in the CSSS is well simulated by the dynamic optimization of the charging price. Then, the relationship among the comprehensive strength, the charging price, and the charging demand is well reflected. Furong District of Changsha is simulated as an example, and the following conclusions are obtained:

1) Charging stations with greater comprehensive strength attract more attention from electric vehicle users, and users are more sensitive to the fluctuation of their charging price. Therefore, the charging station can obtain more profits by setting a lower charging price than the policy price.

2) The competition is more intense for areas with dense charging stations, and the CSSS change caused by charging price fluctuation is also more obvious. On the contrary, the CSSS is more stable with sparse charging stations, and the charging price fluctuation has less impact on the CSSS. It provides a reference for the construction of future charging facilities for operators.

3) With the increase in charging stations participating in the market competition, the profit based on the policy price will gradually decrease. Thus, the profit of charging stations should be improved by setting a real-time charging price based on the CSSS.

It should also be pointed out that the CSSS model should comprehensively consider the influence of regional differences, such as traffic conditions and geographic information, to improve the accuracy and authenticity of simulation results. Thus, the establishment of a complete CSSS model with the regional evaluation index system will be the next topic in future research.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

XY: Formal analysis, Writing–original draft. XT: Methodology, Writing–review and editing. YC: Validation, Writing–review and editing. JW: Data curation, Software, and Writing–original draft. YT: Visualization and writing–review and editing

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the National Natural Science Foundation of China (grant numbers 52277076 and 52307081). Hunan Provincial Nature Science General Project (grant number S2024JJMSXM1107). Excellent Youth Program of Hunan Provincial Department of Education (grant number 23B0334)

Conflict of interest

Author YT was employed by State Grid Hunan Electric Power Company Limited.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1378016/full#supplementary-material

References

Anna, B., Maurizio, C., and Davide, V. (2019). Scale and (quasi) scope economies in airport technology. An application to UK airports. Transp. Res. Part A Policy and Pract. 125 (C), 150–164. doi:10.1016/j.tra.2019.05.013

CrossRef Full Text | Google Scholar

Ca, M. M., Grzanic, M., Pavic, I., Pandžić, H., and Capuder, T. (2022). The effects of household automation and dynamic electricity pricing on consumers and suppliers. Sustain. Energy, Grids Netw. 32, 100931. doi:10.1016/j.segan.2022.100931

CrossRef Full Text | Google Scholar

Chen, C. S., Xiao, L. L., Duan, S. X., and Chen, J. (2019a). Cooperative optimization of electric vehicles in microgrids considering across- time- and- space energy transmission. IEEE Trans. Industrial Electron. 66 (2), 1532–1542. doi:10.1109/tie.2017.2784410

CrossRef Full Text | Google Scholar

Chen, J., Huang, X. Q., Tian, S. M., Cao, Y., Huang, B., Luo, X., et al. (2019b). Electric vehicle charging schedule considering user's charging selection from economics. IET Generation, Transm. Distribution 13 (15), 3388–3396. doi:10.1049/iet-gtd.2019.0154

CrossRef Full Text | Google Scholar

Chen, Y. T., Zeng, X. Z., and Wang, J. X. (2017). Airport service scope research based on improved Wilson model. J. East China Jiaot. Univ. 34 (05), 56–64. doi:10.16749/j.cnki.jecjtu.2017.05.009

CrossRef Full Text | Google Scholar

China News Network (2023). China electric vehicle charging infrastructure promotion alliance: rapid growth of China's charging infrastructure. http://www.ce.cn/xwzx/gnsz/gdxw/202301/12/t20230112_38343857.shtml.

Google Scholar

Dai, D. (2018). Selection of central cities and influence area of Yangzi River city cluster based on gravitational model. Sci. Technol. Perspect. (28), 290–292.

Google Scholar

Gong, L. L., Cao, W., Liu, K. L., and Zhao, J. (2020). Optimal charging strategy for electric vehicles in residential charging station under dynamic spike pricing policy. Sustain. Cities Soc. 63 (0), 102474. doi:10.1016/j.scs.2020.102474

CrossRef Full Text | Google Scholar

ITF Comprehensive electrification and global cooperation under the vision of carbon neutrality. World new energy vehicle congress, Hainan and virtual, August, 2022, 2022,

Google Scholar

Khan, K., Sayed, I. E., and Arboleya, P. (2022). Multi-issue negotiation evs charging mechanism in highly congested distribution networks. IEEE Trans. Veh. Technol. 71 (6), 5743–5754. doi:10.1109/tvt.2022.3175266

CrossRef Full Text | Google Scholar

Lai, S. Y., Qiu, J., Tao, Y. C., and Zhao, J. (2023). Pricing for electric vehicle charging stations based on the responsiveness of demand. IEEE Trans. Smart Grid 14 (1), 530–544. doi:10.1109/tsg.2022.3188832

CrossRef Full Text | Google Scholar

Li, Y. B., Wang, J. N., Wang, W. Y., and Liu, C. (2023a). Dynamic pricing based electric vehicle charging station location strategy using reinforcement learning. Energy 281, 128284. doi:10.1016/j.energy.2023.128284

CrossRef Full Text | Google Scholar

Li, Z., Liu, L., Ding, L., Wang, J. Y., Zhang, S. H., Chen, X. X., et al. (2023b). Scenario-based charging infrastructure planning based on tyson' s multilateral graph. Power Syst. Clean Energy 39 (3), 131–135.

Google Scholar

Liu, H. C. (2022). World new energy vehicle conference: faster, farther, and smarter. Product. Reliab. Rep. 2022, 08. (in Chinese).

Google Scholar

Liu, S. Q., Cui, W., and Zhang, L. (2019). Research on enterprise bidding mode selection and control strategy. Clust. Comput. 22 (6), 14269–14276. doi:10.1007/s10586-018-2285-x

CrossRef Full Text | Google Scholar

Shinde, P., and Shanti, S. K. (2018). Stackelberg game-based demand response in multiple utility environments for electric vehicle charging. IET Electr. Syst. Transp. 8 (3), 167–174. doi:10.1049/iet-est.2017.0046

CrossRef Full Text | Google Scholar

Wang, J. Y., Bharati, G. R., Paudyal, S., Ceylan, O., Bhattarai, B. P., and Myers, K. S. (2019). Coordinated electric vehicle charging with reactive power support to distribution grids. IEEE Trans. Industrial Electron. 15 (1), 54–63. doi:10.1109/tii.2018.2829710

CrossRef Full Text | Google Scholar

Wang, S. Y., Bi, S. Z., and Zhang, Y. J. (2021). Reinforcement learning for real-time pricing and scheduling control in ev charging stations. IEEE Trans. Industrial Inf. 17 (2), 849–859. doi:10.1109/tii.2019.2950809

CrossRef Full Text | Google Scholar

Wilson, A. G. (1972). Entropy in urban and regional modeling [J]. Economic Geography 48 (4), 364–394.

Google Scholar

Wu, J. Q., He, R., Li, X., and Gao, T. (2016). Research on the radiation range of logistics park based on improved breakpoint model. Logist. Eng. Manag. 38 (11), 13–16+31.

Google Scholar

Yang, H. R., Xu, Y. L., and Guo, Q. L. (2023). Dynamic incentive pricing on charging stations for real-time congestion management in distribution network: an adaptive model-based safe deep reinforcement learning method. IEEE Transaction Sustain. Energy 10, 1–13. doi:10.1109/tste.2023.3327986

CrossRef Full Text | Google Scholar

Yang, X. L., Niu, D. X., Sun, L. J., Ji, Z., Zhou, J., Wang, K., et al. (2021). A bi-level optimization model for electric vehicle charging strategy based on regional grid load following. J. Clean. Prod. 325, 129313. doi:10.1016/j.jclepro.2021.129313

CrossRef Full Text | Google Scholar

Yang, X. Y., Guo, X. P., Li, Y., and Yang, K. (2022). The sequential construction research of regional public electric vehicle charging facilities based on data-driven analysis—empirical analysis of Shanxi Province. J. Clean. Prod. 380 (1), 134948. doi:10.1016/j.jclepro.2022.134948

CrossRef Full Text | Google Scholar

Zhang, X. M., Hong, R. Y., Wang, R. J., and Wei, N. (2010). Research on the service capacity of regional logistics parks based on Wilson model. Logist. Technol. 29 (Z1), 41–43.

Google Scholar

Zhou, Z., Liu, Z. T., Su, H., and Zhang, L. (2023a). Planning of static and dynamic charging facilities for electric vehicles in electrified transportation networks. Energy 263, 126073. doi:10.1016/j.energy.2022.126073

CrossRef Full Text | Google Scholar

Zhou, Z., Liu, Z. T., Su, H. Y., and Zhang, L. (2022). Integrated pricing strategy for coordinating load levels in coupled power and transportation networks. Appl. Energy 307, 118100. doi:10.1016/j.apenergy.2021.118100

CrossRef Full Text | Google Scholar

Zhou, Z., Liu, Z. T., Su, H. Y., and Zhang, L. (2023b). Planning of static and dynamic charging facilities for electric vehicles in electrified transportation networks. Energy 263, 126073. doi:10.1016/j.energy.2022.126073

CrossRef Full Text | Google Scholar