Decentralized control strategy of thermostatically controlled loads considering the energy efficiency ratio and measurement error correction

The elimination of traditional thermal generators and the increase of renewable energy source access reduced the inertia of the power system, and thermostatically controlled loads have the potential to provide ancillary services to the power system. This paper introduces a decentralized control strategy for thermostatically controlled loads (TCLs), which focuses on assisting large-scale TCLs in providing frequency support to power systems while considering energy efficiency ratio and measurement error correction. Initially, the nonlinear relationship between heat flow and TCLs’ power is modeled using a polynomial relationship, and the coefficients are determined through a data-driven method to enhance accuracy in TCLs modeling and assess their regulation potential precisely. Subsequently, a decentralized control strategy tailored for power system frequency regulation is developed. To account for measurement errors in TCLs controllers, a measurement error back-correction method is proposed. Simulation examples demonstrate the effectiveness of the proposed control strategy in achieving accurate modeling and control of TCLs and reducing power system frequency fluctuations.

1 Introduction

The elimination of traditional thermal generators and the increase in renewable energy source access reduced the inertia of the power system, resulting in power systems that are more prone to frequency fluctuations (Liang et al., 2022). Scholars usually discuss solutions to this problem from a supply side perspective (Saxena et al., 2021; Kumari et al., 2023). However, as demand-side controllability continues to improve, it is becoming feasible to use demand-side resources to provide ancillary services to the power system (Kumar et al., 2023). The demand side contains a large number of controllable resources, and these controllable resources can provide support for maintaining the stable operation of the power system through reasonable control (Schmitt et al., 2023). Therefore, it is of great significance to study the control problem of demand-side resources.

Thermostatically controlled loads (TCLs), such as air conditioners, refrigerators, and electric water heaters, account for a significant proportion of residential loads. Buildings are reported to consume more than 70% of electricity in the United States, with TCLs being the primary load (Fu et al., 2022). TCLs are well-suited to participate in demand response because of their inherent thermal inertia. Changing the operating state of the load in a short period of time will not significantly reduce the comfort of the user (Franceschelli et al., 2021). TCLs can be further categorized into switching TCLs and continuously controllable TCLs according to their operating characteristics (Hu et al., 2017; Wang et al., 2020). Switching TCLs have only limited power states, i.e., standby power and rated power. On the other hand, the operating power of continuously adjustable TCLs can be freely adjusted between standby power and rated power and thus has higher flexibility. In recent years, the rapid development of power electronics technology has greatly contributed to the popularization of continuously controllable TCLs, so the study of control strategies for power continuously controllable TCLs has a broader prospect.

The individual capacity of TCLs is usually small, and only after a certain number of TCLs are aggregated to form a TCL aggregator does it have the ability to provide frequency support to the power system (Wang et al., 2022). Some scholars have already studied the control strategy of the TCL aggregator (Bao et al., 2023; Jiang et al., 2023; Khan et al., 2023). In terms of communication methods, the existing TCL aggregator control strategies can be divided into centralized control, distributed control, and decentralized control strategies. For the centralized control strategy, Coffman et al. (2023b) proposed an aggregated flexibility capacity evaluation and dispatch method for TCLs while considering cycling constraints. Liu et al. (2021b) designed an optimal control strategy for TCLs that allows TCLs to provide frequency support to the power system. Xie et al. (2022) introduced an aggregated modeling and control scheme for central air conditioning clusters. For the distributed control strategy, Wang et al. (2020) considered optimal control parameter selection while designing a distributed control strategy for TCLs. Wang et al. (2019) investigated the convergence time of the control strategy and designed a distributed finite-time control strategy for TCLs. Wan et al. (2021) considered cyber-attacks in communication and designed an event-triggered control strategy that reduces the consumption of communication resources. In addition, Li et al. (2022) took into account fair scheduling of users when designing control strategies.

However, for both centralized and distributed control, the existence of communication delay can deteriorate the control effect of TCLs (Siu et al., 2022). In contrast, the decentralized control strategy only needs to obtain the local information of TCLs when calculating control commands without additional communication, which can effectively reduce the negative impact of communication delay (Gong et al., 2022). Therefore, when controlling large-scale TCLs, it may be more appropriate to choose decentralized control strategies (Dong et al., 2023). From a game-theoretic point of view, Ding et al. (2021) investigated the possibility of TCLs in assisting the power system in smoothing the tie-line power. Coffman et al. (2023a) further proposed a unified coordination framework for TCLs. Nevertheless, limited by the cost of the terminal controller, the use of decentralized control also faces the problem of insufficient measurement accuracy. Therefore, when applying decentralized control strategies to control the TCL aggregator, it is still necessary to introduce suitable measurement error correction methods (Hongxun et al., 2019).

In addition, when designing the control strategy for TCLs, for determining the power adjustable range of TCLs, it is essential to accurately model the dynamics between the internal temperature of TCLs and the operating power. The most commonly used model for analyzing the internal temperature variation of TCLs is the equivalent thermal parameter model (Liu et al., 2021a; Franceschelli et al., 2021). However, the original equivalent thermal parameter model describes the relationship between heat flow and internal temperature, while the actual physical quantity relevant to the power system is power. Therefore, further analysis of the relationship between heat flow and operating power is required. Wang et al. (2020) assumed that the ratio of power and heat flow is constant, i.e., the energy efficiency ratio does not change with the change in operating power. However, this assumption is not applicable to continuously controllable TCLs. To this end, Jiang et al. (2021) described the relationship between power and heat flow rate in terms of a linear relationship, which improves the model accuracy to some extent.

This paper proposes use of a decentralized control strategy for continuously controllable TCLs that simultaneously considers the energy efficiency ratio and measurement error correction, thus assisting large-scale continuously controllable TCLs in providing frequency support to the power system. First, the relationship between heat flow and power is modeled as a polynomial relationship, and the polynomial coefficients are fitted using a data-driven method to improve the accuracy of TCL modeling, which in turn achieves an accurate assessment of the regulation potential of the TCL. After that, this paper designs a decentralized control strategy for TCLs in power system frequency regulation. Moreover, considering the frequency measurement error, a measurement error back-correction method is proposed to improve the accuracy of TCL control. Simulations show that the proposed control strategy can realize accurate control of TCLs and effectively reduce the frequency fluctuation of the power system under the consideration of the energy efficiency ratio and measurement error correction.

2 Modeling of TCLs

The internal temperature variation of TCLs under the effect of indoor and outdoor cooling and heating sources can be described by a first-order equivalent thermal parameter model in the form of differential equations shown in Eq. 1.

$\frac{d{T}_{\text{in}}\left(t\right)}{dt}=-\frac{1}{RC}{T}_{\text{in}}\left(t\right)+\frac{1}{RC}{T}_{\text{out}}\left(t\right)-\frac{Q_{\text{TCL}}\left(t\right)}{C},(1)$

where T_in(t) is the internal temperature of the TCL at the time t, in units of °C. R is the equivalent thermal resistance, in units of °C/kW. C is the internal air heat capacity, in units of kWh/°C; Q_TCL(t) denotes the heat flux of the TCL at the moment of t, in units of kW. This paper considers the TCL working in the cooling mode, so the sign in front of Q_TCL(t) is negative. Q_TCL(t) is continuously adjustable from 0 to the rated heat flow. T_out(t) is the ambient temperature of the TCL at the moment of t in units of °C.

Consider two moments t_k and t_k+1 separated by Δt, where Δt is a short period of time. Due to Δt typically being in minutes, then between t_k and t_k+1, the change in the heat flow rate and the ambient temperature can be negligible. By solving the ordinary differential Eq. 1 can be discretized as Eq. 2 (Gautschi, 2011)

$\begin{array}{ll}\hfill T_{\text{in}}\left(t_{k+1}\right)& =e^{-\frac{\mathrm{\Delta }t}{RC}}{T}_{\text{in}}\left(t_k\right)+\left(1-e^{-\frac{\mathrm{\Delta }t}{RC}}\right)T_{\text{out}}\left(t_k\right)\hfill \\ \hfill & +\left(1-e^{-\frac{\mathrm{\Delta }t}{RC}}\right)R{Q}_{\text{TCL}}\left(t_k\right).\hfill \end{array}(2)$

Since the actual frequency support task directly affects the system frequency in terms of power rather than heat flow, in order to better use TCLs to provide auxiliary services to the power system, it is necessary to accurately describe the relationship between the operating power and heat flow of TCLs, i.e., the energy efficiency ratio, which in turn rewrites Eqs 2 into 3:

$\begin{array}{ll}\hfill T_{\text{in}}\left(t_{k+1}\right)& =e^{-\frac{\mathrm{\Delta }t}{RC}}{T}_{\text{in}}\left(t_k\right)+\left(1-e^{-\frac{\mathrm{\Delta }t}{RC}}\right)T_{\text{out}}\left(t_k\right)\hfill \\ \hfill & -\left(1-e^{-\frac{\mathrm{\Delta }t}{RC}}\right)R\cdot g\left(P_{\text{TCL}}\left(t_k\right)\right),\hfill \end{array}(3)$

where g (⋅) is a function to be fitted, $g\left(P_{\text{TCL}}(t_k)\right)=Q_{\text{TCL}}(t_k)$ and P_TCL (t_k) is the actual power consumption of the TCL.

3 Energy efficiency ratio correction and regulation potential assessment method for TCLs

Some previous studies treated the energy efficiency ratio of TCLs as a fixed value (Wang et al., 2020), i.e.,

$\frac{P_{\text{TCL}}\left(t_k\right)}{Q_{\text{TCL}}\left(t_k\right)}=\theta ,(4)$

In Eq. 4 θ is a positive constant for cooling TCLs and a negative constant for heating TCLs.

However, the relationship in Eq. 4 is only applicable to describe TCLs with limited power states. In recent years, with the progress of power electronics technology, TCLs with continuously adjustable power, such as inverter air conditioners and refrigerators, have been popularized, and it is inaccurate to use (4) to describe the operating state of such loads. Therefore, this paper proposes an energy efficiency ratio correction, where the heat flux is expressed as the form of Eq. 5.

$\begin{array}{ll}\hfill Q_{\text{TCL}}\left(t_k\right)& =g\left(P_{\text{TCL}}\left(t_k\right)\right)\approx a_n{\left(P_{\text{TCL}}\left(t_k\right)\right)}^n\hfill \\ \hfill & +\cdots +a_1\left(P_{\text{TCL}}\left(t_k\right)\right)+a_0,\hfill \end{array}(5)$

where n is the order of the polynomial, a_i and i = 0, … , n are the coefficients of the polynomial, which can be fitted by the historical operating data of TCLs using data-driven methods. The fitting method selected in this paper is the least squares method. In particular, when n = 1 and a₀ = 0, (5) is the same as the description of the energy efficiency ratio in Jiang et al. (2021). Therefore, the correction method proposed in this paper can also be regarded as an extension of Jiang et al. (2021).

The operating task of TCLs is to ensure that their internal temperature remains within the users’ tolerated range. The user permissible temperature range is denoted as [T_in,min, T_in,max], where T_in,min and T_in,max are the user permissible minimum and maximum temperatures, respectively. Based on the fitted a_i, the minimum and maximum operating power P_TCL,min and P_TCL,max of the TCLs in the current time period can be estimated, and they satisfy the following relationships:

$T_{\text{in,max}}=T_{\text{out}}\left(t_k\right)-R\cdot \left(a_n{\left(P_{\text{TCL,min}}\right)}^n+\cdots +a_1\left(P_{\text{TCL,min}}\right)+a_0\right),(6)$

$T_{\text{in,min}}=T_{\text{out}}\left(t_k\right)-R\cdot \left(a_n{\left(P_{\text{TCL,max}}\right)}^n+\cdots +a_1\left(P_{\text{TCL,max}}\right)+a_0\right).(7)$

By solving (6) and (7), P_TCL,min and P_TCL,max can be obtained.

Remark 1: It can also be observed that in fitting the P_TCL (t_k) and Q_TCL (t_k) relations, as n increases, the difficulty to solve P_TCL,min and P_TCL,max will also increase. Thus, a trade-off is required between accuracy and solving efficiency. In general, for TCLs with simpler structures, such as residential air conditioners and water heaters, it is sufficient to choose the equations of order 3 or less to fit the energy efficiency ratios. The solution of such equations can be directly applied to the mature solution formulas, so it does not bring too much computational burden. For TCLs with more complex structures, such as commercial central air conditioners, fitting the energy efficiency ratio may require higher-order equations. However, since the energy efficiency ratio correction is done before TCLs participate in the demand response program, it is acceptable to take up additional solving time at this stage.

4 Decentralized control strategy and measurement error correction methods for TCLs

When using centralized control policies to manage large-scale TCLs, aggregators will face huge communication and computation burdens. At the same time, centralized control strategies are also prone to leakage of user privacy, which, in turn, reduces users’ willingness to respond. Therefore, this paper proposes to use a decentralized control strategy for continuously controllable TCLs to improve the control effect of large-scale TCLs providing frequency modulation services to the power system.

Consider a load aggregator containing N TCLs, where the operating power of TCLs can be continuously adjusted from 0 to the rated power. The local controller of TCLs can measure the frequency of the power system, and when a frequency deviation occurs in the power system, the controller will dynamically adjust the operating power of TCLs to reduce the frequency fluctuation of the system. The actual frequency deviation of the power system is noted as Δf, which can be measured by the PMU and is defined as Eq. 8:

$\mathrm{\Delta }f\left(t\right)=f_{\text{nom}}-f_{\text{real}}\left(t\right),(8)$

where f_nom is the nominal value of the power system frequency and f_real(t) is the actual frequency of the power system. Denote the maximum allowable frequency and the minimum allowable frequency of the power system as f_max and f_min, respectively.

For the ith TCL, i = 1, … , N, the frequency thresholds f_thr,up,i and f_{thr, down,i} are set to avoid frequent adjustment of the operating power, where f_nom < f_thr,up,i < f_max and f_min < f_thr,up,i < f_nom. The controller changes the operating power of the TCL only when f > f_thr,up,i or f < f_{thr, down,i}.

The steady-state power of a TCL when there is no frequency shift in the power system is denoted as P_nom,i, which is numerically equal to the operating power when the user’s indoor temperature is stabilized at the setpoint. P_nom,i can be approximated using Eqs 3, 5. Design the power upward coefficient β_up,i (t_k) and the power downward coefficient β_down,i (t_k), where ${\beta }_{\text{up},i}(t_k)=\frac{\mathrm{\Delta }f(t_k)-f_{\text{thr,up},i}+f_{\text{nom}}}{\left(f_{\max }-f_{\text{thr,up},i}\right)}$ and ${\beta }_{\text{down},i}(t_k)=\frac{\mathrm{\Delta }f(t_k)-f_{\text{thr,down},i}+f_{\text{nom}}}{\left(f_{\text{thr\hspace{0.17em},down},i}-f_{\min }\right)}$.

The power regulation strategy for TCLs is designed as Eq. 9:

$P_{\mathrm{T}\mathrm{C}\mathrm{L},i}\left(t_k\right)=\left\{\begin{array}{c}{P}_{\mathrm{n}\mathrm{o}\mathrm{m},i}+{\beta }_{\mathrm{u}\mathrm{p}.i}\left(t_k\right)\left(P_{\mathrm{T}\mathrm{C}\mathrm{L},\mathrm{m}\mathrm{a}\mathrm{x}}-P_{\mathrm{n}\mathrm{o}\mathrm{m},i}\right),f\left(t_k\right)>f_{\mathrm{t}\mathrm{h}\mathrm{r},\mathrm{u}\mathrm{p},i}\hfill \\ P_{\mathrm{n}\mathrm{o}\mathrm{m},i}+{\beta }_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n},i}\left(t_k\right)\left(P_{\mathrm{n}\mathrm{o}\mathrm{m},i}-P_{\mathrm{T}\mathrm{C}\mathrm{L},\mathrm{m}\mathrm{i}\mathrm{n}}\right),f\left(t_k\right)<f_{\mathrm{t}\mathrm{h}\mathrm{r},\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n},i}\hfill \\ P_{\mathrm{n}\mathrm{o}\mathrm{m},i},\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.(9)$

In the above control strategy, P_TCL,i (t_k) is the actual operating power of TCLs, and β_up,i (t_k) and β_down,i (t_k) are designed to ensure that TCLs will fully use its regulation potential when the power system frequency reaches the upper and lower tolerance limits. In addition, the designed control strategy is fully decentralized, which is more suitable for large-scale TCLs to participate in power system frequency regulation.

However, in practice, the TCL controller typically cannot directly obtain the frequency measurement value of the phasor measurement unit (PMU). At the same time, the TCL controller is limited by the cost, and its local sampling accuracy of the system frequency is lower than that of the PMU. Therefore, it is difficult to ensure the accuracy of control by relying only on the locally measured system frequency for TCL control. At the same time, there is a communication delay in the process of PMU data transmission to the TCL, so it is difficult to ensure the timeliness of control if the TCL is controlled entirely based on PMU measurement data. Therefore, this paper proposes to use only local measurements for control, while using the actual frequency measured by the PMU to correct the local frequency measurements to improve the control accuracy.

Considering the PMU’s measurement of the system frequency f_PMU as the real value, i.e., f_PMU = f_real, the terminal controller’s measurement of the frequency is denoted as f_TCL,i, and the terminal controller’s measurement error is denoted as $f_{\text{e},i}({\widehat{t}}_k)=f_{\text{PMU}}({\widehat{t}}_k)-f_{\text{TCL},i}({\widehat{t}}_k)$, where ${\widehat{t}}_k$ is the sampling instant of the PMU, and the interval between ${\widehat{t}}_k$ and ${\widehat{t}}_{k+1}$ is much longer than that between t_k and t_k+1. When the PMU sends the frequency measurement value to the TCL controller, it will also send the corresponding sampling instant, i.e., ${\widehat{t}}_k$, together. After receiving the data, the TCL controller calculates $f_{\text{e},i}({\widehat{t}}_k)$ using the local data corresponding to ${\widehat{t}}_k$.

The amount of historical data that can be saved by the terminal controller is S, assuming that the measurement error obeys a normal distribution, with notation U_i = [f_e,i (1), …, f_e,i(S)]; then, the distribution of the frequency measurement error can be expressed as Eq. 10

$U_i\sim N\left({\mu }_i,{\sigma }_i^2\right),(10)$

where μ_i and σ_i are parameters to be approximated later.

In the case where S is large enough, i.e., the amount of historical data is large enough, the distribution of frequency deviations can be estimated by means of, e.g., (11) and (12)

${\mu }_i\approx {\varphi }_i=\frac{1}{S}{\displaystyle \sum _{{\widehat{t}}_k=1}^S}{f}_{\text{e},i}\left({\widehat{t}}_k\right),(11)$

${\sigma }_i^2\approx {\phi }_i^2=\frac{1}{S-1}{\displaystyle \sum _{{\widehat{t}}_k=1}^S}{\left(f_{\text{e},i}\left({\widehat{t}}_k\right)-{\mu }_i\right)}^2,(12)$

where ϕ_i and ${\phi }_i^2$ are estimated values for μ_i and ${\sigma }_i^2$, respectively.

After determining the distribution of frequency deviations, the measured values and deviations of the local frequencies can be corrected in the following way:

${\widehat{f}}_{\text{TCL},i}\left(t_k\right)=f_{\text{TCL},i}\left(t_k\right)-{\varphi }_i,(13)$

${\widehat{f}}_{\text{e},i}\left(t_k\right)=f_{\text{e},i}\left(t_k\right)+{\varphi }_i,(14)$

In Eq. 14 ${\widehat{f}}_{\text{TCL},i}$ and ${\widehat{f}}_{\text{e},i}$ are corrected values for measured values and deviations, respectively.

To achieve better correction results, the value of S needs to be large enough. This results in the above correction method requiring a large amount of data to be stored locally, while the large amount of data also increases the time and space required for computation. Thus, a huge performance requirement is imposed on the TCL controller. To reduce the performance requirements on TCL controllers, this paper proposes a measurement error correction method based on the back-correction method.

Based on Eqs 11 and 12, if new measurement error data are saved, ϕ_i and ${\phi }_i^2$ can be updated using Eqs 15 and 16:

$\begin{array}{ll}\hfill {\widehat{\varphi }}_i& =\frac{1}{S+1}{\displaystyle \sum _{{\widehat{t}}_k=1}^{S+1}}{f}_{\text{e},i}\left({\widehat{t}}_k\right)=\frac{1}{S+1}{\displaystyle \sum _{{\widehat{t}}_k=1}^S}\left(f_{\text{e},i}\left({\widehat{t}}_k\right)+f_{\text{e},i}\left({\widehat{t}}_{k+1}\right)\right)\hfill \\ \hfill & =\frac{S}{S+1}{\varphi }_i+\frac{1}{S+1}{f}_{\text{e},i}\left({\widehat{t}}_{k+1}\right),\hfill \end{array}(15)$

$\begin{array}{cc}\hfill {\widehat{\phi }}_i^2=& \frac{1}{S}{\displaystyle \sum _{{\widehat{t}}_k=1}^{S+1}}{\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_k\right)-{\widehat{\varphi }}_i\right)}^2\hfill \\ \hfill =& \frac{1}{S}\left[{\displaystyle \sum _{k=1}^S}{\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_k\right)-{\widehat{\varphi }}_i\right)}^2+{\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_{k+1}\right)-{\widehat{\varphi }}_i\right)}^2\right]\hfill \\ \hfill =& \frac{1}{S}{\displaystyle \sum _{{\widehat{t}}_k=1}^S}{\left[\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_k\right)-{\varphi }_i\right)+\left({\varphi }_i-{\widehat{\varphi }}_i\right)\right]}^2\hfill \\ \hfill & +\frac{1}{S}{\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_{k+1}\right)-{\widehat{\varphi }}_i\right)}^2\hfill \end{array}$

$\begin{array}{cc}\hfill & =\frac{1}{S}{\displaystyle \sum _{{\widehat{t}}_k=1}^S}\left[{\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_k\right)-{\varphi }_i\right)}^2\right]+\frac{1}{S}{\displaystyle \sum _{{\widehat{t}}_k=1}^S}\left[{\left({\varphi }_i-{\widehat{\varphi }}_i\right)}^2\right]\hfill \\ \hfill & +\frac{1}{S}{\displaystyle \sum _{{\widehat{t}}_k=1}^S}\left[2\left({\varphi }_i-{\widehat{\varphi }}_i\right)\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_k\right)-{\varphi }_i\right)\right]\hfill \\ \hfill & +\frac{1}{S}{\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_{k+1}\right)-{\widehat{\varphi }}_i\right)}^2\hfill \\ \hfill & =\frac{1}{S}{\displaystyle \sum _{{\widehat{t}}_k=1}^S}{\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_k\right)-{\varphi }_i\right)}^2+2\left({\varphi }_i-{\widehat{\varphi }}_i\right)\hfill \\ \hfill & \times \left(\frac{1}{S}{\displaystyle \sum _{{\widehat{t}}_k=1}^S}\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_k\right)-{\varphi }_i\right)\hfill \\ \hfill & +{\left({\varphi }_i-{\widehat{\varphi }}_i\right)}^2+\frac{1}{S}{\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_{k+1}\right)-{\widehat{\varphi }}_i\right)}^2\hfill \\ \hfill & =\frac{1}{S}{\displaystyle \sum _{{\widehat{t}}_k=1}^S}{\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_k\right)-{\varphi }_i\right)}^2+{\left({\varphi }_i-{\widehat{\varphi }}_i\right)}^2\hfill \\ \hfill & +\frac{1}{S}{\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_{k+1}\right)-{\widehat{\varphi }}_i\right)}^2.\hfill \end{array}(16)$

Substituting Eq. 11 into Eq. 16 yields

${\widehat{\phi }}_i^2=\frac{S-1}{S}{\phi }_i^2+{\left({\varphi }_i-{\widehat{\varphi }}_i\right)}^2+\frac{1}{S}{\left(\mathrm{\Delta }{f}_{\text{e},i}\left({\widehat{t}}_{k+1}\right)-{\widehat{\varphi }}_i\right)}^2.(17)$

After the update process in Eq. 16 and Eq. 17, let ${\varphi }_i={\widehat{\varphi }}_i$ and ${\phi }_i^2={\widehat{\phi }}_i^2$ and move on to the next iteration process.

According to the updating method in Eq. 16 and Eq. 17, the terminal controller will not need to store all the historical data, but only the expectation and variance of the normal distribution obtained from the last computation, which reduces the storage capacity and computational requirements of the terminal controller.

After the correction is completed, the final TCL control strategy is

$\begin{array}{cc}\hfill & {\widehat{\beta }}_{\text{up,}i}\left(t_k\right)=\frac{{\widehat{f}}_{\text{TCL},i}\left(t_k\right)-f_{\text{thr,up},i}}{f_{\max }-f_{\text{thr,up},i}},\hfill \\ \hfill & {\beta }_{\text{down},i}\left(t_k\right)=\frac{{\widehat{f}}_{\text{TCL},i}\left(t_k\right)-f_{\text{thr,down},i}}{f_{\text{thr,down},i}-f_{\min }},\hfill \\ \hfill & P_{\mathrm{T}\mathrm{C}\mathrm{L},i}\left(t_k\right)=\left\{\begin{array}{c}{P}_{\mathrm{n}\mathrm{o}\mathrm{m},i}+{\widehat{\beta }}_{\mathrm{u}\mathrm{p}.i}\left(t_k\right)\left(P_{\mathrm{T}\mathrm{C}\mathrm{L},\mathrm{m}\mathrm{a}\mathrm{x}}-P_{\mathrm{n}\mathrm{o}\mathrm{m},i}\right),\widehat{f}\left(t_k\right)>f_{\mathrm{t}\mathrm{h}\mathrm{r},\mathrm{u}\mathrm{p},i}\hfill \\ P_{\mathrm{n}\mathrm{o}\mathrm{m},i}+{\beta }_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n},i}\left(t_k\right)\left(P_{\mathrm{n}\mathrm{o}\mathrm{m},i}-P_{\mathrm{T}\mathrm{C}\mathrm{L},\mathrm{m}\mathrm{i}\mathrm{n}}\right),\widehat{f}\left(t_k\right)<f_{\mathrm{t}\mathrm{h}\mathrm{r},\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n},i}\hfill \\ P_{\mathrm{n}\mathrm{o}\mathrm{m},i},\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.\hfill \end{array}$

Remark 2: A similar method for the frequency measurement error is proposed in Hongxun et al. (2019), where the correction method in Hongxun et al. (2019) defined as Eq. 18.

${\widehat{f}}_{\text{TCL,}i}\left(t_k\right)=f_{\text{TCL},i}\left(t_k\right)-{\gamma }_i\left(t_k\right),(18)$

where γ_i (t_k) obeys a normal distribution with mean ϕ_i and variance ${\phi }_i^2$. However, in practice, the superposition of two normal distributions with opposite means and the same variance will result in another normal distribution with a mean of 0 but a variance twice as large as the original, which in turn amplifies the noise. The back-correction method proposed in this paper introduces only the mean value part when correcting the measured frequency and does not amplify the noise. Simulations will verify that compared to the method in Eq. 18, the method proposed in this paper can effectively avoid frequent changes in the aggregation power of TCLs.

Remark 3: Eq. 16 and Eq. 17 are mathematically equivalent to Eq. 11 and Eq. 12, respectively, so in this way, the accuracy of the estimated measurement error distribution is ensured. In addition, the proposed decentralized control strategy for TCLs can be considered a part of the droop control of the power system, and therefore, does not destabilize the power system.

5 Case study

5.1 Case 1: modeling results of TCLs after energy efficiency ratio correction

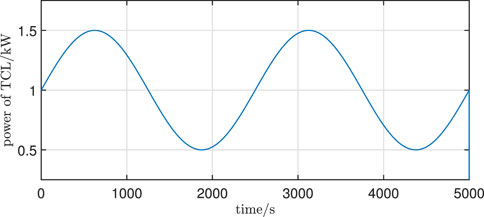
Consider the model as described in Eq. 2 for the TCLs, where R = 2°C/kW, C = 250 kJ/°C, T_out = 32°C. The sampling interval of the temperature is 1s, and the TCL operating power is time-varying, which is described as Eq. 19

$P_{\text{TCL},i}\left(t_k\right)=0.5\sin \left(0.0008t_k\right)+1\left(\text{kW}\right).(19)$

The curve of P_TCL,i (t_k) is shown in Figure 1.

Figure 1

Figure 1. Curve of P_TCL,i (t_k).

The relationship between heat flow and power is

$\ln \left(Q_{\text{TCL},i}\left(t_k\right)\right)=P_{\text{TCL},i}\left(t_k\right)-0.5+{\delta }_i\left(t_k\right),(20)$

where Q_TCL,i is the heat flow rate of the ith TCL. δ_i follows a normal distribution with mean 0 and variance 0.00001.

The temperature curve is fitted using polynomials of different orders. When n = 5, there are

$\begin{array}{cc}\hfill Q_{\text{TCL}}\left(t_k\right)& =g\left(P_{\text{TCL}}\left(t_k\right)\right)\approx 0.0105{\left(P_{\text{TCL}}\left(t_k\right)\right)}^5\hfill \\ \hfill & -0.0429{\left(P_{\text{TCL}}\left(t_k\right)\right)}^4+0.0595{\left(P_{\text{TCL}}\left(t_k\right)\right)}^3\hfill \\ \hfill & +0.0329{\left(P_{\text{TCL}}\left(t_k\right)\right)}^2-0.0034\left(P_{\text{TCL}}\left(t_k\right)\right)+2.713.\hfill \end{array}$

When n = 5, there are

$Q_{\text{TCL}}\left(t_k\right)=g\left(P_{\text{TCL}}\left(t_k\right)\right)\approx -0.0112\left(P_{\text{TCL}}\left(t_k\right)\right)+0.0017.$

The fitting curves are shown in Figure 2. The reference curve is the temperature curve generated based on the relationship between the actual heat flow and power, i.e., (19) and (20). The fitting result is evaluated using the mean absolute error (MAE) and mean square error (MSE) with the reference curve as the benchmark. When the MAE = 0.0816 and MSE = 0.0089, the deviation of the fitted curve from the reference temperature curve is large. When the MAE decreases to 0.0227 and MSE decreases to 0.000894, the fitting effect is significantly improved. This improvement can help the aggregator and the TCL controllers better evaluate the regulation potential of the TCLs.

Figure 2

Figure 2. Temperature profile comparison.

5.2 Case 2: results of back correction in load surge

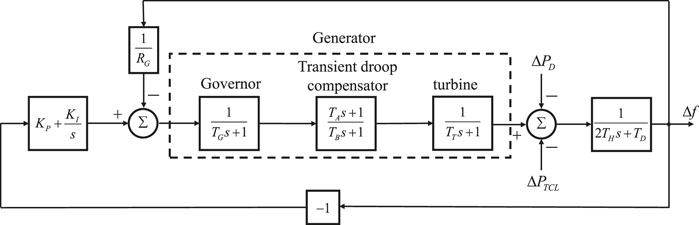
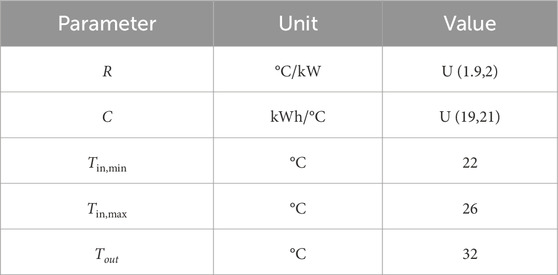
Consider the power system shown in Figure 3. The reheat turbine unit has a generating capacity of 56 MW and a rated frequency of 50 Hz. The average rated power of TCLs is 1.4 kW, and the number of TCLs participating in the system response is 2000. Other TCL parameters are listed in Table 1. The frequency thresholds for loads to participate in the system regulation are set to f_{thr, down,i} = 49.975 Hz and f_thr,up,i = 50.025Hz; meanwhile, the minimum and maximum frequencies allowed by the power system are set to f_min = 49.75 Hz and f_max = 50.25 Hz, respectively. The droop coefficient of primary frequency modulation is R_G = 3.6, and the proportional and the integral coefficient of secondary frequency modulation are K_P = 0.005 and K_I = 0.01, respectively. The governor time constant T_G = 0.30s, while the transient droop compensator time constants are T_A = 4s and T_B = 30s. The inertia constant of the power system T_H = 0.1s, and the load damping coefficient T_D = 0.002s.

Figure 3

Figure 3. Power system architecture.

Table 1

Table 1. Parameters of thermostatically controlled load.

The actual frequency deviation is uniformly measured using the PMU device and periodically sent to the terminal controller of the TCLs; the local frequency deviation of the terminal controller is back-corrected for local load control. The error between the local frequency deviation and the actual frequency deviation is formulated as

${\widehat{f}}_{\text{TCL},i}\left(t_k\right)=f_{\text{PMU}}\left(t_k\right)+{\sigma }_i\left(t_k\right),$

where σ_i follows a normal distribution with a mean 0.05 and variance 0.0001.

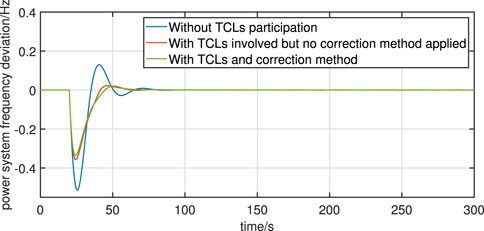
The uncontrollable load of the system at 20 s changes abruptly by 1.12 MW, i.e., 2% of the system capacity. Three scenarios are set up for the comparison experiment: scenario 1, no TCLs are involved in the regulation; scenario 2, TCLs are involved in the regulation, but the back-correction method is not used; scenario 3, TCLs are involved in the regulation, and the back-correction method is used.

The simulation results of the frequency response are shown in Figure 4.

Figure 4

Figure 4. Frequency deviation of the power system.

It can be observed that an effective reduction in the maximum frequency deviation occurs after the TCLs are involved in the frequency support. By comparing the frequency response curves, it can be observed that the maximum frequency deviation of the system is smallest after the introduction of the correction. This is since the presence of the frequency measurement error causes the TCL controller to measure a larger value of frequency, thus delaying the time at which the TCLs begin to respond in the uncorrected case.

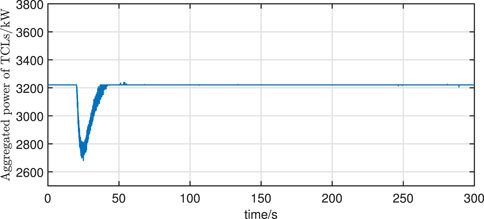
The simulation results of TCLs’ aggregated power when using the proposed correction method or not are shown in Figures 5, 6, respectively. The large frequency measurements also lead to an overall higher response power of the TCLs when no measurement error correction is introduced. In addition, the power of the TCLs is not strictly constant after the power system frequency is restored to its nominal value. Since the fact that the variance in the measurement error cannot be eliminated, the measurement noise may cause some of the TCLs to restart into frequency modulation. This may be mitigated by filtering the measurement signals. However, as shown in Figures 5, 6, it is worth mentioning that the aggregated power fluctuations of TCLs after correction are relatively smaller than that without correction.

Figure 5

Figure 5. Aggregate power for TCLs using the proposed method.

Figure 6

Figure 6. Aggregate power for TCLs without correction.

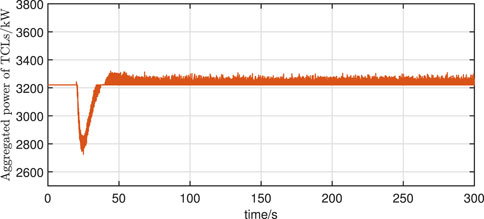
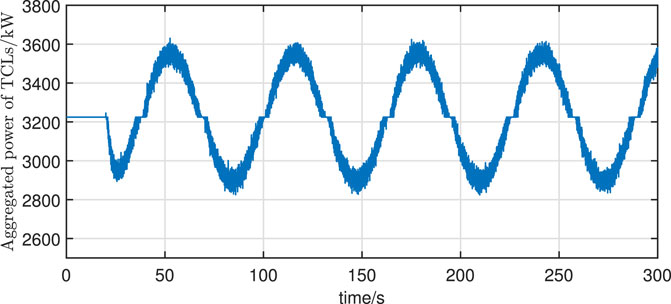
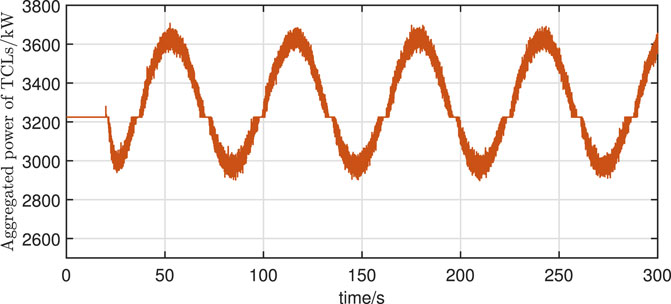
In addition, the frequency response and the aggregated power of TCLs when using the correction method in Eq. 18 are compared with the proposed method. From Figure 5, 7, it can be observed that the fluctuation of the aggregated power of TCLs is more drastic when the correction method in Eq. 18 is used. This is due to the fact that Eq. 18 amplifies the measurement noise, resulting in a frequent response of TCLs after the actual frequency of the power system returns to near the nominal value. Although this frequent response has a small effect on the frequency of the power system, as shown in Figure 8, it may cause a decrease in the willingness of the user to respond.

Figure 7

Figure 7. Aggregate power for TCLs using Eq. 18.

Figure 8

Figure 8. Frequency of the power system when using Eq. 18.

5.3 Case 3: results of back correction in net load oscillations

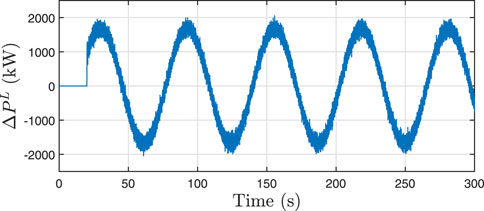
Consider using TCLs to smooth the net load fluctuations due to new energy output uncertainty. The structure and other parameters of the power system are the same as in case 2. The net load fluctuations are shown in Figure 9.

Figure 9

Figure 9. Net load oscillations.

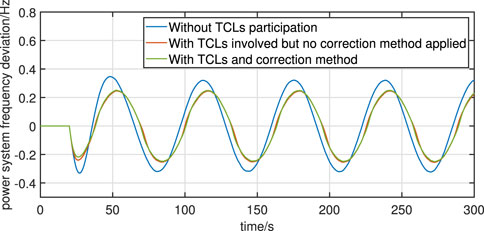
The simulation results of frequency response and aggregated power are shown in Figures 10–12. According to Figure 10, due to the fact that the local measurements of the frequency are large compared to the actual value, the moment of participation of TCLs in the response when the frequency decreased is delayed in the uncorrected case compared to the corrected case, thus resulting in a larger maximum frequency deviation of the system when not corrected. After 100 s, the frequency deviation curves with and without correction almost coincide. This is due to the secondary controls coming into play. However, it can also be observed from Figure 11 and Figure 12 that the aggregated power of the TCLs without using the correction is overall higher than the aggregated power after the correction. This is reflected in practice as the cooling power of TCLs is on the high side, which may lead to a decrease in the user’s comfort and reduce the willingness to respond.

Figure 10

Figure 10. Frequency deviation of the power system.

Figure 11

Figure 11. Aggregate power for TCLs using the proposed method.

Figure 12

Figure 12. Aggregate power for TCLs without correction.

6 Conclusion

A decentralized control strategy is proposed for TCLs to provide frequency support to the power system in this paper. This strategy considers both the energy efficiency ratio and measurement error correction. Using a data-driven approach, the relationship between heat flow and TCLs’ operating power is accurately modeled, enhancing TCL modeling precision. Building upon this model, a decentralized control strategy specifically for TCLs, aimed at regulating power system frequency, is developed. Additionally, a measurement error back-correction method is introduced to account for frequency measurement errors. Simulation examples demonstrate the effectiveness of the proposed control strategy in achieving precise TCL control and reducing power system frequency fluctuations.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

ZM: writing–original draft. TP: writing–review and editing. WZ: writing–review and editing. XJ: writing–review and editing. JH: validation and writing–review and editing. WC: writing–review and editing. KL: writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was funded by Southern Power Grid Corporation Science and Technology Project Funding ([036000KK52222009 (GDKJXM20222125)]).

Conflict of interest

Authors ZM, WZ, JH, and KL were employed by the Power Dispatch Control Center of Guangdong Power Grid Co., Ltd.

Authors TP, XJ, and WC were employed by the Southern Power Grid Scientific Research Institute Limited.

Authors TP, XJ, and WC were employed by Guangdong Power Grid Intelligent Energy Measurement and Advanced Metrology Enterprise Key Laboratory.

The authors declare that this study received funding from the Southern Power Grid Corporation. The funder had the following involvement in the study: study design, collection, analysis, interpretation of data, the writing of this article, and the decision to submit it for publication.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bao, Y.-Q., Yao, Z.-L., and Wu, X.-H. (2023). Thermal parameters estimation of air conditioners based on reduced order equivalent thermal parameters model. Int. J. Electr. Power and Energy Syst. 151, 109149. doi:10.1016/j.ijepes.2023.109149

CrossRef Full Text | Google Scholar

Coffman, A., Bugic, A., and Barooah, P. (2023a). A unified framework for coordination of thermostatically controlled loads. Automatica 152, 111002. doi:10.1016/j.automatica.2023.111002

CrossRef Full Text | Google Scholar

Coffman, A. R., Cammardella, N., Barooah, P., and Meyn, S. (2023b). Aggregate flexibility capacity of tcls with cycling constraints. IEEE Trans. Power Syst. 38, 52–62. doi:10.1109/tpwrs.2022.3160071

CrossRef Full Text | Google Scholar

Ding, Y., Xie, D., Hui, H., Xu, Y., and Siano, P. (2021). Game-theoretic demand side management of thermostatically controlled loads for smoothing tie-line power of microgrids. IEEE Trans. Power Syst. 36, 4089–4101. doi:10.1109/tpwrs.2021.3065097

CrossRef Full Text | Google Scholar

Dong, L., Wu, Q., Hong, J., Wang, Z., Fan, S., and He, G. (2023). An adaptive decentralized regulation strategy for the cluster with massive inverter air conditionings. Appl. Energy 330, 120304. doi:10.1016/j.apenergy.2022.120304

CrossRef Full Text | Google Scholar

Franceschelli, M., Pilloni, A., and Gasparri, A. (2021). Multi-agent coordination of thermostatically controlled loads by smart power sockets for electric demand side management. IEEE Trans. Control Syst. Technol. 29, 731–743. doi:10.1109/tcst.2020.2974181

CrossRef Full Text | Google Scholar

Fu, Y., O’Neill, Z., Wen, J., Pertzborn, A., and Bushby, S. T. (2022). Utilizing commercial heating, ventilating, and air conditioning systems to provide grid services: a review. Appl. Energy 307, 118133. doi:10.1016/j.apenergy.2021.118133

CrossRef Full Text | Google Scholar

Gautschi, W. (2011). Numerical analysis. SpringerLink: bücher. Boston, Massachusetts, USA: Birkhäuser Boston.

Google Scholar

Gong, K., Yang, J., Wang, X., Jiang, C., Xiong, Z., Zhang, M., et al. (2022). Comprehensive review of modeling, structure, and integration techniques of smart buildings in the cyber-physical-social system. Front. Energy 16, 74–94. doi:10.1007/s11708-021-0792-6

CrossRef Full Text | Google Scholar

Hongxun, H., Yi, D., Yonghua, S., and Saifur, R. (2019). Modeling and control of flexible loads for frequency regulation services considering compensation of communication latency and detection error. Appl. Energy 250, 161–174. doi:10.1016/j.apenergy.2019.04.191

CrossRef Full Text | Google Scholar

Hu, J., Cao, J., Chen, M. Z. Q., Yu, J., Yao, J., Yang, S., et al. (2017). Load following of multiple heterogeneous tcl aggregators by centralized control. IEEE Trans. Power Syst. 32, 3157–3167. doi:10.1109/tpwrs.2016.2626315

CrossRef Full Text | Google Scholar

Jiang, T., Ju, P., Wang, C., Li, H., and Liu, J. (2021). Coordinated control of air-conditioning loads for system frequency regulation. IEEE Trans. Smart Grid 12, 548–560. doi:10.1109/tsg.2020.3022010

CrossRef Full Text | Google Scholar

Jiang, W., Lu, C., and Wu, C. (2023). Robust scheduling of thermostatically controlled loads with statistically feasible guarantees. IEEE Trans. Smart Grid 14, 3561–3572. doi:10.1109/TSG.2023.3238997

CrossRef Full Text | Google Scholar

Khan, B., Shafiq, S., and Al-Awami, A. T. T. (2023). Artificial-neural-network-based autonomous demand response controller for thermostatically controlled loads. IEEE Syst. J. 17, 5014–5022. doi:10.1109/JSYST.2023.3280927

CrossRef Full Text | Google Scholar

Kumar, N., Singh, B., and Panigrahi, B. K. (2023). Voltage sensorless based model predictive control with battery management system: for solar pv powered on-board ev charging. IEEE Trans. Transp. Electrification 9, 2583–2592. doi:10.1109/TTE.2022.3213253

CrossRef Full Text | Google Scholar

Kumari, P., Kumar, N., and Panigrahi, B. K. (2023). A framework of reduced sensor rooftop spv system using parabolic curve fitting mppt technology for household consumers. IEEE Trans. Consumer Electron. 69, 29–37. doi:10.1109/TCE.2022.3209974

CrossRef Full Text | Google Scholar

Li, L., Dong, M., Song, D., Yang, J., and Wang, Q. (2022). Distributed and real-time economic dispatch strategy for an islanded microgrid with fair participation of thermostatically controlled loads. Energy 261, 125294. doi:10.1016/j.energy.2022.125294

CrossRef Full Text | Google Scholar

Liang, H., Ma, J., and Lin, J. (2022). Robust distribution system expansion planning incorporating thermostatically-controlled-load demand response resource. IEEE Trans. Smart Grid 13, 302–313. doi:10.1109/tsg.2021.3121658

CrossRef Full Text | Google Scholar

Liu, G., Tao, Y., Xu, L., Chen, Z., Qiu, J., and Lai, S. (2021a). Coordinated management of aggregated electric vehicles and thermostatically controlled loads in hierarchical energy systems. Int. J. Electr. Power and Energy Syst. 131, 107090. doi:10.1016/j.ijepes.2021.107090

CrossRef Full Text | Google Scholar

Liu, H., Xie, H., Luo, H., Qi, J., Goh, H. H., and Rahman, S. (2021b). Optimal strategy for participation of commercial hvac systems in frequency regulation. IEEE Internet Things J. 8, 17100–17110. doi:10.1109/jiot.2021.3076434

CrossRef Full Text | Google Scholar

Saxena, V., Kumar, N., Singh, B., and Panigrahi, B. K. (2021). An mpc based algorithm for a multipurpose grid integrated solar pv system with enhanced power quality and pcc voltage assist. IEEE Trans. Energy Convers. 36, 1469–1478. doi:10.1109/TEC.2021.3059754

CrossRef Full Text | Google Scholar

Schmitt, K., Bhatta, R., Chamana, M., Murshed, M., Osman, I., Bayne, S., et al. (2023). A review on active customers participation in smart grids. J. Mod. Power Syst. Clean Energy 11, 3–16. doi:10.35833/mpce.2022.000371

CrossRef Full Text | Google Scholar

Siu, J. Y., Kumar, N., and Panda, S. K. (2022). Command authentication using multiagent system for attacks on the economic dispatch problem. IEEE Trans. Industry Appl. 58, 4381–4393. doi:10.1109/TIA.2022.3172240

CrossRef Full Text | Google Scholar

Wan, Y., Long, C., Deng, R., Wen, G., Yu, X., and Huang, T. (2021). Distributed event-based control for thermostatically controlled loads under hybrid cyber attacks. IEEE Trans. Cybern. 51, 5314–5327. doi:10.1109/TCYB.2020.2978274

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Chen, H., Li, Y., and Liu, S. (2022). A review of air conditioning load aggregation in distribution networks. Front. Energy Res. 10. doi:10.3389/fenrg.2022.890899

CrossRef Full Text | Google Scholar

Wang, Y., Tang, Y., Xu, Y., and Xu, Y. (2020). A distributed control scheme of thermostatically controlled loads for the building-microgrid community. IEEE Trans. Sustain. Energy 11, 350–360. doi:10.1109/tste.2019.2891072

CrossRef Full Text | Google Scholar

Wang, Y., Xu, Y., and Tang, Y. (2019). Distributed aggregation control of grid-interactive smart buildings for power system frequency support. Appl. Energy 251, 113371. doi:10.1016/j.apenergy.2019.113371

CrossRef Full Text | Google Scholar

Xie, K., Hui, H., Ding, Y., Song, Y., Ye, C., Zheng, W., et al. (2022). Modeling and control of central air conditionings for providing regulation services for power systems. Appl. Energy 315, 119035. doi:10.1016/j.apenergy.2022.119035

CrossRef Full Text | Google Scholar